Week 1 - Introduction to Probability and Probability Distributions

Lesson 1 - Introduction to Probability

What is Probability?

• Probability가 무엇인지 알아보기 위해 예제를 준비했다.

  • 아이들이 축구를 하기 위해 축구공을 뽑는 사건이 주어진다고 하자.

  • 이때, 축구공을 뽑아 축구를 할 수 있는 확률은 얼마일까?

    • 기호로는 $P(soccer)$라고 표현한다.

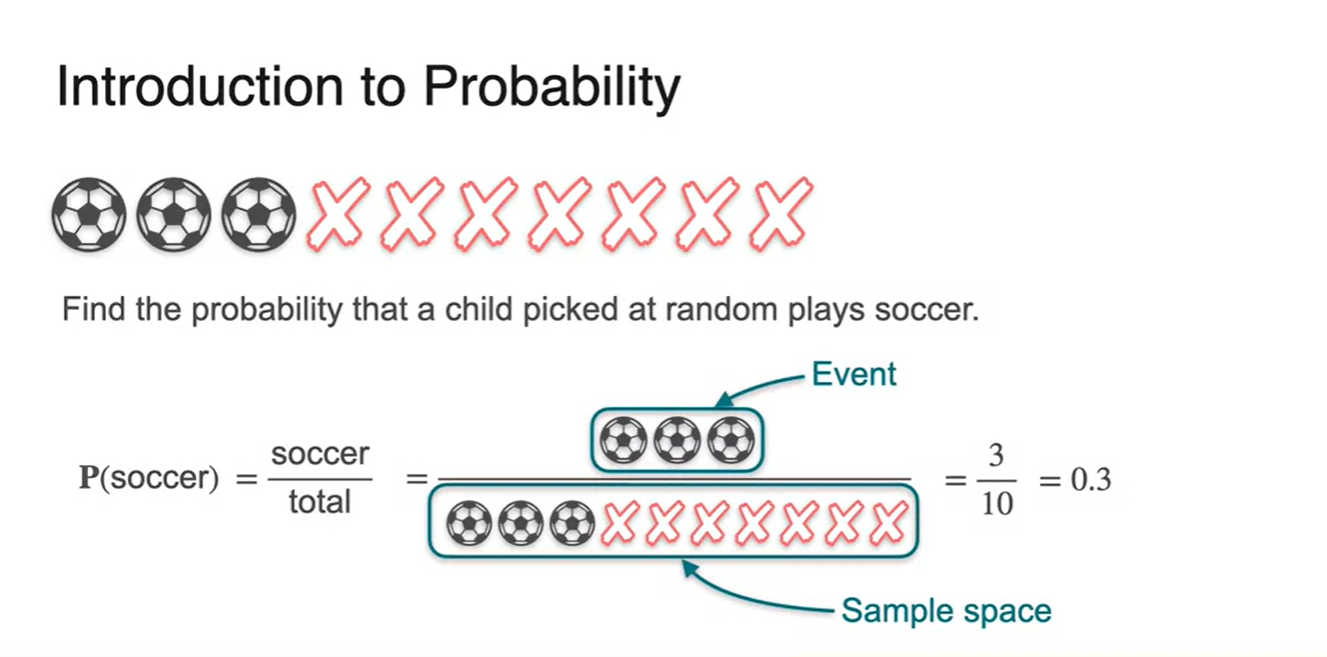
• 전체 sample space가 모든 경우의 수로 주어지고, event가 우리가 알고자 하는 특정한 사건이라면 다음과 같이 확률(Probability)을 정의할 수 있다

  • $\displaystyle P(soccer) = \frac{soccer}{total} = \frac{event}{sample \; space} = \frac{3}{10} = 0.3$

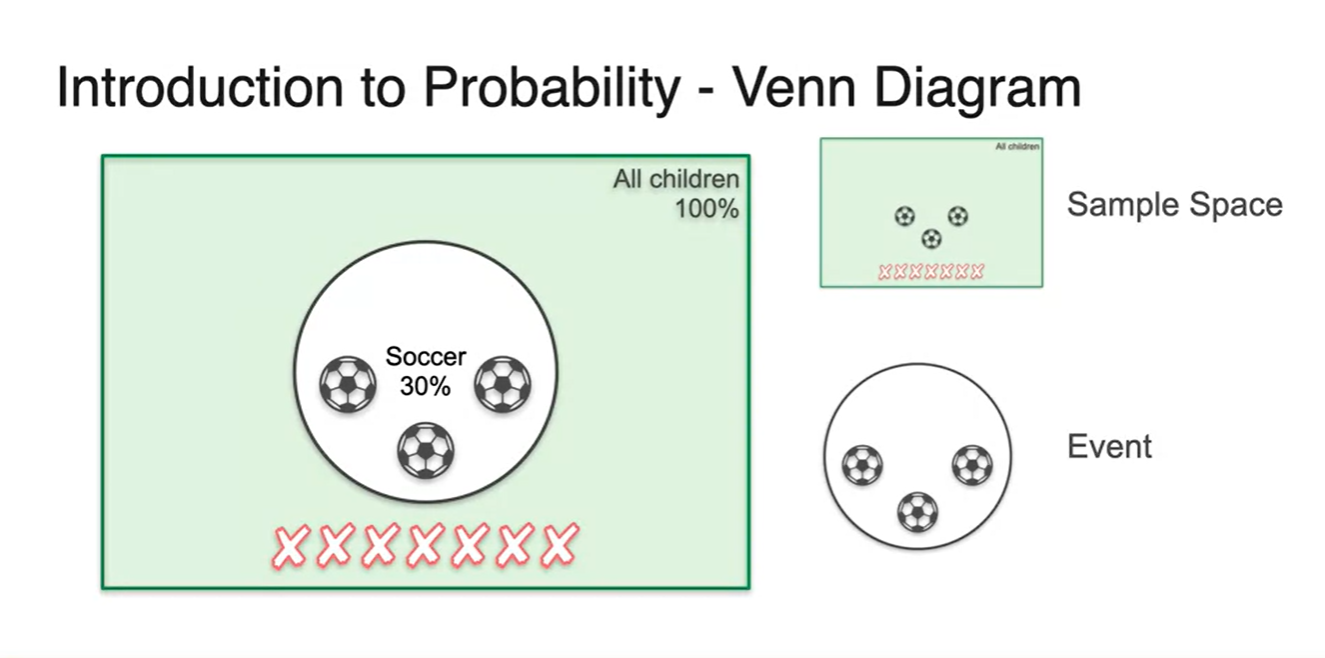
• 이를 벤다이어 그램으로 표현해보자.

  • 전체 경우의 수를 나타내는 sample space는 모든 공간을 차지한다.

  • 특정 사건을 나타내는 축구공을 뽑는 경우의 수 event는 sample space의 일부를 차지한다.

    • 만일 축구공을 뽑지 "않는" 경우의 수를 찾고 싶다면 아래 X가 그려진 space가 event space가 되었을 것이다.

• 이번에는 flip coin 예제를 다뤄보자.

  • H와 T 두 가지 상황으로 experiment가 가능하며 우리가 찾고 싶은 확률은 heads만 나올 확률이다.

    • 기호로는 $P(heads)$라 표현한다.

• 두 번의 시행으로 $P(HH)$를 찾겠다면 모든 경우의 수를 고려해보는 것으로부터 출발하자.

  • 첫 번째 시행에서는 H와 T이, 두 번째 시행헤서는 각각의 H와 T가 만들어진다.

    • 즉, ${HH, HT, TH, TT}$인 4개의 모든 경우의 수를 찾았다.

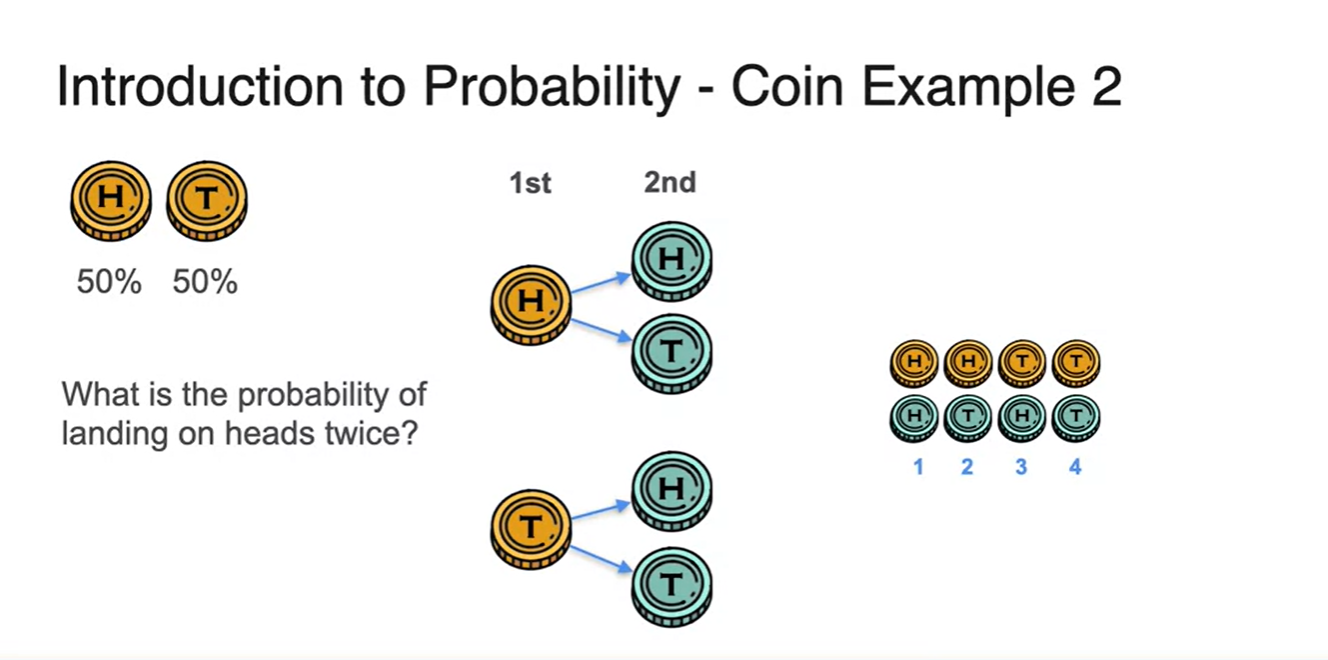
• 이러한 sample space에서 우리가 찾고 싶은 event는 $HH$에 해당한다.

  • 따라서 확률은 $\displaystyle \frac{1}{4} = 0.25$로 계산된다.

• 세 번의 시행으로 $P(HHH)$를 찾는 과정 또한 모든 경우의 수를 구하는 것부터 시작이다.

  • 첫 번째 시행과 두 번째 시행, 세 번째 시행 단계에서 모두 각각의 H와 T가 만들어진다.

    • 즉, ${HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}$ 8개의 모든 경우의 수를 찾았다.

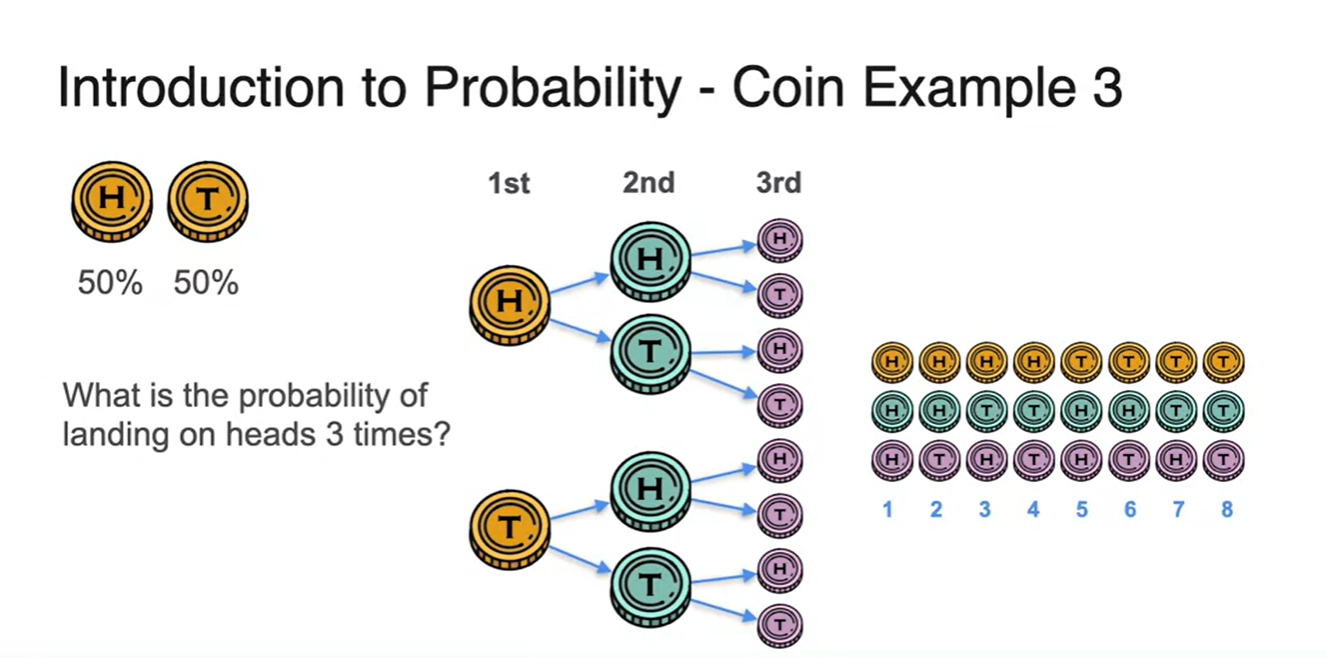
• 이러한 sample space에서 우리가 찾고 싶은 event는 $HHH$다.

  • 따라서 확률은 $\displaystyle \frac{1}{8} = 0.125$로 계산된다.

What is Probability? - Dice Example

• 이번에는 dice 하나를 가지고 6이 나올 확률을 추정해보자.

  • 주사위의 눈금 개수가 6개이므로 한 번의 시행에서 눈금이 나올 수 있는 모든 sample space의 경우의 수는 6개다.

    • 이 중 우리가 찾고 싶은 event는 6이 나오는 단 1개이므로 $P(6)$ 확률을 계산하면 $\displaystyle \frac{1}{6}$이 계산된다.

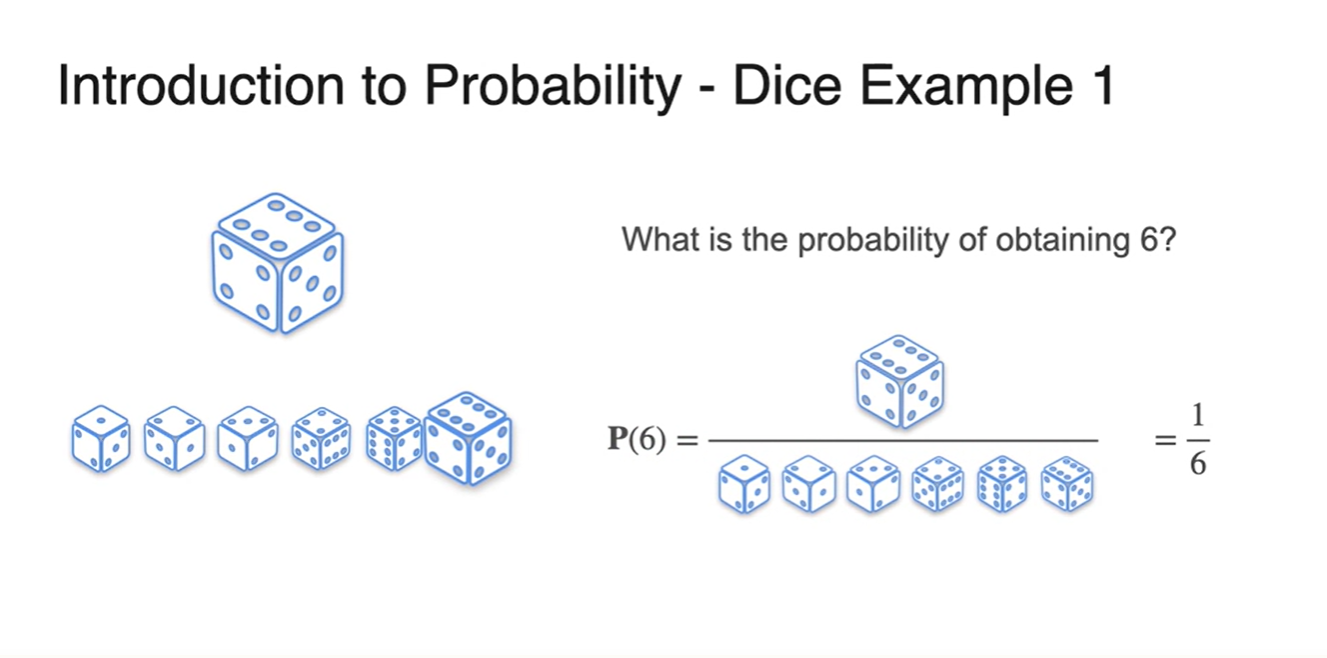
• 주사위 두 개를 이용하여 $P(6, 6)$을 계산한다면 관측될 수 있는 모든 경우의 수가 36개로 세어진다.

  • 따라서 우리가 찾고 싶은 event $P(6, 6)$은 $\displaystyle \frac{1}{36}$으로 계산된다.

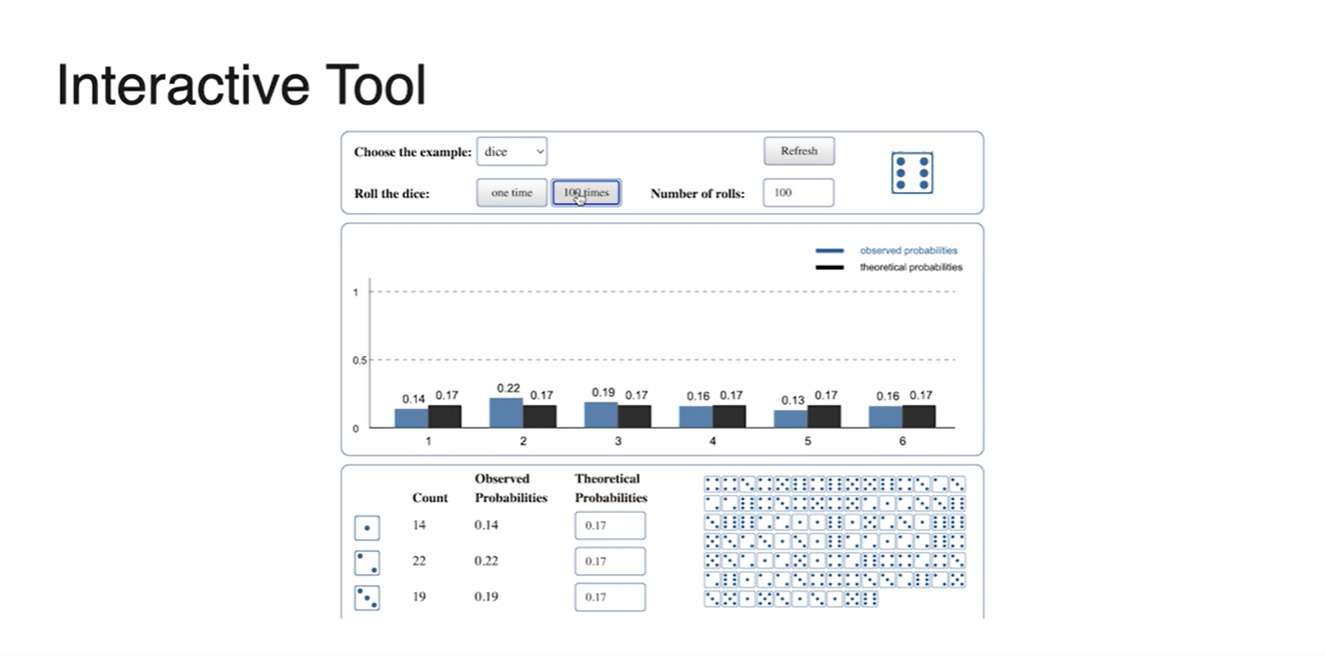
• 강의에서 제공된 Interative Tool을 이용해 100번의 시행으로 분포 함수를 그려보자.

  • 실제로 엄청나게 큰 숫자로 해당 event를 반복하면, 산술적인 $\displaystyle \frac{1}{2}$이나 $\displaystyle \frac{1}{6}$과 같은 확률이 균등하게 그려진다고 한다.

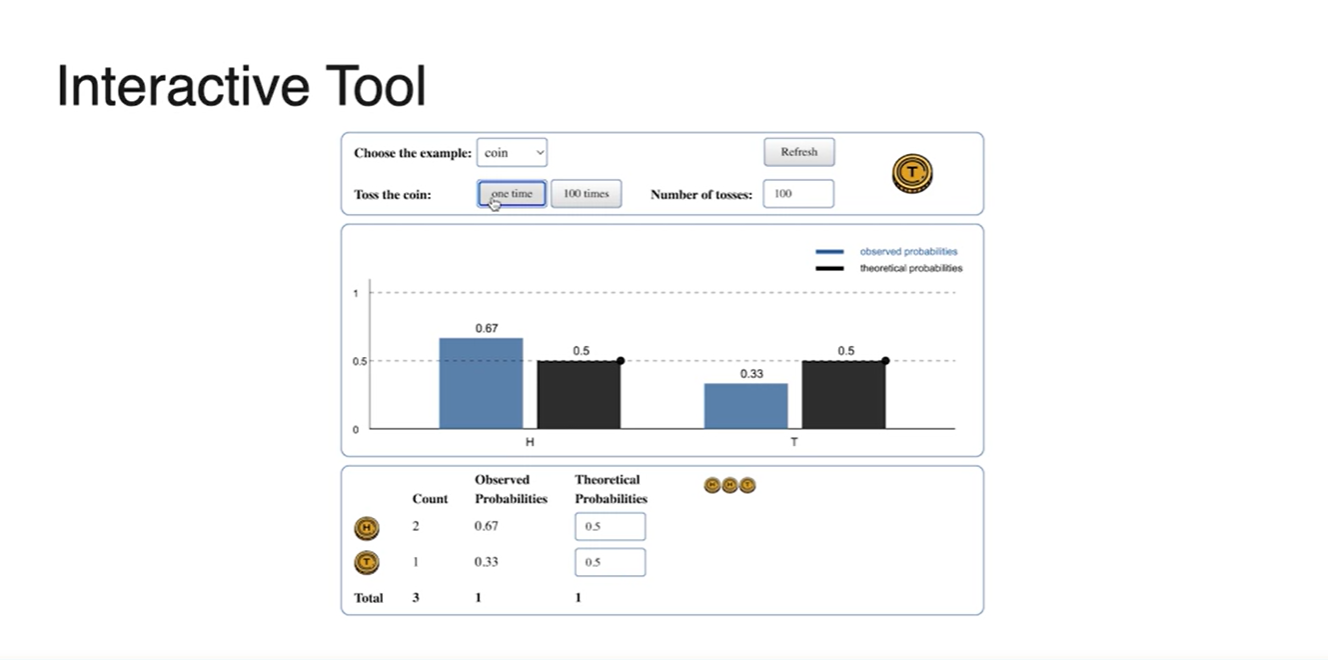
Complement of Probability

• 확률의 Complement rule, 여사건에 대하여 알아보자.

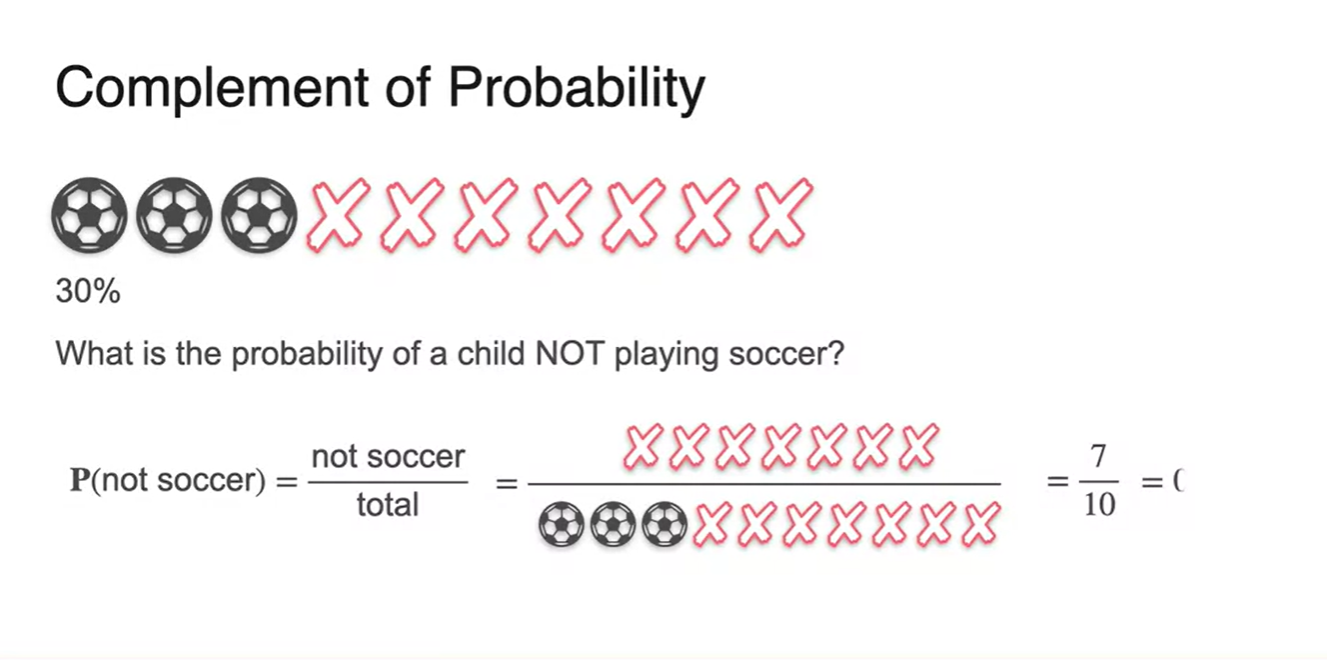
  • 아이들이 축구공을 고를 확률이 30%였다면, 축구공을 고르지 못할 확률은 얼마일까?

    • 기호로는 $P(not \; soccer)$로 표현하며, 이번에는 축구공을 고르지 못하는 경우의 수가 event로 주어지므로 값은 $\displaystyle \frac{7}{10}$으로 계산된다.

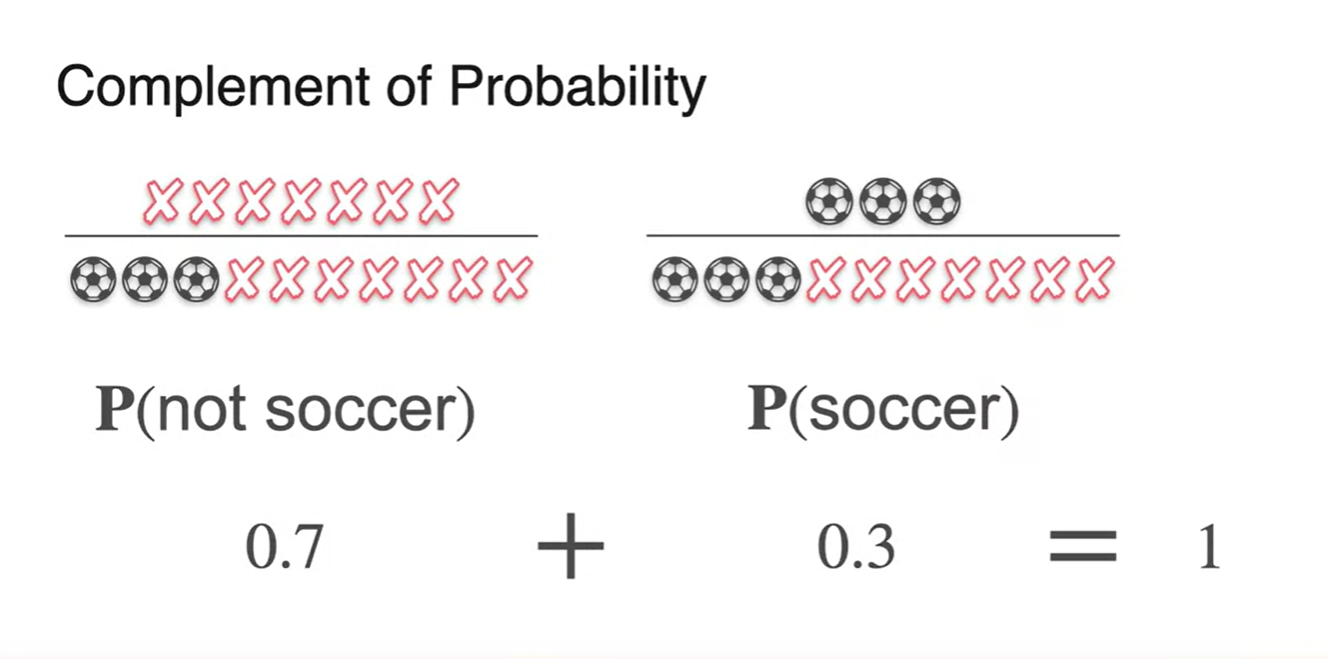
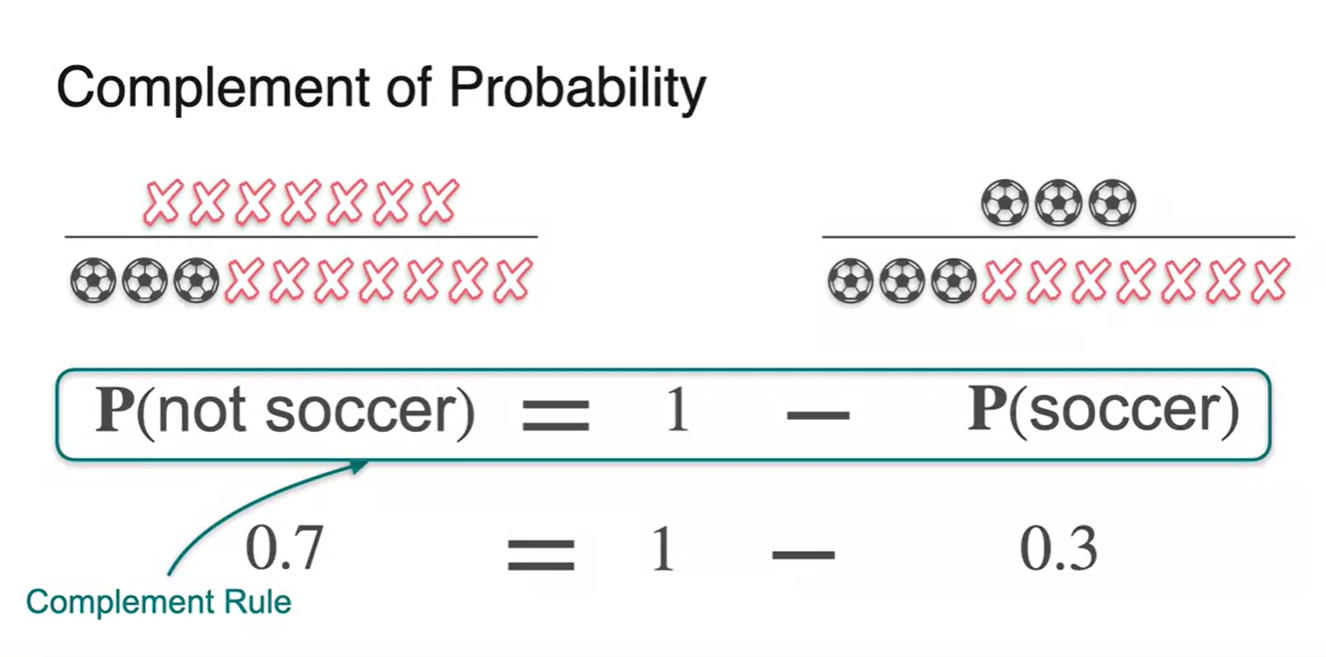
• $P(not \; soccer)$과 $P(soccer)$의 합은 1이다.

  • 다시 말해, $P(not \; soccer)$는 $1- P(soccer)$라는 것과 같다.

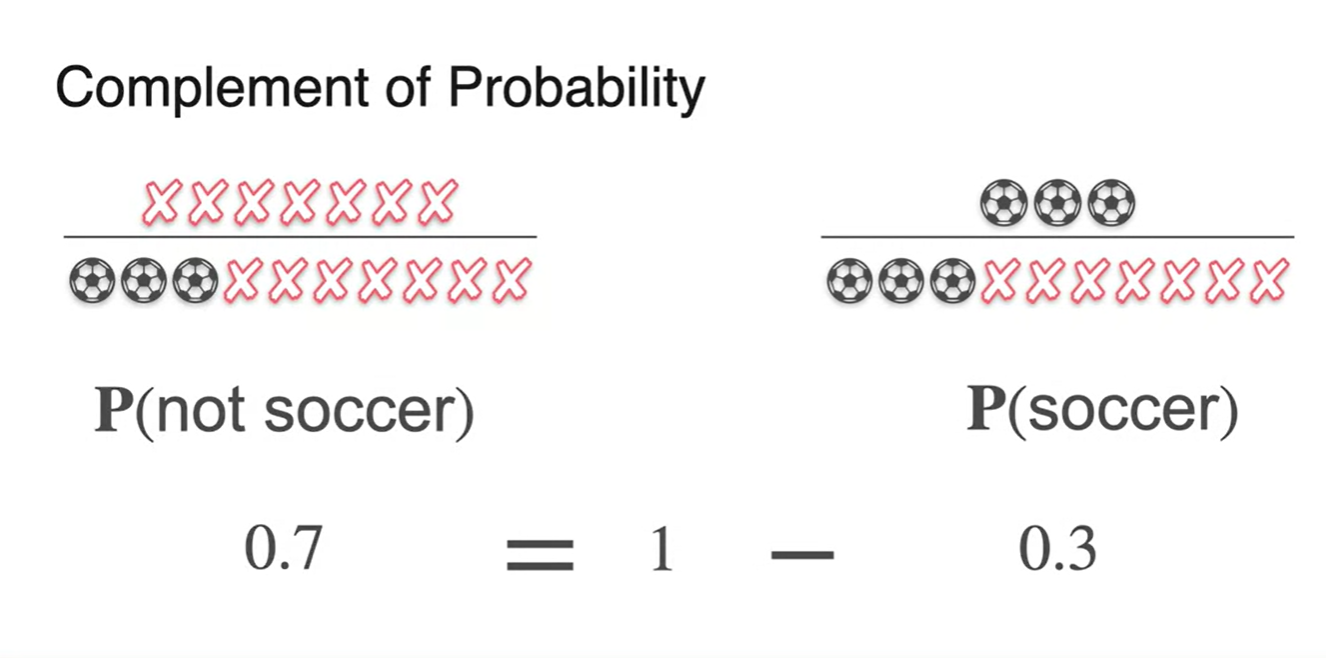
• 이러한 법칙을 Complement Rule이라 하며, 한글로는 "여사건"이다.

• 수식으로 표현하면 $P(A') = 1 - P(A)$로 정리할 수 있다.

  • $A$가 하나의 event라면 $A'$이 해당 event의 여집합에 속한다고 보면 된다.

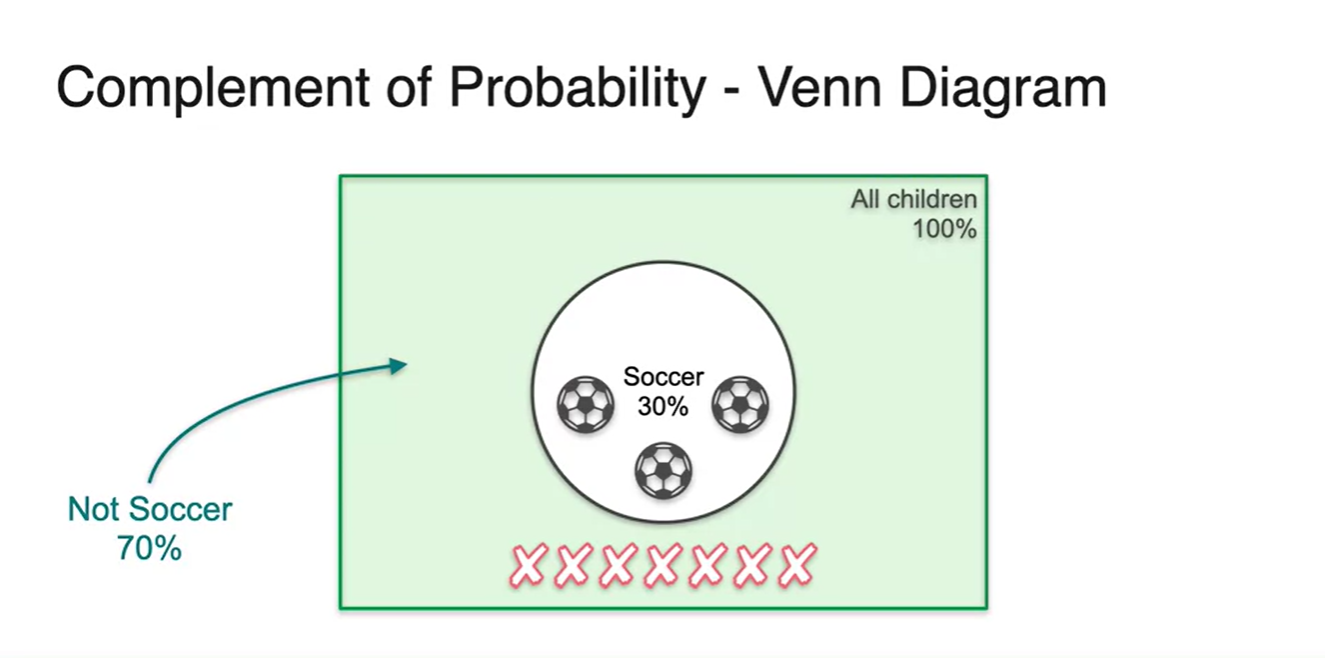
• 이를 벤다이어 그램으로 표현한다면 축구공을 고른 event의 여백이 바로 Not soccer zone이다.

  • 전체 sample space는 벗어나지 않는다.

• Coin example에서 $P(HHH)$의 complement $P(not \; HHH)$는 $\displaystyle \frac{7}{8}$이다.

• Dice example에서 $P(6)$의 complement $P(not \; 6)$는 $\displaystyle \frac{5}{6}$이다.

Sum of Probabilities (Disjoint Events)

• 확률의 disjoint event, 배반 사건에 대해 알아보자.

  • 어떤 학교에서 아이들이 단 하나의 sport만을 선택하여야 한다면, 전체 학생들 중 soccer를 하거나 basketball을 선택할 확률은 얼마일까?

    • Hint: kids는 10명이다.

• 10명의 아이들이 있으므로 전체 sample space에서의 경우의 수는 10개다.

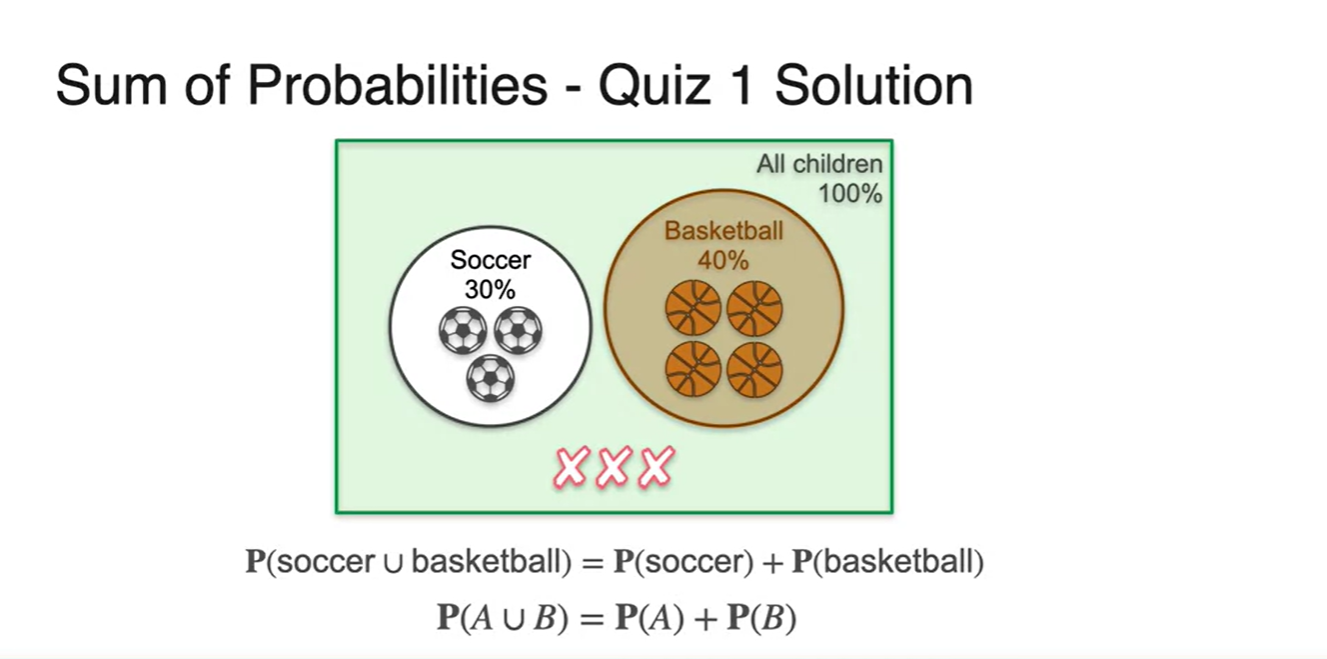
  • 이 중 soccer 3명, basketball 4명이라면 우리가 찾고자 하는 event $P(soccer \; or \; basketball)$은 $\displaystyle \frac{3+4}{10} = 0.7$이다.

    • 즉, 두 경우의 수를 단순 합하여 표혆할 수 있다는 뜻이다.

• 첫 번째 예제인 disjoint event는 합집합 표현이 가능하다.

  • 합집합의 확률은 모든 사건의 합의 확률이라 할 수 있다.

    • 기호로는 $P(A \cup B) = P(A) + P(B)$라고 표현한다.

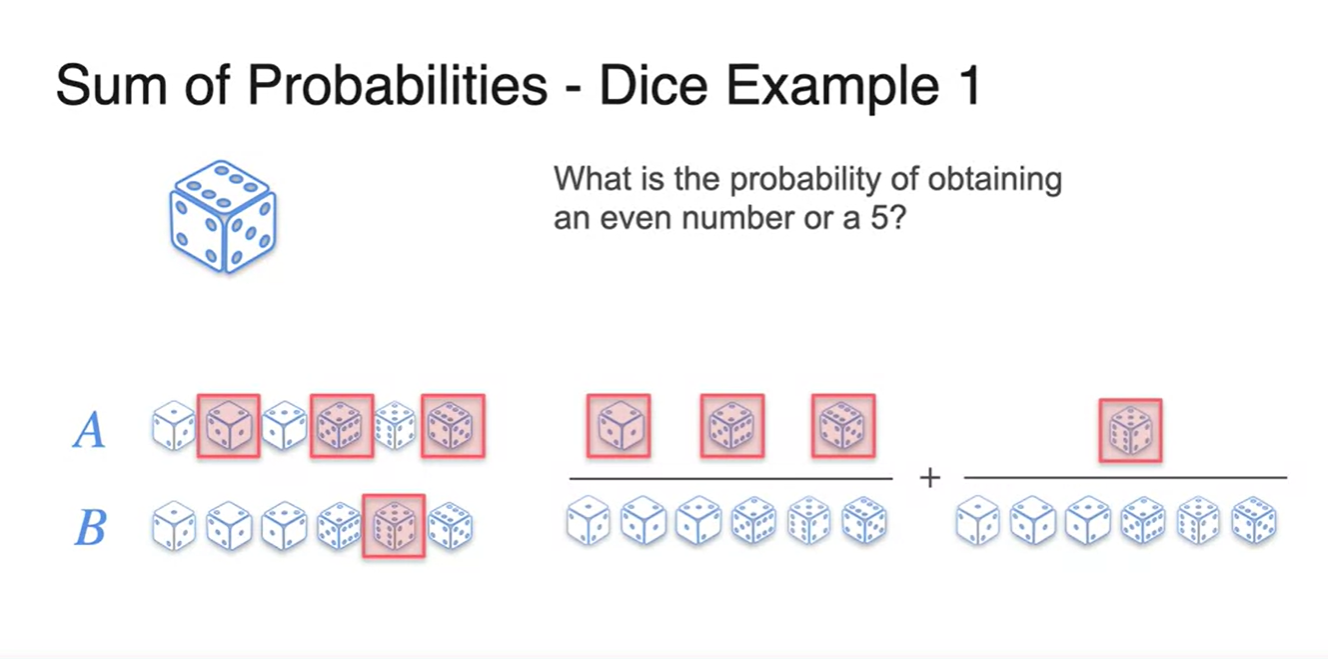
• 이번에는 dice example을 통해 disjoint event를 다뤄보자.

  • 사건 $A$가 짝수가 나올 event, 사건 $B$가 5가 나올 event라고 하자.

    • 우리가 찾고자 하는 event는 짝수이거나 5일 확률이다.

• 두 사건을 단순 합하여 $P(even \; number \; or \; 5)$를 찾는다면

  • $P(even \; number)$와 $P(5)$를 더한 $\displaystyle \frac{4}{6} = \frac{2}{3}$로 계산된다.

• 이번에는 두 주사위를 굴려 숫자의 합이 7이 나오거나 10이 나올 확률을 찾아보자.

• 모든 경우의 수를 고려하여 각 사건 $A$와 $B$의 경우의 수를 걸러내면 아래와 같다.

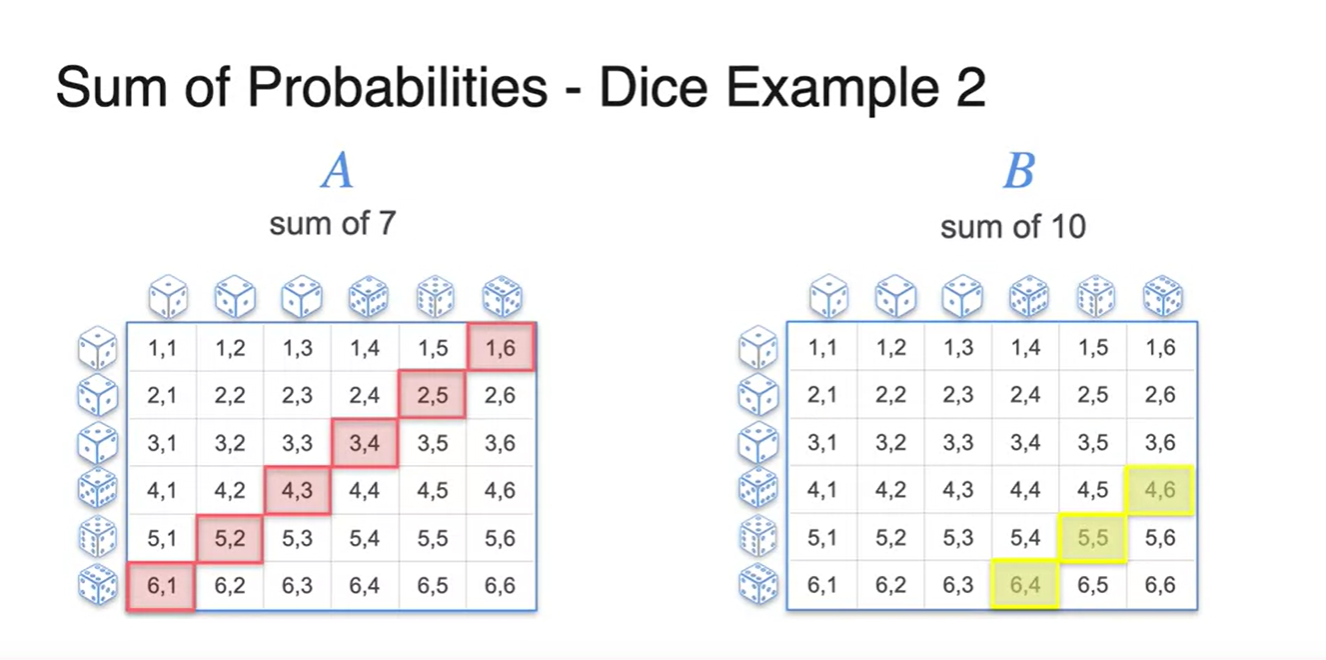
• 우리가 찾는 event는 $A \; or \; B$이므로 두 경우의 수를 합해 본 결과가 아래 그림과 같다.

• $P(sum \; of \; 7)$과 $P(sum \; of \; 10)$의 합은 $\displaystyle \frac{9}{36} = \frac{1}{4}$로 계산되었다.

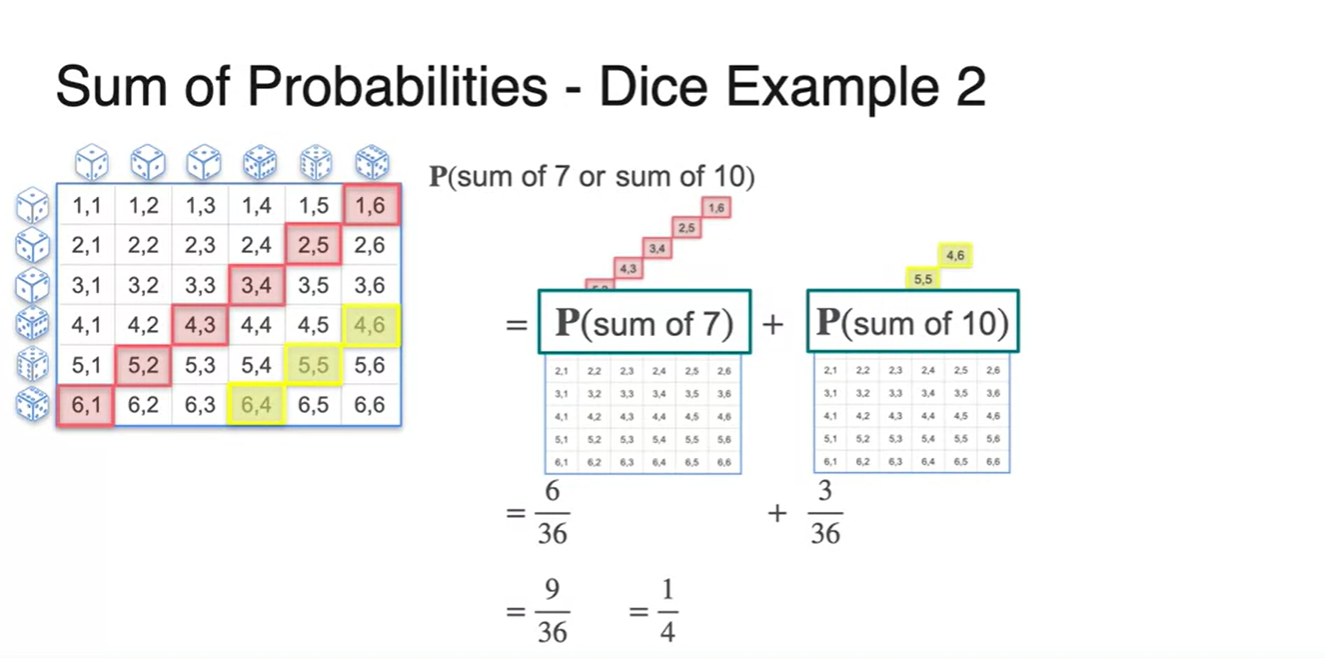
• 이번에는 두 주사위를 굴렸을 때 숫자의 차가 2가 나오거나 1일 확률을 구해보자.

• 마찬가지로, 전체 경우의 수에서 각 사건 $A$와 $B$의 경우의 수를 걸러내 보면 아래 그림과 같이 그려진다.

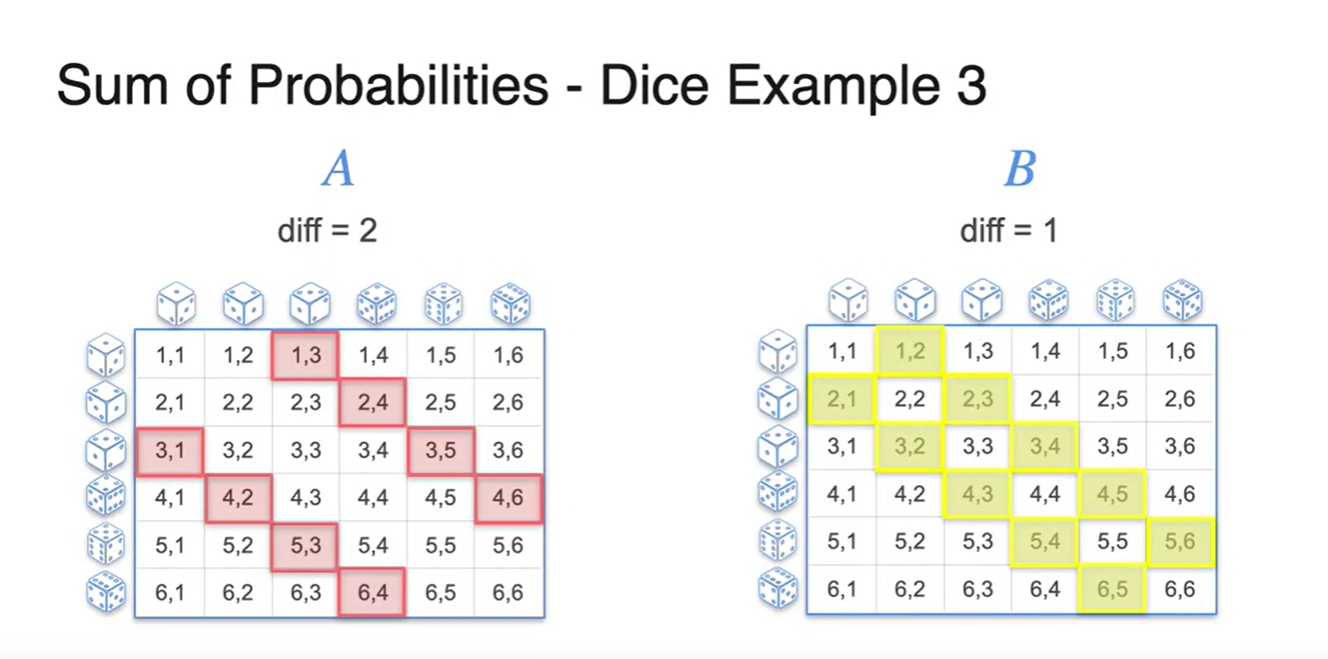
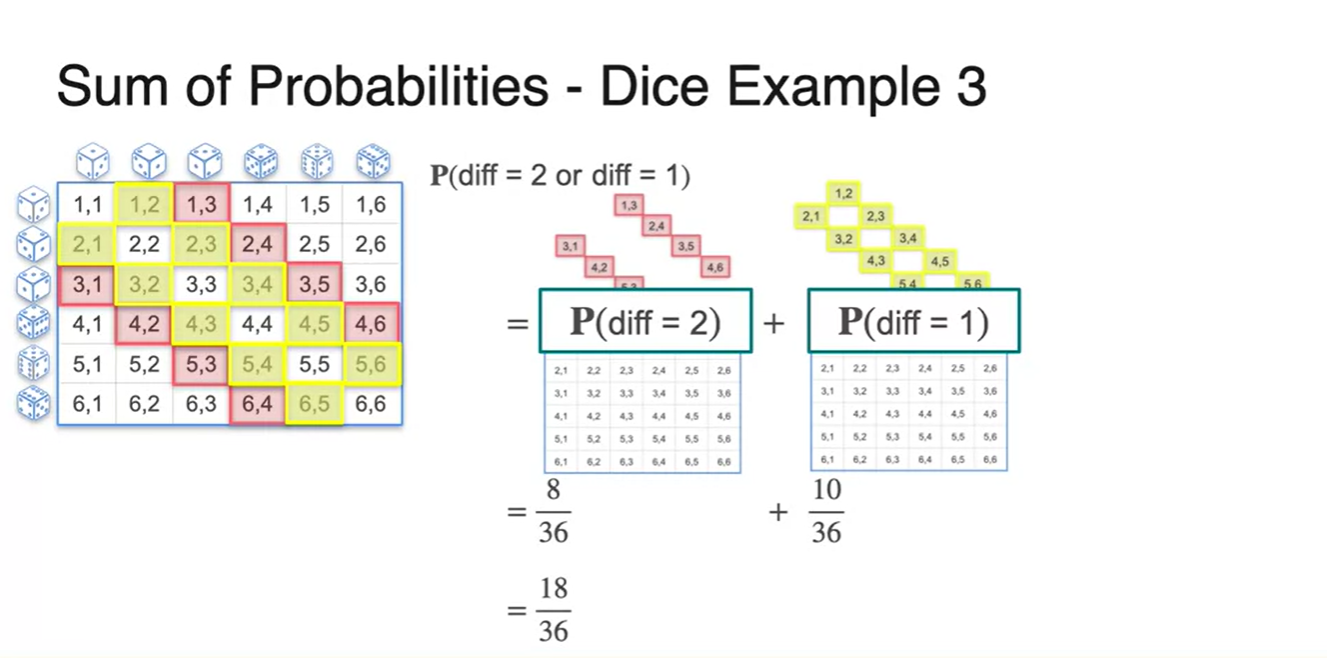
• 두 사건을 합한 $A \; or \; B$의 event를 표시하면 아래와 같다.

• $P(diff \; 2)$과 $P(diff \; 1)$의 합은 $\displaystyle \frac{18}{36} = \frac{1}{2}$로 계산되었다.

Sum of Probabilities (Joint Events)

• 확률의 joint event, 결합 확률에 대해 알아보자.

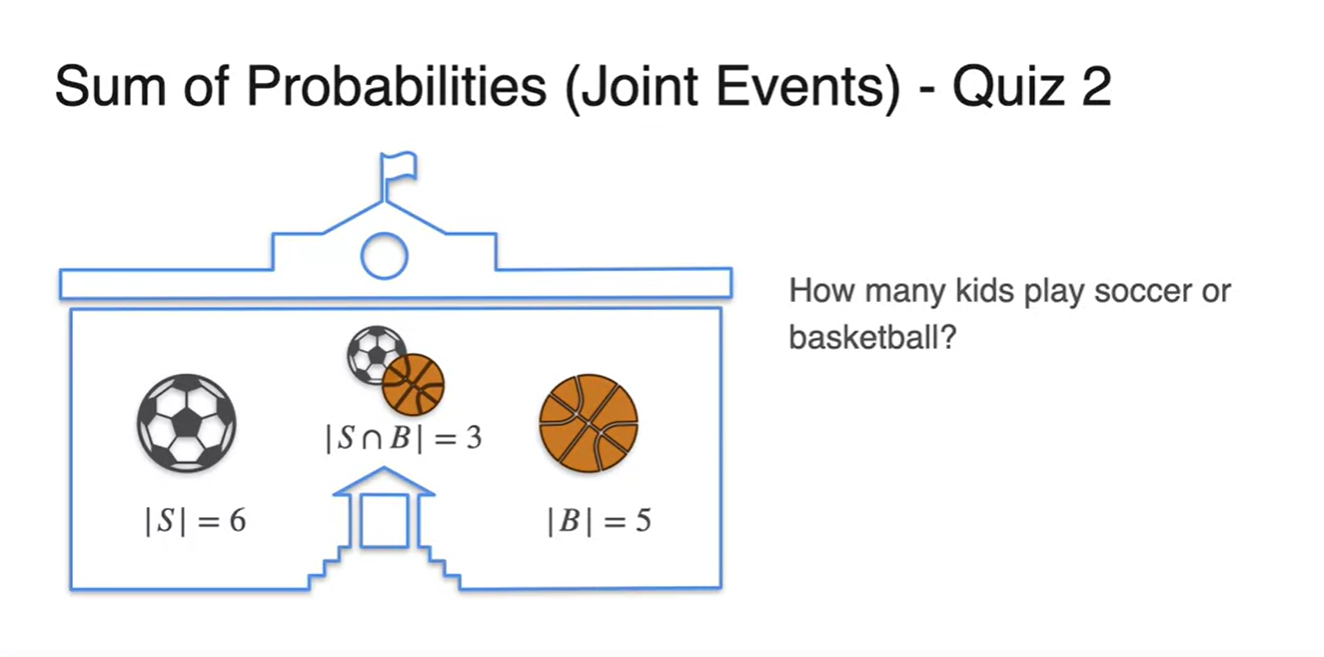
  • 어떤 학교에서 soccer와 basketball 중 개수에 상관 없이 아이들이 원하는 대로 sports를 선택할 수 있게 해주었다고 하자.

    • 이때, 10명의 학생들 중에서 soccer와 basketball을 할 확률이 각각 $0.6$, $0.5$로 주어졌다면 soccer나 basketball을 할 확률의 합은 얼마일까?

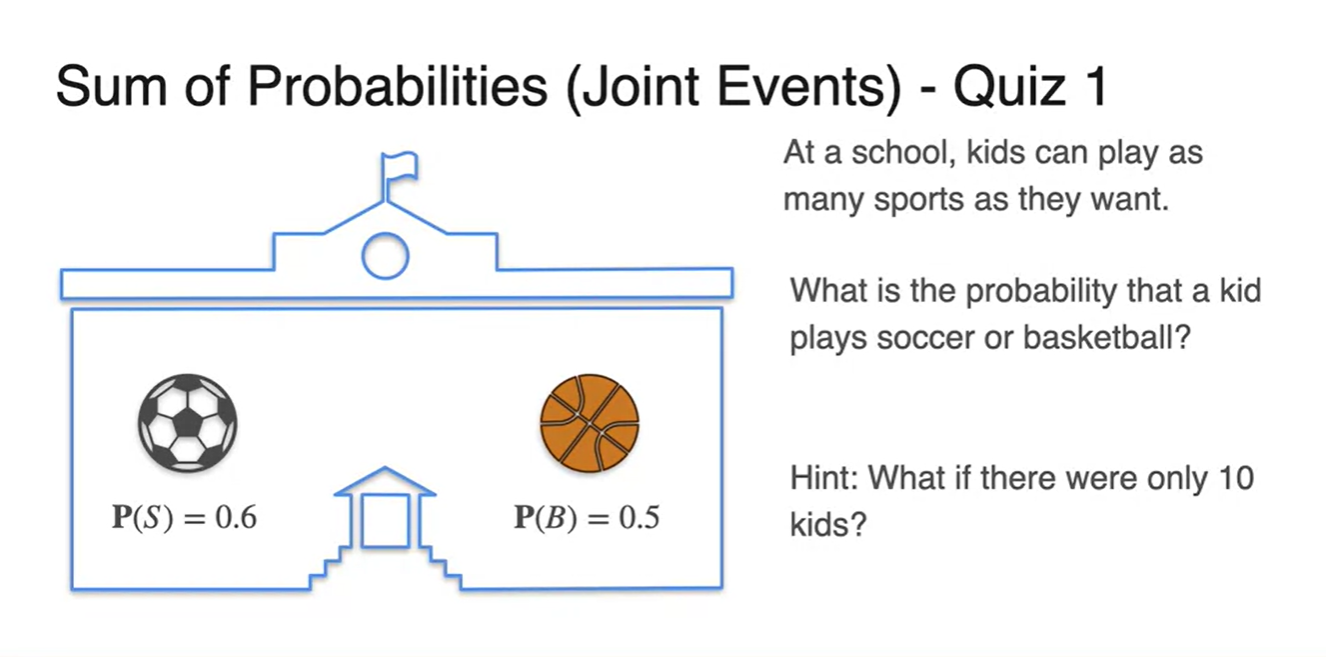
• 우리가 찾고자 하는 event는 $P(soccer \cup basketball)$이며 몇 명의 친구들이 두 sports를 동시에 골랐는지는 아직 알 수 없다.

  • 이러면 우리는 정보가 부족하여 확률을 구할 수 없다.

    • 아직 몇 명의 학생이, "도대체 누가" 중복되었는지를 알지 못하기 때문이다.

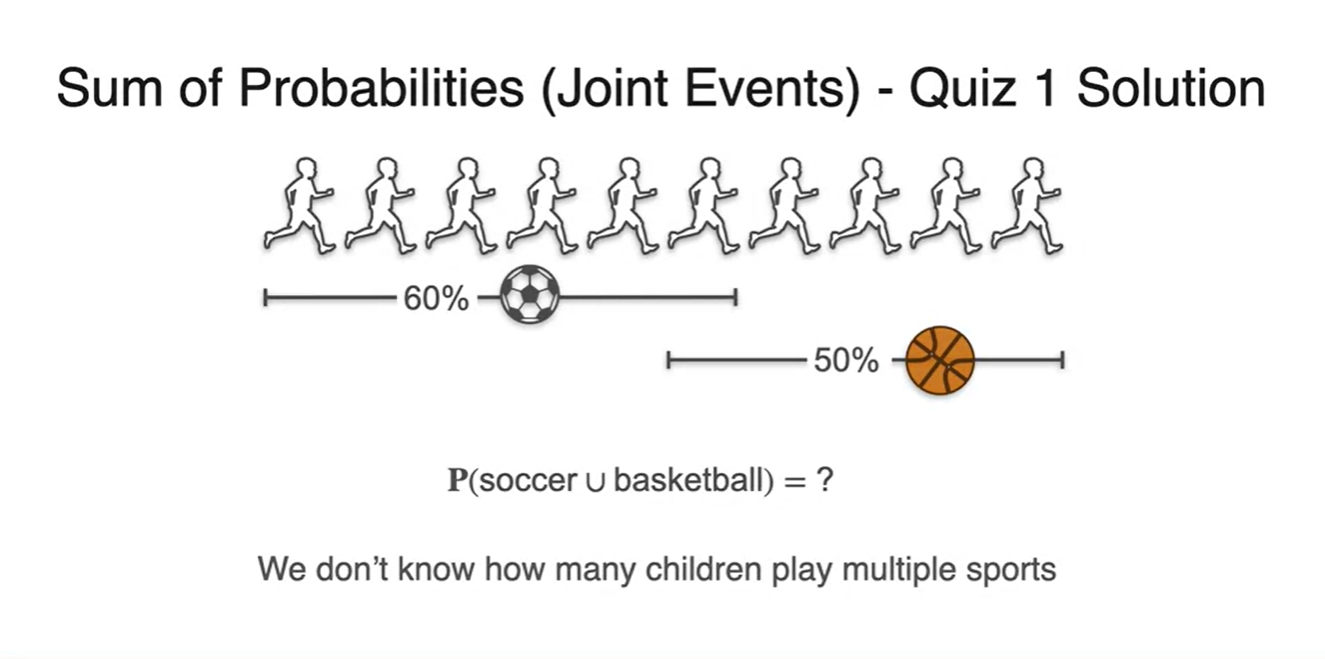
• 두 sports를 모두 고른 학생이 아래와 같이 한 명일 수도 있고 세 명일 수도 있다.

  • 핵심은 중복되어 더해지는 값이 있다는 것이다.

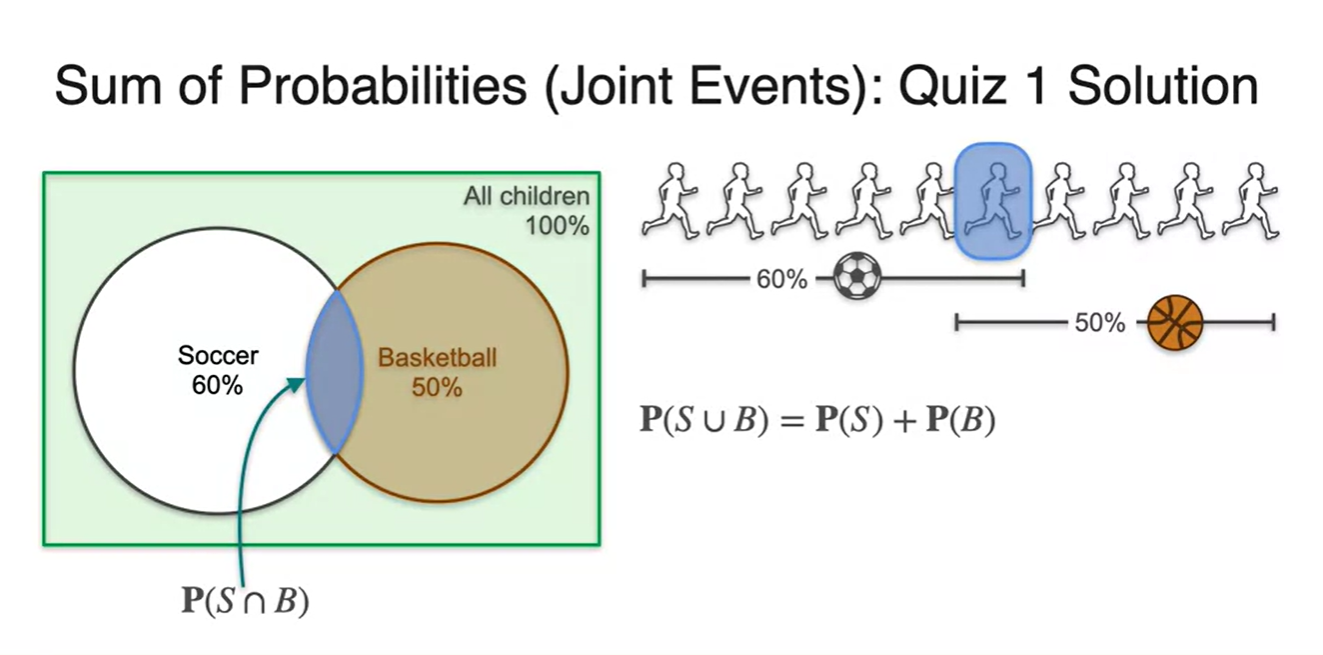
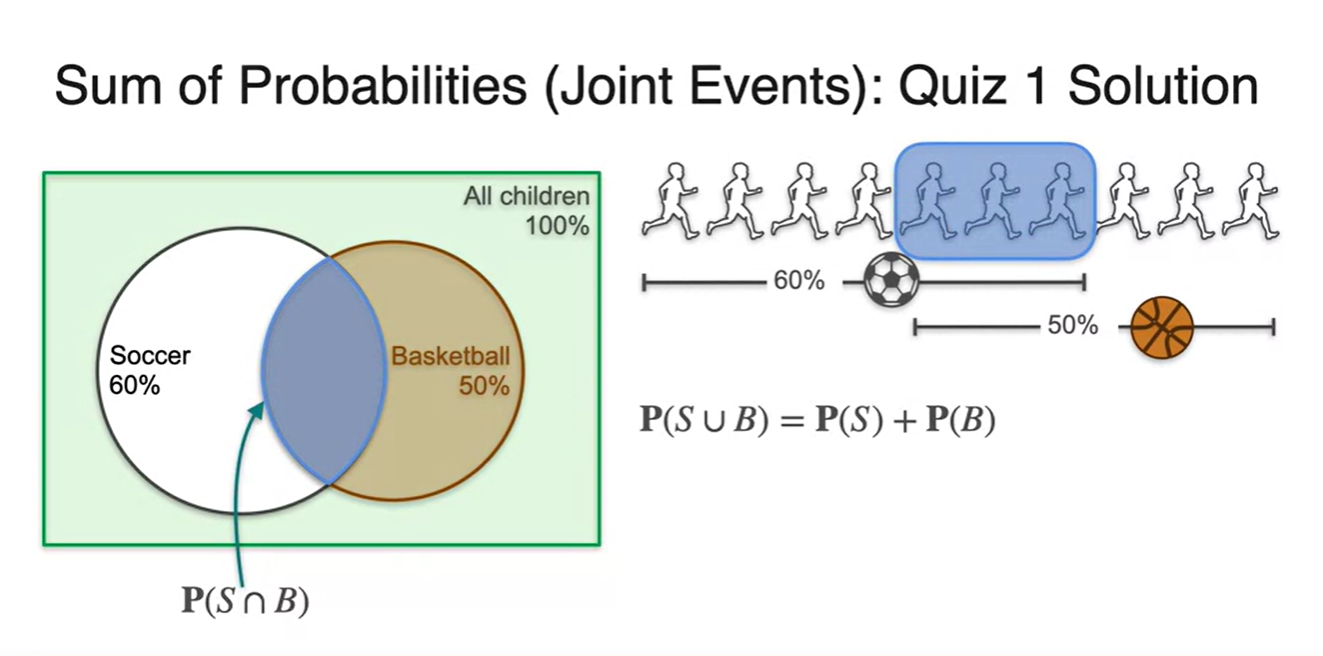
• 만일 두 sports를 고른 학생들이 10명 중 3명이라고 하자.

  • 위 학생들은 soccer를 선택한 경우의 수에도 포함되고, basketball을 고른 경우에 수에도 포함되었을 것이다.

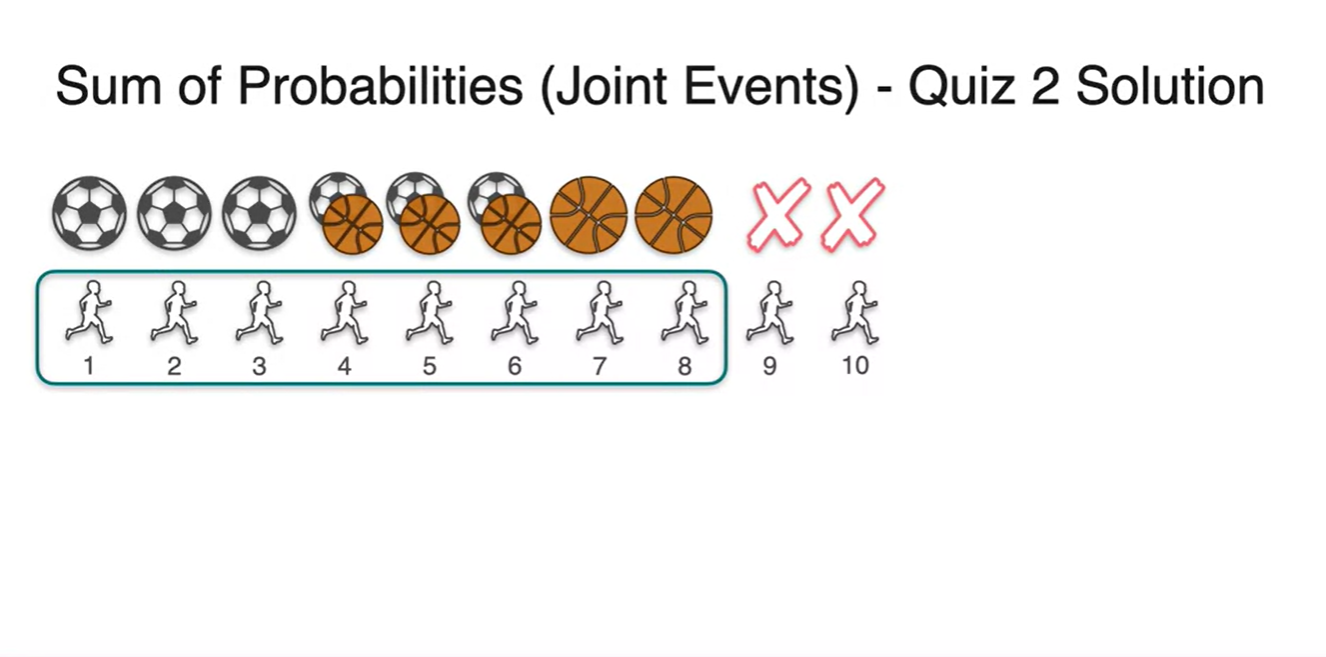
• 즉, 10명 중 3명이 중복된 선택을 했다고 볼 수 있다.

  • 따라서 전체 학생 10명 중 soccer나 basketball을 선택한 경우의 수는 모두 8명이라는 사실을 알 수 있다.

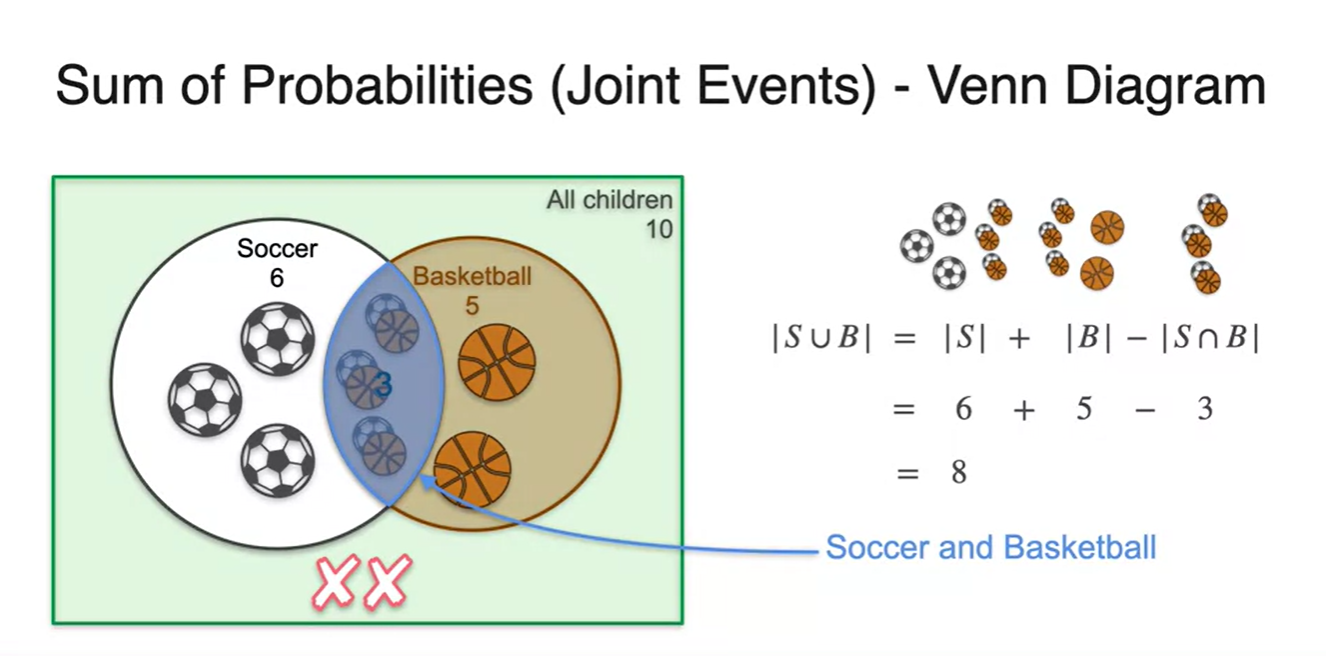
• 우리는 이러한 사건을 inclusion exclusion problem으로 치환하여 볼 수도 있다.

  • 즉, 각 독립된 사건의 합에서 교집합을 빼면, 합집합을 구할 수 있다는 사실을 안다면 말이다!

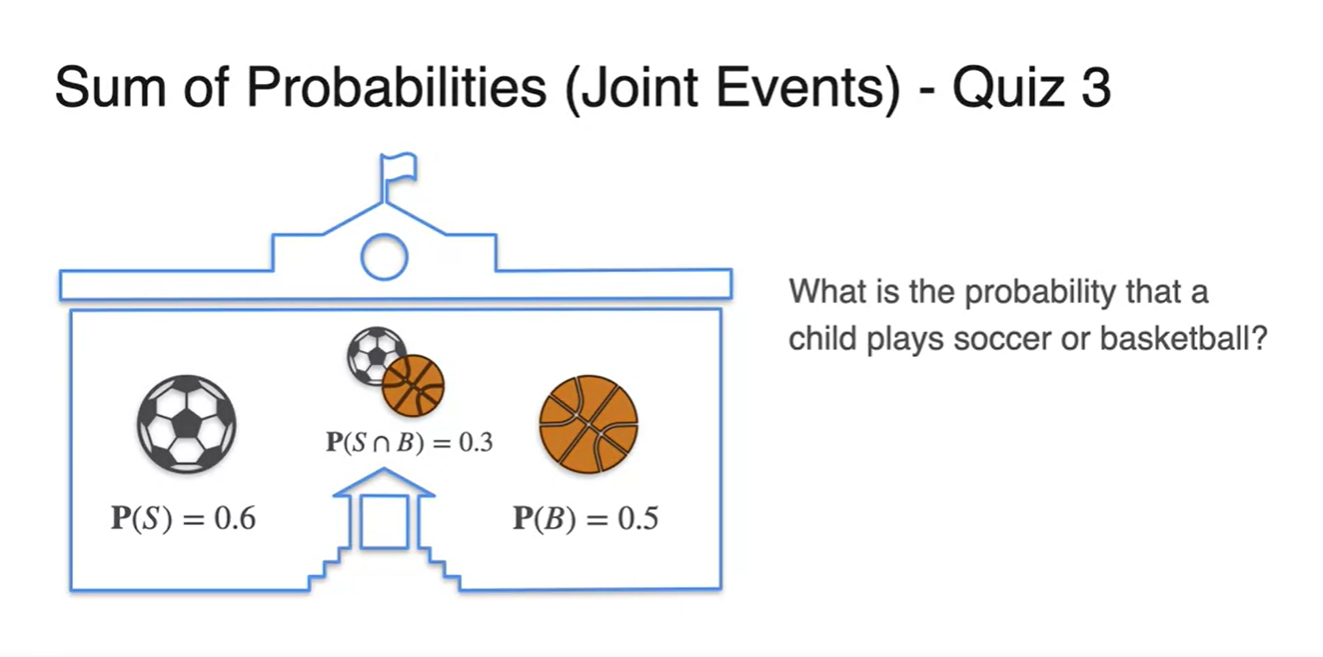
• 경우의 수가 아닌 확률로 주어졌을 때에도 마찬가지다.

  • $P(S) = 0.6$, $P(B) = 0.5$가 주어졌을 때 $P(S \cap B) = 0.3$이라면 전체 합집합은 얼마인가?

• 정답은 $P(S \cup B) = P(S) + S(B) - S(S \cap B)$를 계산하여 구할 수 있다.

  • $P(S \cup B) = 0.6 + 0.5 - 0.3 = 0.8$

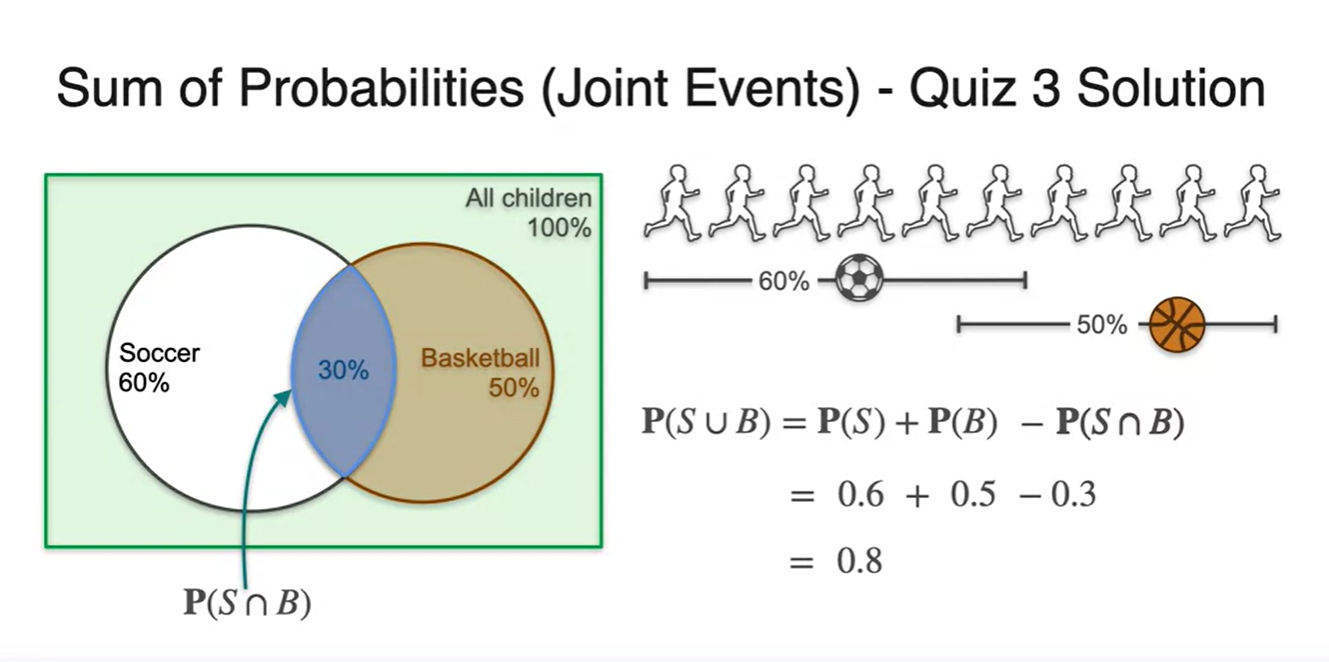
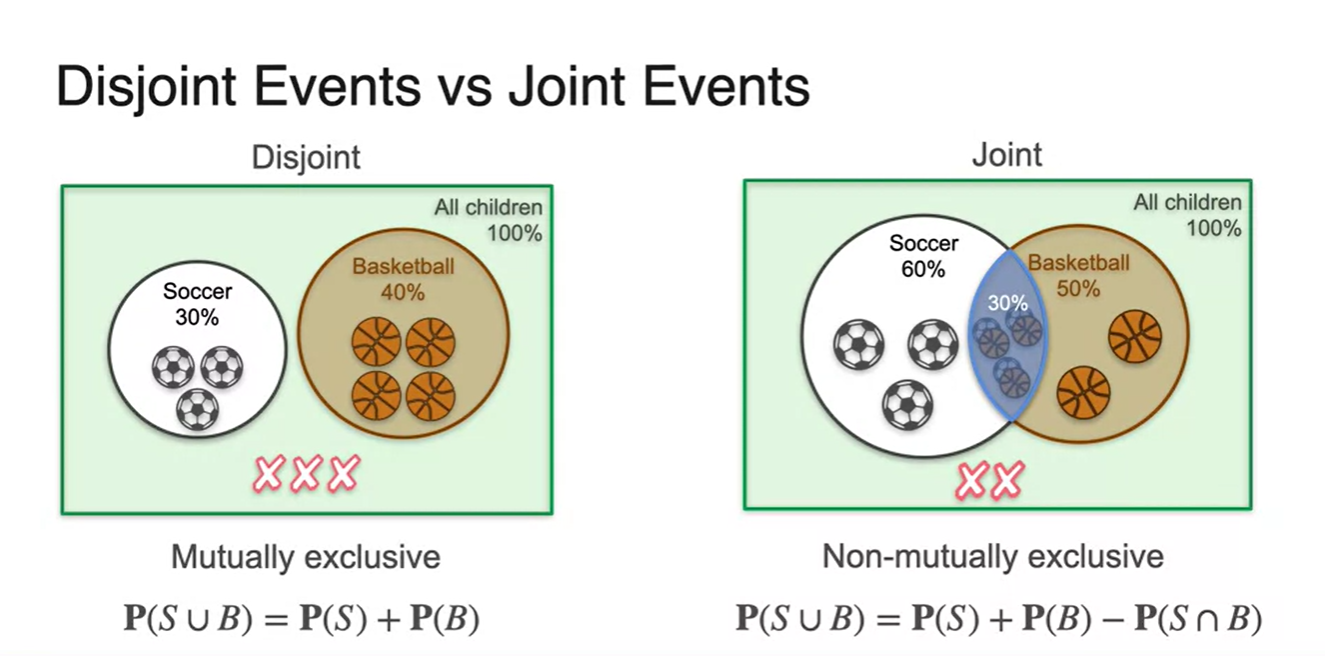
• 벤다이어 그램으로 표현한다면 Disjoint와 Joint의 차이를 확연히 구별할 수 있다.

  • 한글 용어는 다소 어려우나, disjoint가 배반 사건인 이유는 두 사건이 서로 연관될 수 없는 확률이기 때문이 아닐까 추측한다.

• 두 주사위를 굴렸을 때 숫자의 합이 7이 나오거나 차이가 1일 확률은 얼마일까?

• 두 사건을 각각 $A$와 $B$로 하여 경우의 수를 찾아보면 아래 그림과 같다.

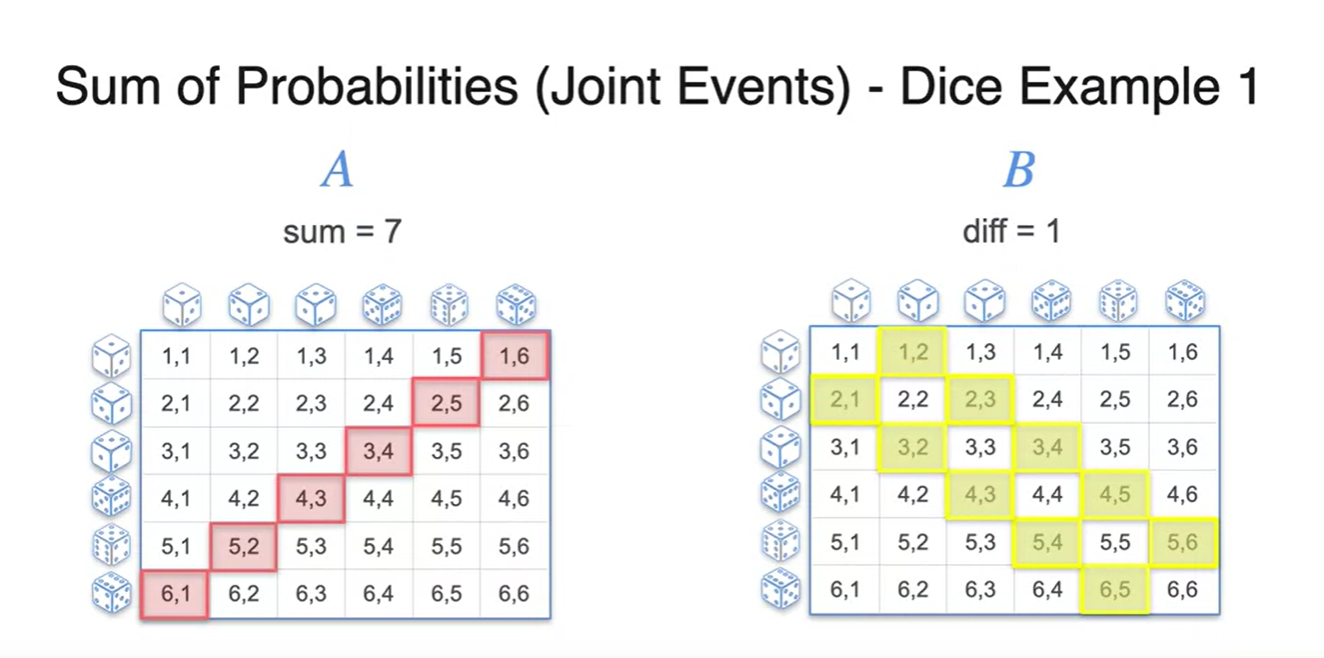
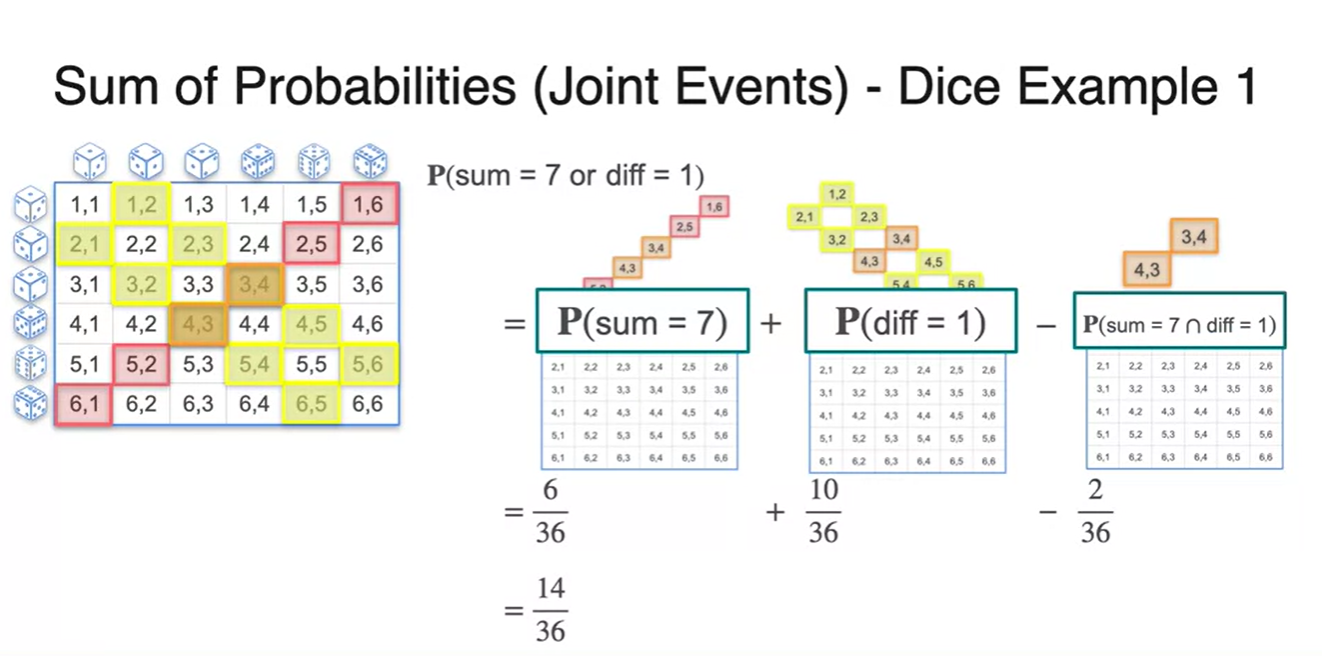
• 아까와 다르게 $A \; or \; B$의 사건을 합쳐보니 double count된 경우의 수가 존재한다.

  • 중복된 부분을 다뤄줘야 하는게 joint event의 핵심이다.

• 계산 과정은 아래와 같다.

  • $P(sum=7 \; or \; diff = 1)$은 $P(sum=7)$과 $P(diff=1)$에서 $P(sum=7 \cap diff=1)$을 빼주는 과정으로 해결 가능하다.

    • $P(sum=7 \; or \; diff=1) = \displaystyle \frac{6}{36} + \displaystyle \frac{10}{36} - \displaystyle \frac{14}{36}$

Independence

• 확률의 Independence, 독립 사건에 대해 알아보자.

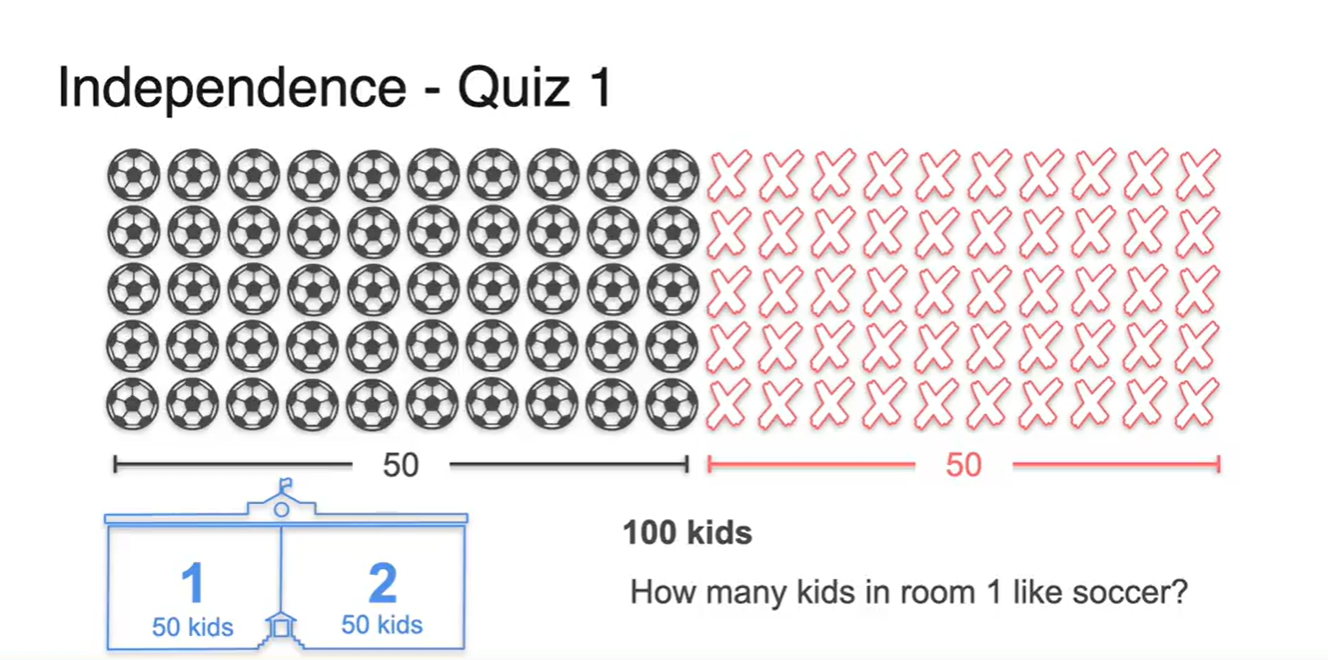
  • 예를 들어 전체 학생이 100명인 학교에서 50명의 학생이 축구를 했고, 한 반에 50명씩 2반이 있는 상황이 주어진다고 가정하자.

    • 이 때 각 반에서 축구를 한 사람의 숫자는 몇 명일까?

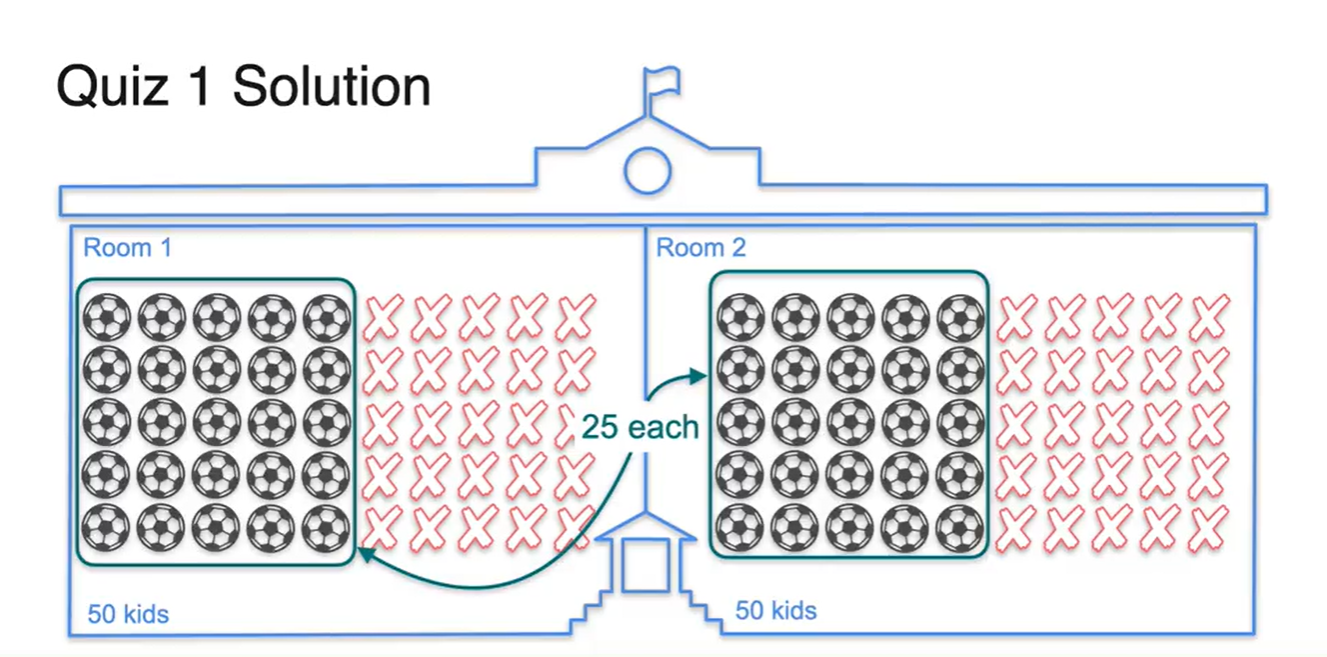
• 유추해보건대, 두 반의 사람 명수가 똑같다면 50명 중 절반인 25명씩 찢어져서 나뉘었을 것이라 생각할 수 있다.

  • 확률 계산으로 따지면 $\displaystyle \frac{1}{2} * \frac{1}{2} = \frac{1}{4}$이다.

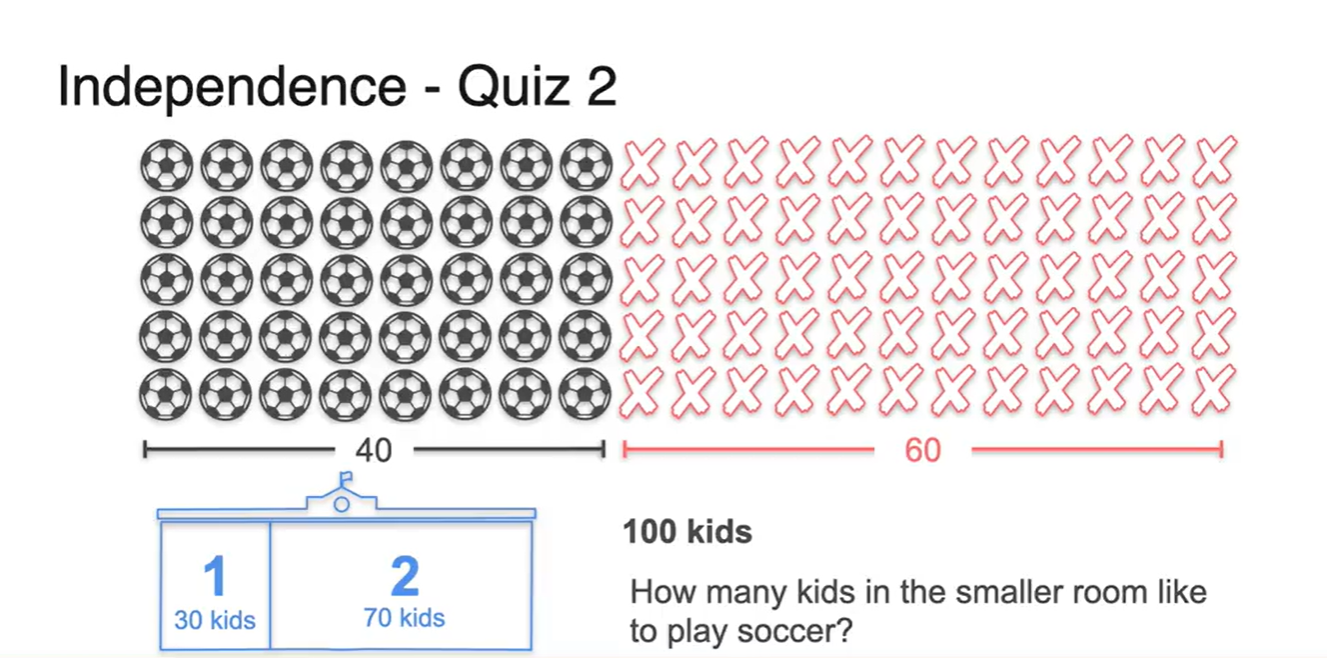
• 그렇다면 이번엔 1반이 30명, 2반이 70명인 상황에서는 어떨까?

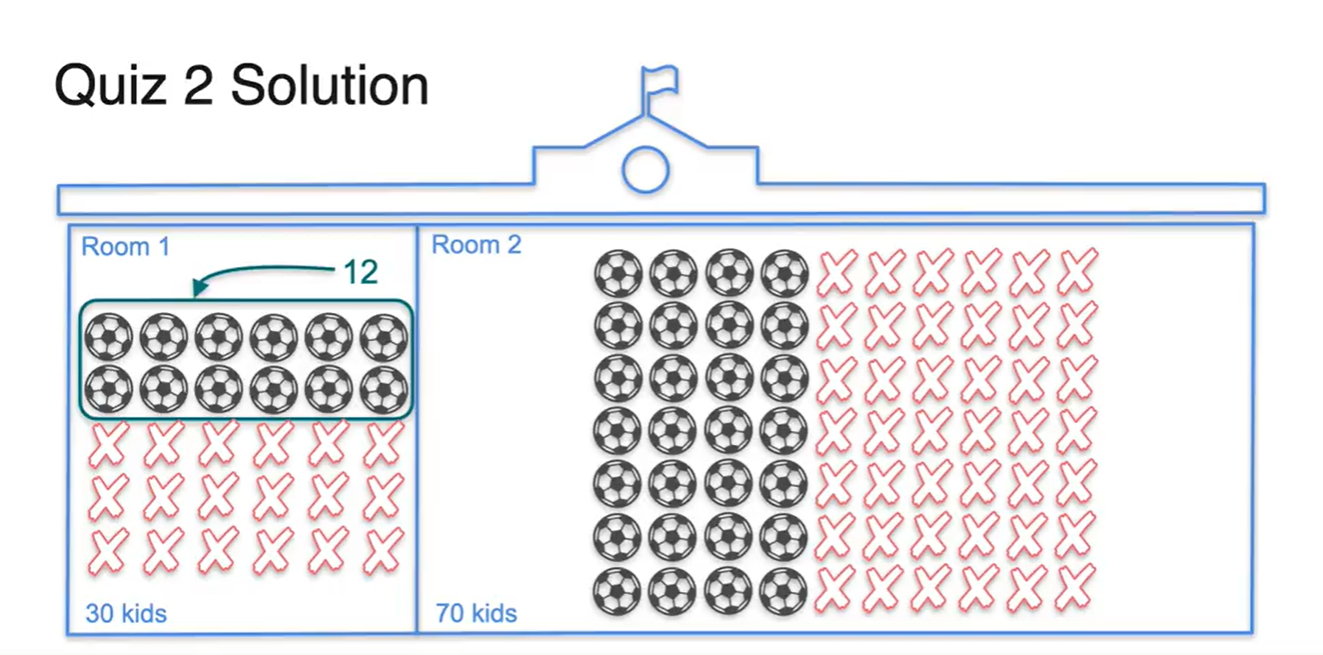
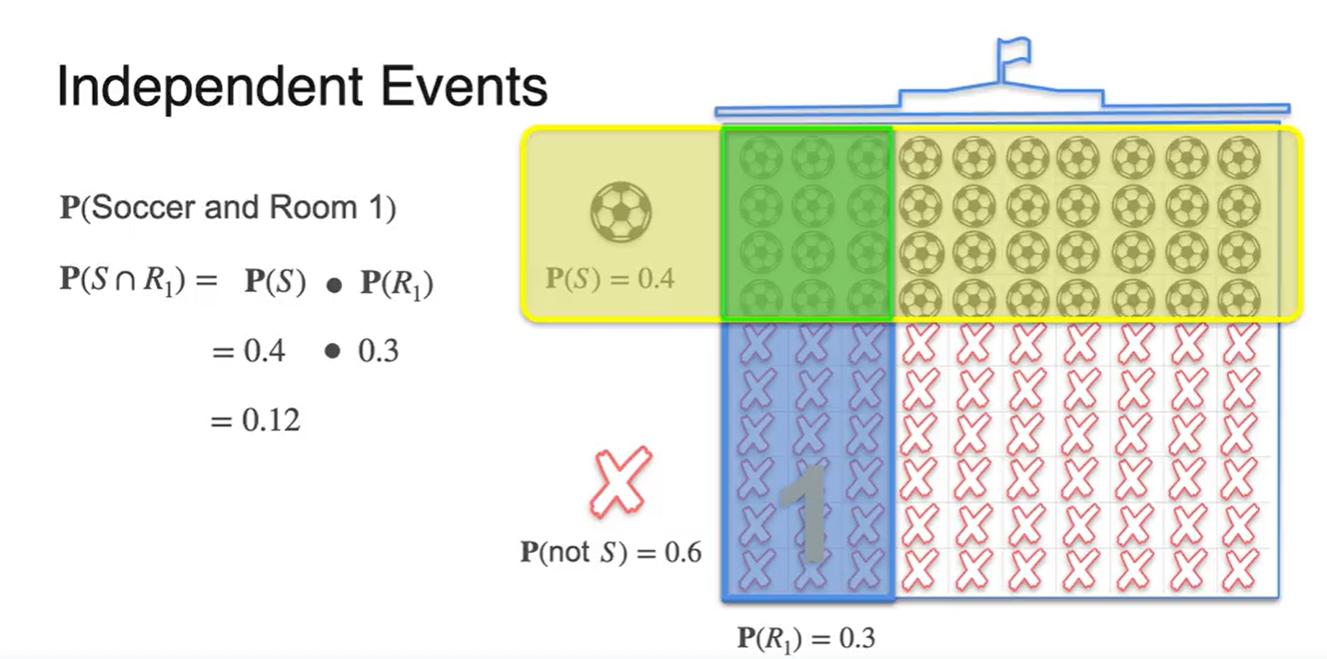
• 전체 확률인 100명중 40명이 축구를 했다는 정보와 100명 중 30명이 1반이라는 정보는 사실 서로 독립된 사건이다.

  • 따라서 $\displaystyle \frac{40}{100} * \frac{30}{100} = \frac{12}{100}$의 확률로 총 12명이 1반이면서 축구를 한 학생으로 계산된다.

• 두 확률의 교차점을 그림으로 나타낸 결과는 아래와 같다.

  • 독립 사건의 확률 계산은 $P(S \cap R_1) = P(S) * P(R_1)$ 각 확률의 곱이다.

• 두 동전을 던졌을 때 모두 Head가 나올 확률은 얼마인가?

  • $\displaystyle \frac{1}{2} * \frac{1}{2} * \frac{1}{2} * \frac{1}{2} = \frac{1}{4}$이다.

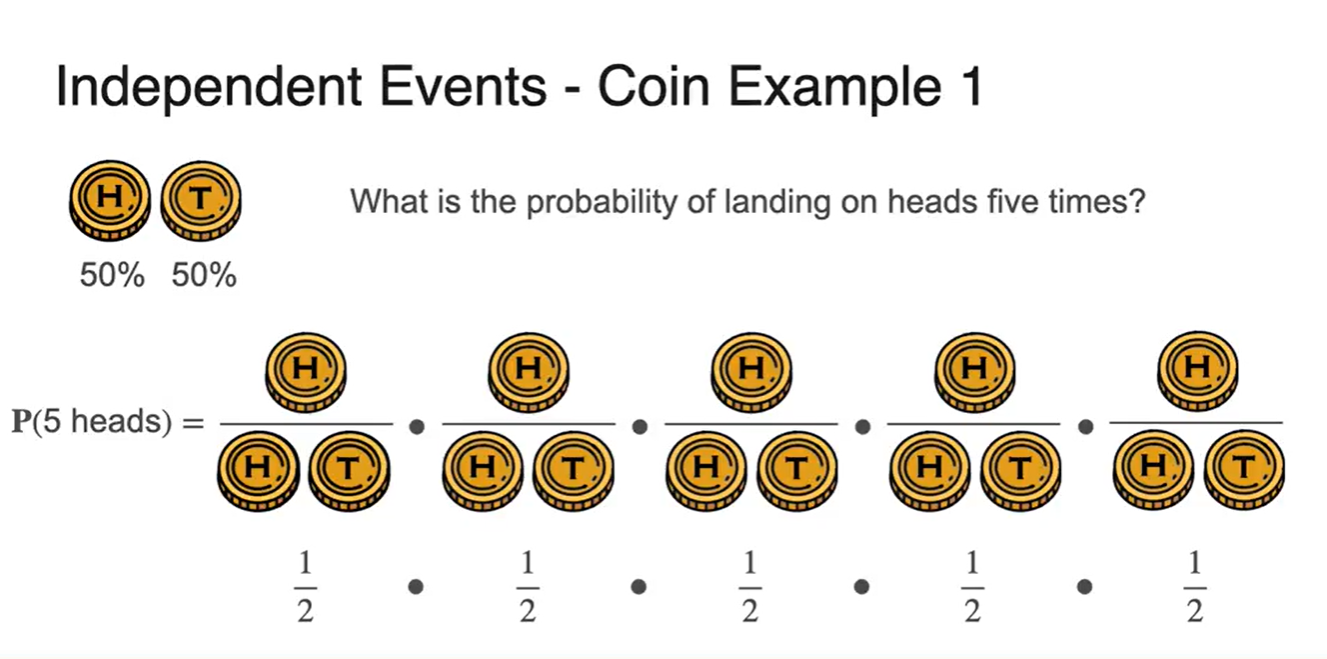
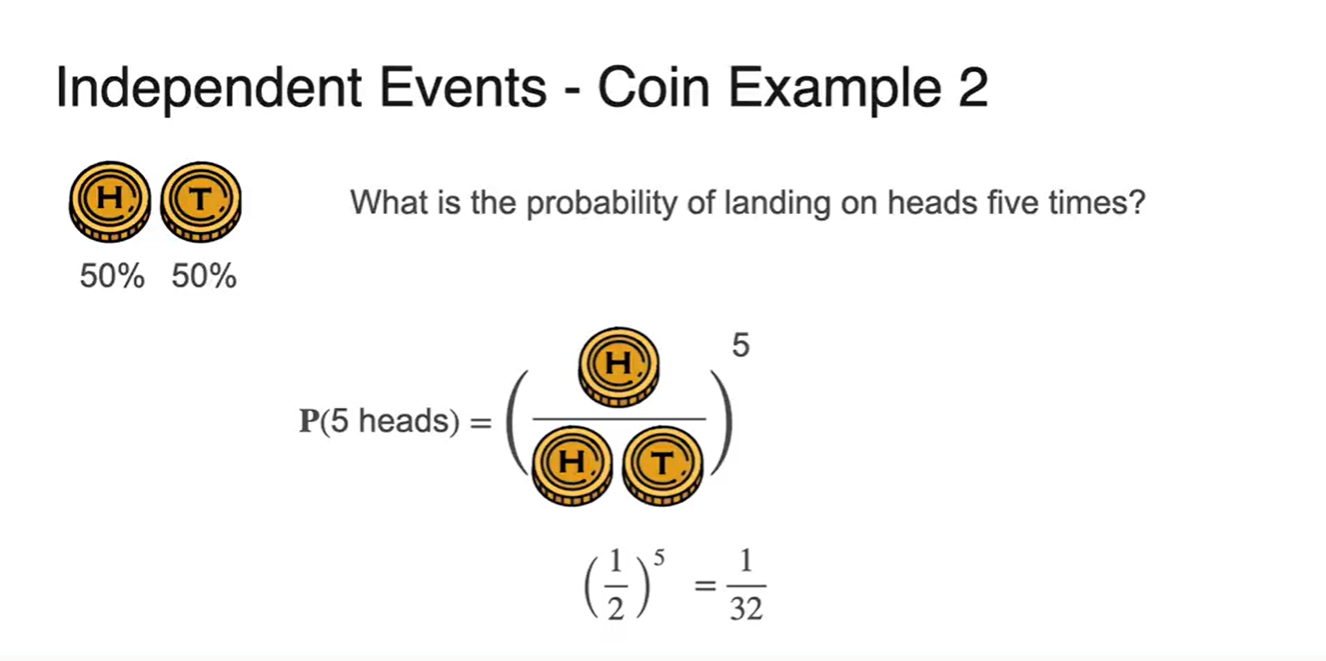
• 만약 5번 던졌을 때 모두 Head가 나올 확률은?

  • $\displaystyle (\frac{1}{2})^{5} = \frac{1}{32}$이다.

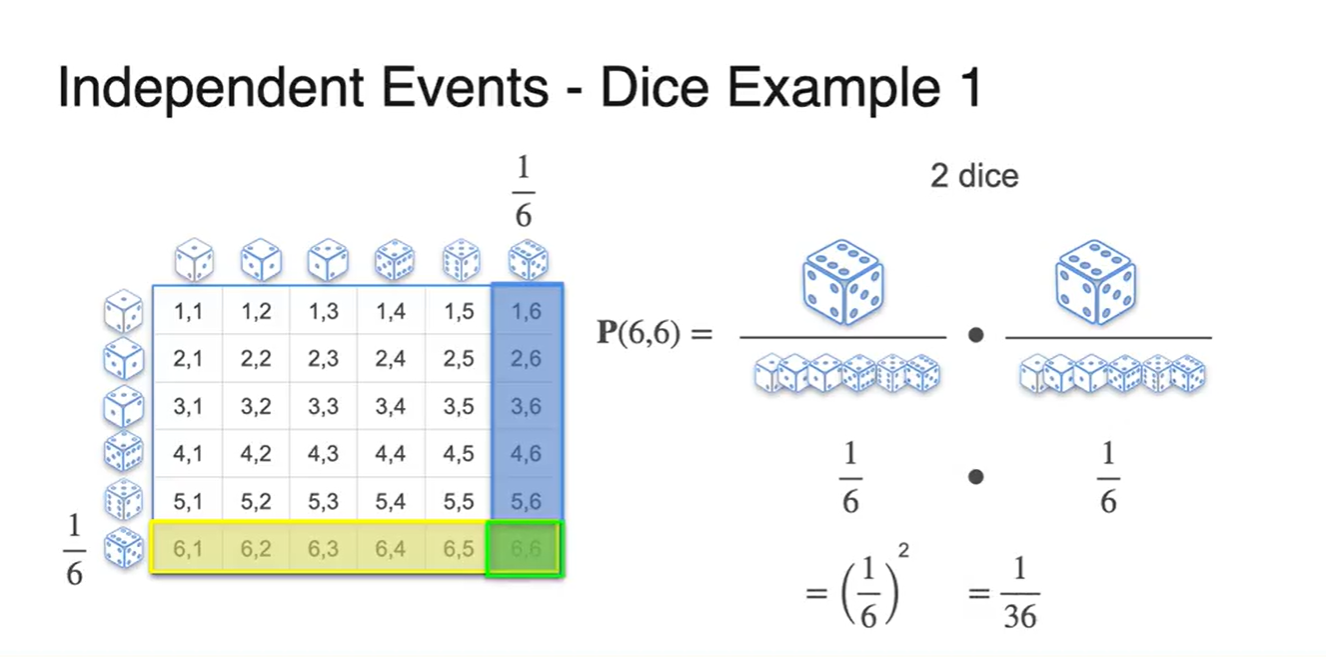
• 주사위를 두 개를 던졌을 때 모두 6이 나올 확률은 $\displaystyle \frac{1}{6} * \frac{1}{6} = \frac{1}{36}$이다.

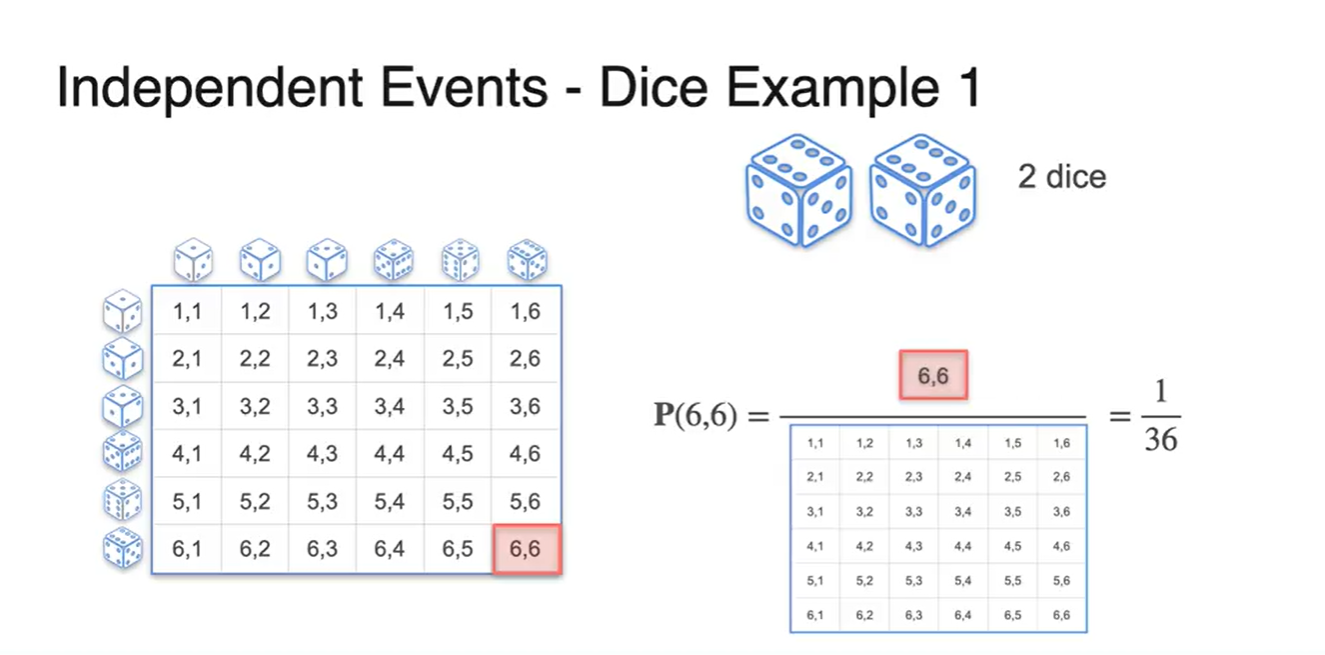
• 두 사건의 교차점이 36개 중 단 하나의 경우의 수로 주어지기 때문이다.

• 만약 10번 던졌을 때 모두 6이 나올 확률은?

  • $\displaystyle (\frac{1}{6})^{10}$이다.

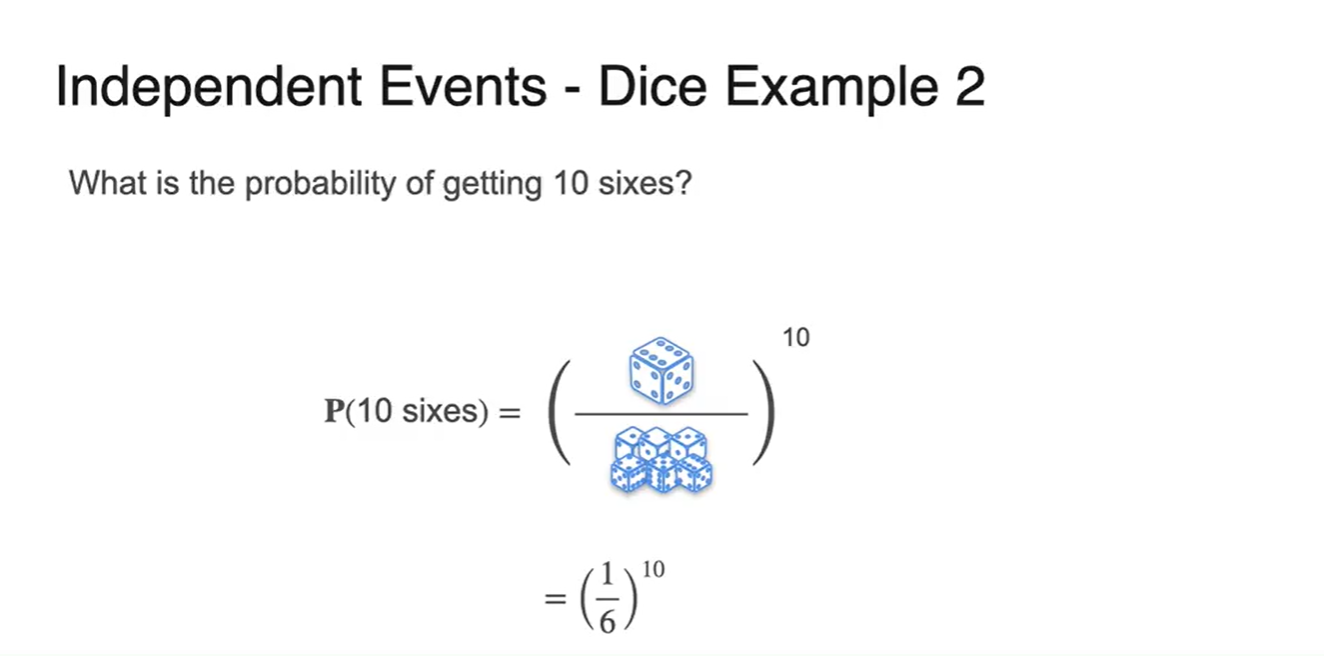
Birthday problem

• 사실 2명의 친구들이 만났을 때 둘 다 생일이 똑같을 확률은 그리 크지 않을 것이다.

  • 결론부터 말하자면 23명의 사람이 모였을 때, 두 명의 사람이 생일이 똑같을 경우의 수는 확률적으로 꽤나 크다고 한다.

• 예를 들어, 30명의 친구들이 party에 모인다고 하자.

  • 여기에 두 사람의 생일이 똑같을 확률은 얼마일 것으로 추정하는가?

    • 적어도 두 명은 생일이 같을 것이라 추정하는가?
    • 아니면 아무도 생일이 같지 않을 것이라 추정하는가?

• 정답은 random하게 뽑힌 2명의 생일은 같을 확률이 높다.

  • 무려 0.3의 유의미한 확률로 말이다.

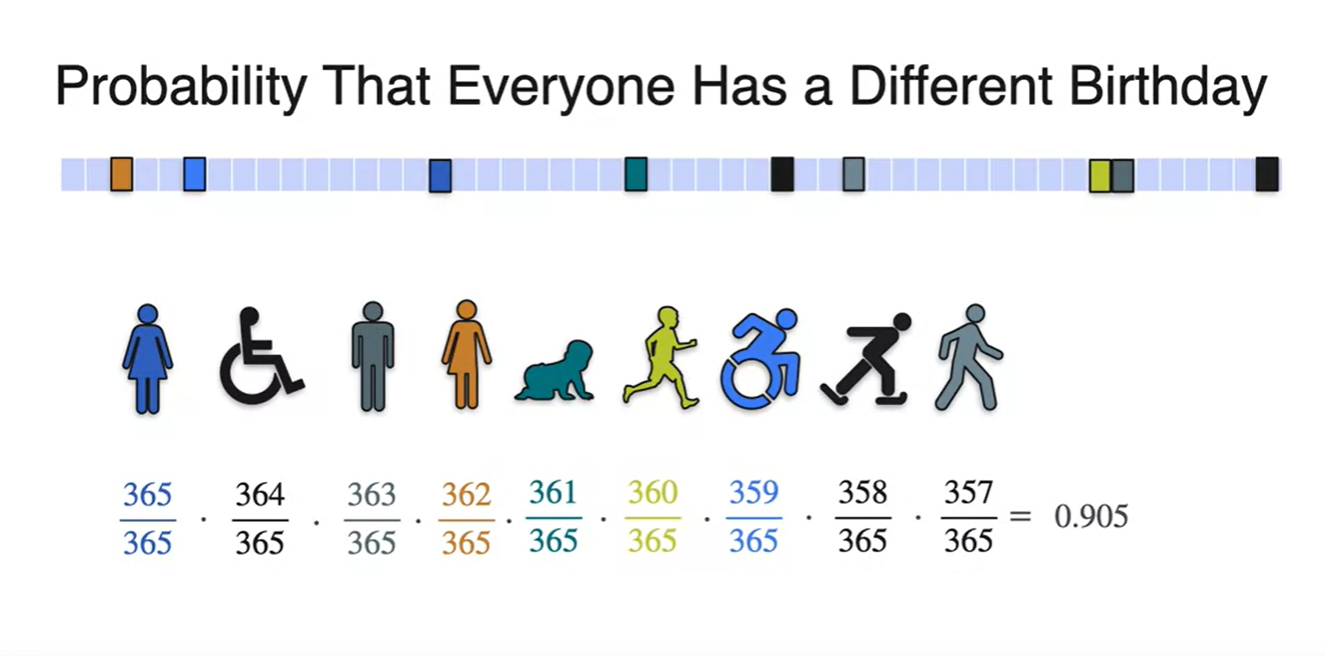
• 사람들의 생일이 모두 중복되지 않는다고 가정하며 독립 사건을 다뤄보자.

  • 첫 번째 사람은 365일 중에 365일 모두 생일일 수 있으므로 $\displaystyle \frac{365}{365}$ 확률을 갖는다.

  • 두 번째 사람은 365일 중에 364일 모두 생일일 수 있으므로 $\displaystyle \frac{364}{365}$ 확률을 갖는다.

  • 세 번째 사람은 365일 중에 363일 모두 생일일 수 있으므로 $\displaystyle \frac{363}{365}$ 확률을 갖는다.

    • 이런 식으로 모든 사건을 곱하면, 9명의 사람이 있을 때 모든 사람의 생일이 다 다를 확률이 0.9로 계산되어 나온다.

    • 다시 말해, 0.1의 확률로 두 사람의 생일이 겹칠 수 있는 것이다!

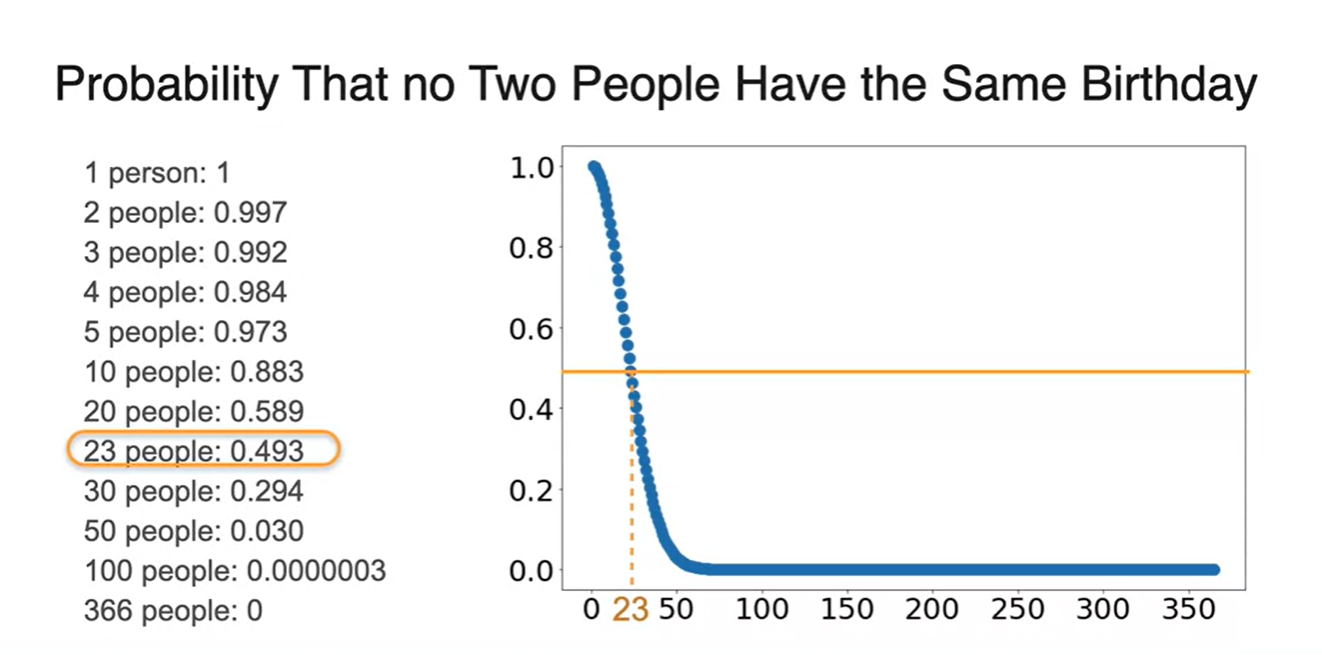
• 모인 사람 수를 늘려가며 확률을 계산해보면 아래와 같은 결과를 얻을 수 있다.

  • 재미있는 점은 23명의 사람의 모였을 때, 0.5의 확률로(반반) 두 사람의 생일이 같을 수 있다는 점이다.

    • 이는 각 사람의 생일이 독립된 사건으로 계산되기 때문이다.
    • random한 원소를 뽑는다고 해서 모든 원소가 다를 확률의 경우의 수가 오히려 나타나기 더 어렵다는 것을 뜻한다.

Conditional Probability - Part 1

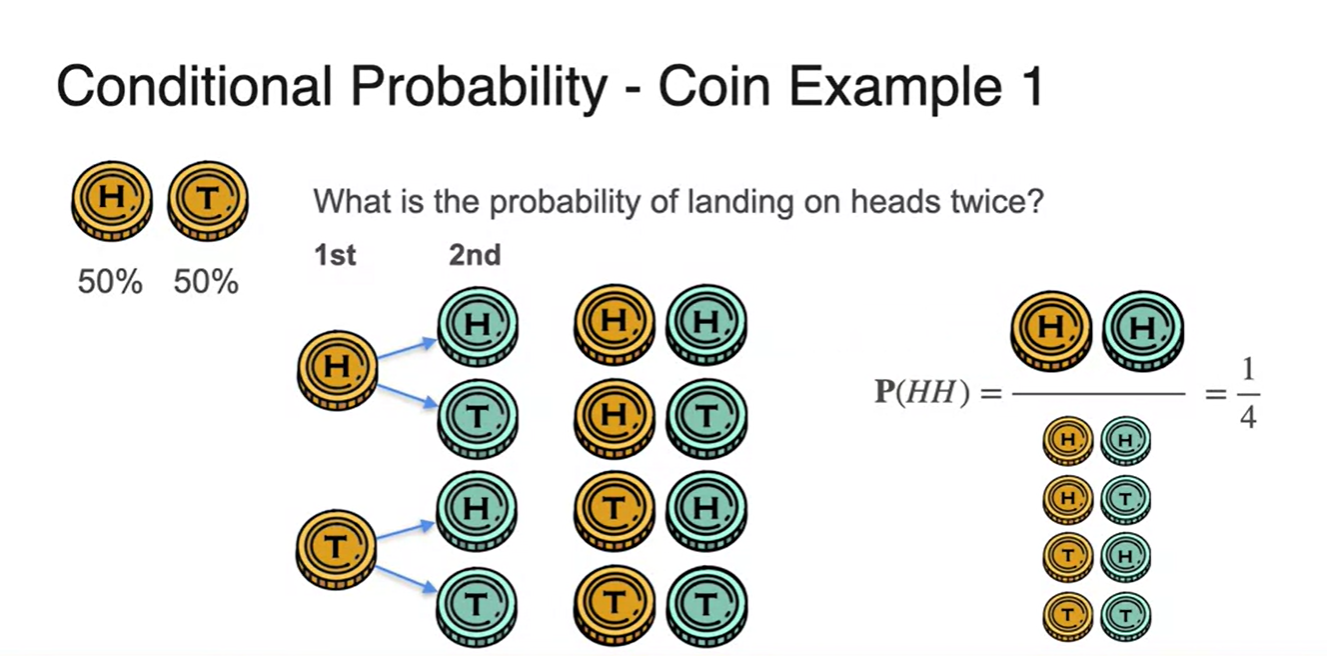
• 동전을 두 번 던져 두 번 모두 Head가 나올 확률은 얼마였는가?

  • 전체 sample space의 경우의 수가 4개, 우리가 찾고자 하는 $HH$ 경우의 수가 1개로 $\displaystyle \frac{1}{4}$의 확률이 나온다.

• 만약, 첫 번째 시행의 결과가 Head임을 알고 난 후에 또 다시 Head가 나올 확률은 얼마일 것으로 추정하는가?

  • 기호로는 $P(HH \; | 1st \; is \; H)$로 표기하며 이 때는 전체 sample space가 2개, 찾는 경우의 수가 1개이기 때문에 총 $\displaystyle \frac{1}{2}$의 확룔로 계산된다.

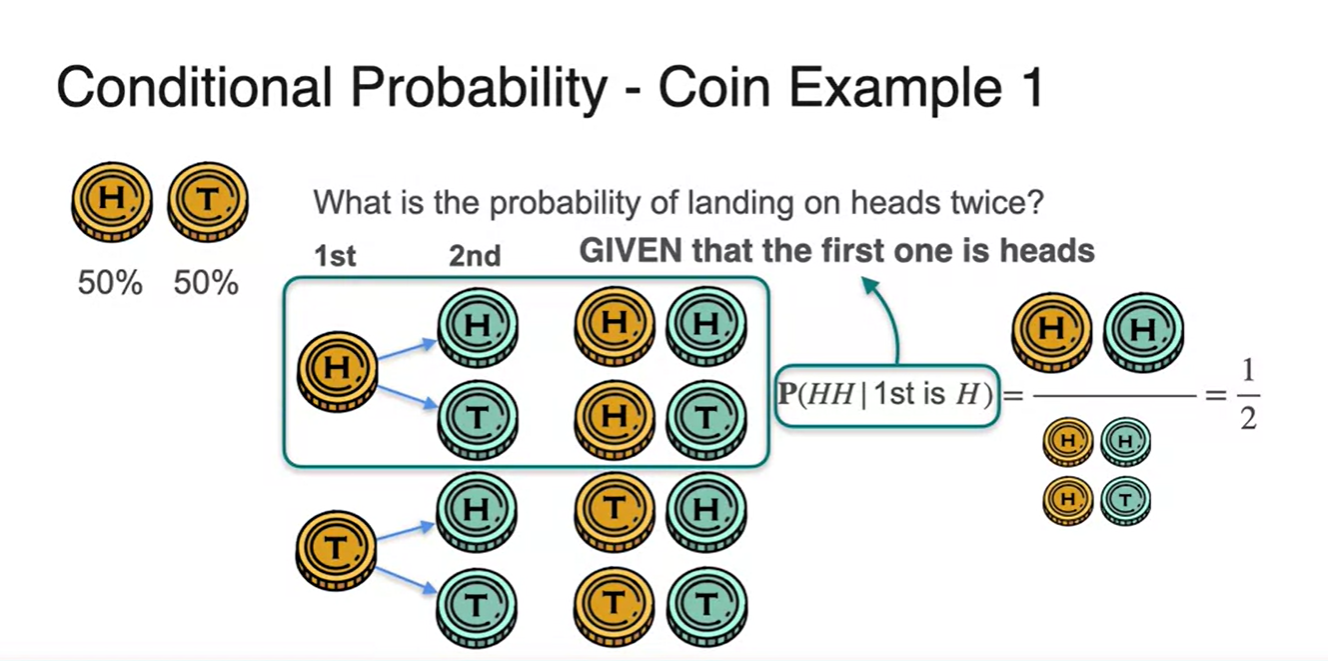
• 첫 번째 시행 결과가 Head라는 사실은 확률의 정의에서 conditional 즉, 조건문에 해당한다.

• 모든 경우의 수를 표로 정리한다면 아래 표와 같고, 첫 시행의 결과가 head라는 사실을 나타내면,

  • 첫 시행의 결과가 Tail이 나온 아래 두 경우의 수를 생각하지 않는다는 의미로 지워버리는 것과 같다.

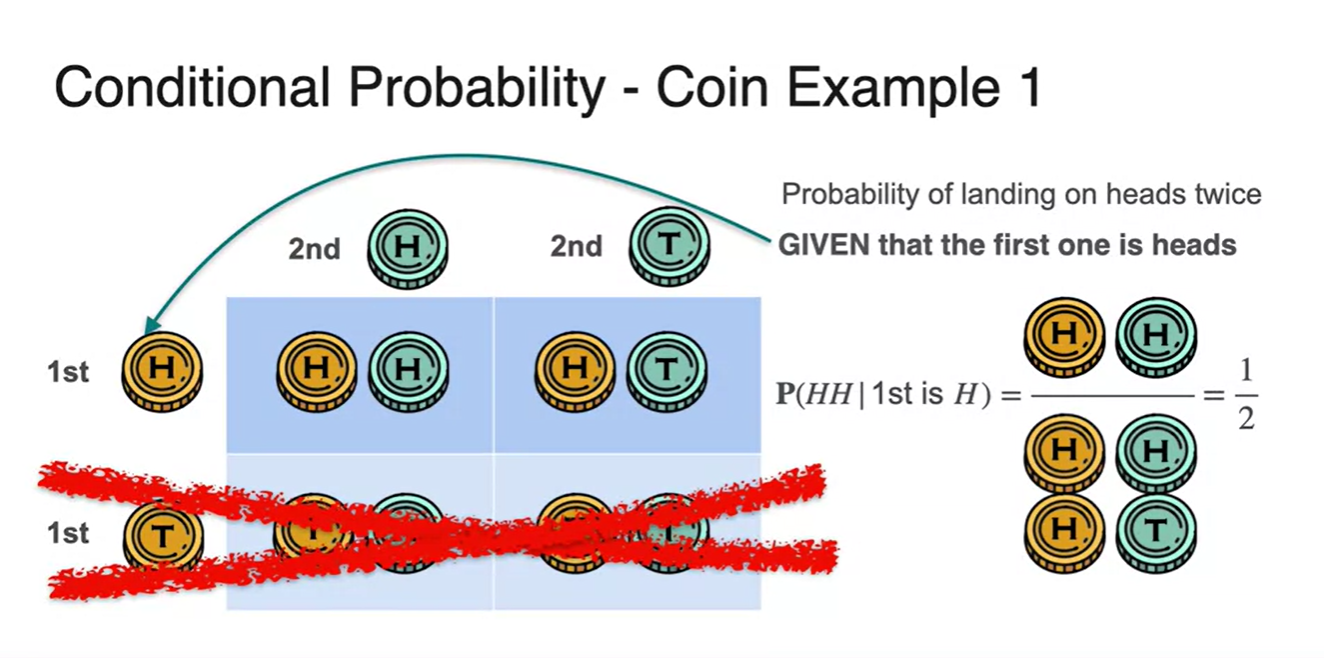
• 그렇다면 이번엔 첫 시행 결과가 Tail이 나온 상황에서 두 동전이 모두 Head가 나올 확률은 얼마일지 예상해보자.

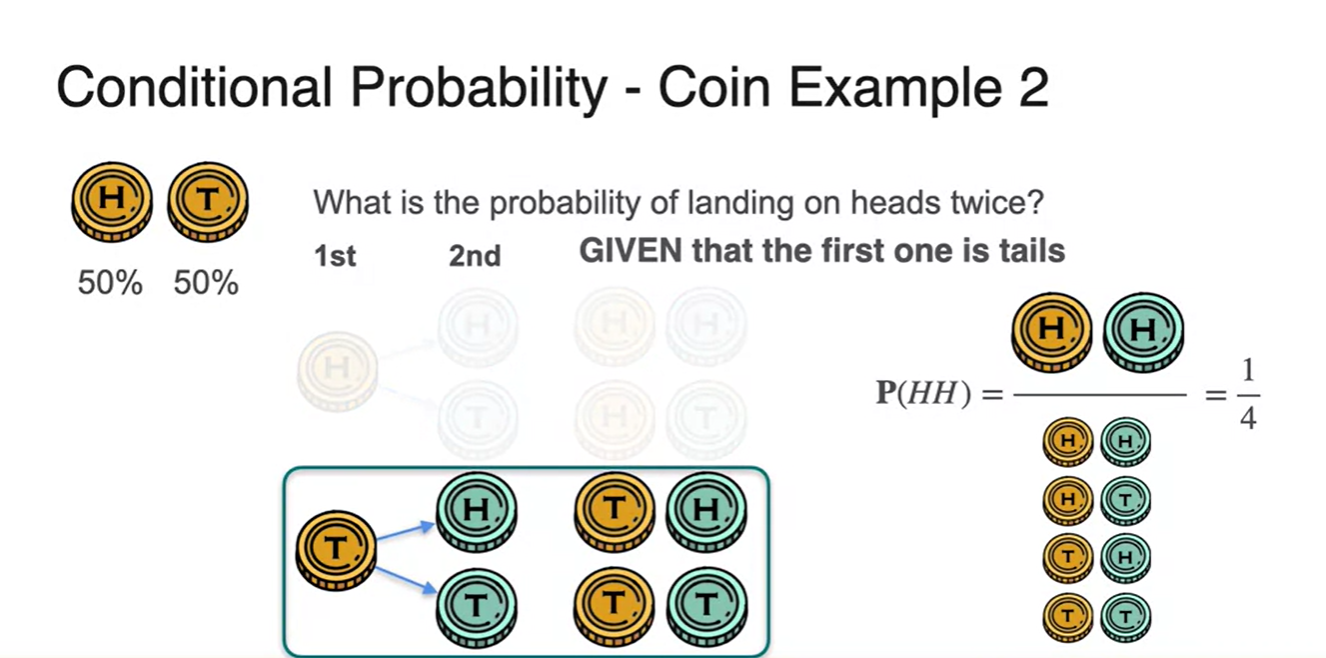
• 어떠한 경우에도 Tail이 한 번 나온 이상 Head 두 개가 번갈아 나오는 경우의 수는 존재하지 않는다.

  • 기호로는 $P(HH \; | 1st \; is \; T)$로 표기, 계산한 결과 $\displaystyle \frac{0}{2} = 0$이라는 것을 알 수 있다.

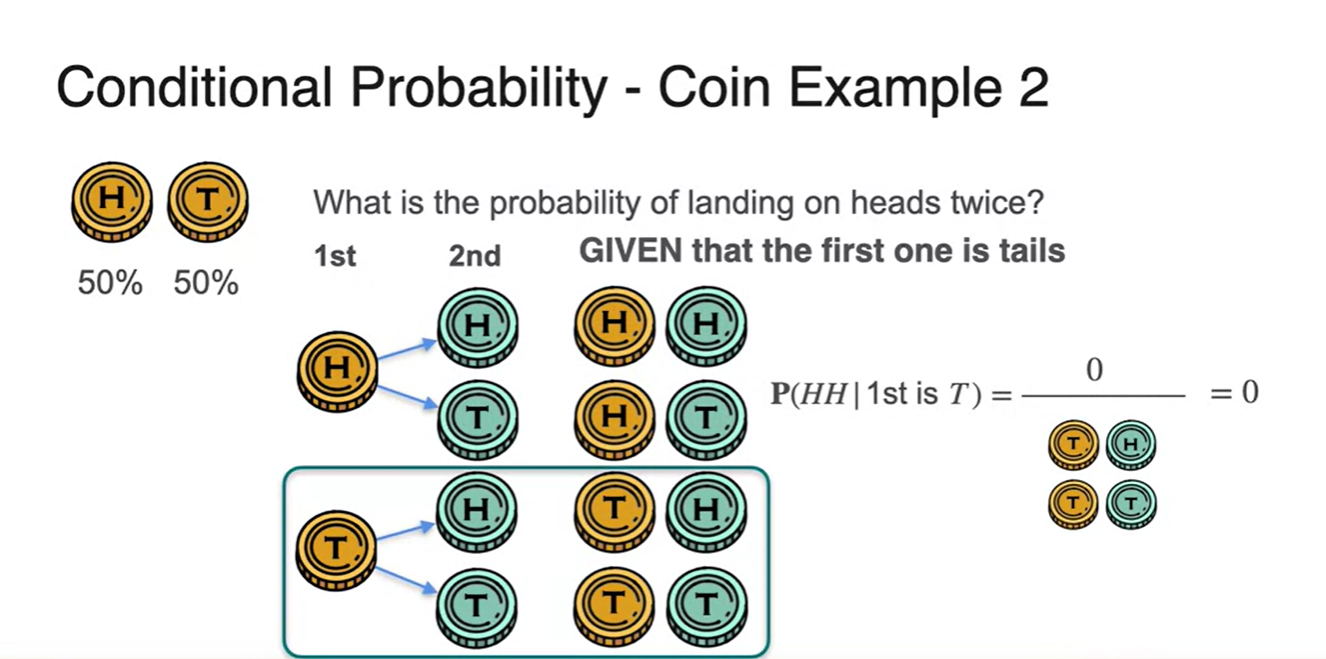
• 마찬가지로 첫 시행이 Tail이라는 조건이 주어진 순간, 모든 경우의 수 중 첫 시행이 Head인 경우의 수는 지워버리는 것과 같다.

  • 그러나 아래 두 경우 모두 $HH$의 결과는 나타날 수 없기 때문에 이 때의 확률은 $0$으로 계산된다.

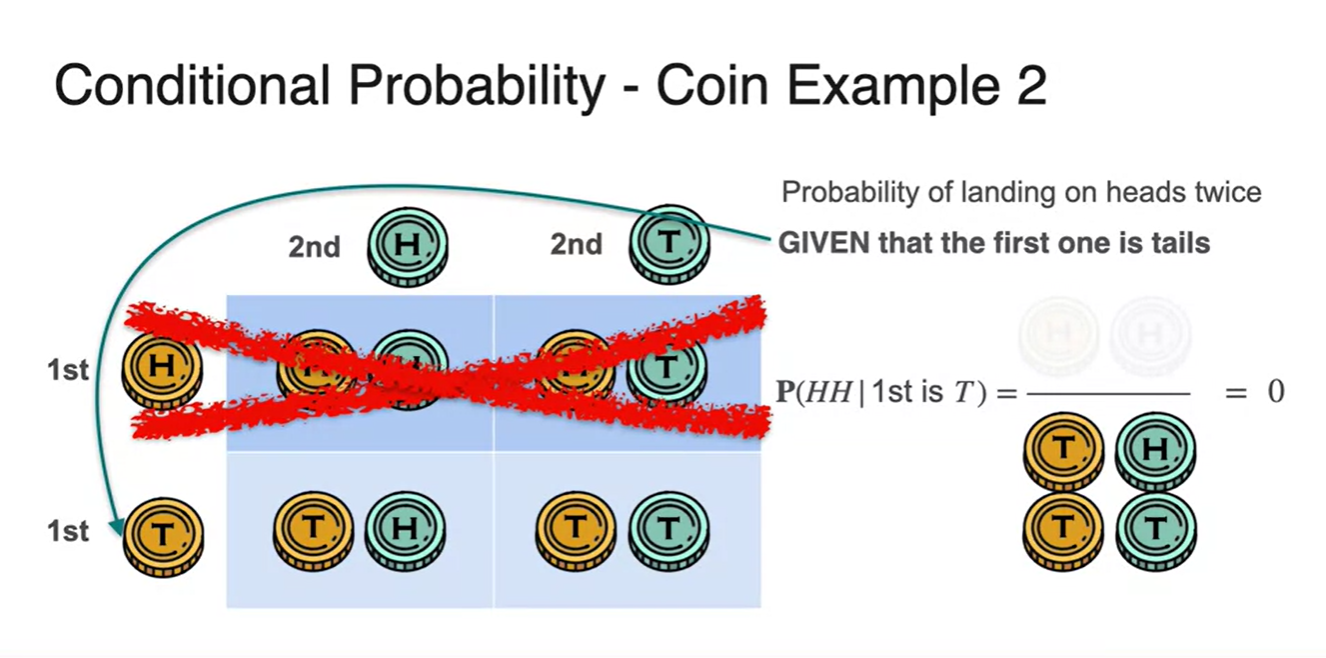
• 사건이 서로 독립적일 때에 두 사건의 교차 확률은 $P(A \cap B) = P(A) * P(B)$로 전개된다.

  • 이를 확률의 Product Rule이라 한다.

• 주사위 문제로 넘어와서, 두 주사위를 던지는 상황을 가정해보자.

  • 첫 시행의 결과가 6이고 두 시행의 합이 10이 되는 확률을 구한다면 얼마의 확률값을 갖는가?

    • 전체 sample space는 36, 우리가 찾는 경우의 수는 (6, 4) 1개 이므로 $\displaystyle \frac{1}{36}$이다.

• 두 사건을 조금 더 풀어서 전개해보자.

  • 첫 번째 사건은 주사위 눈금이 6이 나올 확률인 $P(1st \; is \; 6) = \displaystyle \frac{1}{6}$이었다.

  • 두 번째 사건은 첫 시행이 6이 나올 확률 중에서 합이 10인 확률이므로 $P(sum=10 \; | 1st \; is \; 6) = \displaystyle \frac{1}{6}$이다.

    • 두 확률의 곱으로 $P(1st \; is \; 6 \cap sum=10)$ 확률인 $\displaystyle \frac{1}{36}$이 계산될 수 있다!

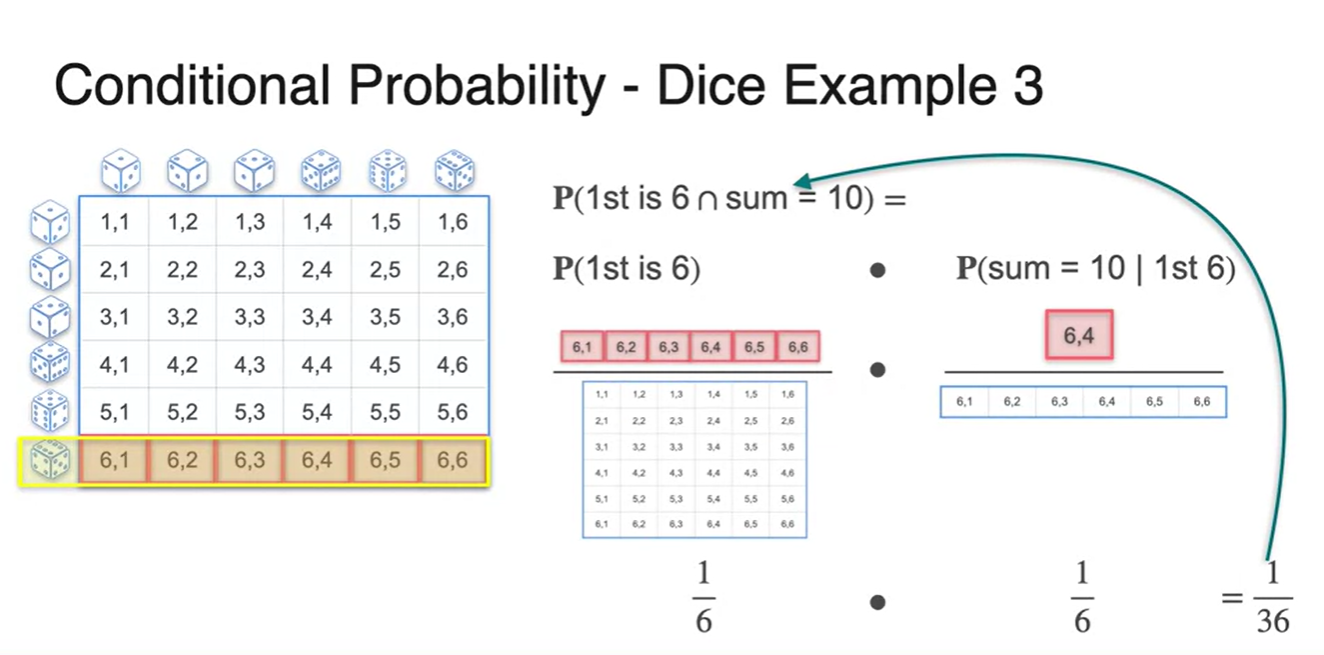
• 이를 통해 Conditional probability, 조건부 확률의 공식이 무엇인지 유도된다.

  $P(A \cap B) = P(A) * P(B|A)$

• 만일 두 사건이 독립적인 경우라면 $P(B|A) = P(B)$이다.

  • B 사건이 A 사건의 시행 결과에 영향을 받지 않을 때의 상황이다.

• $P(sum=10)$ 즉, 두 번의 주사위를 던졌을 때의 합이 10이 나올 확률은 얼마인가?

  • 전체 sample space 경우의 수가 36, 찾는 경우의 수가 3이므로, $\displaystyle \frac{3}{36} = \frac{1}{12}$다.

• 만일 첫 시행에서의 주사위 눈금이 6이 나왔다면 $P(sum=10 \; | 1st \; is \; 6)$은 얼마일까?

  • 전체 sample space가 6, 찾는 경우의 수가 1이므로 $\displaystyle \frac{1}{6}$으로 계산된다.

• 만일 첫 시행의 주사위 눈금이 1이 나왔다면 $P(sum=10 \; | 1st \; is \; 1)$은 얼마인가?

  • 불행하게도 첫 시행의 눈금이 1일 때는 두 눈금의 합이 10이 될 수 없다.

    • 즉, 확률은 $0$이다.

Conditional Probability - Part 2

• 위에서 다뤘던 예제와 비슷하게, 이번에는 1반에만 TV가 놓여져 있다고 가정해보자.

  • 1반에서만 축구를 볼 수 있는 상황에서 축구를 좋아하는 친구들이 각 반에 몇 명일지 추정해보자.

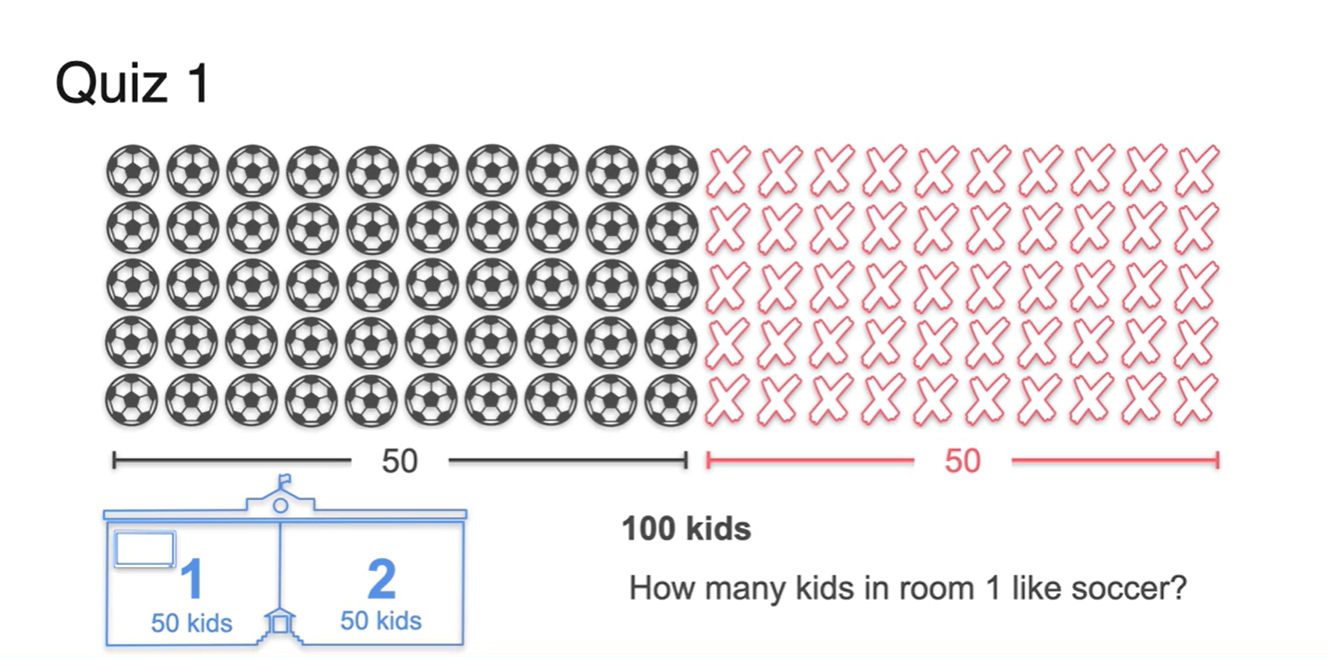
• 정답은 50명의 친구들이 모두 1반으로 가있을 것이라 예상할 수 있다.

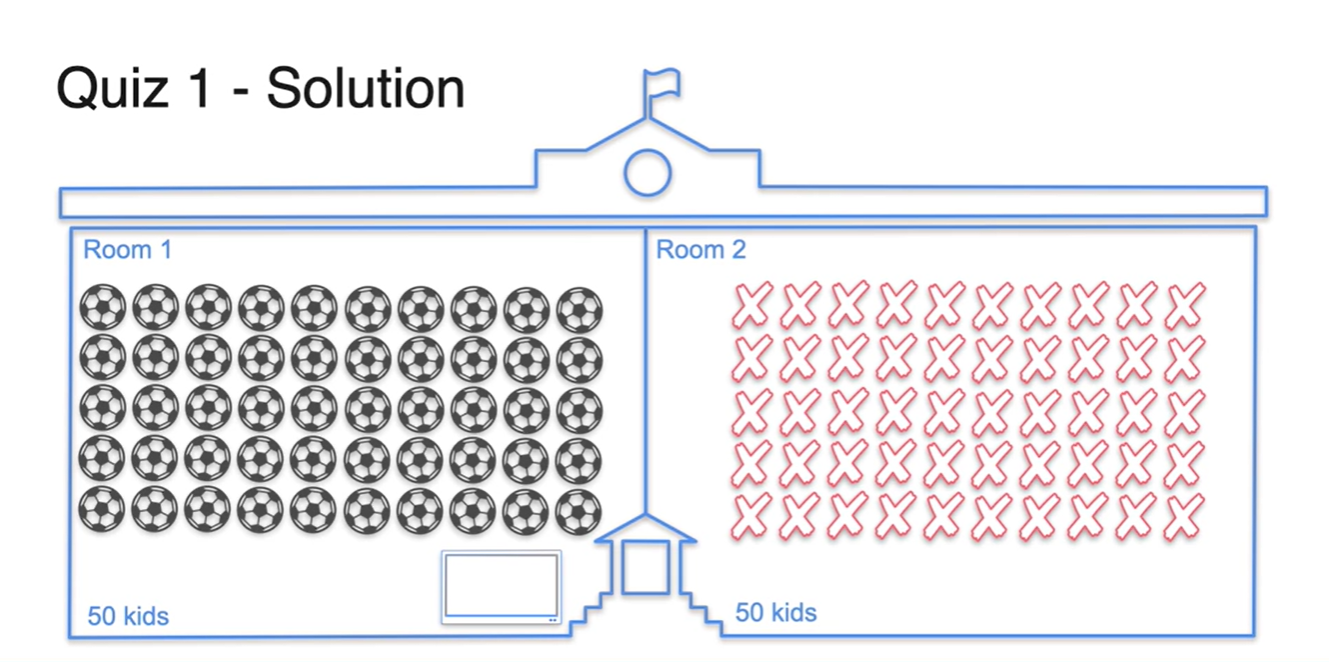
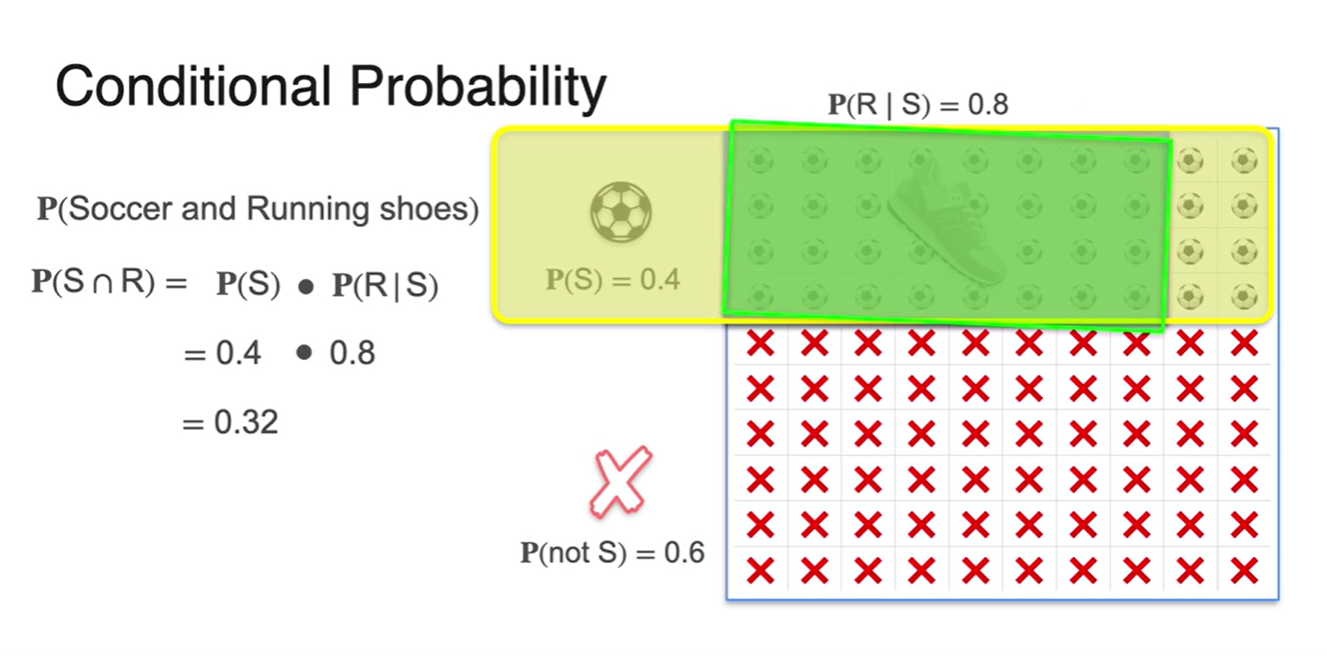
• 이번에는 100명중 40명의 친구들이 축구를 할 줄 아는 상황이 주어진다고 가정해보자.

  • 전체의 80% 비율로 운동화를 가진 학생들이 존재한다면, 총 몇 명의 친구들이 운동화를 가지고 있는가?

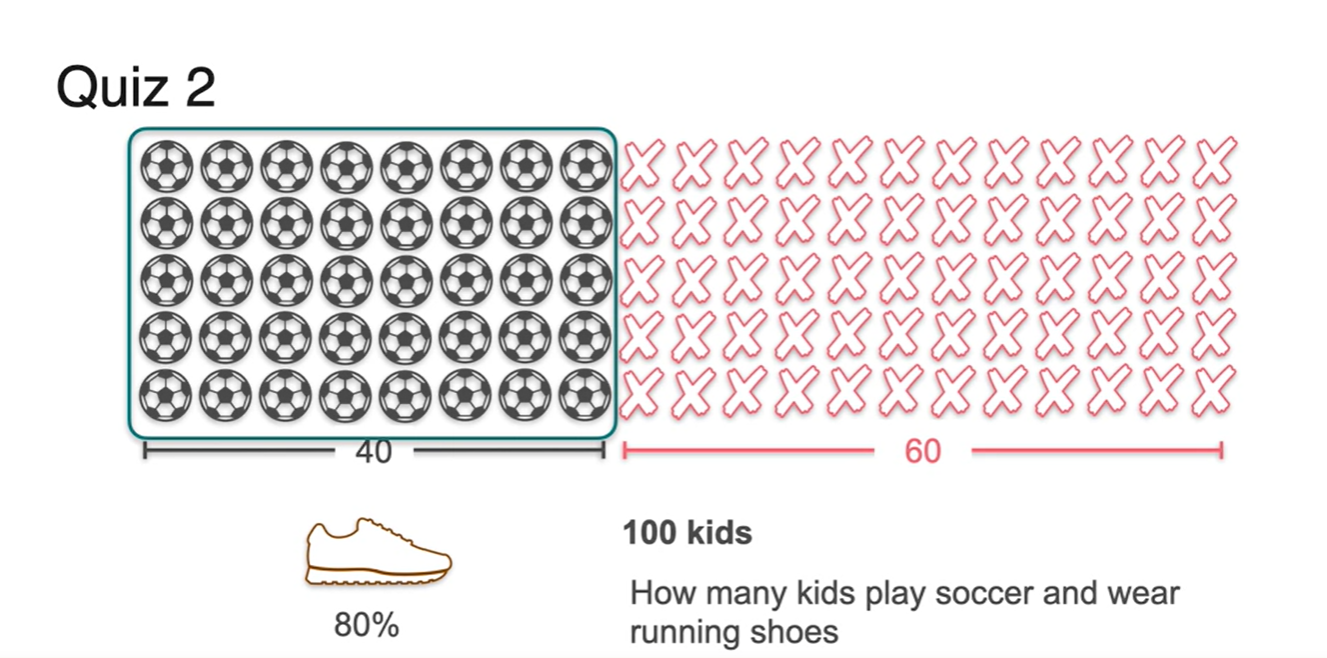
• 이러한 상황에서는 전체 sample space의 경우의 수가 100명이 아닌 40명으로 한정된다.

  • 이 중 80%의 비율이면 32명의 학생이 운동화를 가지고 있다는 사실을 알 수 있다.

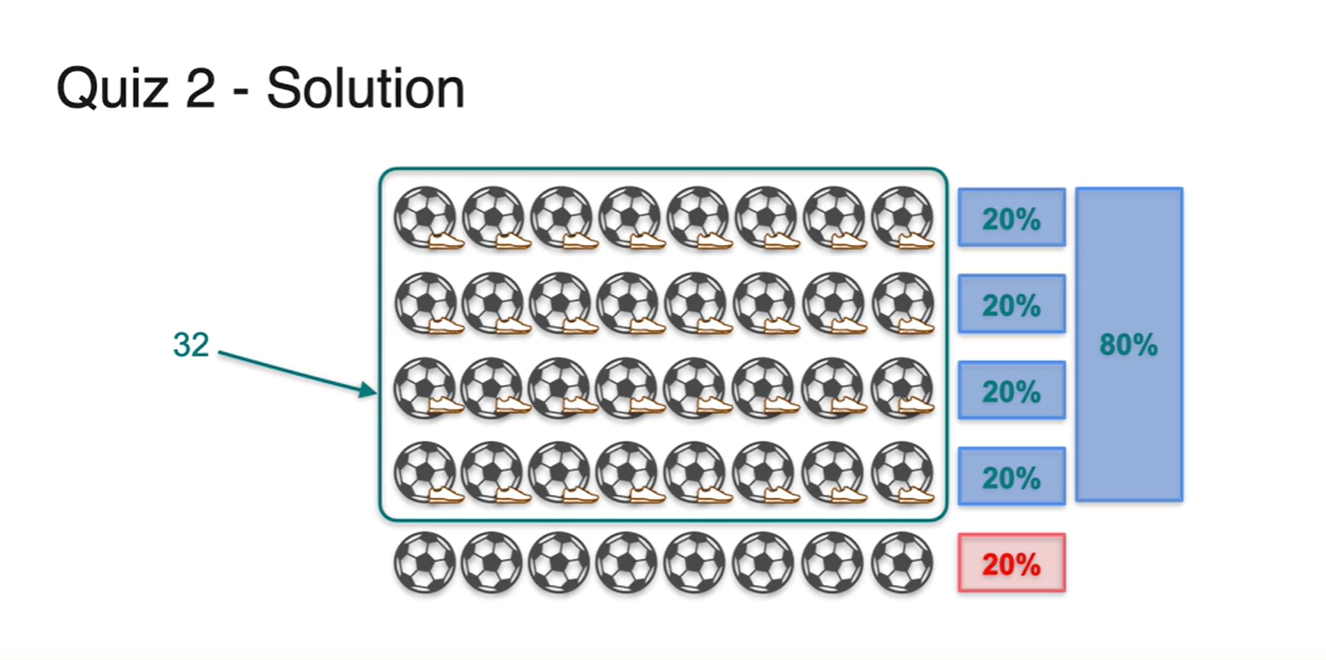
• 두 사건의 조건부 확률을 공식으로 정리해보자.

  • $P(Soccer \; and \; Running \; shoes) = P(S \cap R) = P(S) * P(R|S) = 0.4 * 0.8$

    • 두 사건의 교차 확률은 축구를 할 수 있는 학생의 확률과 운동화를 신고 있는 학생의 확률을 곱한 값이다.

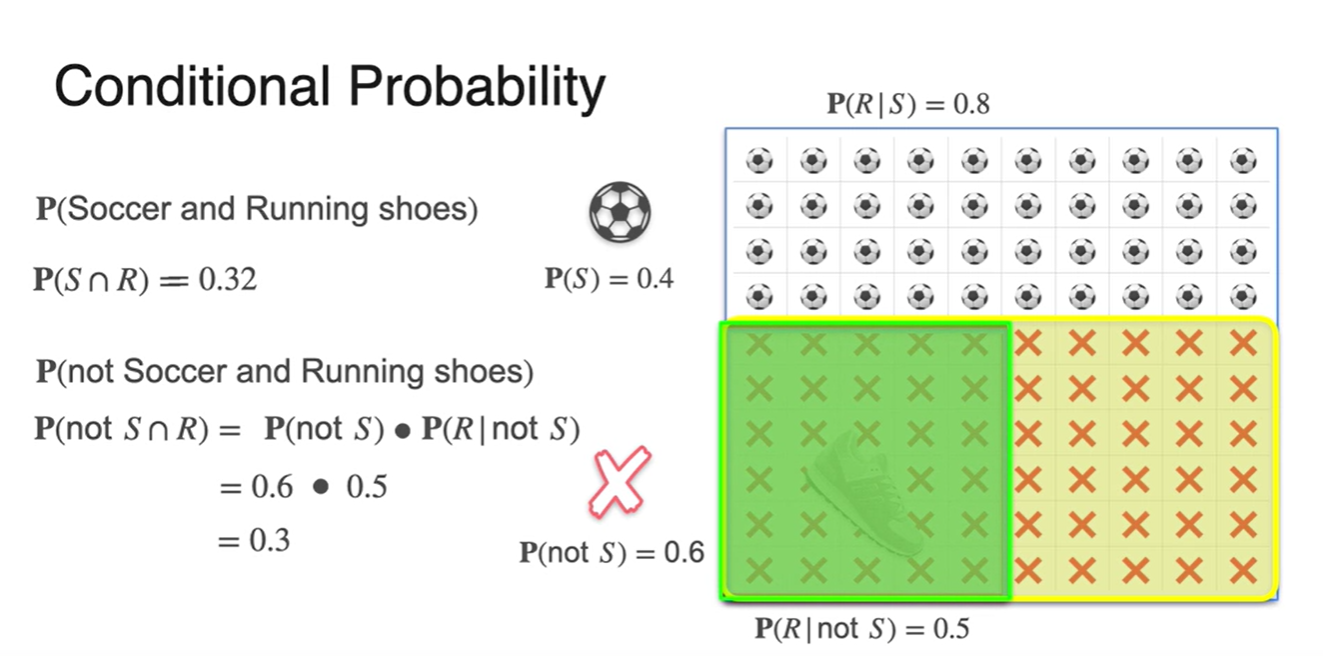
• 만일 축구를 하지 않는 학생들 중 운동화를 가지고 있는 학생의 비율이 50%라는 정보를 제공했다고 가정해보자.

  • $P(not \; Soccer \; and \; Running \; shoes) = P(not \; S \cap R) = P(S) * P(R|not \; S) = 0.6 * 0.5$

    • 두 사건의 교차 확률은 축구를 하지 않는 학생의 확률과 운동화를 신고 있는 학생의 확률을 곱한 값이다.

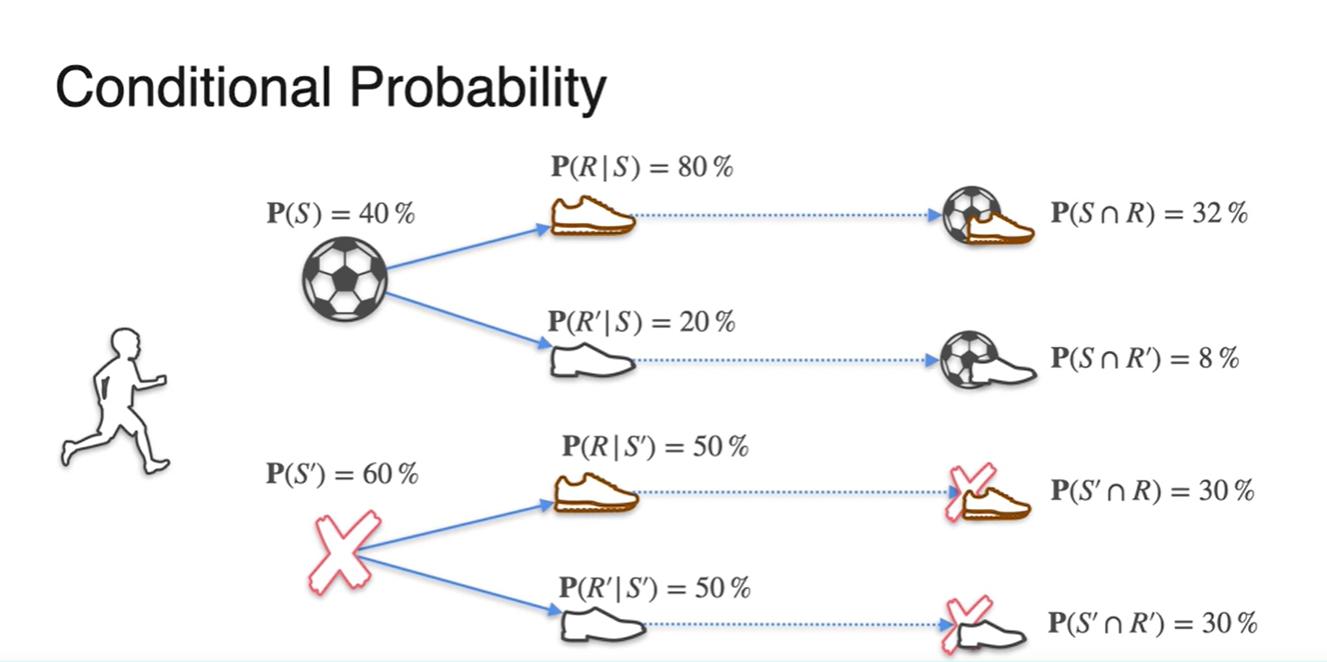
• 모든 가능한 경우의 수를 정리해보면 다음과 같다.

  • 재밌는 점은 축구를 한 학생과 하지 않은 학생의 확률의 합과 각 집단 속에서 운동화를 신은 확률과 신지 않은 확률의 조건부 확률의 합이 모두 1이라는 점이다.

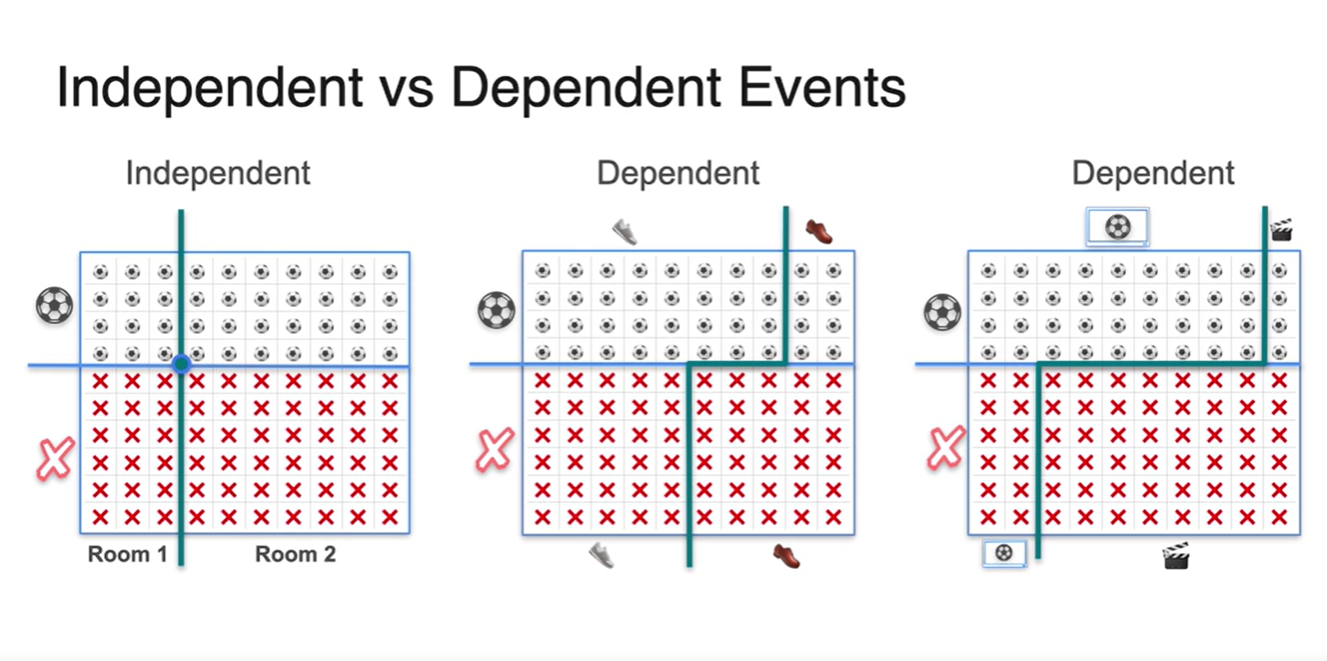
• 아래 그림은 여러 조건에 따른 비율의 변화를 나타낸다.

  • 세 가지의 예시를 나타낸다.

Bayes Theorem - Intuition

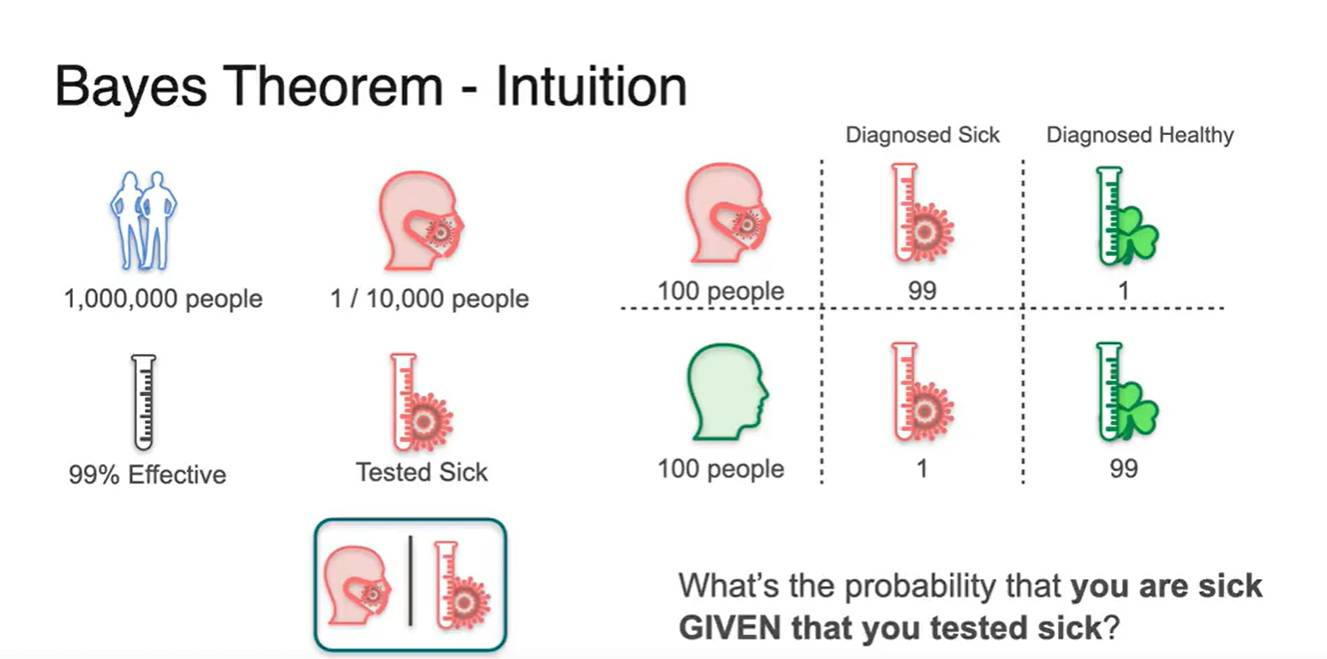
• 1,000,000명의 사람들 중에서 1/10,000의 확률로 아픈 사람이 존재한다고 가정해보자.

  • 그리고 99%의 정확도를 갖는 양성 반응 테스트기가 있다.

    • 100명의 아픈 사람이 테스트를 진행할 때에는 99명은 제대로 진단 받고, 1명이 검출되지 않는다.
    • 100명의 건강한 사람이 테스트를 진행할 때에는 1명이 아픈 사람이라 진단 받으며, 99명이 제대로 진단 받는다.

  • 그렇다면 아픈 사람으로 진단 받은 사람들 중에 그들이 실제로 아픈 사람일 확률은 얼마일까?

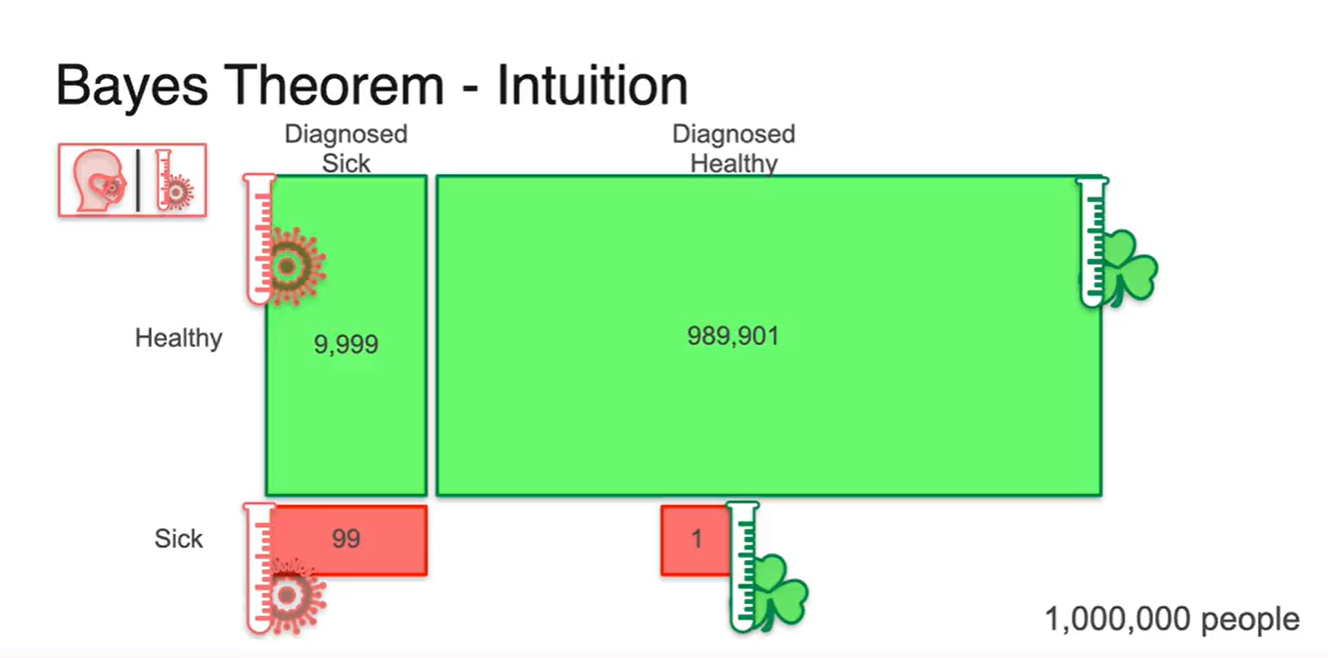
• 전체 사람이 1,000,000명이라면 999,900명의 건강한 사람이 건강하다고 진단받고, 100명의 사람이 병이 있는 것으로 진단 받는다.

  • 그 중 99%의 확률로 각각 정확한 진단을 받는다고 할 때, 건강한 사람 중 아프다고 진단 받는 사람의 숫자가 9,999명인 것에 주목해 보라.

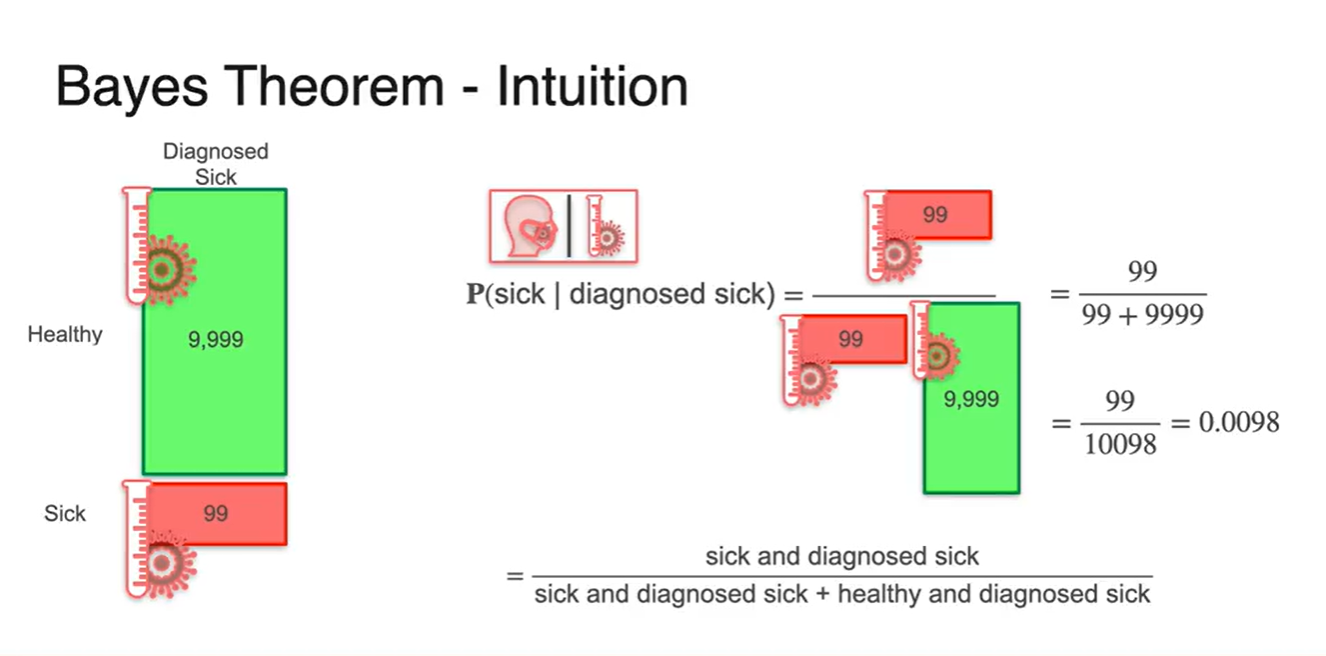
• 우리는 이것을 기호로 $P(sick \; | \; diagnosed \; sick)$이라 표현할 수 있다.

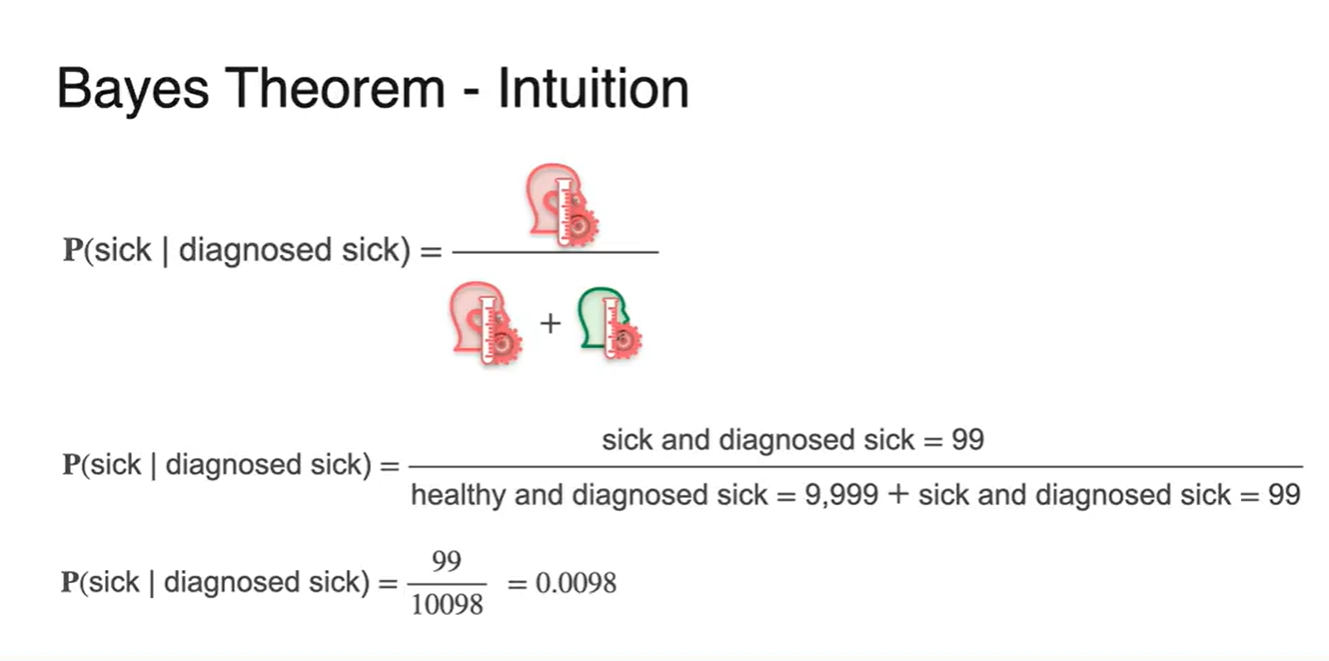
  • 놀랍게도, 아프다고 진단받은 사람들 중 진짜로 아픈 사람일 확률은 0.0098로 계산된다.

    • 즉, 1%도 안되는 매우 낮은 확률을 갖는다.

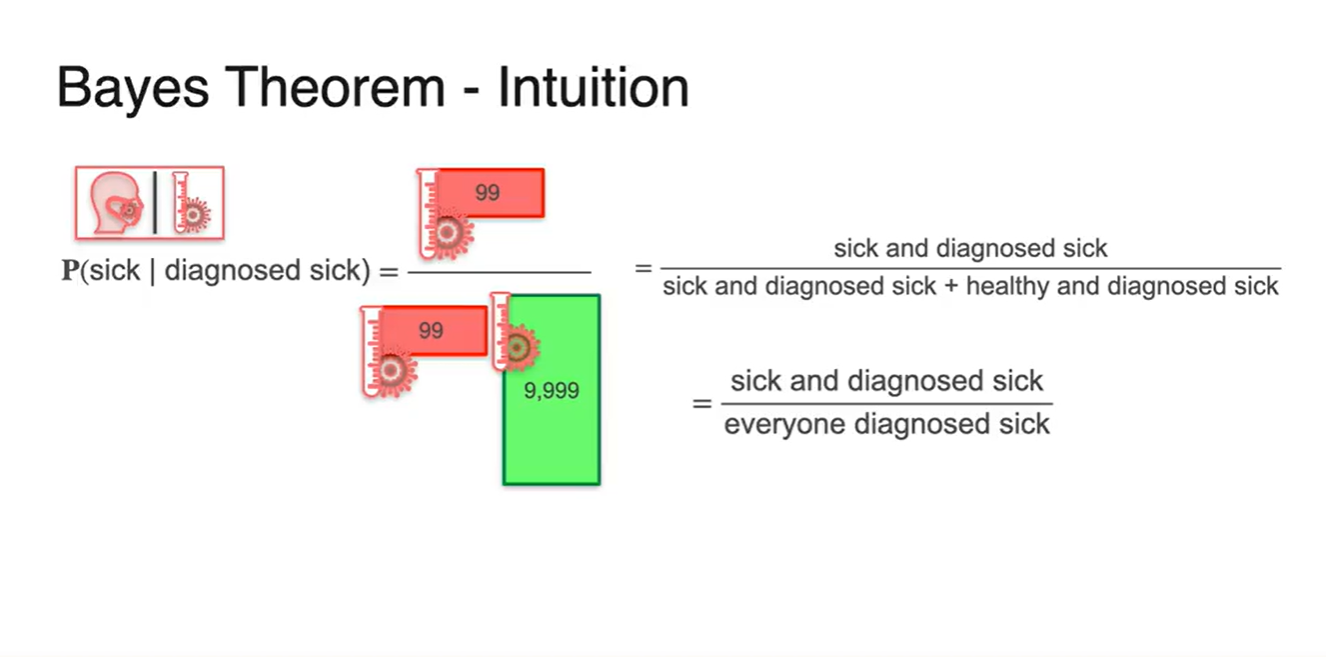
• 아프다고 진단 받았지만 실제로 아픈 사람일 확률은 1% 미만이다.

  • 이는 건강한 사람의 1%의 비율인 9,999명이 > 실제로 아픈 사람의 99% 비율보다 더욱 많은 숫자를 기록하기 때문이다.

• 모든 경우의 수를 정리하면 아래 그림과 같다.

  • 각 확률을 계산하여 조건에 따른 사람의 숫자를 기록해 놓은 결과다.

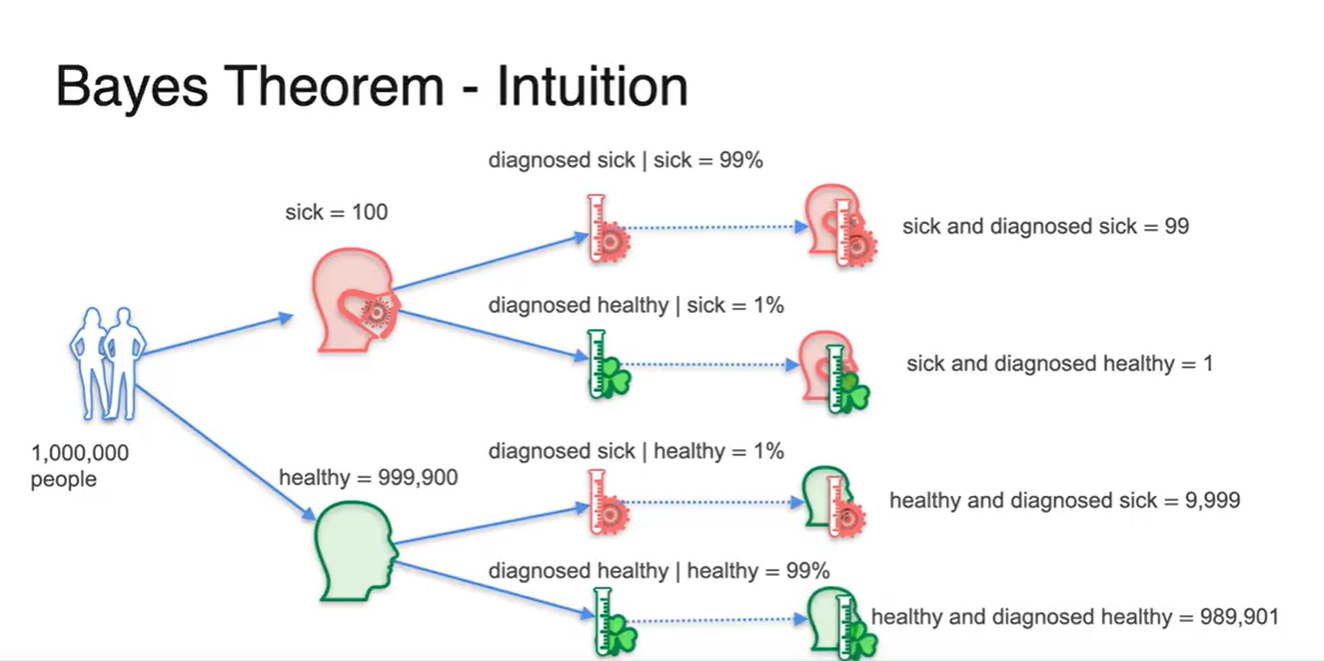
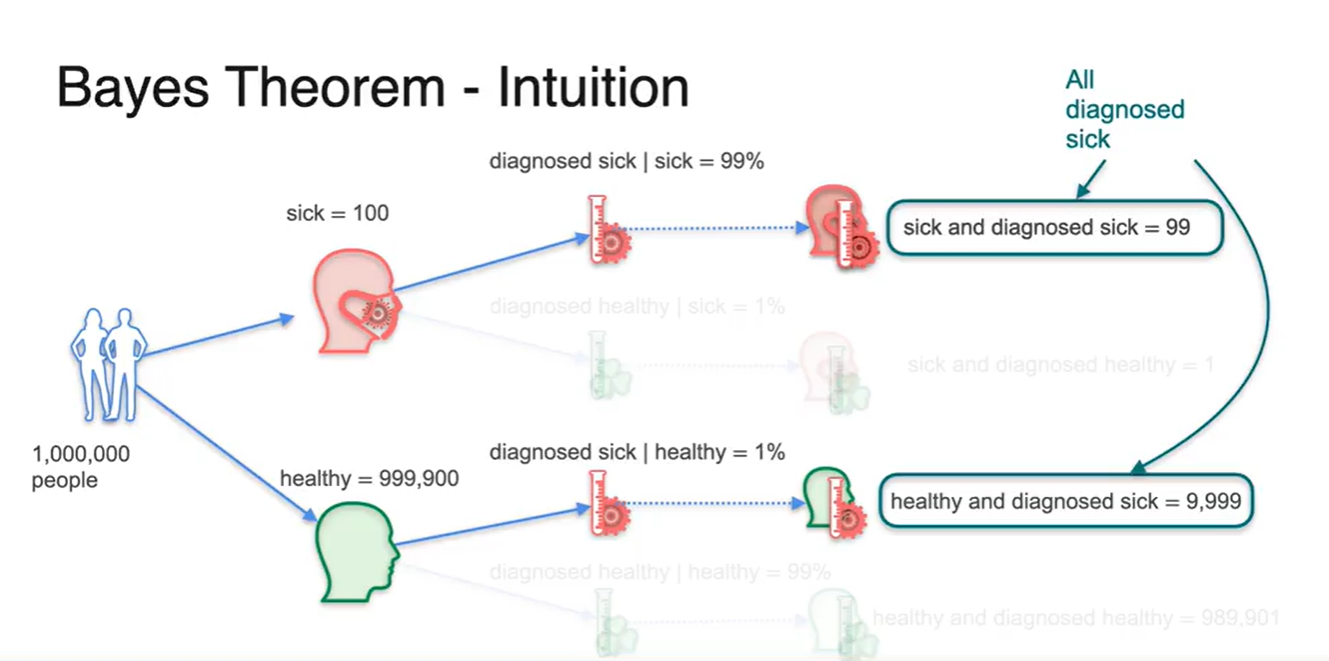
• 이들 중 아프다고 진단 받은 사람의 숫자를 세어보면 99명과 9,999명의 합으로 계산될 수 있다.

• 다시 한 번 정리하면 다음과 같은 식으로 Bayes Theorem 예시를 전개할 수 있다.

  • $P(sick \; | \; diagnosed \; sick) = \displaystyle \frac{99}{9,999 + 99} = 0.0098$

Bayes Theorem - Mathematical Formula

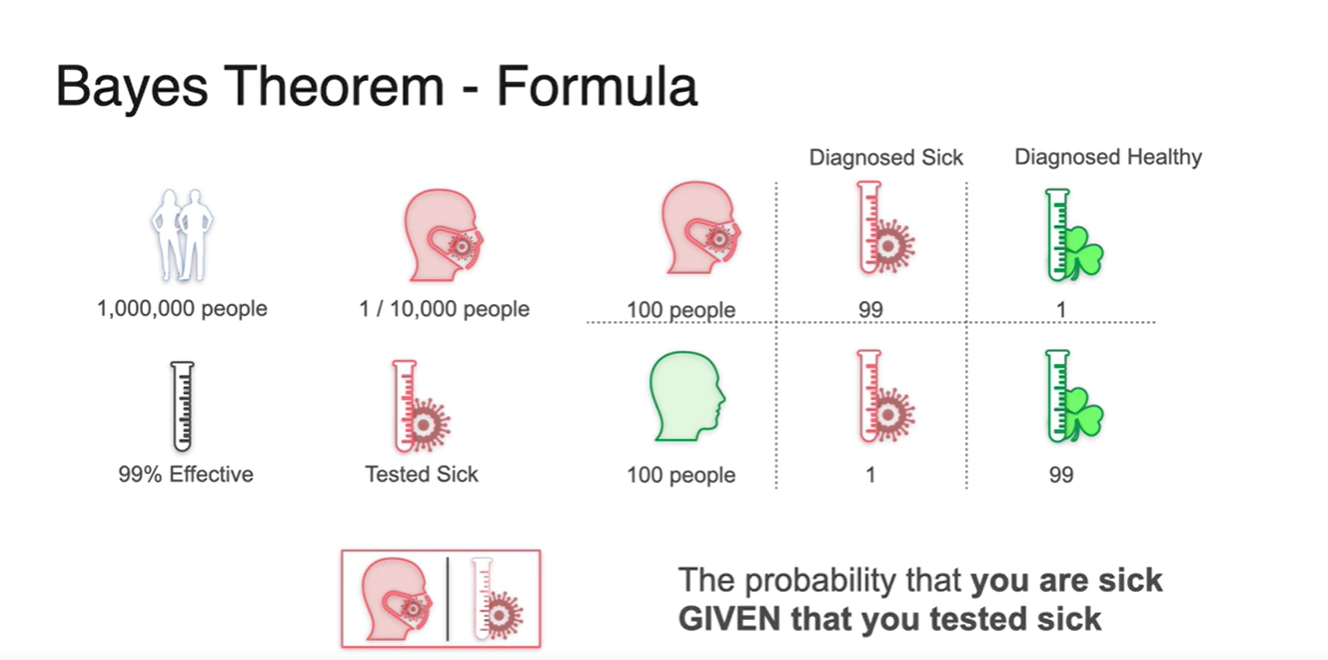
• 자, 그럼 이제 양성 반응 테스트를 한 사람들 중 실제로 아픈 사람일 확률을 구해보자.

  • 알고 있는 정보는 테스트기의 정확도와 병에 걸릴 수 있는 사람의 확률 뿐이다.

• 1/10,000의 확률로 병에 걸릴 수 있다는 것과 테스트기의 정확도가 99%라는 정보는 어떤 결과를 유도해낼까?

  • $P(sick) = 0.01\%$ : 전체 사람들 중 아픈 사람일 확률

  • $P(not \; sick) = 99.99\%$ : 전체 사람들 중 건강한 사람일 확률

  • $P(diagnosed \; sick \; | \; sick) = 99\%$ : 실제로 아픈 사람이 아프다고 진단 받을 확률

  • $P(diagnosed \; sick \; | \; not \; sick) = 1\%$ : 실제로는 건강한 사람이 아프다고 진단 받을 확률

    • 이렇게 총 4가지 확률을 유도해낼 수 있다.

• $A$ 사건이 실제로 아픈 사람을 나타내고 $B$ 사건이 아프다고 진단 받을 확률을 나타낸다고 하자.

  • $P(A|B) = \displaystyle \frac{P(A \cap B)}{P(B)}$ : Conditional Probability를 통해 사건을 전개해 보면 다음과 같다.

    • $P(A|B) = \displaystyle \frac{P(sick \; and \; diagnosed \; sick)}{P(diagnosed \; sick)}$

• 우리가 알고 있는 정보는 왼쪽의 4가지 정보 뿐이며. 오른쪽의 조건부 확률을 계산하기 위해서는 $P(sick \; and \; diagnosed \; sick)$과 $P(diagnosed \; sick)$을 알아야 한다.

  • 두 확률 값을 구하기 위해 Bayes Theorm이 도움이 될 것이다.

• $P(sick \; and \; diagnosed \; sick)$을 조건부 확률의 정의로 전개하면 다음과 같다.

  • $P(sick \; and \; diagnosed \; sick) = P(sick) * P(diagnosed \; sick \; | \; sick)$이다.

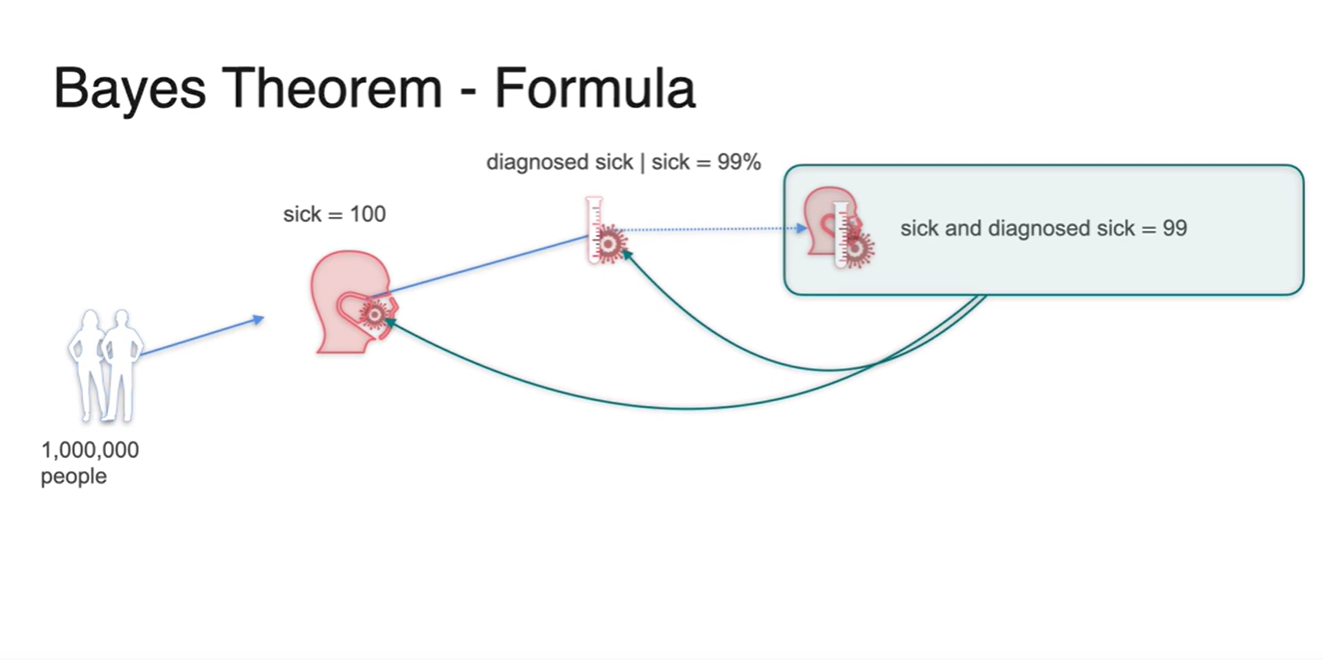
• 모든 경우의 수를 tree로 놓고 보았을 때, 위 경우는 아픈 사람이자 병을 진단 받을 확률이므로 아래와 같은 한 가지로 뻗어 나감을 알 수 있다.

  • {1,000,000명의 사람 * 0.01 = 100명} * {아픈 사람들 중 실제로 아픈 사람일 확률(테스트기의 정확도) 0.99}를 곱해서 얻어진 결과는 99명이다.

• 그러면 $P(diagnosed \; sick)$은 어떻게 구할까?

  • 아까 구했던 $P(sick \; and \; diagnosed \; sick)$는 조건부 확률에 의해 두 확률의 곱으로 나뉘어 전체 확률의 분자로 들어갔다.

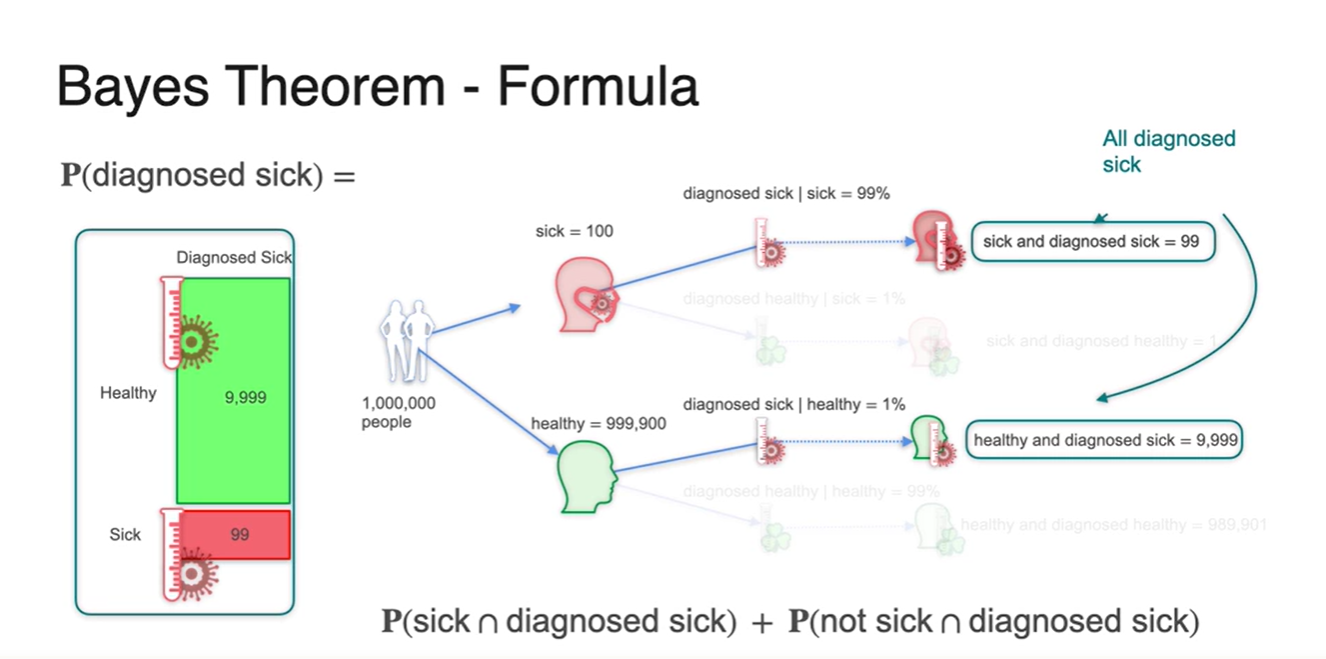
• 아프다고 진단 받은 사람의 경우의 수를 둘로 쪼개보면 {실제로 아픈 사람일 경우}와 {실제로는 건강한 사람일 경우}가 있다.

  • 이 두 확률의 합이 전체 sample space인 {아픈 사람이라고 진단 받을 확률}이다.

    • 기호로는 $P(sick \cap diagnosed \; sick) + P(not \; sick \cap diagnosed \; sick)$이라 표현한다.

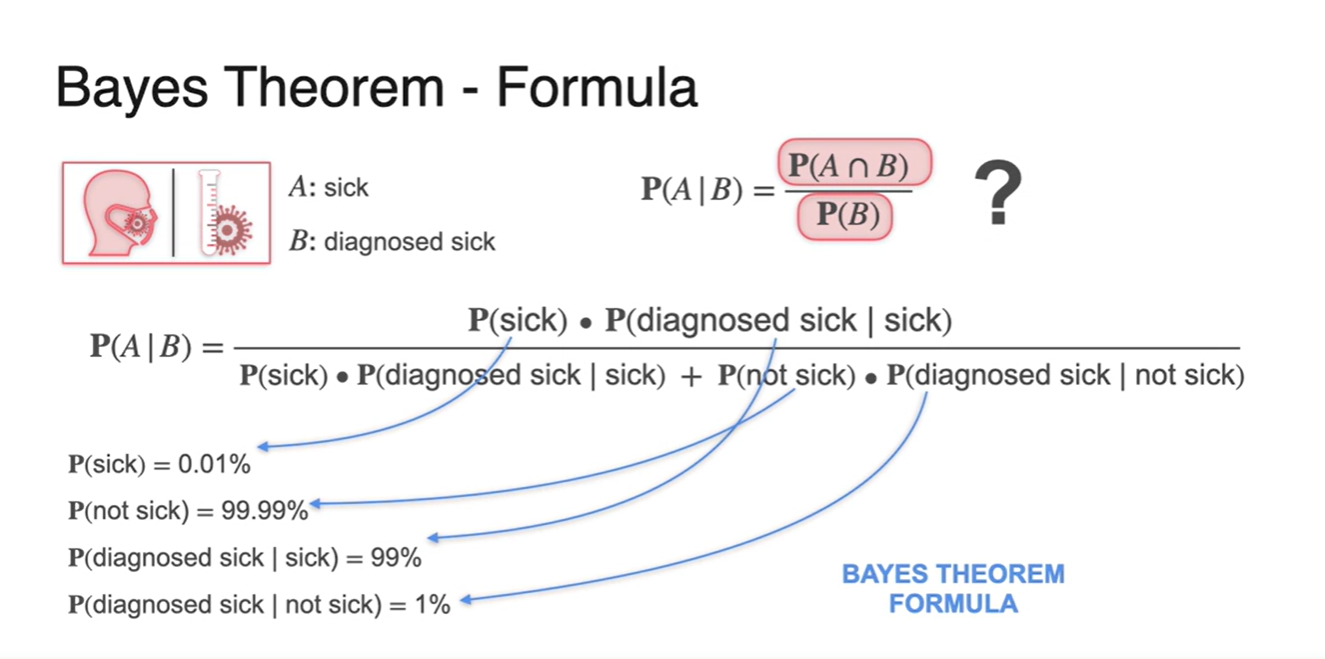
• 아래 식을 $A$와 $B$ 두 사건으로 정리하면 다음과 같다.

  • $P(A|B) = \displaystyle \frac{P(A) * P(B | A)}{P(A \cap B) + P(A' \cap B)} = \frac{P(A) * P(B | A)}{P(B)}$

• 우리가 구하고자 했던 $P(sick \; | \; diagnosed \; sick)$의 확률은 Bayse Theorm을 사용함으로써 우리가 알고 있는 확률들의 값으로 표현 가능해진다.

  • 각 확률들을 매칭한 결과가 다음 그림과 같다.

• 조금 더 수식적으로 정리하면 아래와 같다.

  • $P(A|B) = \displaystyle \frac{P(A) * P(B|A)}{P(A) * P(B|A) + P(A') * P(B|A')}$

• 모든 확률 값을 대입하여 찾고자 하는 확률을 구한다면, 0.0098로 아까 전에 구했던 답과 정확하게 일치한다.

  • $P(A|B) = \displaystyle \frac{0.0001 \times 0.99}{(0.0001 \times 0.99) + (0.9999 \times 0.01)} = 0.0098$

Bayes Theorem - Spam example

• Spam example을 통해 Bayes Theorem을 정리해보자.

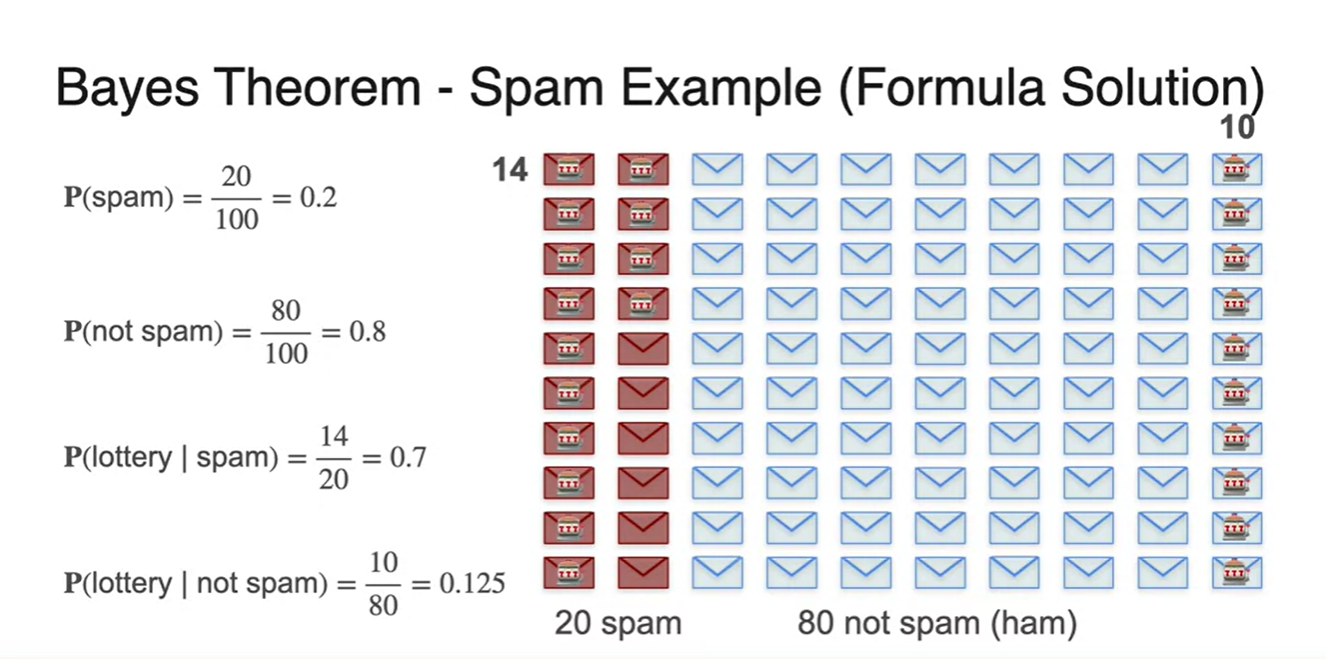
  • 예를 들어, 100개의 메일 중에서 spam 메일을 받을 확률이 $\displaystyle \frac{20}{100} = 0.2$라고 가정 해보자.

• lottery 단어가 들어있는 메일이 실제로 spam 메일일 확률은 얼마일까?

  • 기호로 표기하면 $P(spam \; | \; lottery)$를 찾고자 하는 것이다.

• Conditional probability의 공식은 $P(A|B) = \displaystyle \frac{P(A \cap B)}{P(B)}$로 정리할 수 있다.

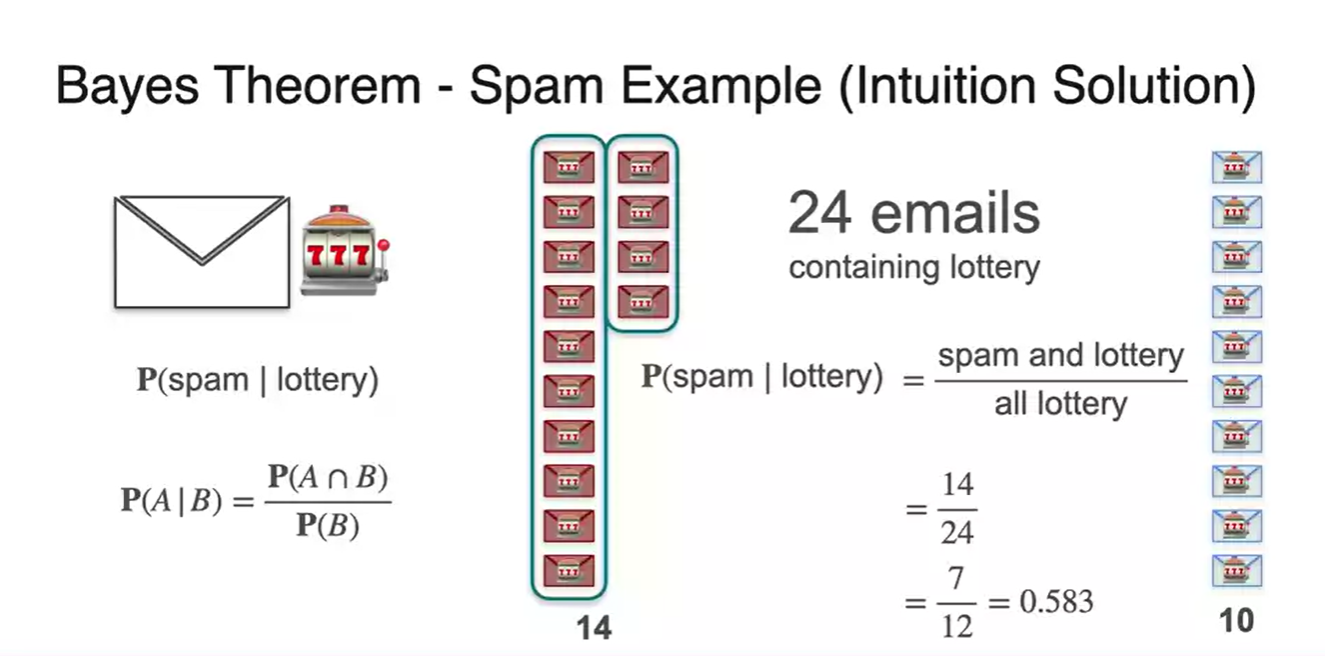
  • 다시 말해, lottery 단어가 들어있는 메일들 중 사실상 spam 메일인 확률이므로 교집합 경우의 수를 고려해야 한다.

    • $P(spam \; | \; lottery) = \displaystyle \frac{spam \; and \; lottery}{all \; lottery}$

  • 즉, 24개의 "lottery"가 들어있는 메일 중에서 14개의 메일이 실제 spam 메일이기 때문에 우리가 판별하고자 하는 task를 수행하는 모델이 뽑아낼 logit이라 보면 된다.

• $A$ 사건이 spam 메일인 사건, $B$ 사건이 "lottery"가 들어있는 메일에 대한 사건일 때 우리가 알고 있는 확률들로 이를 정리해보자.

  • 사전 확률인 $P(spam)$에 대한 확률
  • lottery가 있다고 판명된 관측 결과 확률 $P(lottery \; | \; spam)$
  • lottery가 없다고 판명된 관측 결과 확률 $P(lottery \; | \; not \; spam)$

• 각 확률값을 계산해보면 아래와 같이 계산된다.

  • $P(spam) = \displaystyle \frac{20}{100} = 0.2$
  • $P(not \; spam) = \displaystyle \frac{80}{100} = 0.8$
  • $P(lottery \; | \; spam) = \displaystyle \frac{14}{20} = 0.7$
  • $P(lottery \; | \; not \; spam) = \displaystyle \frac{10}{80} = 0.125$

• 따라서 Bayes theorem으로 사후 확률을 계산해보면 아래와 같이 $0.583$의 확률로

  처음 구했던 $\displaystyle \frac{14}{24}$의 확률과 똑같은 값이 계산된다.

  • $P(spam \; | \; lottery) = \displaystyle \frac{0.2 \times 0.7}{(0.2 \times 0.7) + (0.8 \times 0.125)} = 0.583$

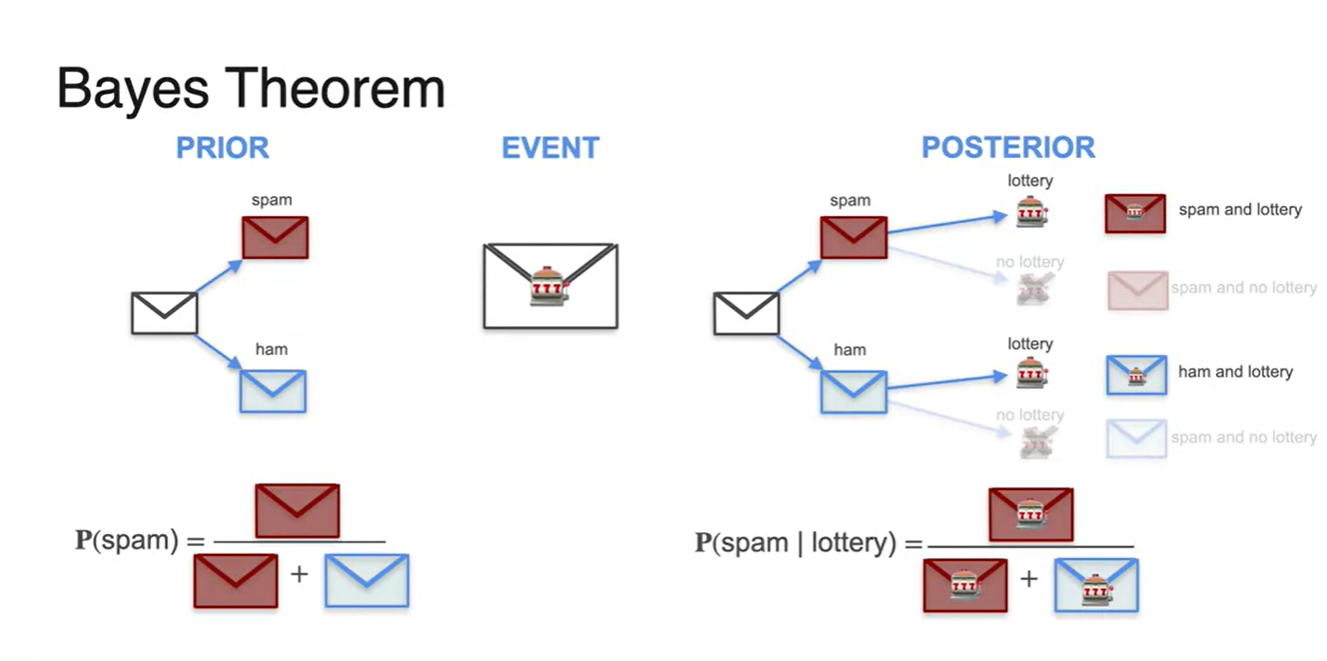
Bayes Theorem - Prior and Posterior

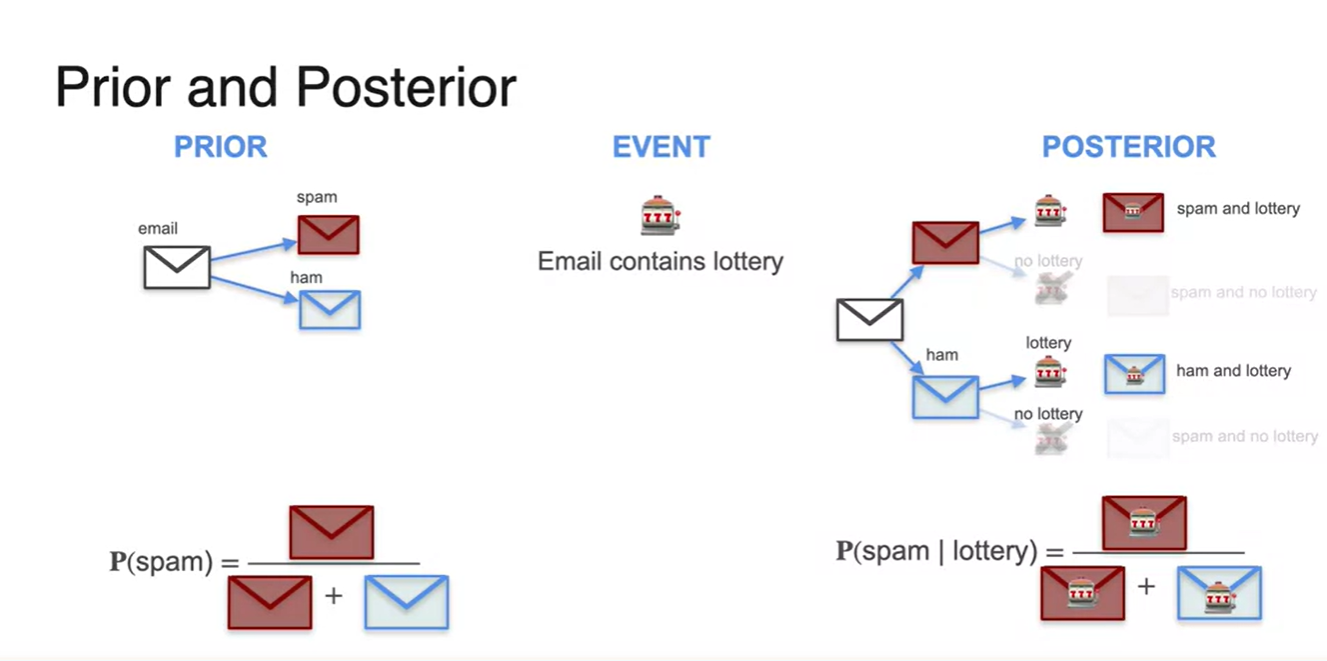
• Prior probability는 $P(A)$, 특정 Event는 $E$, Posterior probability는 $P(A|E)$이다.

  • $E$라는 Event가 주어졌을 때(given), $A$라는 사건이 일어날 확률을 뜻한다.

• Spam 메일을 받을 확률인 Prior probability는 {spam 메일을 받는 경우의 수}를 {spam + not spam}으로 나눈 값으로 계산된다.

  • 마찬가지로 "lottery"가 들어있는 메일들 중 실제로는 spam 메일일 Posterior probability를 구하고자 한다면, {Spam $\cap$ lottery} 경우의 수를 {lottery가 들어있다고 주장한 메일의 수}로 나누면 된다.

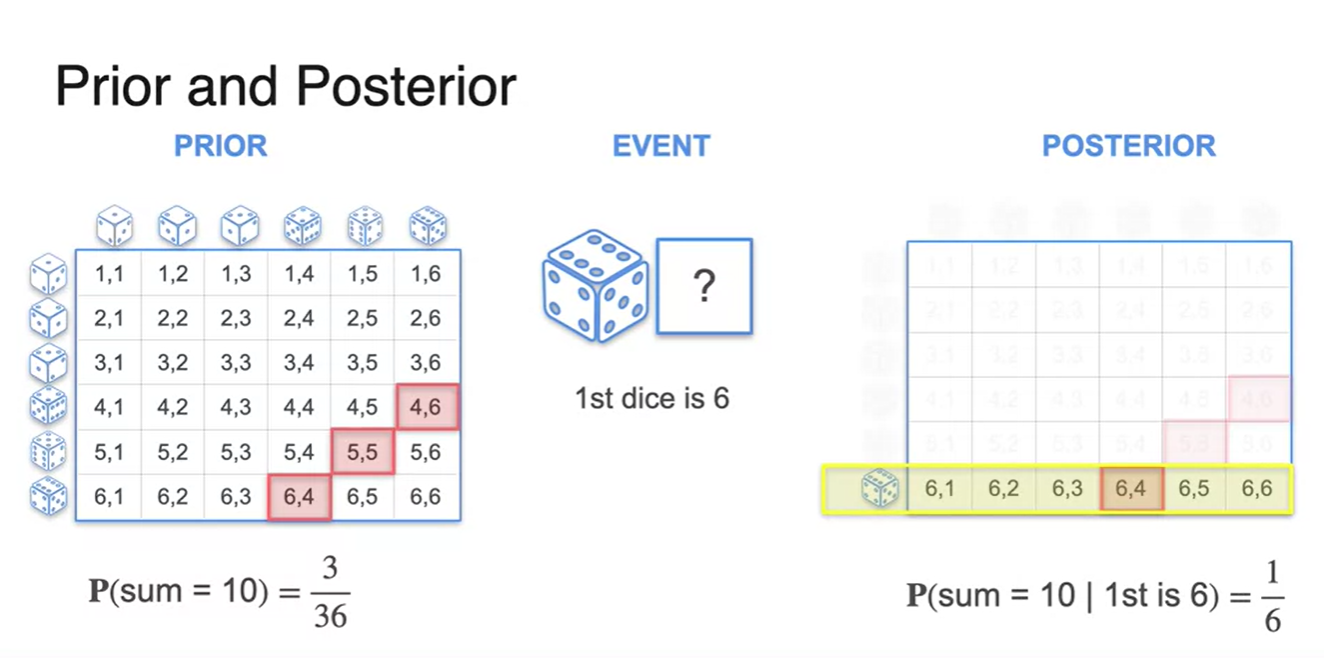
• 주사위를 굴렸을 때의 결과도 마찬가지다.

  • 두 번의 주사위를 굴리고자 할 때, 합쳐서 10이 나올 확률은 사전 확률, 첫 번째 시행에서 6이 나올 확률은 하나의 특정한 사건 event다.

    • 강의에서 말하기를 우리가 다른 분포에서 살았기 때문에, 어떤 새로운 사건이 주어졌을 때 기존 사건이 change 된다고 본다고 한다.

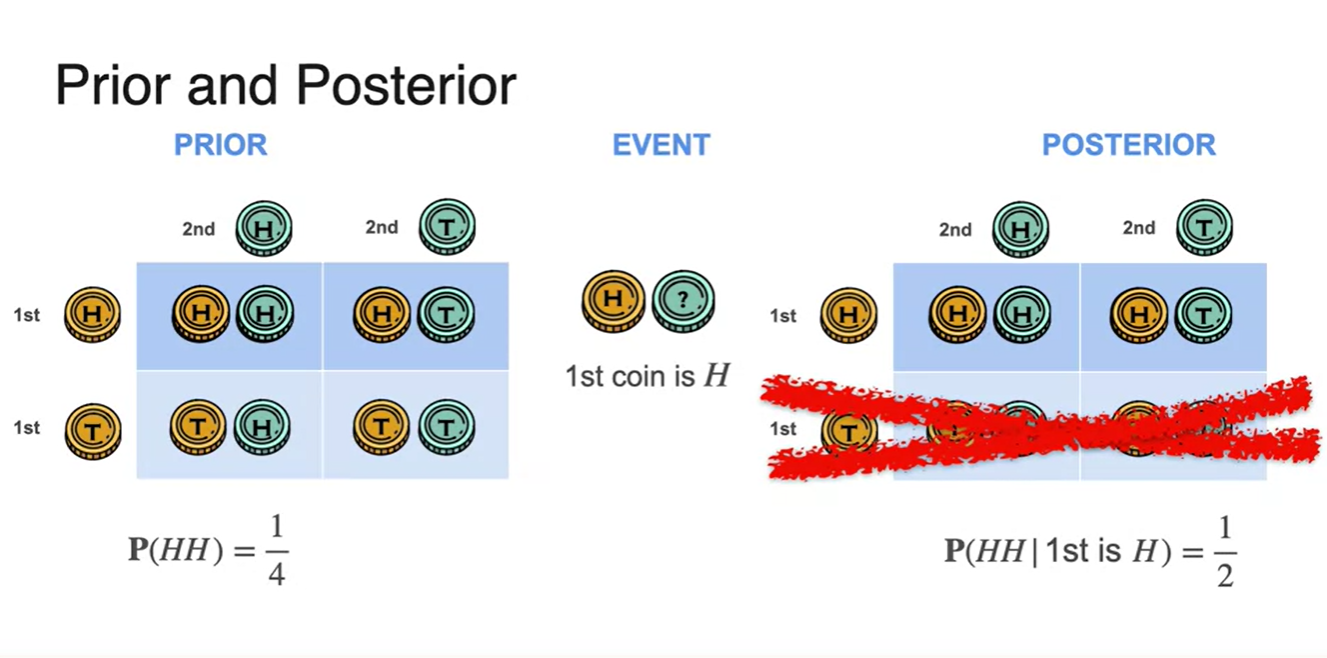
• 동전 두 번 던지는 예제에서도 마찬가지이다.

  • $P(HH)$ Head가 두 번 나올 확률은 $\displaystyle \frac{1}{4}$인 상황에서 첫 번째 시행이 Head였다고 한다면 오른쪽 표의 아래 두 경우의 수는 고려 대상이 아니다.

    • 즉, 첫 시행의 결과로 인해 기존 확률의 분포가 바뀐 것이라 생각하면 된다.

Bayes Theorem - The Naive Bayes Model

• 두 event가 모두 발생했을 때의 경우는 어떨까?

  • 기존에는 "lottery" 단어만 들어간 경우의 spam 메일만을 판별했다면 이번에는 "winning"이라는 단어까지 들어간 경우를 고려해보자.

    • $P(spam \; | \; lottery)$와 $P(spam \; | \; winning)$을 이용해 두 교차점 확률을 어떻게 구하는 게 좋을까?

• "lottery"와 "winning"이라는 단어가 모두 들어간 spam메일의 확룔을 구하고자 Bayes Theroem을 이용해 전개해보았다.

  • $P(spam \; | \; lottery \& winning) = \displaystyle \frac{P(spam) * P(lottery \& winning \; | \; spam)}{P(lottery \& winning)}$로 전개할 수 있다.

    • $P(lottery \& winning) = P(spam) * P(lottery \& winning \; | \; spam) + P(ham) * P(lottery \& winning \; | \; ham)$다.

• Event가 100개 가량으로 더욱 많아진다면 어떨까?

  • 핵심은 $P(w_1, ... w_100 \; | \; spam)$를 구하는 일이지만, 0과 1사이의 확률을 여러 번 곱하면 값이 $0$에 가까워지므로 2개의 사건만 우선 다뤄보도록 하자.

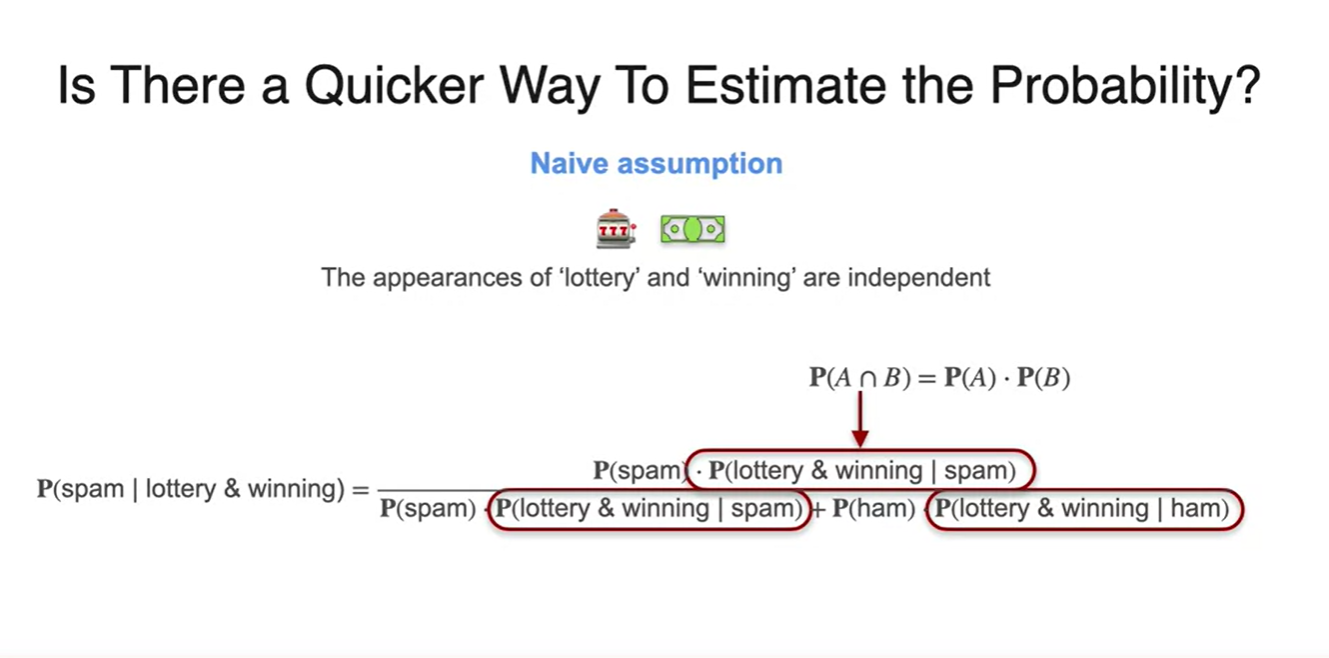
• 계산을 빠르고 효율적으로 해내기 위해 Naive한 가정을 세워보자.

  • 조건부 확률을 기준으로, 두 사건이 independent하다면 $P(A \cap B) = P(A) * P(B)$ 공식으로 전개가 가능하다.

    • $P(lottery \& winning \; | \; spam)$를 독립 사건으로 가정하여 다시 풀어써보자.

• 두 사건을 독립 사건으로 가정하면 아래와 같이 수식이 다시 전개된다.

  • 즉, 우리가 구할 수 있는 $P(lottery \; | \; spam)$, $P(winning \; | \; spam)$, $P(lottery \; | \; ham)$, $P(winning \; | \; ham)$ 확률들을 써먹을 수 있게 됐다.

• 100단어를 예측해야하는 task에서도 마찬가지다.

  • 모든 사건을 독립적이라 가정한다면 spam 메일 중 각 단어가 나온 확률을 모두 곱하여 전체 문장의 추정 확률을 계산할 수 있는 것이다.

• "lottery" 단어가 포함된 메일을 기준으로 아래 네 가지 확률을 각각 계산해보자.

  • $P(spam) = \displaystyle \frac{20}{100} = 0.2$

  • $P(ham) = \displaystyle \frac{80}{100} = 0.8$

  • $P(lottery \; | \; spam) = \displaystyle \frac{14}{20} = 0.7$

  • $P(lottery \; | \; ham) = \displaystyle \frac{10}{80} = 0.125$

• "winning" 단어가 포함된 메일을 기준으로 두 확률을 추가로 계산해보자.

  • $P(winning \; | \; spam) = \displaystyle \frac{15}{20} = 0.75$

  • $P(winning \; | \; ham) = \displaystyle \frac{8}{80} = 0.1$

• 사후 확률인 $P(spam \; | \; lottery \& winning)$은 아래의 수식을 거쳐 계산된다.

  • 관측 결과인 $P(lottery \; | \; spam)$나 $P(winning \; | \; spam)$ 등을 이용하여 전체 확률을 계산할 수 있게 된다.

Probability in Machine Learning

-Bayes Theorem은 Maching Learning의 핵심 개념이다.

• Prior prob, Event Posterior를 가지고 likelihood를 modeling하는 것이 머신러닝이다.

  • 위의 예제에서는 $P(spam \; | \; lottery)$가 likelihood다.

• Image recognition problem에서의 기대 확률은 $P(cat \; | \; image)$다.

  • Image는 여러 픽셀들의 경우의 수로 이루어져 있으므로 $P(cat \; | \; pixel_1, pixel_2, ... , pixel_n)$로 전개할 수 있다.

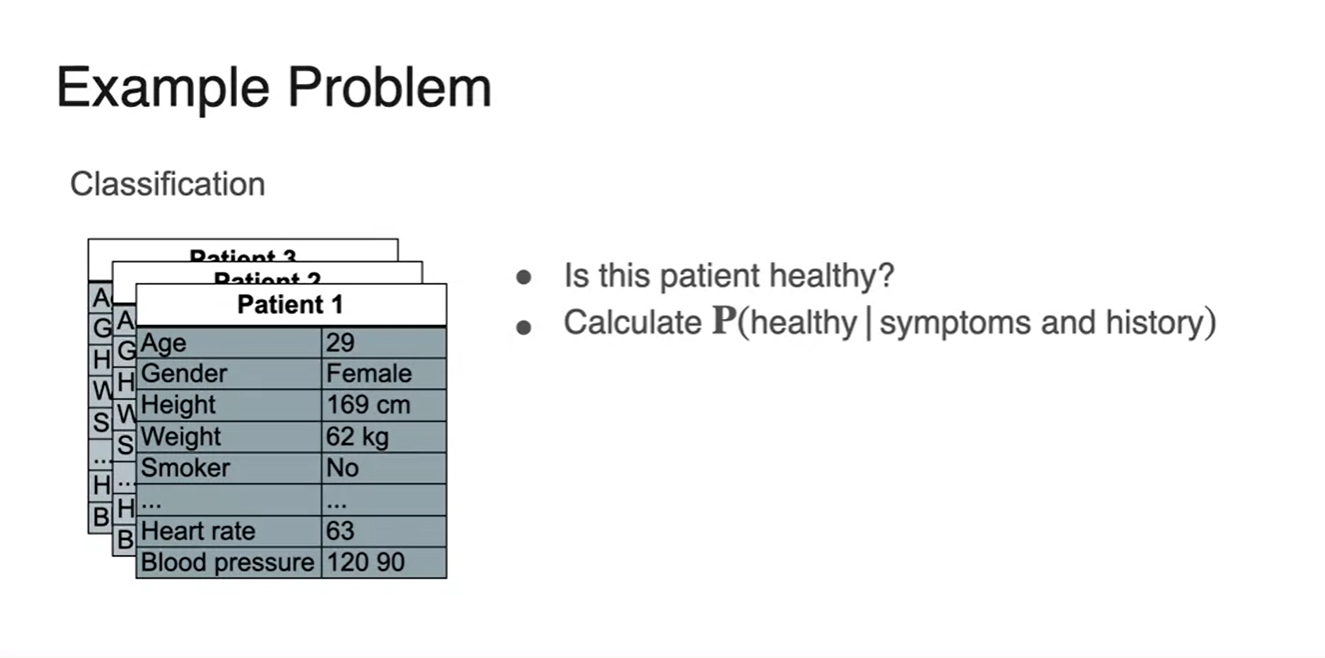
• Classification Disease problem에서의 기대 확률은 $P(healthy \; | \; symptoms \; and \; history)$이다.

  • 이들의 symptoms 경우의 수와 history 경우의 수를 사건으로 놓는다.

• Sentimental analysis에서의 기대 확률은 $P(happy \; | \; words \; in \; the \; sentence)$다.

  • 각 문장의 probability 곱을 통해 happy인지 unhappy인지 예측하는 것이다.

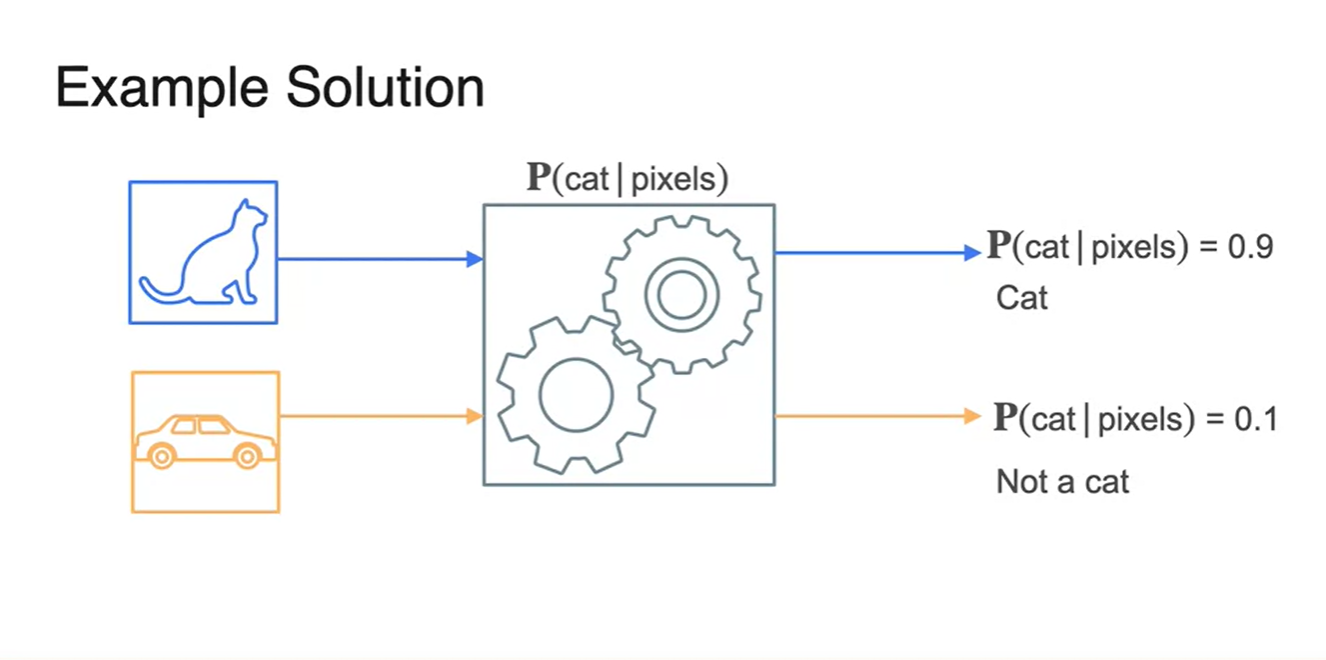
• 만약 cat 사진을 판별하는 모델을 모델링 했다고 가정해보자.

  • 그렇다면 cat 사진이 들어왔을 때에는 $P(cat \; | \; pixels) \approx 1$를 기대 확률로 생각한다.

  • 반대로 car 사진이 들어왔을 때에는 $P(cat \; | \; pixels) \approx 1$를 기대 확률로 생각한다.

• Generative model의 task는 image를 human 사진과 아주 유사하게 생성해내는 모델이다.

  • 즉, $P(face \; | \; pixels)$의 기대 확률을 높아지게 만드는 task라 할 수 있다.

Lesson 2 - Probability Distributions

Random Variables

• 동전 던지기 예제로 돌아가보자.

  • Random variable이란 "head가 나타날 횟수"와 같은 변수를 말한다.

    • 기호로는 $X$로 표현한다.

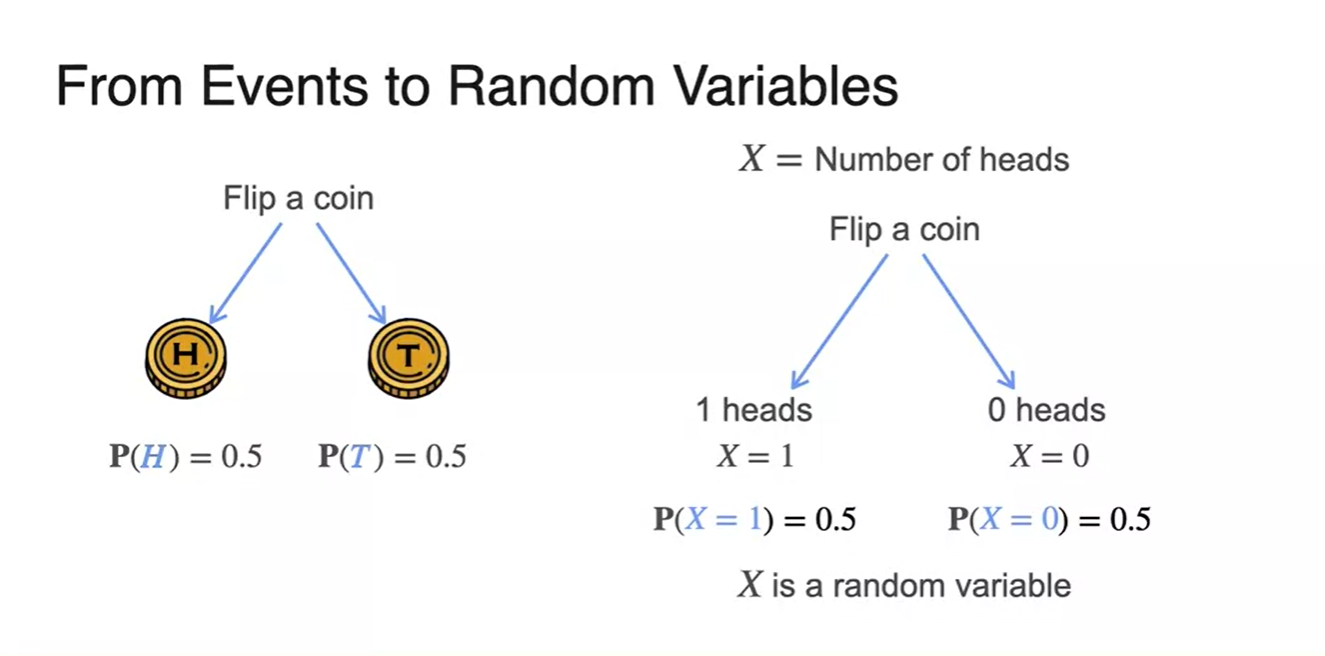
• 10번의 동전을 던졌을 때 $X$개의 head가 나올 확률은 얼마일까?

  • Head가 한 번 나올 확률은 $P(H) = 0.5$이다.

    • 시행 횟수가 10번일 때, 9번일 때, 8번일 때... 1번일 때, 0번일 때의 확률은?

• Possible outcomes는 0~10까지이다.

  • $X=5$일 때의 경우의 수는 사실 한 가지가 아니라 여러 경우일 수 있다.

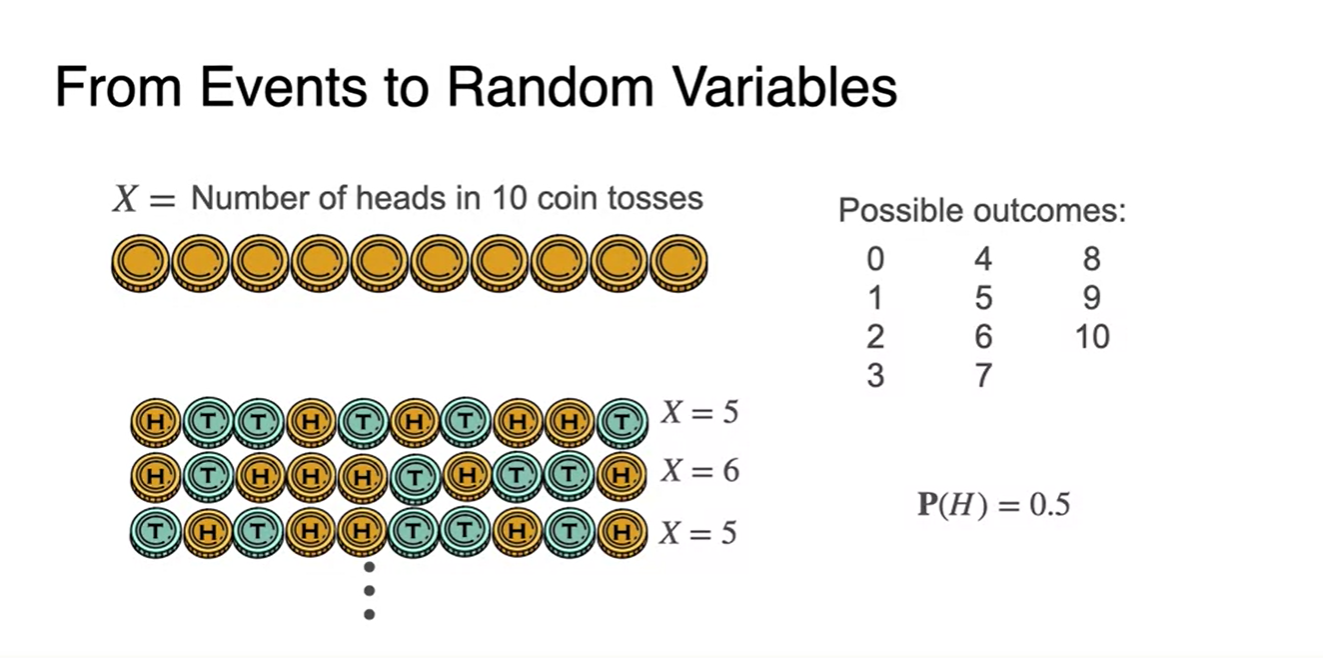
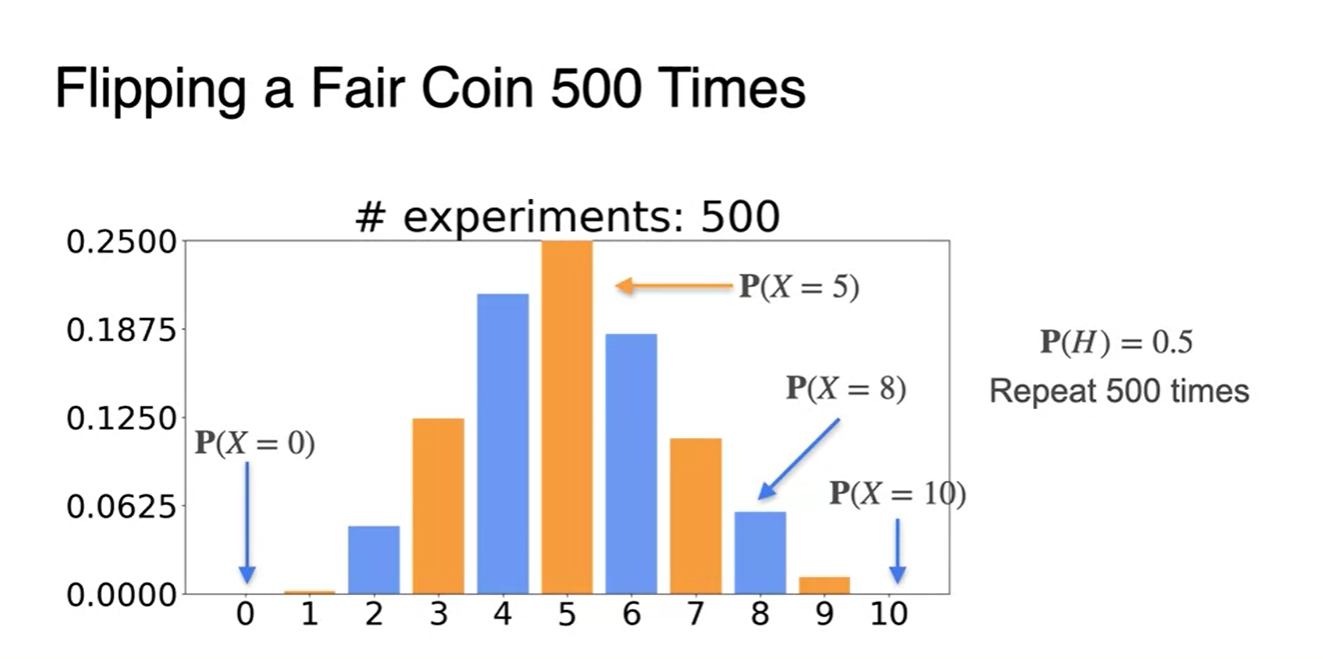
• 500번의 시행으로 각 random variable의 확률을 히스토그램으로 표현한 결과다.

  • $P(X=0)$이나 $P(X=10)$의 확률은 매우 적은 반면, 중앙값인 $P(X=5)$는 매우 확률이 높은 것을 알 수 있다.

• 왜 Random variable을 사용하는 것일까?

  • Random variable은 한 번의 시행에서 모델이 뽑아낼 수 있는 모든 가능한 결과를 나타낸다.

    • $X$는 음수일 수도 있고, float형일 수도 있고 모든 실수가 가능하다.

• 여러 Random variable의 예시를 살펴보자.

  • 시간, 높이, 적재량, 날씨 모든 예시의 확률 변수가 다 가능하다.

• Random variables는 Discrete vs. Continous한 경우로 나뉜다.

  • Discrete한 경우는 countable하고, Continuous는 interval하다.

• Random variable과 Deterministic variable의 차이는 다음과 같다.

  • Deterministic은 $x$가 특정 함수로 mapping되는 경우로, outcome이 정해져있는 상황이다.

  • Random variable은 uncertain outcome을 야기한다.

Probability Distributions (Discrete)

• Discrete한 경우의 Probability Distributions, 확률 분포를 알아보자.

  • $X=0$, $X=1$, $X=2$, $X=3$일 때의 경우의 수를 모두 정리하면 다음과 같다.

    • Multiple option이 가능하다.

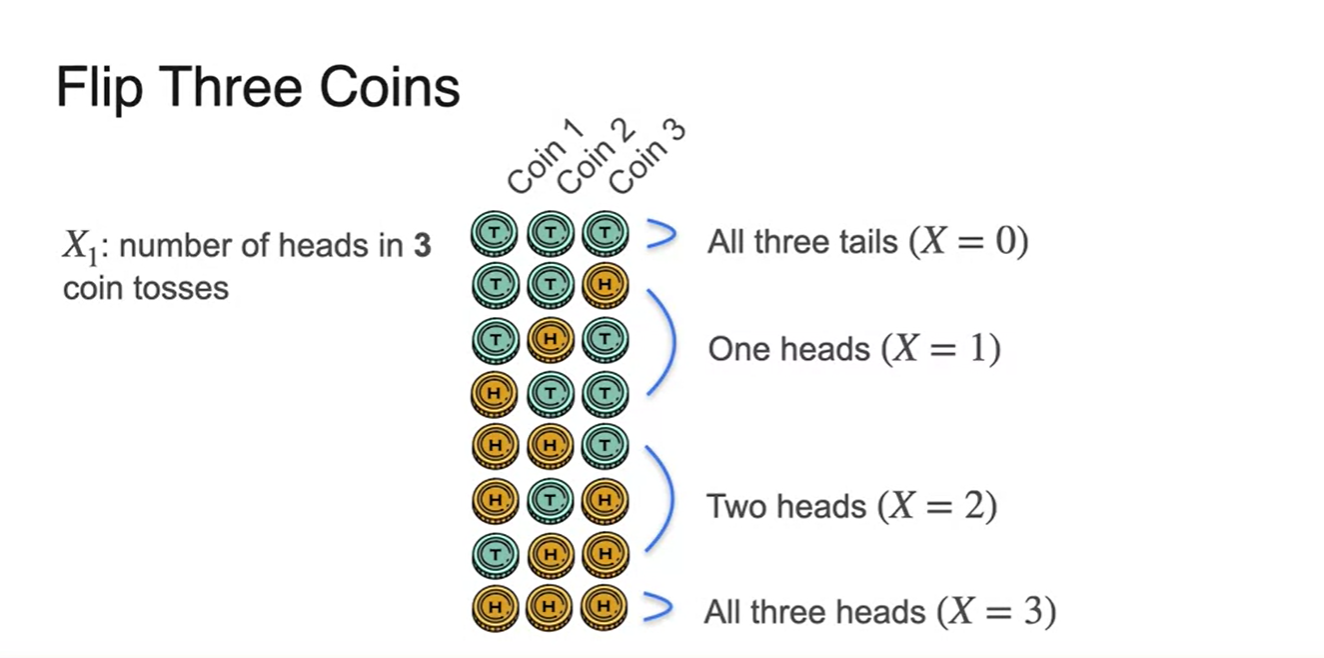
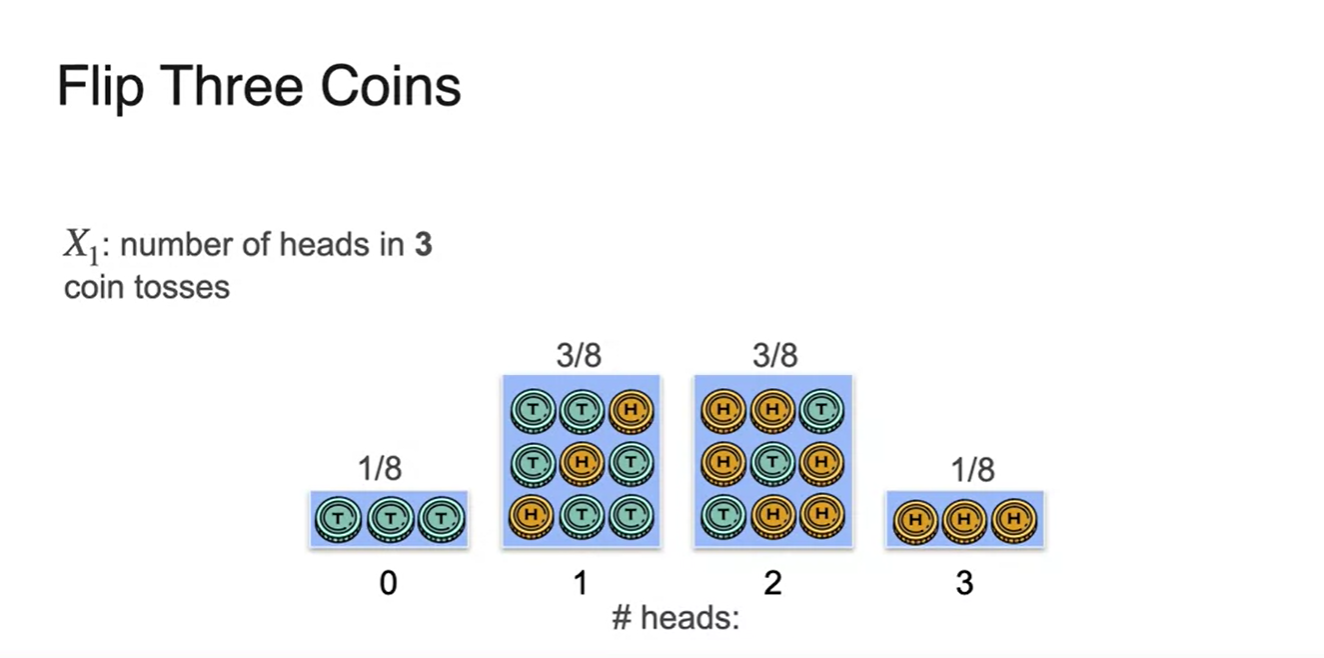
• Normal histogram으로 그려보자.

  • # of heads가 확률 변수가 되어 각 확률의 값을 그래프로 표현하였다.

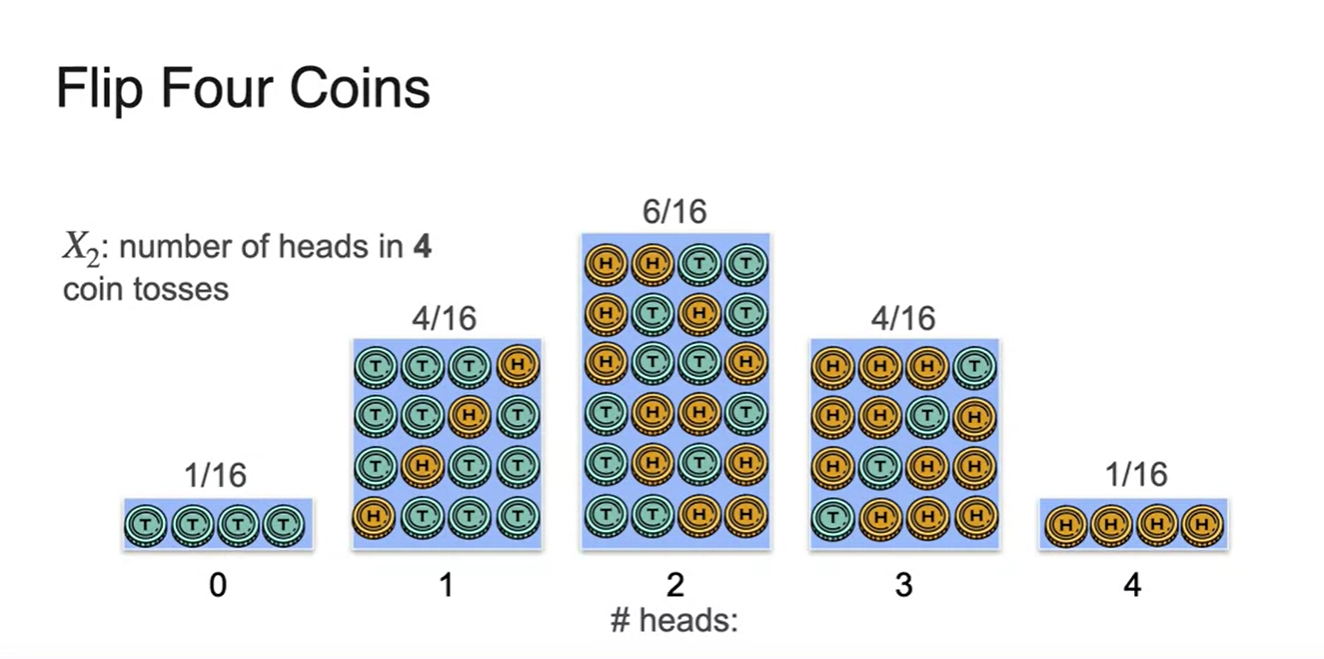
• 4번의 동전 던지기를 했다면 어떨까?

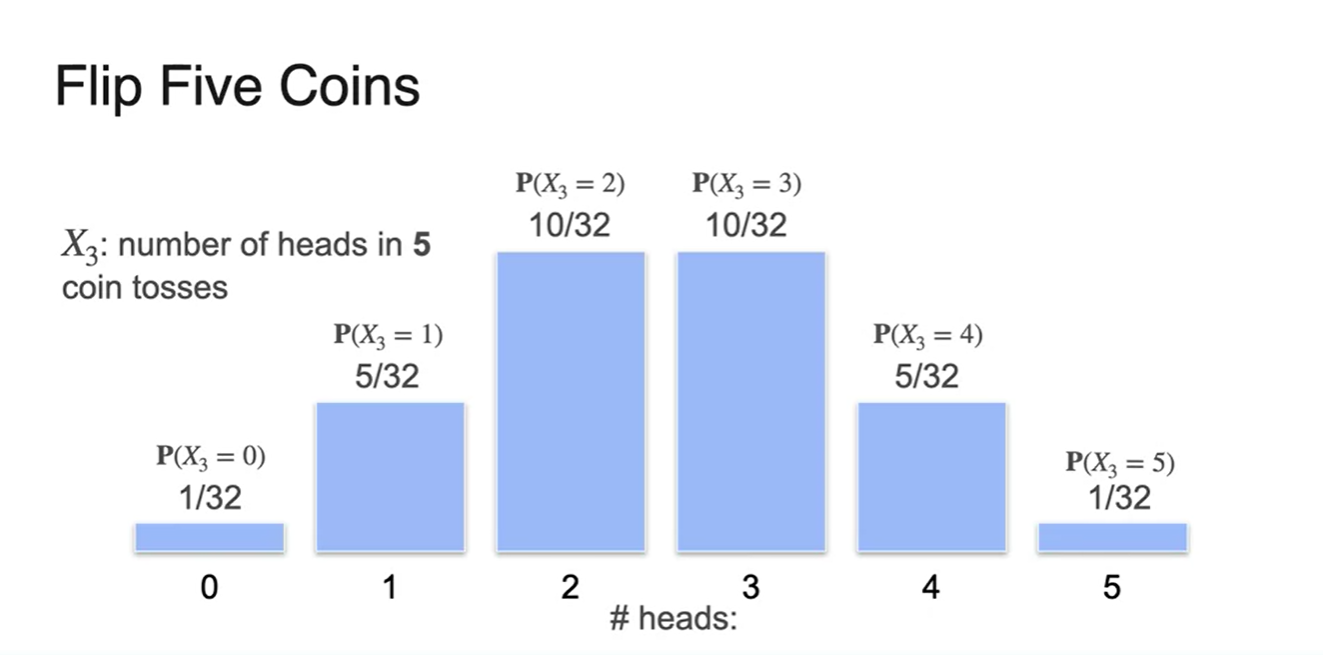
• 5번의 동전 던지기를 한 결과는 다음과 같다.

• Random variable에 따른 확률 분포 함수는 PMF(Probability Mass Function)라 한다.

  • Random variables가 discrete한 경우에 각 확률 또한 특정 값으로 discrete하게 표현되며, 수식은 $p_x(x), \;$ ex. $x=0, 1, 2, 3, 4, 5$로 표현한다.

  • 이 때 모든 확률은 양수($p_x(x) \ge 0$)여야 하며 전체 확률 값을 더했을 때
    ($\displaystyle \sum_{x} p_x(x) = 1$) 1을 만족해야 한다.

• 지금까지 $n$번의 시행으로 얻을 수 있는 확률에 대해 알아보았다.

  • 가능한 모든 경우의 수로부터 만들 수 있는 single model은 뒤에서 다룰 Binomial distribution에 의해 결정될 것이다.

Binomial Distribution

• 5번의 동전 던지기를 통해 2번의 head를 얻을 수 있는 확률은 얼마인가?

  • 아래 두 경우의 수는 엄연히 다른 경우에 해당하지만 확률은 모두 동일하다.

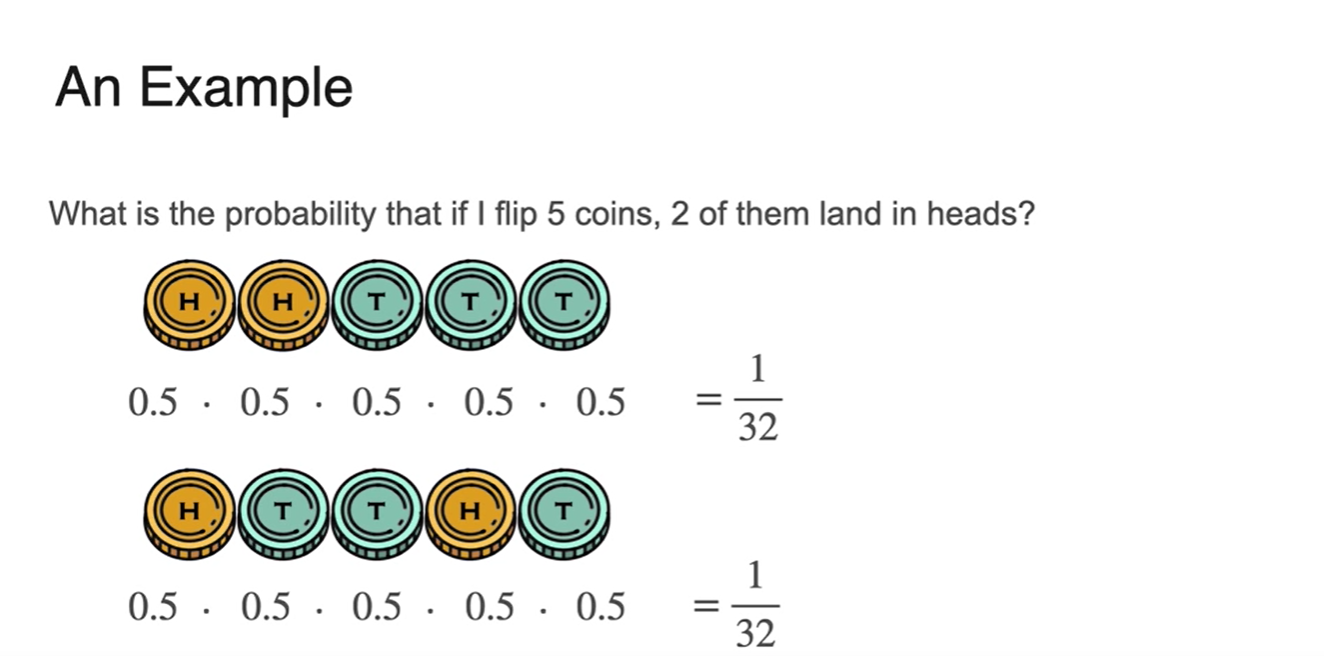
• 가능한 모든 경우의 수를 찾게 되면 모두 10개라는 사실을 알게 된다.

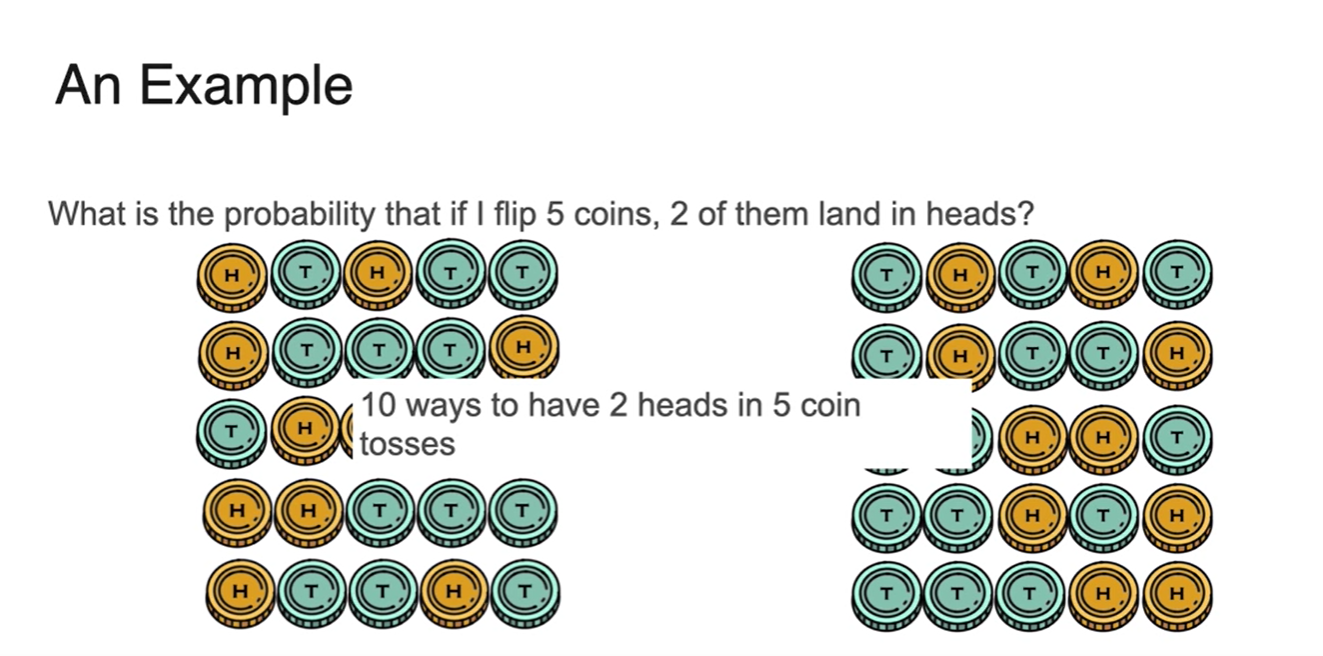
• 이를 수식으로 표현하면 다음과 같다.

  • $10 = \displaystyle \frac{5!}{2! (5-2)!}$

    • n번의 시행을 {H의 개수, T의 개수}로 나눈다.

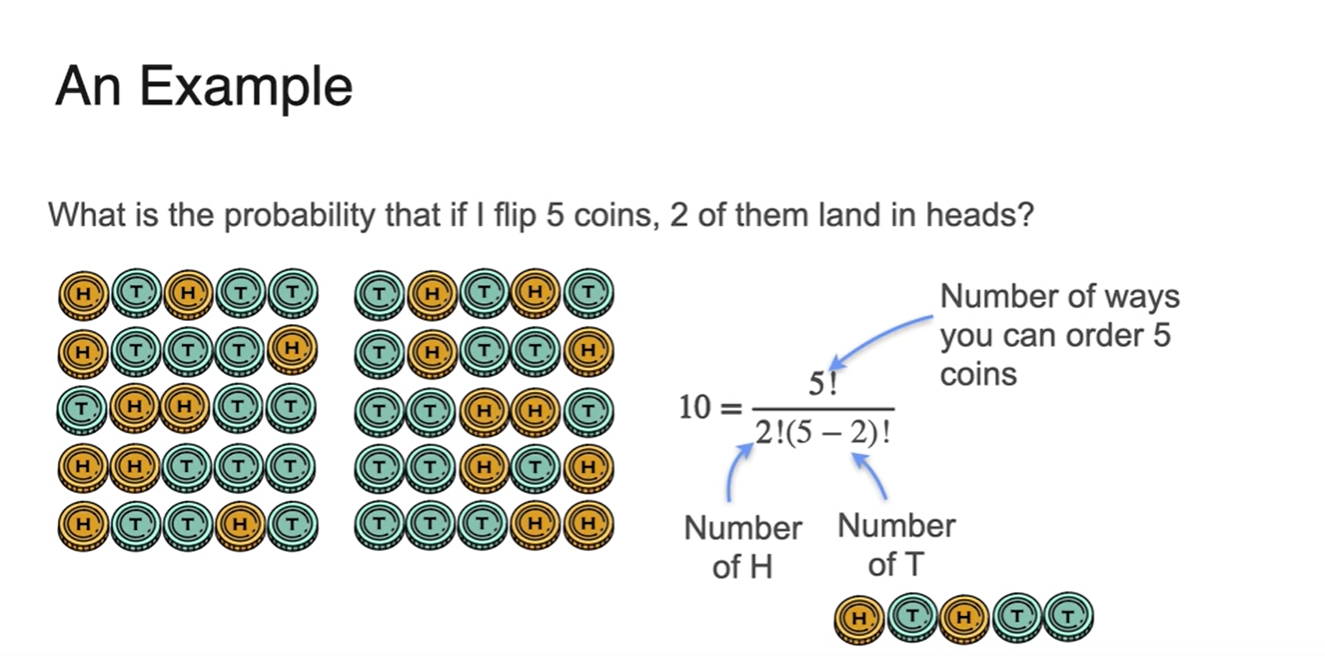
• 이는 $\displaystyle {n \choose k}$로 나타내며 k를 선택하는 것과 그렇지 않은 n-k를 선택하는 경우가 동일하다.

  • 따라서 symmetric한 성질을 가진다.

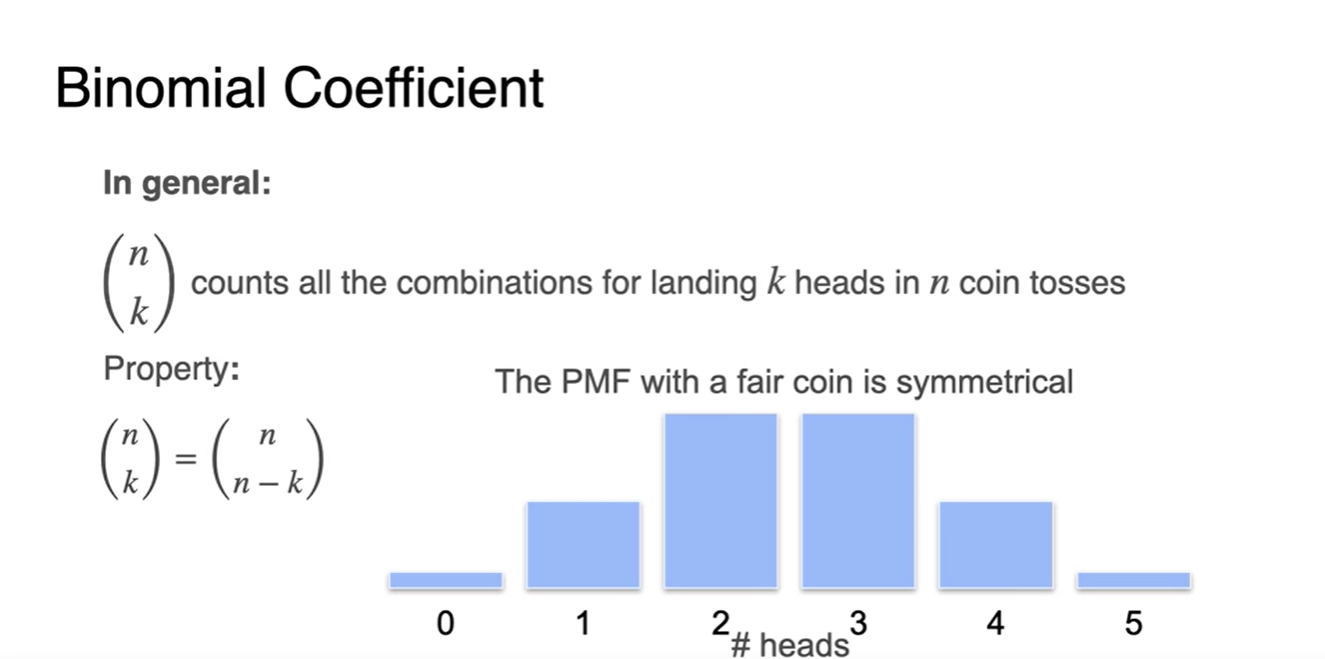
• $P(H) = p$임을 알고 있을 때의 5번의 시행 횟수에 대한 General PMF를 알아보자.

  • $p_x(x) = \displaystyle {5 \choose k} p^x (1-p)^{5-x}$

• 이를 Binomial Distribution이라 하며 기호로는 아래와 같이 쓴다.

  • $X \sim Binomial(5, p)$

• 마치 parameter의 역할을 하는 $n$과 $p$를 고정시켜 분포로 표현해보자.

  • $p=0.5$일 때는 분포의 모양이 symmetric하다.

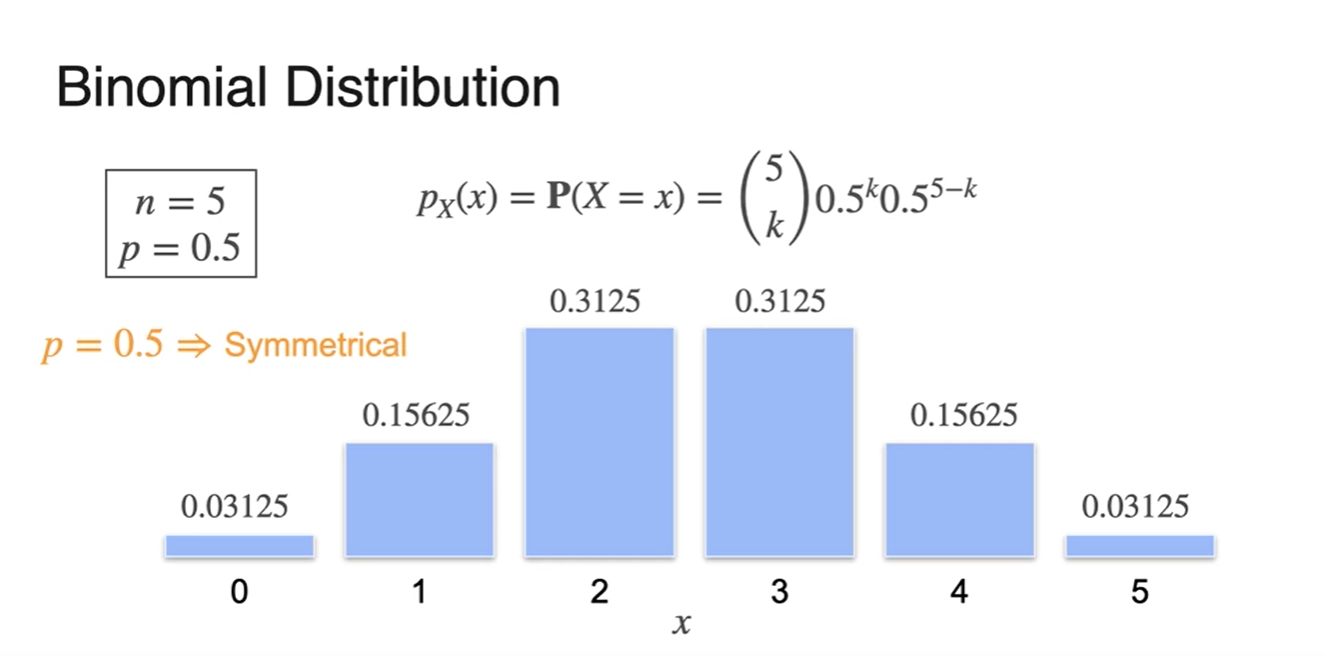
• 만약 Biased coin을 사용한다면 분포는 살짝 달라진다.

  • 더 이상 symmetric하지 않고 살짝 치우친 형태를 띈다.

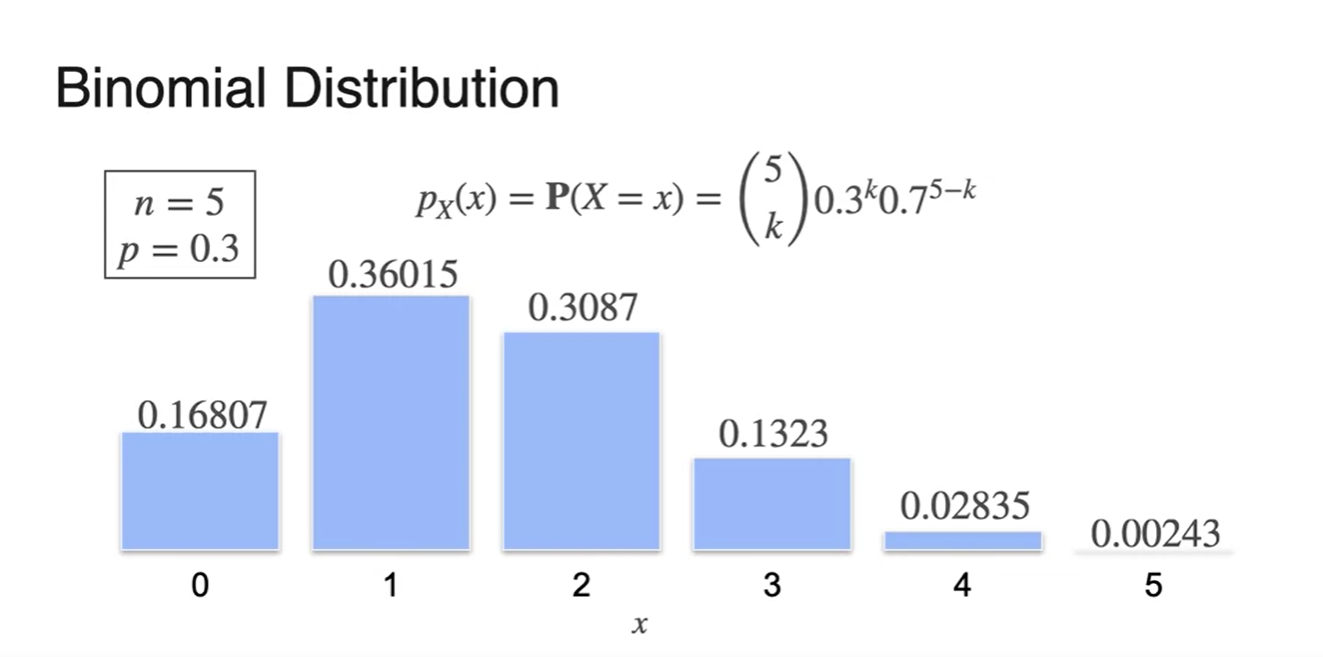
• 일반적으로, $n$번의 시행 횟수에 대한 PMF는 아래와 같이 정의한다.

  • $p_x(x) = {n \choose k} p^x (1-p)^{n-x}$, $x=0, 1, 2, ..., n$

  • $X \sim Binomial(n, p)$

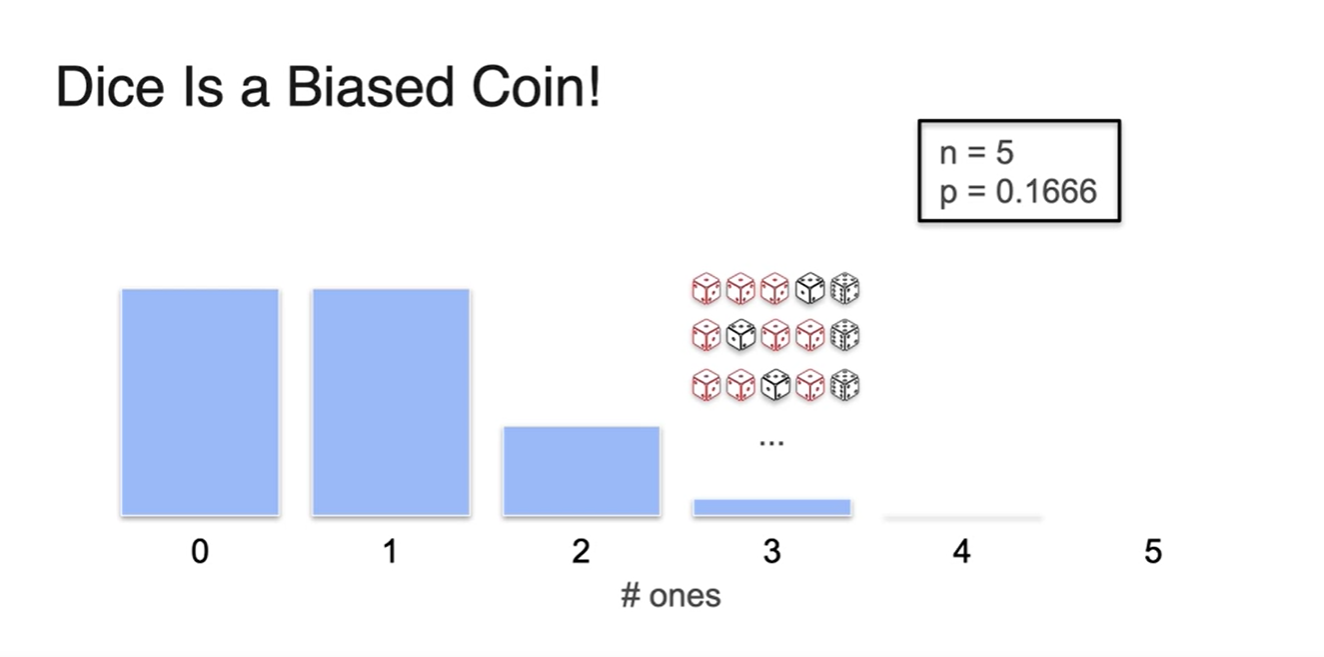
• Quiz. 5번의 주사위를 던져 1이 3번 나올 확률은?

  • $\displaystyle {5 \choose 3} (\frac{1}{6})^3 (\frac{5}{6})^2$

• Dice는 마치 Biased coin과 같다.

  • 가능한 확률 $p$는 $\displaystyle \frac{1}{6}$, 반대 확률 $1-p$는 $\displaystyle \frac{5}{6}$다.

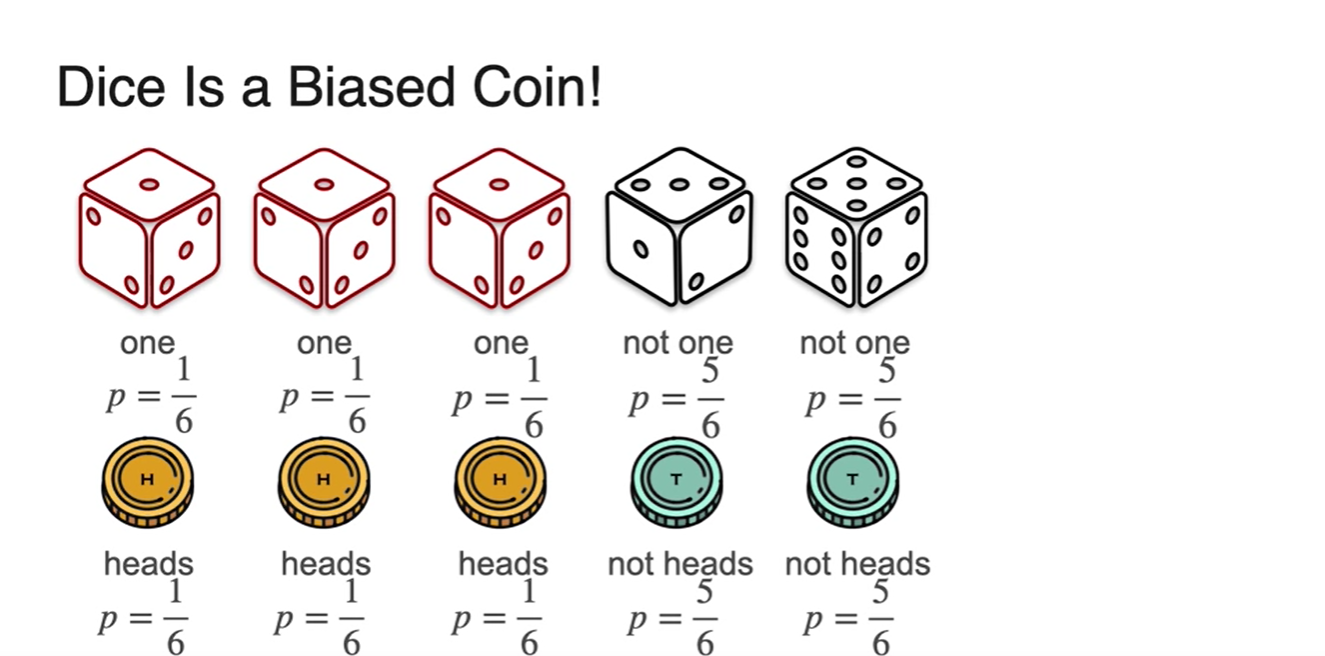
• 위 사건의 Binomial distribution의 함수 모양은 Biased coin histogram과 비슷하다.

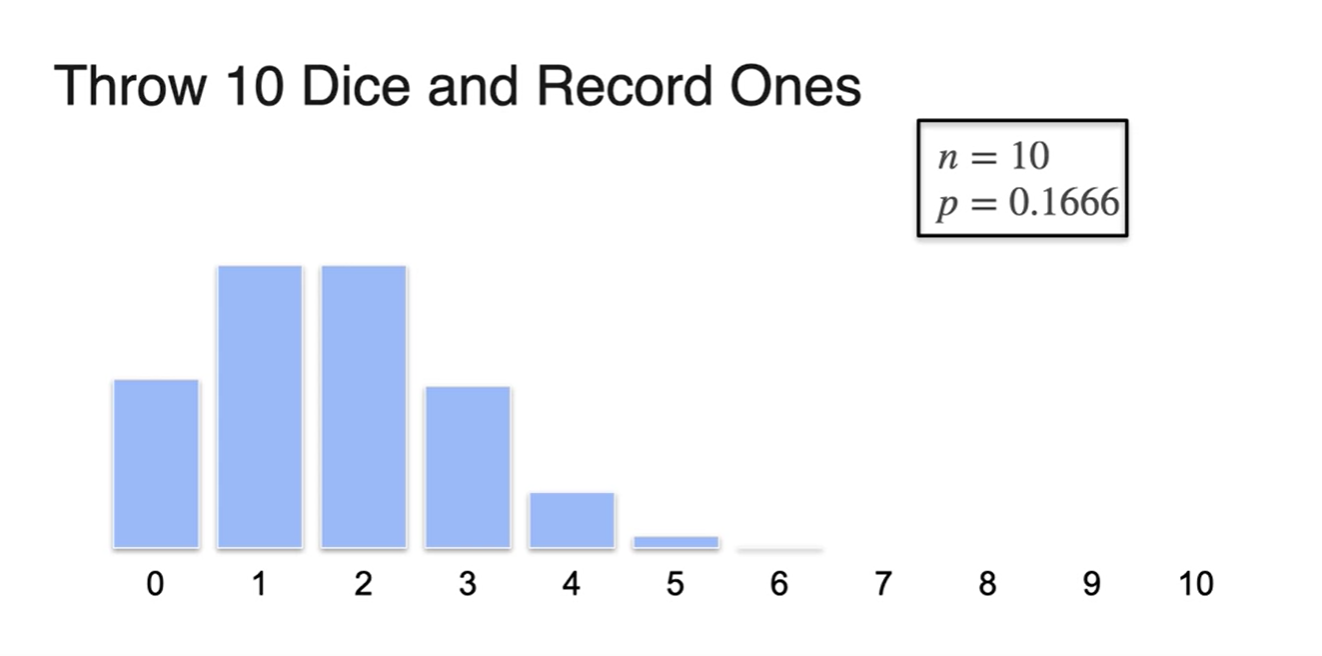
• Quiz. Binomial distraibution의 parameters는 무엇인가?

  • $n=10, p=\displaystyle \frac{1}{6}$가 parameters라고 볼 수 있다.

• 10번의 시행으로 Binomial distribution을 그려보면 아래와 같이 그려진다.

(Optional) Binomial Coefficient

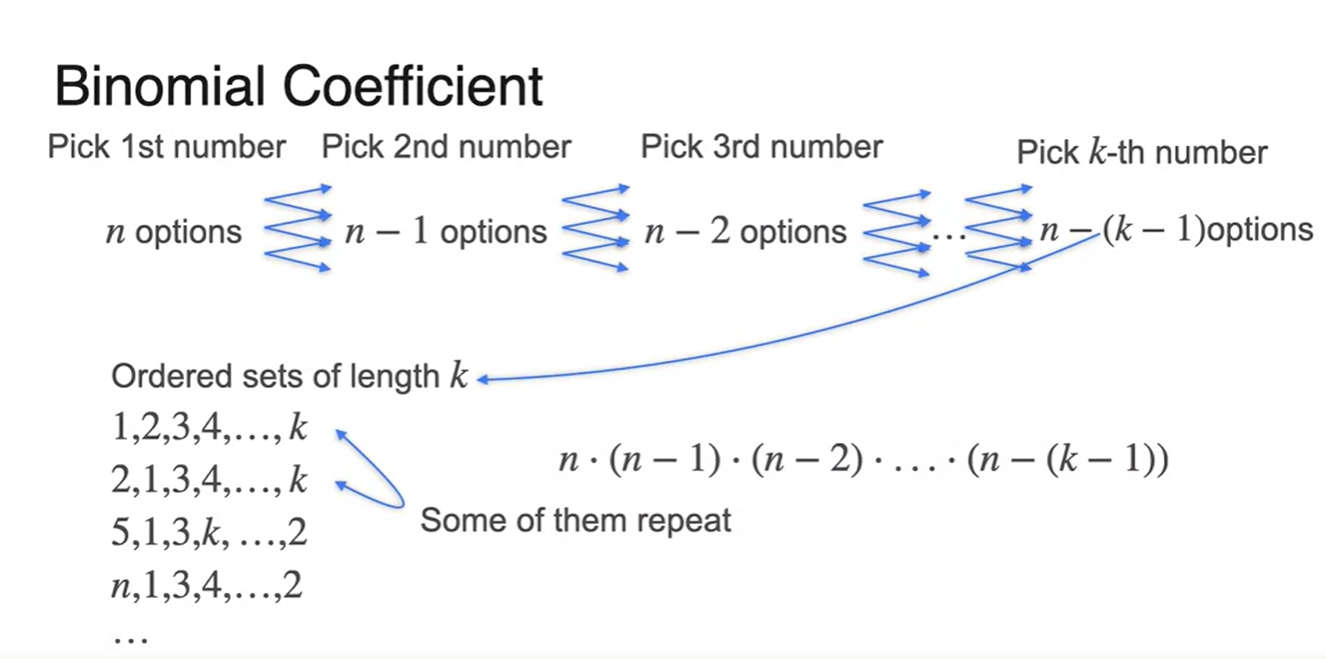
• Binomial Coefficient가 어떻게 유도되는지 알아보자.

  • k번의 시행으로 option이 선택되었을 때, 중복을 고려하지 않는다면 뽑아지는 경우의 수 개수는 $n * (n-1) * (n-2), ... (n-(k-1))$이다.

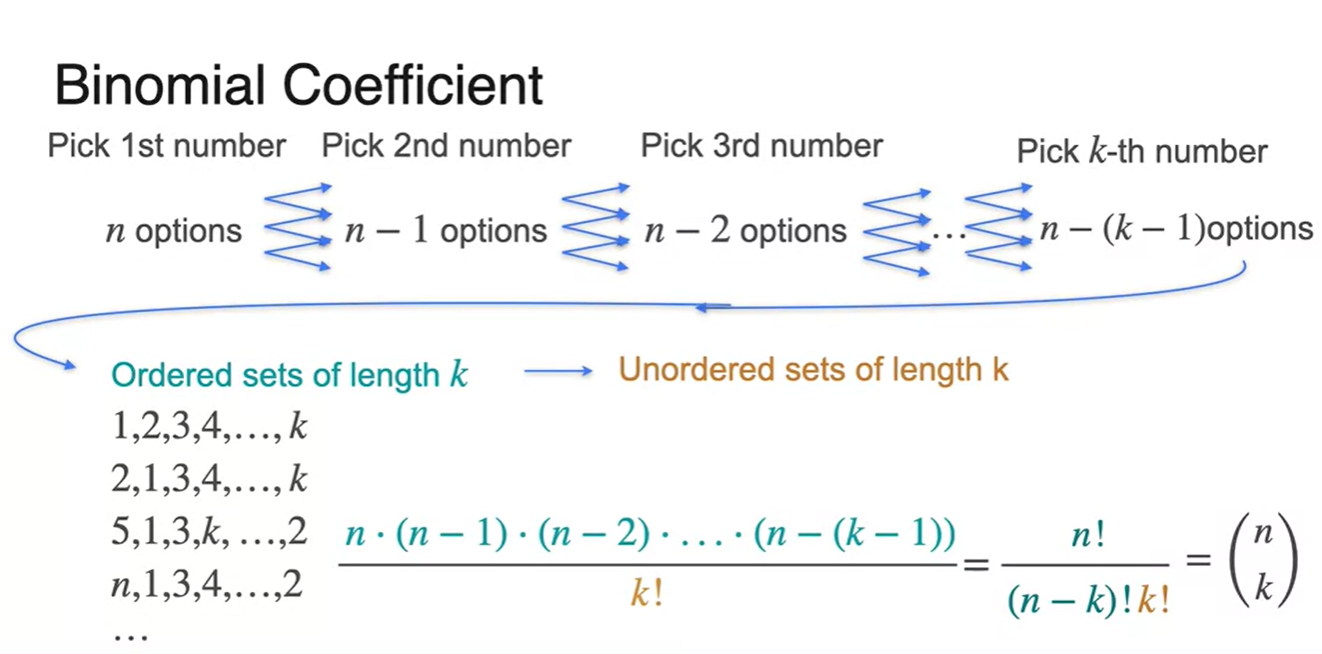
• 중복되는 ordered set의 개수는 n번의 시행 횟수의 factorial로 설명할 수 있다.

  • 위의 예제에서는 k개를 뽑았기 때문에 $k!$의 경우의 수 만큼 중복이 일어난다.

• 수식으로 정리하면 다음과 같다.

  • $\displaystyle \frac{n * (n-1) * (n-2) * ... * (n-(k-1))}{k!} = \frac{n!}{(n-k)! k!} = {n \choose k}$

• $0!$은 1이다.

  • 0번의 head가 나올 경우의 수가 단 한 번 존재하기 때문이다.

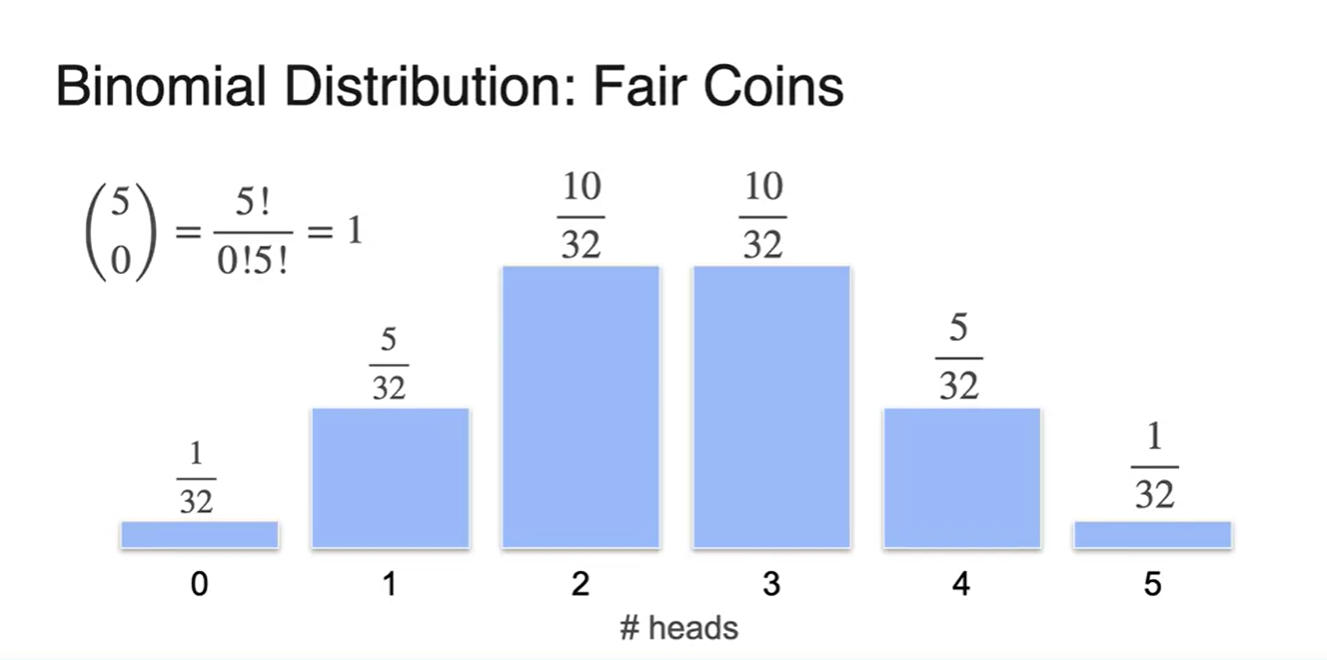
• Unbiased coins라면 앞면 확률이 $0.5$, 뒷면 확률이 $0.5$다.

• Biased coins라면 앞면 확률이 $0.3$, 뒷면 확률이 $0.7$이다.

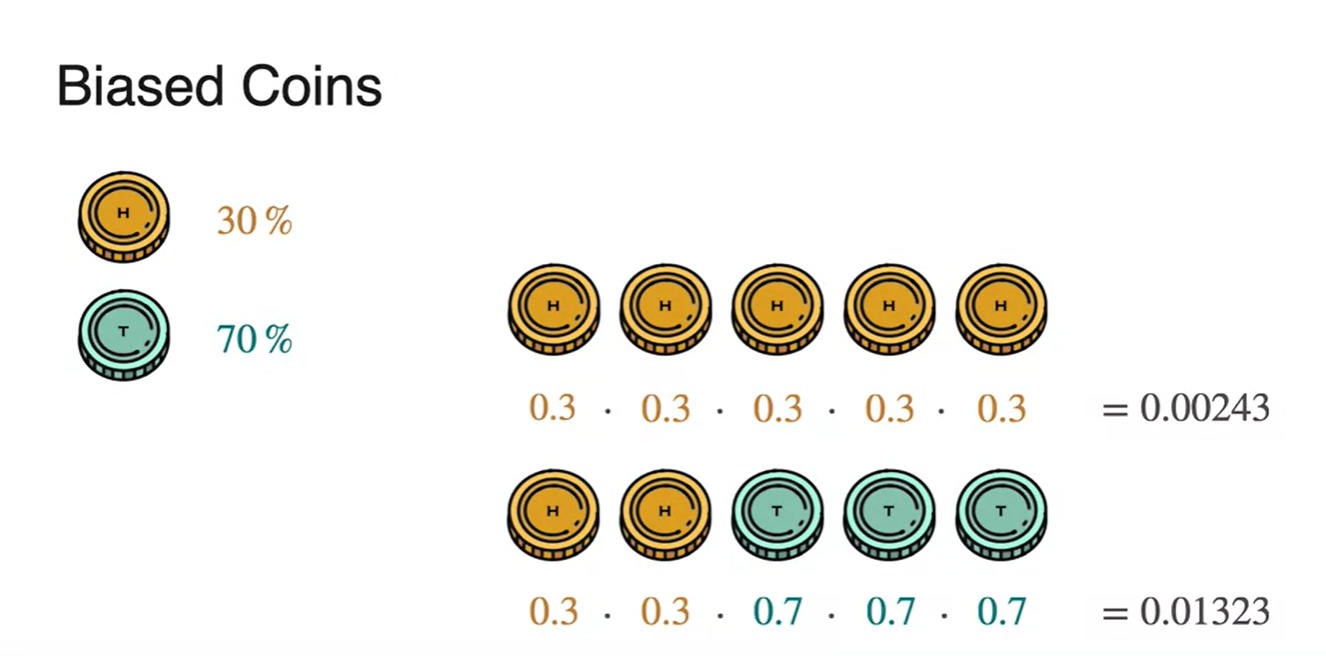
• Biased coin을 던져 구할 수 있는 random variable의 확률을 계산하면 아래 그림과 같다.

• 이 때 한 random variable당 중복되는 경우의 수가 $\displaystyle {n \choose k}$이므로 이를 곱하여 중복 처리해준다.

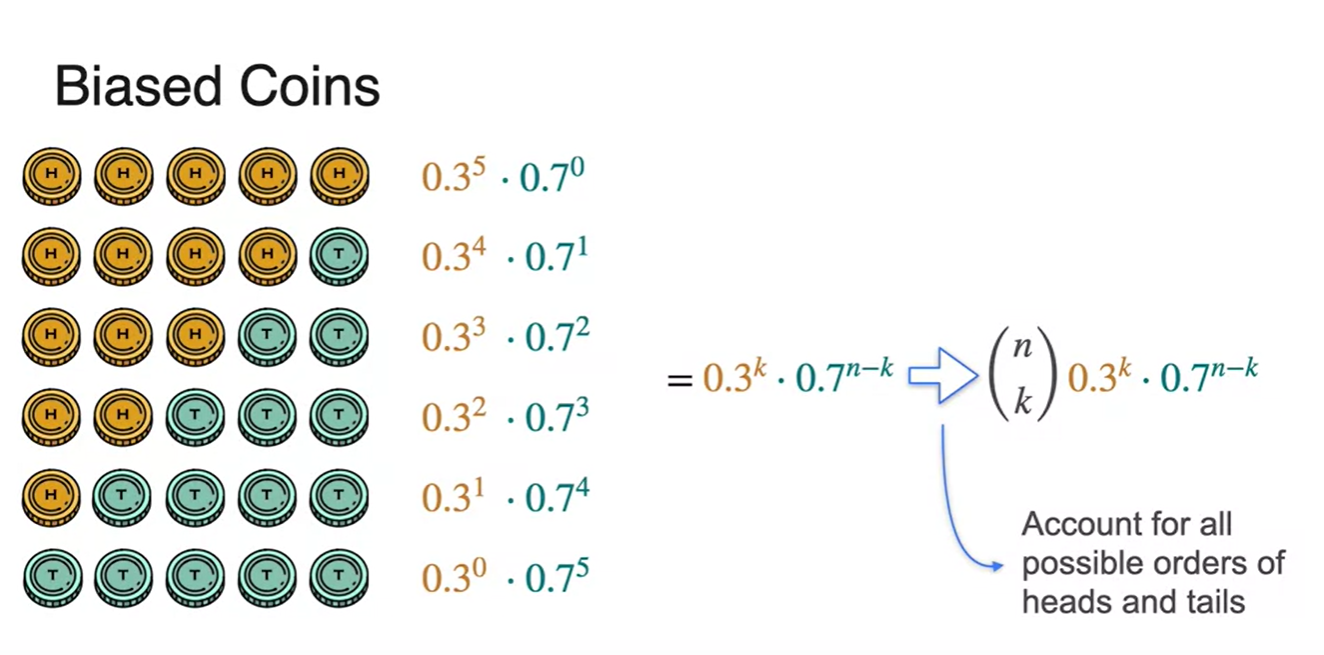
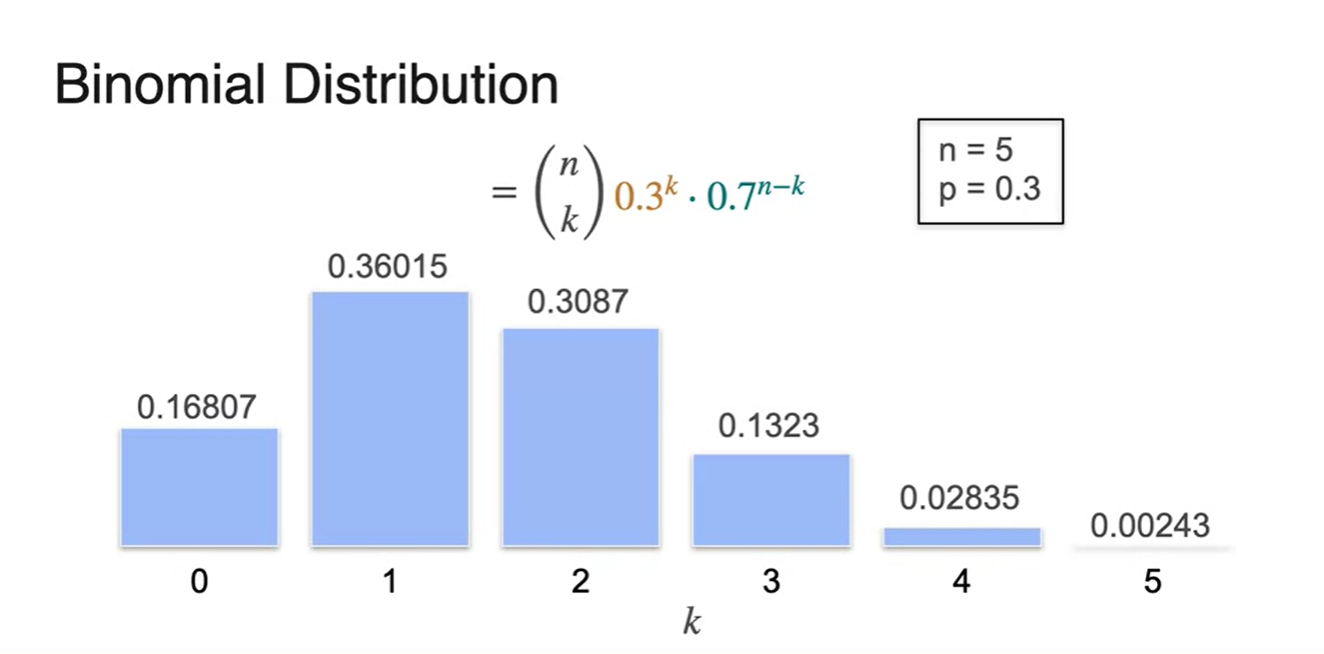
• Biased coin으로 binomial distribution 히스토그램를 나타내면 아래 그림과 같이 그려진다.

  • k가 random variable, pameter는 각각 $n=5$, $p=0.3$일 때의 분포다.

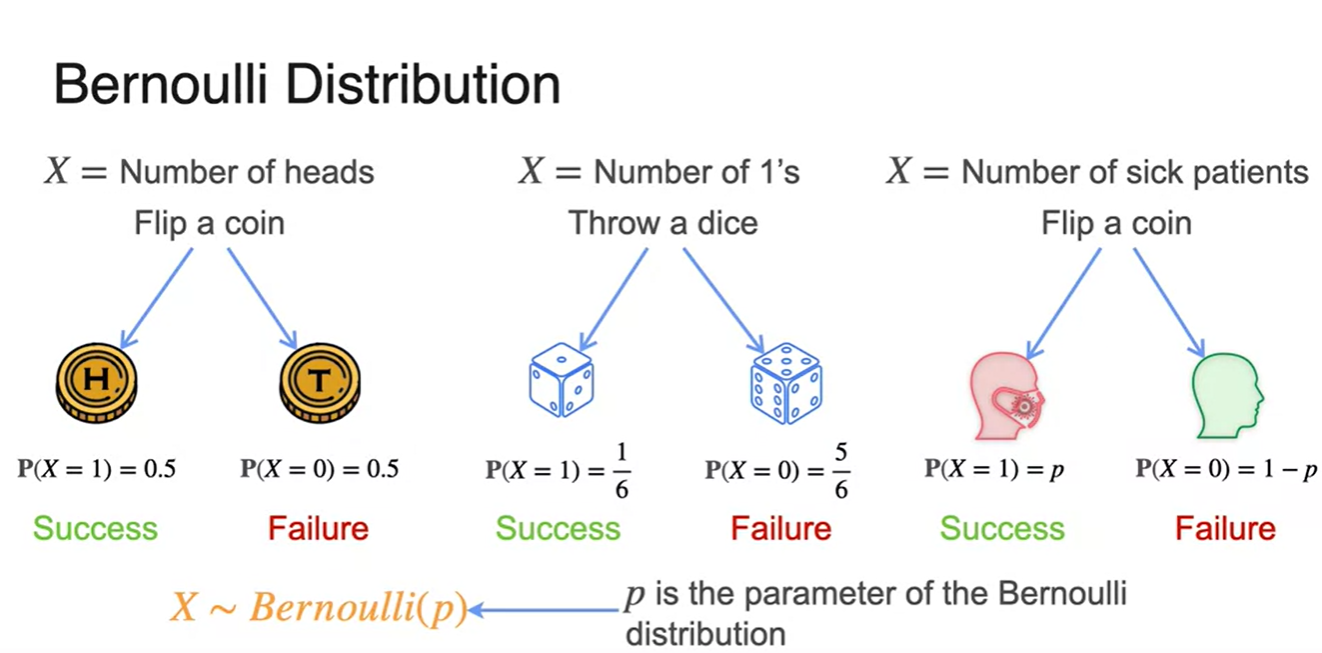
Bernoulli Distribution

• Bernoulli Distribution은 한 번의 시행에서 얻어낼 수 있는 success와 failure의 확률을 나타낸다.

  • $p$는 성공 확률, $1-p$는 실패 확률이며 각 시행에서 나타날 수 있는 경우의 수가 성공 or 확률 두 가지일 때 사용한다.

Probability Distributions (Continuous)

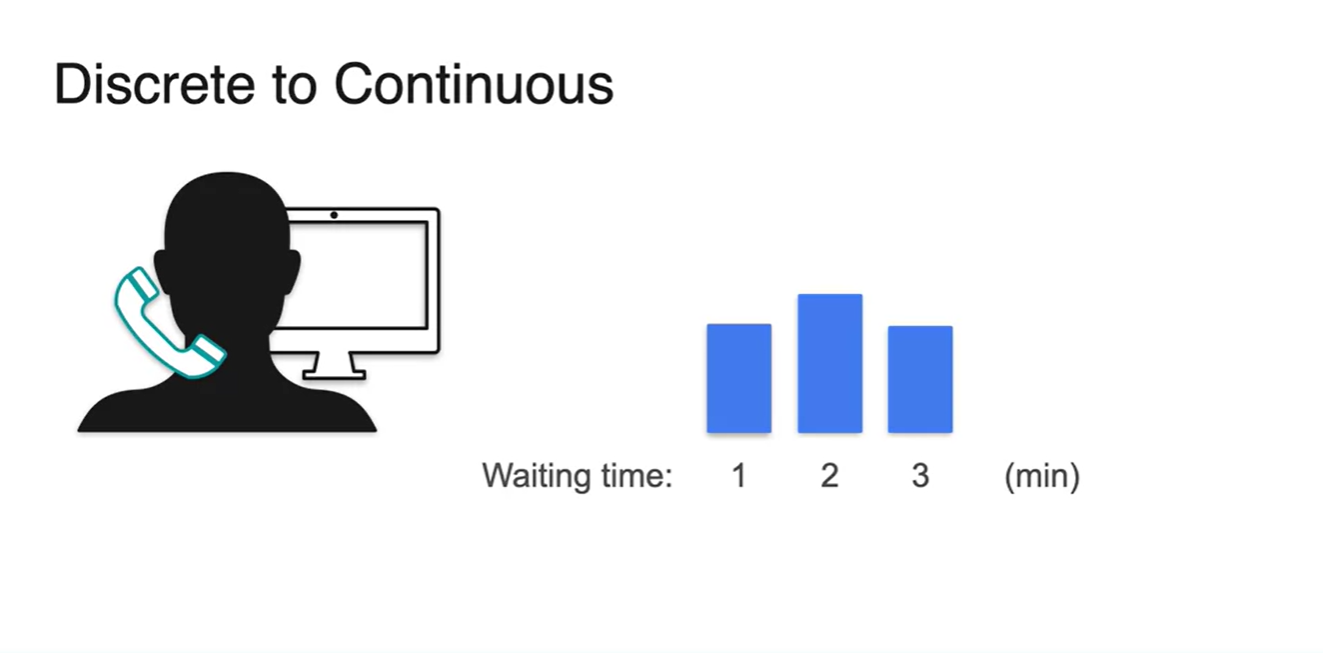
• 콜센터에 전화하였을 때 기다려야하는 시간에 대한 확률을 알아보자.

  • Waiting time이 1, 2, 3분으로 딱딱 떨어진다면 discrete한 random variables를 다루는 것이다.

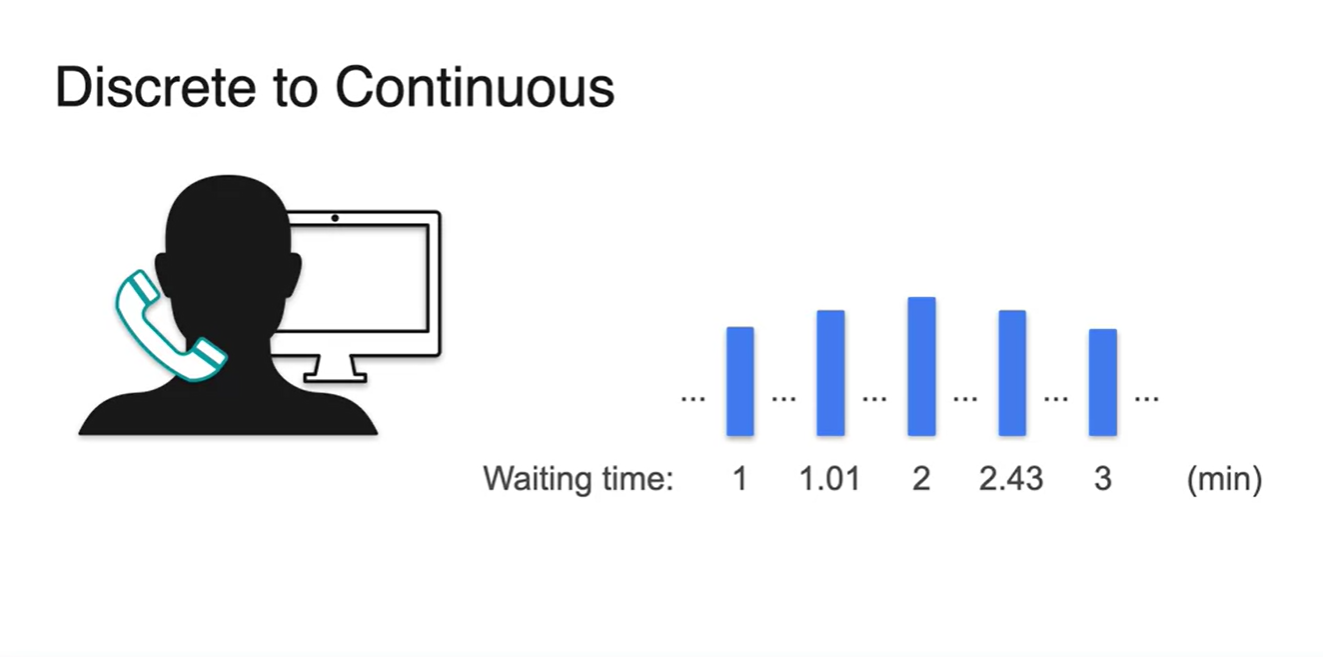
• 그러나 사실 기다린 시간은 1.01, 2.43과 같이 매우 다양할 수 있다.

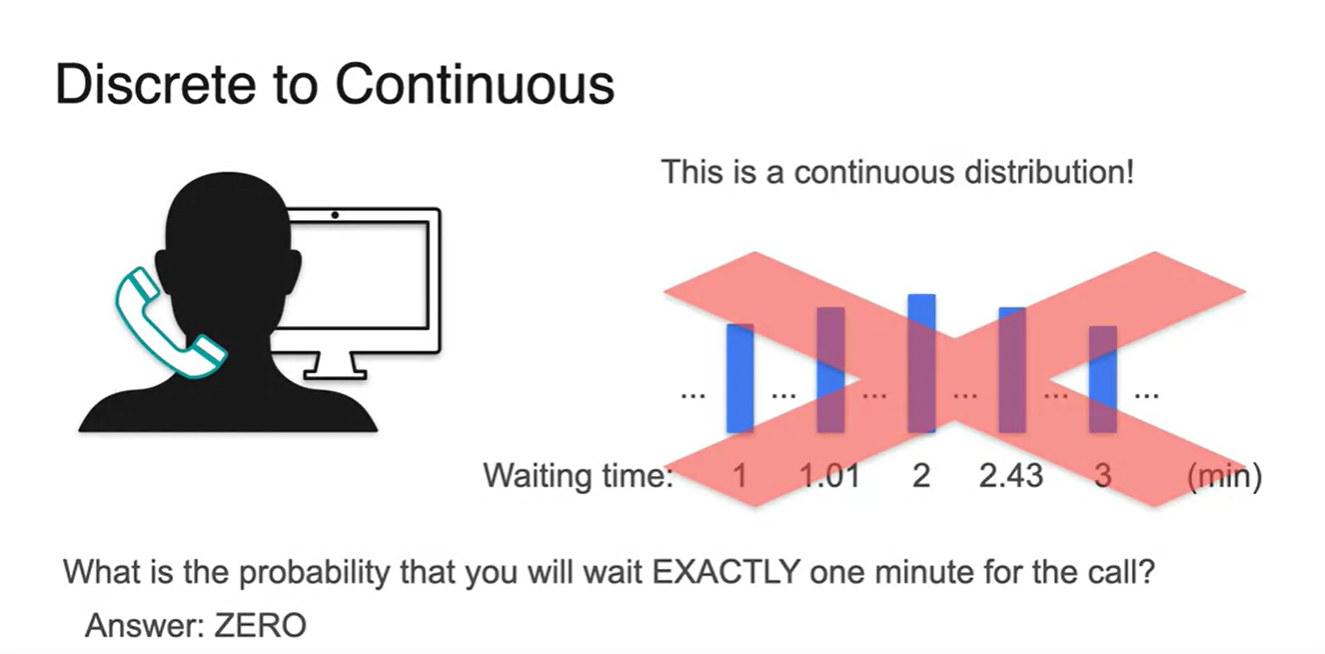
• 따라서 사실상 기다린 시간이 1분인 사람의 확률을 구하는 것은 거의 $0$에 가깝다고 볼 수 있다.

  • 즉, continuous한 random variable을 다뤄야 한다.

• Discrete한 변수를 잘게 쪼개서 1분 단위로 확률을 합하여 표현해 보자.

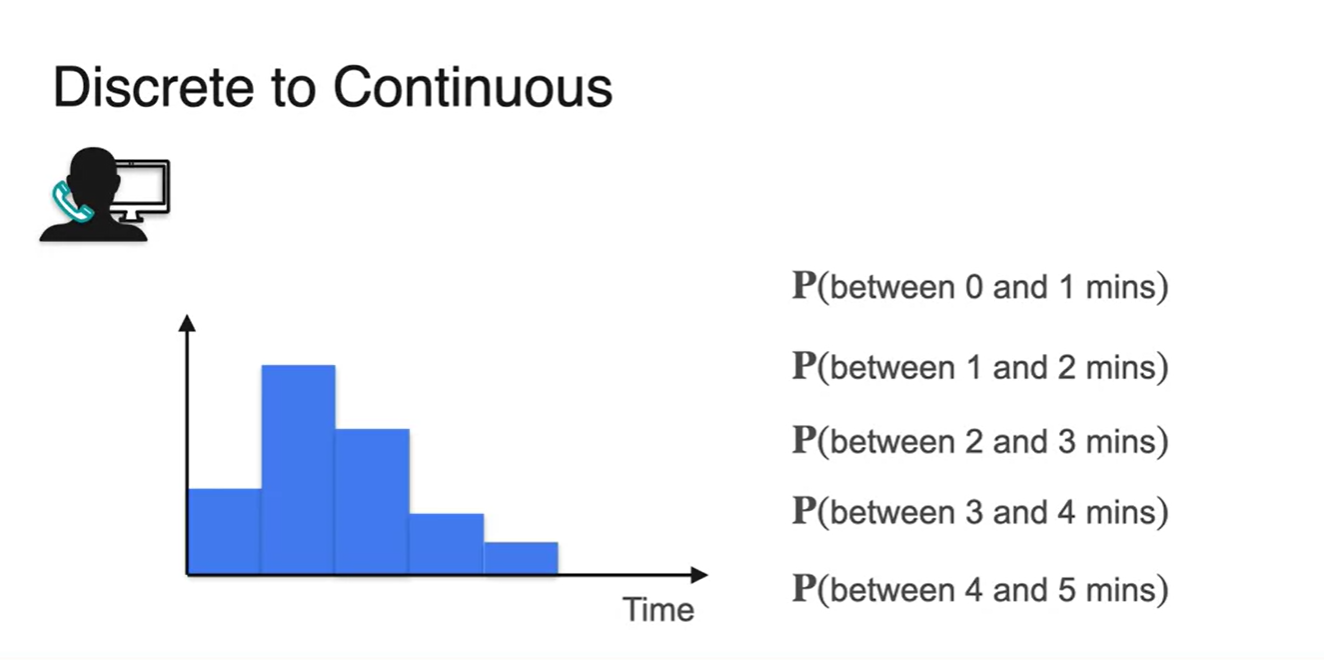
• 0.5분 단위로 확률을 합하여 표현한 결과와 0.25분 단위로 합하여 표현한 결과가 아래와 같다.

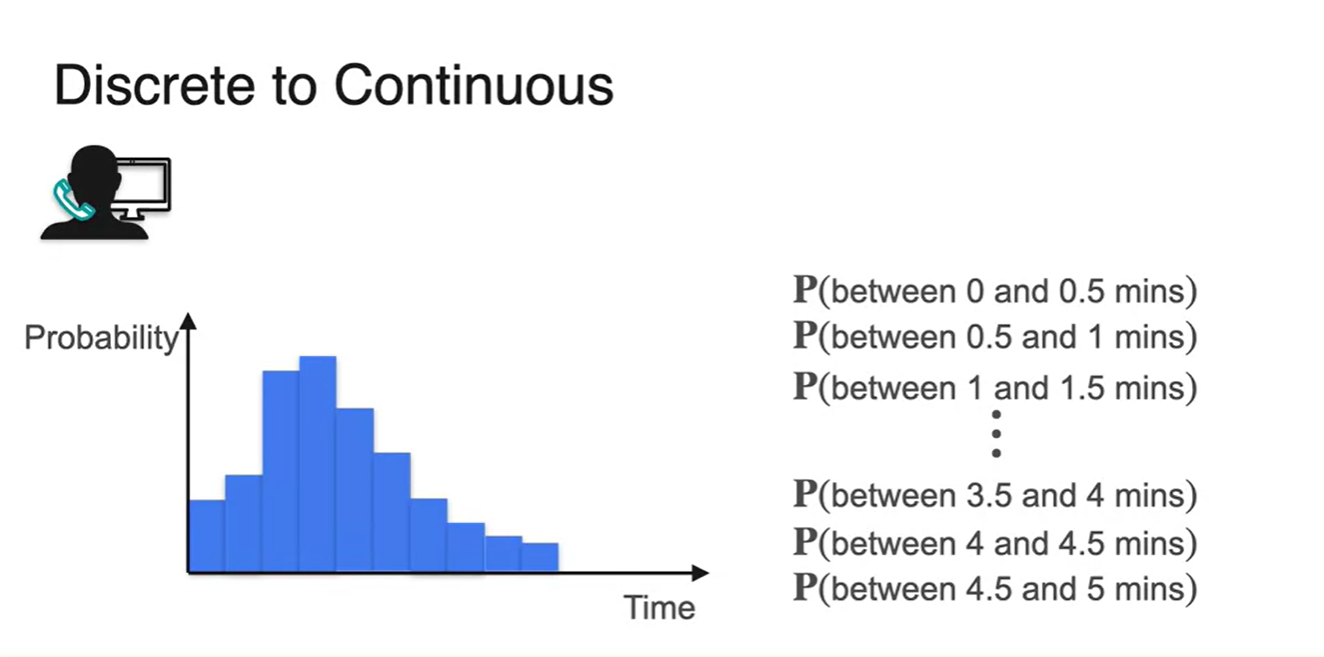
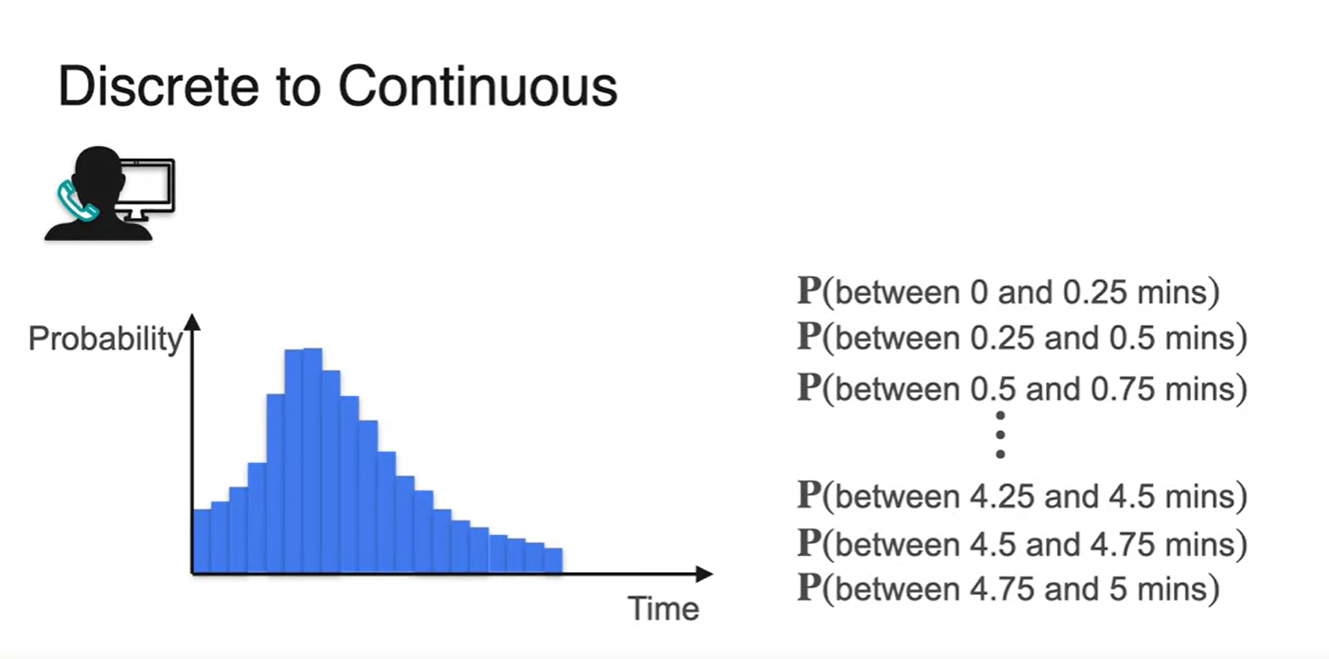
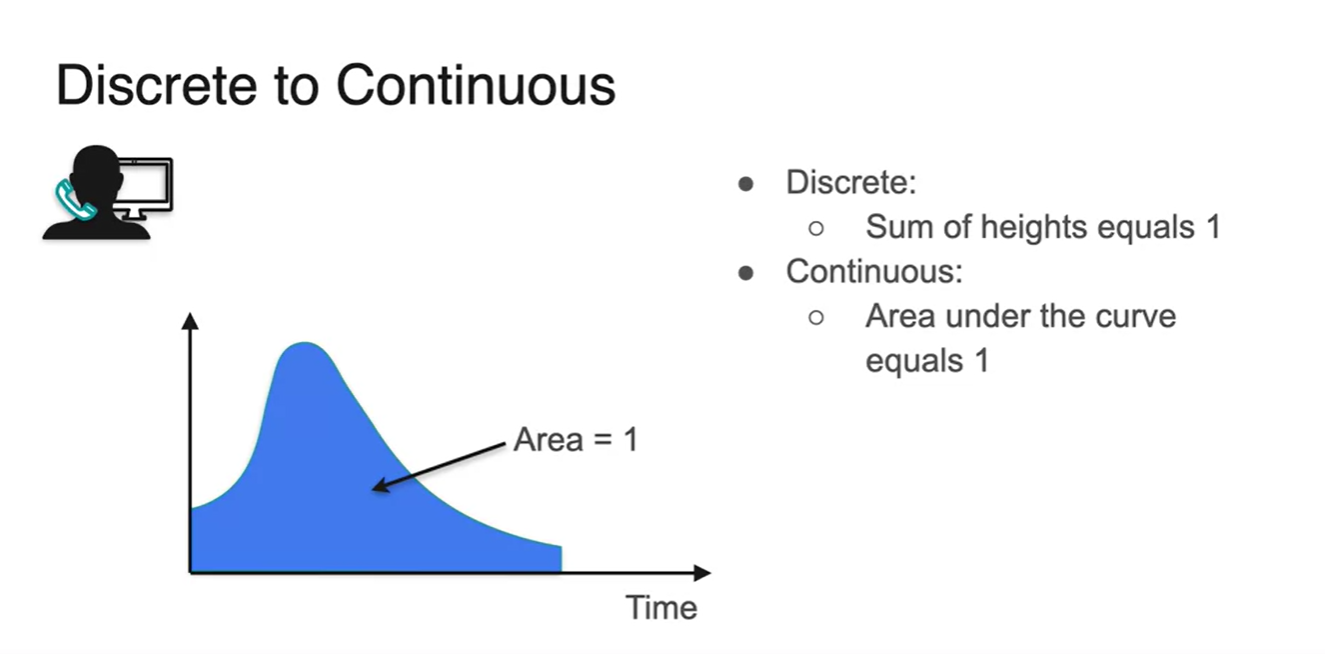
• 확률 변수를 계속해서 잘게 쪼개다 보면 아래 그림과 같이 smooth한 함수로 그래프가 그려진다.

  • 전체 확률의 합은 항상 1이어야 하는 성질로부터 그래프 아래 면적이 1이라는 것을 알 수 있다.

Probability Density Function

• 위의 예시에서 random variable을 1분 단위로 쪼개고 각 확률의 값이 동일하다고 가정해보자.

  • 이 때, 전체 확률 합이 1이어야 한다는 성질로부터 $P(2 \le X \le 3)$는 1/5임을 알 수 있다.

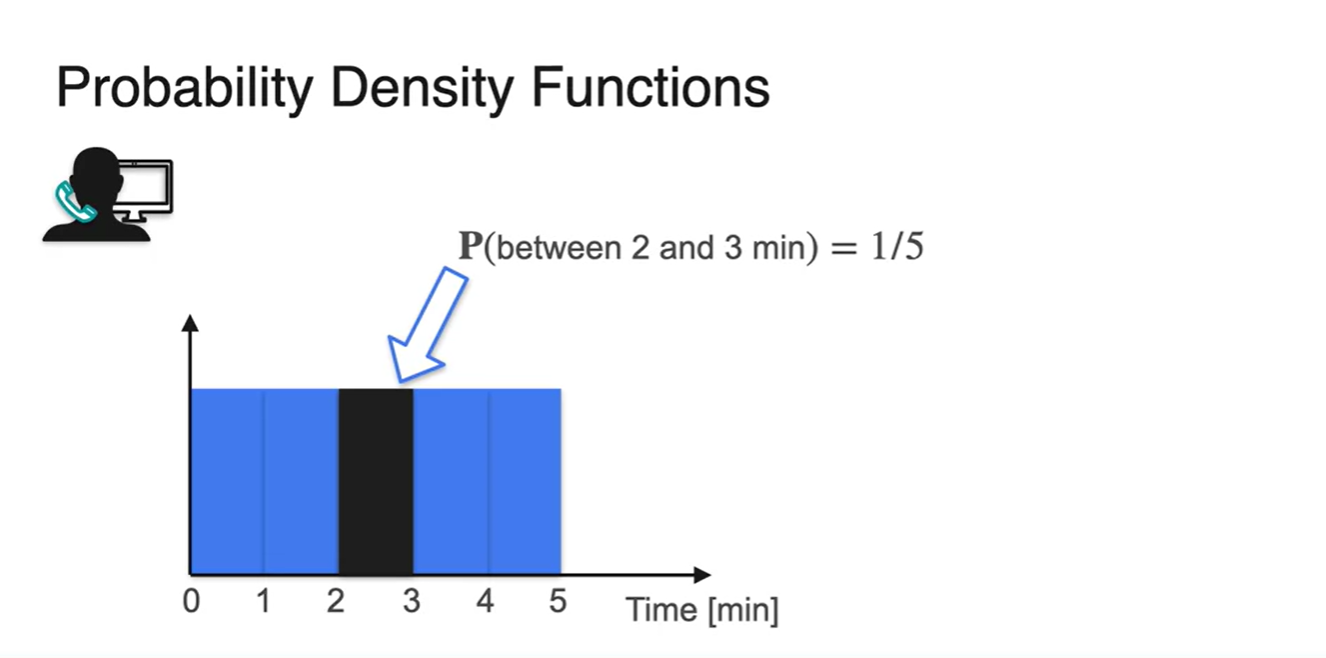
• 이번에는 random variable을 0.5분 단위로 쪼개고 각 확률의 값이 동일하다고 가정하자.

  • 전체 확률 합이 1인 동일한 bar가 10개 있으므로 $P(2 \le X \le 2.5)$는 1/10(0.1)임을 알 수 있다.

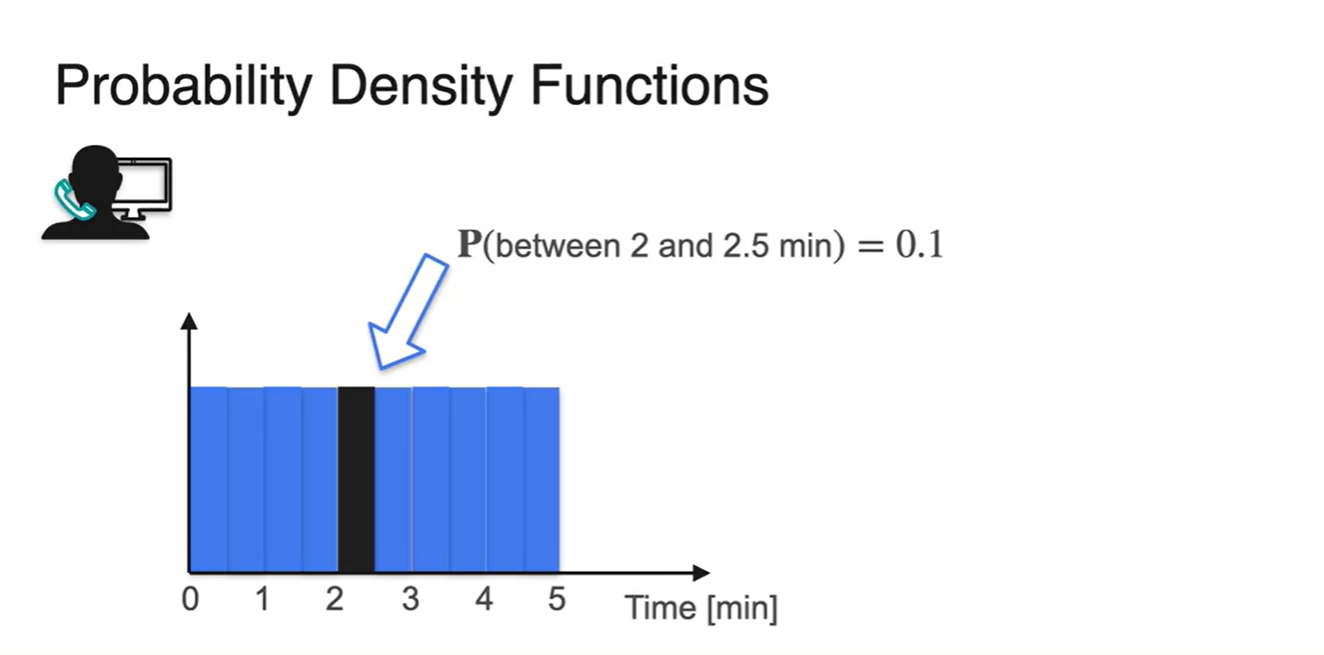
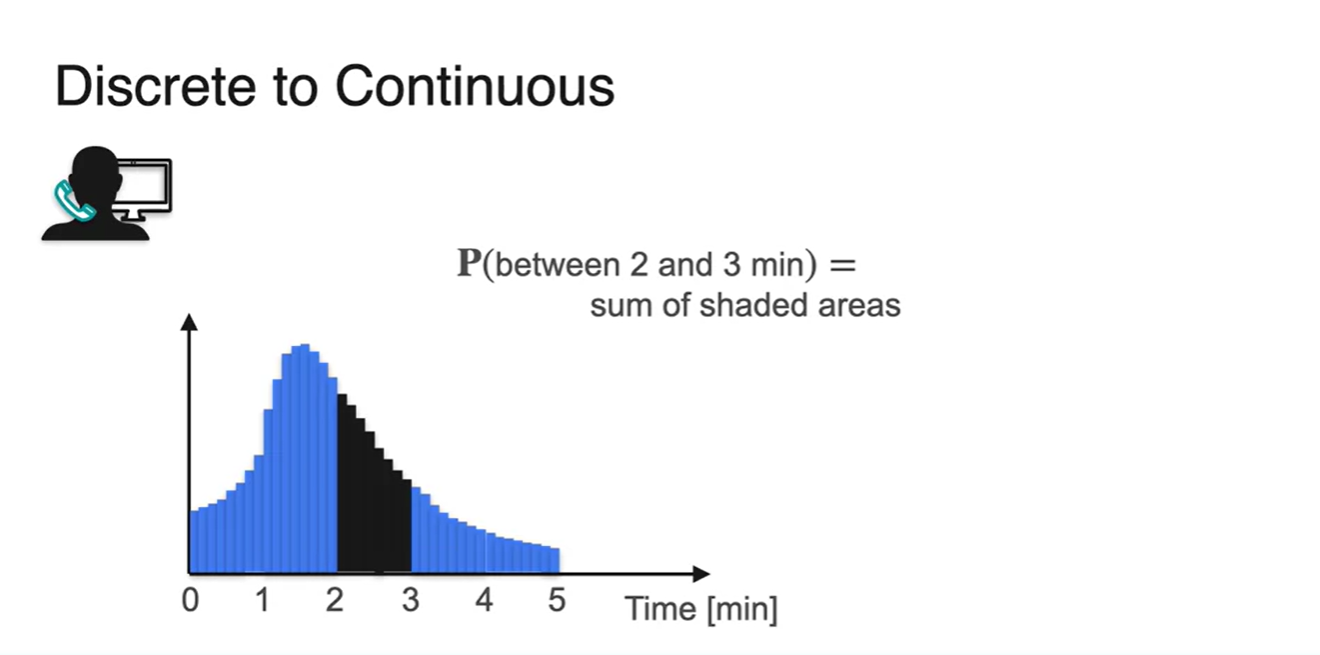
• Random variable을 계속해서 잘게 쪼개다 보면 기존에 구하고자 했던 $P(2 \le X \le 3)$는 여러 bar의 확률을 더한 결과와 같다는 것을 알게 된다.

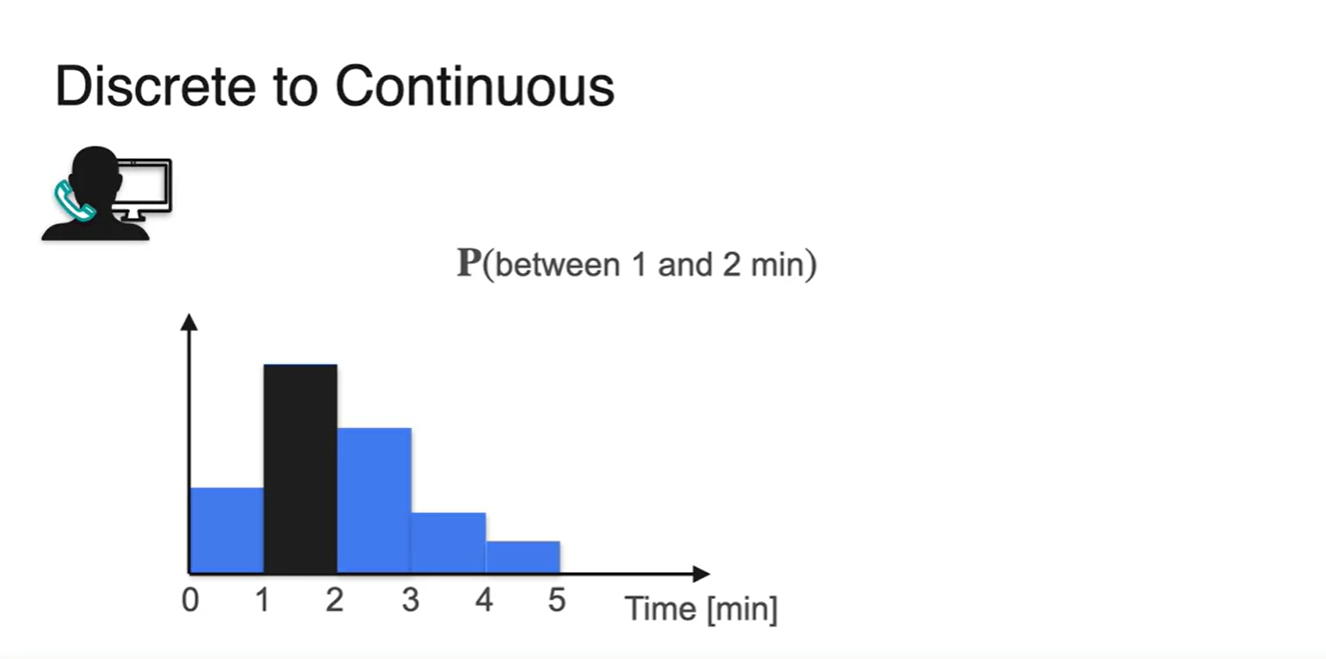
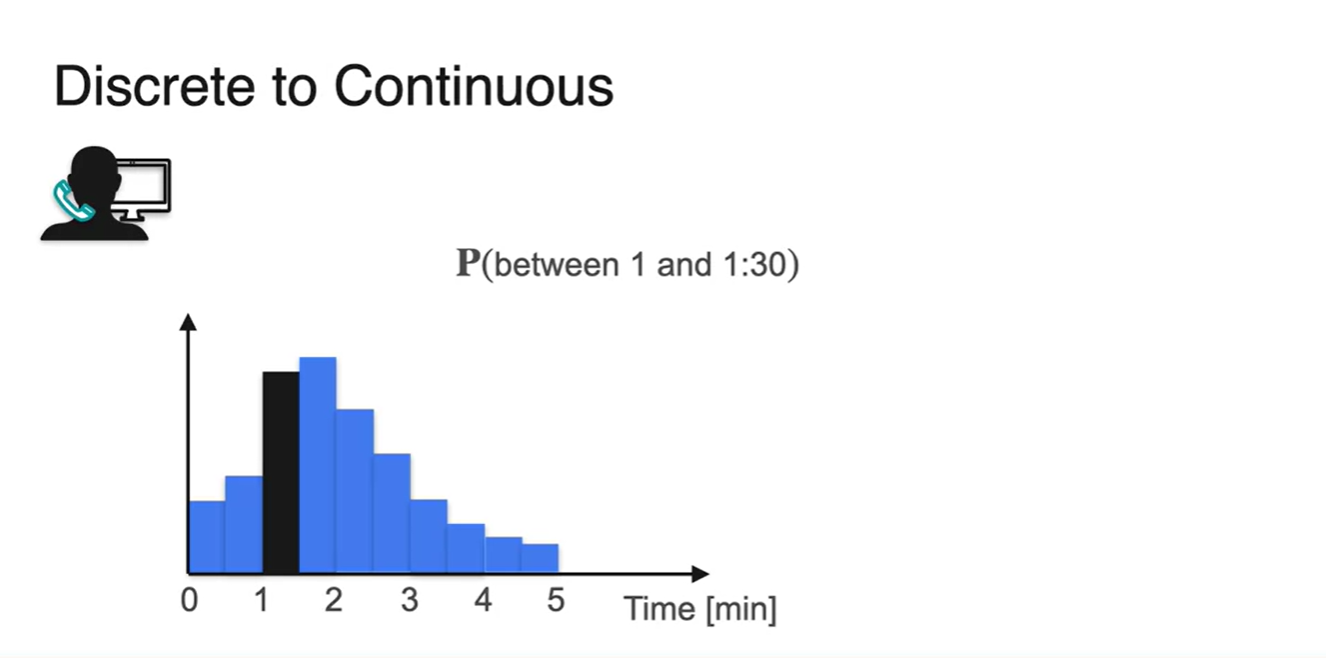
• Finite한 interval of bar의 넓이의 합은 smooth한 그래프 아래 면적과 같다.

  • 즉, 그래프 아래 적분 값(area)을 구함으로써 구간의 확률을 알 수 있게 된다.

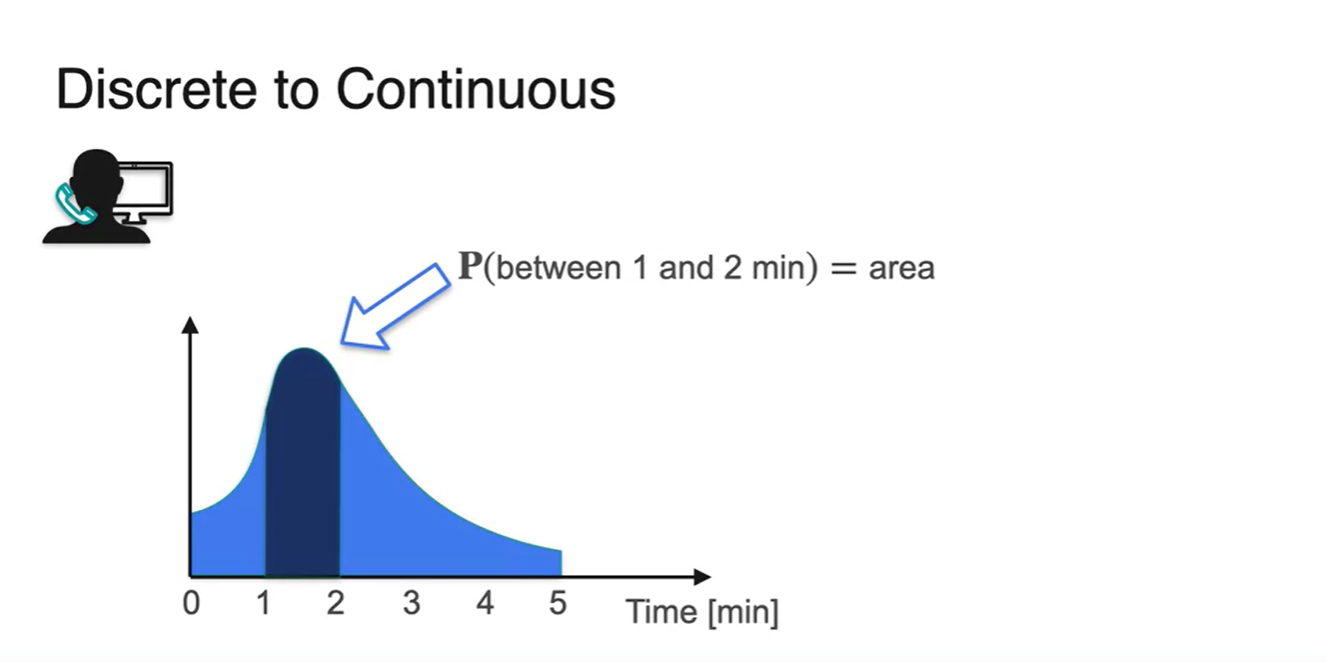
• Question. 시간이 명확하게 2분인 확률은 얼마일까?

  • $P(EXACTLY \; 2 \; min)$은 bar의 넓이가 존재하지 않으므로 0이다.

    • 따라서 continuous한 variable을 갖는 확률을 구할 때에는 명확한 "값"의 확률은 구할 수 없으며, 구간의 확률만을 다룰 수 있다.

• Summary

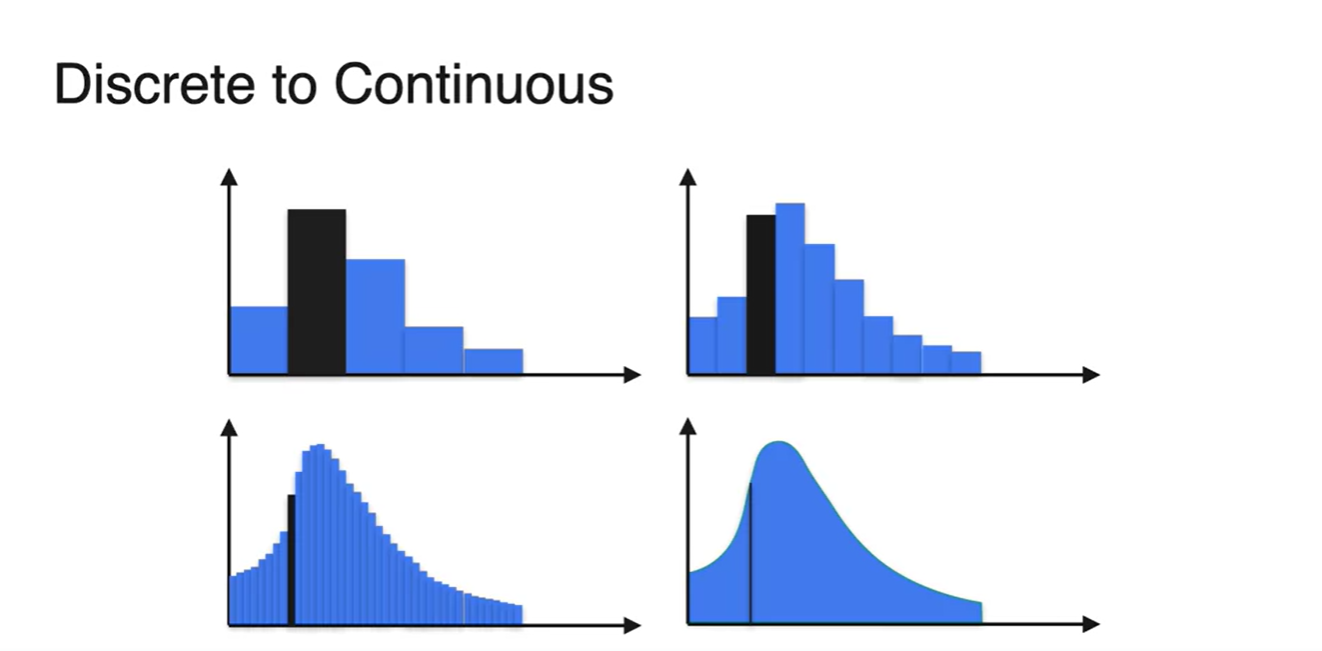
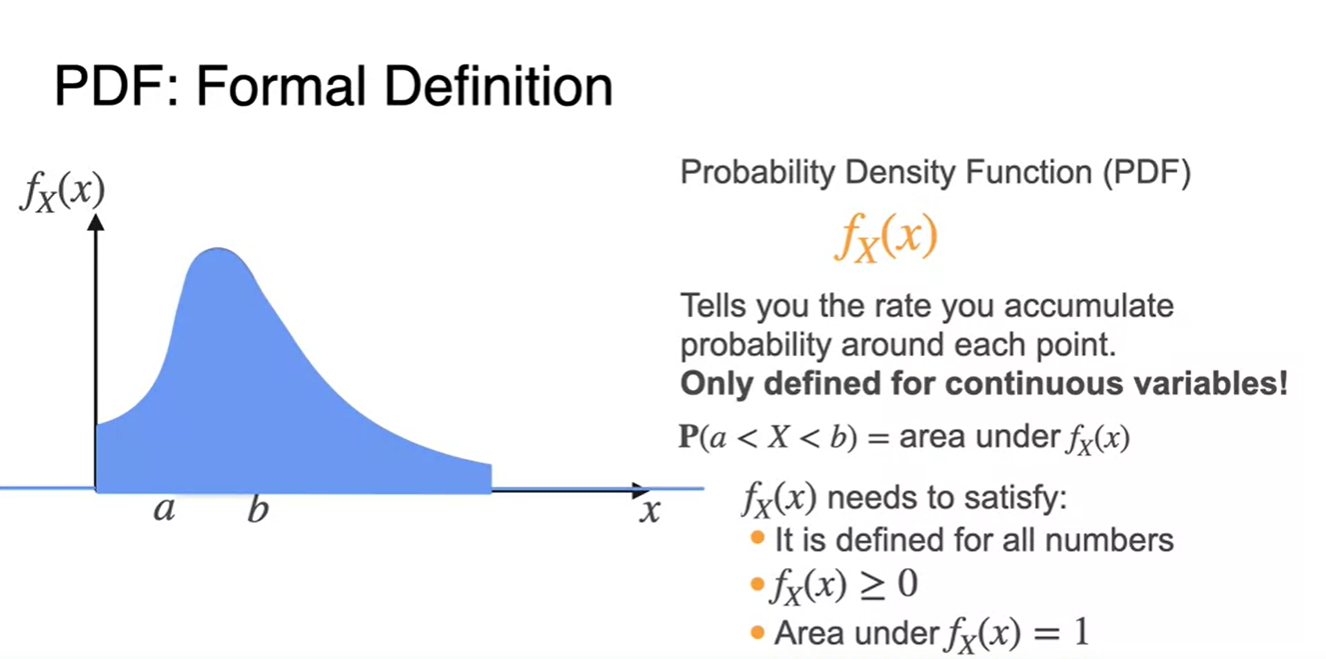
• PDF(Probability Density Function)를 기호로 나타내면 $f_X(x)$다.

  • 확률 변수가 continous한 경우, 구간의 확률 $P(a < X < b)$는 a부터 b까지의 $f_X(x)$ 아래 면적을 의미한다.

  • 또한, 세 가지 조건을 만족해야 한다.

    1. All numbers에 대해 정의되어야 한다.
    2. $f_X(x) \ge 0$, 확률은 양수여야 한다.
    3. $f_X(x)$ 아래 면적의 전체 합은 항상 1이다.

• Discrete vs Continous Random Variables의 경우를 정리해보자.

  • Discrete : 확률 변수는 finite하며 PMF를 통해 각 변수의 확률을 얻어낼 수 있다.
  • Continous : 확률 변수는 infinite하며 PDF를 적분(area)하여 interval 확률을 얻어낼 수 있다.

Cumulative Distribution Function

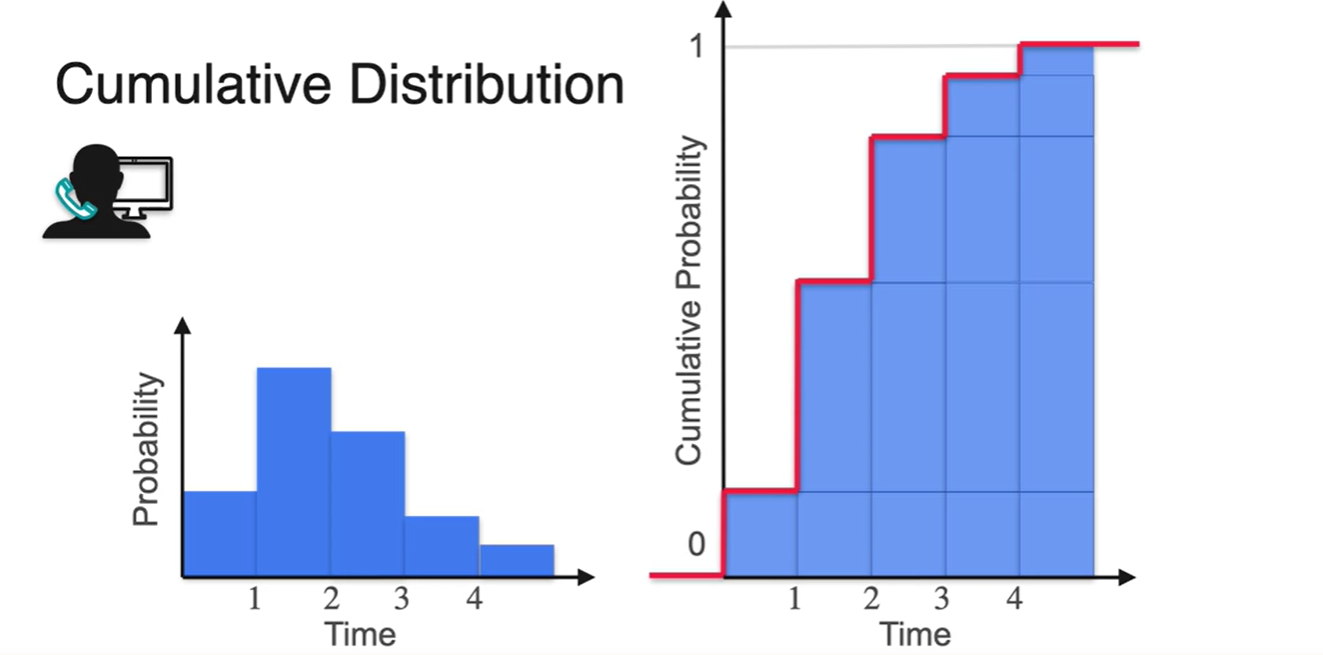
• Cumulative Distribution Function, CDF에 대해 알아보자.

  • Cumulative 즉, 누적 확률 분포를 의미한다.

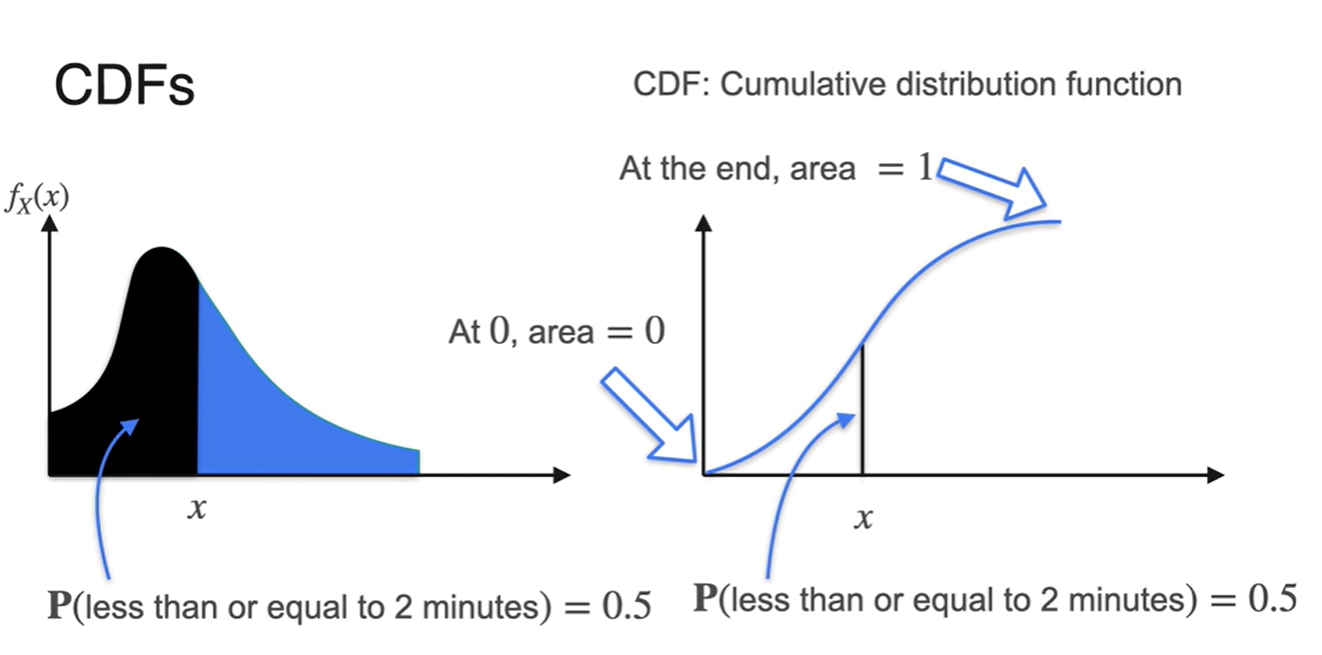
• CDF는 PDF의 구간 면적의 값을 나타내는 적분형 함수다.

  • 0에서의 area는 0이라는 점과 end point의 area는 1이라는 특징을 가지고 있다.

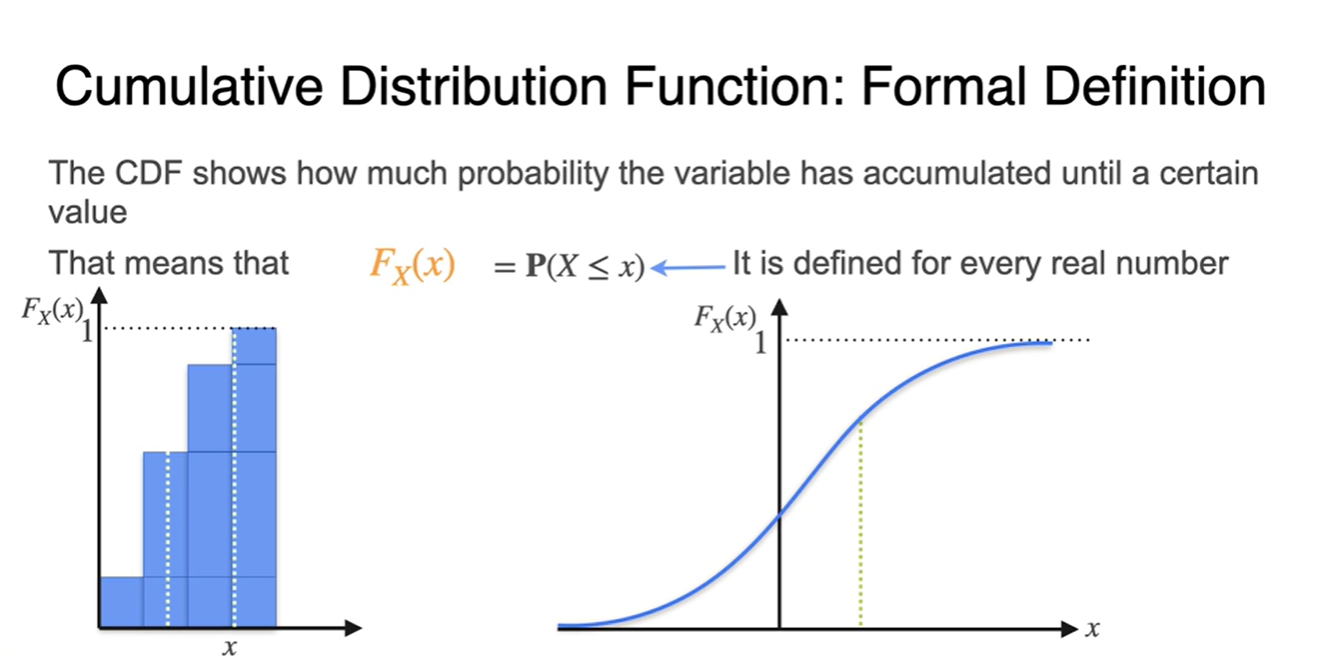
• CPF는 우리가 알고자 하는 certain value 까지의(until) 누적 확률을 나타낸다.

  • 기호로는 $F_X(x)$로 대문자 표기하며, 모든 $x$ variable에 대해 $P(X \le x)$ 값을 정의내릴 수 있는 함수다.

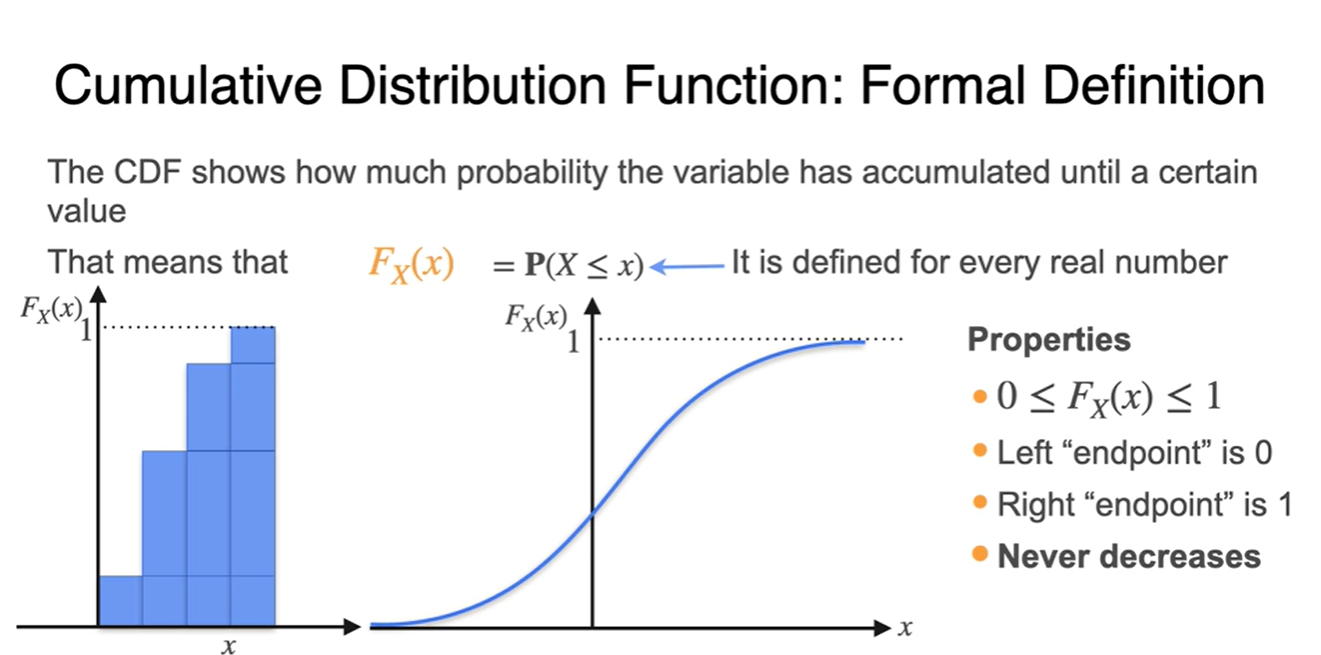
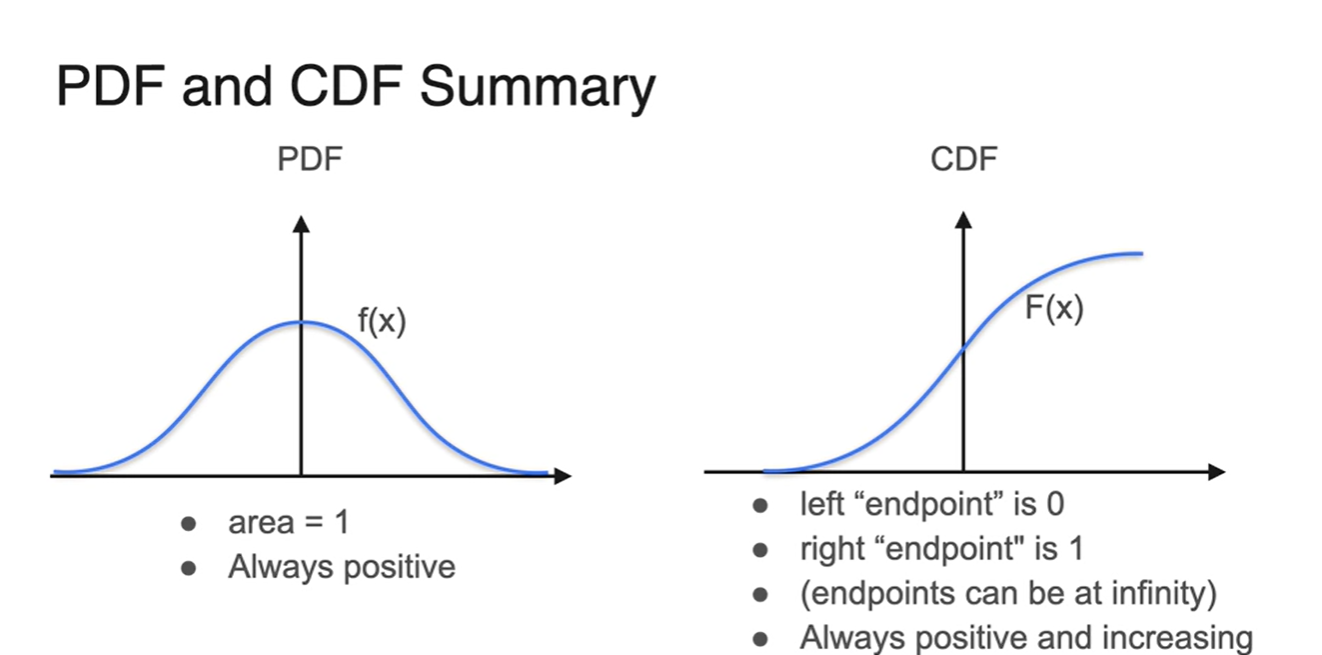
• PDF의 properties는 아래와 같다.

  • $0 \le F_X(x) \le 1$ : 모든확률은 0과 1 사이의 값을 가진다.
  • 가장 왼쪽의 endpoint는 0이다.
  • 가장 오른쪽의 endpoint는 1이다.
  • 절대로 감소하지 않는다.

• PDF와 CDF의 차이는 아래와 같이 설명될 수 있다.

  • 다시 말해 PDF의 적분은 CDF, CDF의 미분은 PDF다.

Uniform Distribution

• 아래와 같은 상황을 가정해보자.

  • 0에서 15분 사이의 어떠한 시간대에든 대답을 할 수 있다.

    • 그러나 시간 안에 대답을 하지 못하면 전화 연결이 끊어진다.

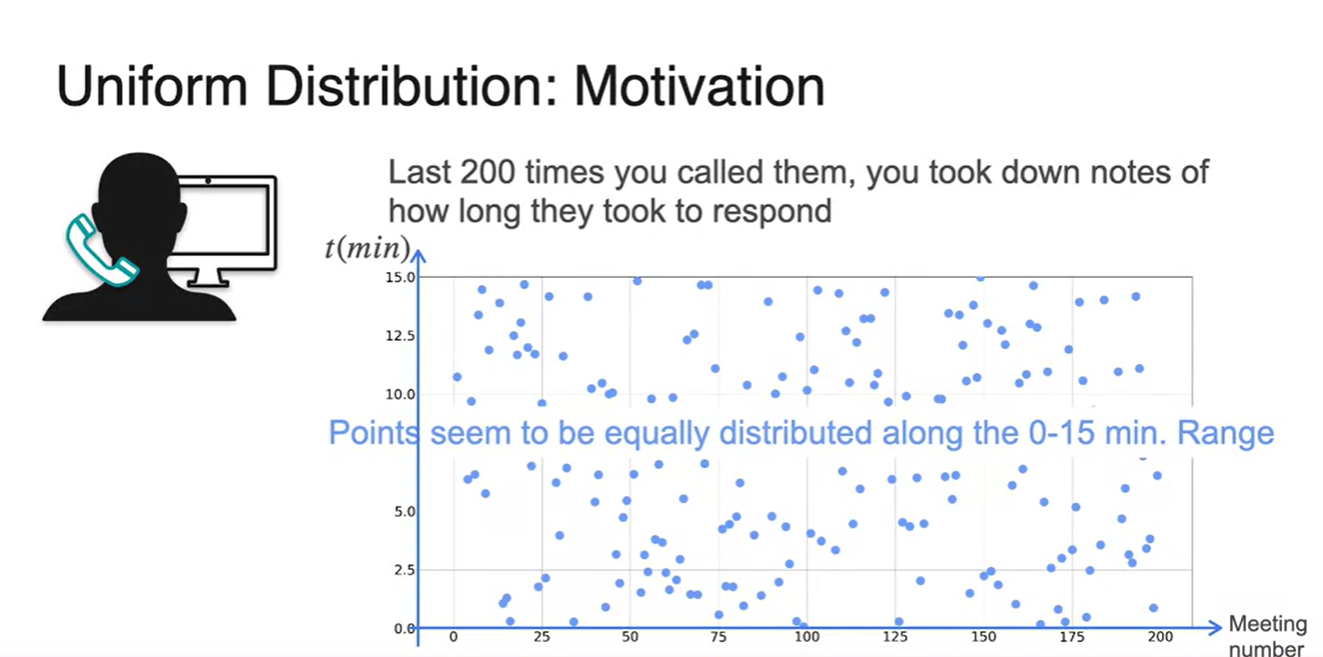
• 200번의 시행을 반복하였을 때, 대답한 시각을 점 찍어 보자.

  • 0-15분 사이의 시간에 존재하는 점들은 equally distributed하다.

    • 구간에 "존재"한다는 점만 놓고 보면 말이다.

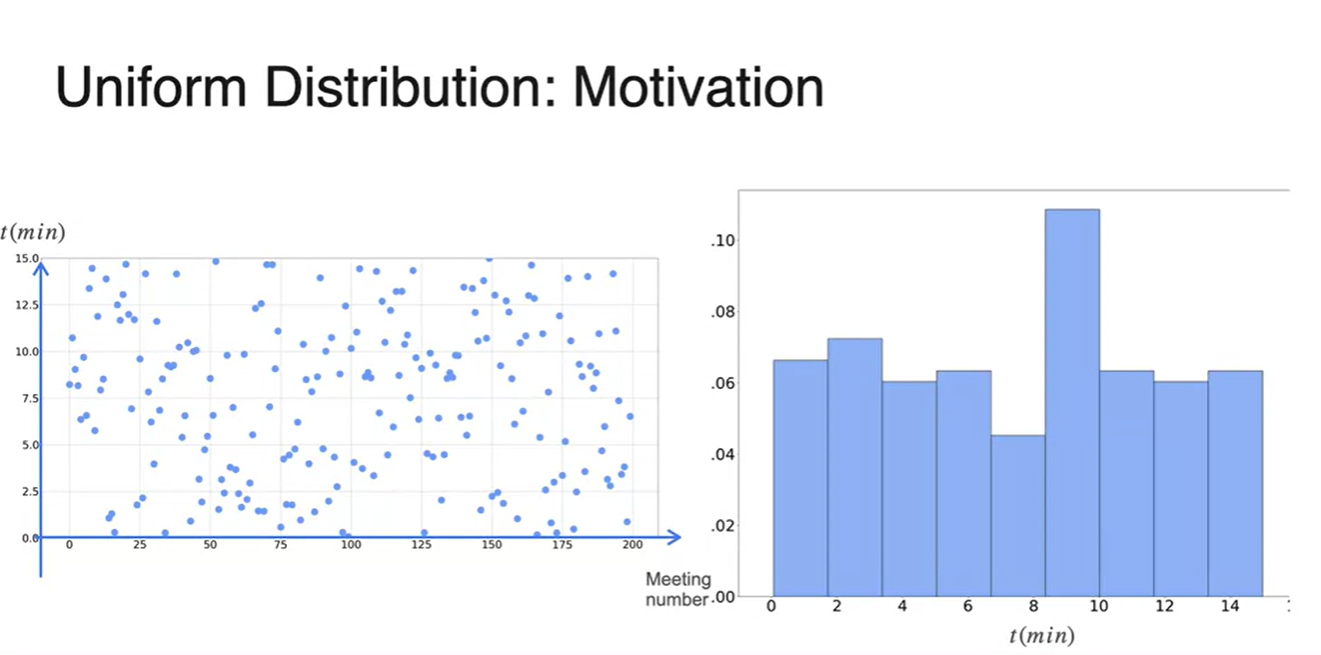
• Time을 잘게 쪼개어 확률 분포로 표현하면 오른쪽과 같은 그림의 histogram이 나온다.

  • Uniform distribution은 이러한 관점을 다르게 바라본다.

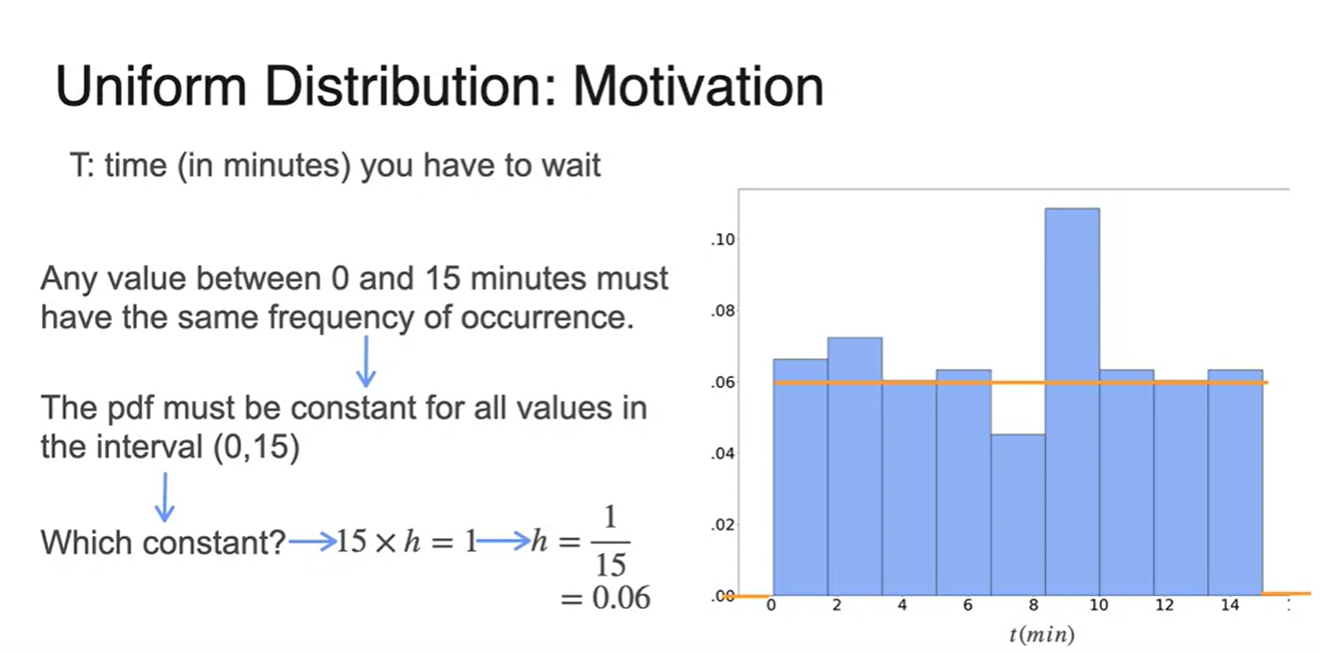
• (0, 15) 사이의 값이 same frequency를 가진다면, 해당 interval 확률은 모두 동일하다.

  • 이를 주황색 line으로 나타내어 Uniform distribution의 PDF를 완성한다.

    • 0부터 15분까지가 random variables로 주어지므로 일정한 확률 $p = \displaystyle \frac{1}{15}$를 갖는다.

• Uniform distribution의 parameters는 각 구간의 endpoint $a$와 $b$이다.

  • PDF 수식은 아래와 같다.

    $f_X(x) = \begin{cases} \displaystyle \frac{1}{b-a} & {a < x < b} \\ 0 & {x \notin (a, b)} \end{cases}$

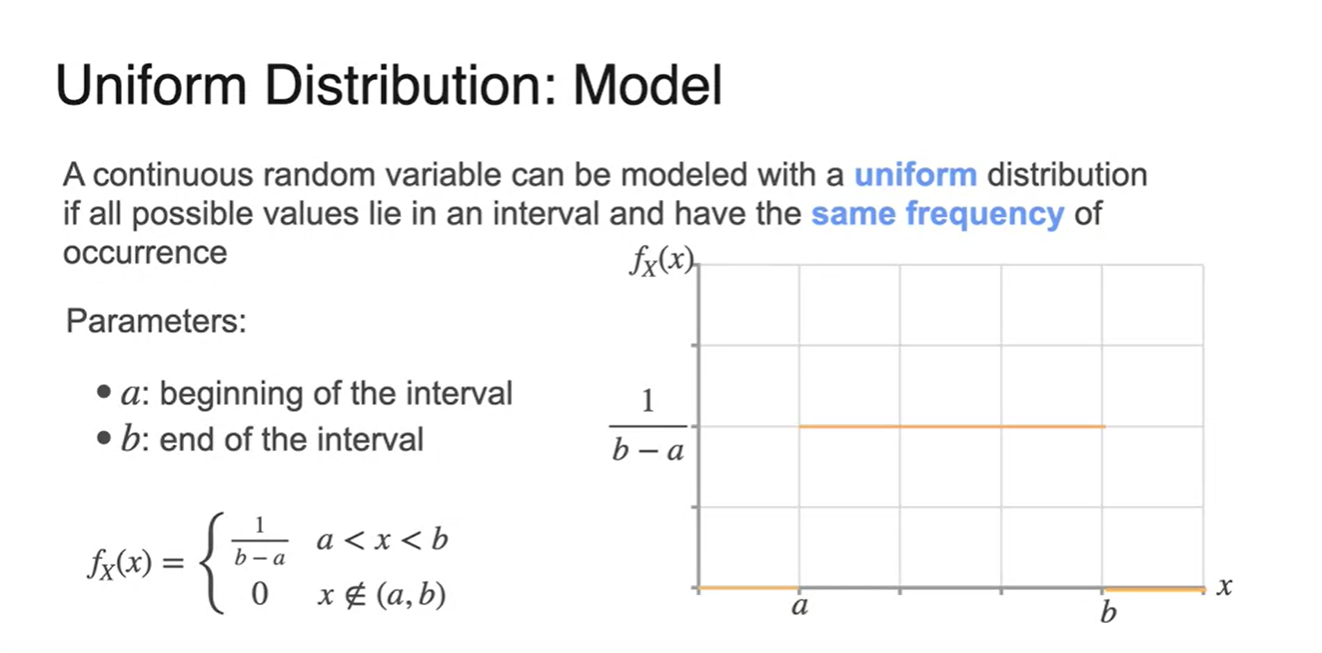
• 그래프로 표현하면 다음과 같이 특정 구간에만 같은 확률을 갖는 분포를 갖는다.

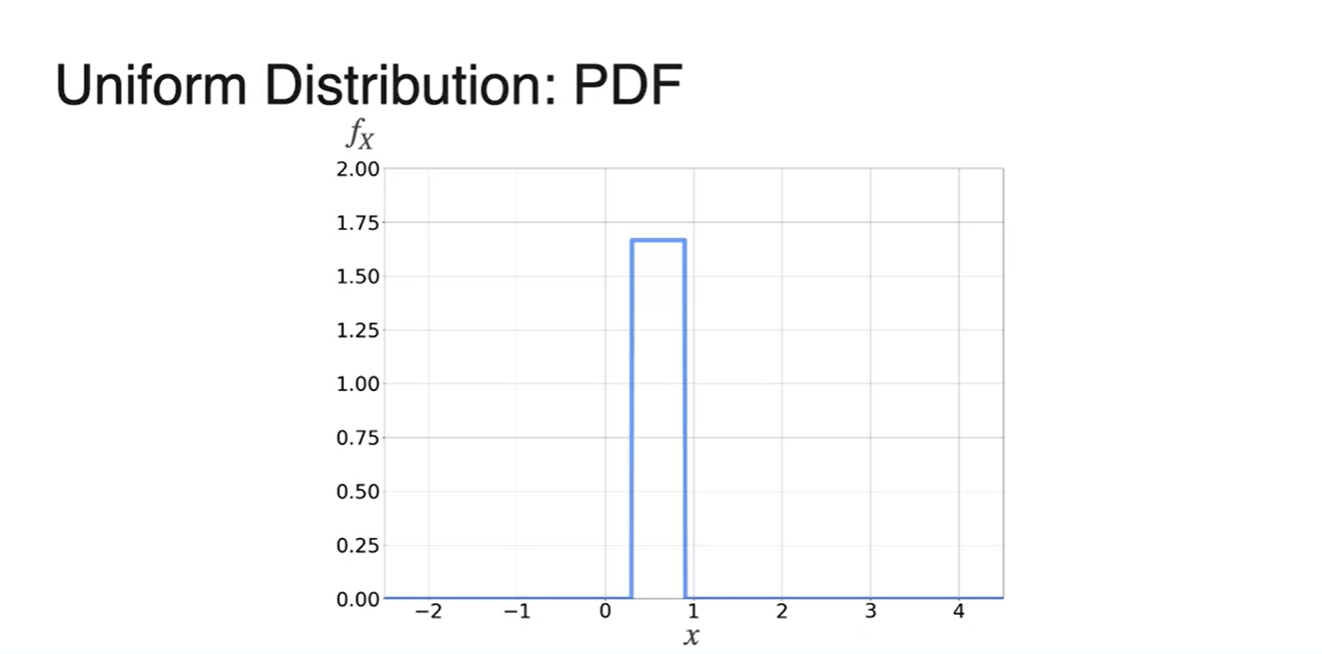
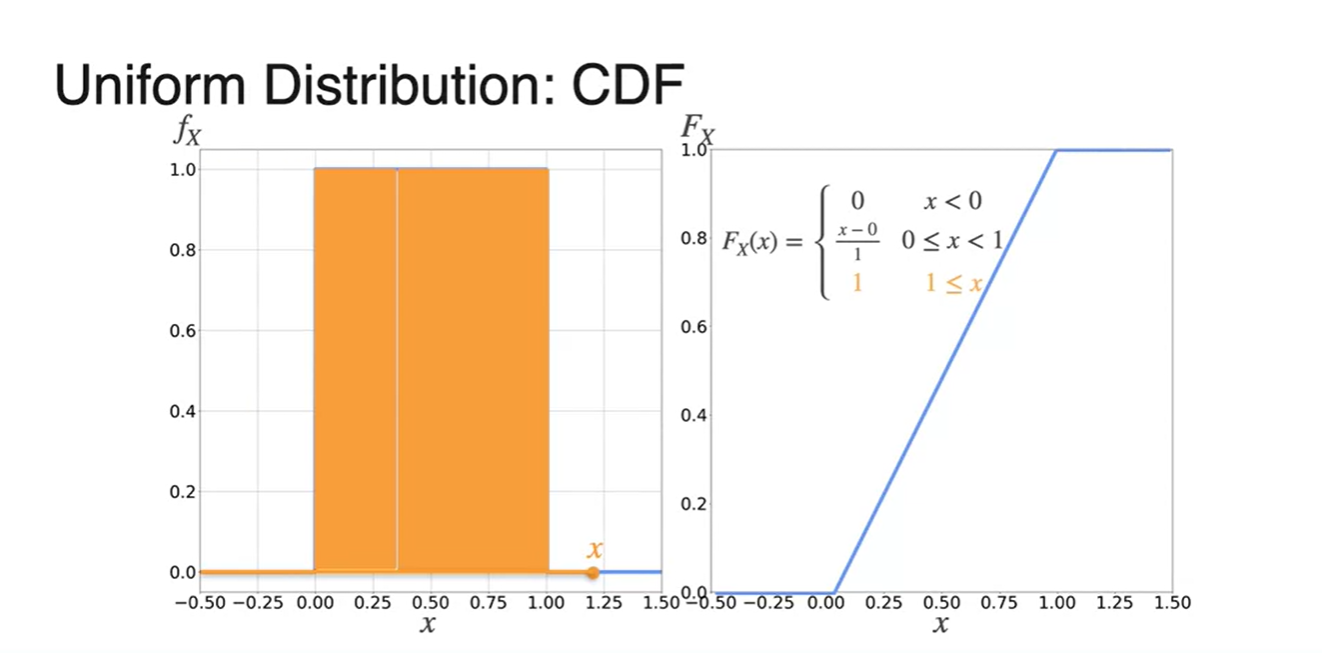
• PDF를 활용해 CDF를 그리는 과정을 각 $x$마다 쪼개서 나타낸 결과는 아래와 같다.

  • $x \le 0$일 때는 확률이 0
  • 구간의 확률은 증가하는 1차 함수
  • $1 \le x$에서는 1이다.

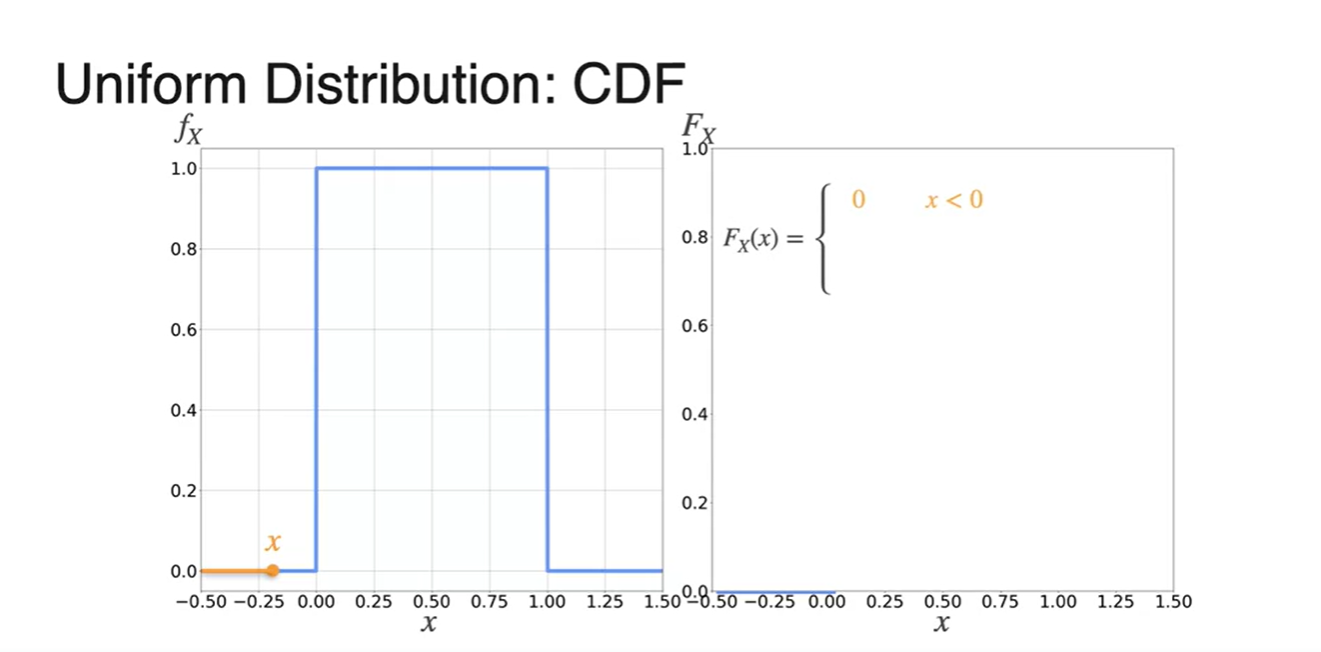
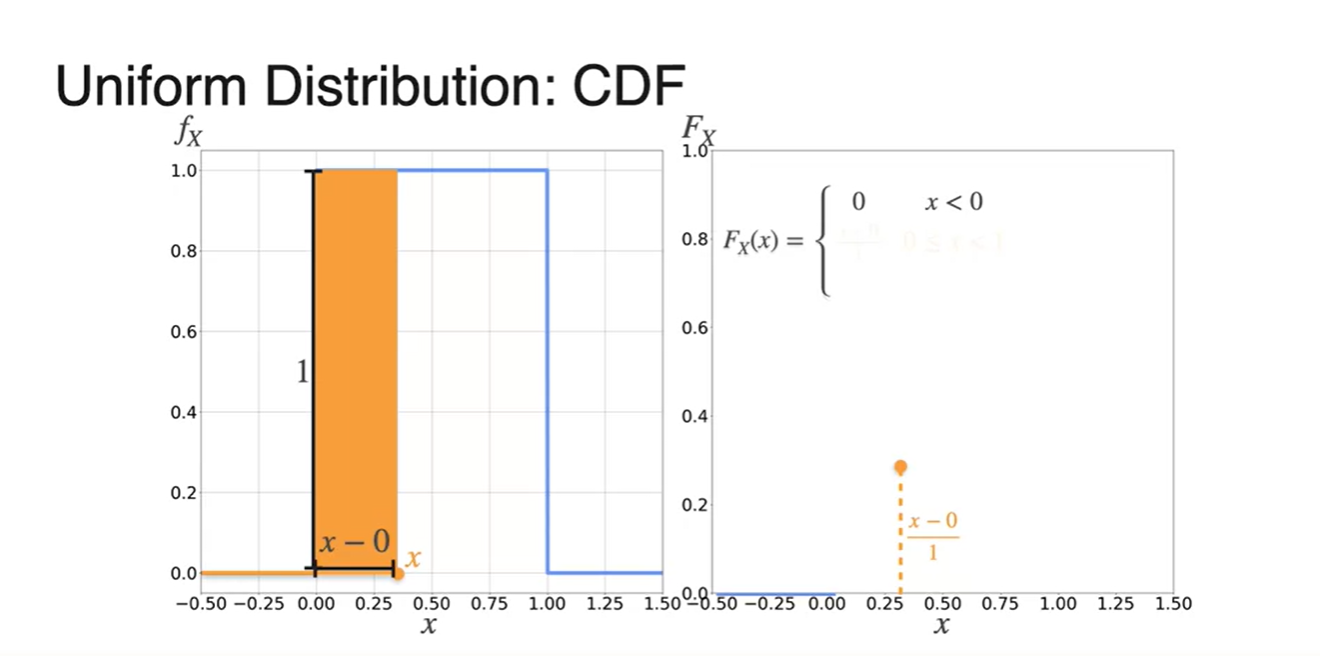
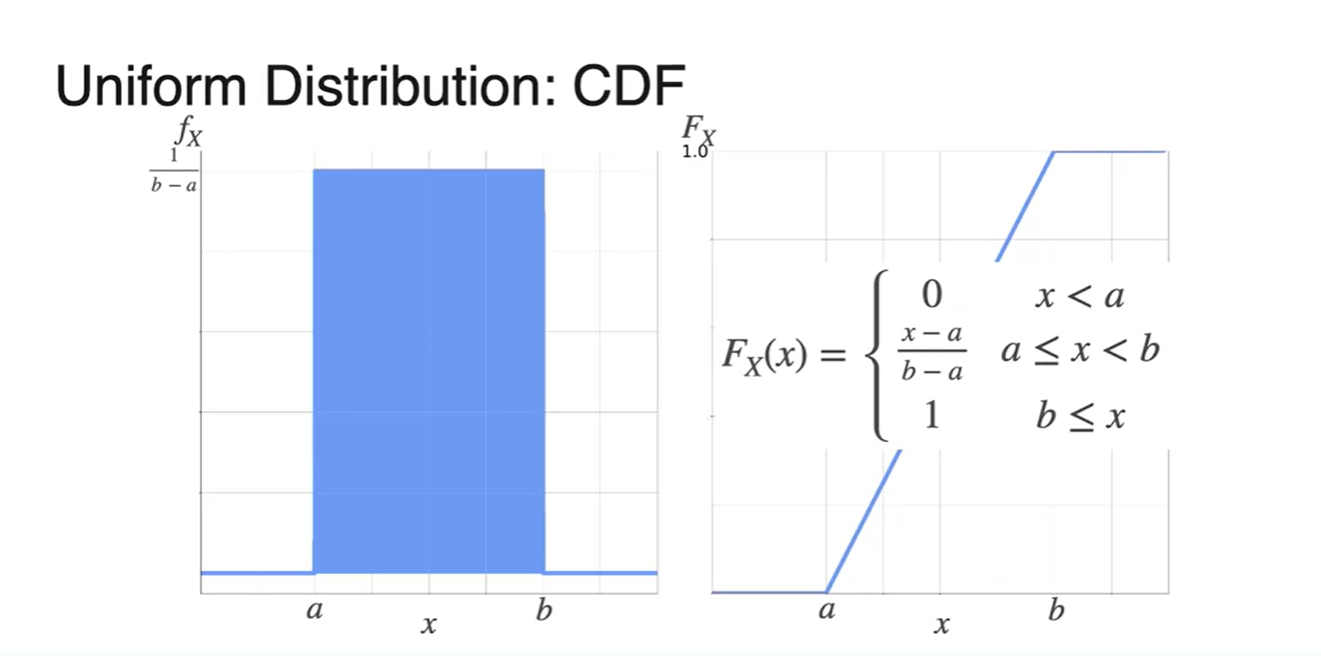
• Uniform distribution의 CDF를 수식으로 나타내면 다음과 같다.

  $f_X(x) = \begin{cases} 0 & {x < a} \\ \displaystyle \frac{x-a}{b-a} & {a \le x < b} \\ 1 & {b \le x} \end{cases}$

Normal Distribution(Gaussian Distribution)

• 가장 보편적이고 중요한 확률 분포인 Normal Distribution(Gaussian Distribution)에 대해 알아보자.

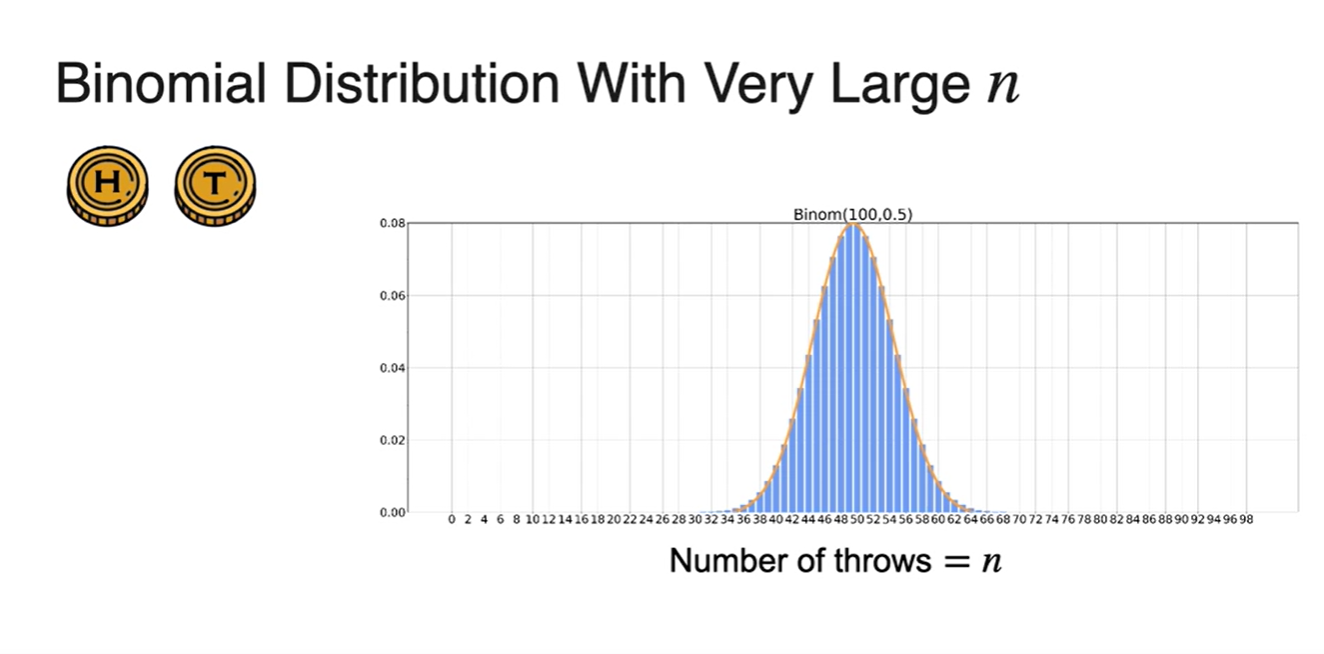
  • Binomial Distribution을 따르는 시행을 무한히 큰 $n$에 대하여 시행했을 때의 분포는 아래와 같은 그래프 모양을 가진다.

  • 이와 같은 Bell shaped curve 그래프가 Normal distribution의 그래프 형태와 비슷한 모양을 갖는다.

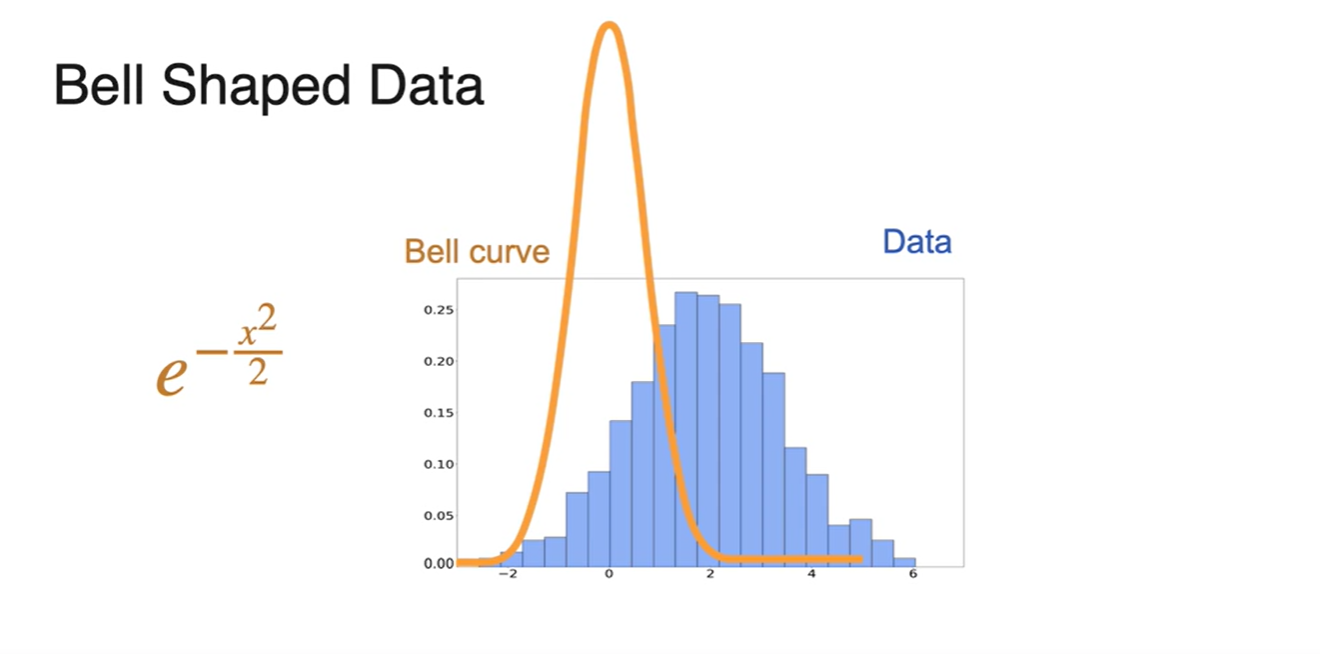
• Bell shaped curve function인 $e^{\displaystyle -\frac{x^2}{2}}$ 함수는 0이 중심인 함수다.

  • 우리의 data 분포는 오른쪽 파란색 그래프와 같이 중점 부분이 치우쳐진 함수다.

    • 위 함수를 조금씩 조정하여 data 분포 함수에 가깝게 만들어보자.

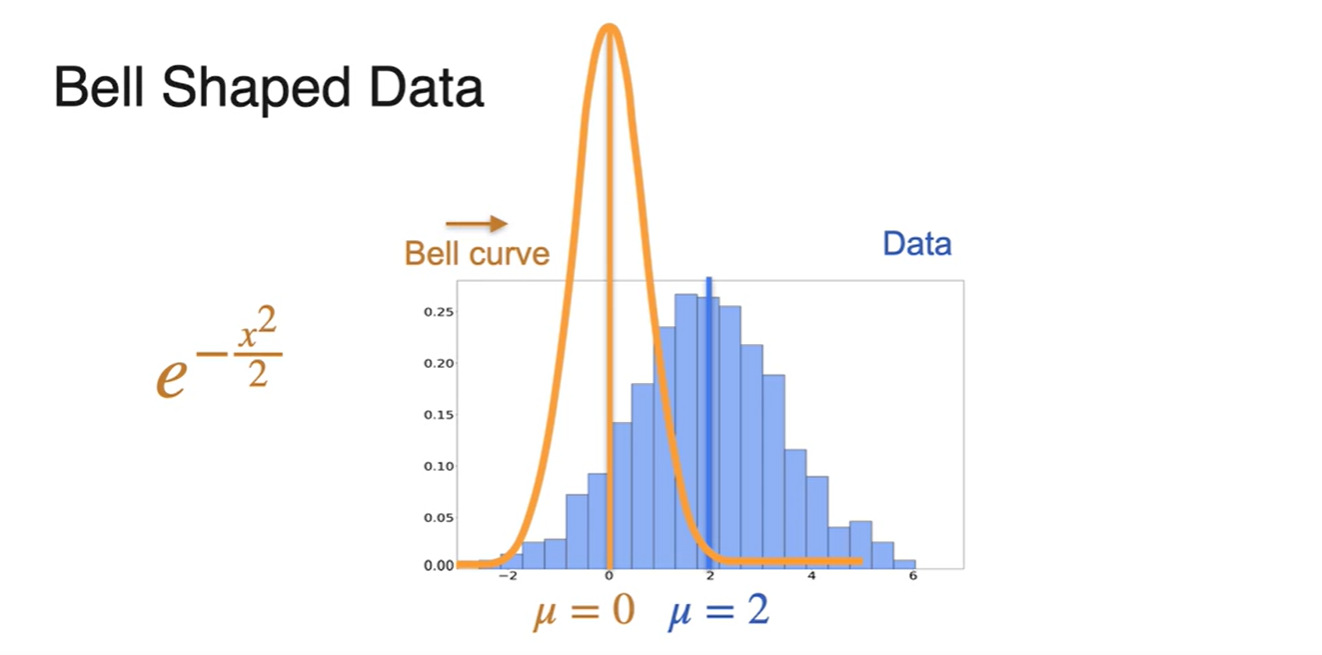
• $e^{\displaystyle -\frac{x^2}{2}}$의 중심인 $\mu$는 0이고 data 분포의 $\mu$는 2다.

  • 우리는 bell curve를 오른쪽으로 움식여야만 한다.

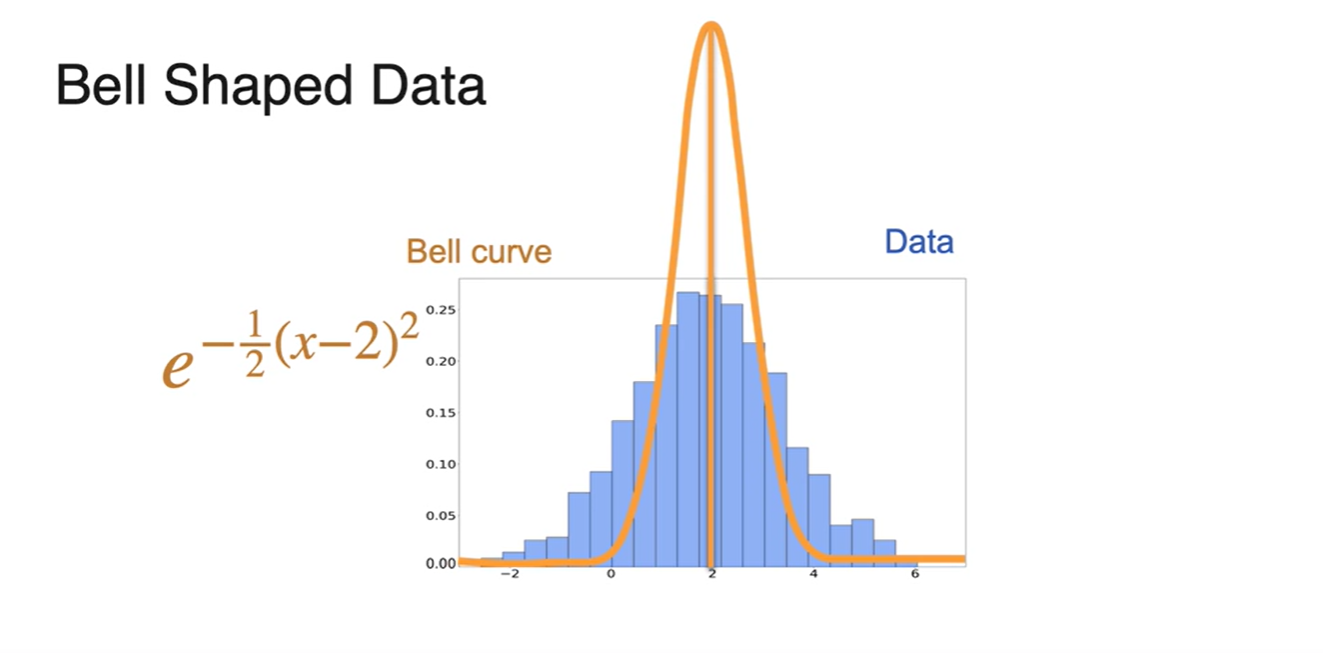
• x를 오른쪽으로 움직일 방법은 $x$를 $x-2$로 치환하면 된다.

  • 따라서 bell curve function이 $e^{\displaystyle -\frac{1}{2}(x-2)^2}$이 되었다.

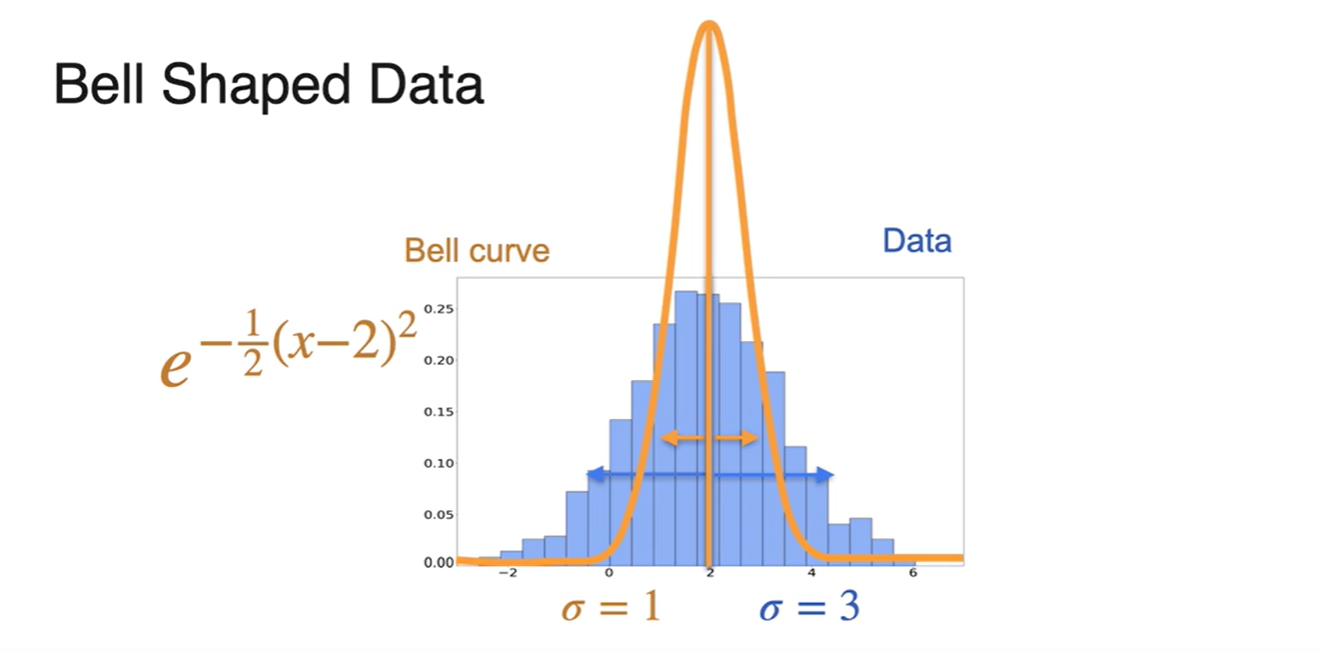
• 이제는 너비를 조정해야 한다.

  • Bell curve의 width $\sigma$는 1, data 분포의 width $\sigma$는 3이다.

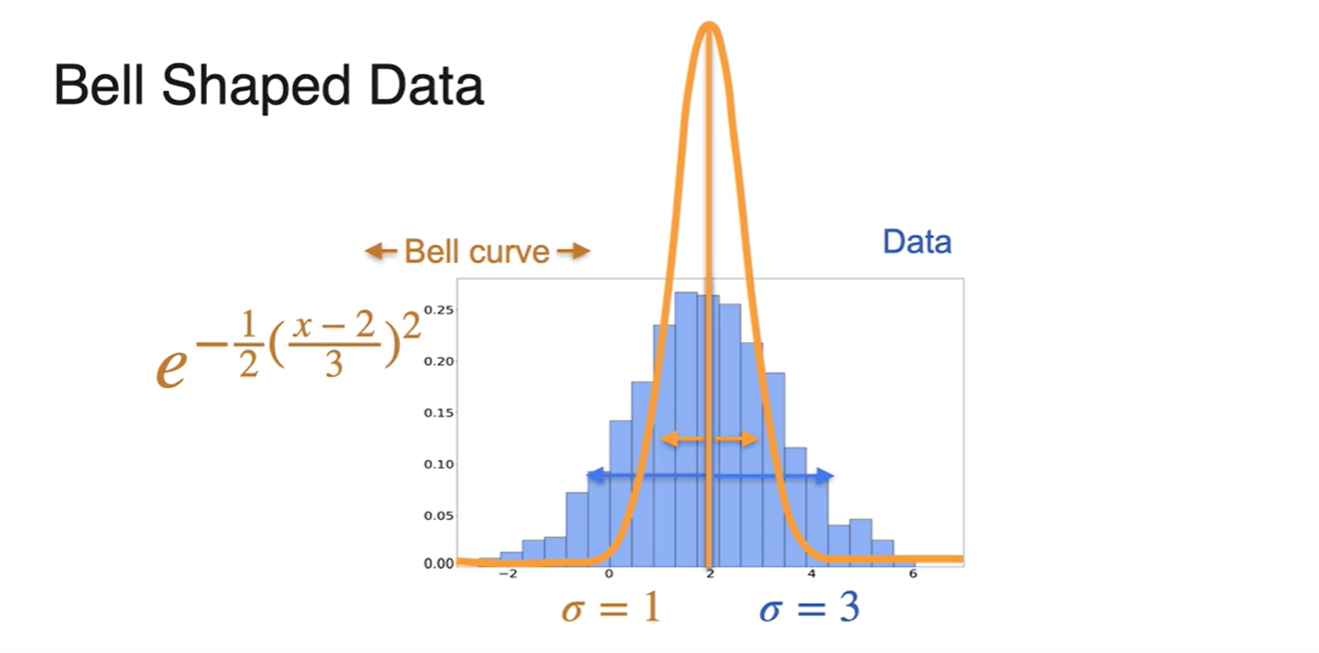
• 너비를 넓히는 일은 변수를 넓히고자 하는 값으로 나누어 치환하는 방법을 사용한다.

  • 따라서 bell curve function이 $e^{\displaystyle -\frac{1}{2}(\frac{x-2}{3})^2}$이 되었다.

• 마지막으로 높이를 변경해야 한다.

  • 높이가 달라지면 확률 전체의 합이 1을 벗어나는 것과 연관성이 있다.

    • 현재 bell curve의 area가 $3 \sqrt{2 \pi}$이므로 이 값으로 전체 함수를 나눠주면 $\displaystyle \frac{1}{3 \sqrt{2 \pi}} e^{\displaystyle -\frac{1}{2}(\frac{x-2}{3})^2}$함수가 된다.

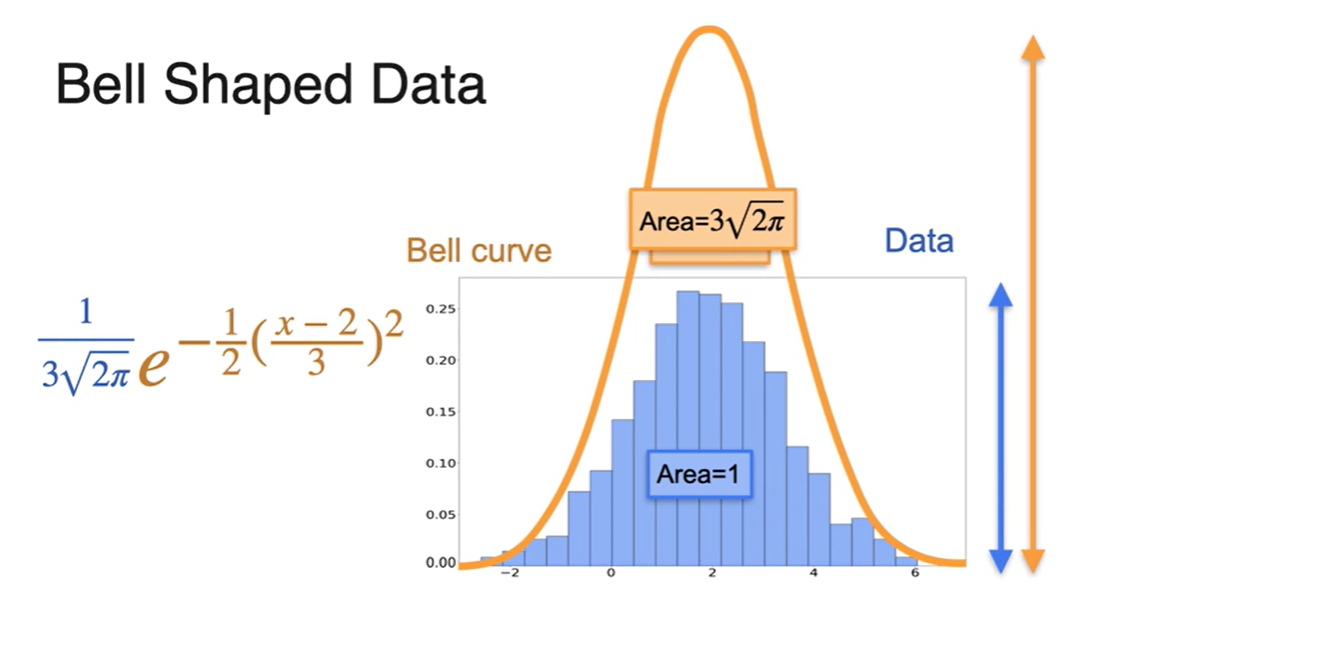
• 최종 bell curve가 data 분포와 거의 동일해진 결과를 나타내면 아래 그림과 같다.

  • $\mu$는 Mean(평균)이며, $\sigma$는 Standard deviation(표준 편차)다.

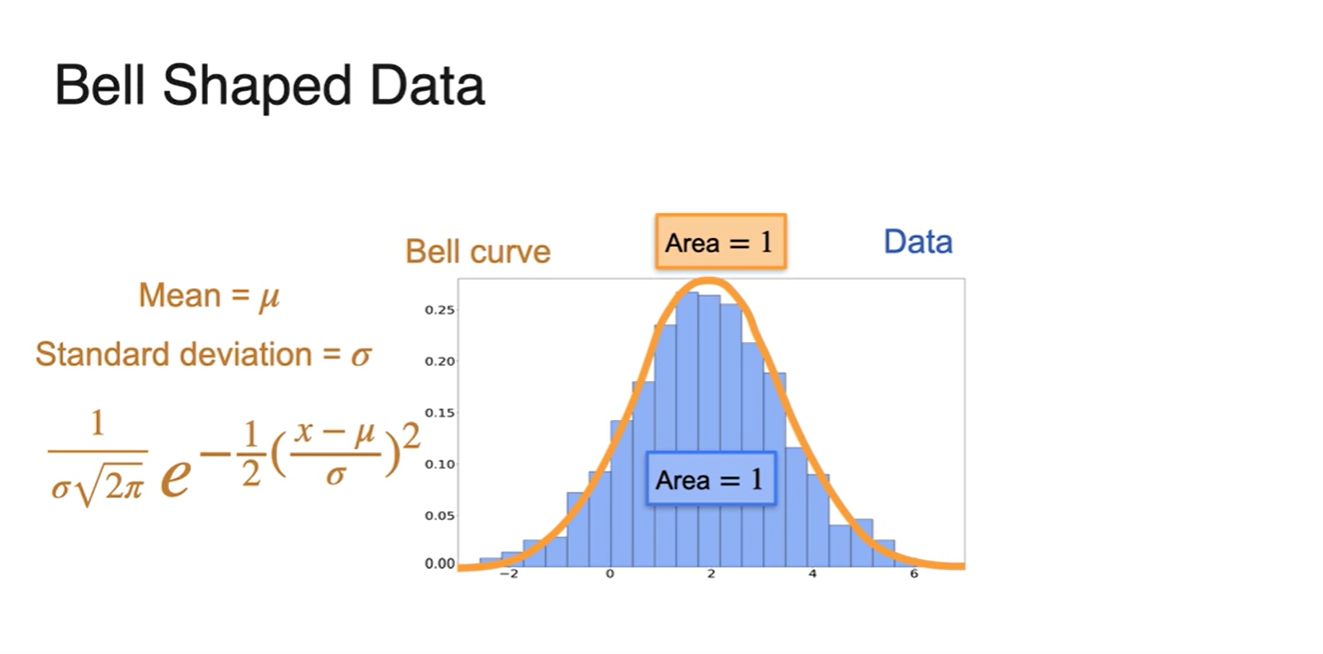
• $\mu$는 중앙 random variable, $\sigma$ function의 width에 해당한다.

  • Normal Distribution의 fundtion 형태는 $\displaystyle \frac{1}{\sigma \sqrt{2 \pi}} e^{\displaystyle -\frac{1}{2}(\frac{x- \mu}{\sigma})^2}$다.

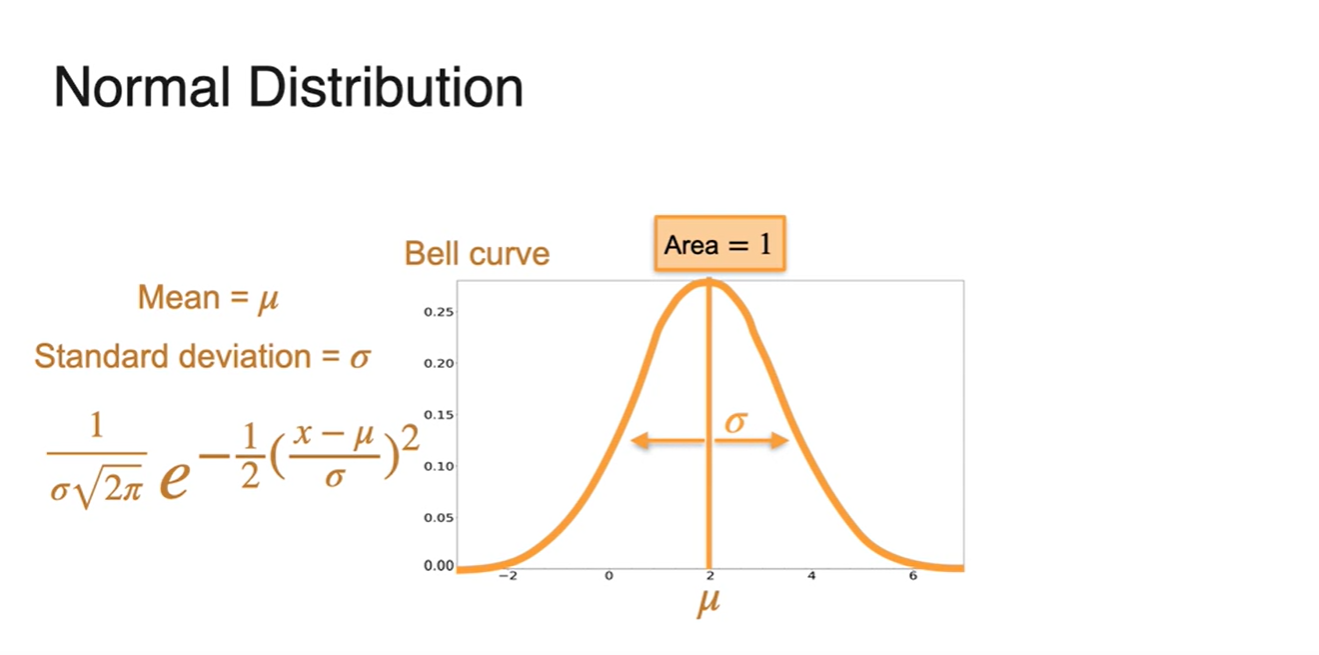
• $\mu$는 center of the bell, $\sigma$ spread of the bell이다.

  • Normal Distribution은 Symmetri한 성질을 띄며 Range가 all real number여야 한다.

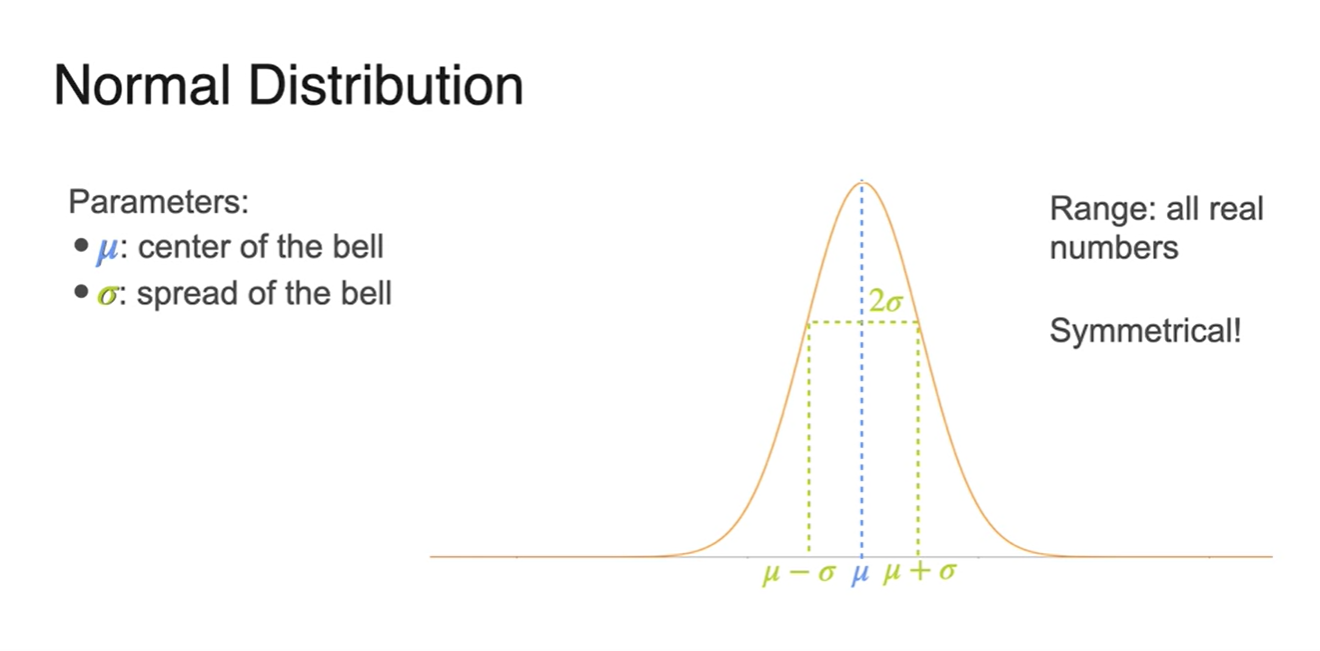
• 앞에 상수로 놓인 $\displaystyle \frac{1}{\sigma \sqrt{2 \pi}}$는 Scailing constant로 쓰인다.

  • Width 의 1/2이 $\sigma$라는 사실도 있다.

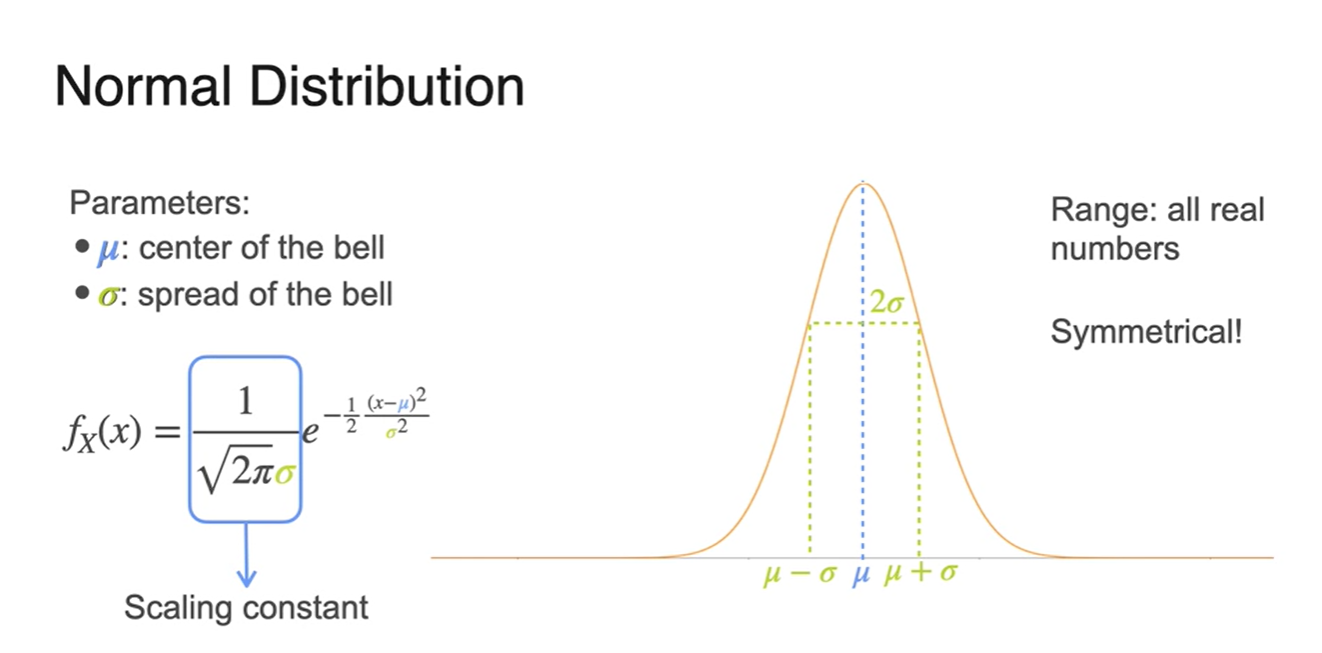
• $\mu$와 $\sigma$는 parameter로서 작용하며, 그래프 모양을 결정하는 요인이다.

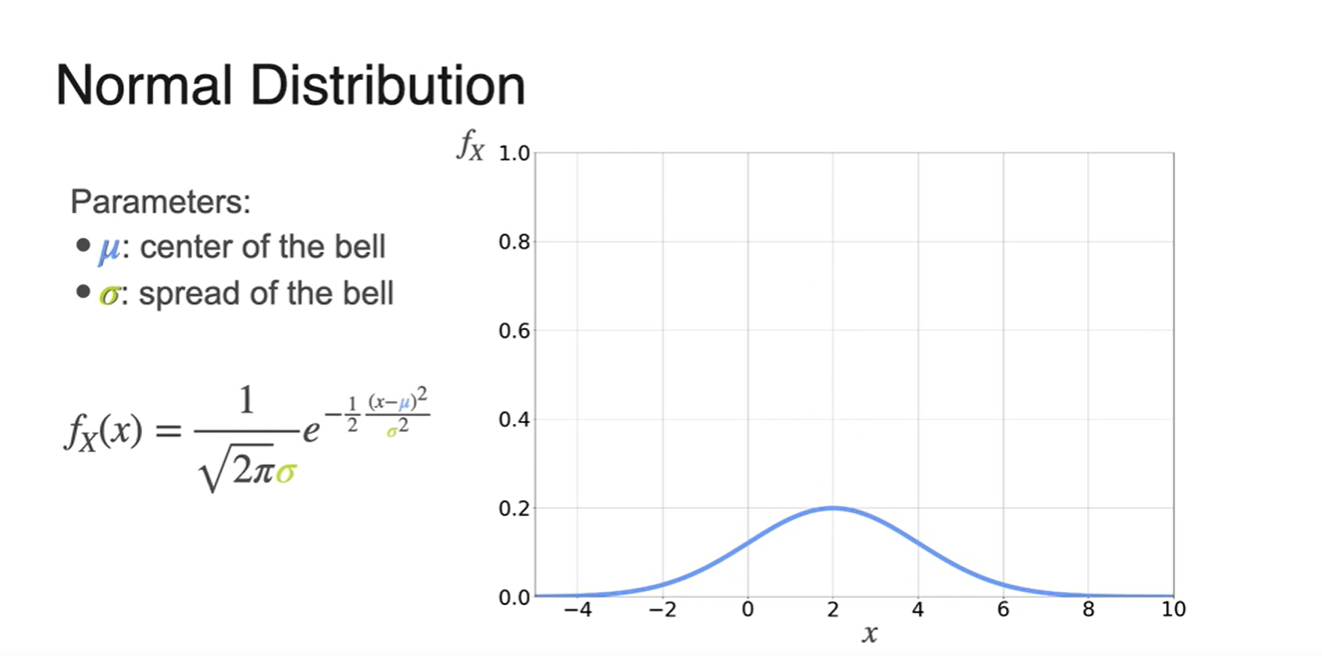
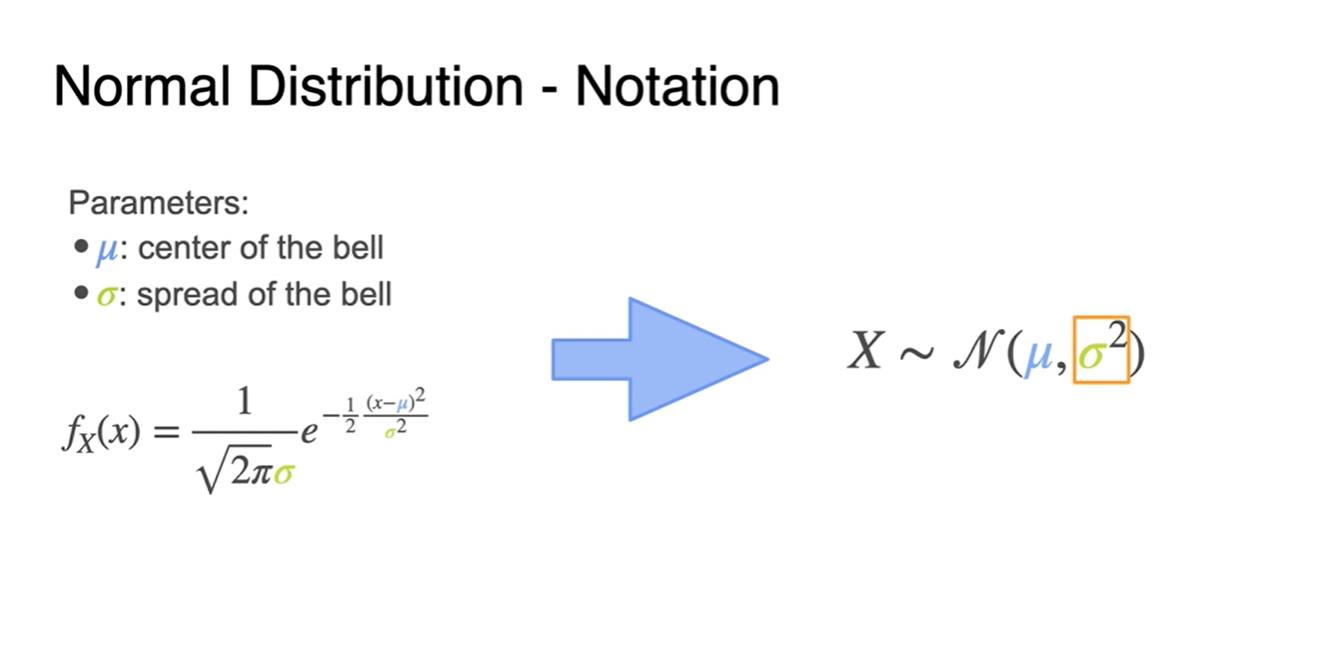
• Normal Distribution의 Notation은 $X \sim N(\mu, \sigma^2)$로 표현하며 $\sigma^2$은 variation(분산)이다.

• 만약 $\mu$가 0, $\sigma$가 1이라면 아래와 같은 그래프와 함수 식이 만들어진다.

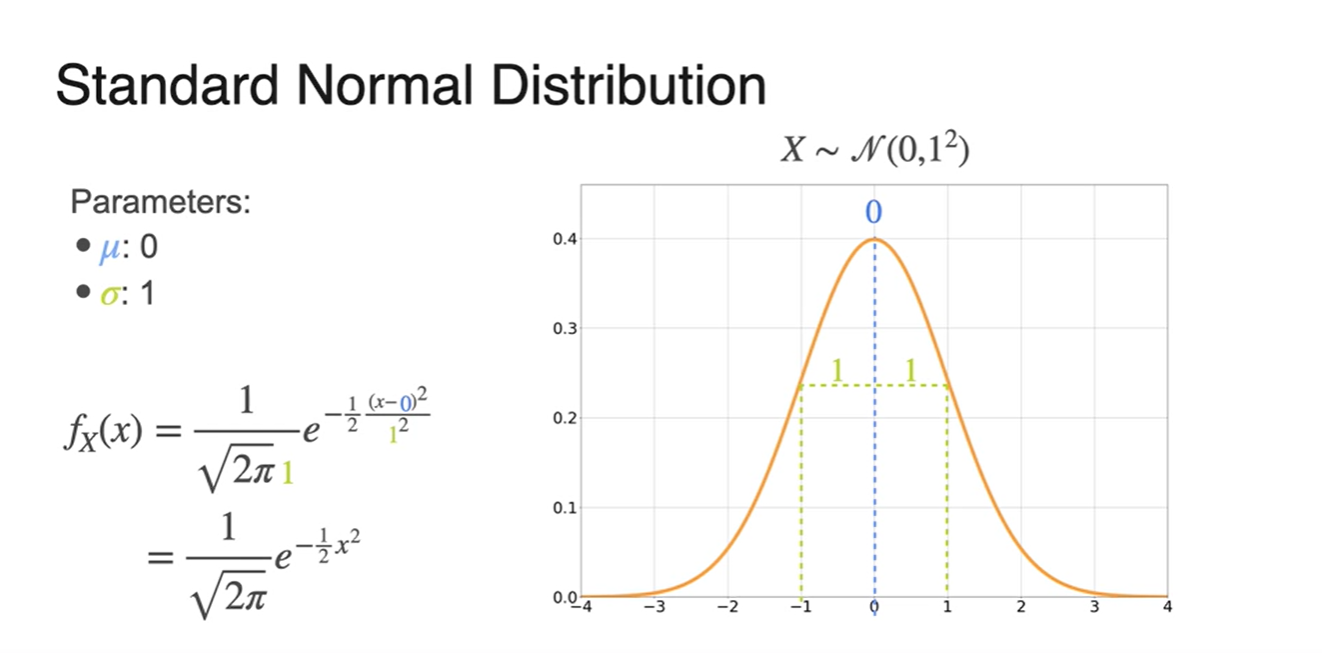
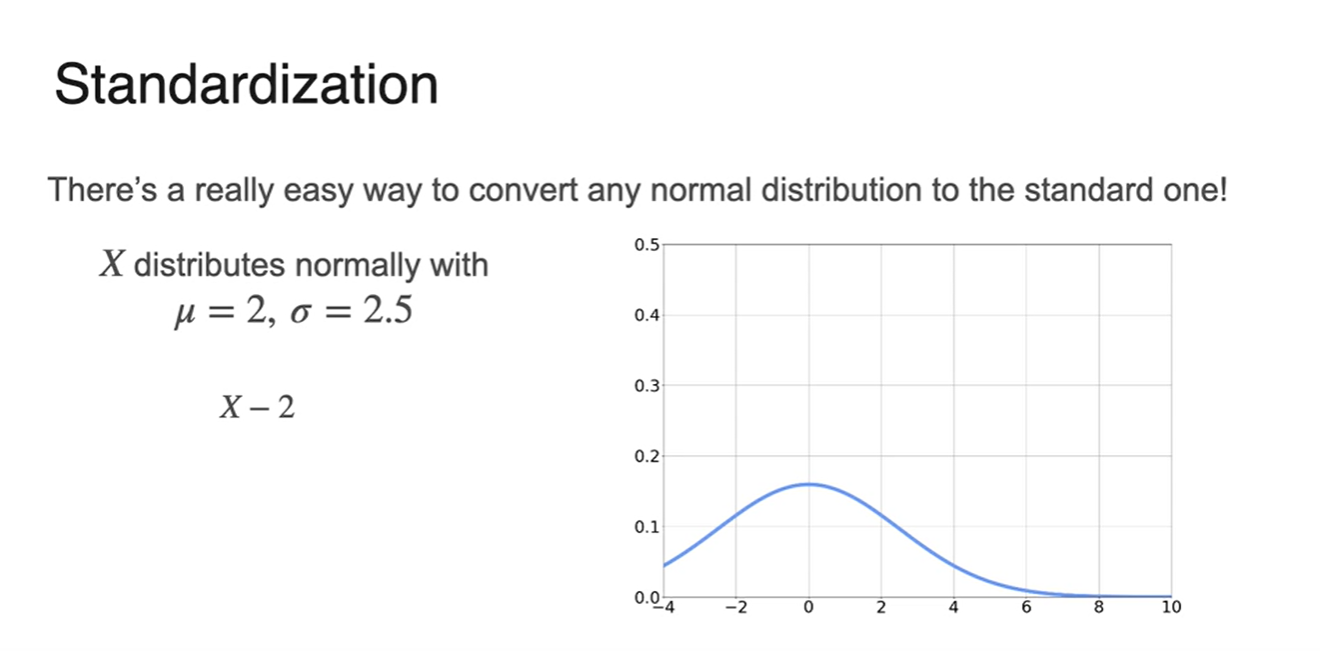
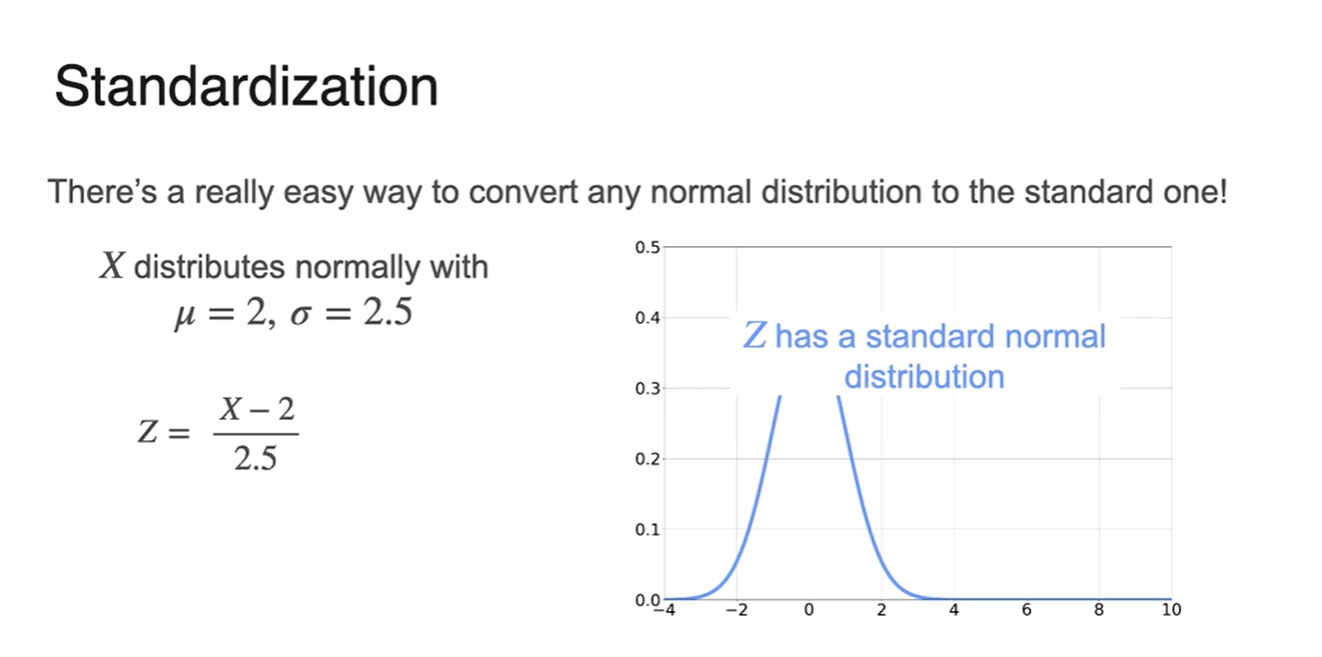
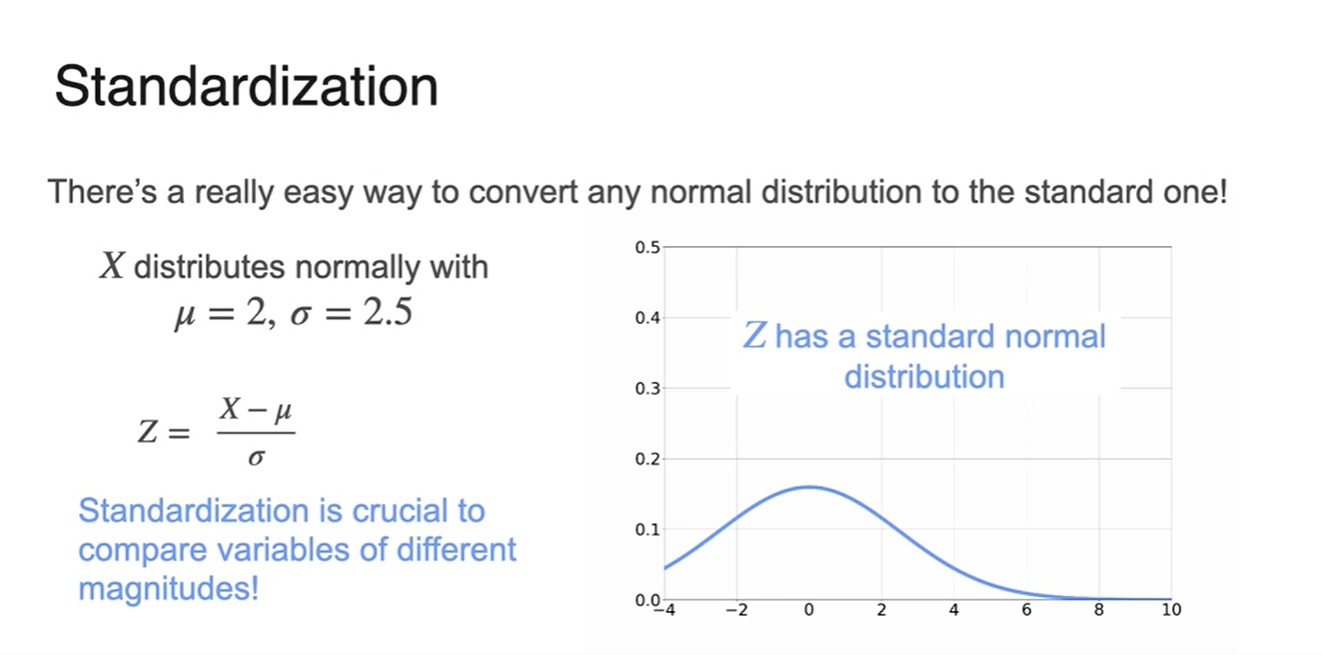
• Normal Distribution으로 standard한 분포를 만드는 일은 매우 쉽다.

  • $\mu$와 $\sigma$만 알았을 때 그래프를 그리는 과정은 다음 그림에 첨부되어 있다.

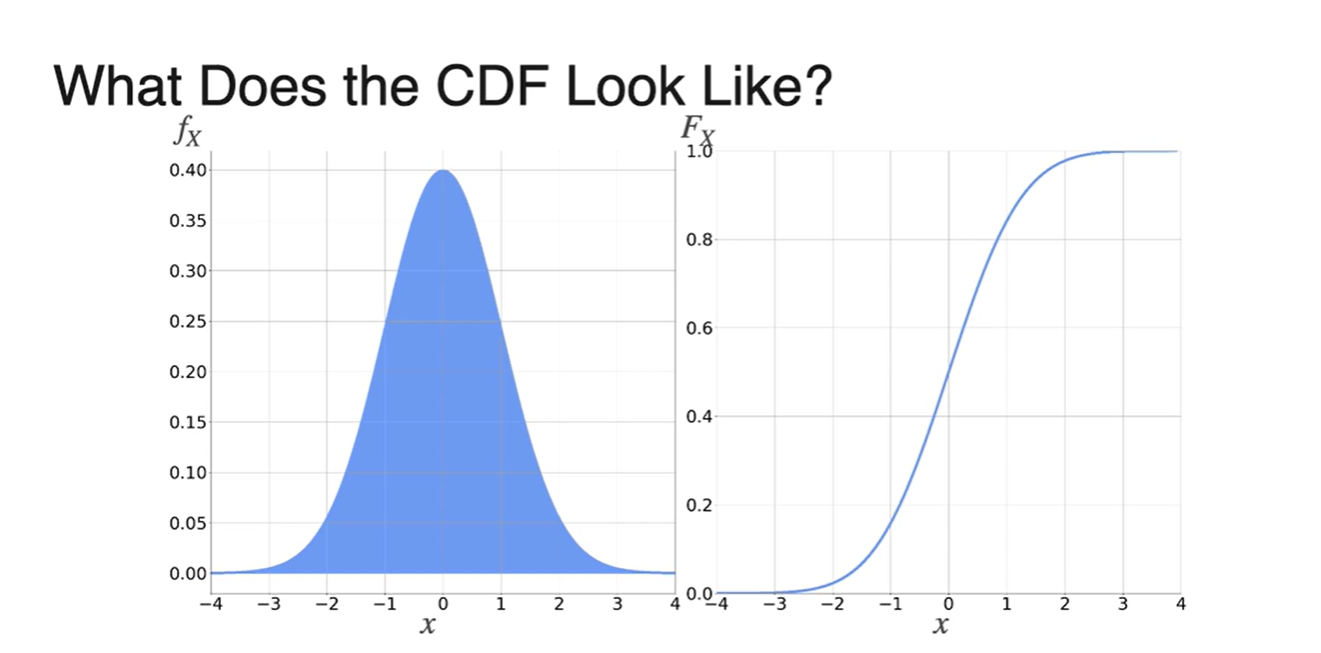
• Normal Distribution의 CDF는 어떻게 그려질까?

  • Smooth하게 증가하는 함수로 다뤄진다.

• 확률을 계산하는 일은 더이상 손으로 불가능하다..

  • 예전에는 table data를 모두 적어 가능했을지 몰라도 지금은 컴퓨터가 한다.

• Normal Distribution이 쓰이는 예시들은 아래의 상황에서 주로 쓰인다.

  • 실제 삶과 연관되는 매우 다양한 case들이 normal distribution을 따르며 ML에서 또한, 특히 이 분포를 중요하게 여긴다.

(Optional) Chi-Squared Distribution

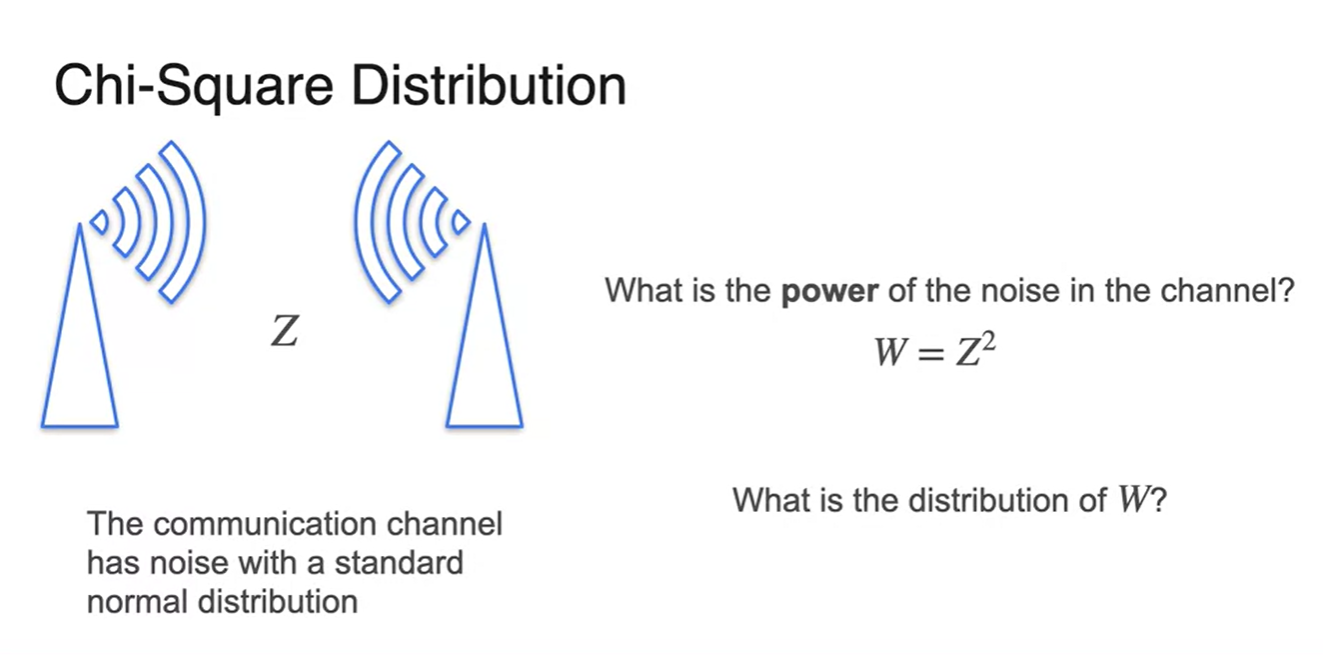
• Chi-Squared Distribution, 만약 전파를 주고 받는 두 송전탑이 있다고 해보자.

  • Atmospheric condition과 예상치 못한 변수들로 인해 수신한 정보에 noize가 섞이게 된다면, 이는 기존 10010 값에 $Z$가 더해진 형태로 출력된다고 볼 수 있다.

• Noise $Z$가 standard normal distribution을 따른다면, power of noise $Z^2$은 얼마일까?

  • $Z^2$을 $W$로 치환하여 $W$의 확률 분포를 알아내보자.

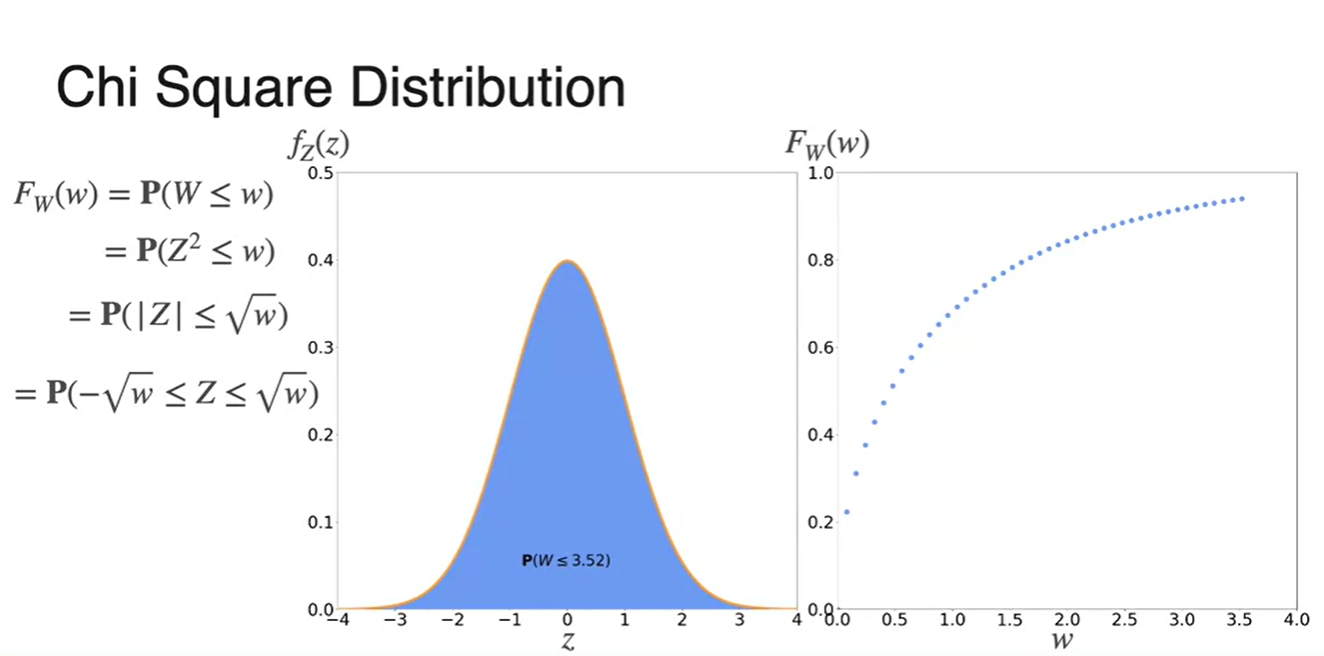
• 우리가 알고자 하는 누적 확률 CDF는 $z$에 대한 $f_Z(z)$로부터 유도될 수 있다.

  • $F_W(w) = P(W \le w)$

    $= P(Z^2 \le w)$

    $= P(|Z| \le \sqrt{w})$

    $= P(-\sqrt{w} \le Z \le \sqrt{w})$

  • $Z$가 normal distribution을 따르기 때문에 해당 그래프의 구간 적분 값이 $W$의 CDF다.

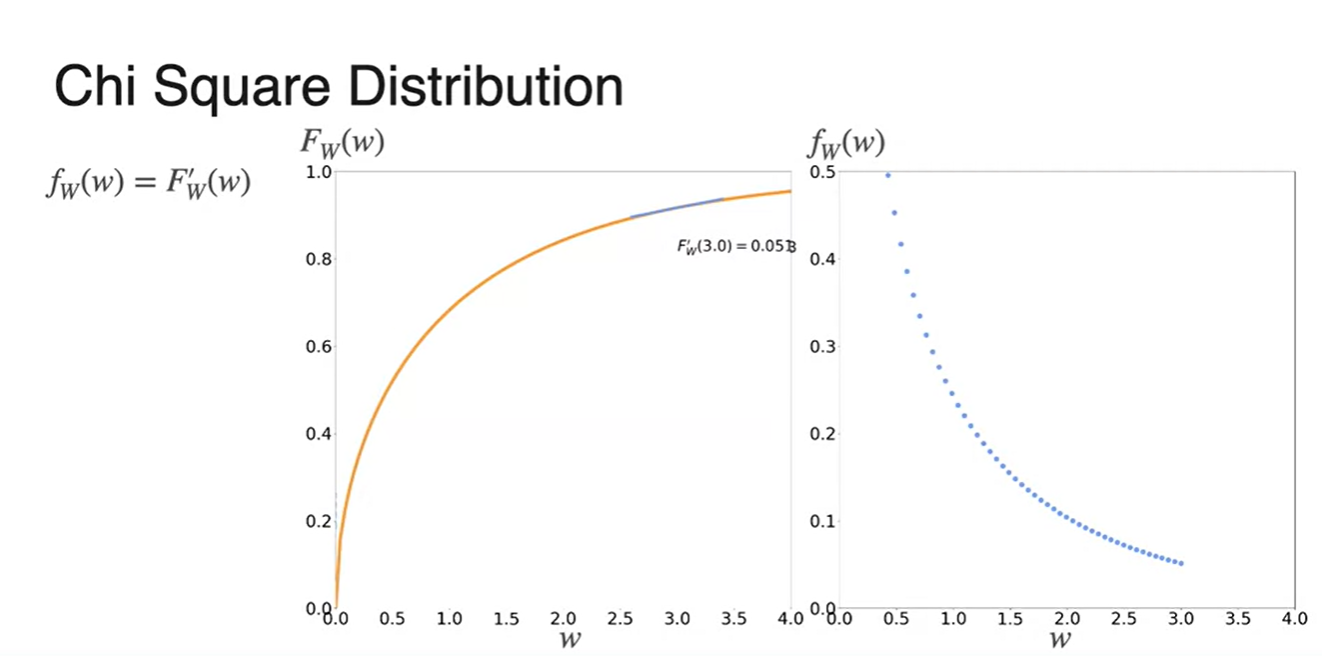
• $W$의 PDF를 알고 싶다면 CDF인 $F_W(w)$를 미분함으로써 구할 수 있다.

  • 관계를 정리하면 $f_W(w) = F'_W(w)$임을 알 수 있다.

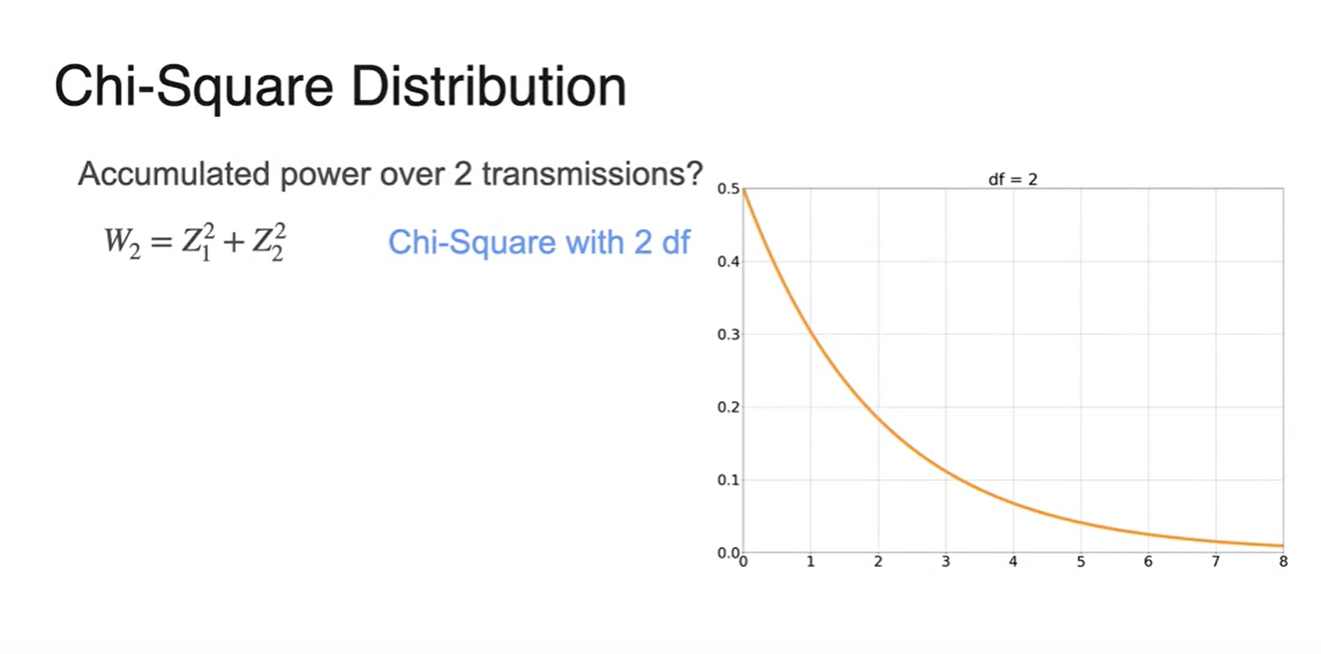
• Chi-Square Distribution은 normal distribution을 확률 분포로 갖는 여러 개의 $Z$의 합을 모델링하고 싶을 때 쓰인다.

  • 만약 $W_2 = Z_1^2 + Z_2^2$라면 degrees of freedom은 2개며 그래프 형태는 아래와 같다.

• 만약 $W_5 = Z_1^2 + Z_2^2 + Z_3^2 + Z_4^2 + Z_5^2$라면 degrees of freedom은 5이며 그래프 형태가 조금 더 퍼진 형태를 띤다.

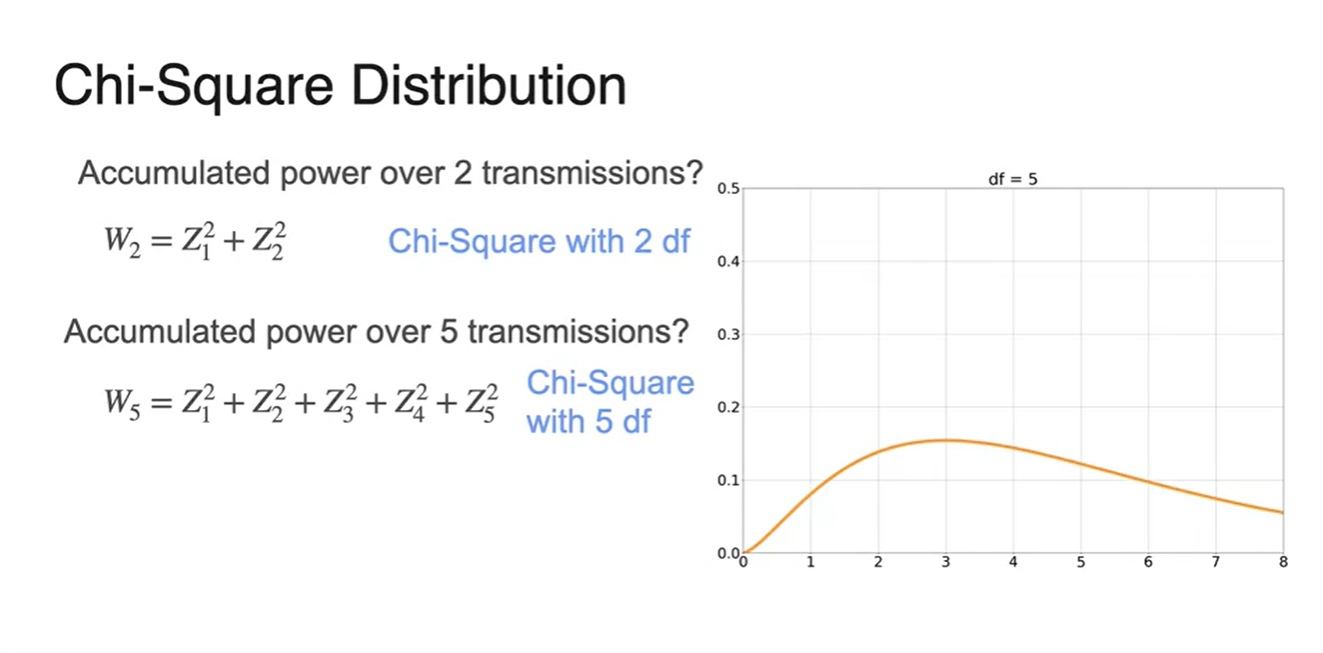
• 더해지는 noise가 클수록 분포는 more spread, more symmetrical해진다는 특성이 있다.

  • k transmissions일 때, $W_k = \displaystyle \sum_{i=1}^{k} Z_i^2$를 모델링하면 오른쪽 그래프 형태를 띤다.

    • 참조 : 카이제곱 분포

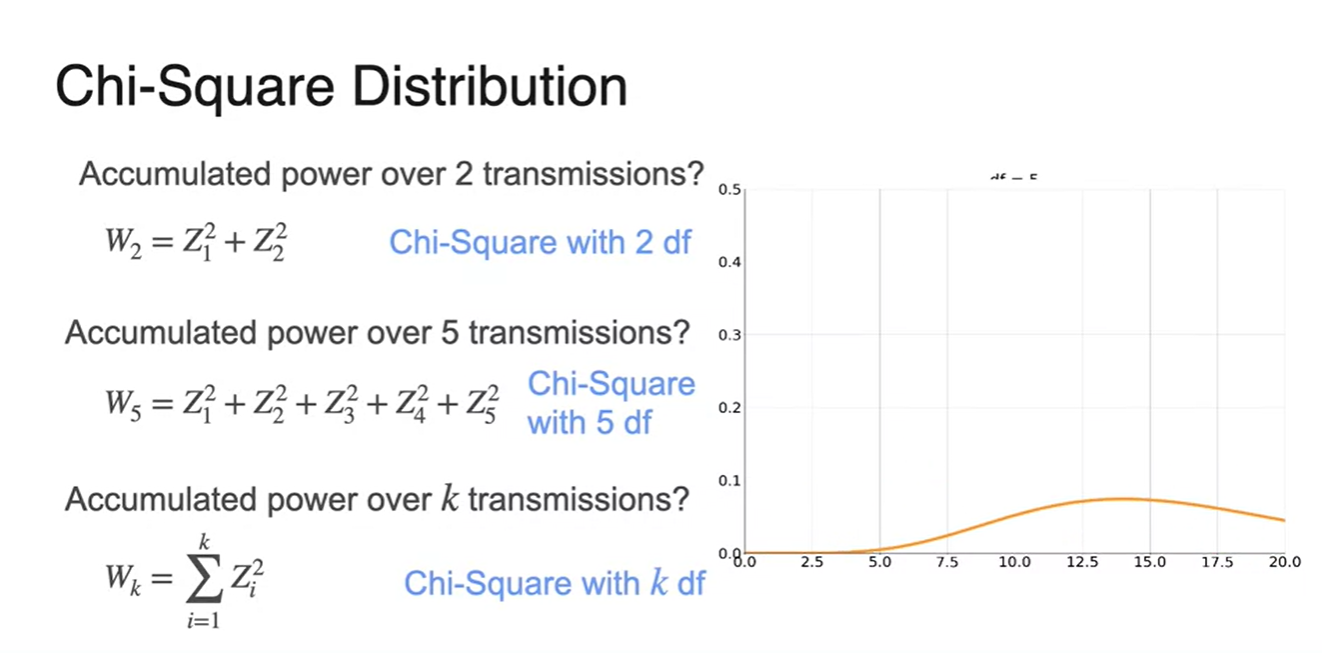
Sampling from a Distribution

• Distribution이 결정되어 있을 때 변수를 Sampling하는 방법에 대해 알아보자.

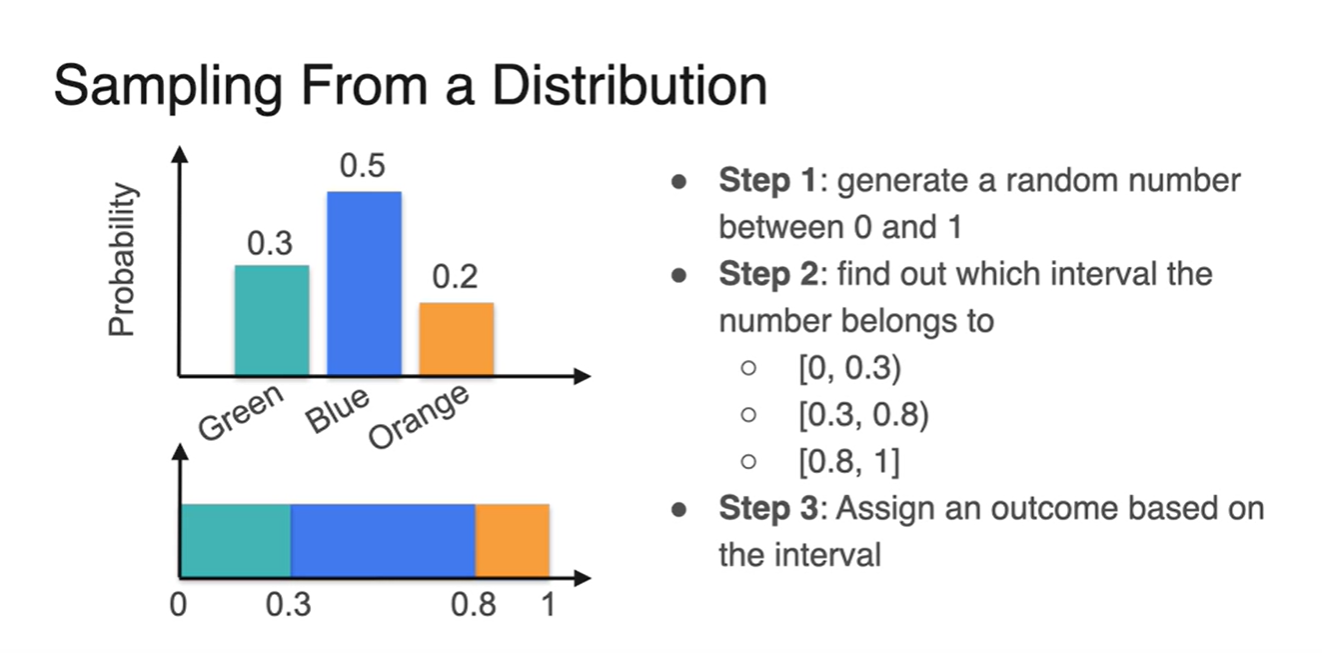
  1. 0과 1 사이의 값을 random하게 generate한다.

  2. Generate한 값이 [0, 0.3), [0.3, 0.8), [0,8, 1) 세 구간 중 어느 구간에 속하는지 알아낸다.

  3. 결과를 interval에 표시한다.

     • 몇 가지 변수들만이 존재할 때, 확률의 크기가 크면 클수록 Blue 변수의 개수가 다른 색들의 변수 개수보다 좀 더 많을 것이다.

     • 따라서 각 구간의 확률 크기에 따라 random 변수가 놓일 구간의 확률도 결정된다.

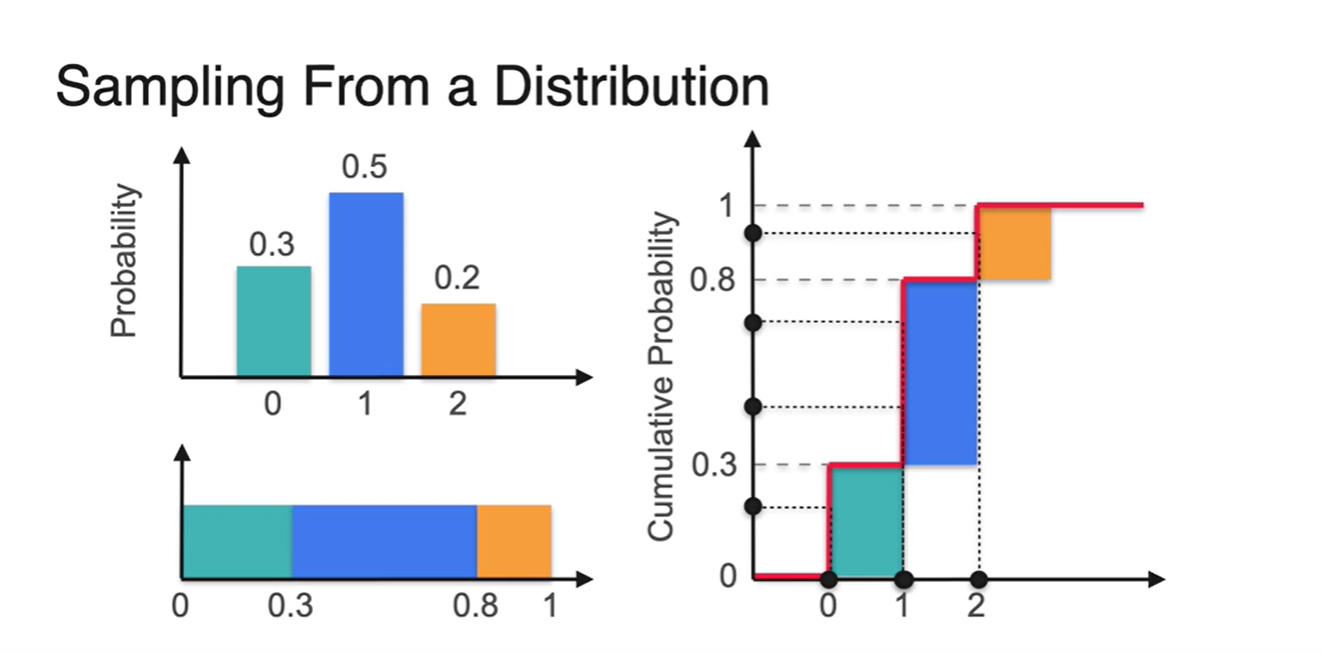
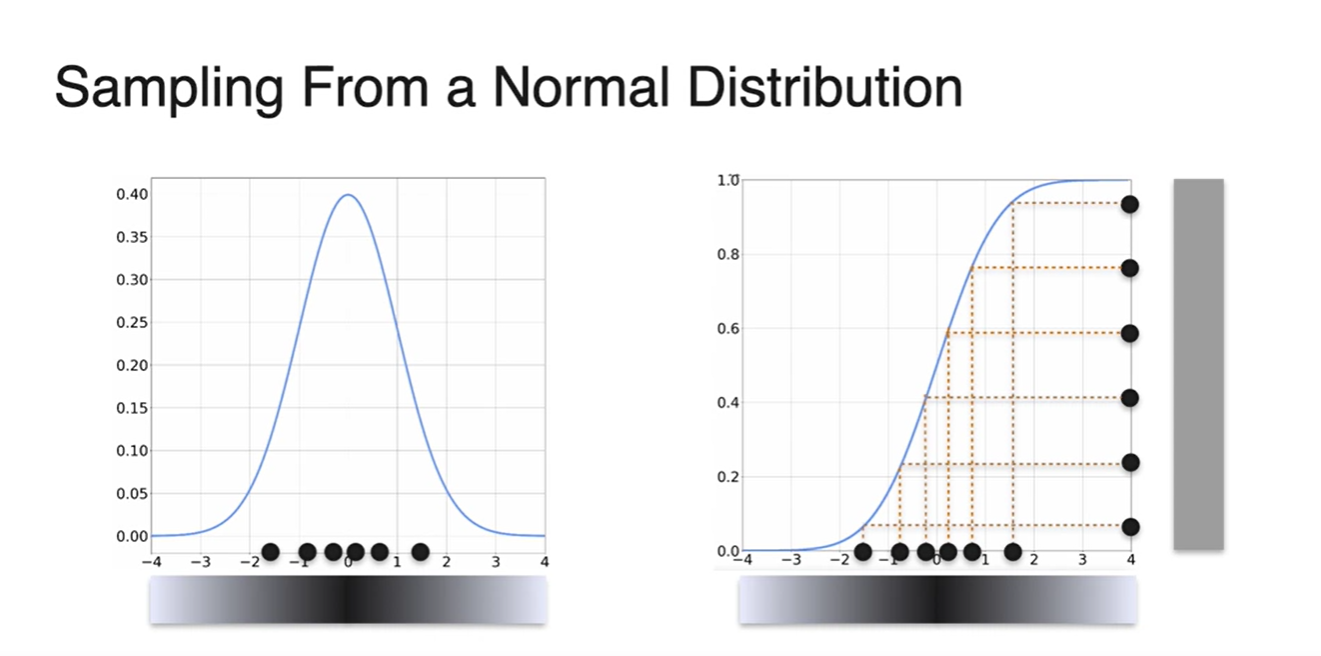
• 아래 분포를 CDF로 나타내면 오른쪽 그림과 같이 그려진다.

  • 그래프를 오른편에서 바라보았을 때 Orange, Blue, Green 각각의 확률(y축)을 찍어 해당 변수(x축)가 어떤 값인지 기록해보자.

    • 2가 1번, 1이 2번, 0이 1번 나왔다.

• Normal Distribution의 CDF를 통해 Random variables를 Sampling하는 방법 또한 마찬가지다.

  • CDF의 확률을 잡아 sampling된 변수들의 분포를 그라데이션으로 나타내면, PDF에서의 확률 분포와 동일한 분포를 얻어낼 수 있다.

---

• 출처 : [Coursera] Mathmatics for Machine Learning and Data Science