[MMD] Probability & Statistics for Machine Learning & Data Science Week 2
Week 2 - Describing probability distributions and probability distributinos with multiple variables
Lesson 1 - Describing Distributions
Expected Value
-
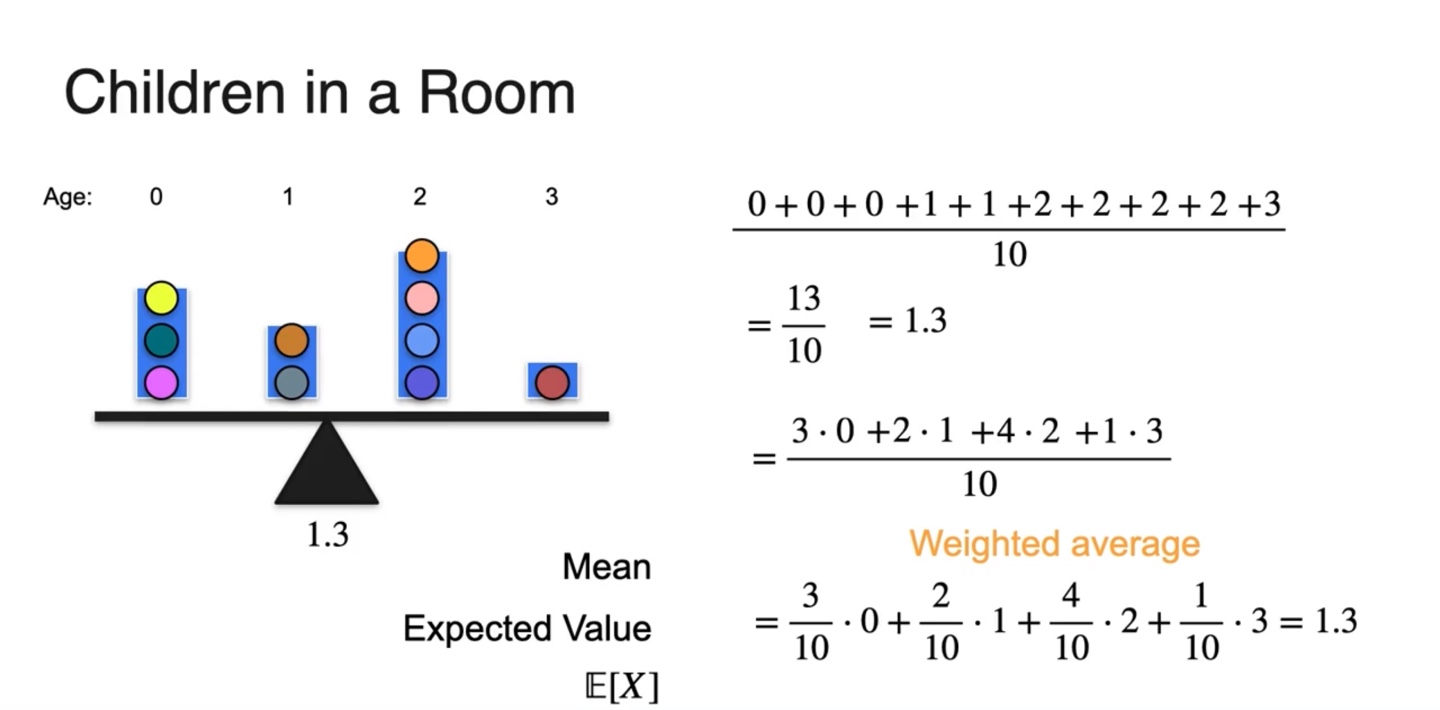
연령대에 따른 사람들의 분포를 아래에 나타내 보자.
- 0세부터 3세까지의 나이만을 나타내었다.
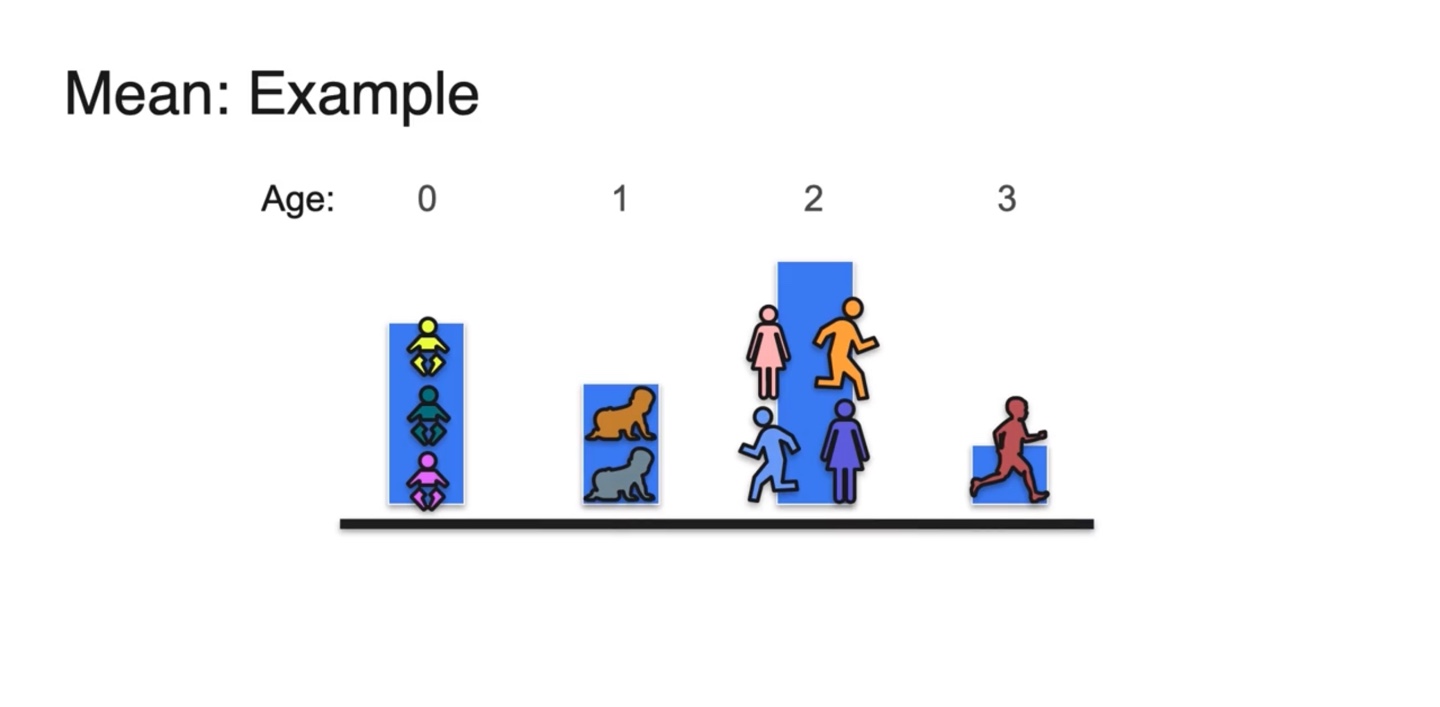
-
그림을 단순화하여 색깔 있는 공으로 히스토그램을 다시 표현해 보자.
- 그리고 각 공은 age만큼의 무게를 지닌다고 가정한다.
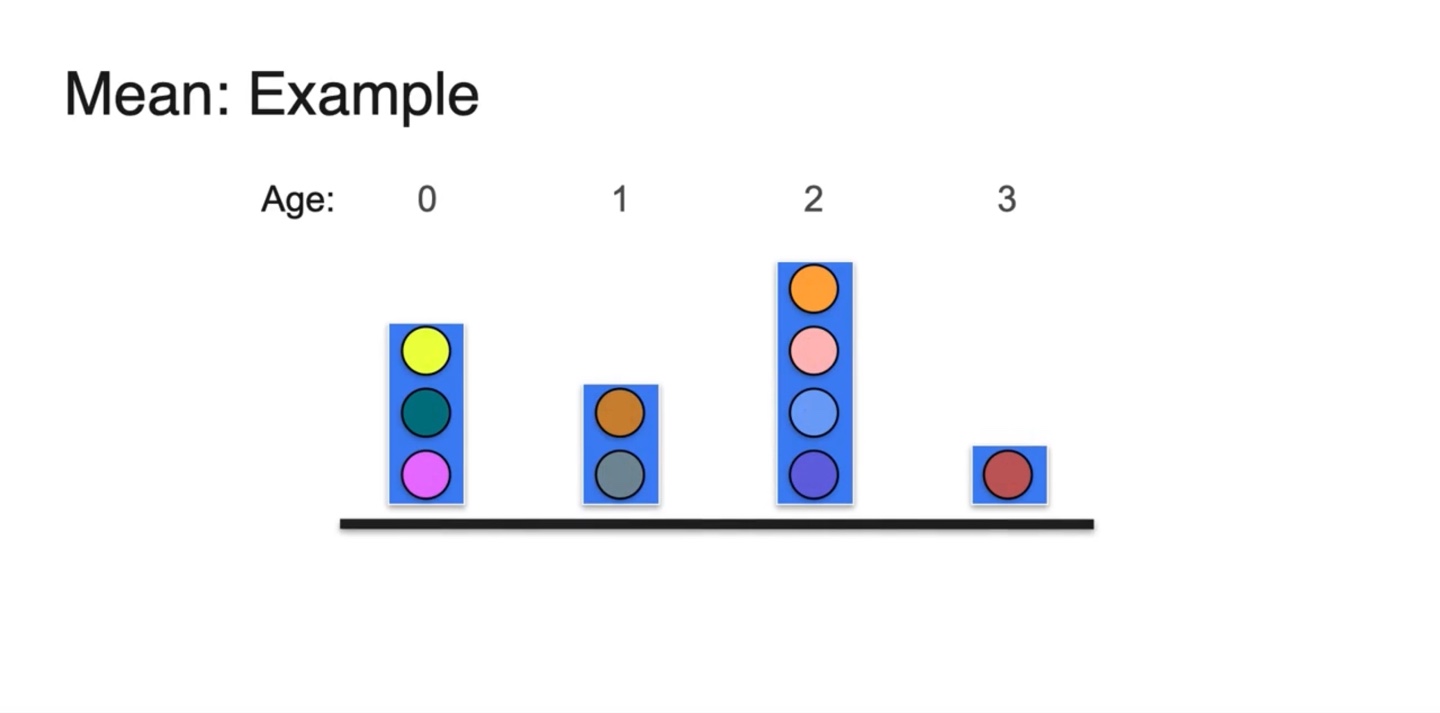
-
이들의 무게 중심을 찾으면 1.3의 age에 위치한다는 것을 알 수 있다.
- 어떻게 계산되었을까?
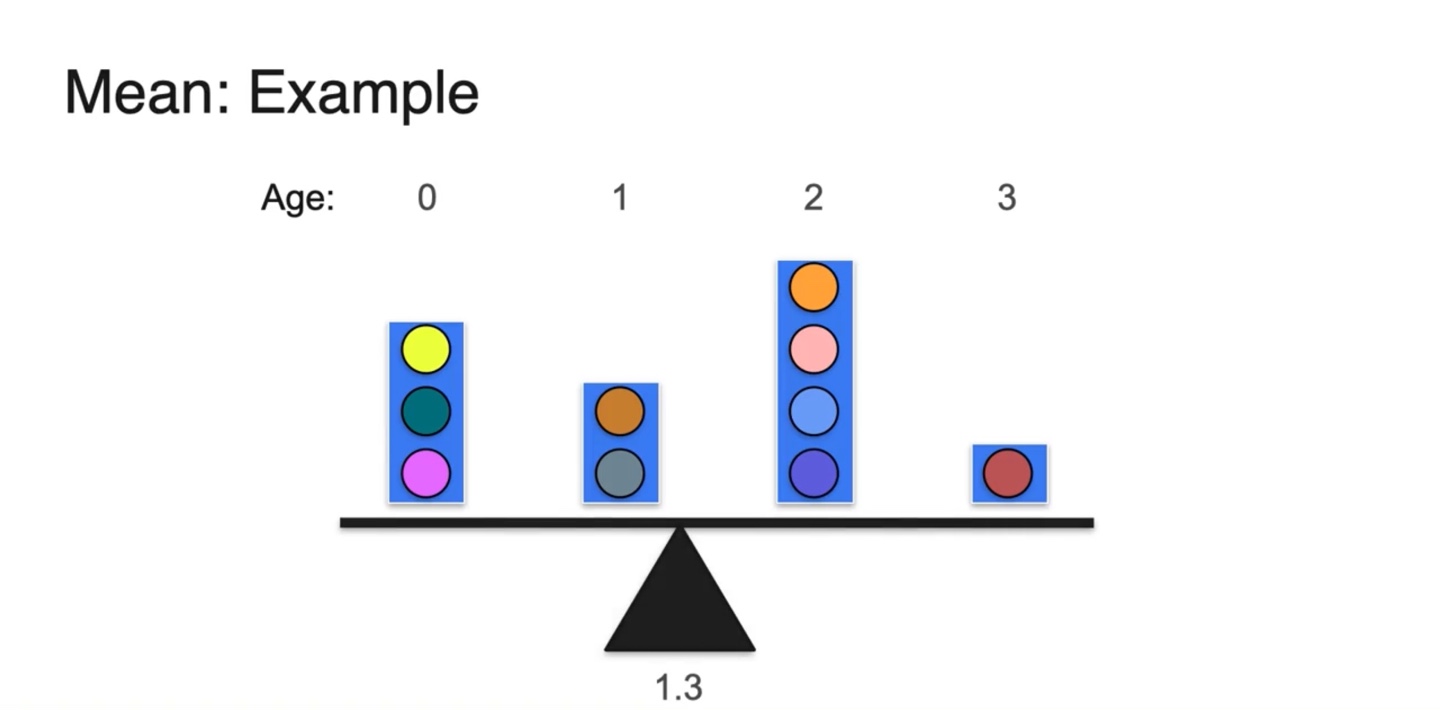
-
무게가 age인 공들의 전체 무게를 평균 내면 의 결과가 나온다.
- 즉, 평균값은 무게 중심의 위치와 동일하다!
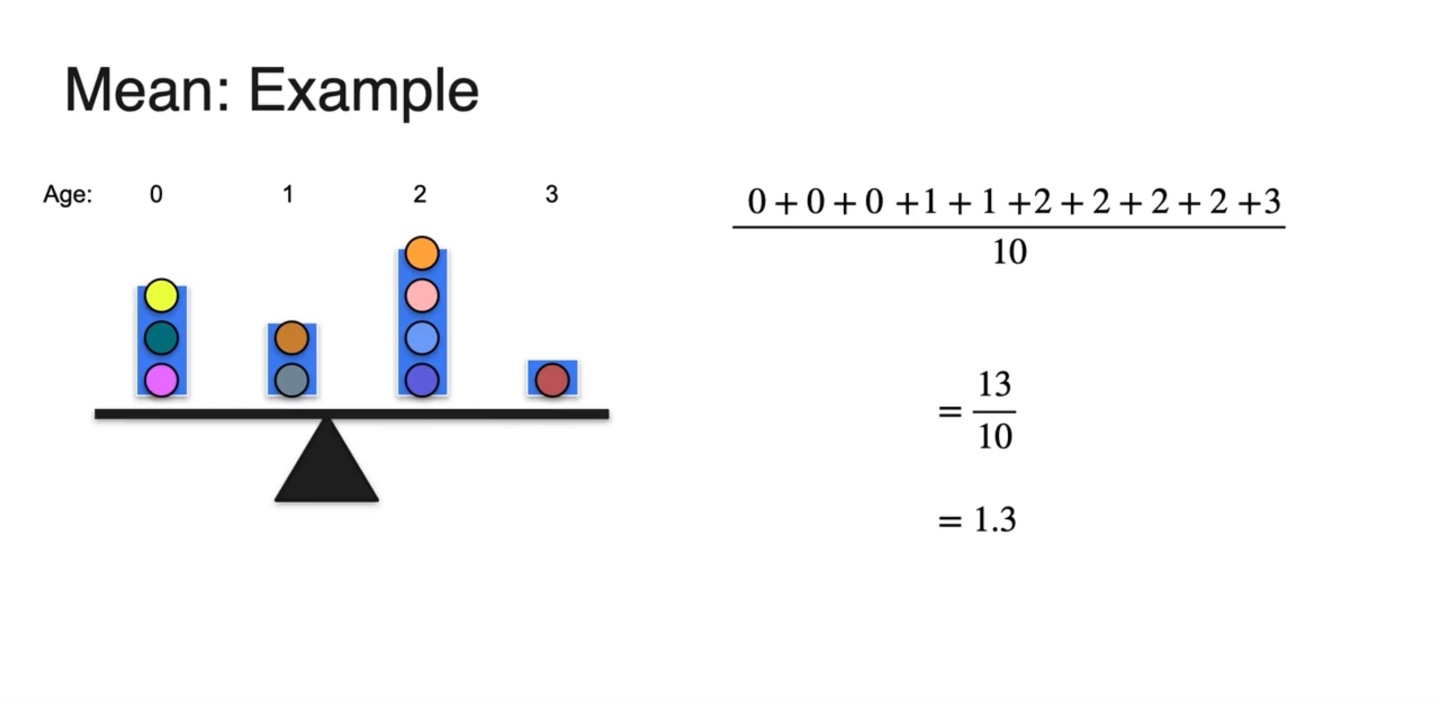
-
각 age와 개수의 곱 그리고 전체 합으로 나타낸다면 다음과 같이 표현된다.
-
-
전체 개수의 비율 즉, {확률 * 확률 변수(Random variable)}로 표현되며, weighted average가 평균의 정의이다.
-
Expected value라고 하며 기호로는 라 표기한다.
-
-
-
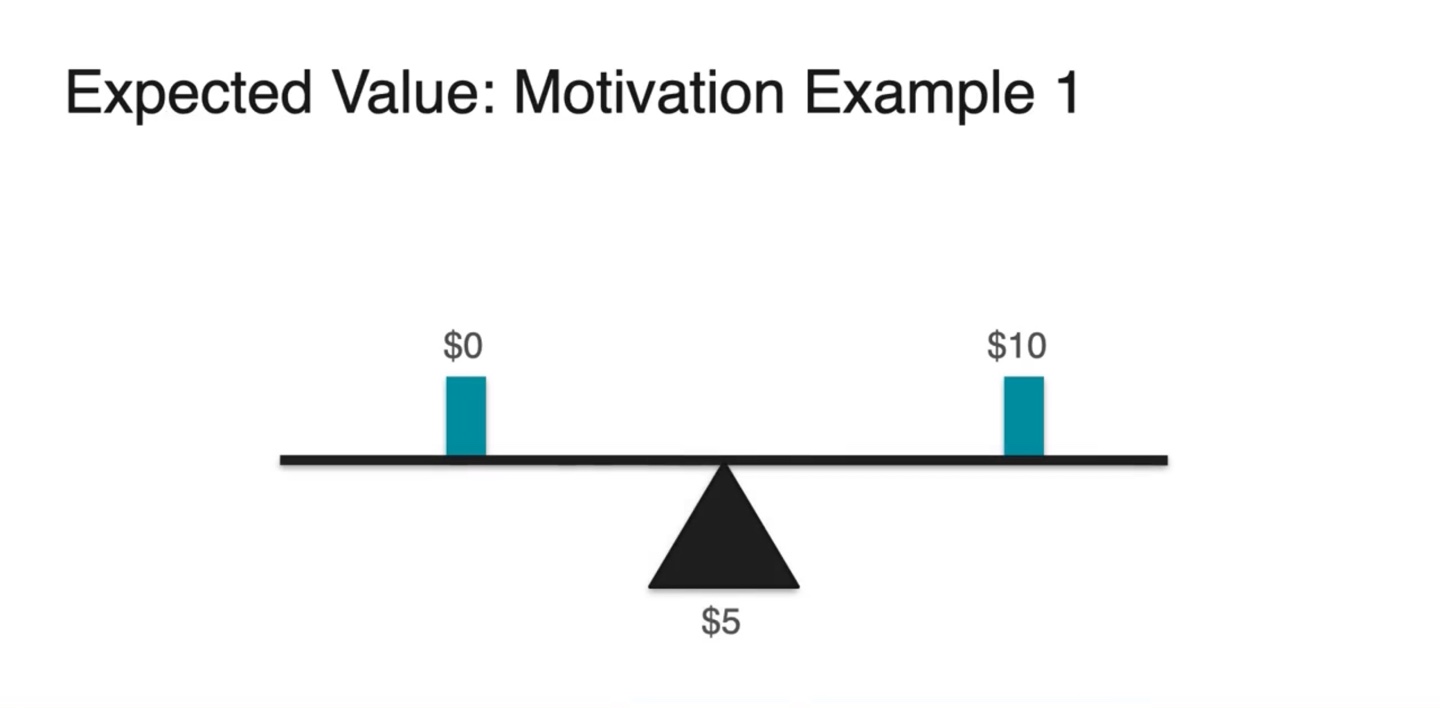
예를 들어, 친구와 동전 던지기 게임을 한다.
-
Head가 나오면 $10를 받고, Tail이 나오면 아무 것도 받지 못한다.
- Question: 참가비는 얼마가 적당할까? $6일까 $4일까?
-


-
정답은 $5이다.
- 이길 수 있는 확률의 기댓값은 1/2(0.5), 질 수 있는 확률도 1/2(0.5)이기 때문에 절반은 얻고 절반은 잃어도 손해는 보지 않는다.

- $0과 $10이 random variable이면 확률의 weight가 동일할 때 중앙값인 $5가 된다.
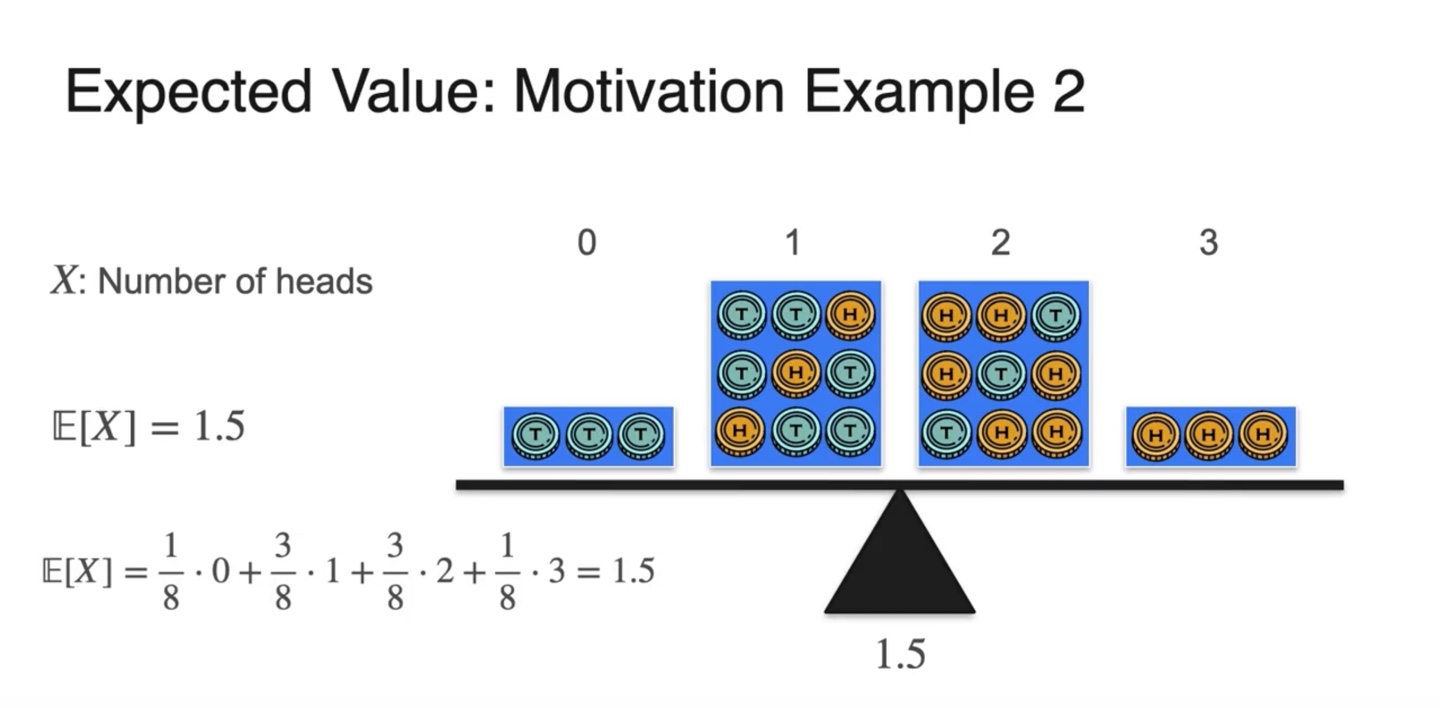
- 만약 user가 동전을 세 번 던질 수 있고 head가 나오면 $1을 받는다고 할 때, 참가비는 최대 얼마로 설정하면 좋을까?

-
각 확률 변수(random variable)은 , 확률(weight)은 이 되어 기댓값이 계산된다.
-
확률 변수가 discrete한 경우에는 아래와 같이 공식이 쓰여진다.
-
PMF of X :
-
-

-
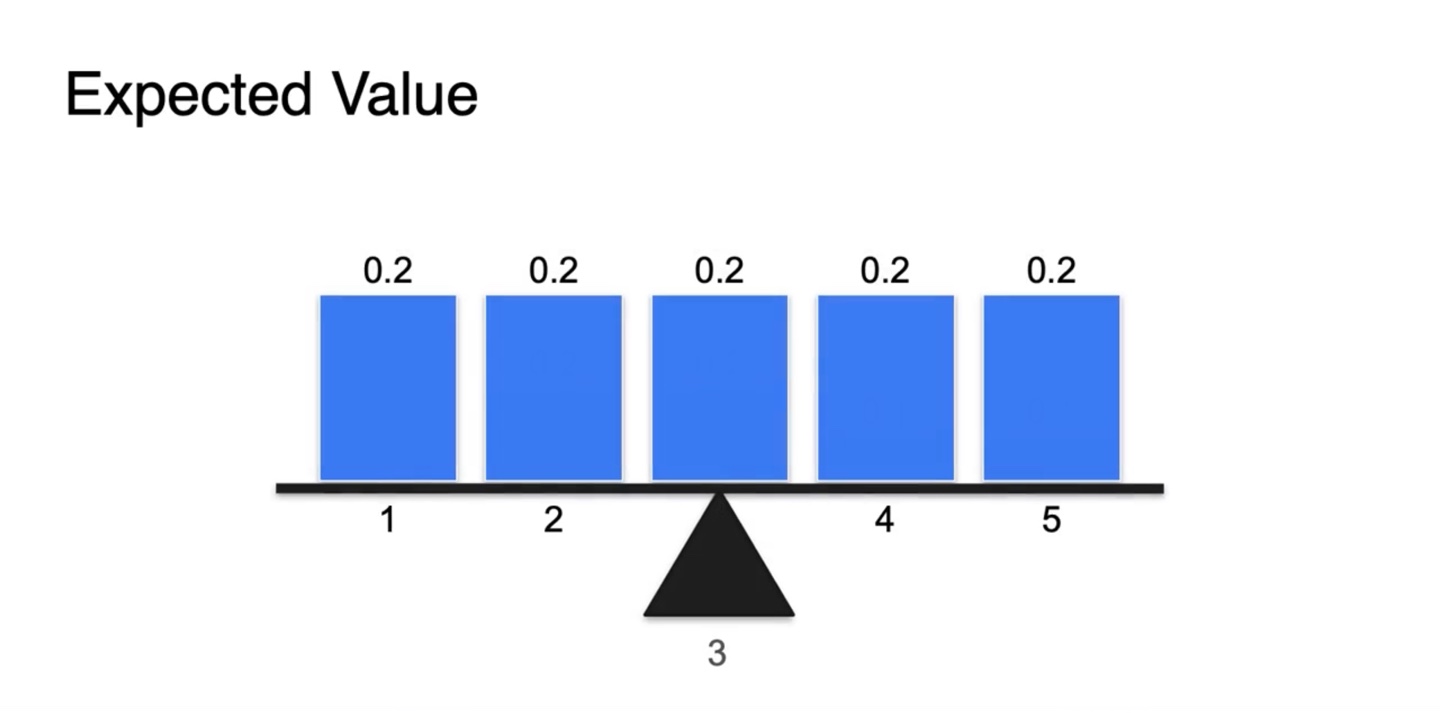
만일 Uniform distribution이라면 어떨까?
- 확률의 weight값은 동일하므로 확률 변수 random variable의 평균값인 3이 Expected value가 된다.
-
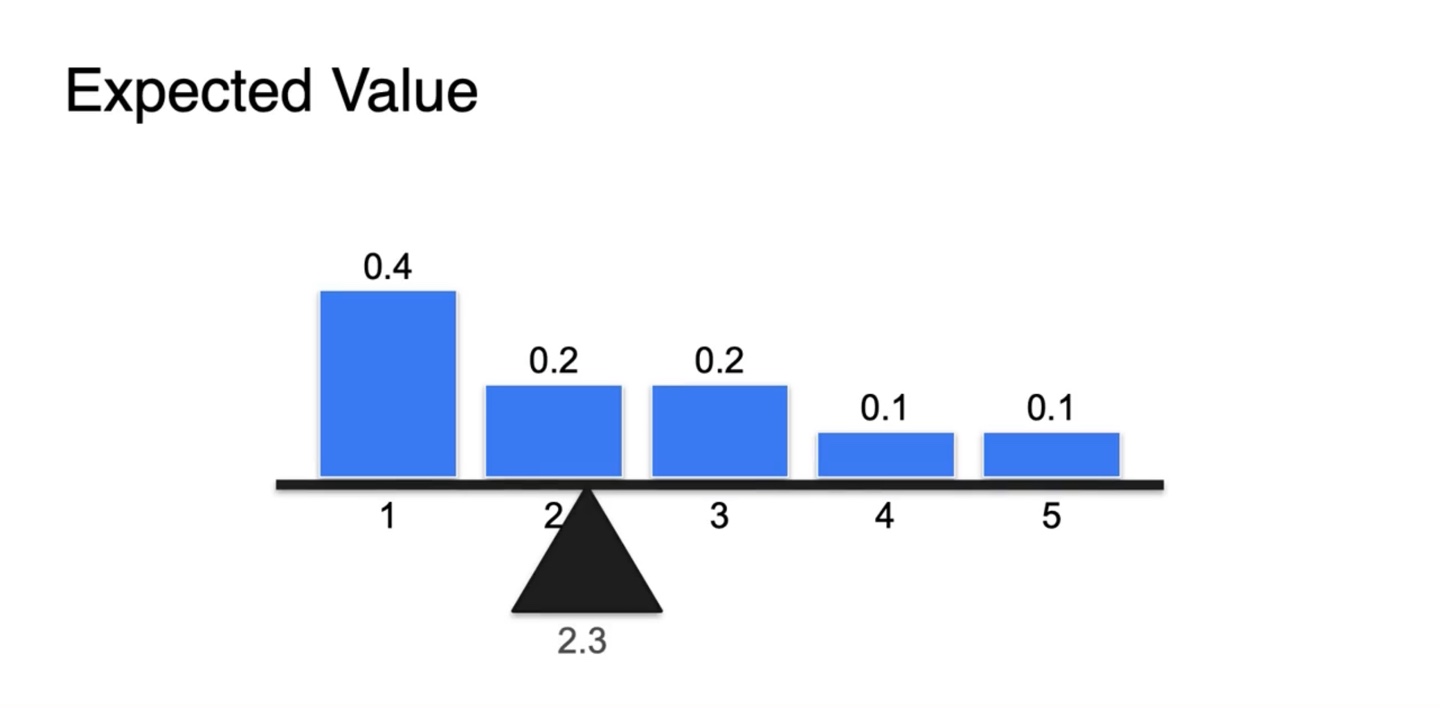
만약 확률인 weight 값이 동일하지 않다면 어떨까?
-
Expected value는 3보다 약간 적은 2.3으로 계산됨을 알 수 있다.
- 기댓값은 {확률 변수 * 확률}이므로 두 값을 모두 고려하여 평형점을 찾았을 때 확률이 더 높은 쪽으로 치우칠 수 밖에 없다.
-
-
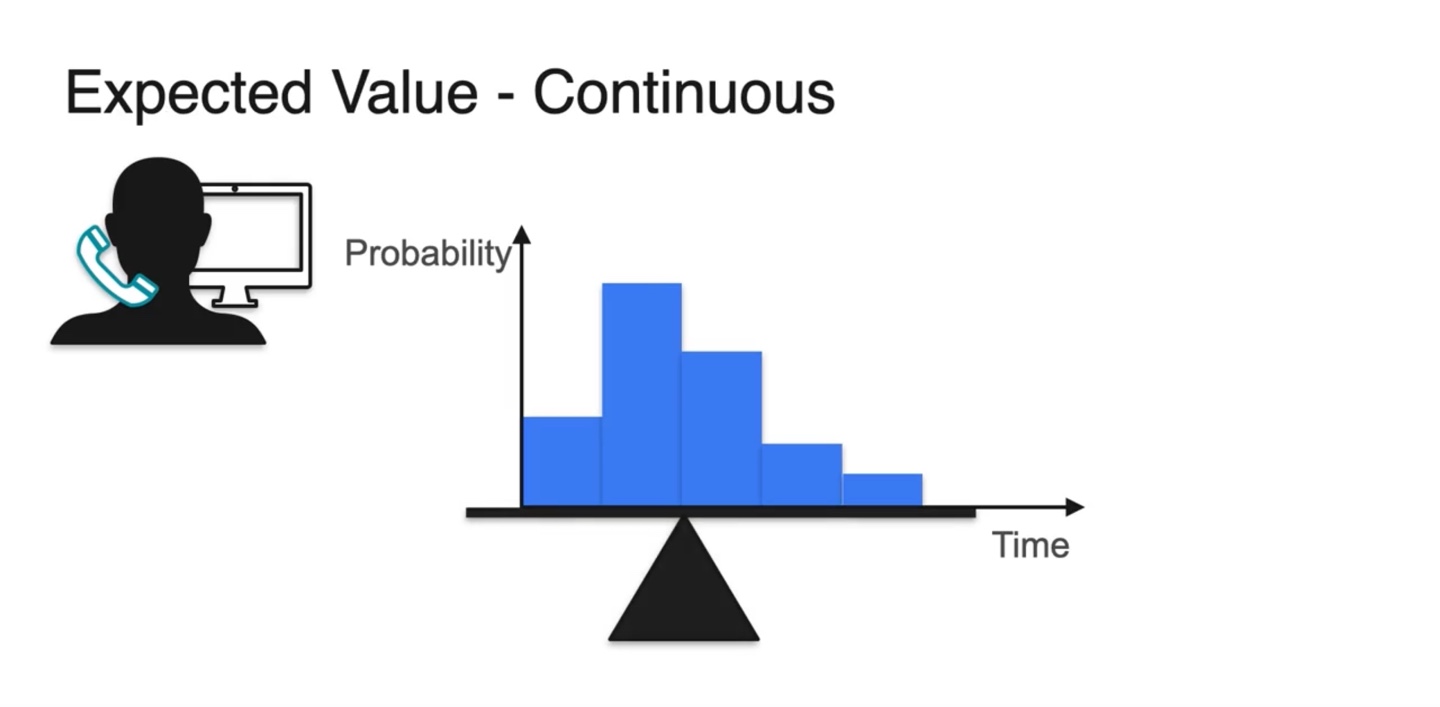
Continuous한 variables라면 어떨까?
- Discrete한 variables의 평형점은 아래 그림과 같이 찾을 수 있었다.
-
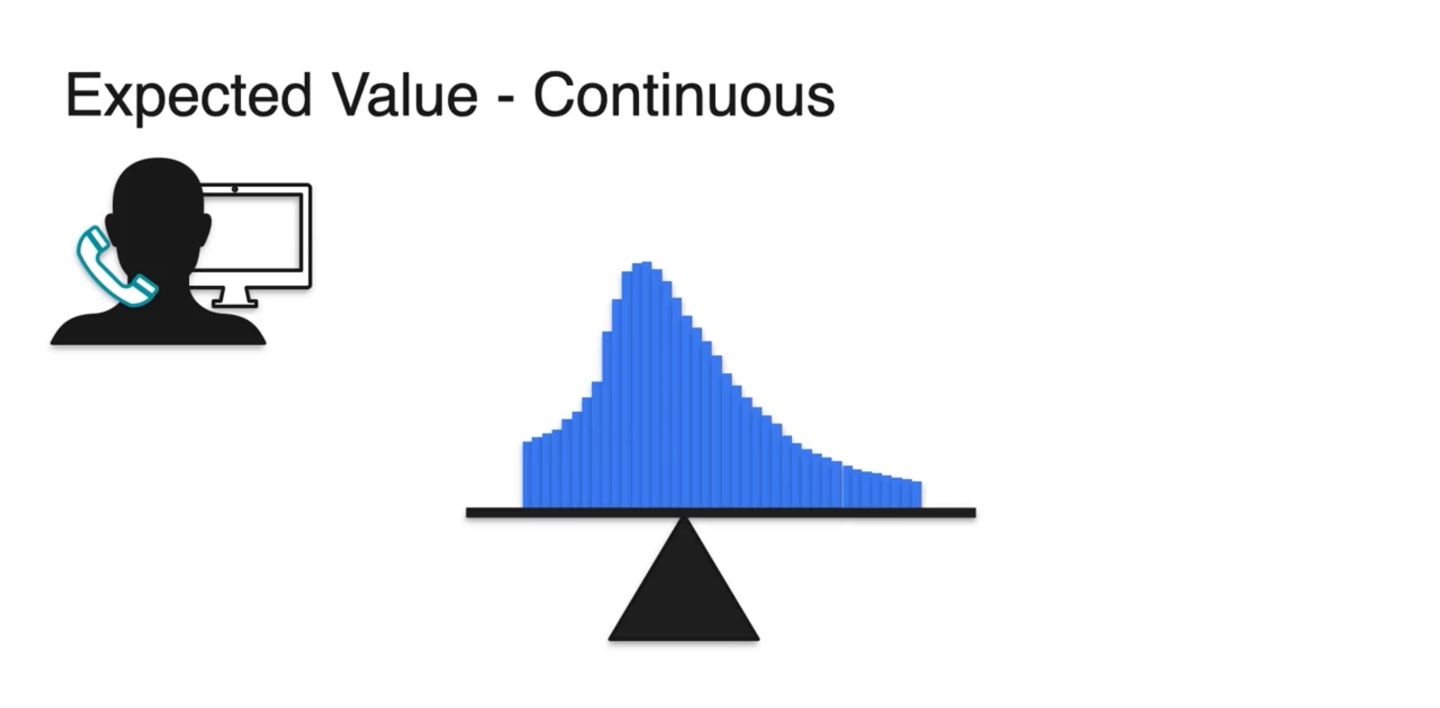
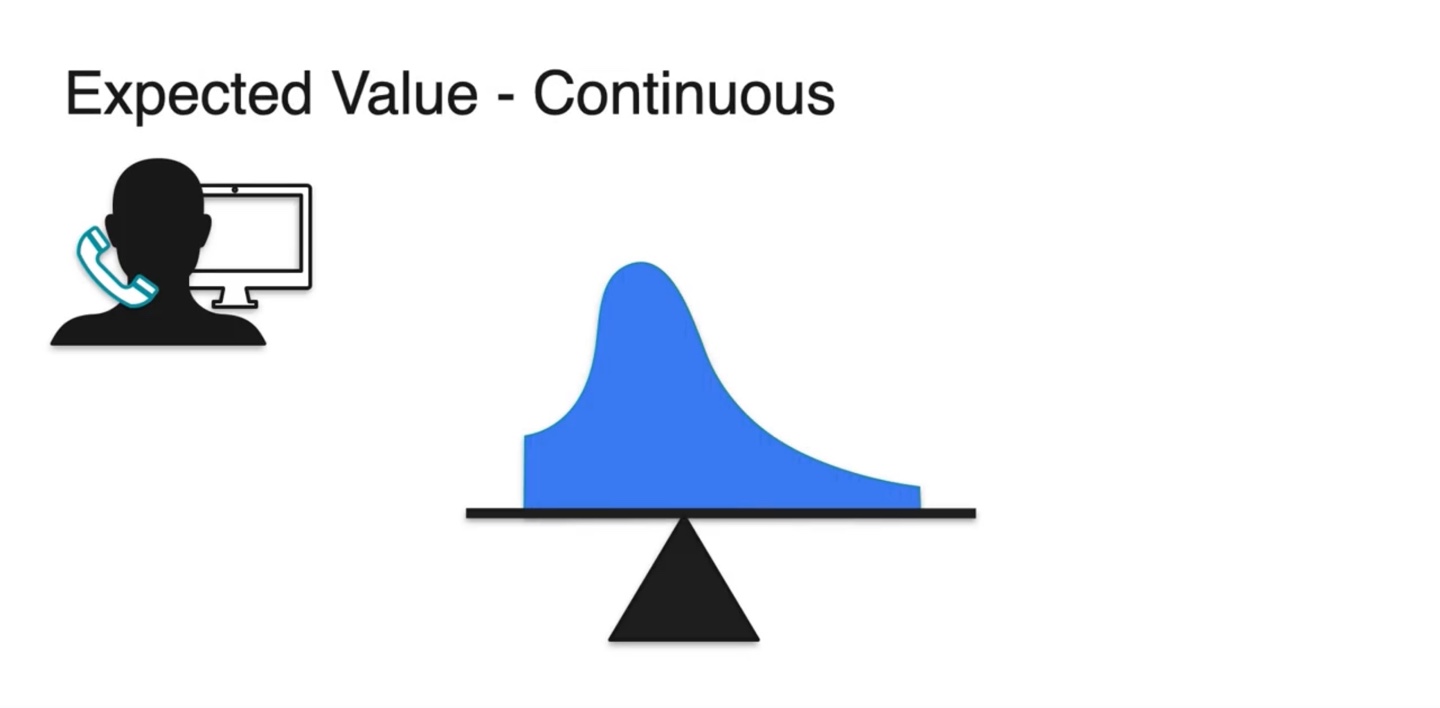
Continuous variables는 Discrete한 variables를 잘게 쪼개진 꼴이다.
- 아주 잘게 자르면 smooth한 bar들의 모임이 전체 확률 분포 PDF가 됨을 알 수 있다.
-
Contionuous한 variables와 Discrete한 variables의 Expected value는 아래와 같이 정의된다.
-
Discrete :
-
Continuous :
-

-
버스 기다린 시간을 하루 하루 측정하여 전체 기다린 시간의 평균값이 얼마인지 구해보고 싶다고 하자.
- 기다린 시간을 수직선 분포로 표시하여 Average를 찾으면 27.833의 값으로 계산됨을 알 수 있다.
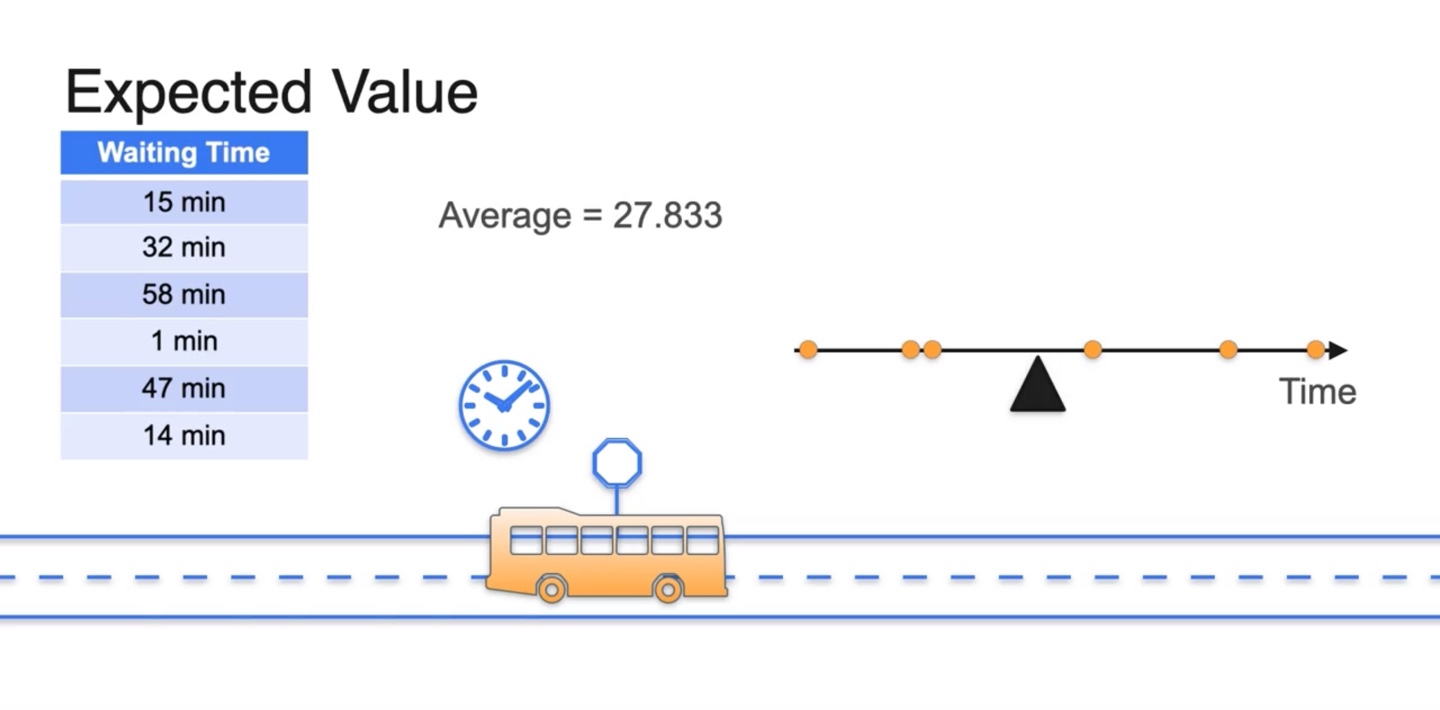
-
만약 여러 번의 측정으로 다음과 같은 분포를 얻어내었다고 하자.
- 기다린 시간의 확률 변수(random variable)가 매우 다양할 때 Average 즉, Expected value는 해당 변수의 중앙값이자 평균값인 30으로 계산된다.
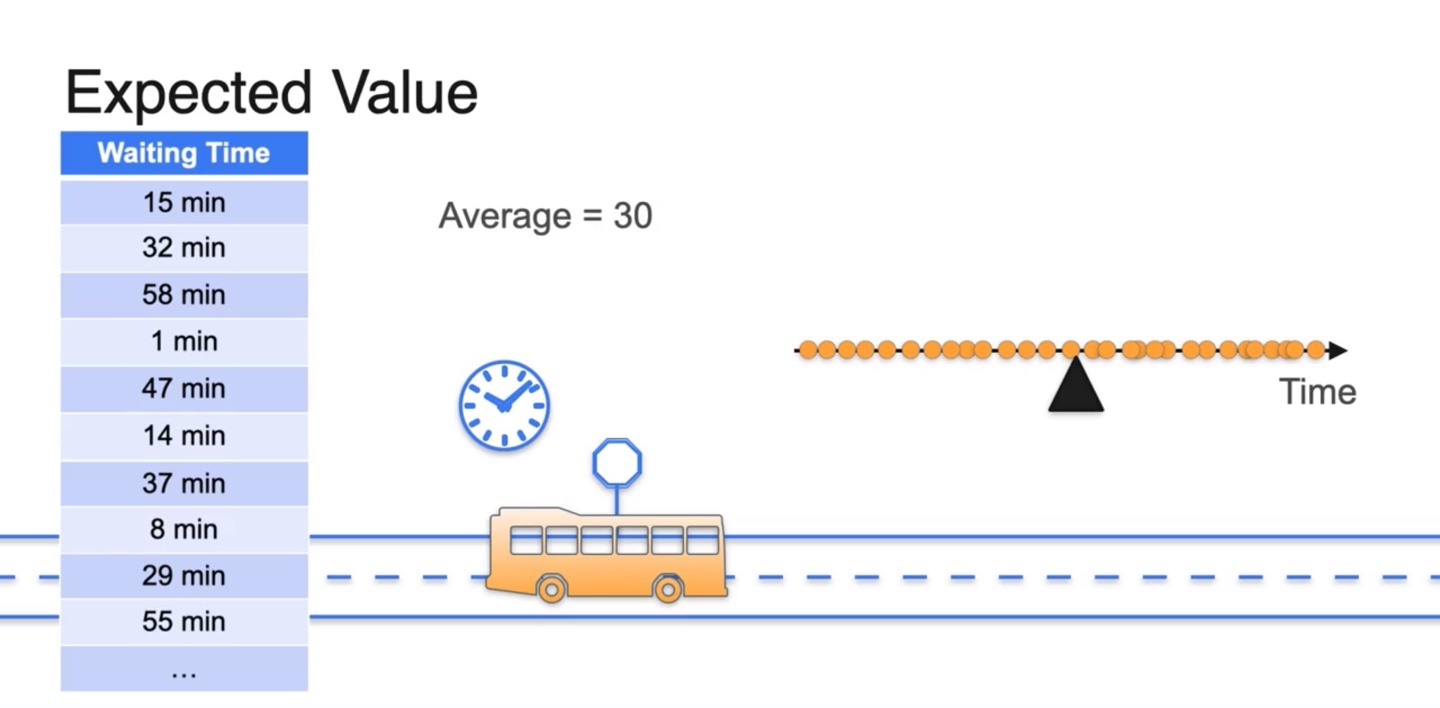
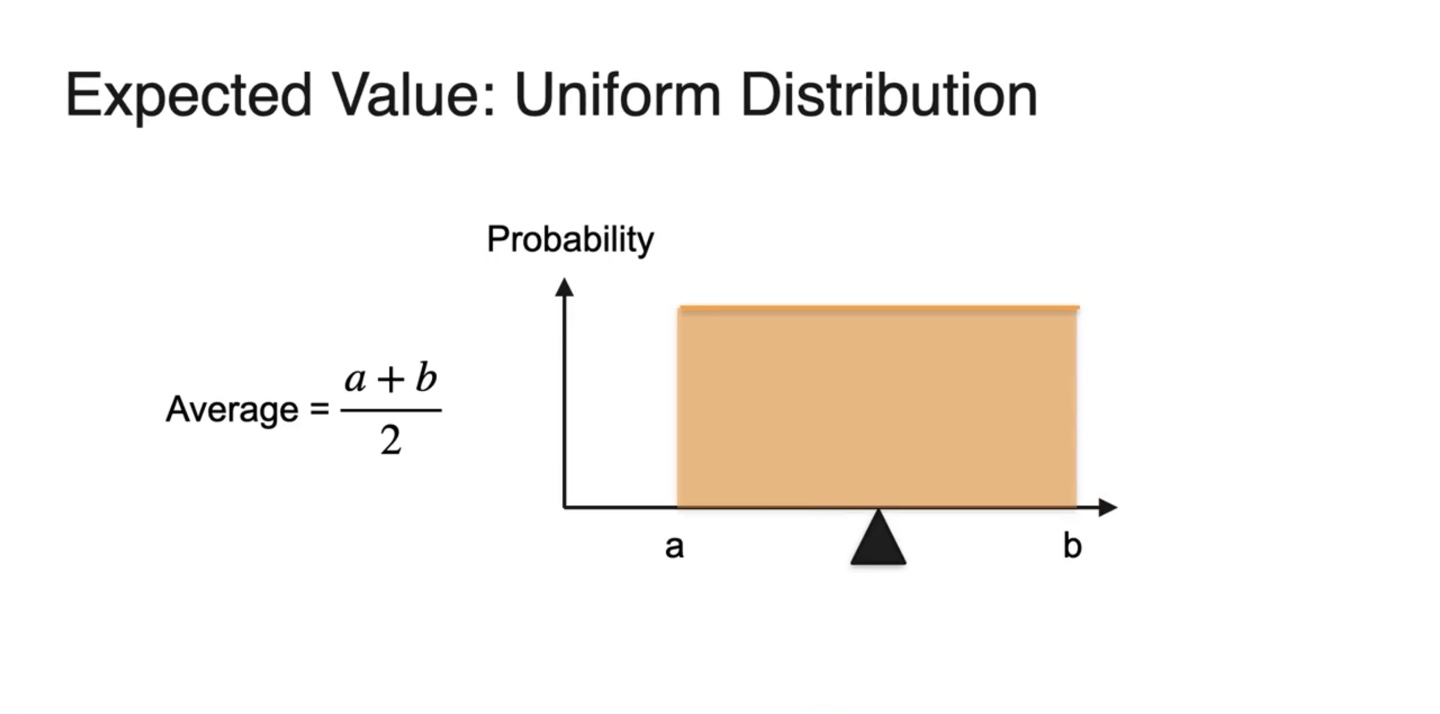
- 전체 확률 분포가 Uniform distribution을 따를 때, Expected value는 전체 확률 변수의 평균값이다.
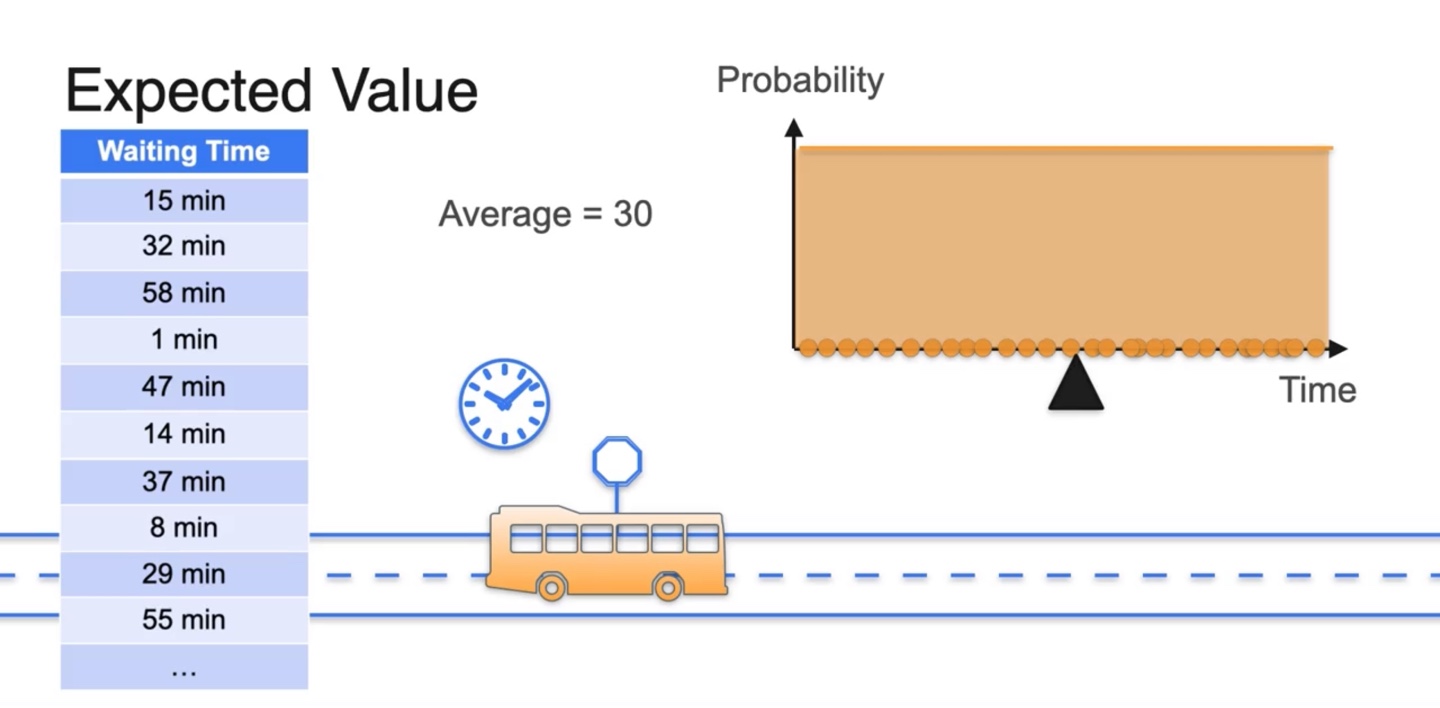
- 만일 확률 변수가 0~1 사이의 값이고 uniform distribution을 따른다면 Average는 0.5다.
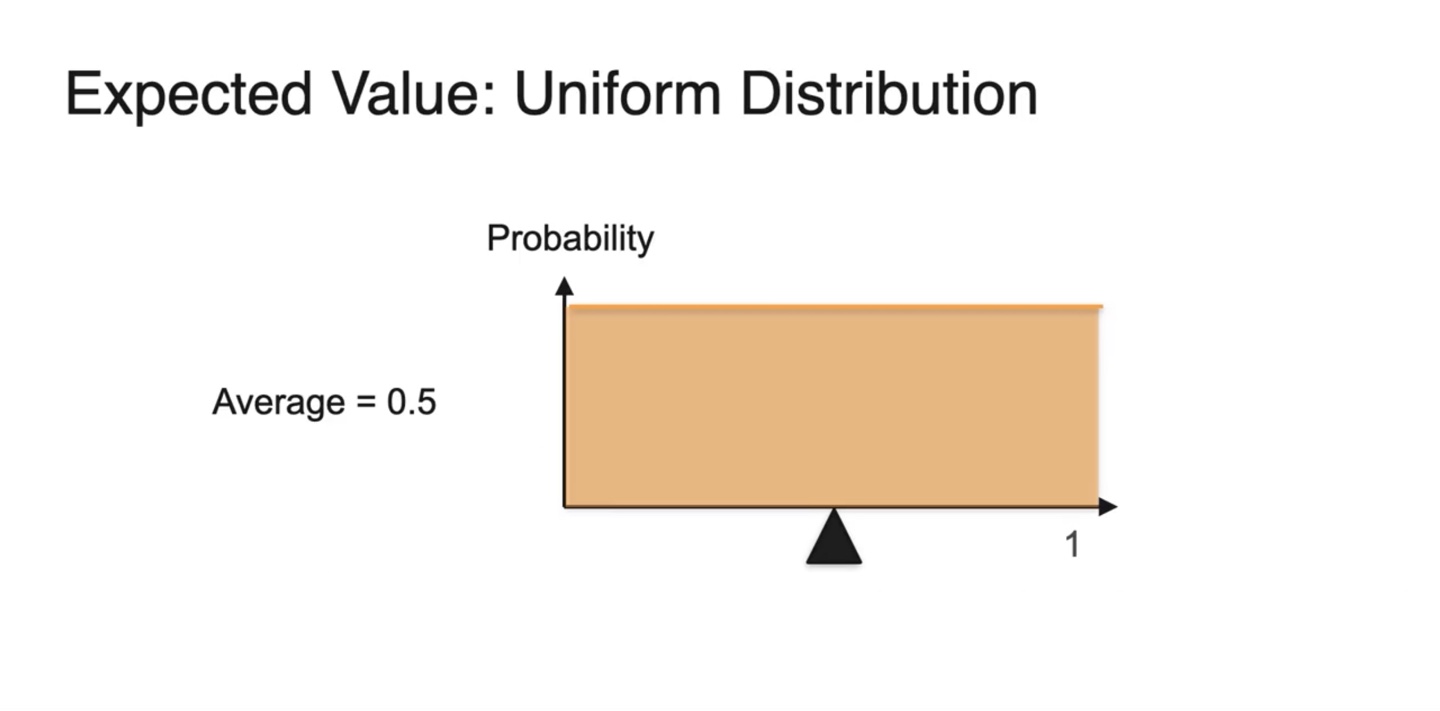
-
만일 확률 변수가 에서부터 까지일 때, uniform distribution을 따르는 분포를 따른다면
- Expected value는 다.
-
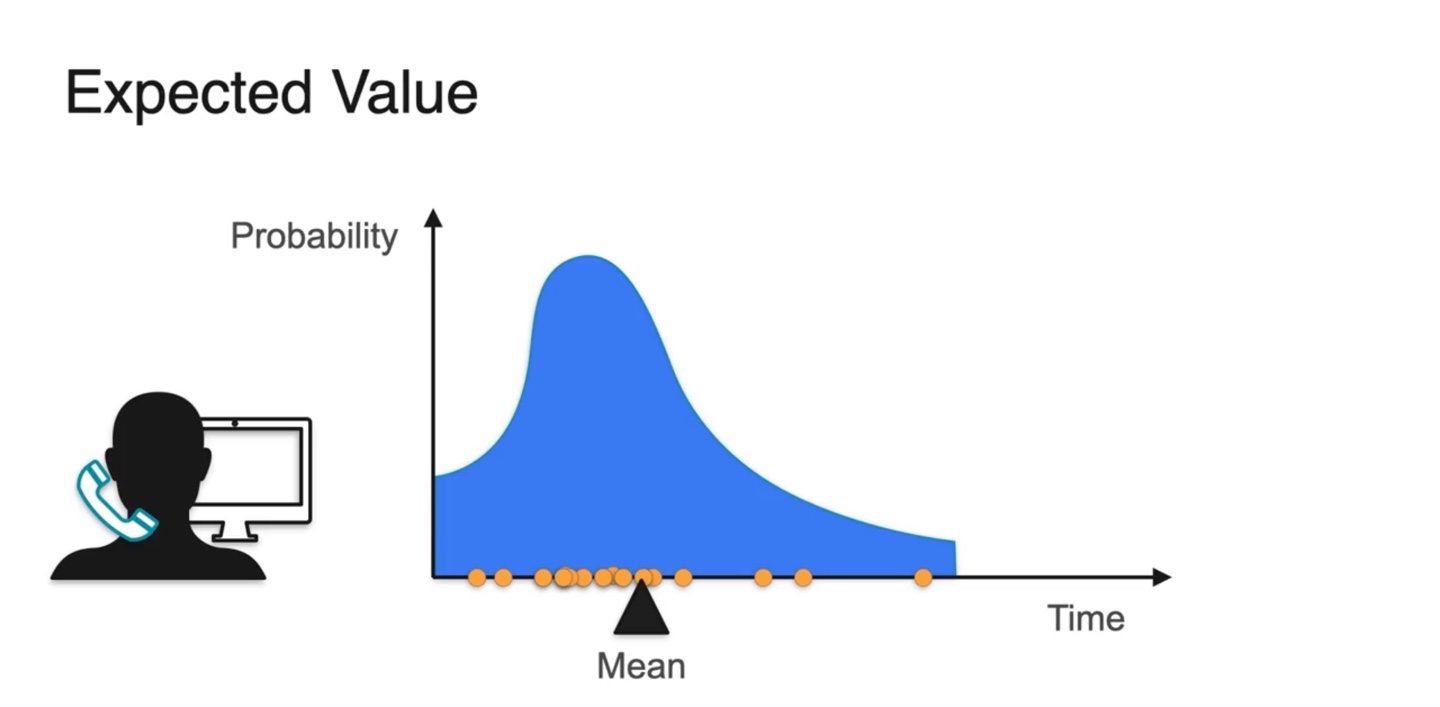
아래와 같은 분포를 가진다면 어떨까?
-
확률에 따라 random variable을 sampling해보면 대부분 확률이 높은 값에서 확률 변수들이 결정된다는 것을 알 수 있다.
- 따라서 mean값은 확률이 큰 값 쪽에 대부분 위치한다.
-
-
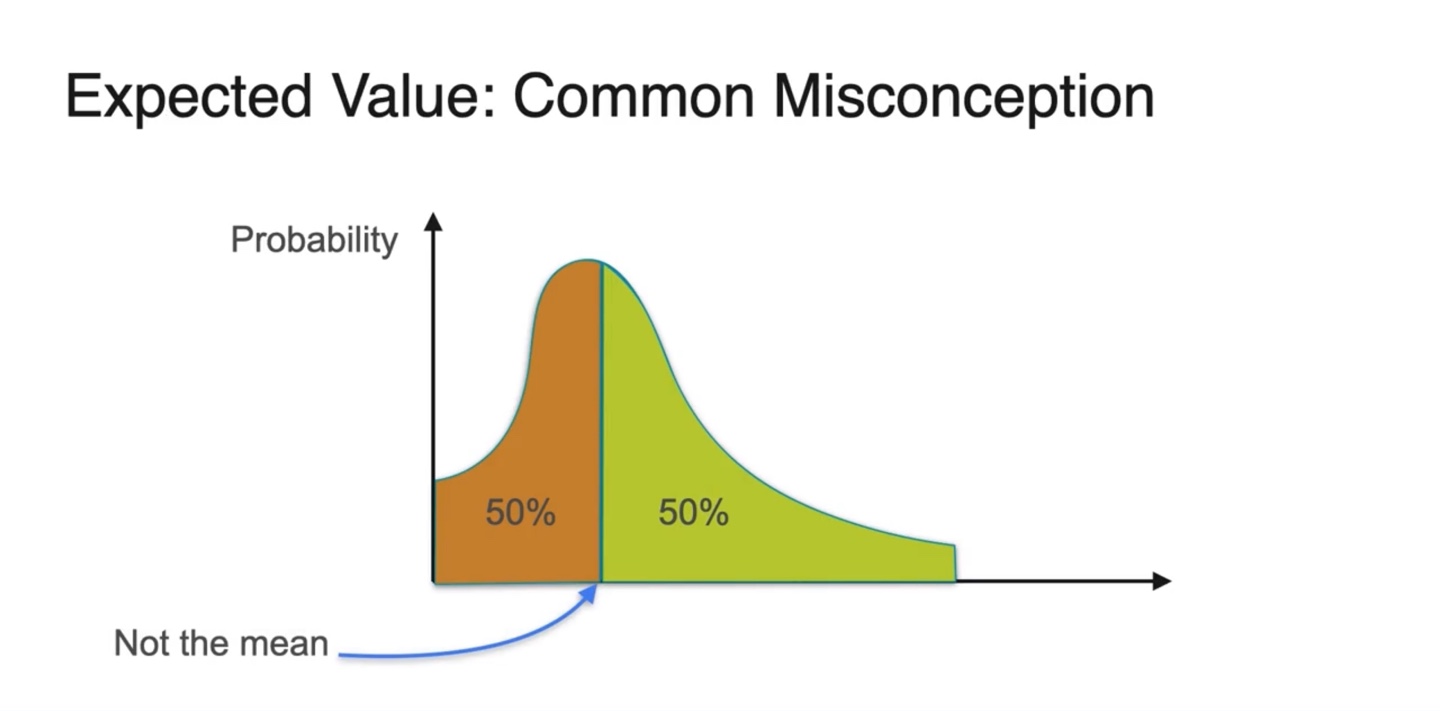
그러나 한 가지 큰 Misconception을 갖게 될 수 있다.
- Mean은 확률 밀도 함수(PDF)의 면적 즉, 확률이 정확하게 50% / 50%인 곳에 위치하는 것이 아니다.
-
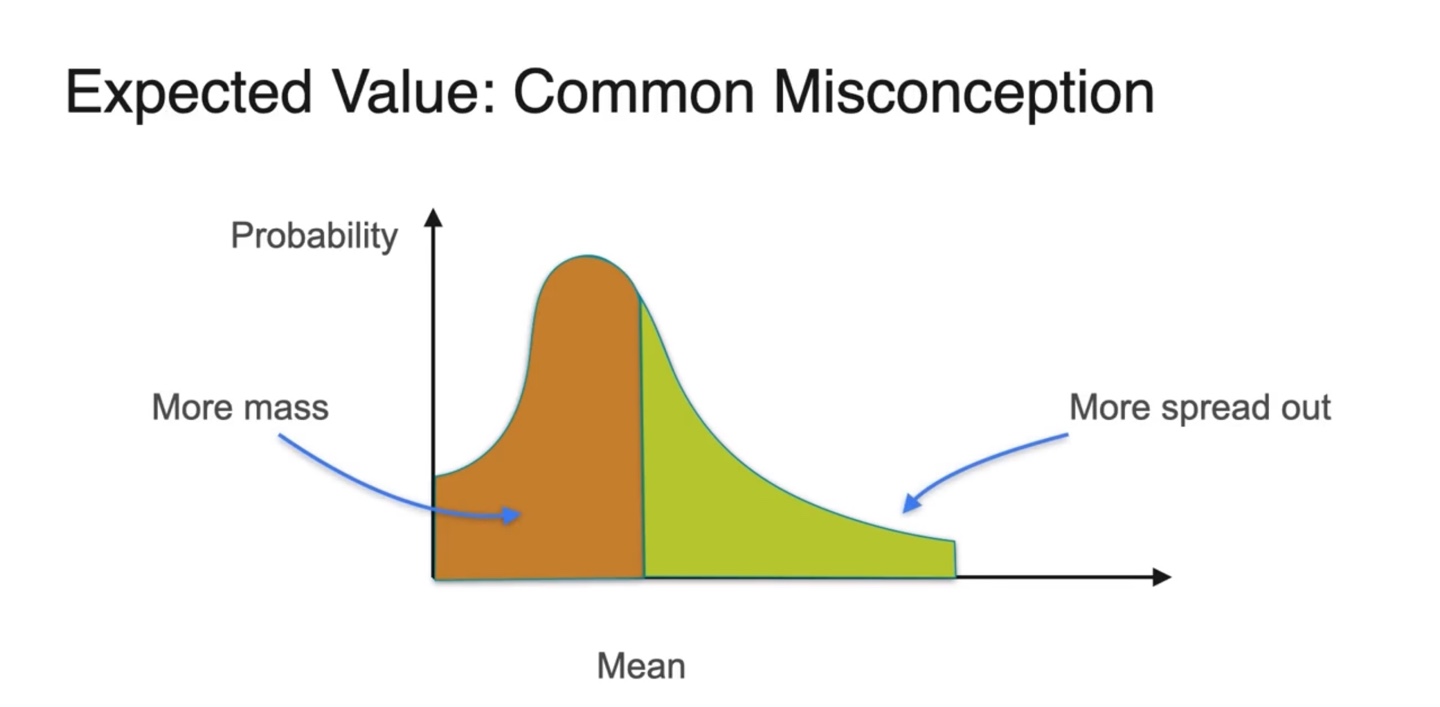
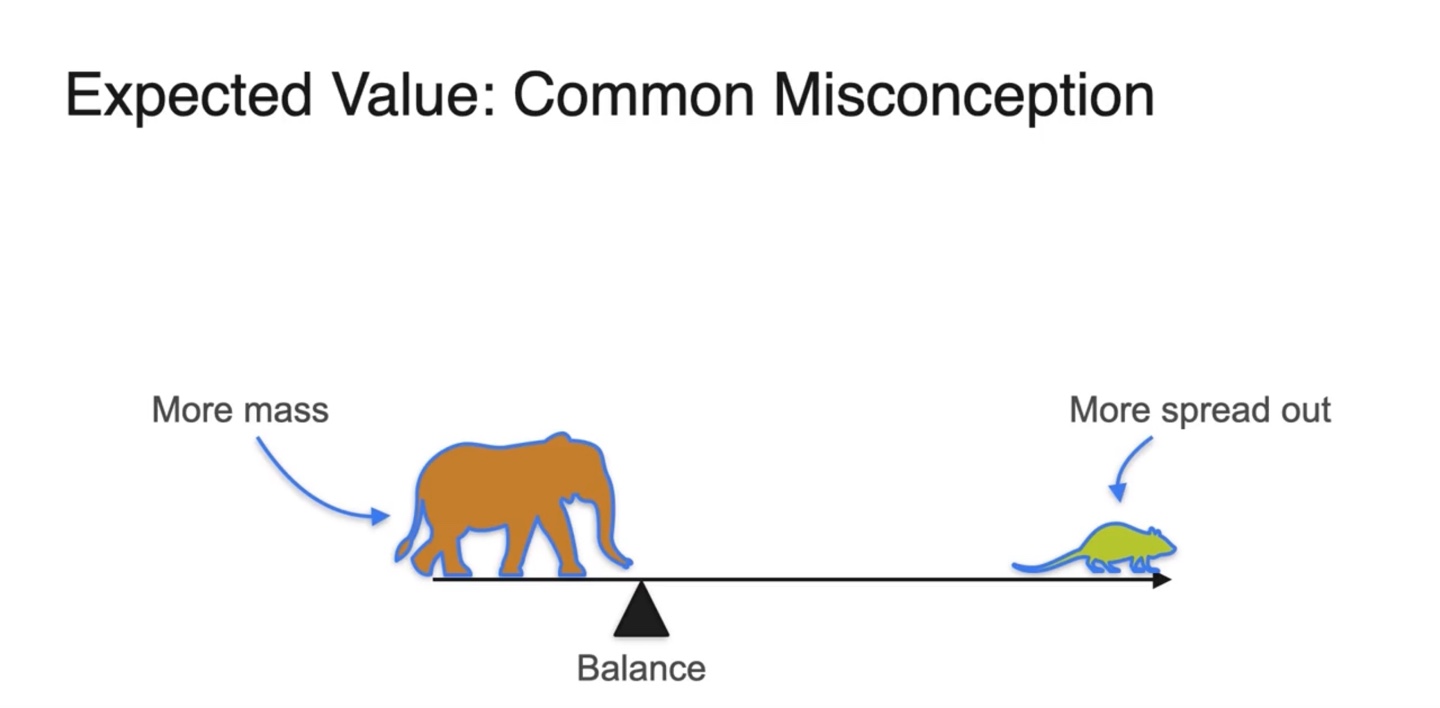
실제 Expected value의 위치는 more mass와 more spread out으로 나뉜 면적을 취한 곳에 위치한다.
- 이는 {확률 변수 * 확률}인 기댓값의 정의를 따르기 때문이다.
-
코끼리와 쥐의 예시를 통해 이해해보자
-
무게 중심의 평형점은 {질량 * 거리}로 정의된다.
- 따라서 질량은 확률, 평형점으로부터의 거리는 확률 변수로 치환되어 곱하였을 때 balance를 맞춰야만 한다.
-
-
정리하자면 아래와 같다.
- Expected value의 기호는 다.
- Mean은 Balancing point다.
- Discrete와 Continuous random variables에 따라 다르게 정의된다.
- PMF나 PDF의 weighted average가 기댓값이다.

Other measures of central tendency: median and mode
-
Motivation: 1980년대 North Carolina 대학의 평균 연봉은 $250,000인 반면, 다른 나라의 대졸 평균 연봉은 $22,000이었다.
-
왜 이러한 차이가 났던 것일까?
- 이유는 한 학생의 연봉이 매우 높았기 때문이었다.
- 그는 바로 마이클 조던이다.
-
- 졸업한 학생들의 Salary 분포를 나타내보면 아래와 같이 그려진다.
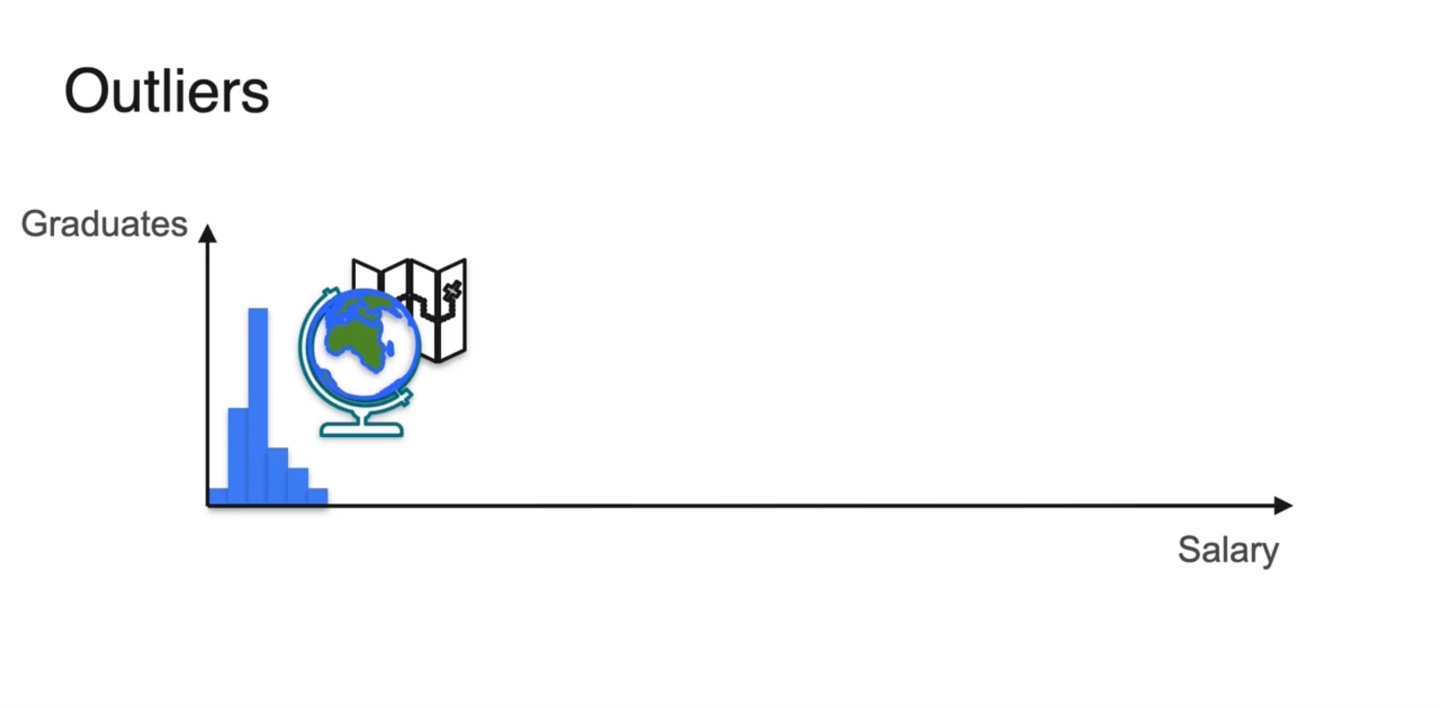
- 만약 대부분의 분포가 왼쪽에 치우친다면 무게 중심인 기댓값 또한 왼쪽 편에 위치함을 알 수 있다.

-
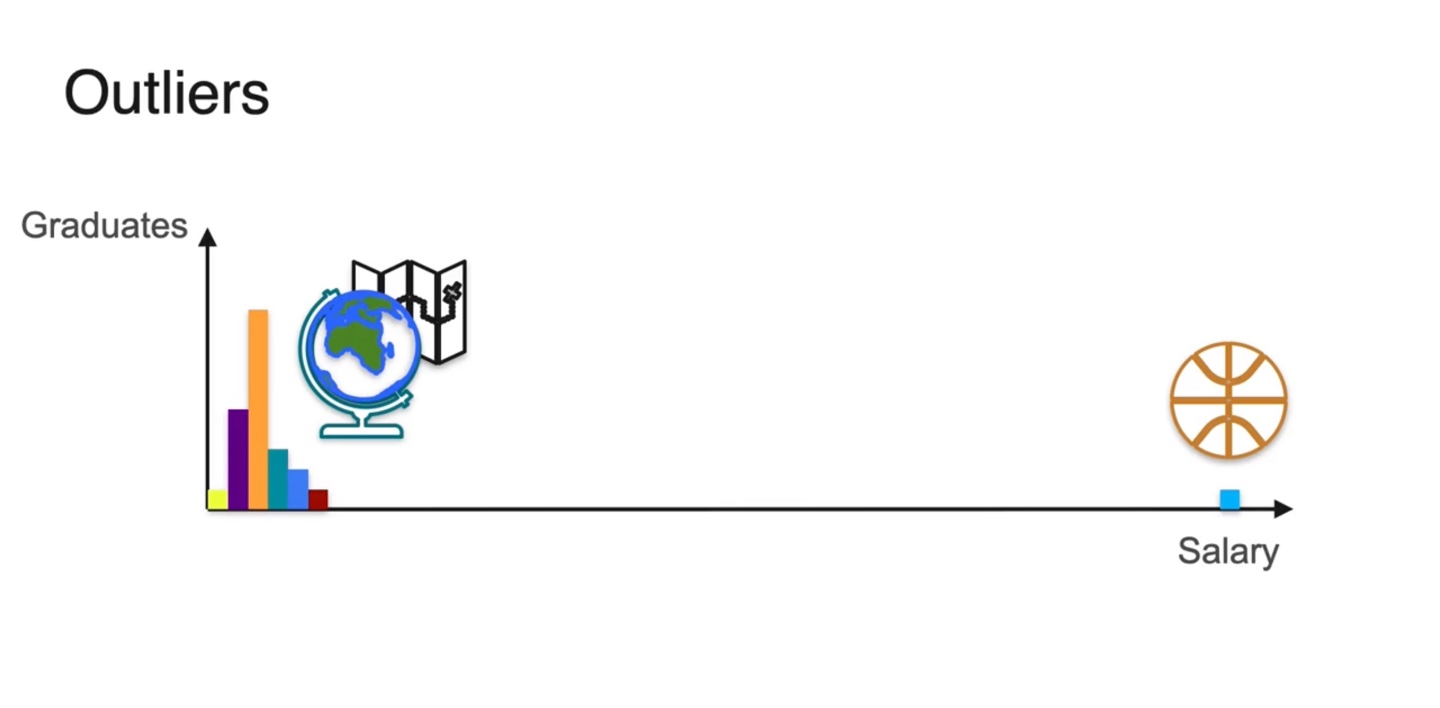
그러나 Outlier인 마이클 조던의 연봉이 매우 높아, 전체 확률을 금방 상쇄시킬 만큼의 변수를 갖는다면 어떨까?
- 무게 중심은 한 사람의 outlier에 의해서도 쉽게 치우치게 된다.
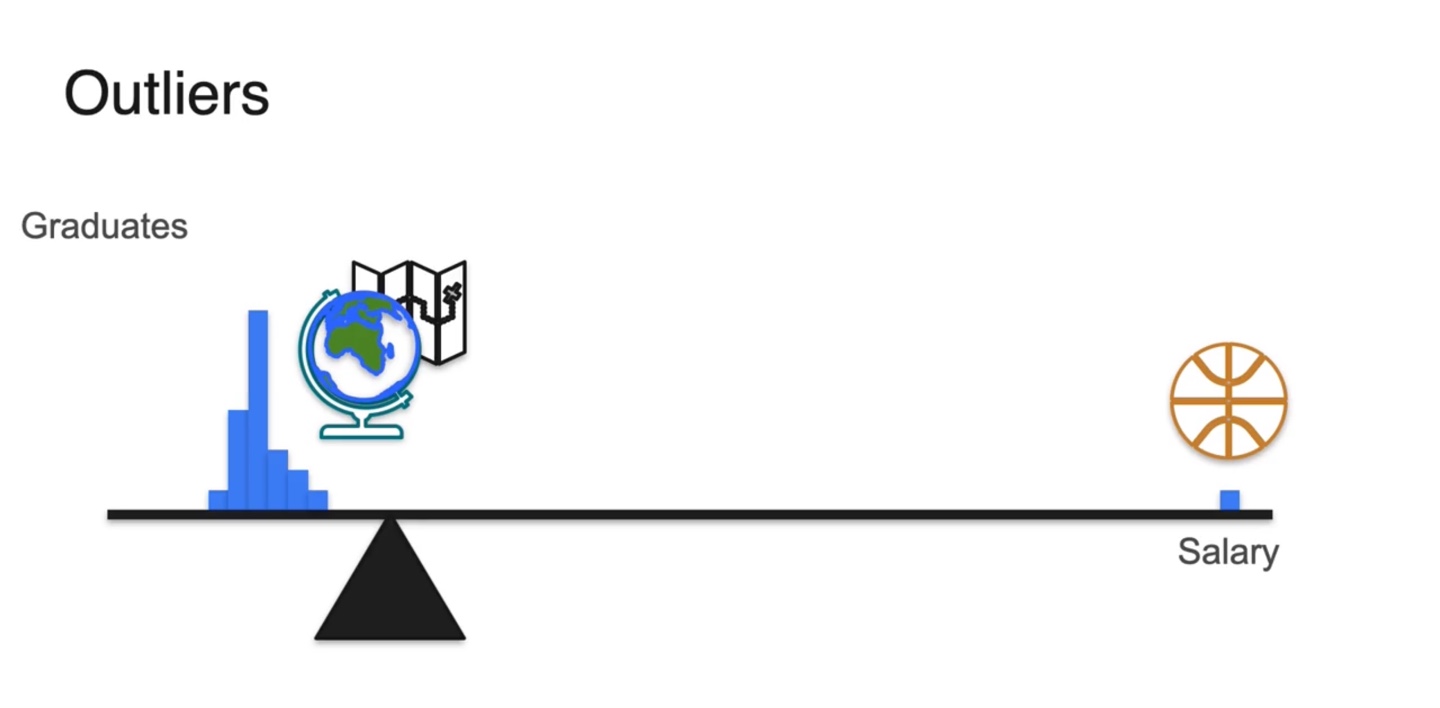
- 그렇다면 이제, 전체 분포에 색깔을 칠해 분포를 펼쳐보도록 하자.
-
각 variable이 특정 weight를 갖지 않는다면 같은 거리로 전체 분포가 펼쳐짐을 알 수 있다.
- 이 때 확률이 가장 높은 random variable은 주황색이다.

-
이 중 중앙값인 median은 주황색 variable이다.
- Median을 구할 때에는 weight가 무시되기 때문에, outlier의 영향력이 약해진다는 점이 중요한 핵심이다.
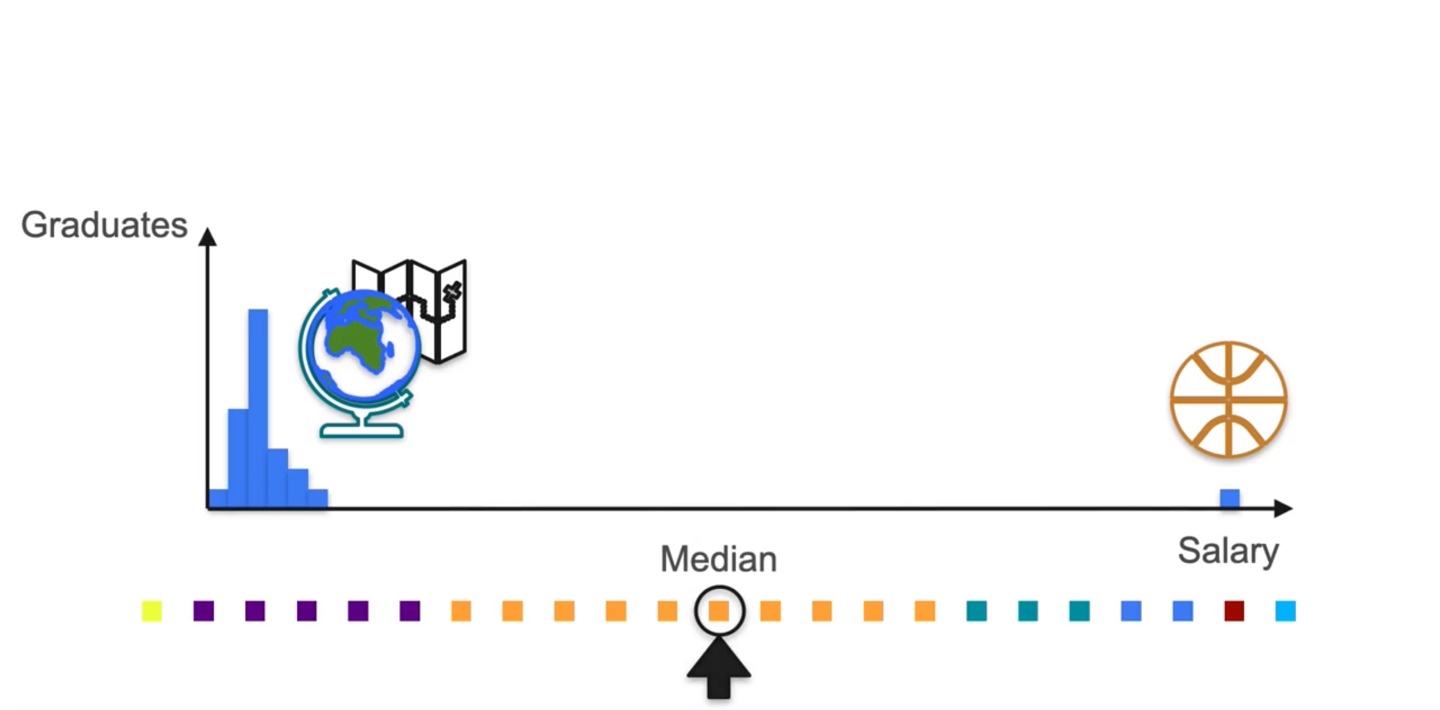
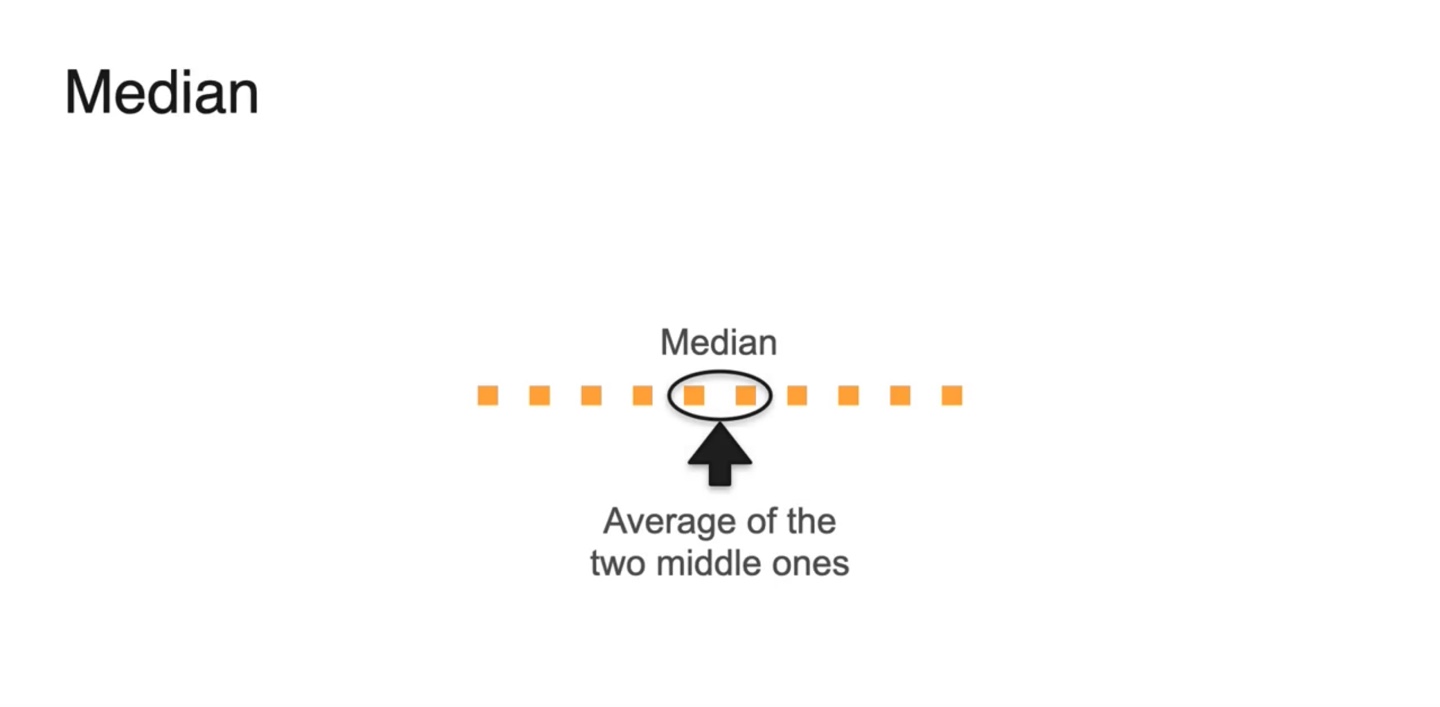
- 만약 전체 variable의 개수가 짝수(even)면 중앙값인 두 값의 평균으로 계산할 수 있다.
- Mode는 최대 확률을 갖는 random variable을 말한다.
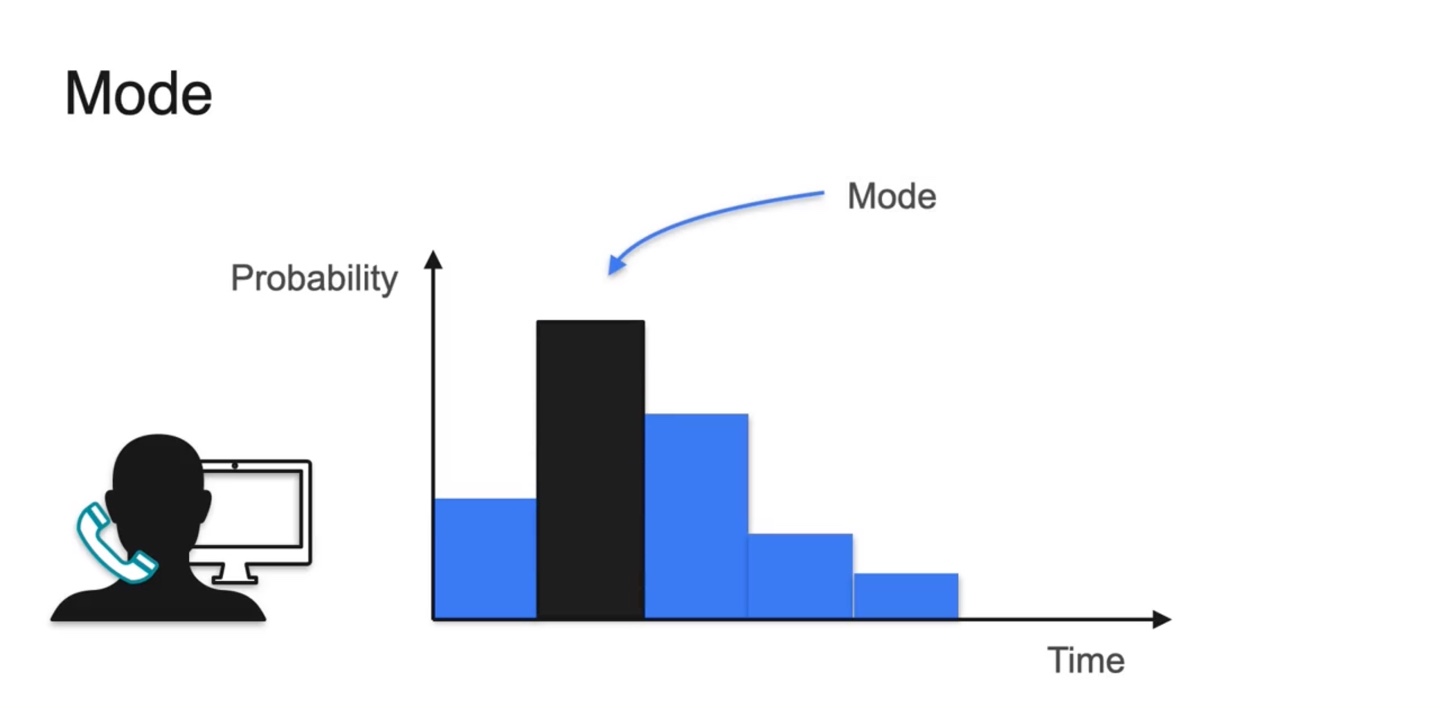
- Discrete한 경우일 때와 Continuous한 경우일 때를 나타내었을 때의 mode를 찾은 결과다.
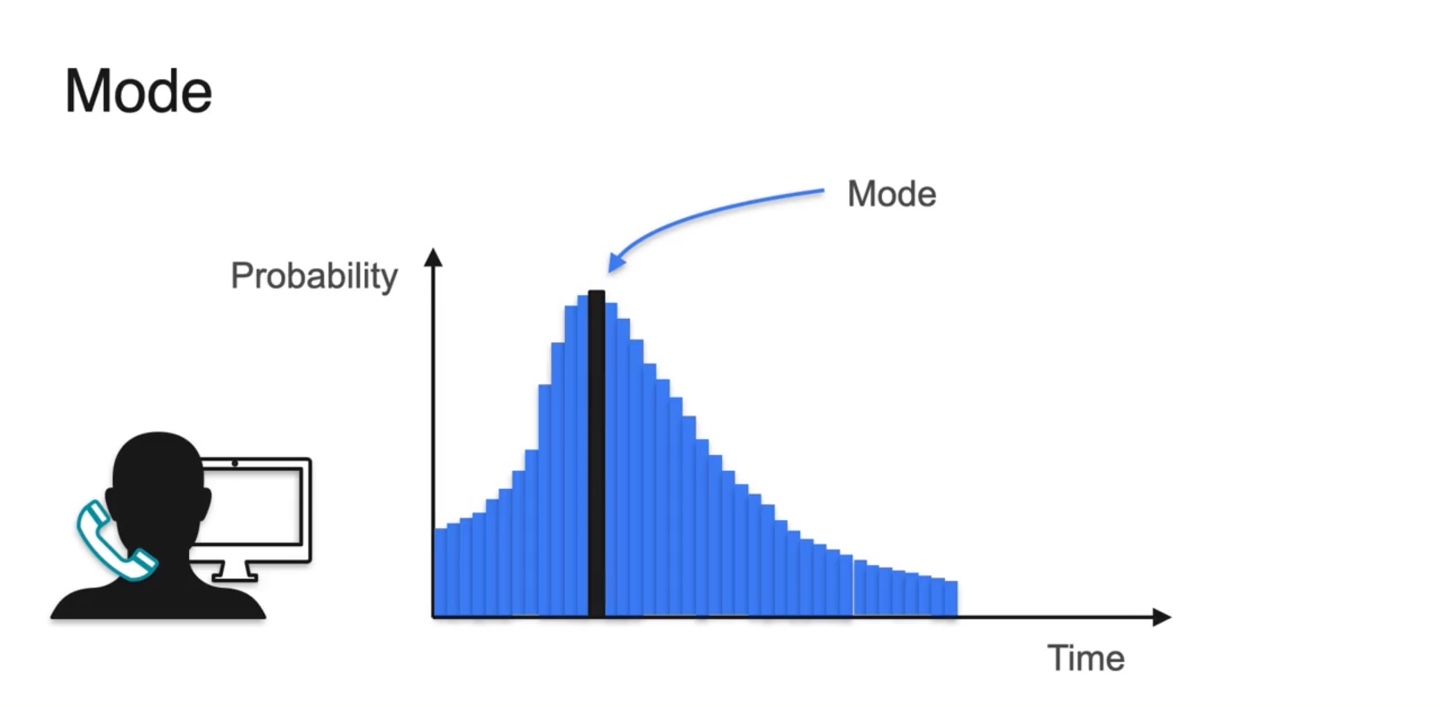
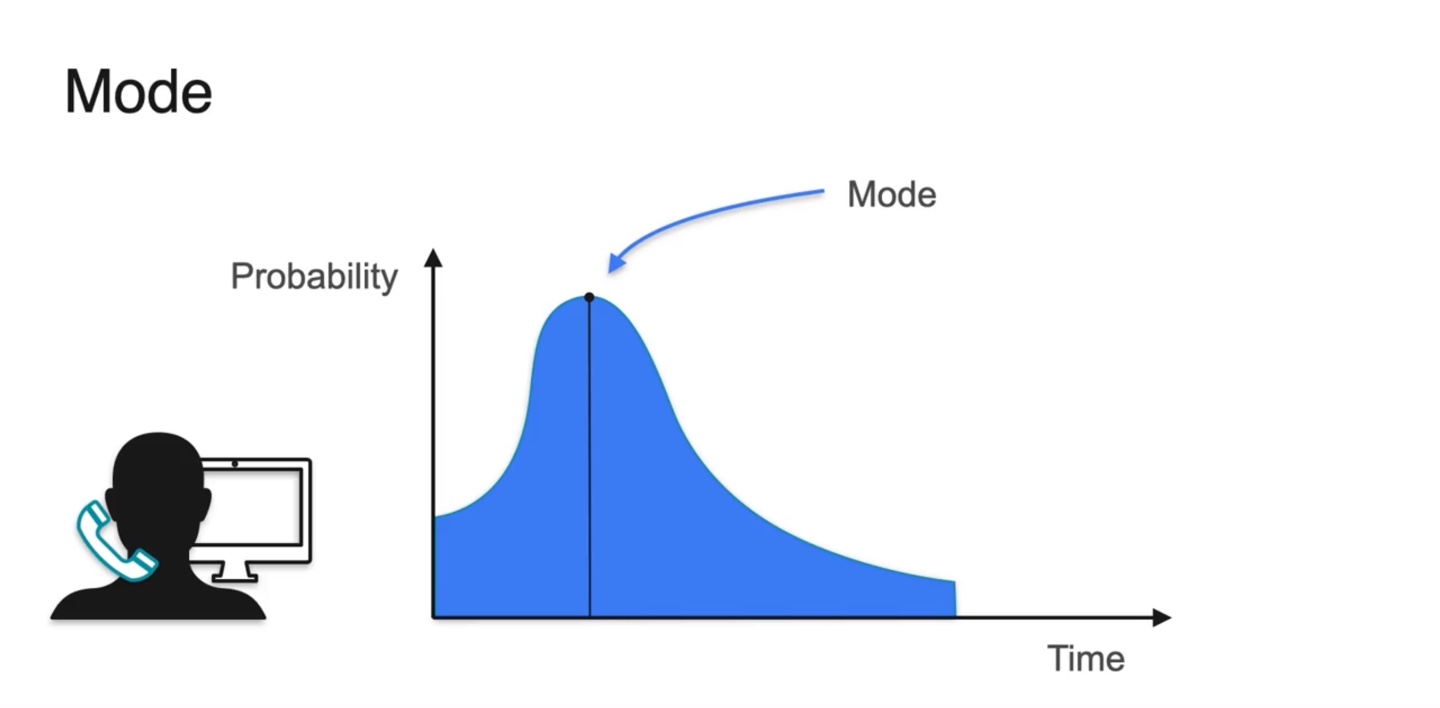
-
만약 최대 확률을 갖는 random variable이 여러 개 있다면 multimodal distribution이라 부른다.
- Mode는 여러 개일 수 있다.
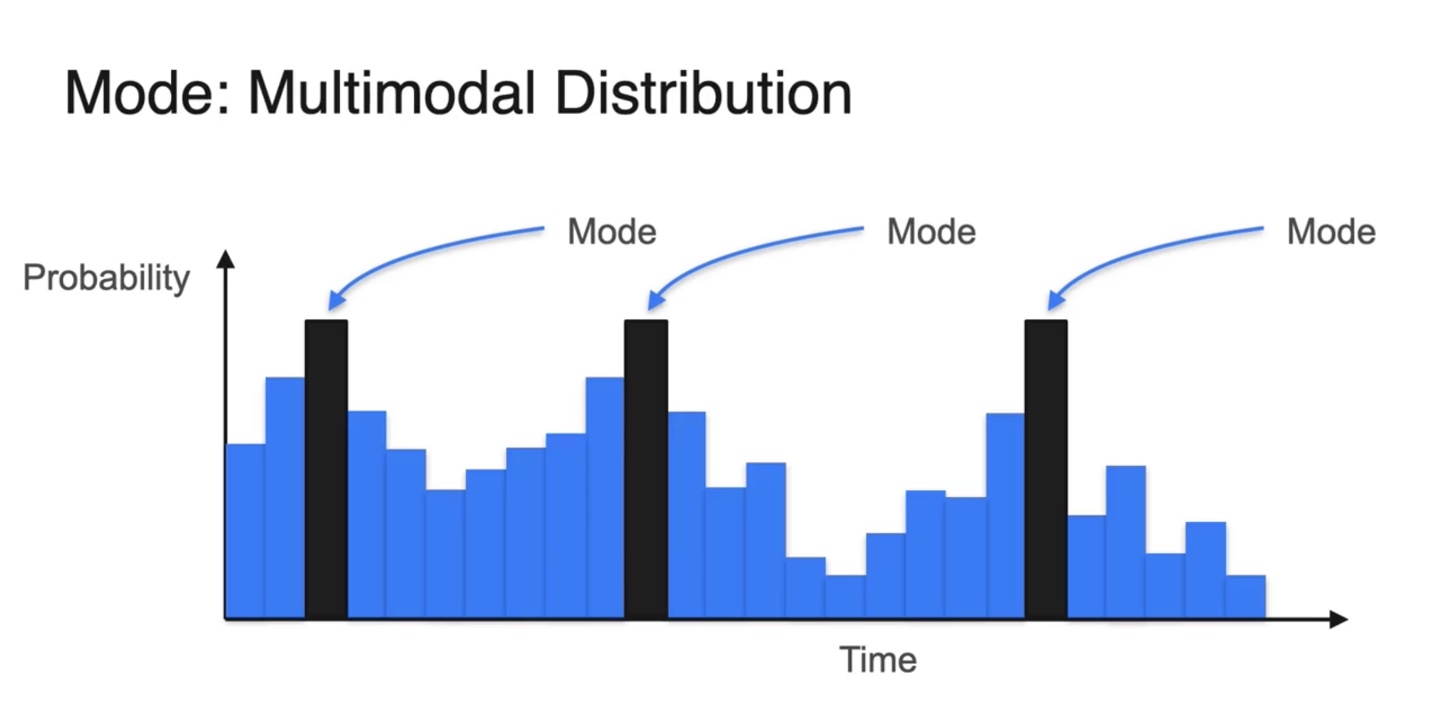
- 아래와 같은 이항 분포를 따를 때, mean, median, mode를 찾아 표기한 결과를 나타내면 다음과 같다.
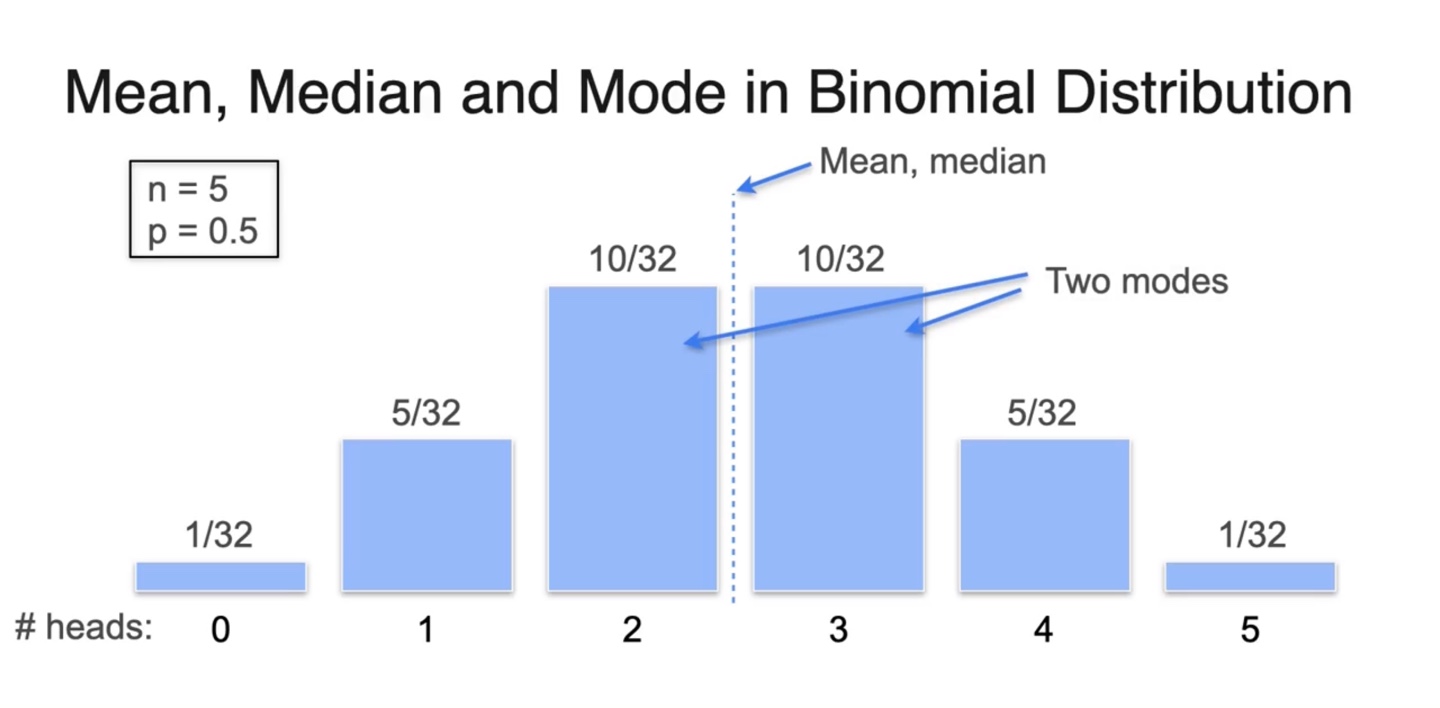
- Biased 이항 분포를 따를 때의 mean, median, mode는 아래와 같다.
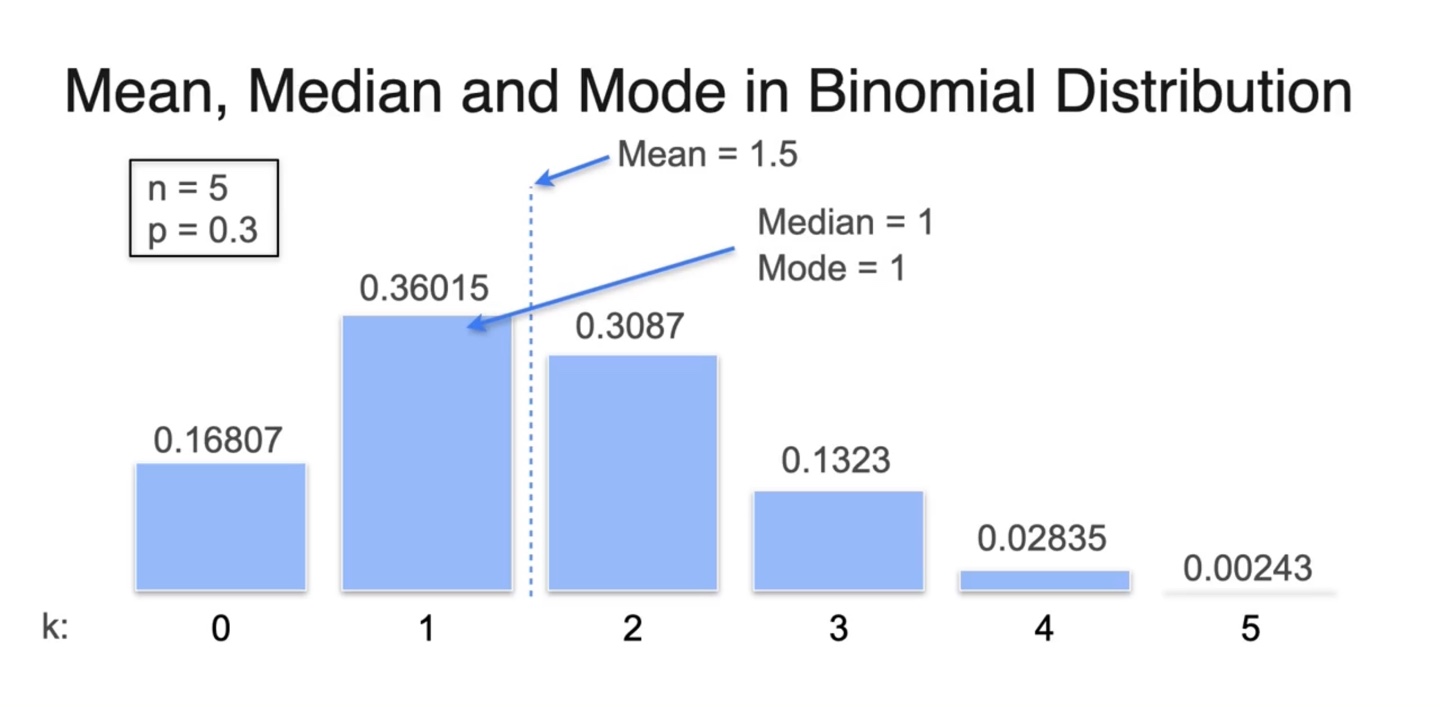
-
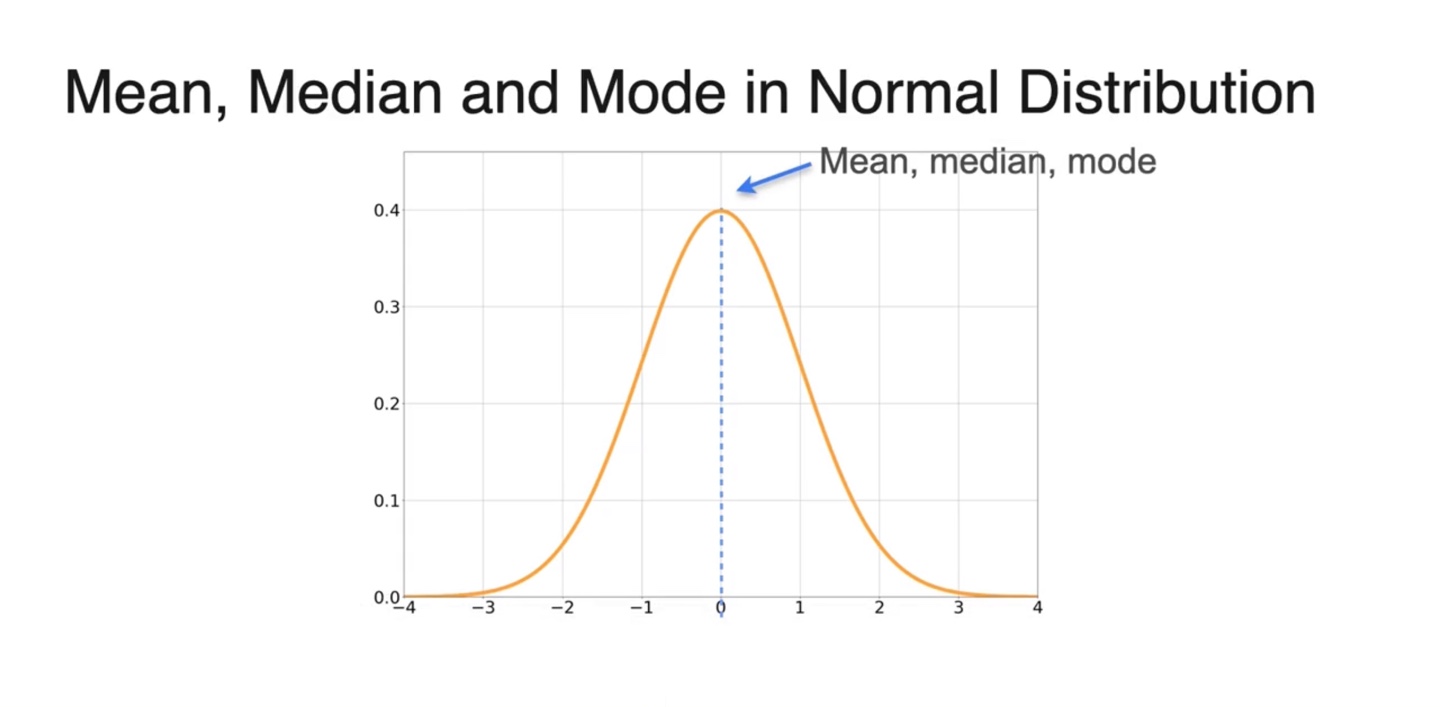
만약 Normal distribution이라면 mean, median, mode가 모두 같은 값을 가리킨다.
- 의 분포를 따른다면 말이다.
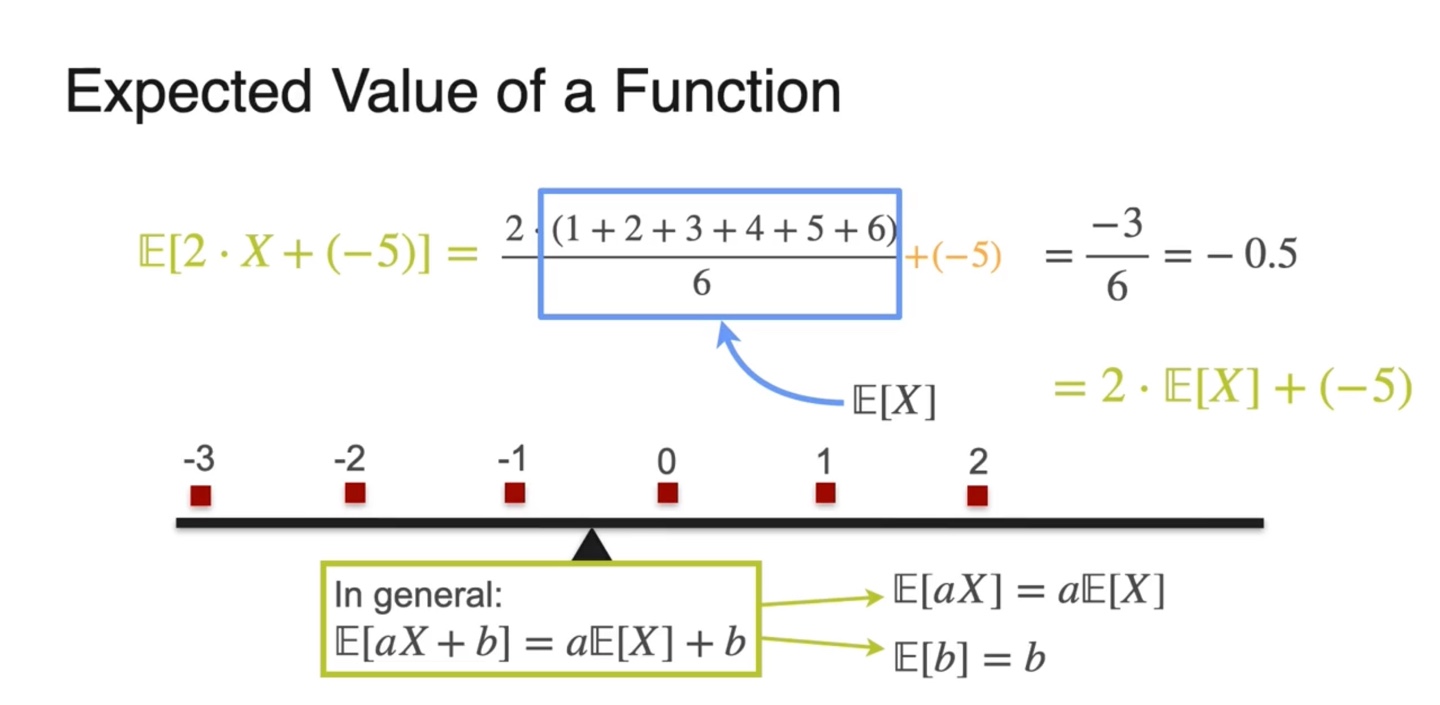
Expected value of a Function
-
아래와 같은 확률 변수와 확률을 가질 때, Expected value를 구해보자.
-
수식으로는 로 표기한다.
- 이 때 변수는 이며 이를 인 함수로 치환하여 합성할 수 있다.
-

-
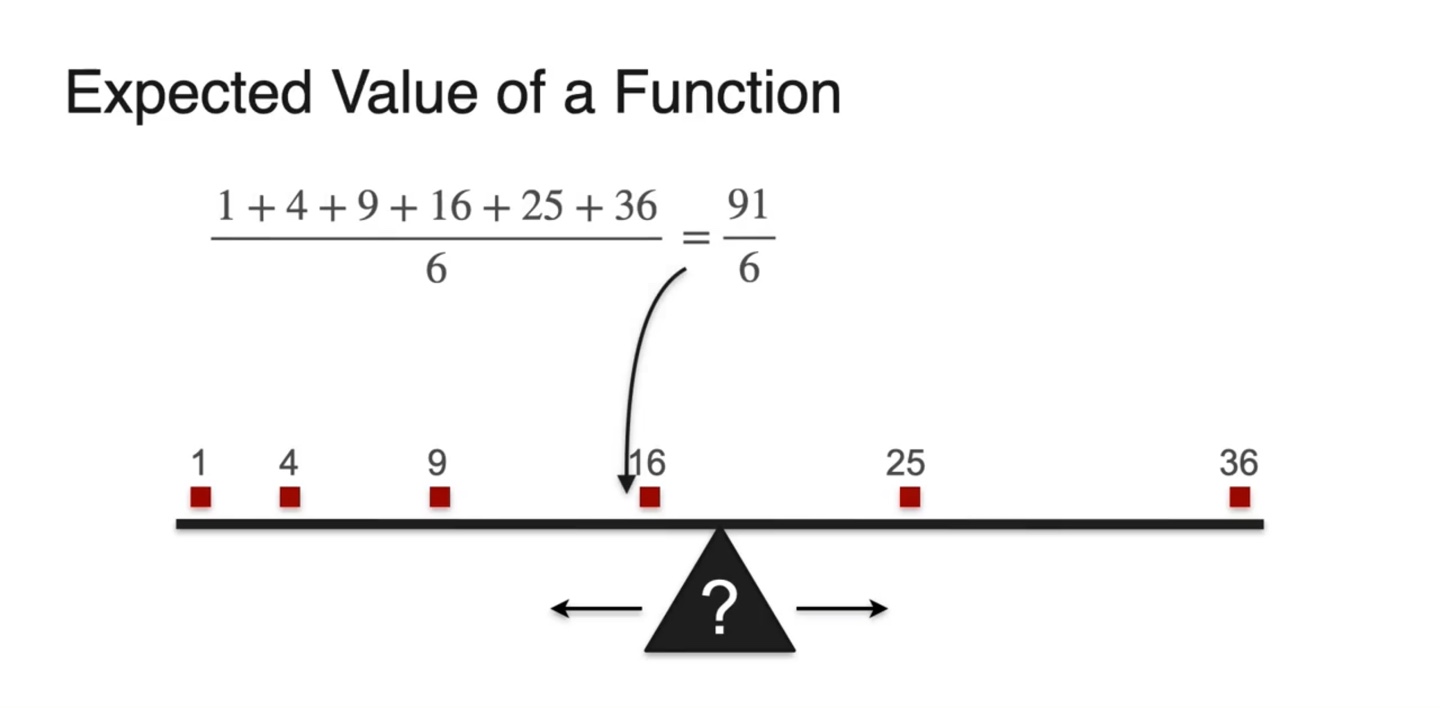
만약 변수의 제곱을 확률 변수로 취하고자 한다면 어떨까?
- 아래와 같이 주사위를 던지는 상황이라고 가정하여 변수에 제곱을 취해보자.
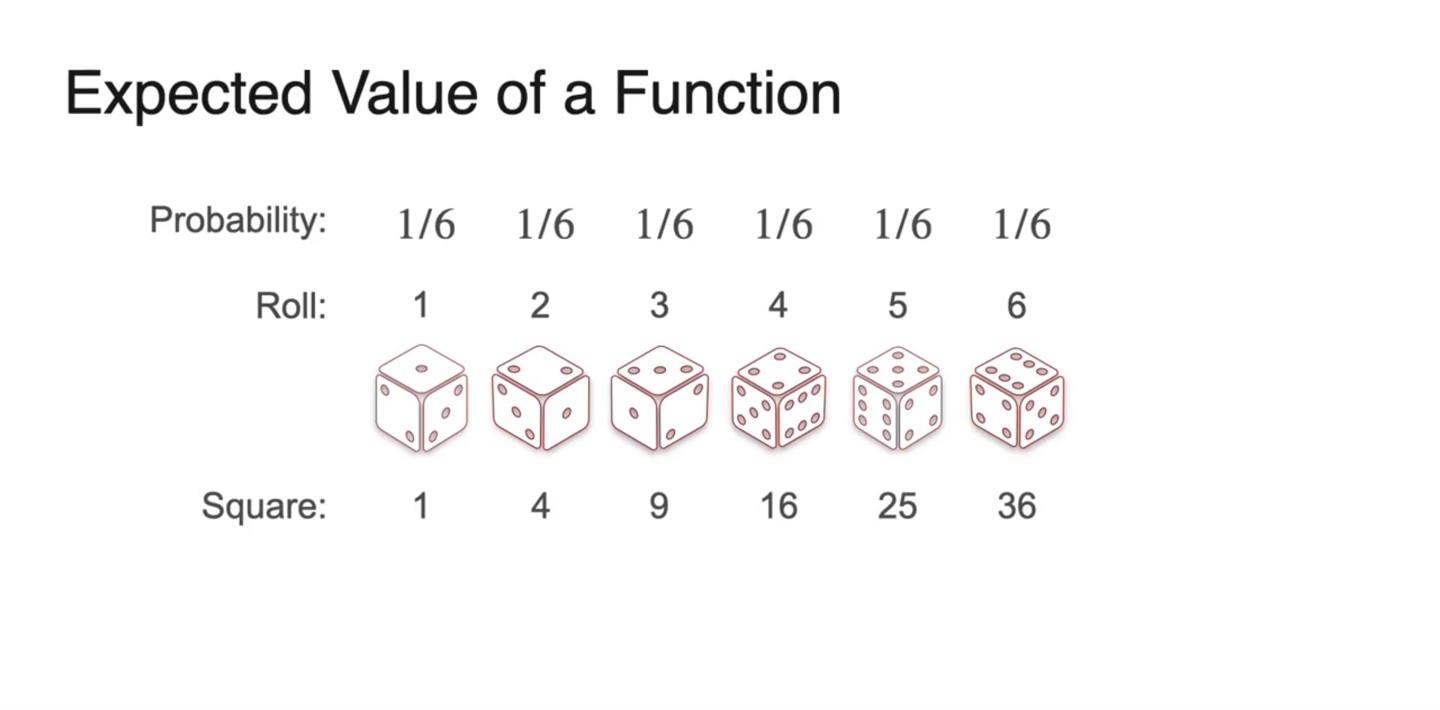
- Expected value를 구하기 위해 weight인 확률과 확률 변수의 분포를 히스토그램화 해보자.
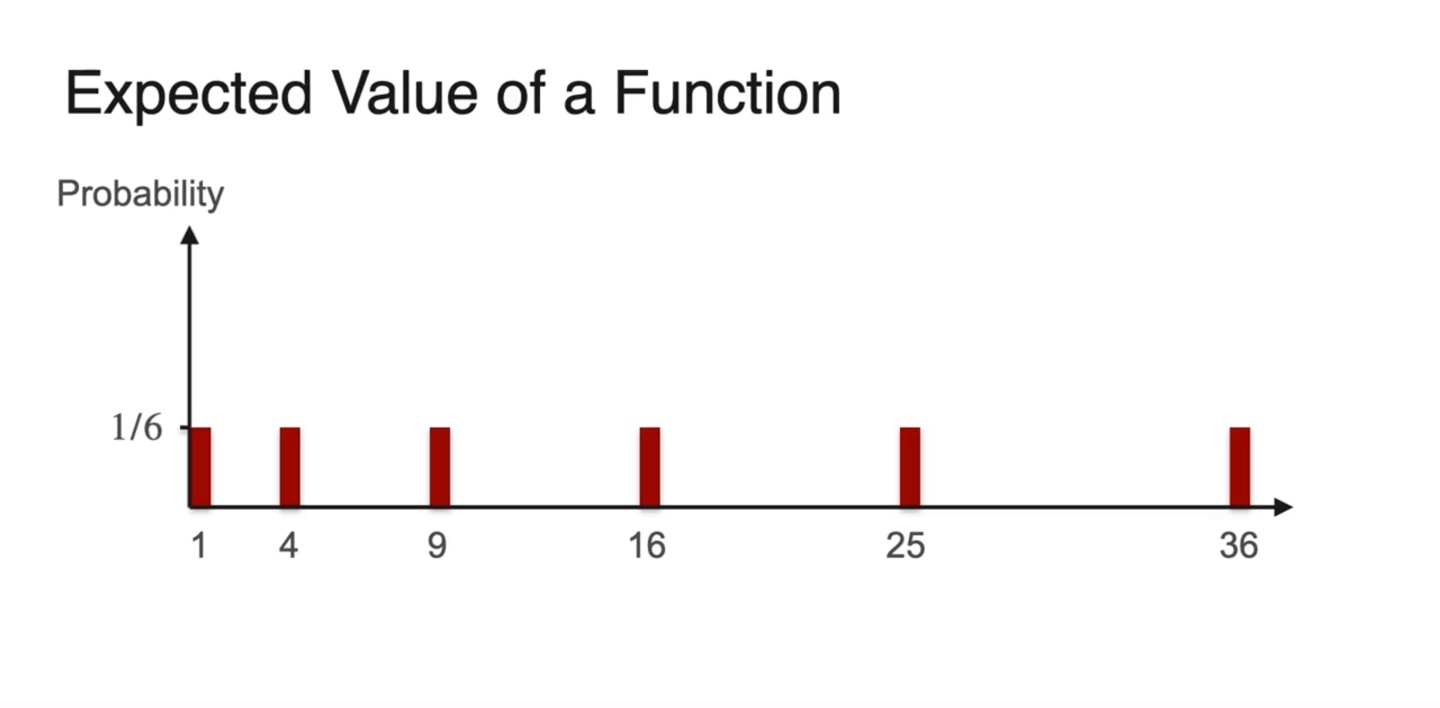
-
이 분포의 평균은 어디에 위치할까?
- 기존 의 평균에 비해 얼마나 달라질지를 계산해보면 차이를 알 수 있다.
-
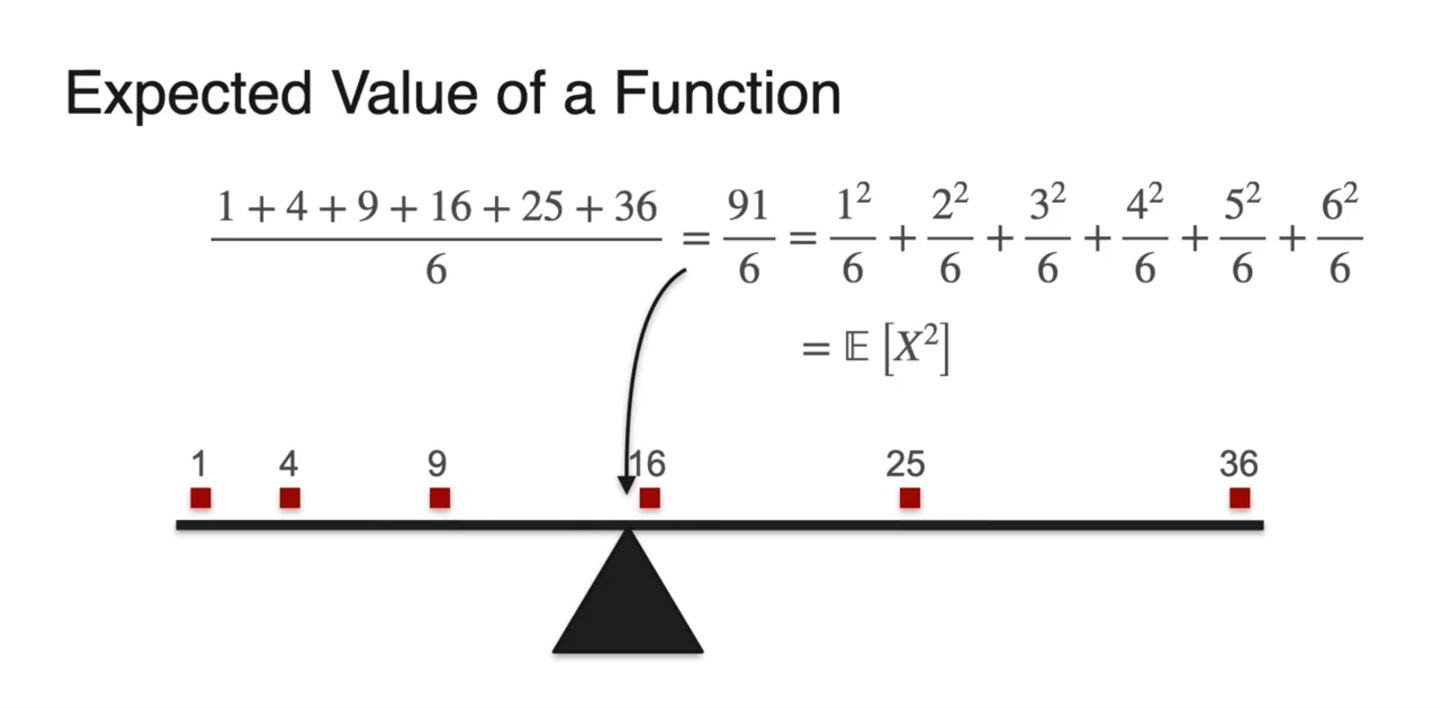
의 값은 로 계산되었다.
-
확률 분포가 uniform일 때 은 중앙값이 곧 평균값이었다.
- 그러나 는 살짝 왼쪽으로 치우쳐진 분포를 갖는다.
-
-
이번에는 Linear function의 Expected value를 찾아보자.
- Random variable에 를 곱하고 를 취하여 기댓값을 계산해보도록 하겠다.
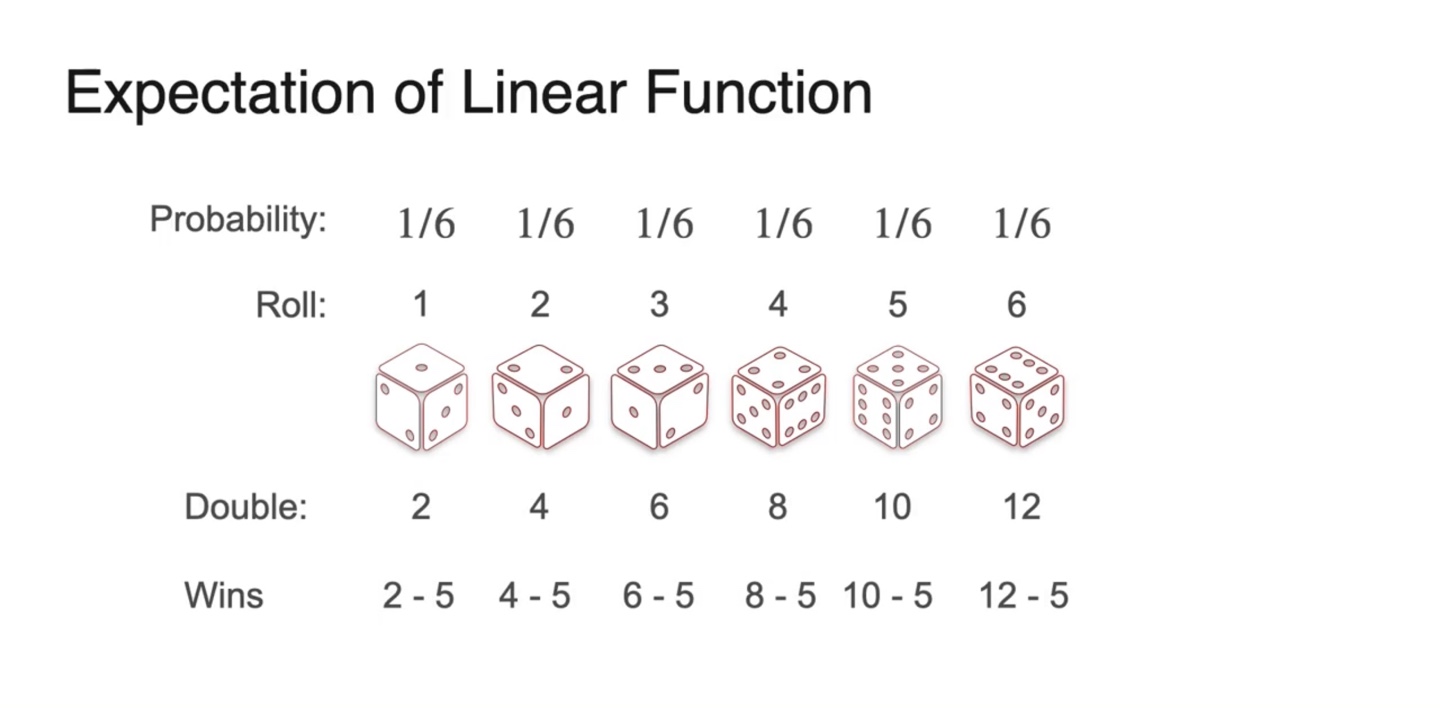
- 확률 분포는 uniform distribution을 따르고 random variable은 아래와 같다.
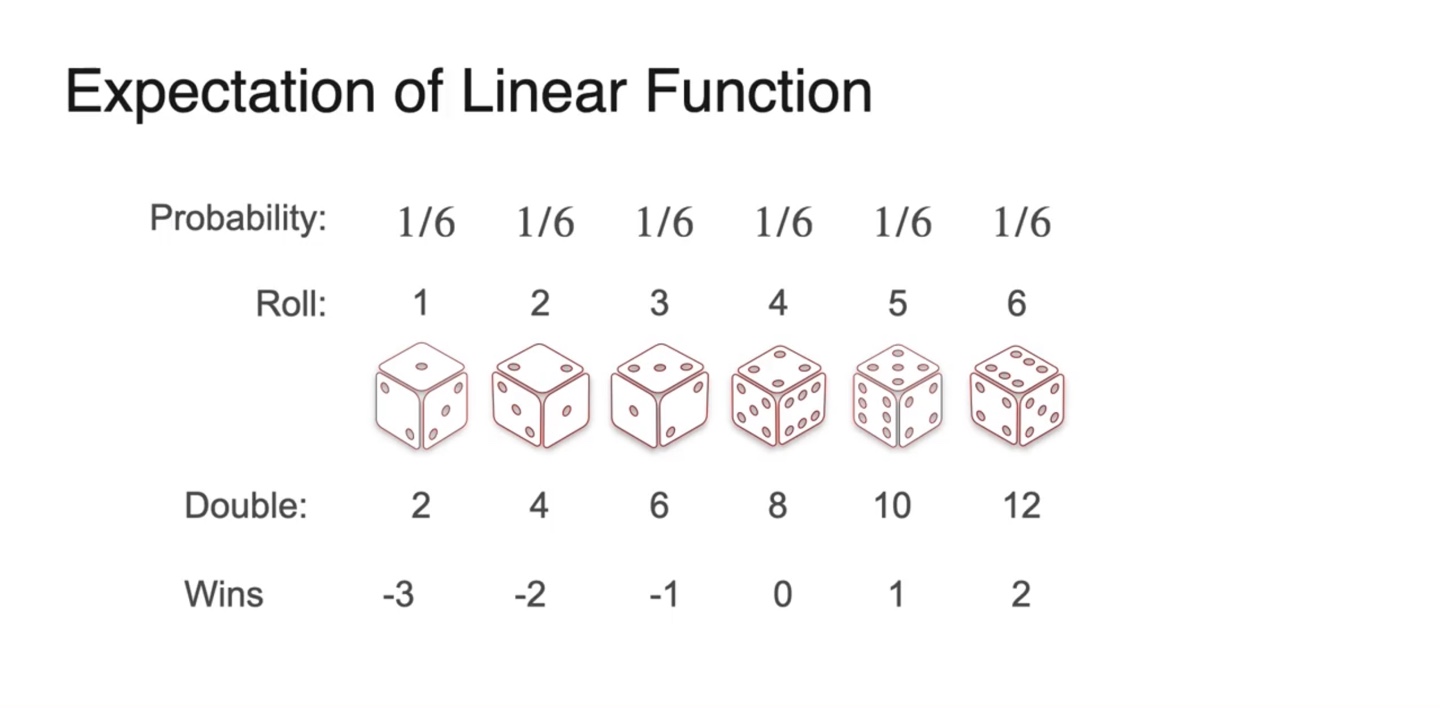
- 이를 히스토그램으로 펼쳐보면 아래와 같이 그려진다.
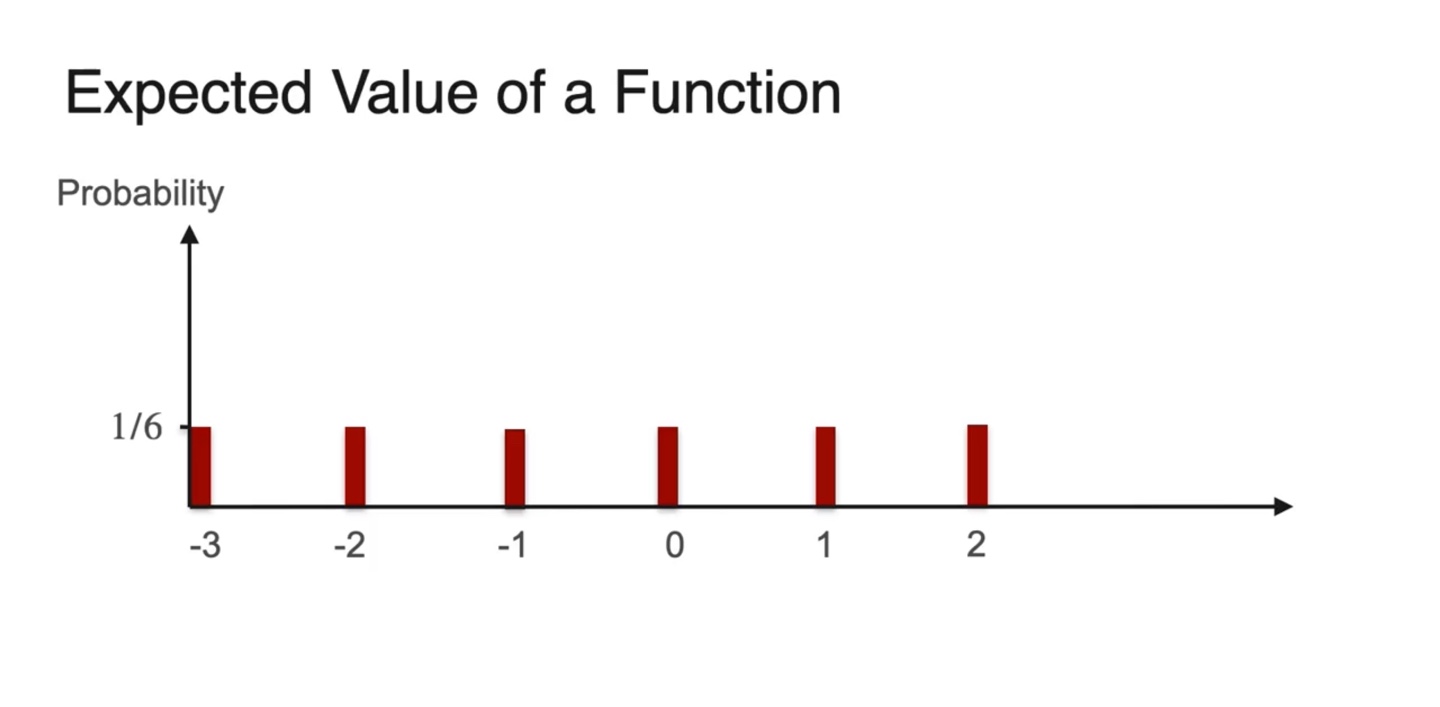
- 기댓값은 기존 variable 의 평균값과 비슷하게 중앙값이 곧 평균값을 따른다.
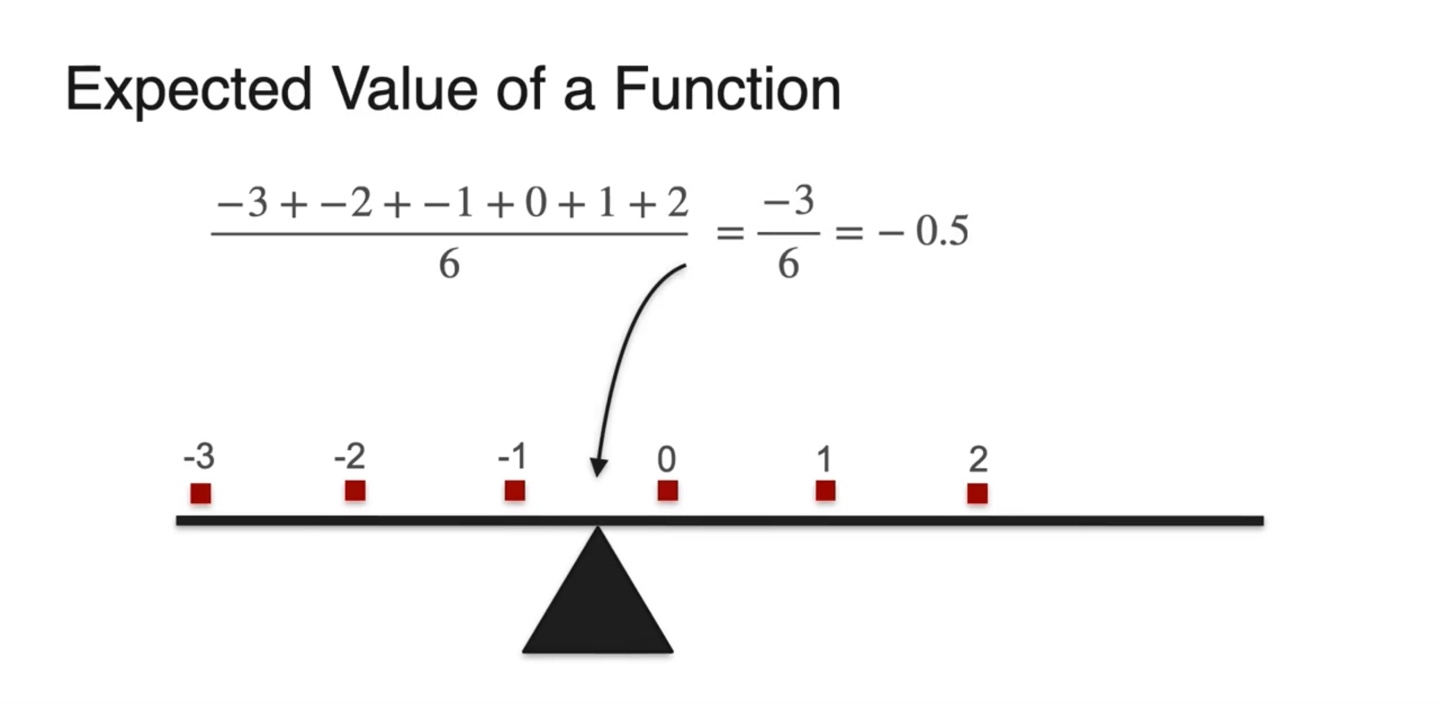
- 원래의 변수 와 확률 분포로 수식을 다시 표현하면 를 곱하고 를 취한 결과가 그대로 반영되어 나타난다.
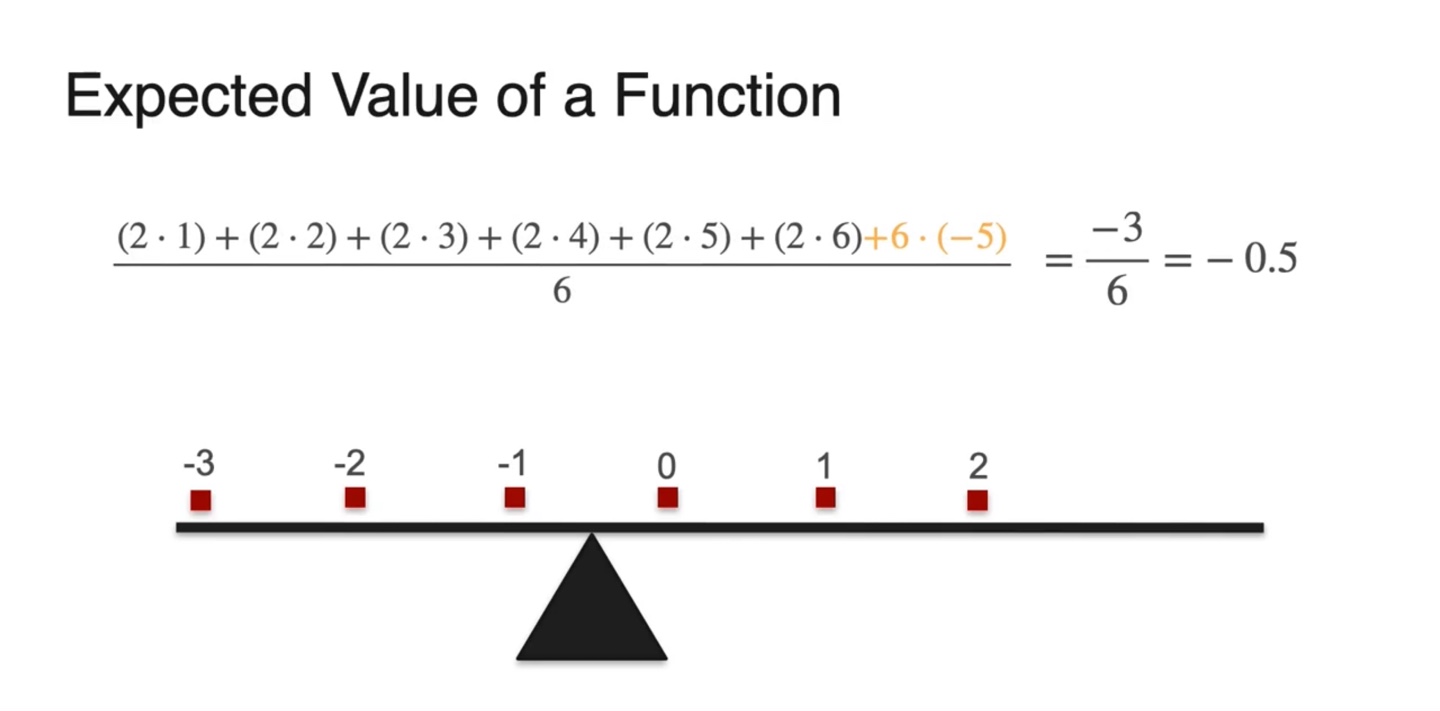
- 즉, 선형 변환 이후의 기댓값인 가 기존 기댓값인 에 를 곱하고 해준 값과 같다는 것이다.
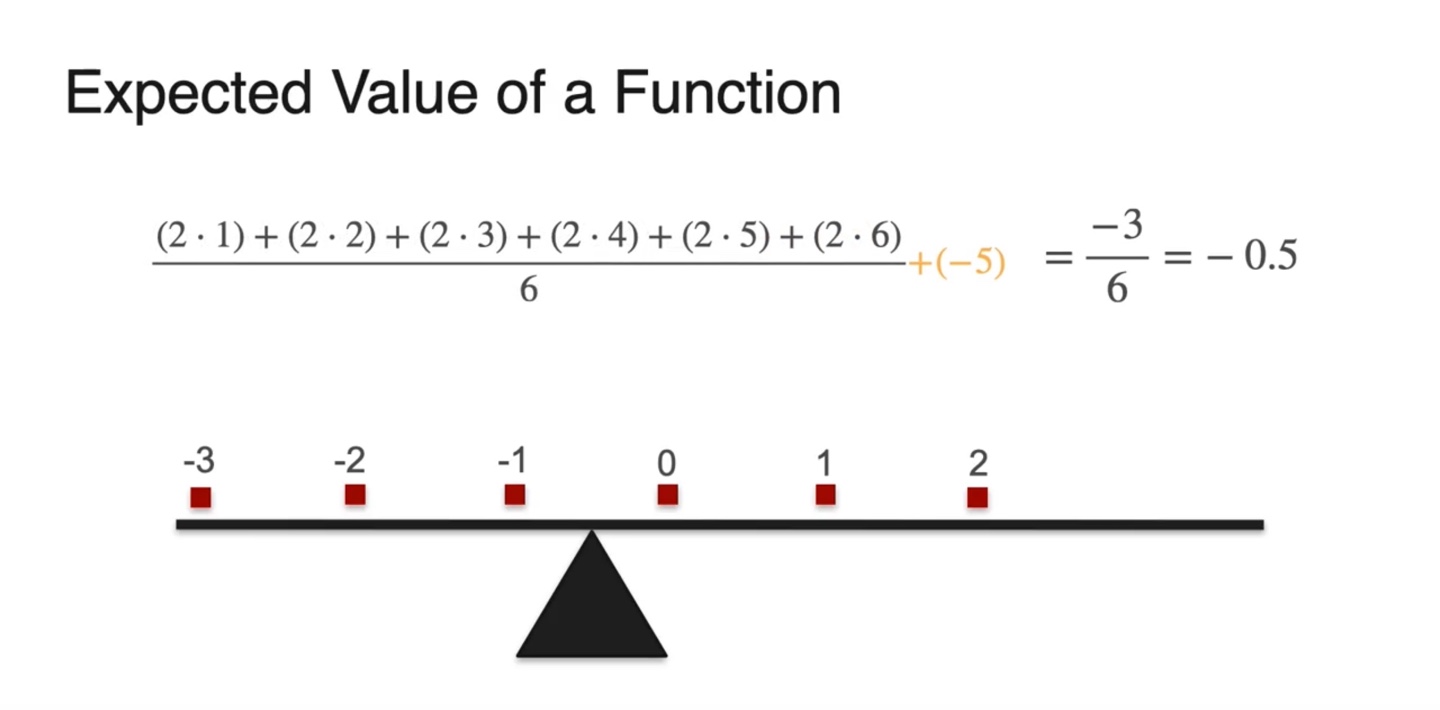
-
정리하자면 다음과 같다.
Sum of expectations
-
만일 동전을 던져 head가 나오면 $1, tail이 나오면 아무것도 받지 못한다고 하자.
-
그리고 주사위를 던져 주사위의 눈금만큼의 금액을 받을 수 있는 상황이다.
- 당신이 이 게임을 이겨 받을 수 있는 평균 금액은 얼마일까?
-

-
동전을 던져 이겼을 때의 평균 금액은 이다.
-
주사위를 던져 이겼을 때의 평균 금액은
다.
-
이 두 평균을 합한 값은 곧 전체 평균과 같다.
-

-
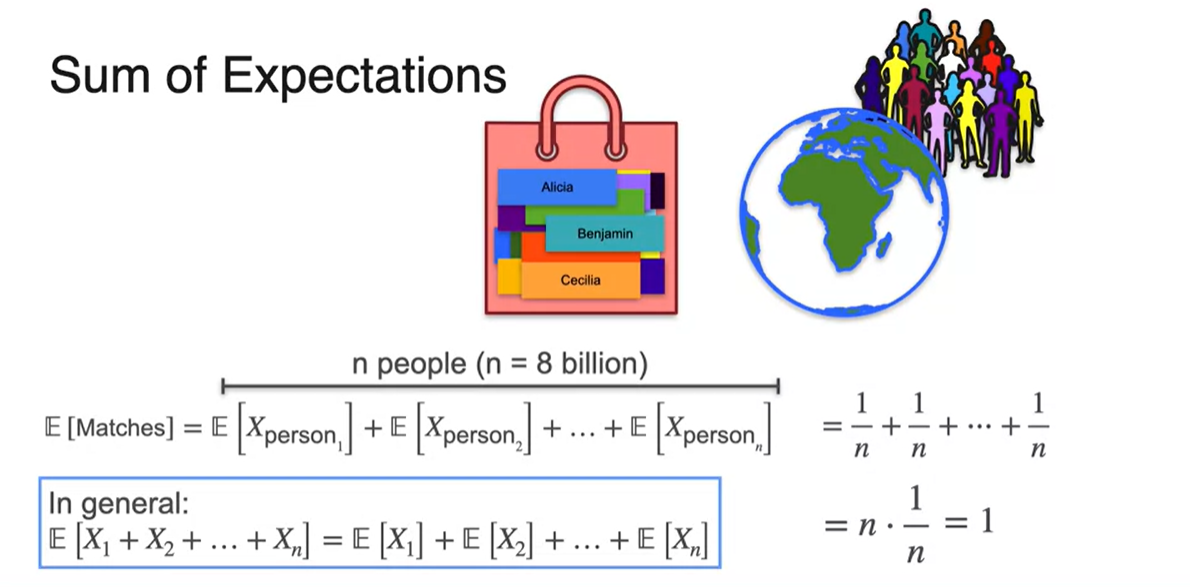
전 세계 80억명의 사람 이름이 unique하다고 가정하여, 이들의 이름이 들어있는 bag에서 각자 이름을 뽑는 상황이라고 생각해보자.
- 자신의 이름을 뽑은 사람의 평균값은 얼마일까?
-
정답은 1이다.
- 아래 예시에서는 Bo Bleepityblop이라는 사람이 본인의 이름을 뽑았다고 한다.
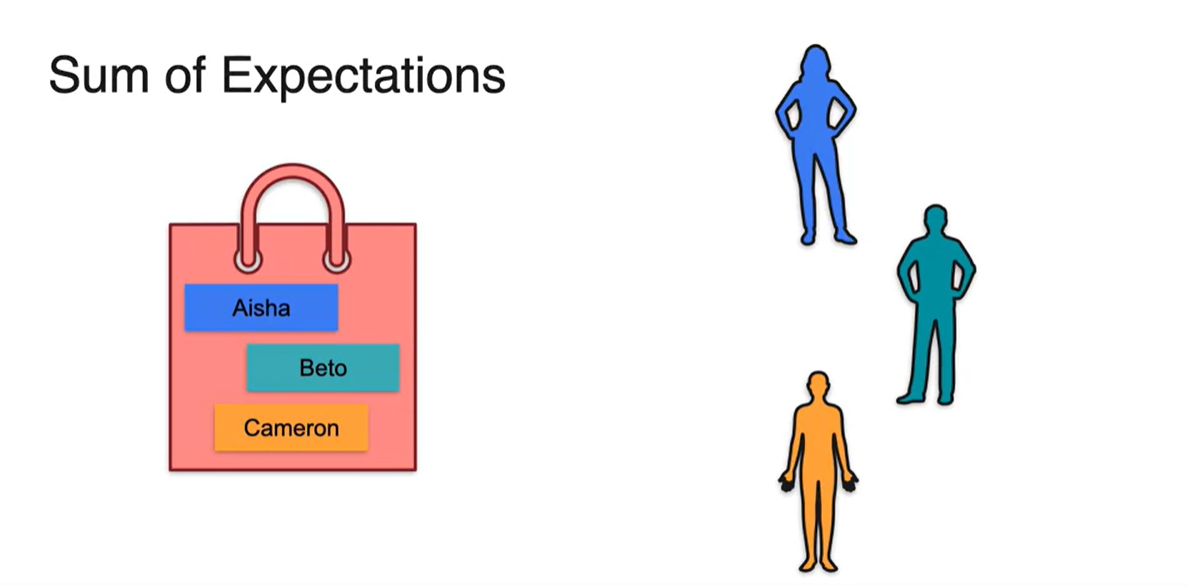
- 만약 3명의 사람이 이름 뽑기를 했다고 가정해보자.
-
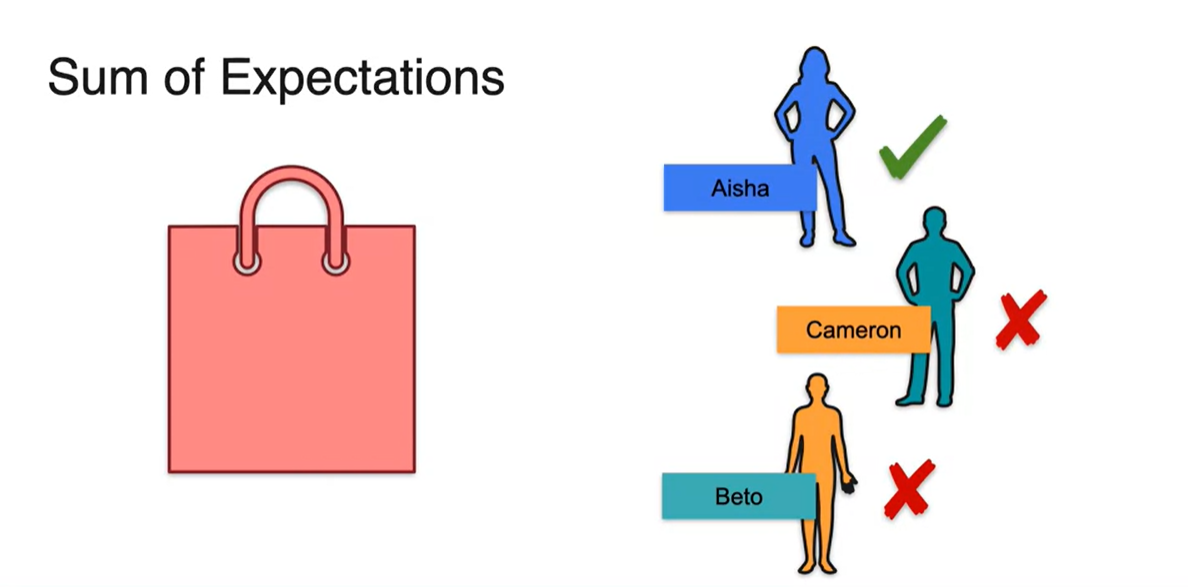
Aisha는 Aisha 본인을, Beto는 Cameron을 Cameron은 Beto를 뽑았다.
- 이 때 자신의 이름을 뽑은 사람은 Aisha 1명이다.
-
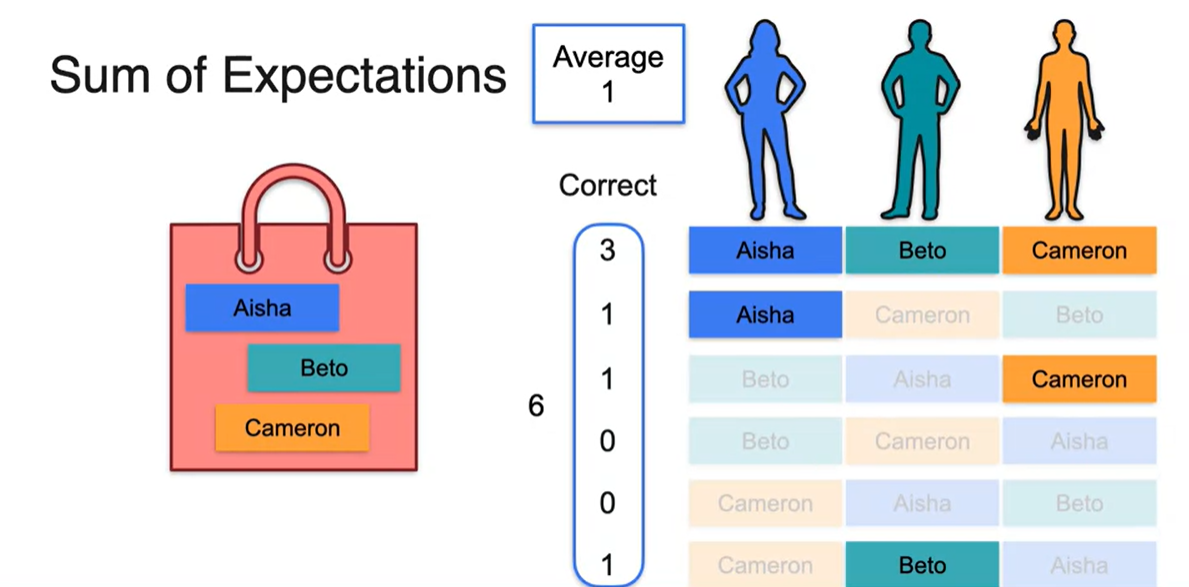
여러 번의 시행을 하여 자신의 이름을 뽑은 사람의 정확도를 평균 내어보자.
- 항상 명확하게 1의 평균값을 가지긴 힘들겠으나, 여러 번의 시행으로 정확도를 평균 내면 결국 1에 수렴하게 될 것이다.
-
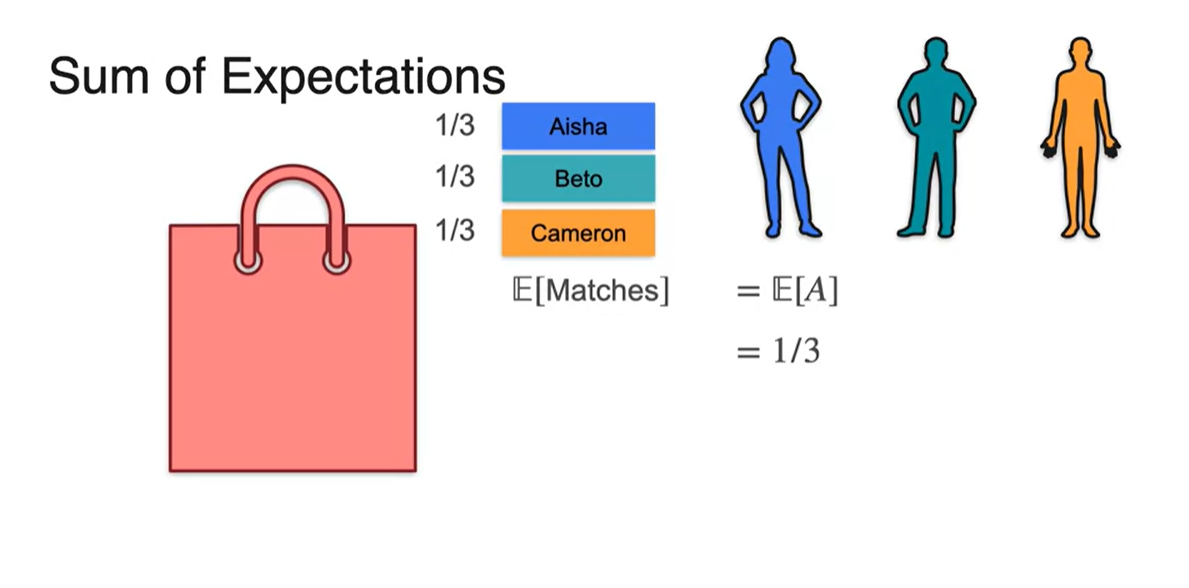
이번에는 각 사람마다의 평균값을 구해보자.
- Aisha는 총 세 가지의 선택지를 가지고 있고, 이 선택지의 확률이 1/3이기 때문에 자신의 명찰을 뽑는 expected value는 이다.
-
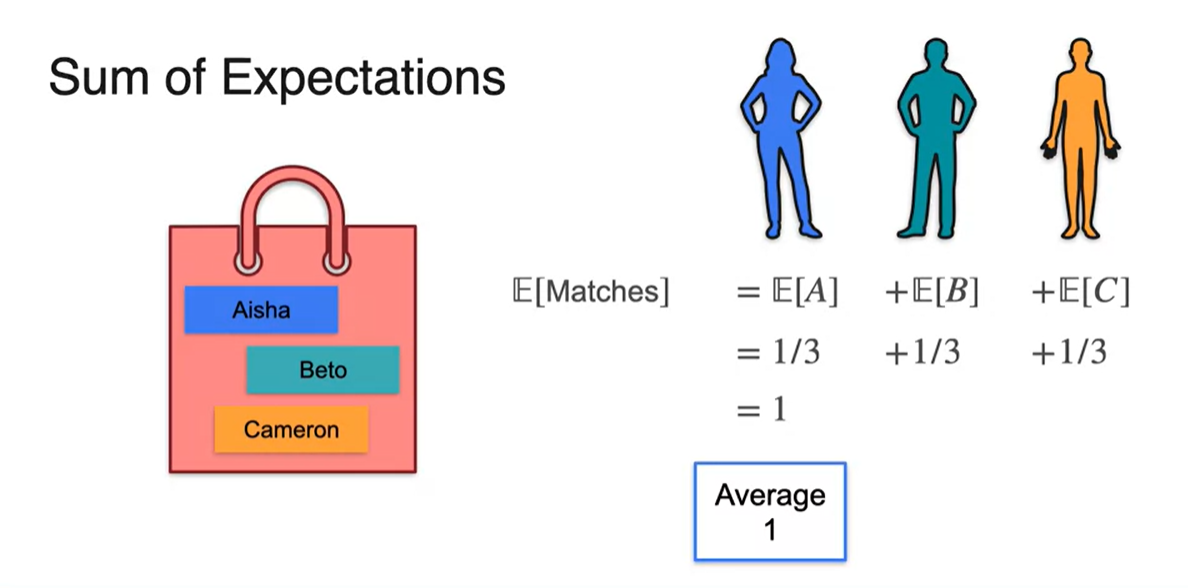
Beto나 Cameron의 expected value 또한 마찬가지다.
- 즉, 한 사람 한 사람의 정확도를 모두 더해 를 구하면 Average는 똑같이 1이 얻어짐을 알 수 있다.
-
80억명의 사람 중에서 자신의 이름표를 뽑은 사람의 평균값 또한 마찬가지다.
- 한 명당 의 expected value를 가지므로 명의 평균값을 모두 더한 값,
이 전체 평균과 같다.
- 한 명당 의 expected value를 가지므로 명의 평균값을 모두 더한 값,
Variance
-
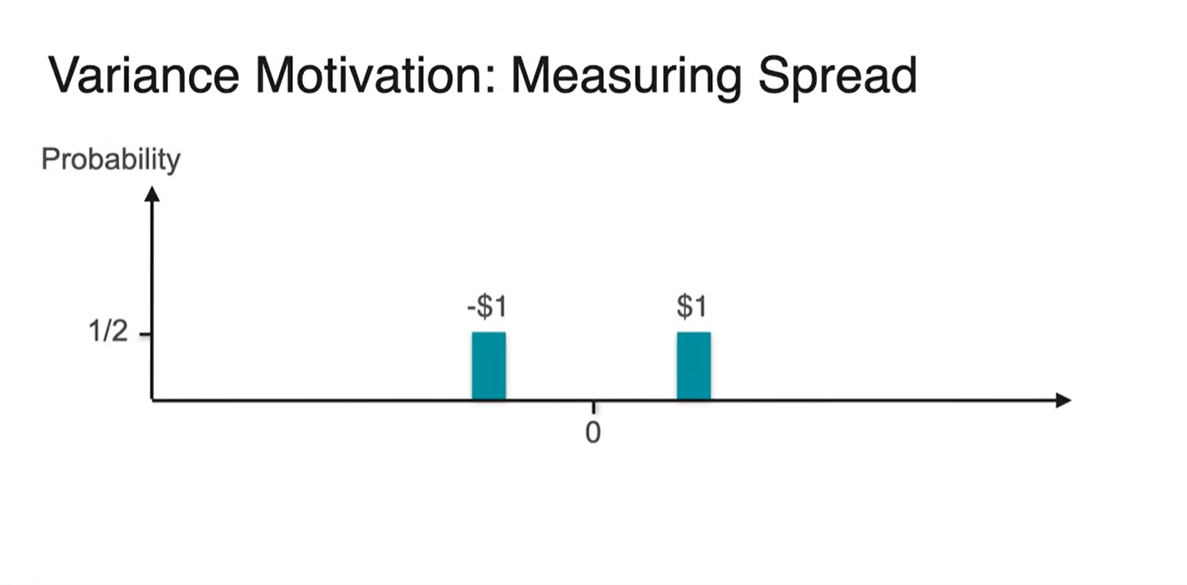
동전을 던져 head가 나오면 $1, tail이 나오면 -$1 을 받는 게임을 한다고 해보자.
- 이 게임의 Expected value는 이다.


-
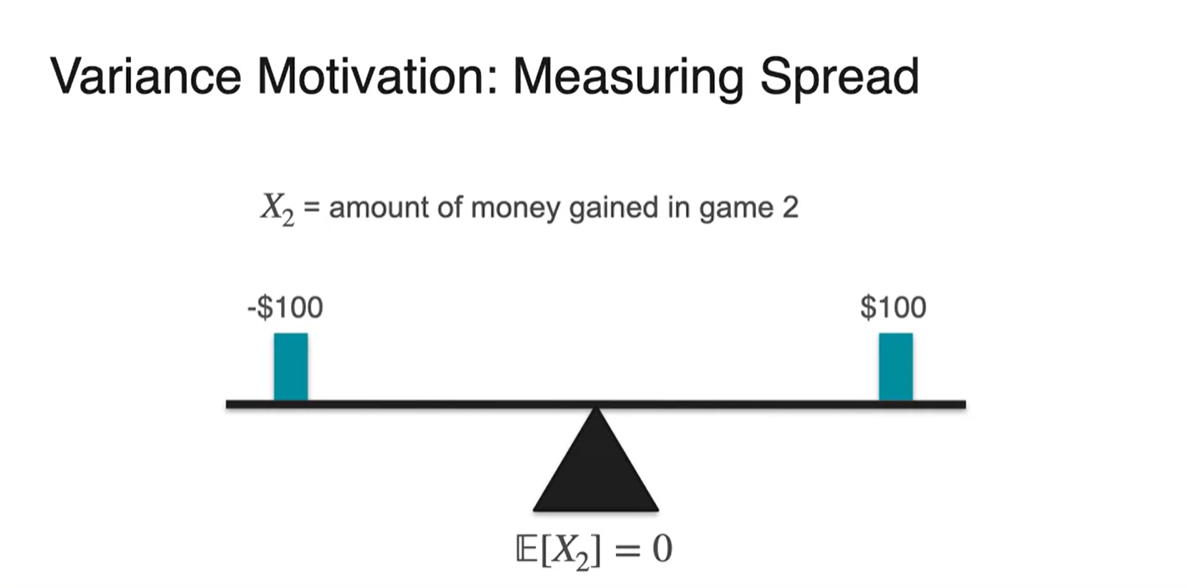
똑같은 게임을 head가 나오면 $100, tail이 나오면 -$100 을 받도록 해보자.
- 놀랍게도 이 게임의 Expected value 또한 이다.


-
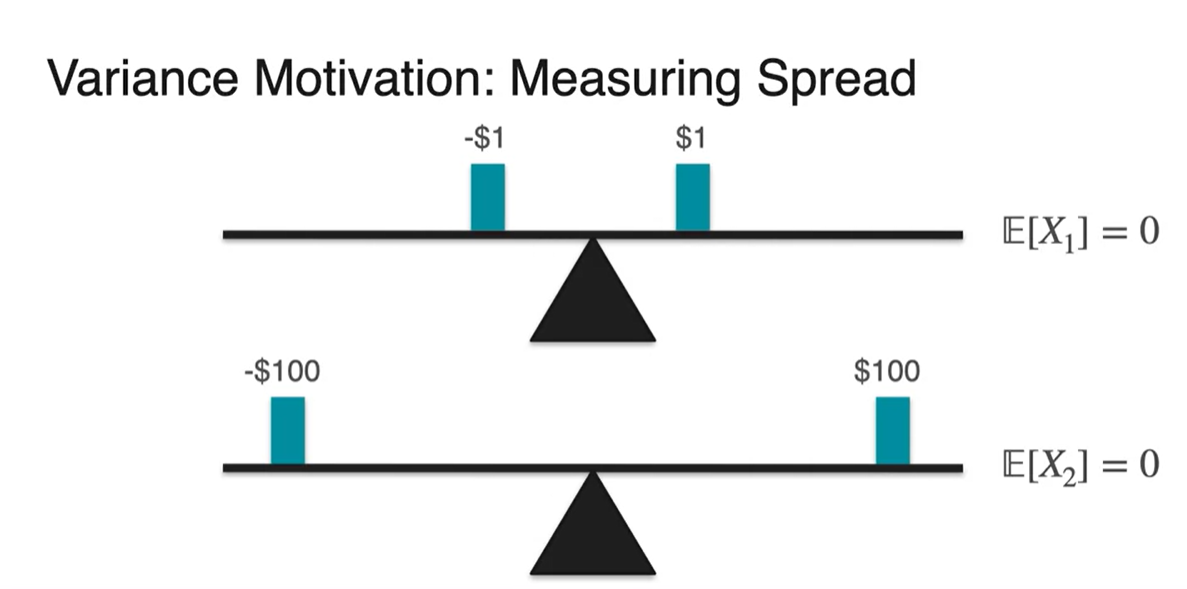
분산(Variance)의 개념은 spread를 측정하는 것이다.
- 확률 변수와 확률 분포로 ploting하면 아래와 같은 그림이 그려진다.
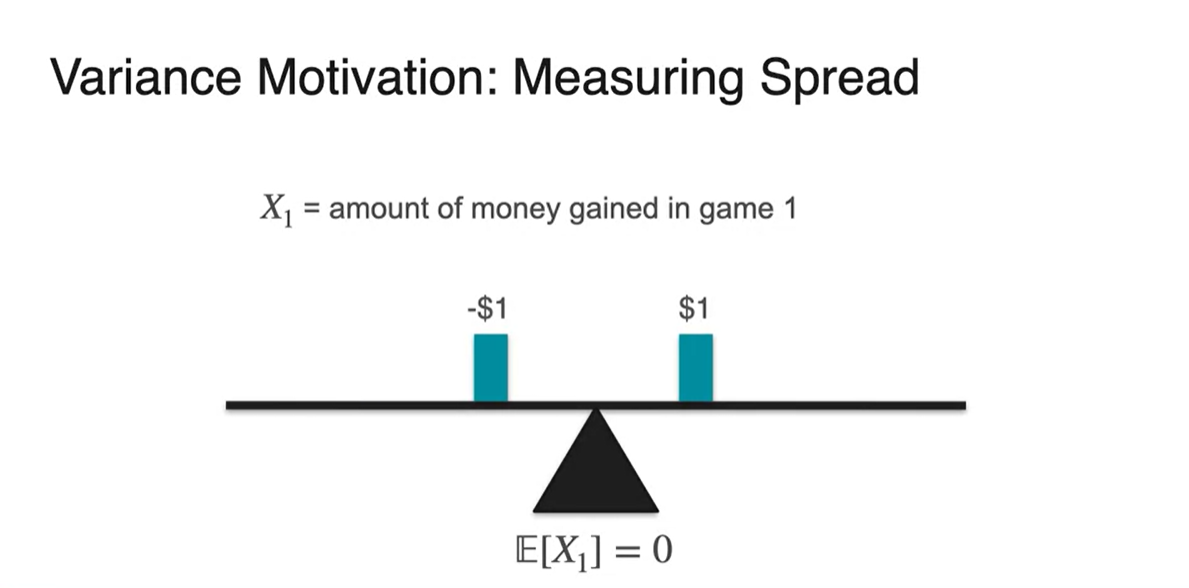
- 첫 번째 게임의 expected value, 무게 중심은 0이다.
-
두 번째 게임의 expected value, 무게 중심 또한 0이다.
- 여기까지는 평균을 계산하는 방법이다.
-
Variance는 어찌 보면 그 게임의 위험도를 판별할 때 필요한 수치임을 알 수 있다.
- Expected value로는 $1를 받는 게임이나 $100를 받는 게임이 동일하게 0이기 때문에 위험 수치로 비교하기에는 적절하지 않다.
-
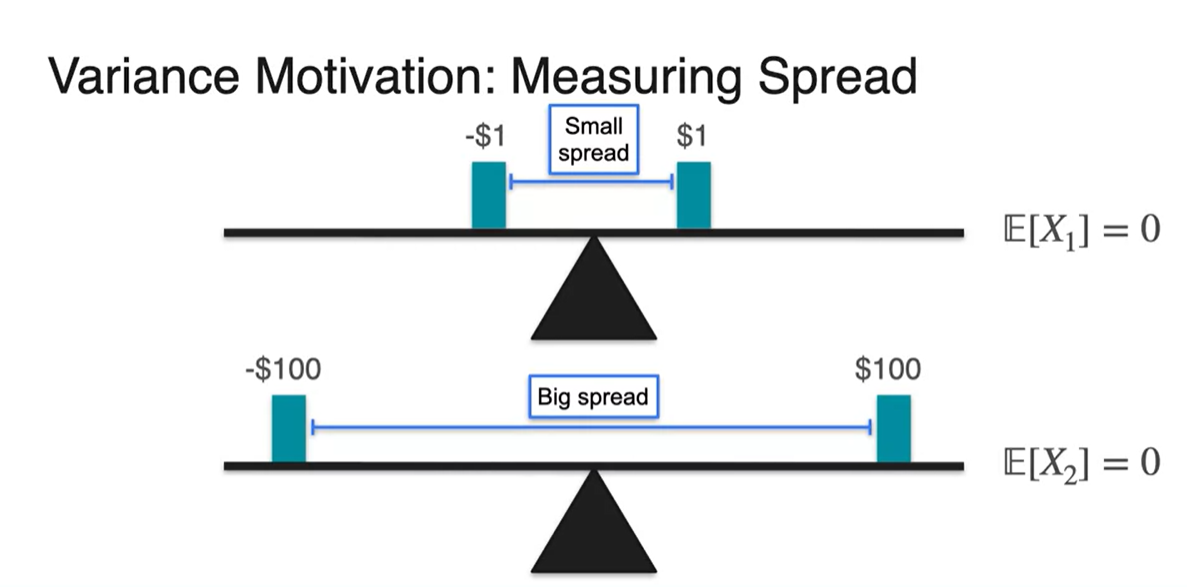
Variance는 각 변수들의 떨어진 정도, spread로 판별한다.
- 아래 그림에서는 $100 게임이 more spread하다.
-
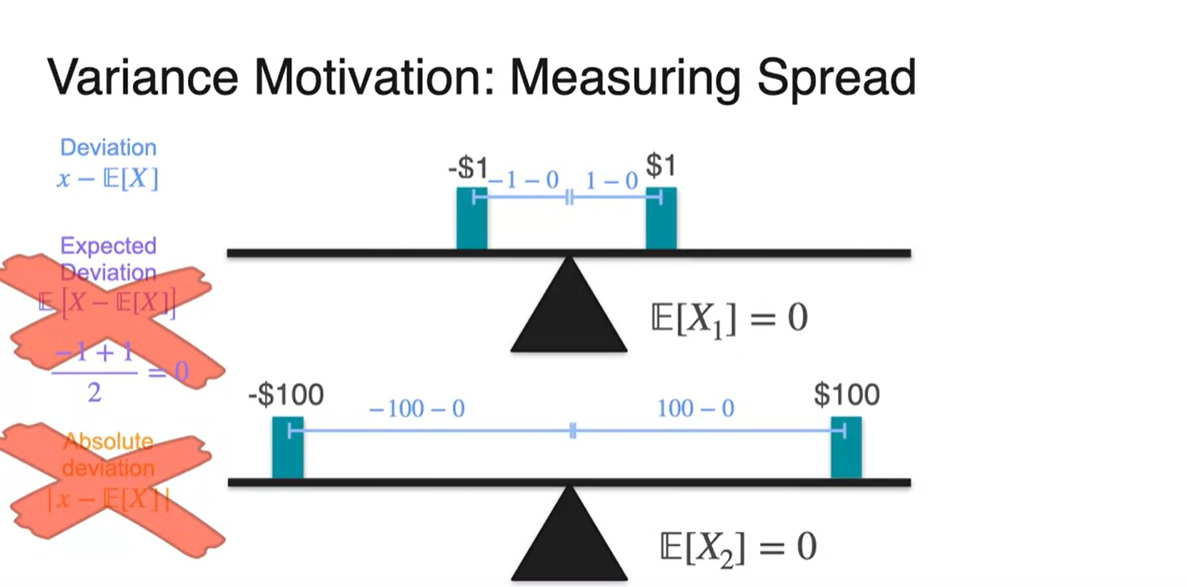
편차(Deviation)는 확률 변수() - 평균()이다.
-
편차의 평균을 내면 양수 음수의 값이 서로 상쇄되기 때문에 spread를 측정하기에 알맞지 않다.
-
편차의 절댓값(Absolute)으로 계산하면 절댓값의 특성 상 massive mathmatical properties를 가진다고 설명하고 있기 때문에 적절하지 않다고 한다.
- 가장 대표적인 특징 중에 하나는 절댓값 함수가 뾰족점이 존재하여 미분할 수 없는 함수라는 점이다.
-
-
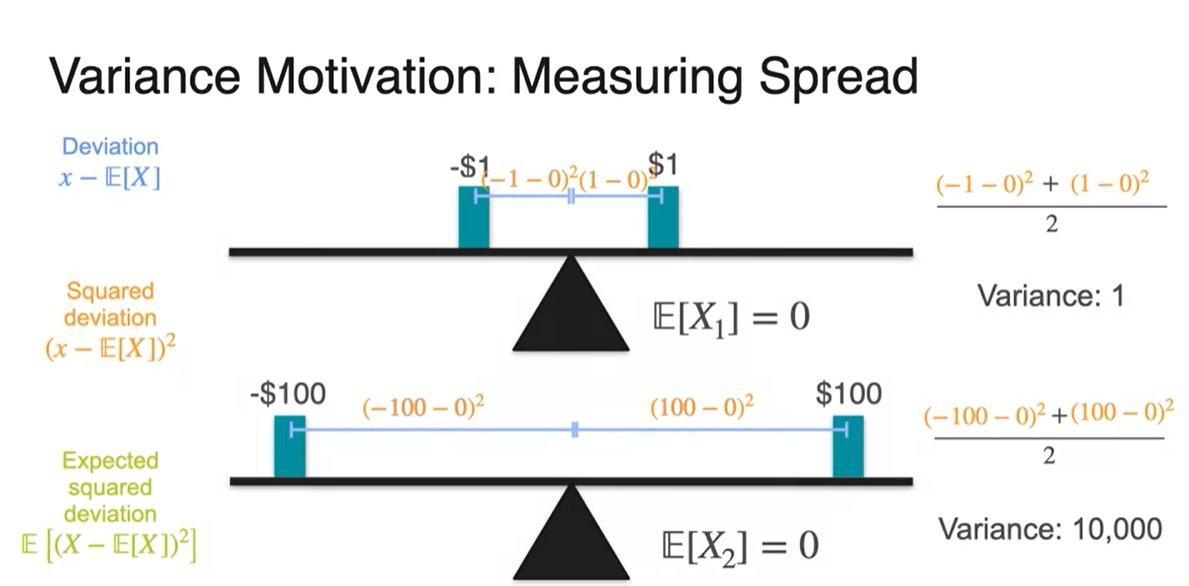
따라서 우리는 편차 제곱의 평균으로 variance를 정의한다.
- 두 게임의 variance를 비교해보면 10,000으로 계산된 두 번째 게임이 위험도가 더 높음을 알 수 있다.
-
공식으로 표기하면 다음과 같다.
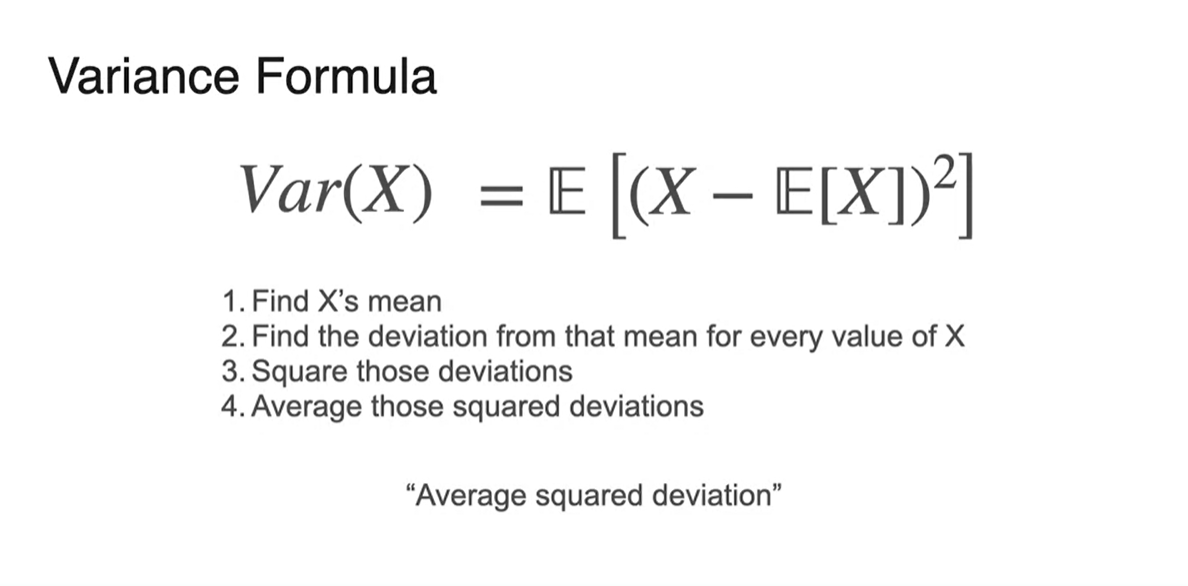
-
이번에는 $2, -$2 / $3, -$1을 받는 두 게임의 분산을 계산해보자.
- 결과적으로 두 variance는 동일하다.


-
두 게임의 Expected value는 각각 0, 1이다.
- 확률 변수에 평균을 뺀 즉, 편차 제곱의 평균을 구하면 4의 값으로 동일하다.


- Variance는 로도 표기할 수 있다.
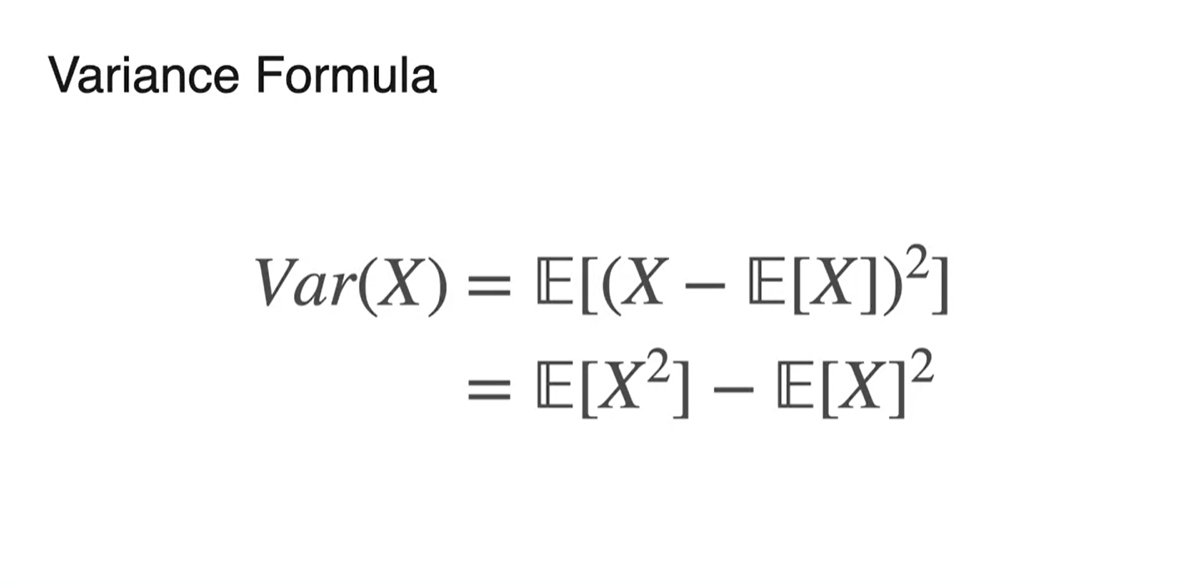
-
편차 제곱의 평균을 전개하면 증명할 수 있다.
: Linear
: Multiply constant, Expectation of constant

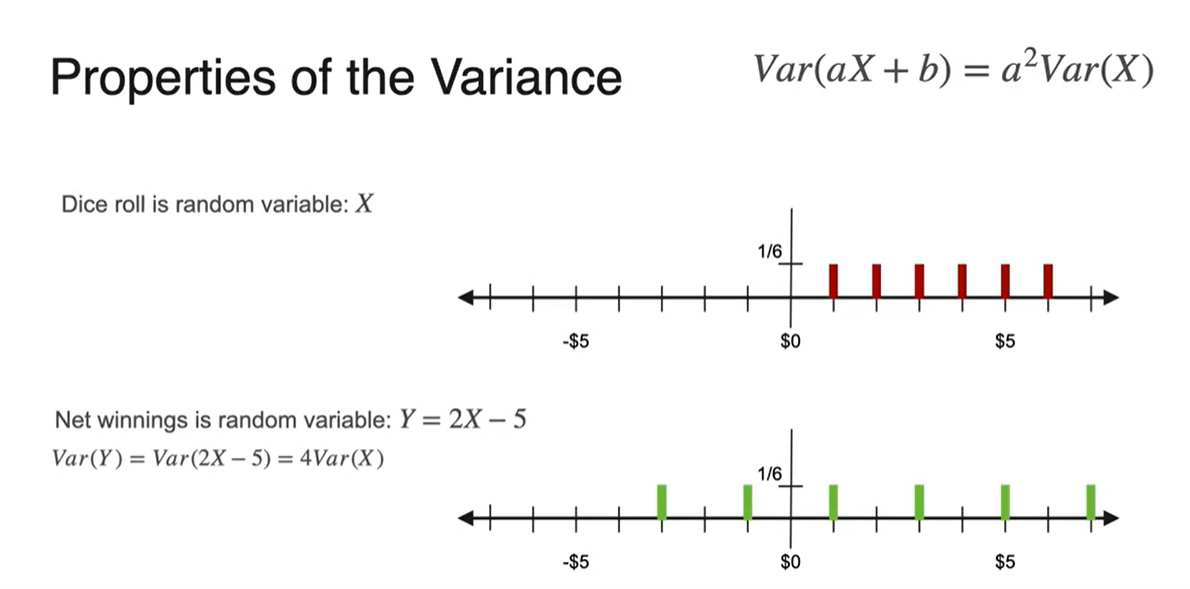
- 주사위 던지는 예제로 다시 넘어가서, 를 곱하고 를 취한 의 분산을 구해보자.

-
분포를 펼쳐보면 아래와 같이 그려진다.
- 결론적으로 분산의 선형 변환은 공식을 만족한다.
-
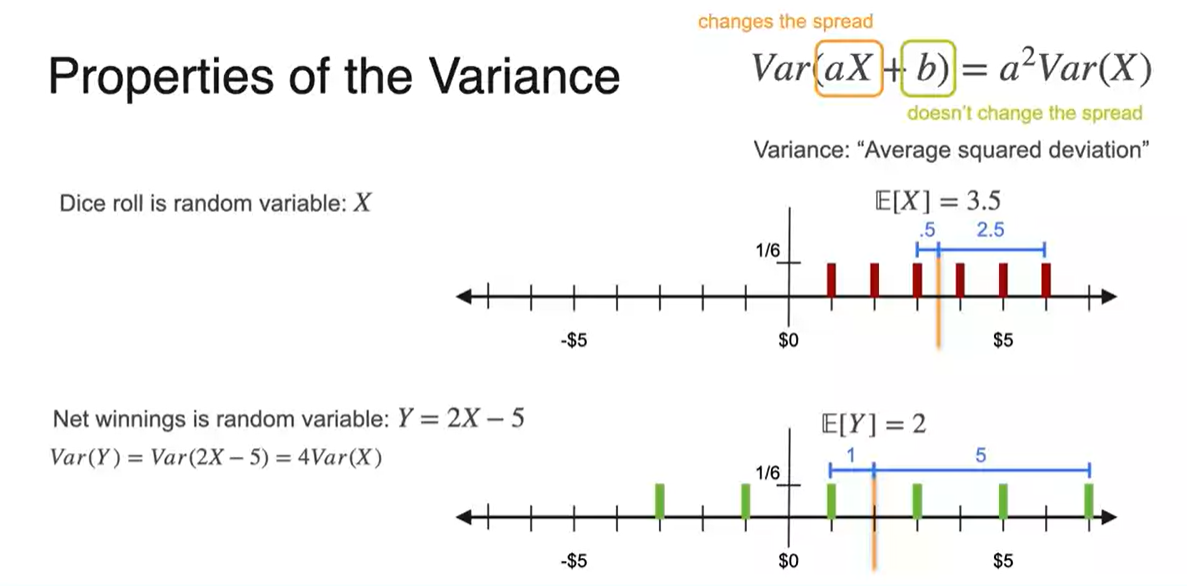
평균으로부터의 거리를 구해보면 기존 분포에서의 편차는 0.5, 2.5인 반면 의 분포는 1, 5로 딱 2배씩 증가했음을 알 수 있다.
- 더해진 는 영향을 미치지 않고, 편차의 제곱이 곧 분산으로 계산되어 최종식은 곱해진 value {의 제곱 * 기존 variance}로 분산이 정의된다.
Standard Deviation
-
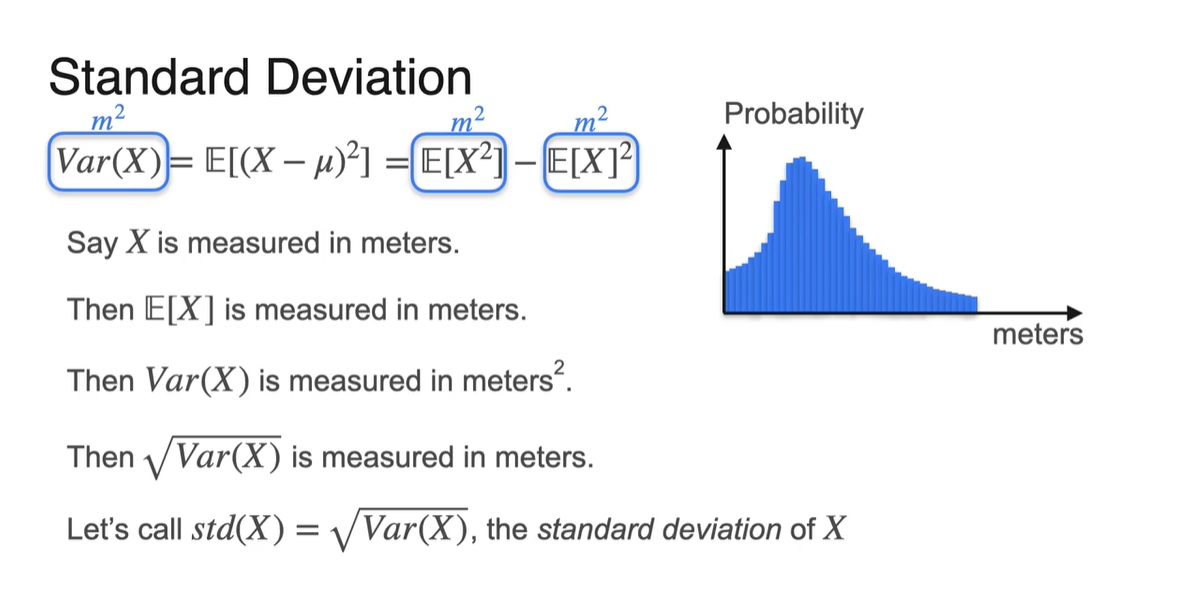
분산(Variance)으로 spread를 측정하면 단위가 제곱배가 되어 해석이 어려워진다.
-
만약 한 class의 학생들의 키를 측정하여 확률 분포를 표현하면, Variance의 단위는 meter 제곱()이 된다.
- 이를 해결하기 위해 표준 편차(Standard Deviation) 개념이 등장하였고, 분산의 square root 즉, 로 정의한다.
-
-
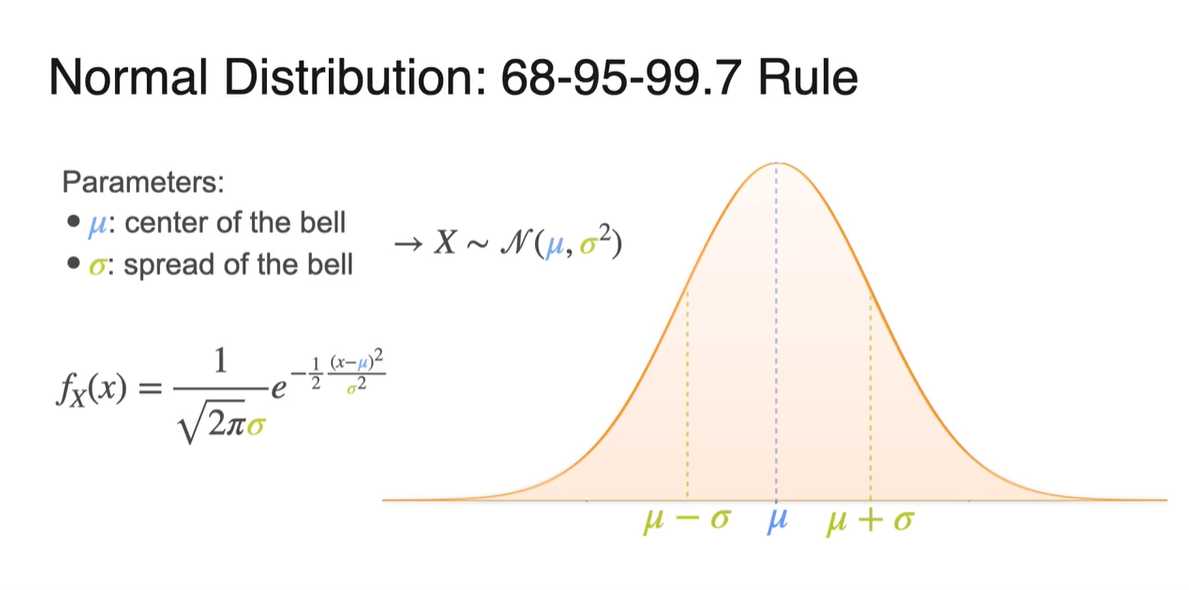
Normal distribution에서의 가 가리키는 값이 바로 표준 편차다.
- 평균으로부터의 좌우 width를 표현한다.
-
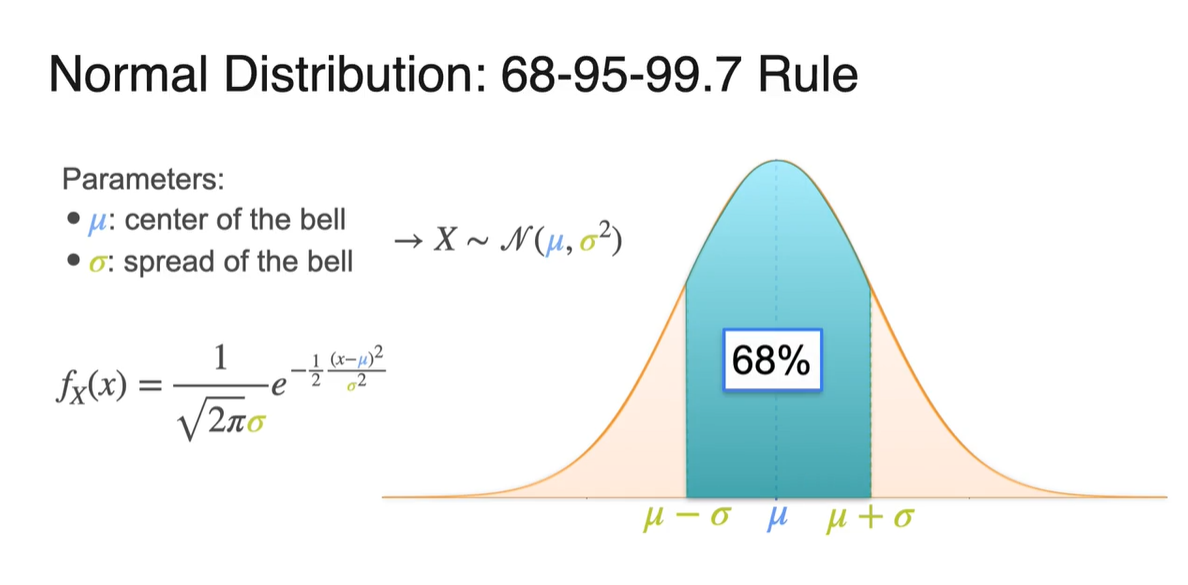
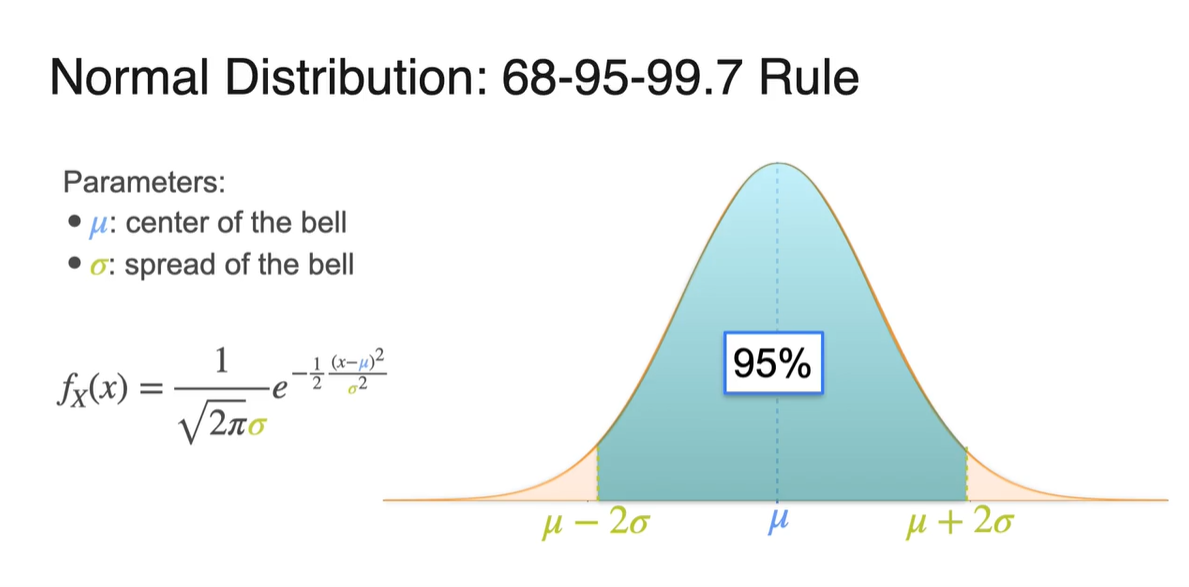
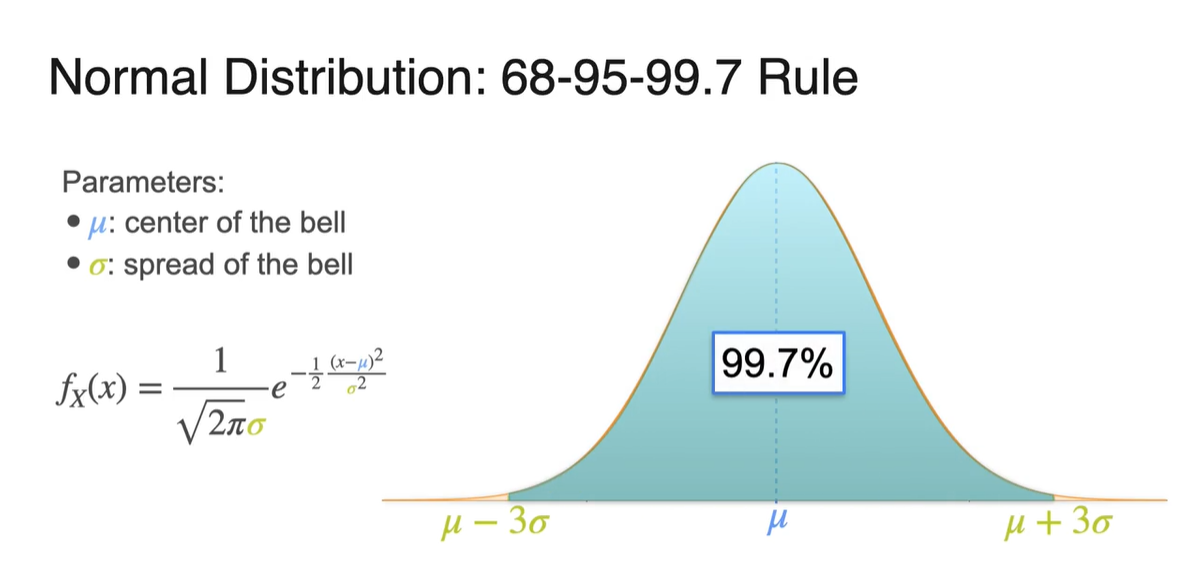
확률 변수 가 와 사이를 가질 때의 면적은 전체 면적의 68%를 차지한다.
- 와 사이는 95%를, 와 사이는 99.7%의 면적을 차지한다.
-
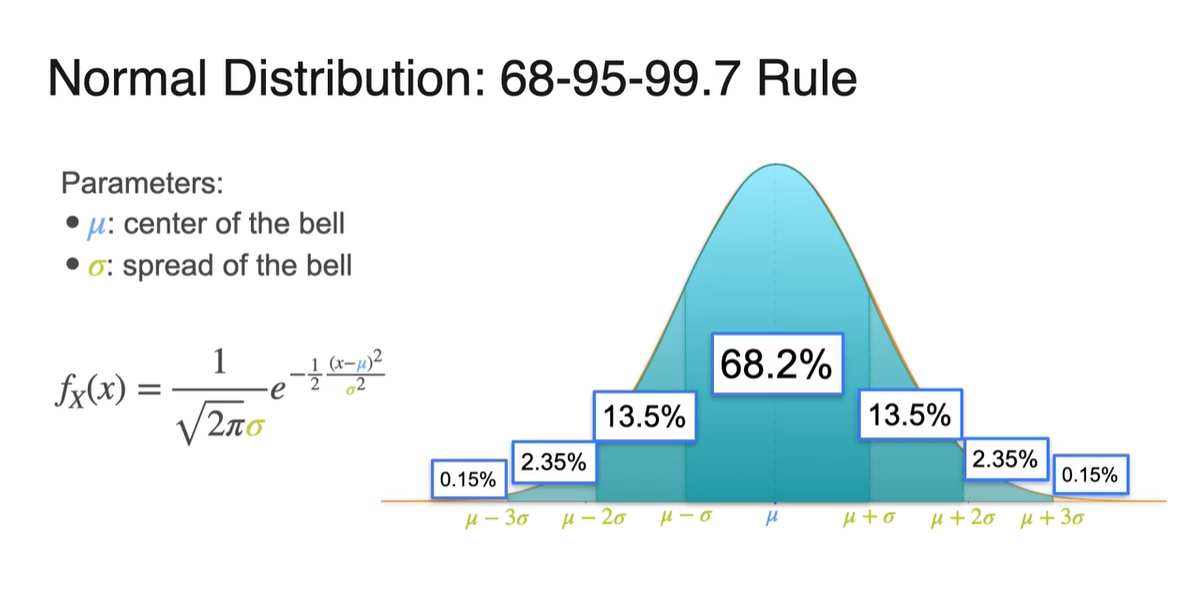
전체 확률이 1이므로 전체 면적은 100%로 나타낼 수 있으며, 아래 그림은 각 구간의 면적을 계산해 둔 결과값을 나타낸다.
- Standard deviation이 얼마인지에 따라 신뢰 구간을 설정할 수 있다는 점도 알아두자.
Sum of Gaussians
-
만약 두 Gaussian 분포를 더한 분포를 알고 싶다면 어떨까?
-
일반적으로 컴퓨터의 Response time()은 Processing time()과 Network latency()에 따라 결정된다.
-
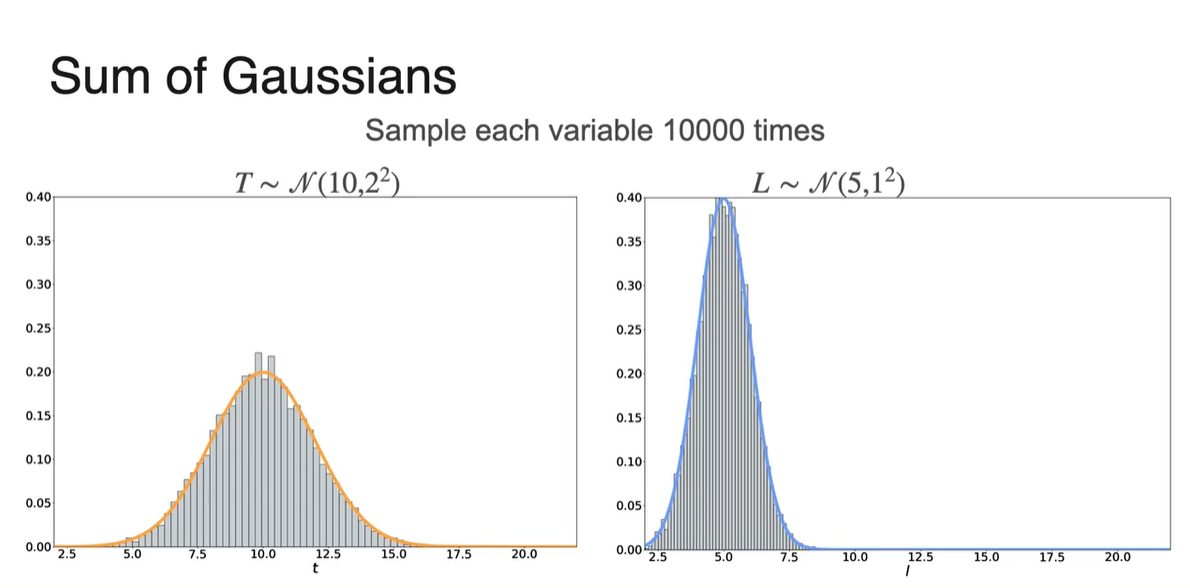
전체 분포의 확률 변수가 이고, 와 이 평균과 표준 편차가 각각 다른 gaussian 분포를 따른다면 의 분포는 무엇일까?
- 을, 을 따르며 두 확률 변수는 Independent 하다!
-

-
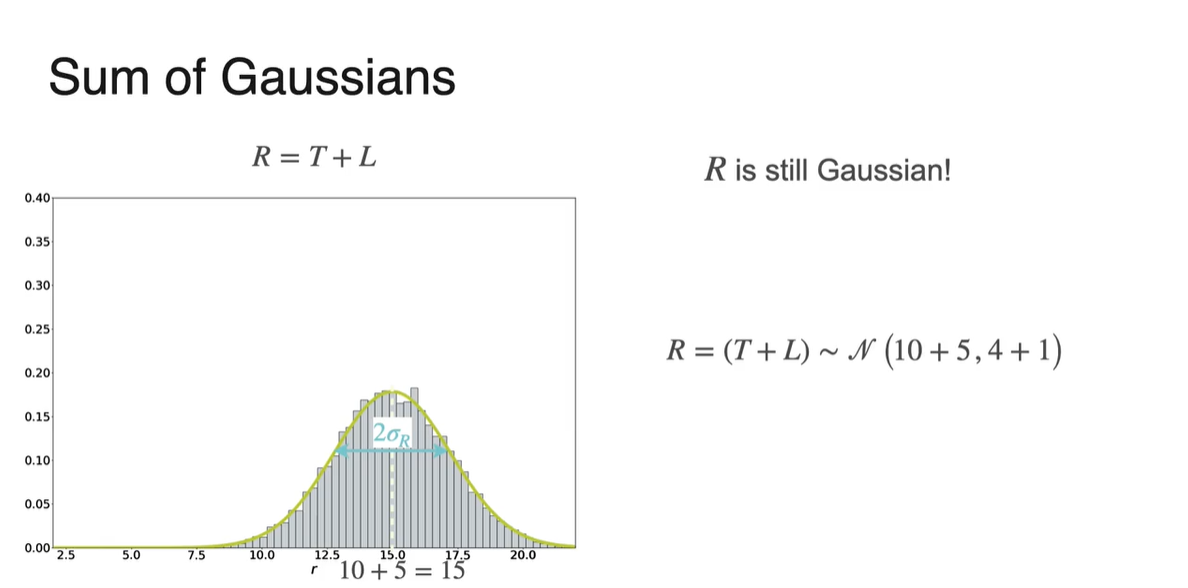
두 분포의 graph를 표현한 그림은 아래와 같다.
- 10,000번의 sample을 뿌렸을 때의 분포 결과를 나타낸다.
-
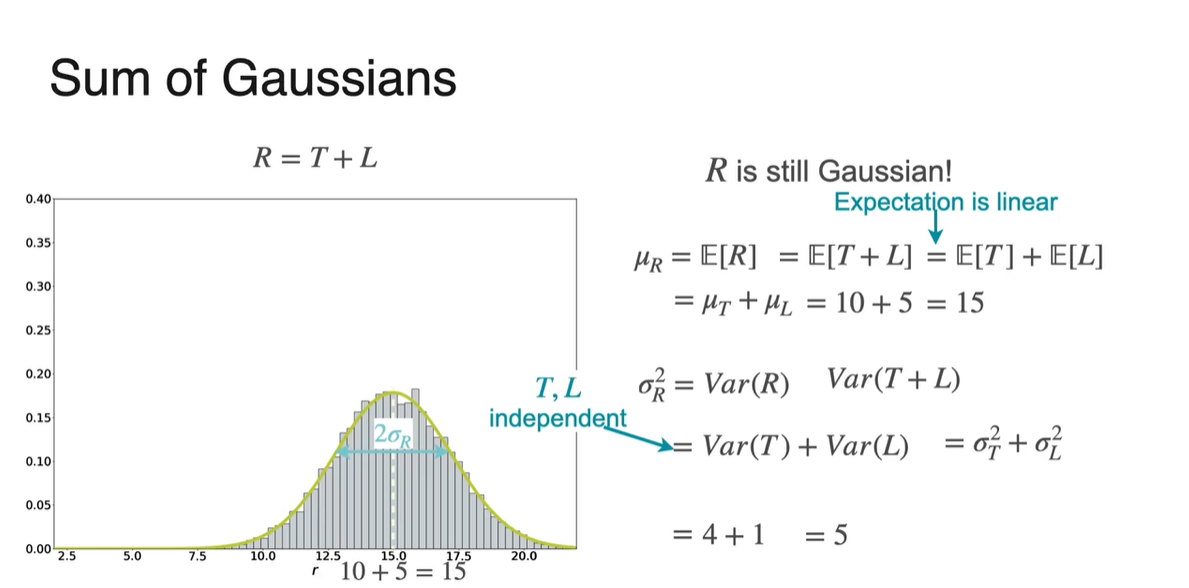
결론부터 말하자면, 의 분포 또한 Gaussian(Normal) distribution을 따른다!
- 독립적인 두 확률 분포의 Expected vaule의 합도 linear하고, Variance의 합도 linear하기 때문이다.
-
일 때, 분포는 을 따른다.
- Graph 모양 또한 종(bell) 모양임을 알 수 있다.
-
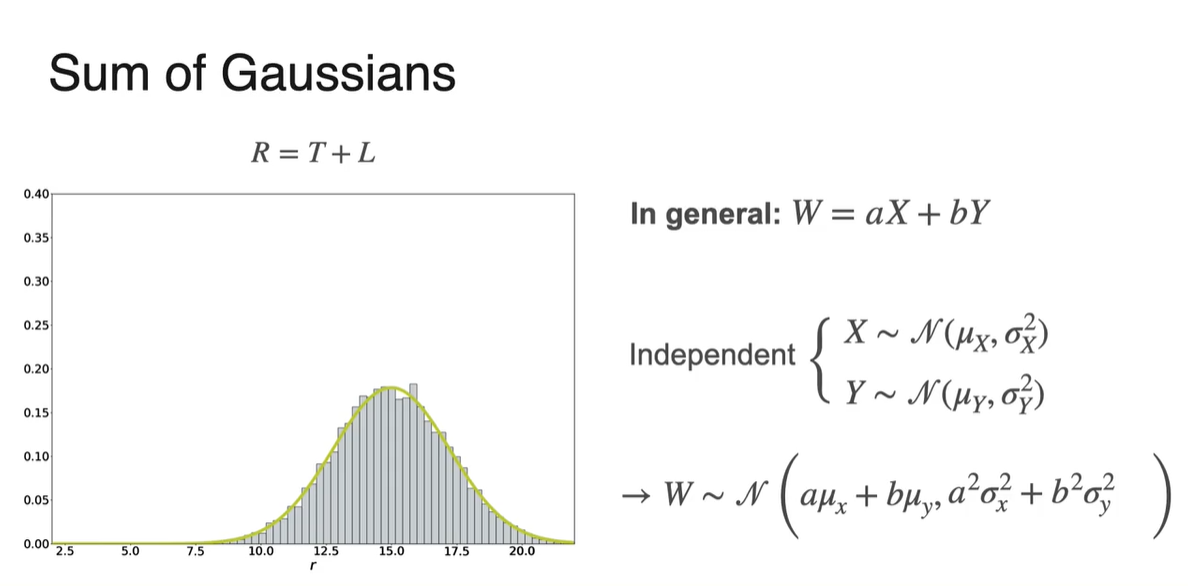
In general: 인 선형 변환을 거친 확률 변수의 분포는 기댓값과 분산(표준 편차)의 선형 변환으로도 표현 가능하다.
- 단, 두 분포가 독립적(independent)일 때에 성립한다.
Standardizing a Distribution
-
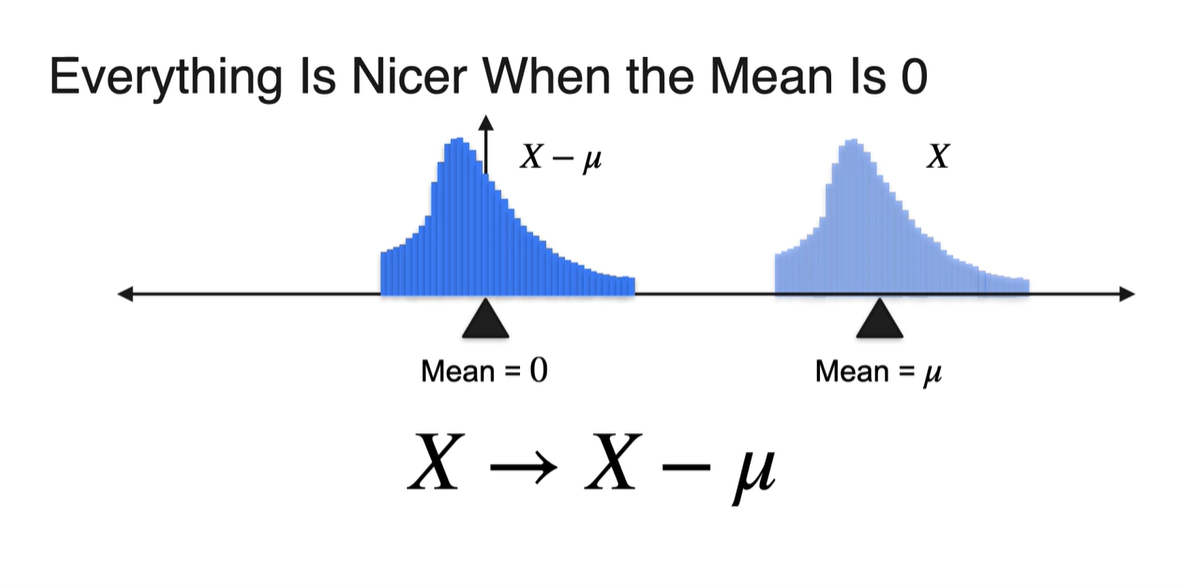
기존 확률 변수 에 기댓값 를 빼면 평균은 항상 0이다.
- 일 때 이다.
-
이는 Expected value의 linear property에 의해 유도된다.
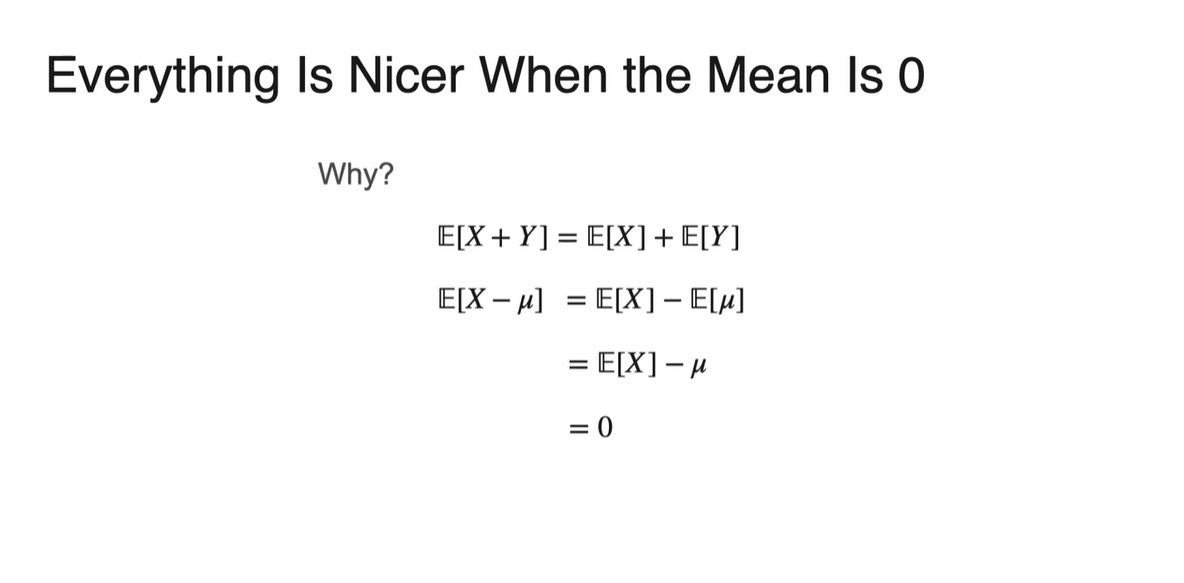
-
표준 편차(Standard deviation)가 인 분포는 width가 넓다.
- 만약 로 보낸다면 표준 편차는 항상 1이 된다.
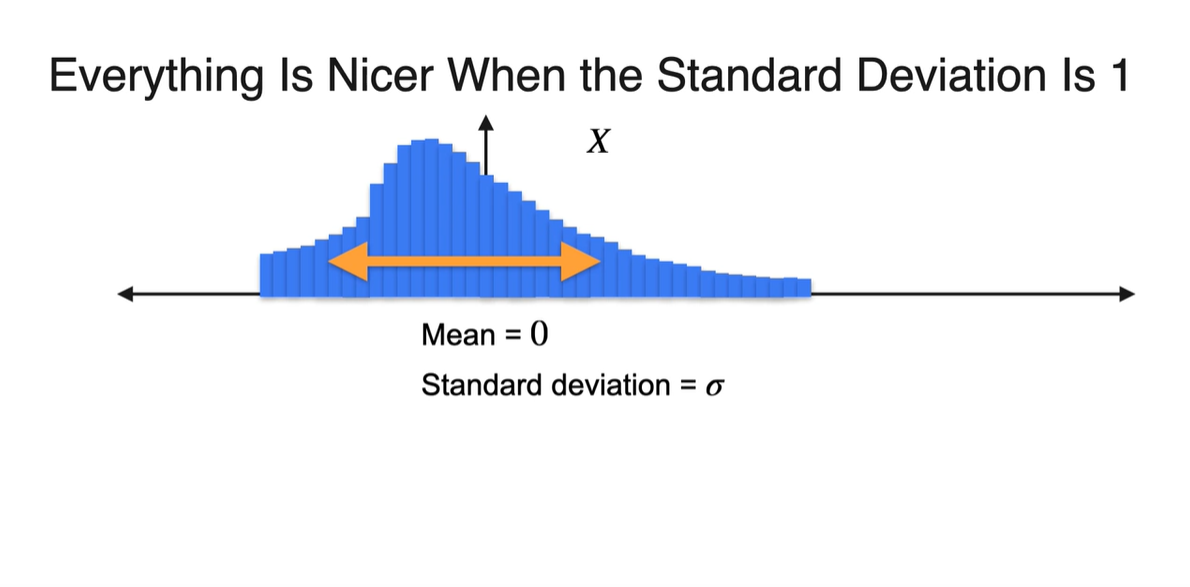
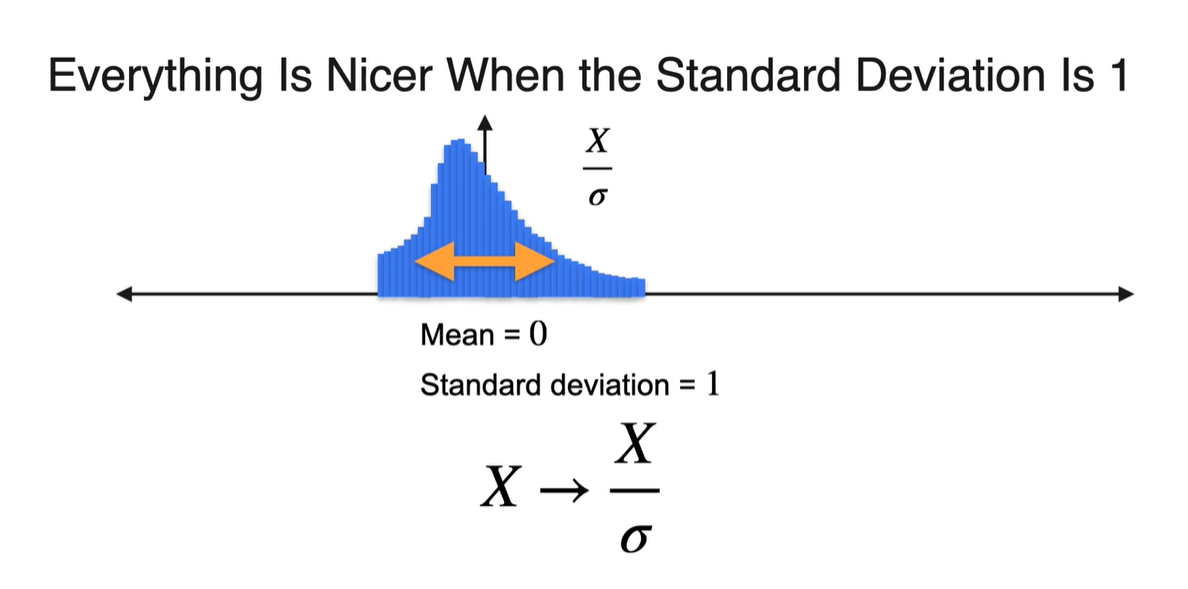
-
마찬가지로 Variance와 Standard deviation의 property에 의해 유도된다.
-

-
기존 Gaussian 분포를 정규화(Standardize)하여 얻을 수 있는 이점은 무엇일까?
-
Comparability between different datasets : 서로 다른 데이터셋의 비교가 용이함
-
Simplification of statistical analysis : 통계적 분석이 용이함
-
Improved performance of machine learning models : 모델의 패턴 인식 능력 향상
- All of the above라고 설명한다.
-
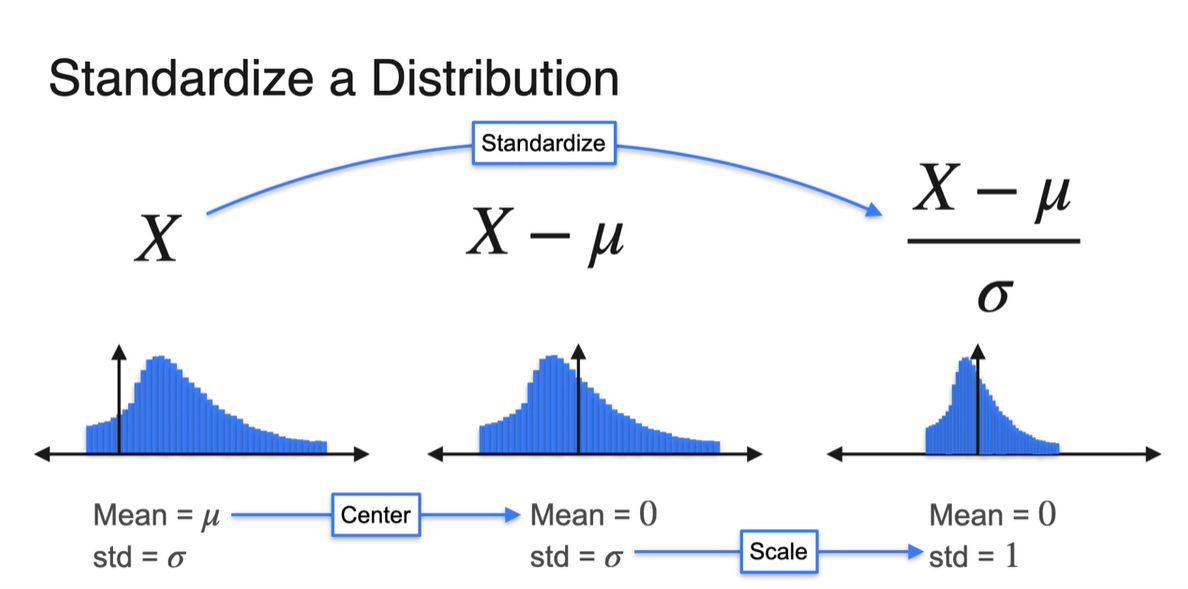
Skewness and Kurtosis: Moments of a Distribution
-
라는 Random variable의 확률 분포가 다음과 같다고 하자.
-
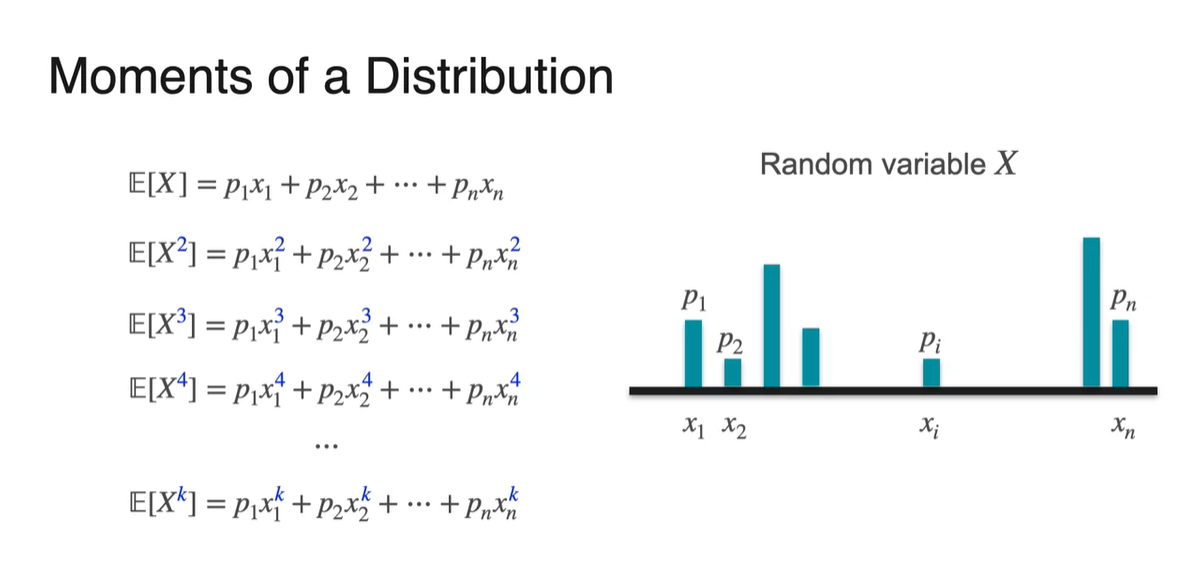
우리는 와 를 계산하여 각각 평균과 분산으로 활용했다.
- 마찬가지로 , , ... 더 나아가 를 계산하는 것이 가능하다.
-
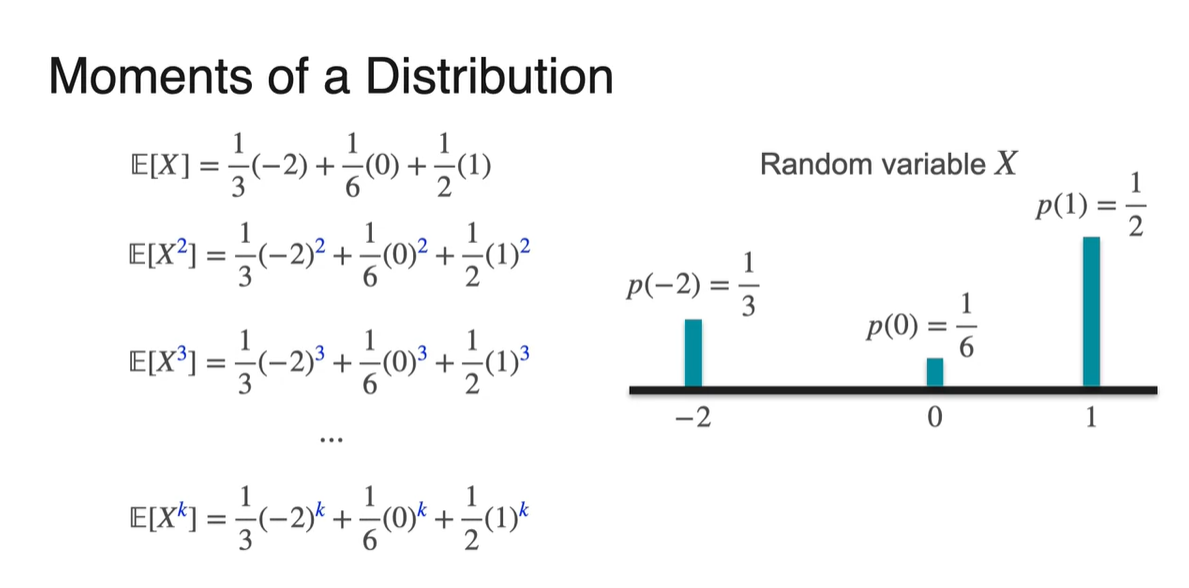
- , , , , ... 더 나아가 를 활용한 정의에 대해 알아보자.
Skewness and Kurtosis - Skewness
-
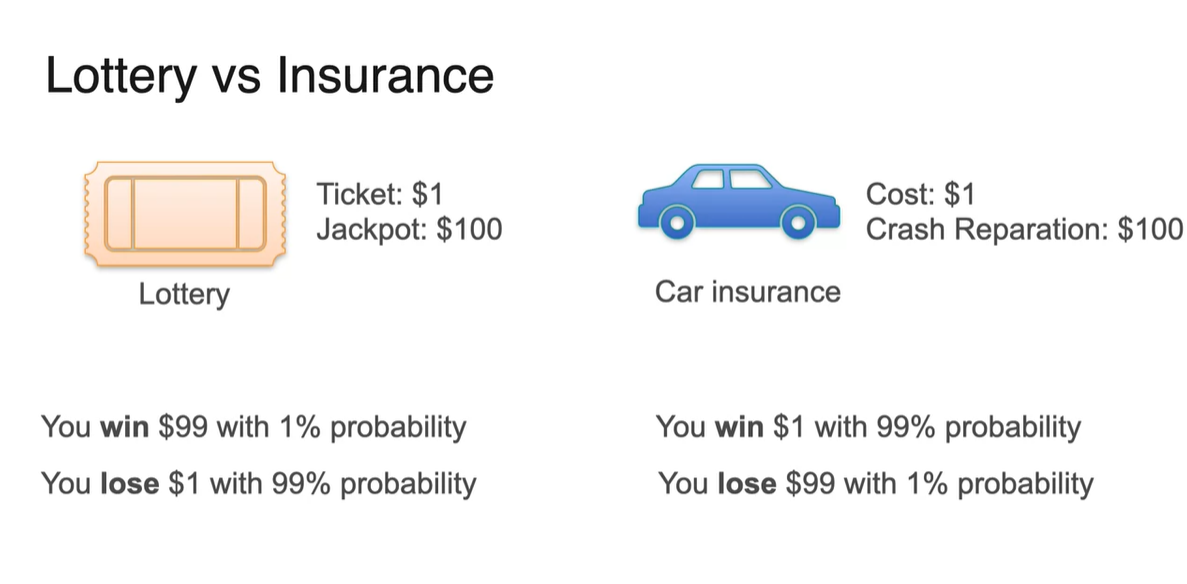
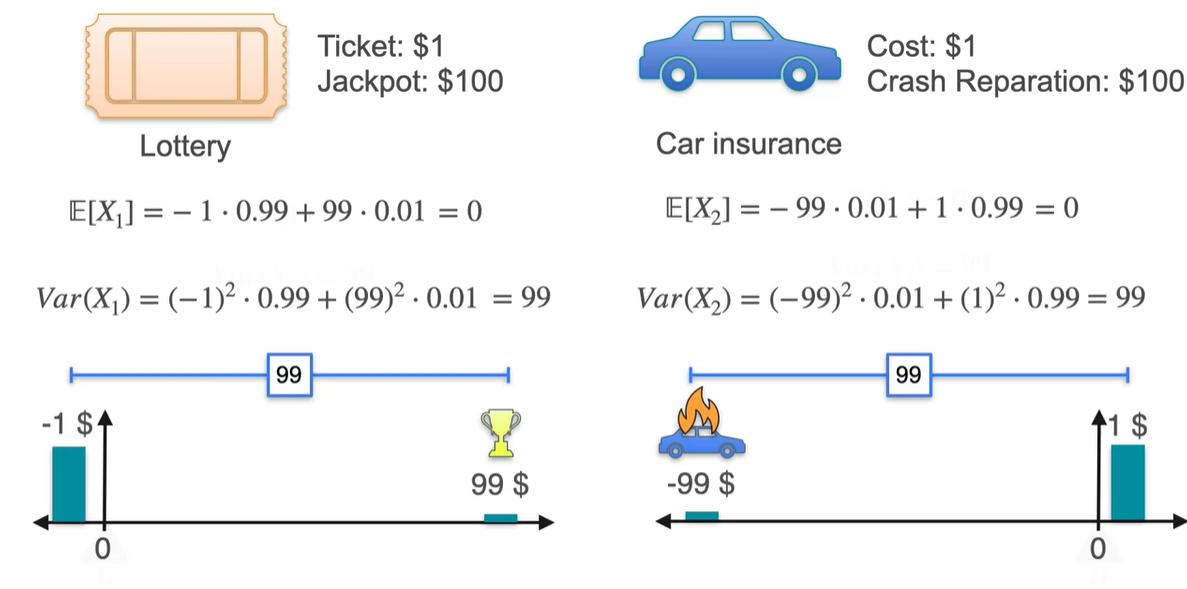
Lottery에 당첨되는 상황과 Car insurance 보험 적용을 받을 때의 상황을 가정해보자.
- Lottery는 1%의 확률로 $99를 얻고, 99%의 확률로 $1를 잃는다.
- Car insurance는 99%의 확률로 $1를 얻고, 99%의 확률로 $99를 지불한다.
-
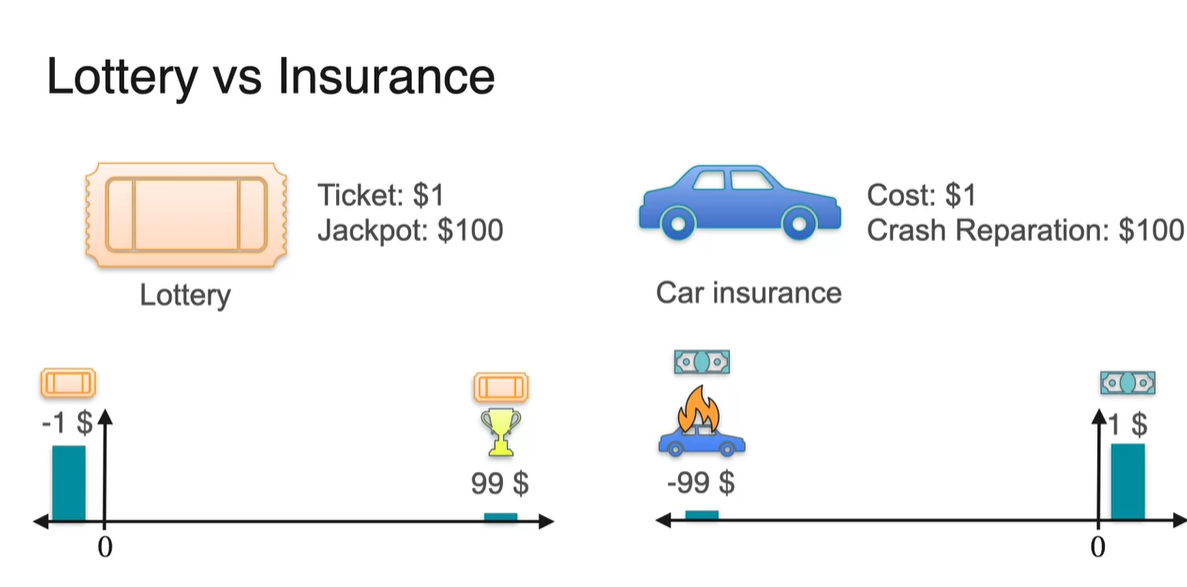
두 확률 분포를 그림으로 나타내면 아래와 같다.
- 평균과 분산은 각각 얼마일까?
-
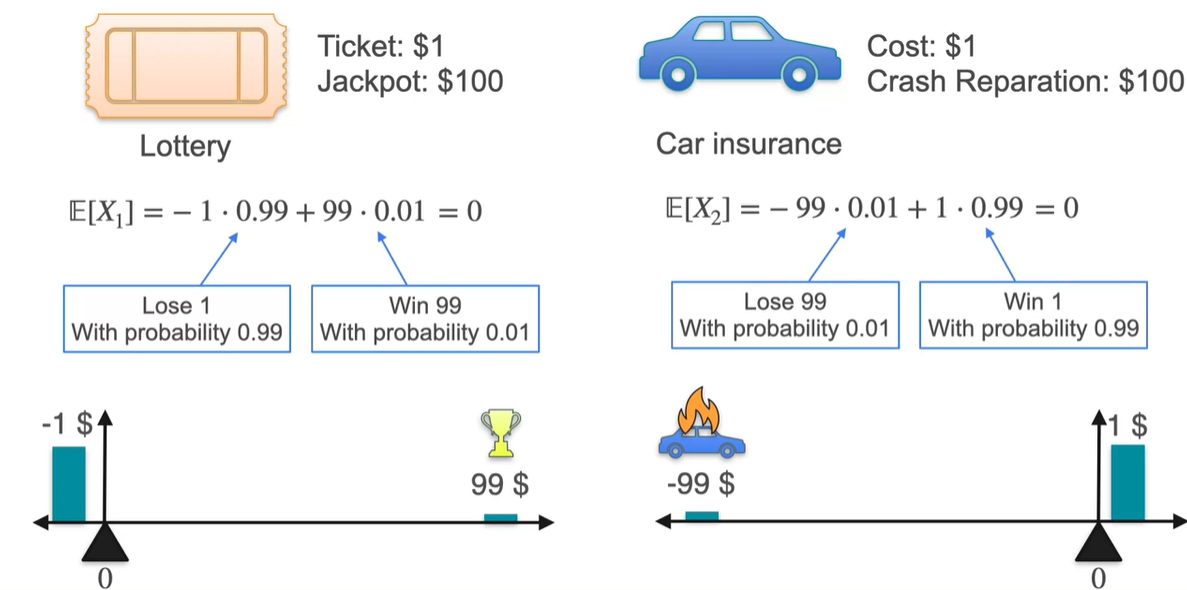
안타깝게도 평균 와 분산 모두 동일한 값을 갖는다.
- 분명 위험도가 다른 분포임에도 불구하고, 평균과 분산이 같다는 점은 두 분포의 차이를 만들지 못한다.
-
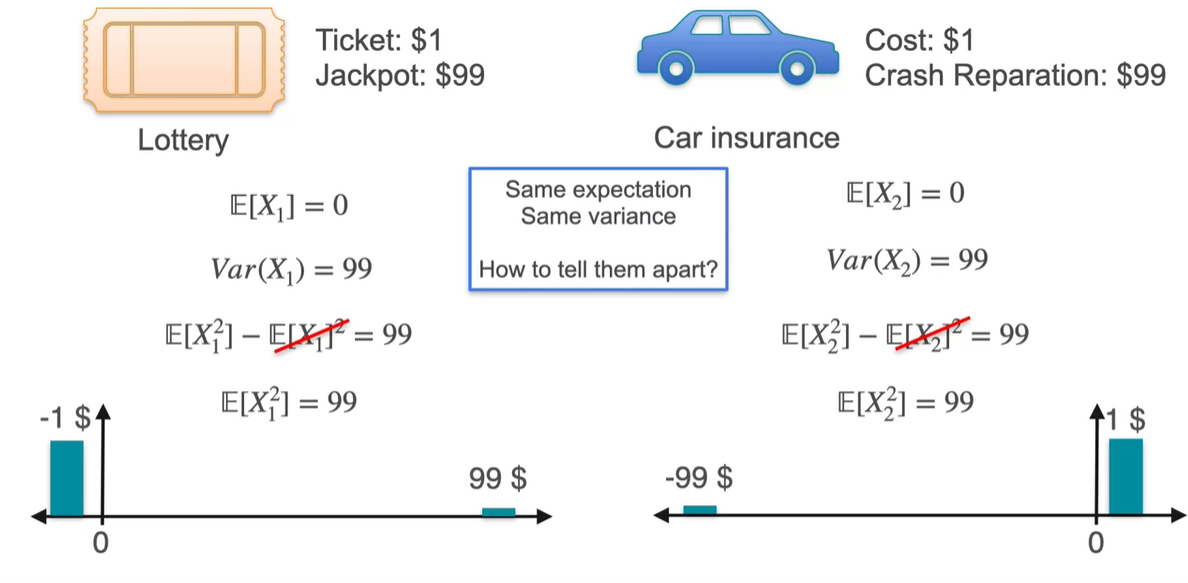
구체적으로 분산의 식은 로 계산된다.
- 위에서 구한 확률 변수의 제곱의 기댓값 와 기댓값 을 이용해 계산하면 두 분포는 평균과 분산에서의 차이가 없음을 알 수 있다.
-
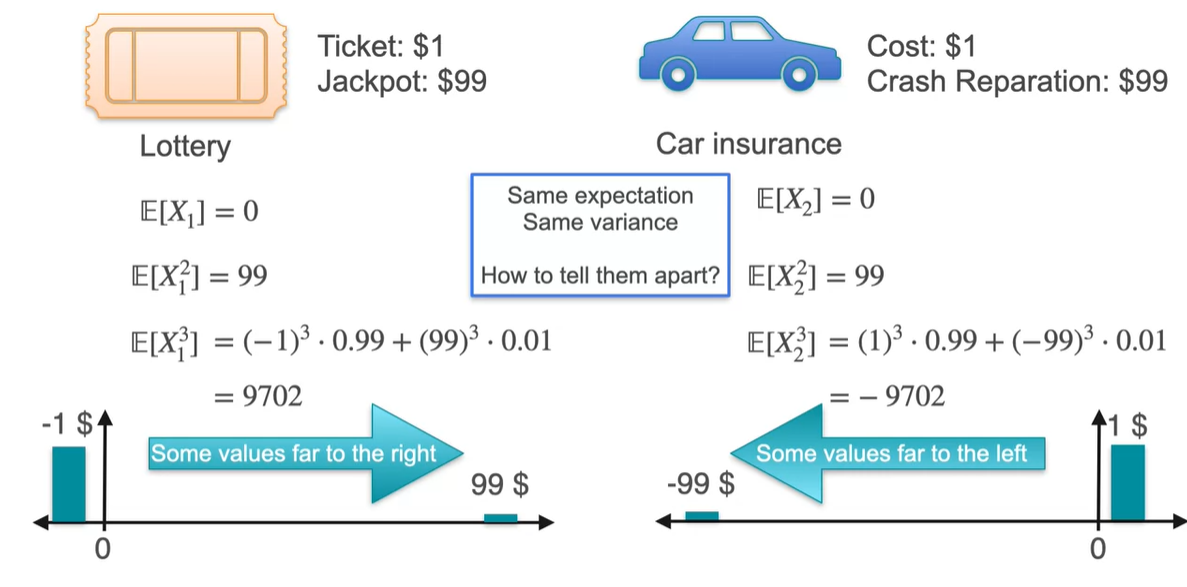
그러나 를 구하면 차이가 나타난다!
-
Lottery 분포는 양수 값으로 계산되는 반면, Car insurance 분포는 음수로 계산된다.
- 가 양수일 때는 some value가 오른쪽으로 멀리 떨어져 있음을 알린다.
- 가 음수일 때는 some value가 왼쪽으로 멀리 떨어져 있음을 알린다.
-
-
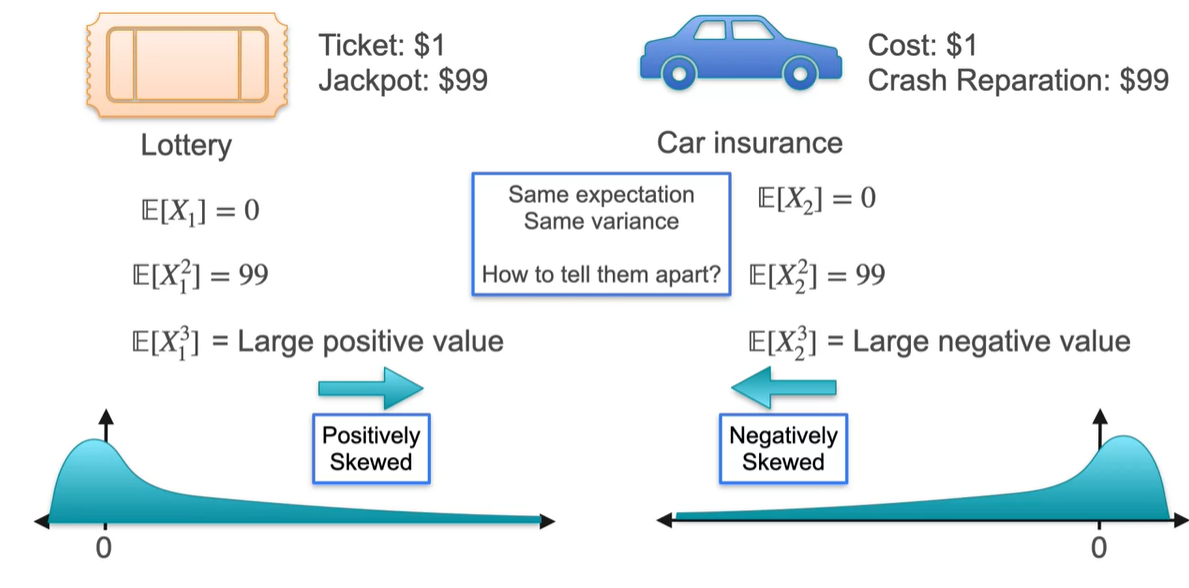
이를 Skewed 되었다고 말하며, 한글로는 "왜도"라 표현한다.
- 양수라면 large value가 일부의 확률로 존재한다는 것을 뜻하며, 음수라면 small value가 일부의 확률로 존재한다는 것을 나타낸다.
-
Skewness는 으로 정의될 수 있지만 이대로는 사용하지 못한다.
- 정규화가 필요하다.

-
명확한 정의는 다음과 같다.
- Skewness =
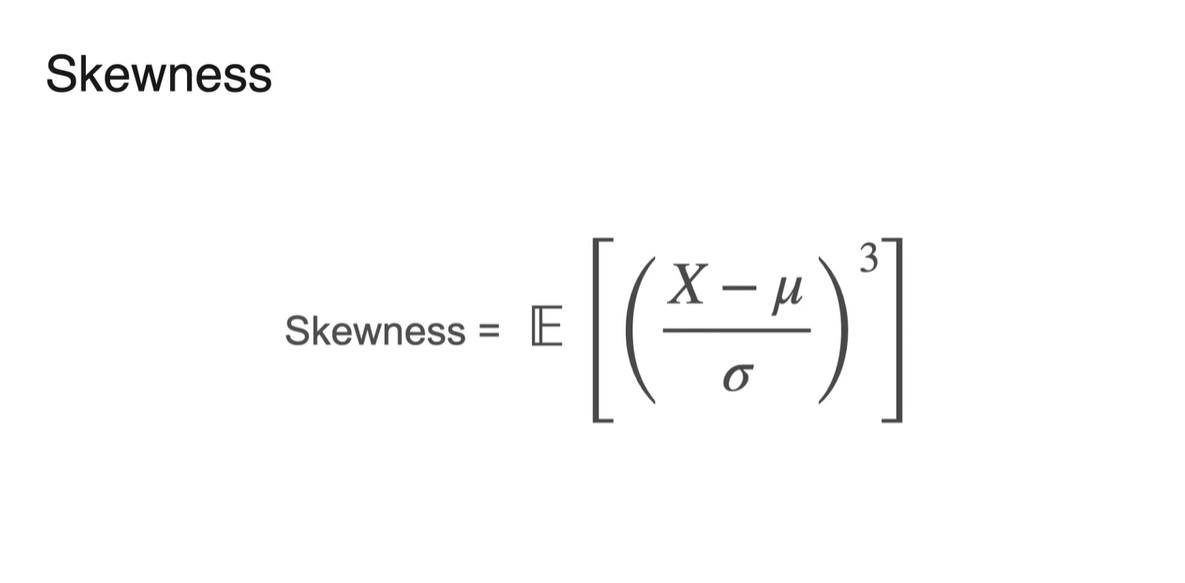
-
Skewness의 부호에 따라 세 가지 케이스의 분포로 나뉜다.
- > 0 : Positively Skewed
- = 0 : Not Skewed
- < 0 : Negatively Skewed
Skewness and Kurtosis - Kurtosis
-
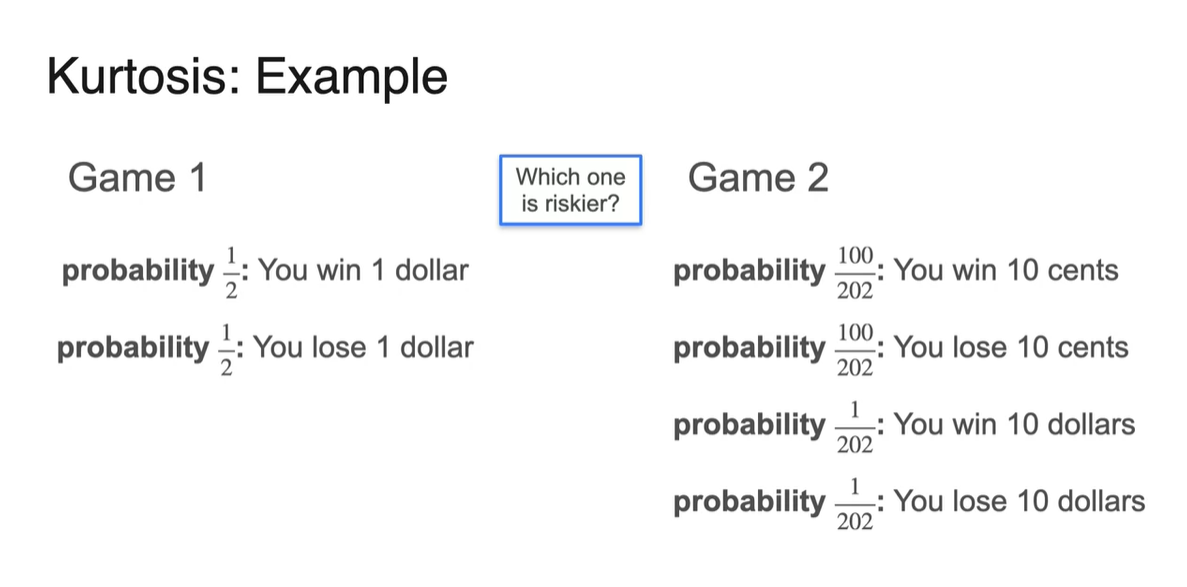
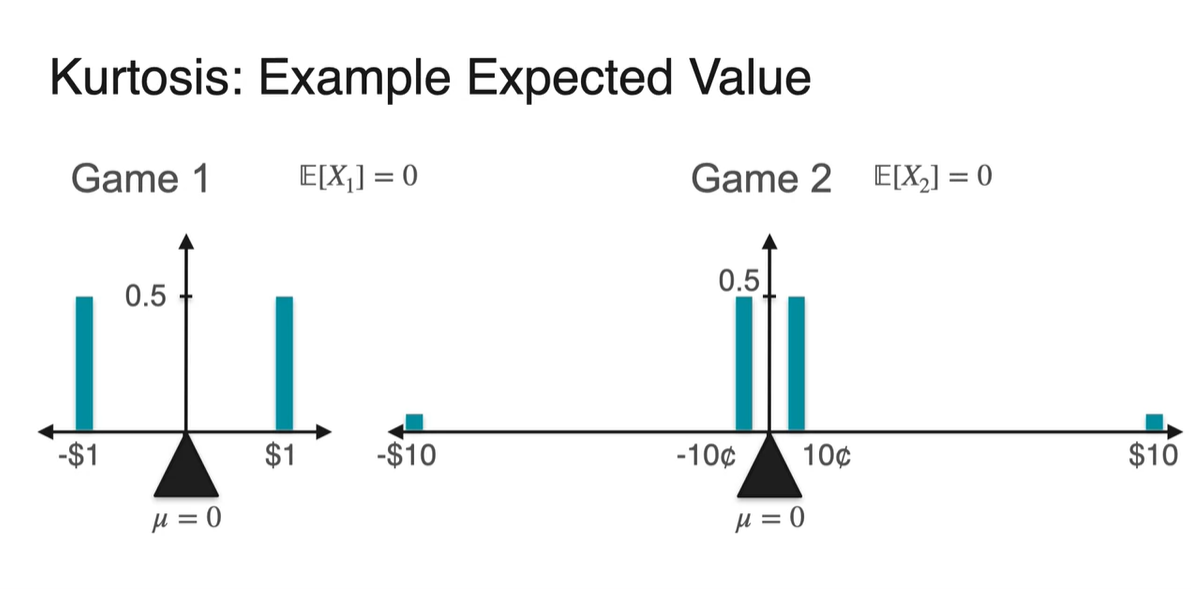
두 게임의 예시를 비교해보자.
-
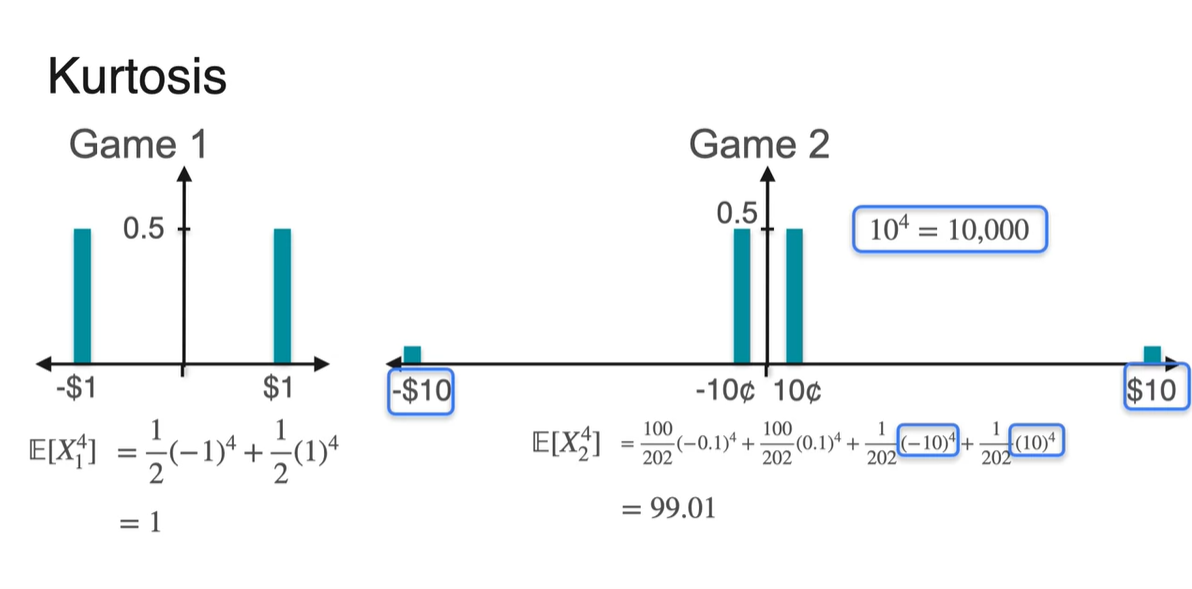
첫 번째 게임은 50%의 확률로 $1를 얻고 50%의 확률로 $1를 잃는다.
-
두 번째 게임은 의 확률로 10 cents를 얻고, 의 확률로 10 cents를 잃는다.
- 그리고 의 확률로 $10를 얻고, 의 확률로 $10를 잃는다.
-
-
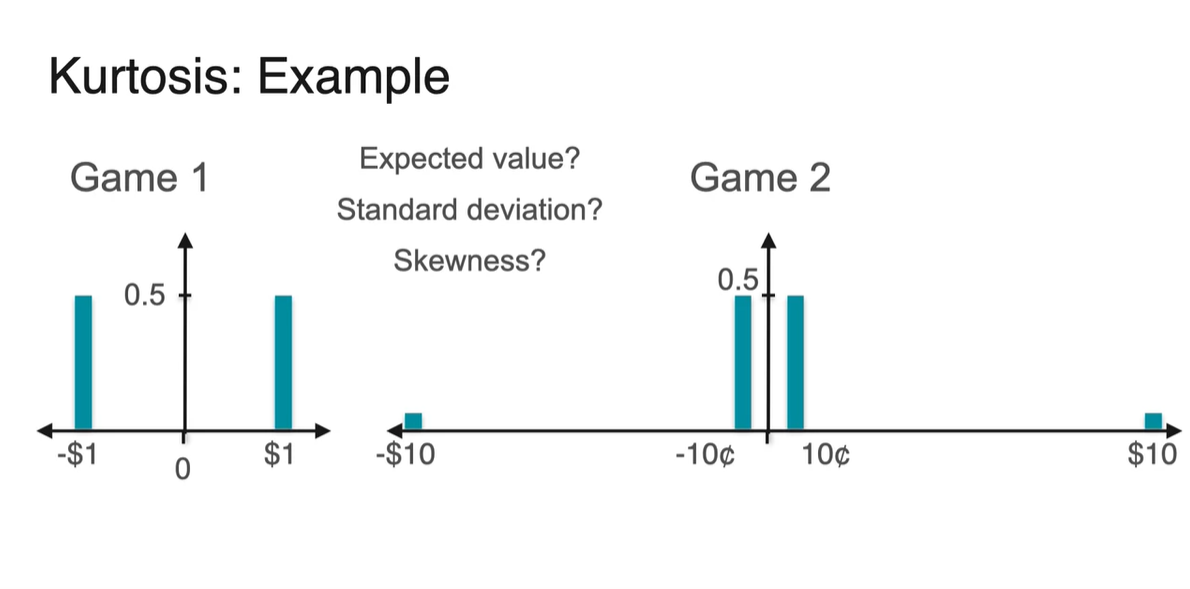
이제 두 분포를 비교해보자.
- Expected value()와 Standard deviation(), Skewness()는 각각 얼마일까?
-
기댓값 은 두 분포 모두 0이다.
- Symmetric ditribution이기 때문에 무게 중심은 가운데 지점 0이다.
-
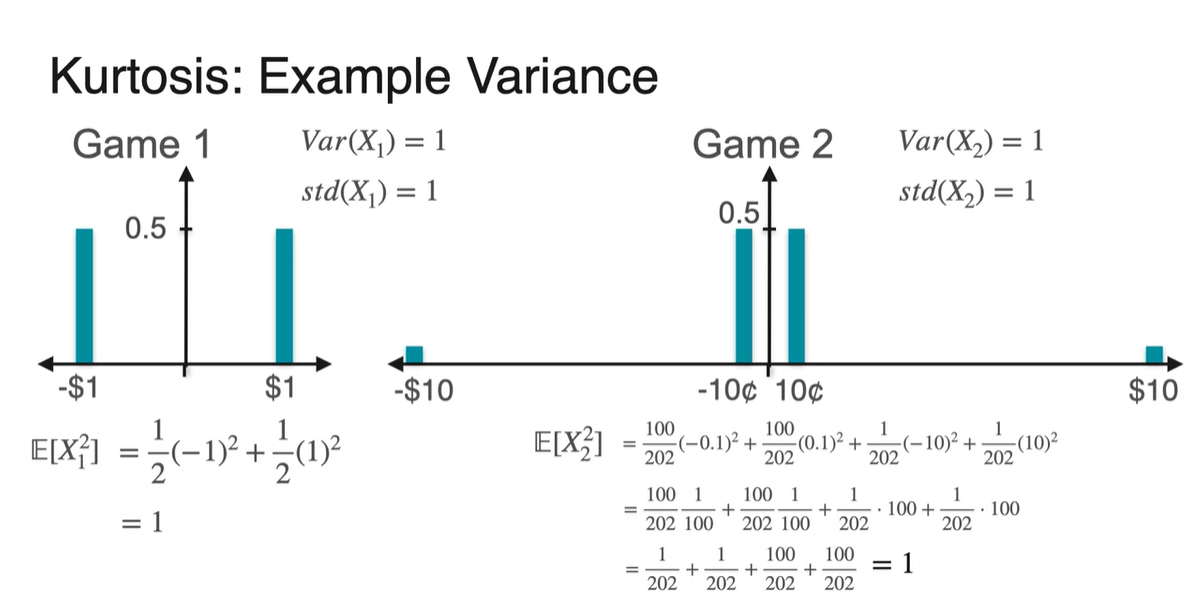
분산 Variance와 표준 편차 Standard deviation은 두 분포 모두 1이다.
- 를 구해보면 1의 값을 가지며, 기댓값의 제곱을 빼도 1이다.
-
안타깝게도 Skewness 또한 같다.
-
Symmetric distribution은 치우친 정도가 없기 때문에 항상 0의 값을 가진다.
- 정규 분포(Normal distribution)의 Skewness가 항상 0인 것처럼 말이다.
-
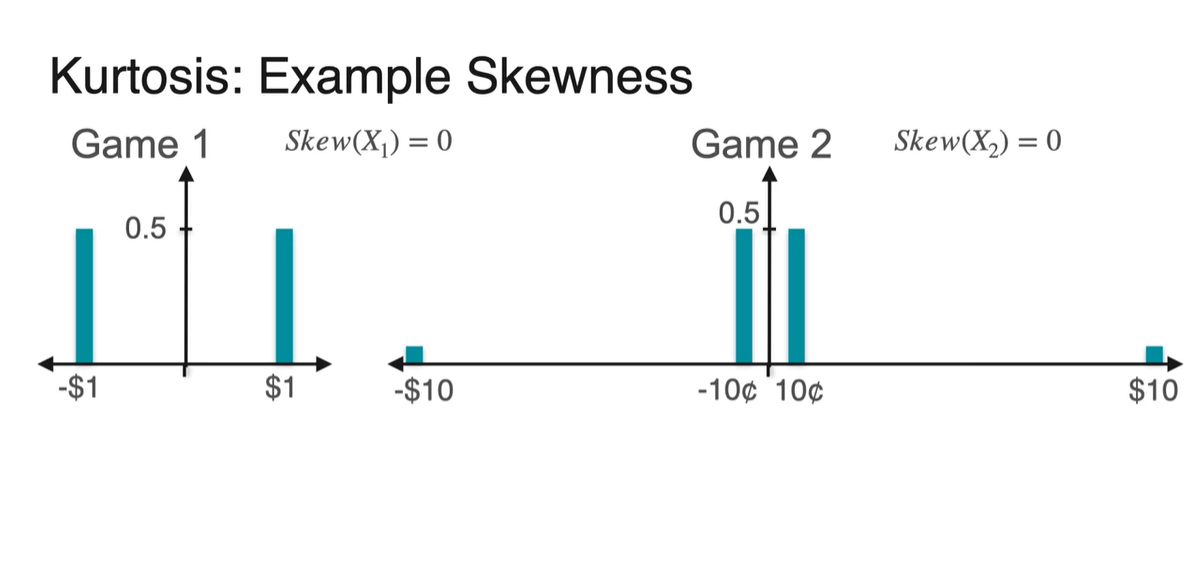
-
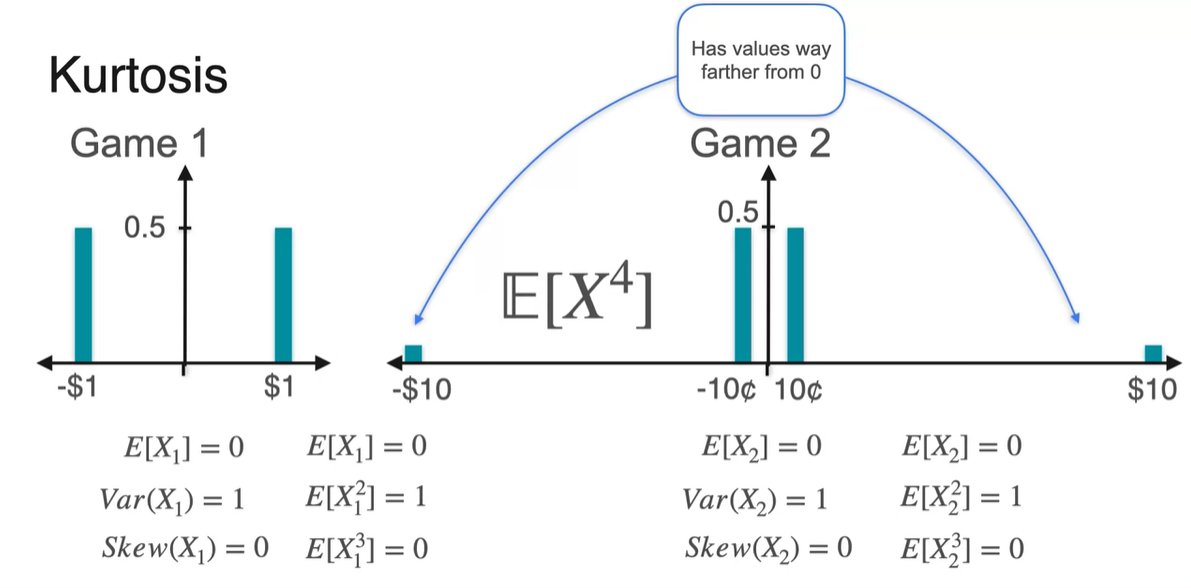
그러나 현재 두 분포는 엄연히, 퍼진 정도에 있어 매우 다른 특징을 갖는다.
- Some values가 서로 멀리 떨어져 있는 정도를 나타내려면 를 구해봐야 한다.
-
를 계산해보니 차이가 극명하게 드러났다.
- 오른쪽 분포는 값이 매우 큰 Random variable이 존재하기 때문에 가 다소 큰 값을 가짐을 알 수 있다.
-
이러한 값을 나타내는 지표를 우리는 Kurtosis, 한글로는 "첨도"라고 한다.
- 마찬가지로 정규화 과정이 추가적으로 필요하다.

-
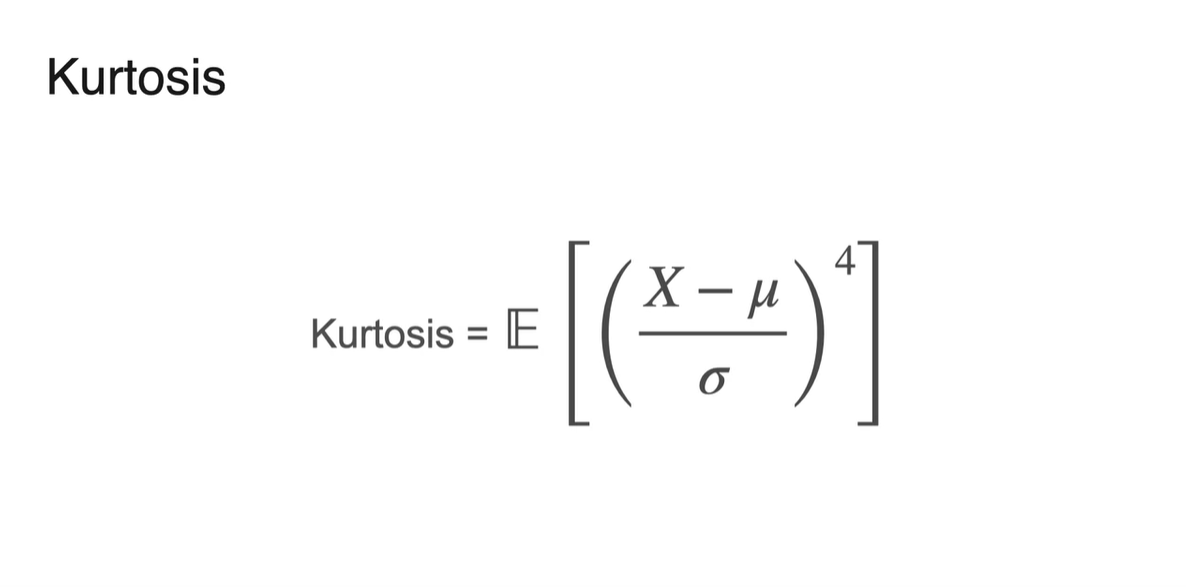
명확한 정의는 다음과 같다.
- Kurtosis =
-
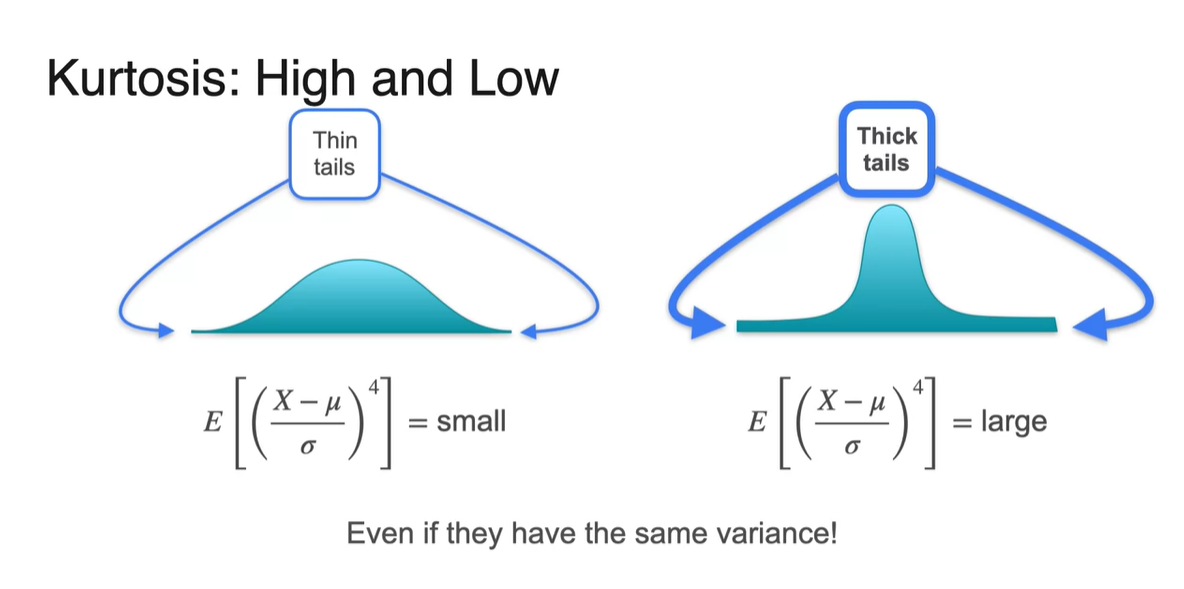
Kurtosis의 크기에 따라 tail의 thickness를 알아낼 수 있다.
- Kurtosis가 작다면 Thin tails 분포를 가진다.
- Kurtosis가 크다면 Thick tails 분포를 가진다.
Quantiles and Box-Plots
-
Quantile, 표본의 관측치를 나누는 분위수에 대해 알아보자.
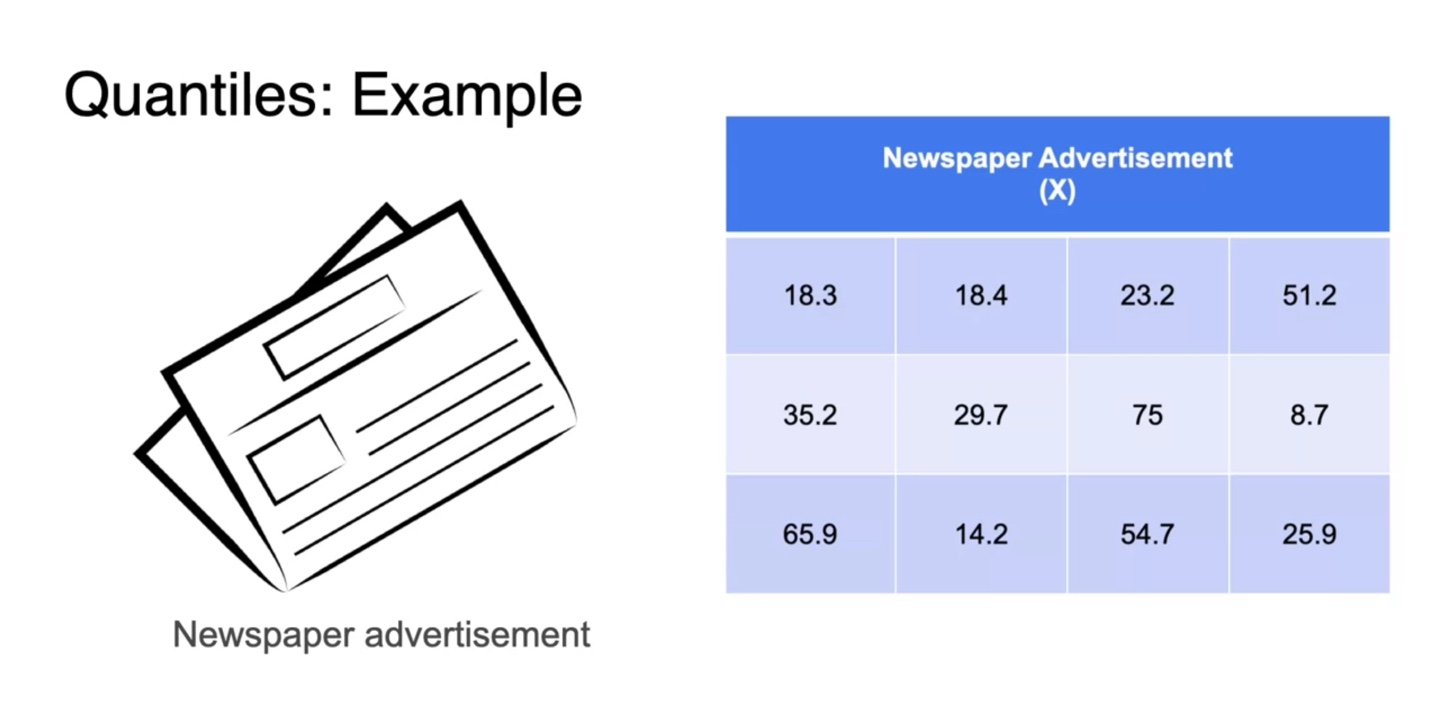
- 광고 예산 X에 따른 판매 수익 예제를 통해 살펴보도록 하겠다.
-
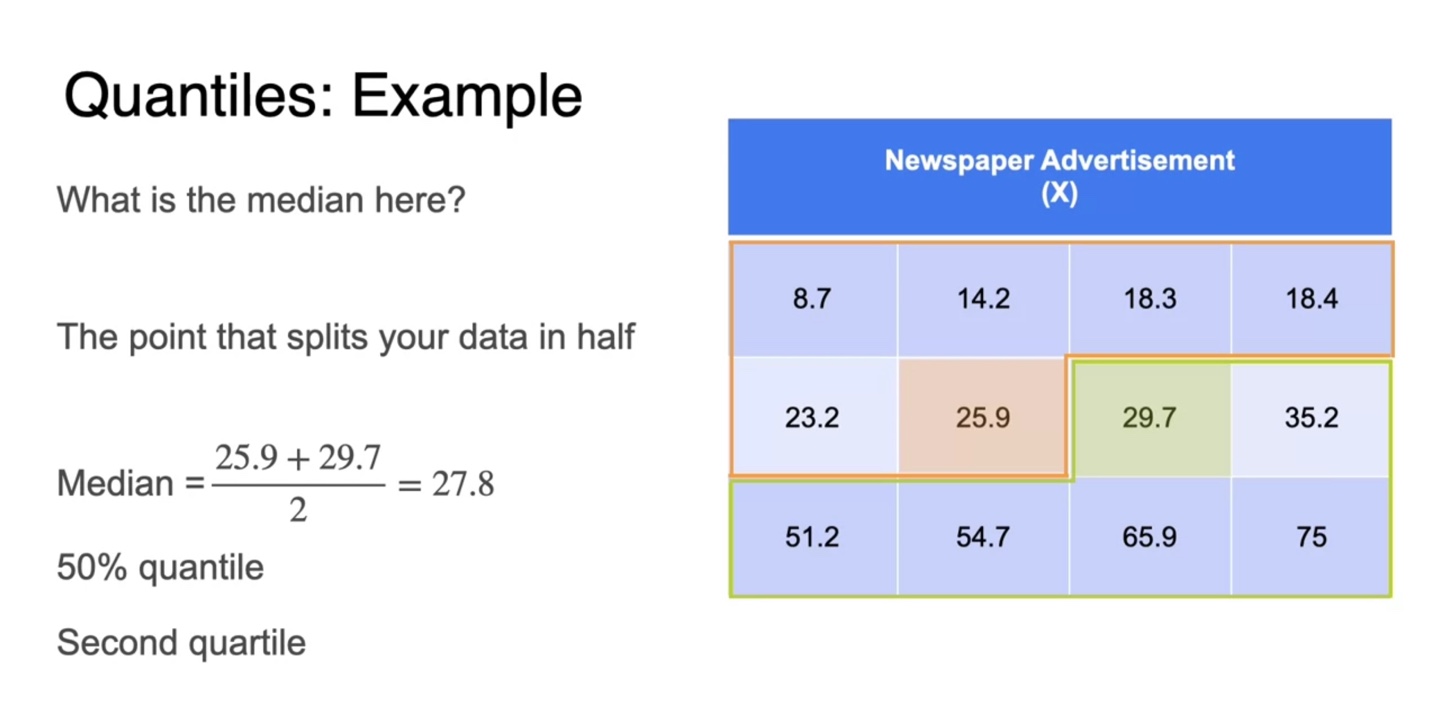
먼저 12개의 sample을 오름차순으로 정렬하여 median 값을 찾아보자.
-
데이터셋을 절반으로 나누었을 때, 중앙에 위치한 두 관측값의 평균으로 median을 정의한다.
- 이를 50% quantile이라고 하며, 2nd quartile이라고 부르기도 한다.
-
-
25% quantile은 데이터를 1/4, 3/4으로 나누었을 때의 중앙값을 평균 낸 값이다.
- 이를 1st quartile이라고도 한다.

-
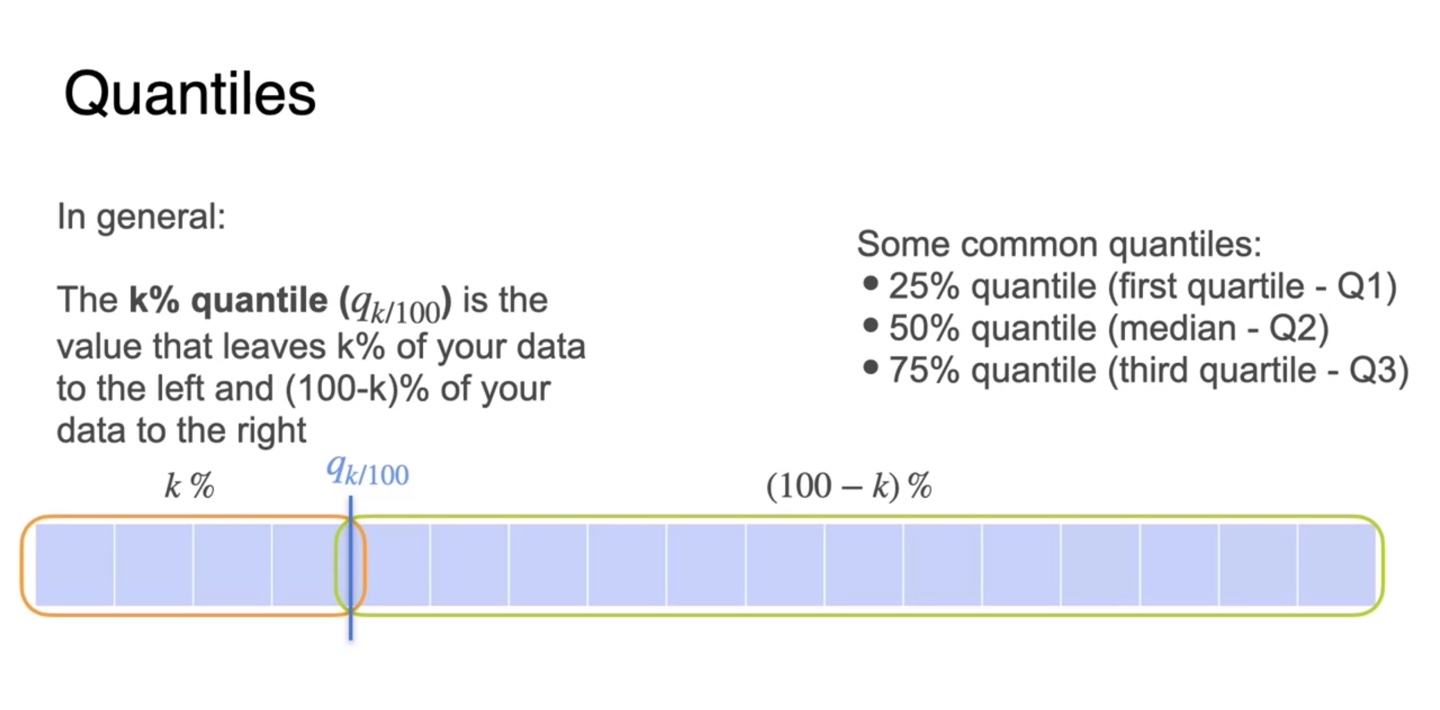
일반적으로 k% quantile은 데이터를 k%, (100-k)%로 분해했을 때의 중앙값 평균을 의미한다.
-
25% quantile, 50% quantile, 75% quantile을 각각 Q1, Q2, Q3라고 표현한다.
- 25% quantile은 1st quartile
- 50% quantile은 median
- 75% quantile은 3rd quartile
-
-
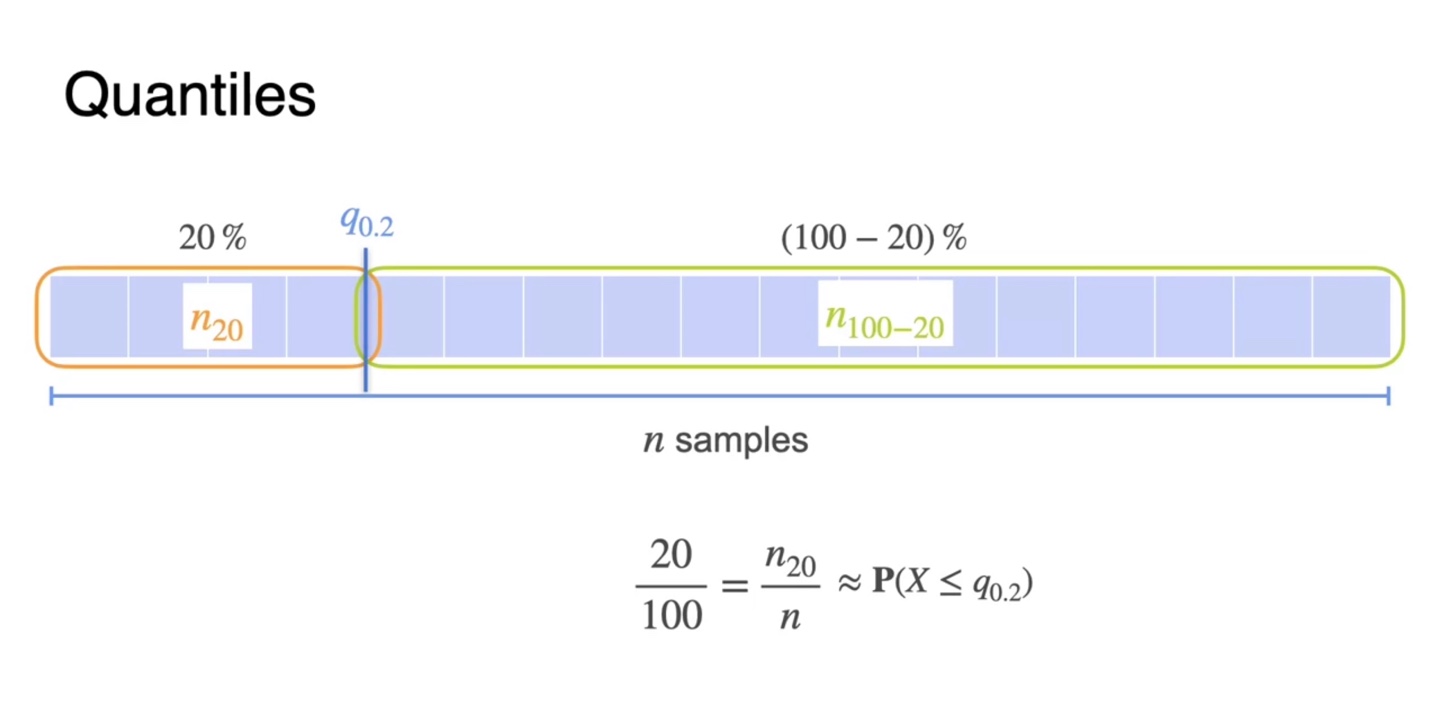
총 개의 sample이 존재한다면 는 데이터의 20%를 cutting한 지점까지를 나타낸다.
- 나머지 sample은 자연스럽게 전체 sample의 80%를 차지한다.
-
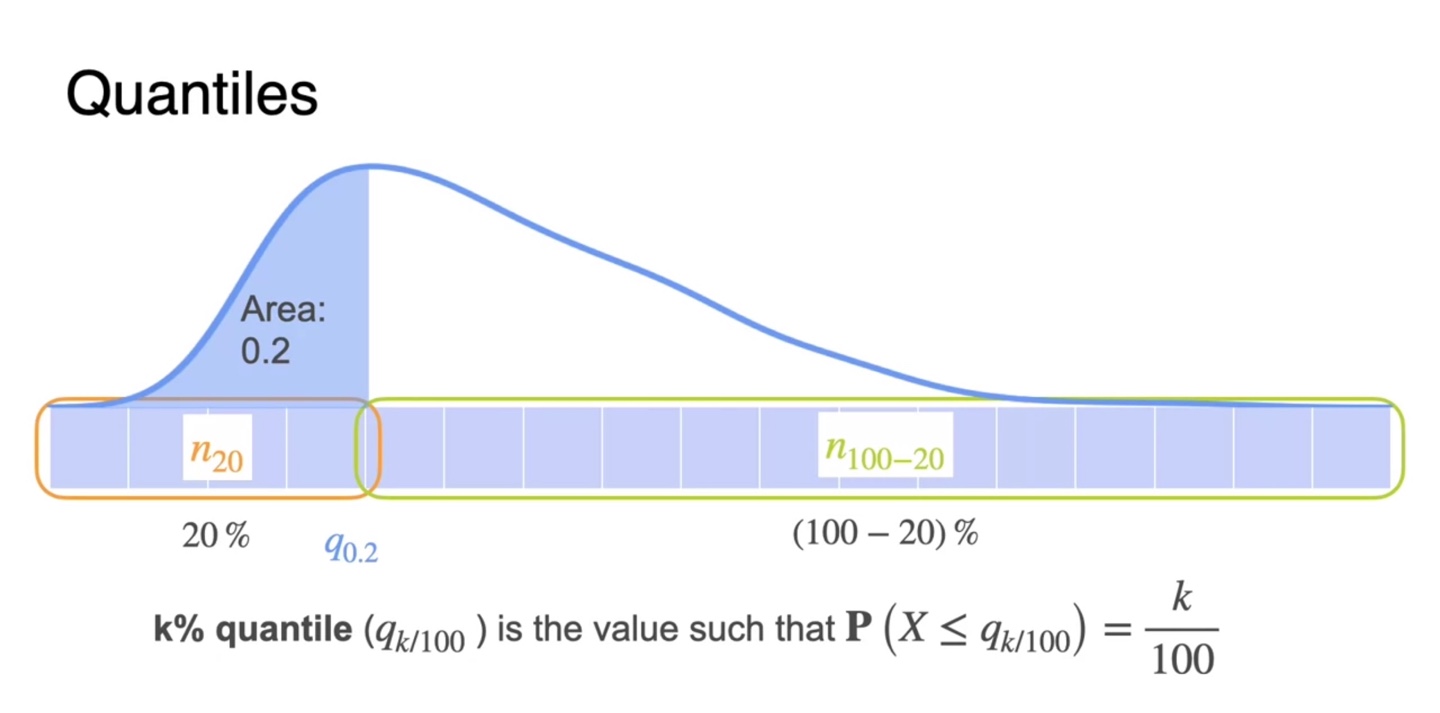
일반화하면, k% quantile은 확률 분포의 면적(area) 즉, 확률이 인 지점까지의 sample들을 자른 부분을 말한다.
Visualizing data: Box-Plots
-
Box-Plot을 그리면 quantile과 median, outlier까지도 시각화할 수 있다.
- 위 데이터 확률 변수를 다시 한 번 오름차순 정렬하여 나타내보자.
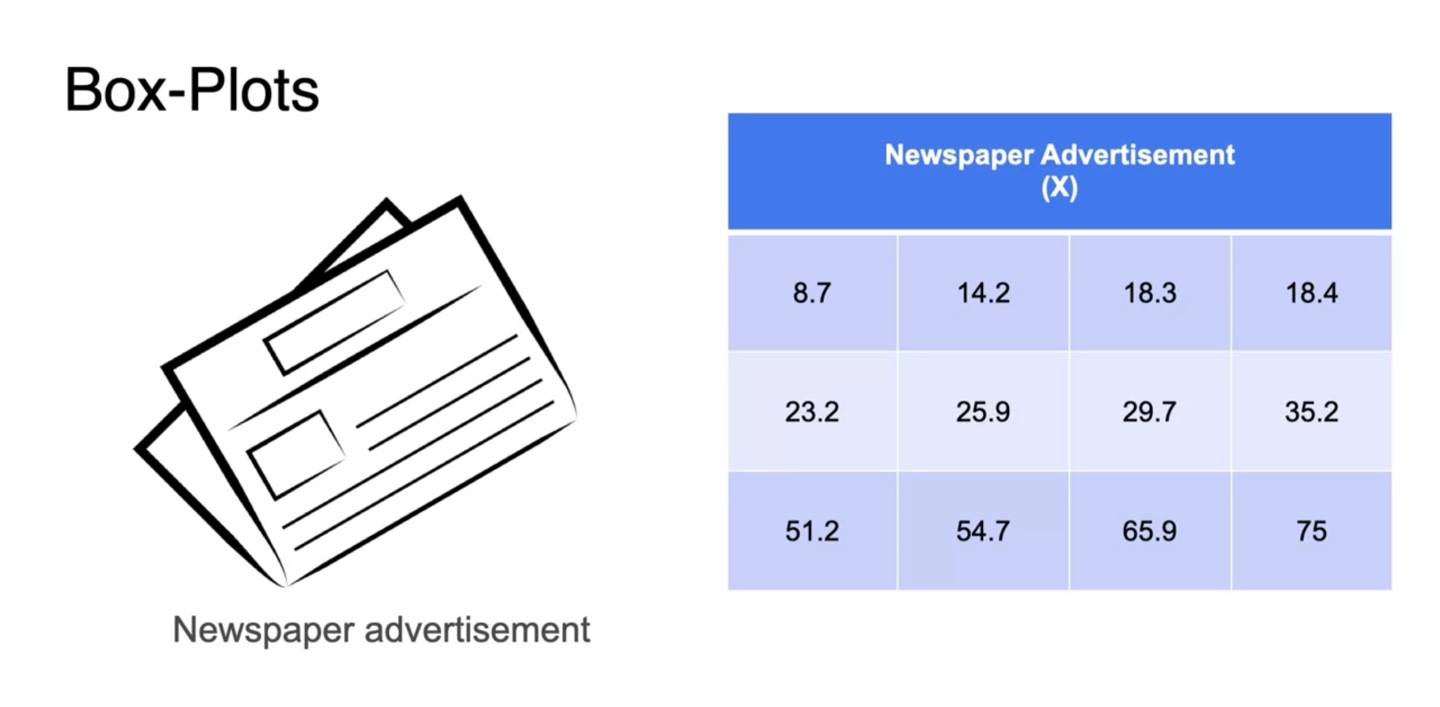
-
전체 데이터가 12개이므로 Q1은 3개, Q2는 6개, Q3는 9개까지 자른 부분에서의 중앙값의 평균이다.
- 오름차순 정렬하였으므로 Q1, Q2, Q3 또한 증가하는 값을 가진다.
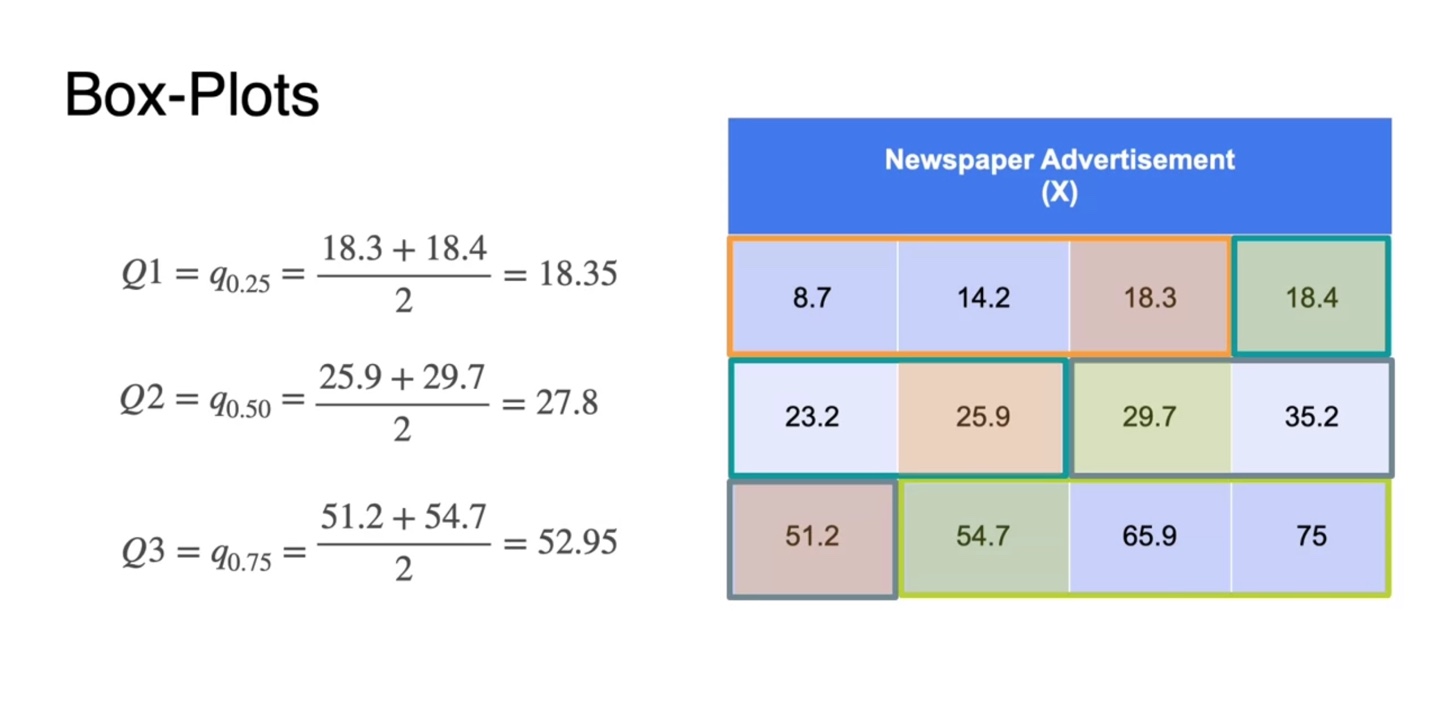
-
Interquartile range(IQR)은 Q3와 Q1을 뺀 값으로 정의한다.
- 즉, box-plot에서의 박스의 영역을 나타내는 것이다.
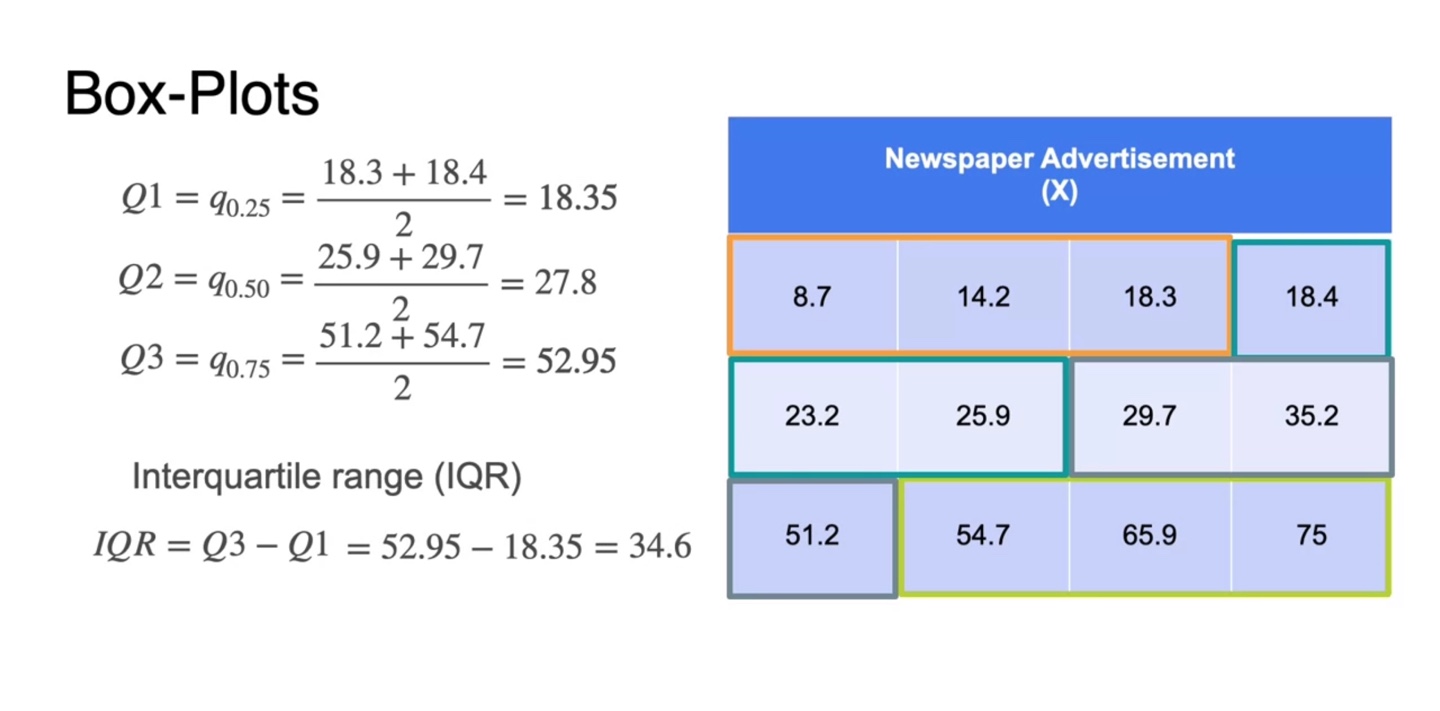
-
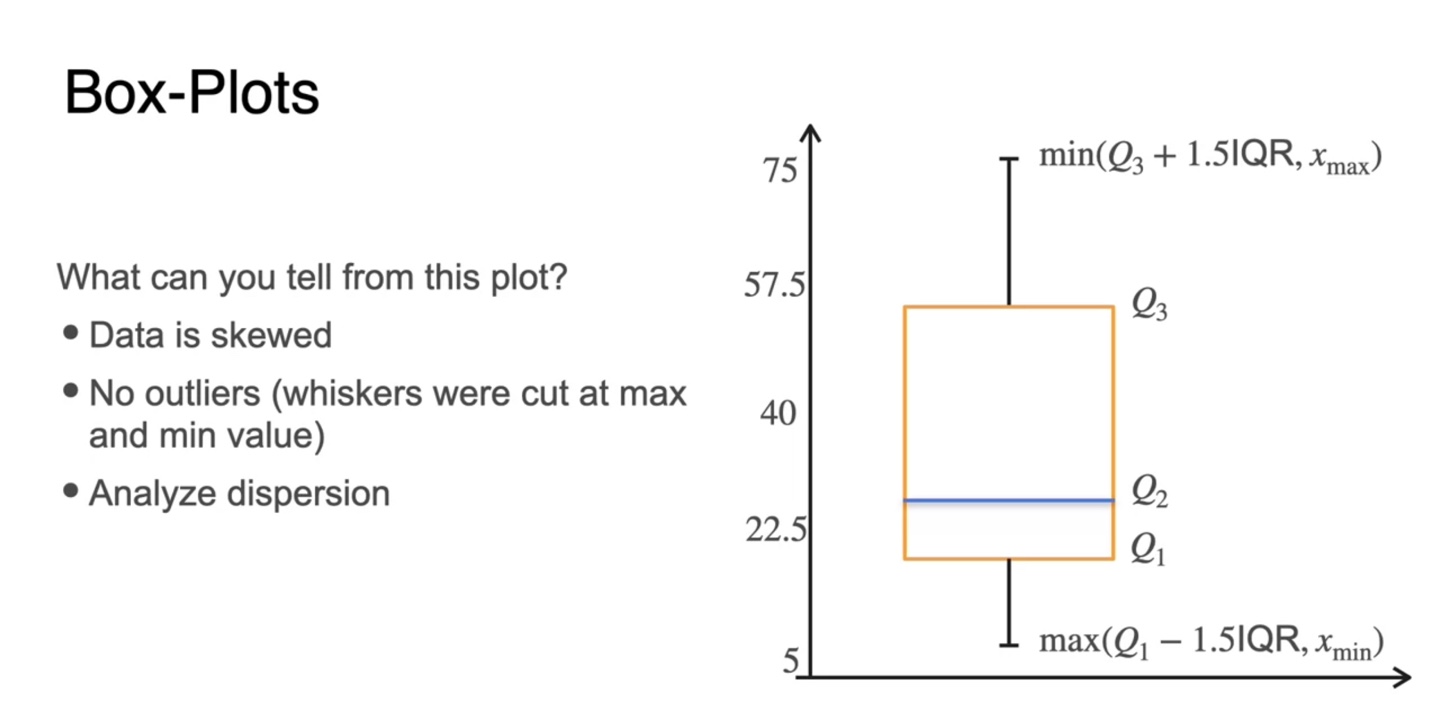
주황식으로 색칠된 부분이 박스의 영역을 나타내는 Q1과 Q3이며, 파란색 색칠 부분은 중앙값 median이다.
- 전체 데이터에서의 min값과 max값까지 추가로 확인하여 Q1-1.5*min, Q3+1.5*max까지 표현하면 outlier sample이 있는지에 대해서도 확인할 수 있다.
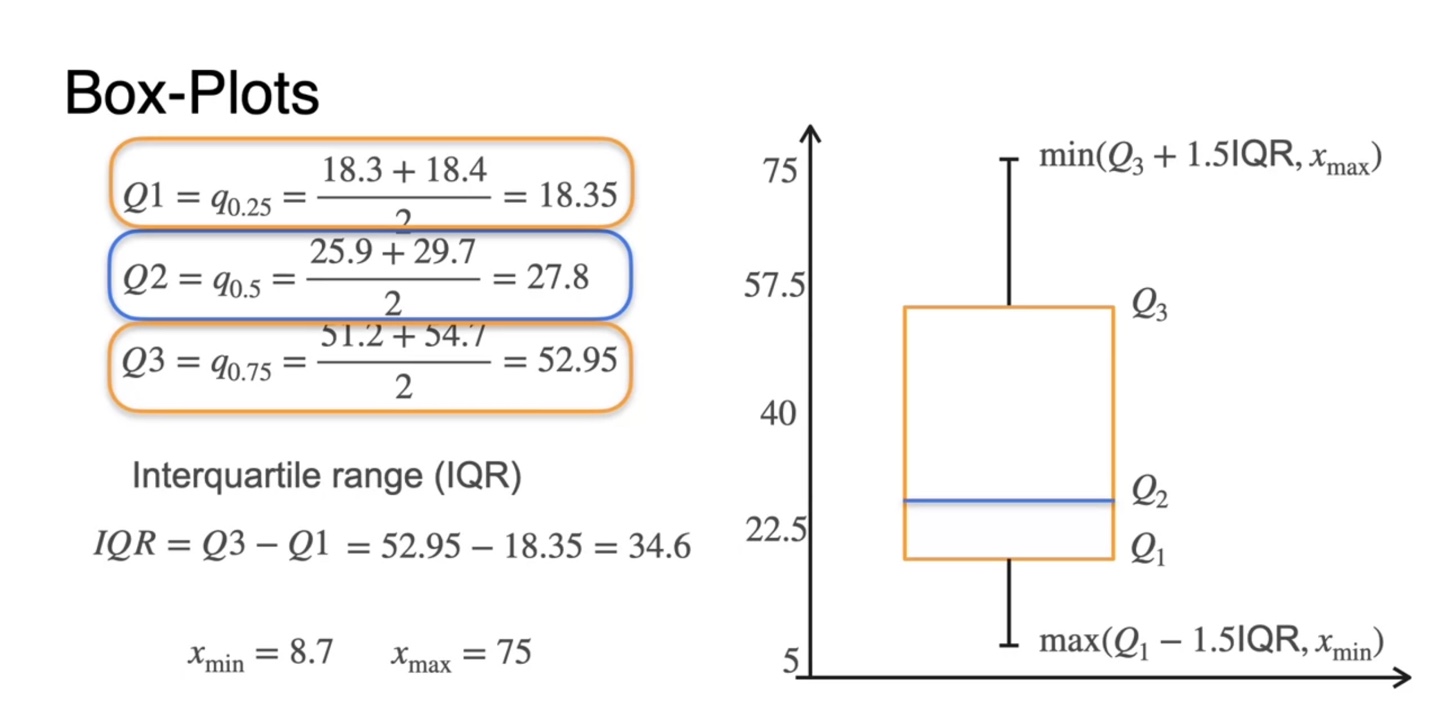
-
이렇게 그린 box-plot을 해석해보자.
- 데이터 분포는 median 값을 기준으로 다소 skewed, 치우쳐져 있다.
- Whiskers(구렛나룻)를 벗어난 값이 존재하지 않기 때문에 Outliers 존재하지 않는다.
- 이제 상자의 길이와 whiskers를 통해 분산(dispersion)을 분석할 수 있다.
-
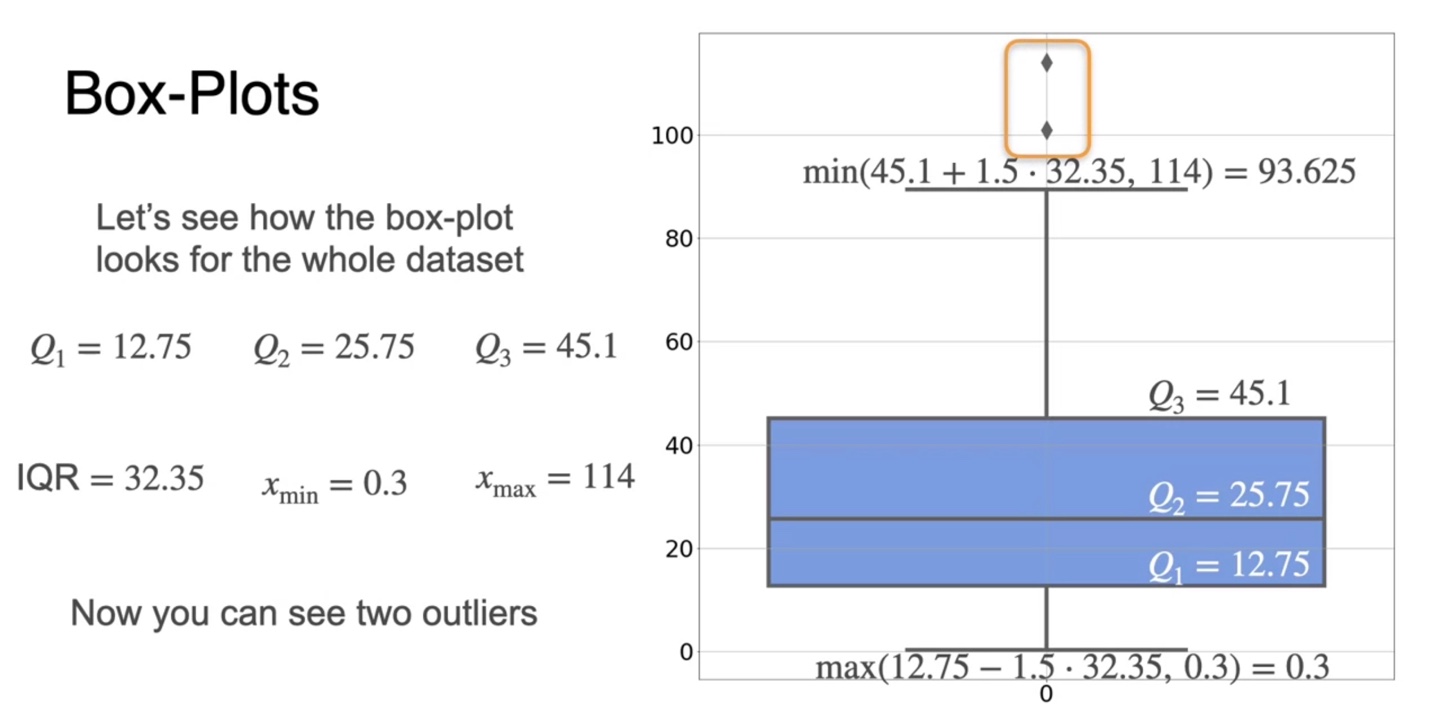
12개의 samples와 더불어 모든 데이터셋의 분포를 시각화해보면 아래와 같은 box-plot이 그려진다.
- Q1, Q2, Q3로부터 IQR을 계산하고 min & max로 whiskers를 그려 점을 찍어보니, 확률 변수가 다소 큰 outlier가 존재한다는 것을 알아낼 수 있게 되었다.
Visualizing data: Kernel density estimation
-
이제 확률 밀도 함수(PDF)를 추정하는 방법에 대해 알아보자.
- Density Estimation을 말한다.
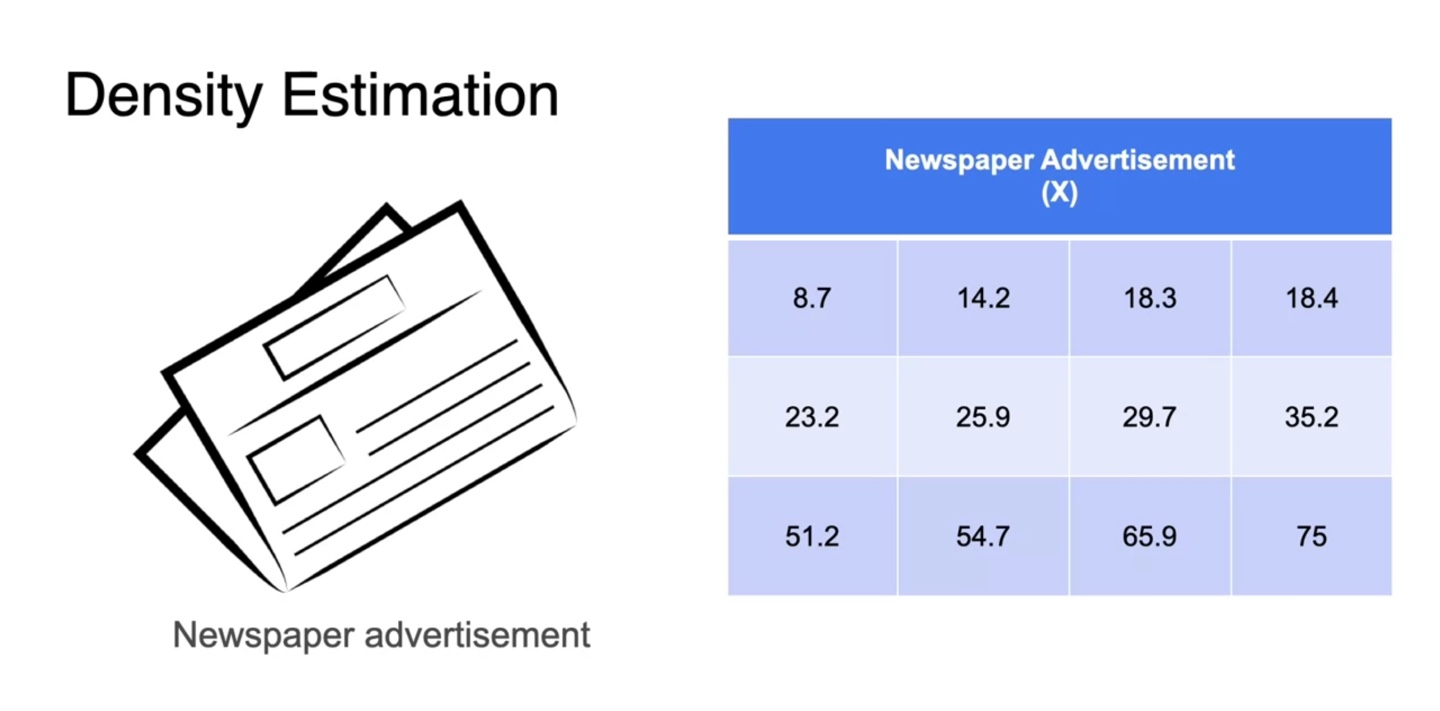
-
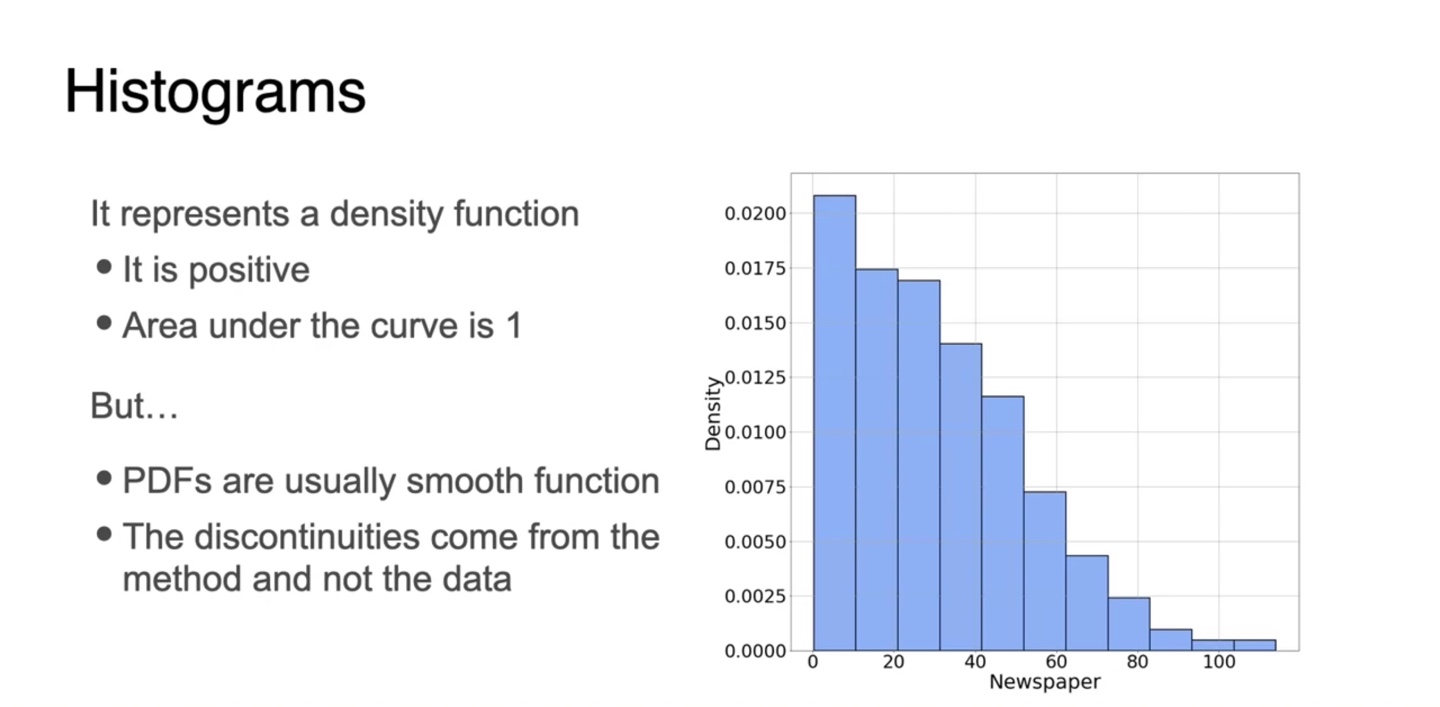
확률 변수에 따른 분포를 histogram화 해보면 아래와 같이 그려진다.
-
Density function의 특성 상 함수값은 모두 양수이며 전체 넓이는 1을 만족해야 한다.
- 그러나 PDF는 smooth한 function이다.
- 따라서 discontinuous한 현재의 histogram을 continuous하게 만드는 estimation method가 새롭게 필요하다.
-
-
이를 Kernel Density Estimation(KDE)라고 명명한다.
- 먼저, 확률 변수 X에 대한 관측값을 모두 기록한다.
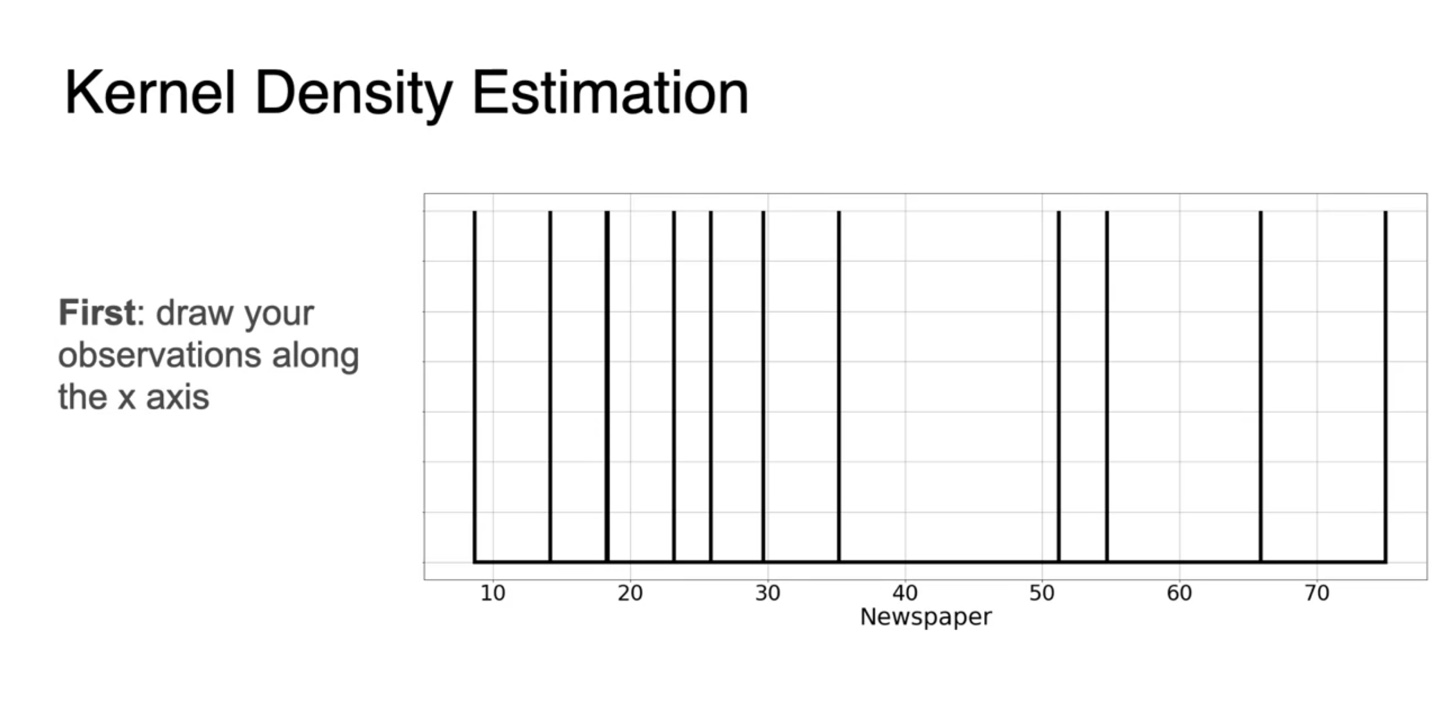
-
관측된 random variables를 각각의 평균으로 하는 gaussian 분포를 생성한다.
- 분포는 standard deviation, 에 따라 뾰족할수도 있고 넓을 수도 있다.
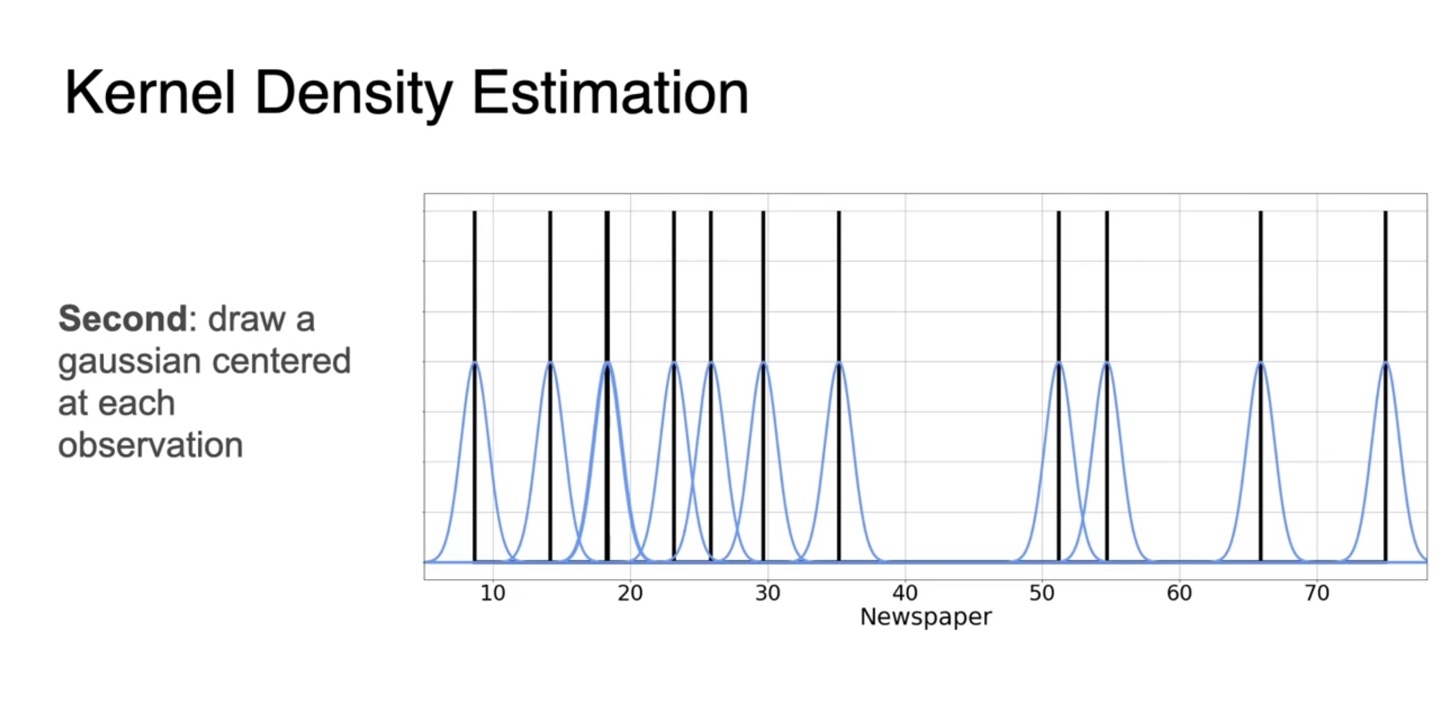
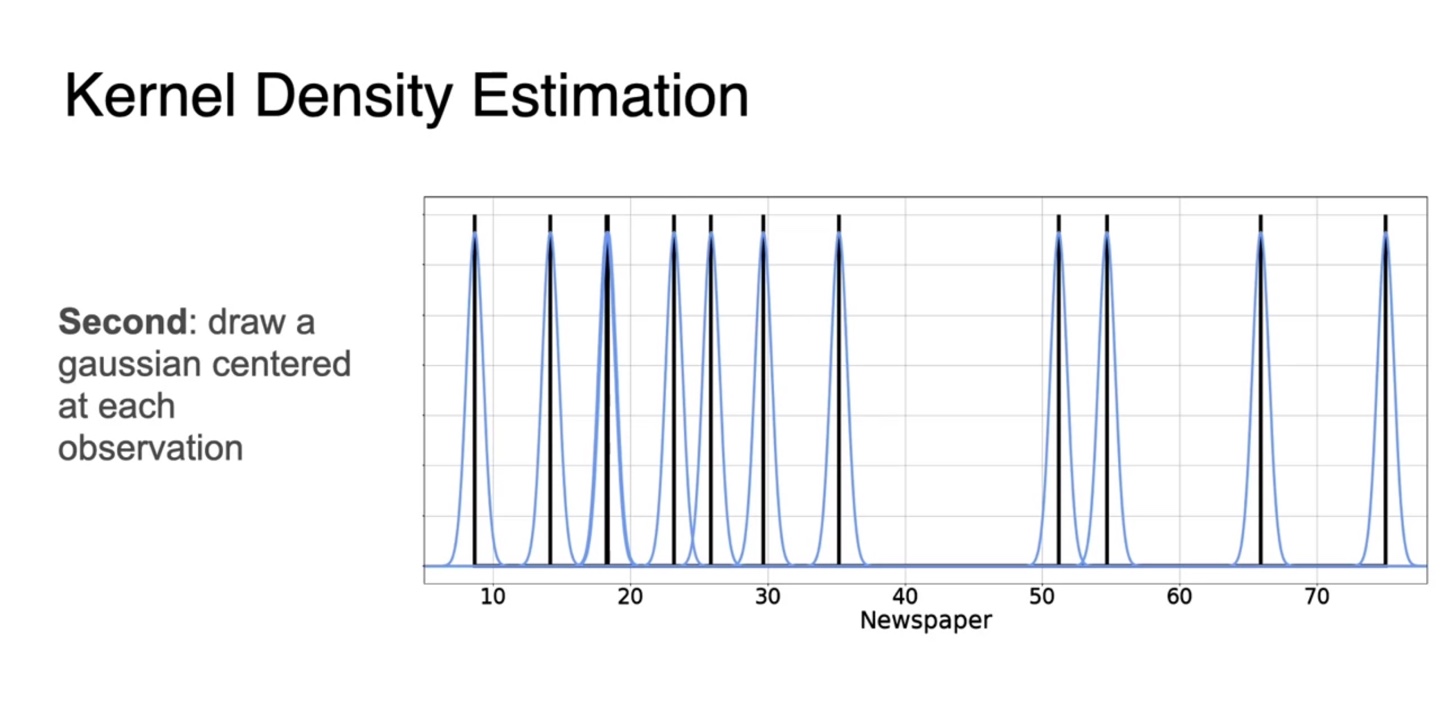
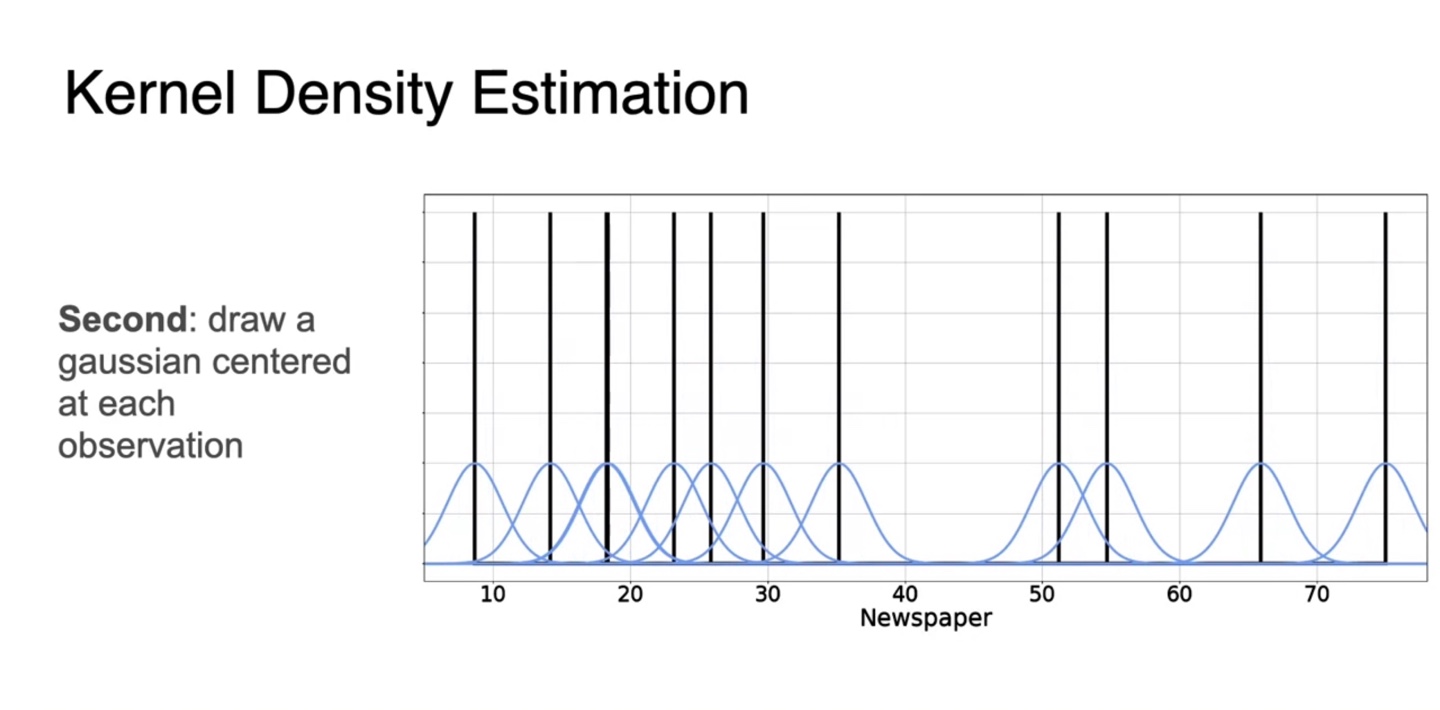
-
Gaussian 분포의 합은 또 다른 gaussian 분포를 만들 수 있다고 했었다.
- 따라서 위에서 정의한 모든 관측치들의 개별적인 gaussian 분포를 모두 더해, 으로 평균내어 전체 gaussian 분포를 구한다.
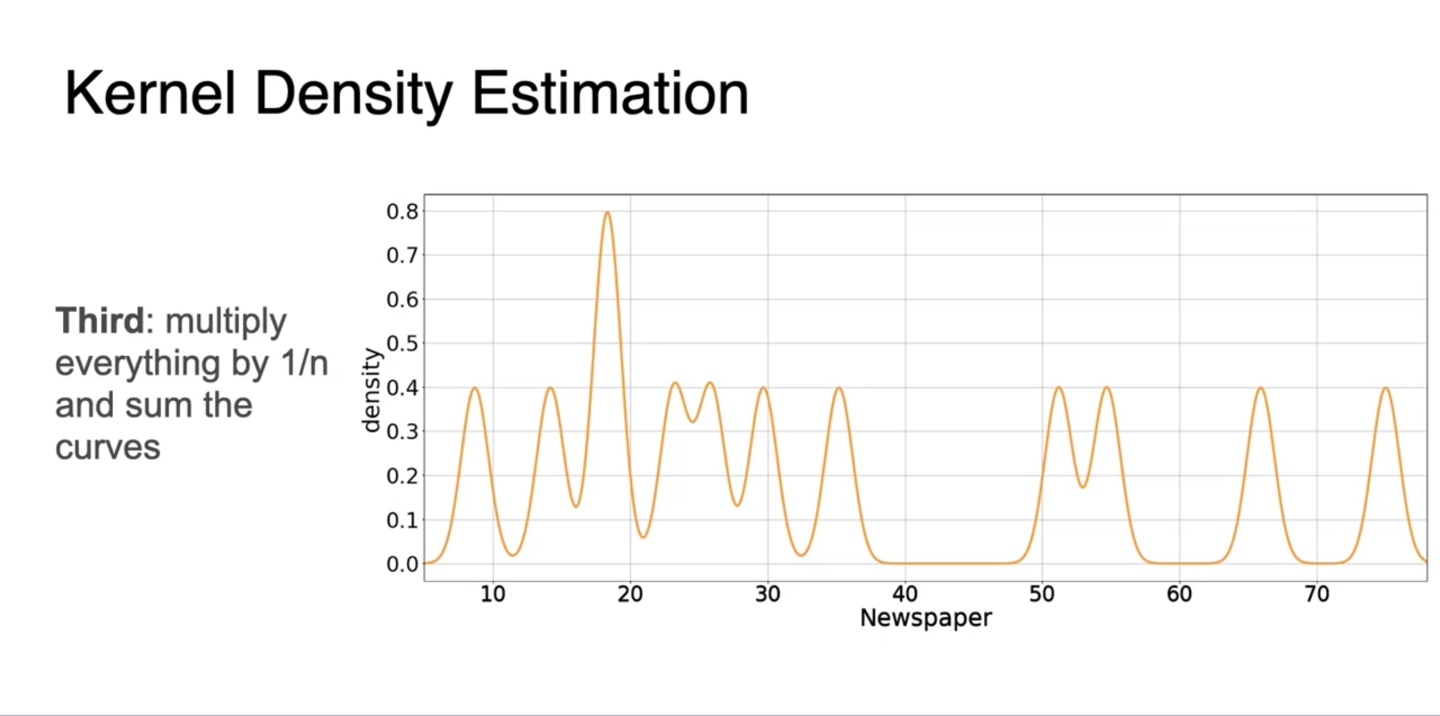
- 모든 관측치에 대한 값으로 gaussian 분포를 그리면 아래와 같은 추정 PDF가 완성된다.
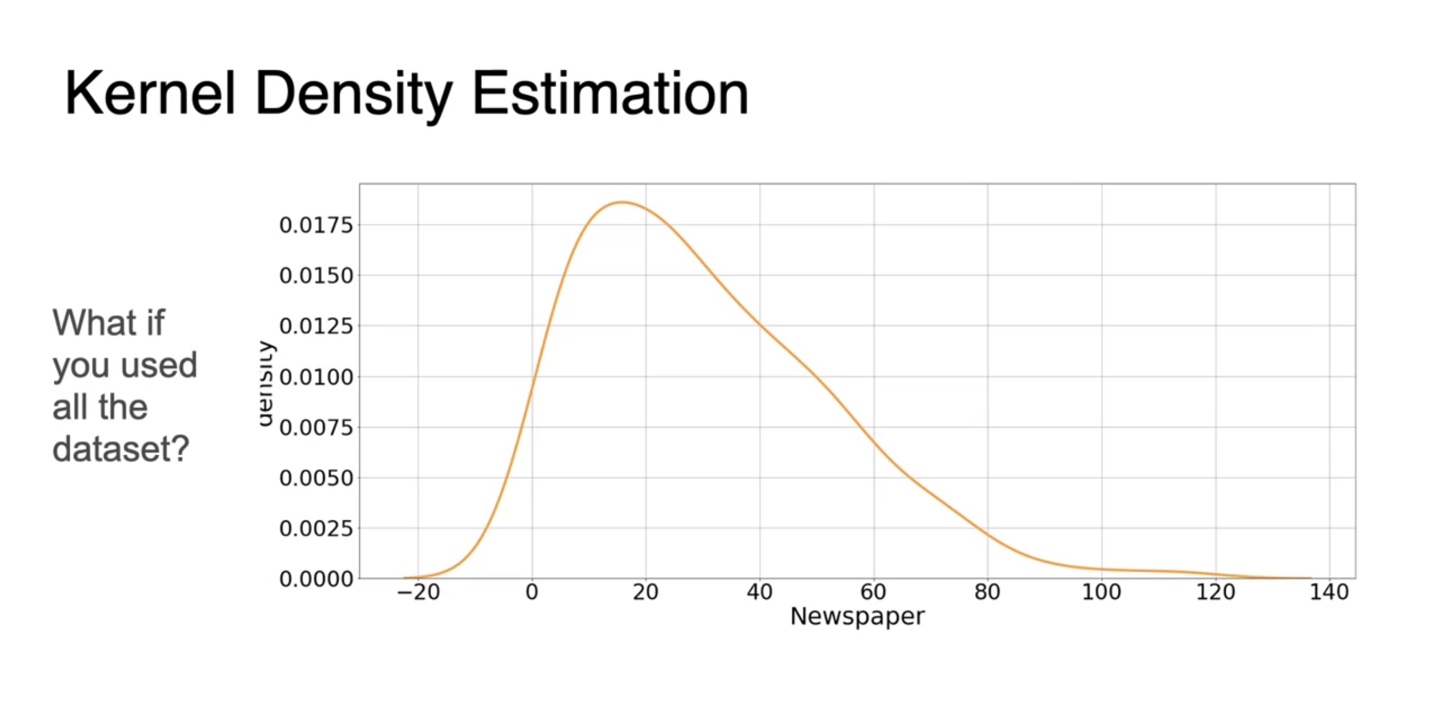
Visualizing data: Violin Plots
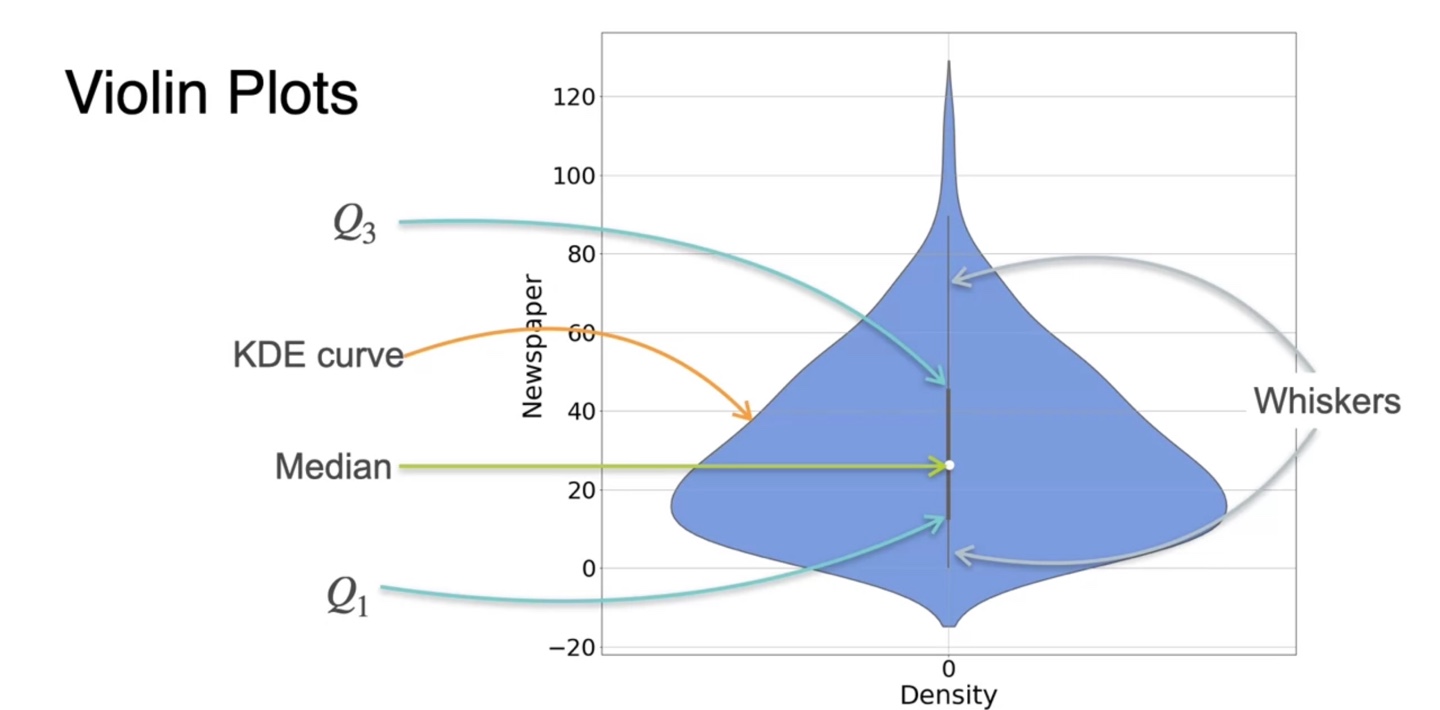
- Violin plot은 box-plot과 Kernel Density Estimation을 모두 고려한 그래프다.
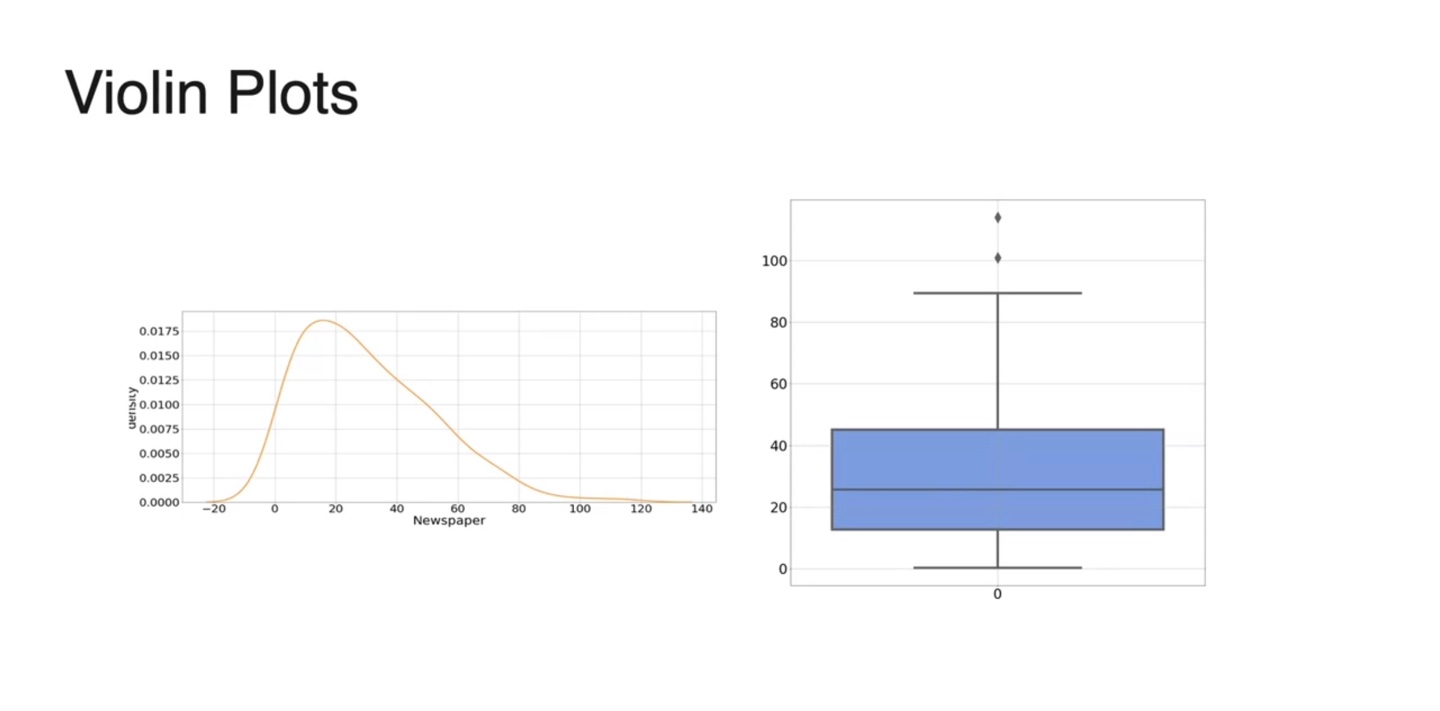
- 기존 box-plot에 KDE function을 옆으로 spread하게 갖다 붙인 형태라고 볼 수 있다.
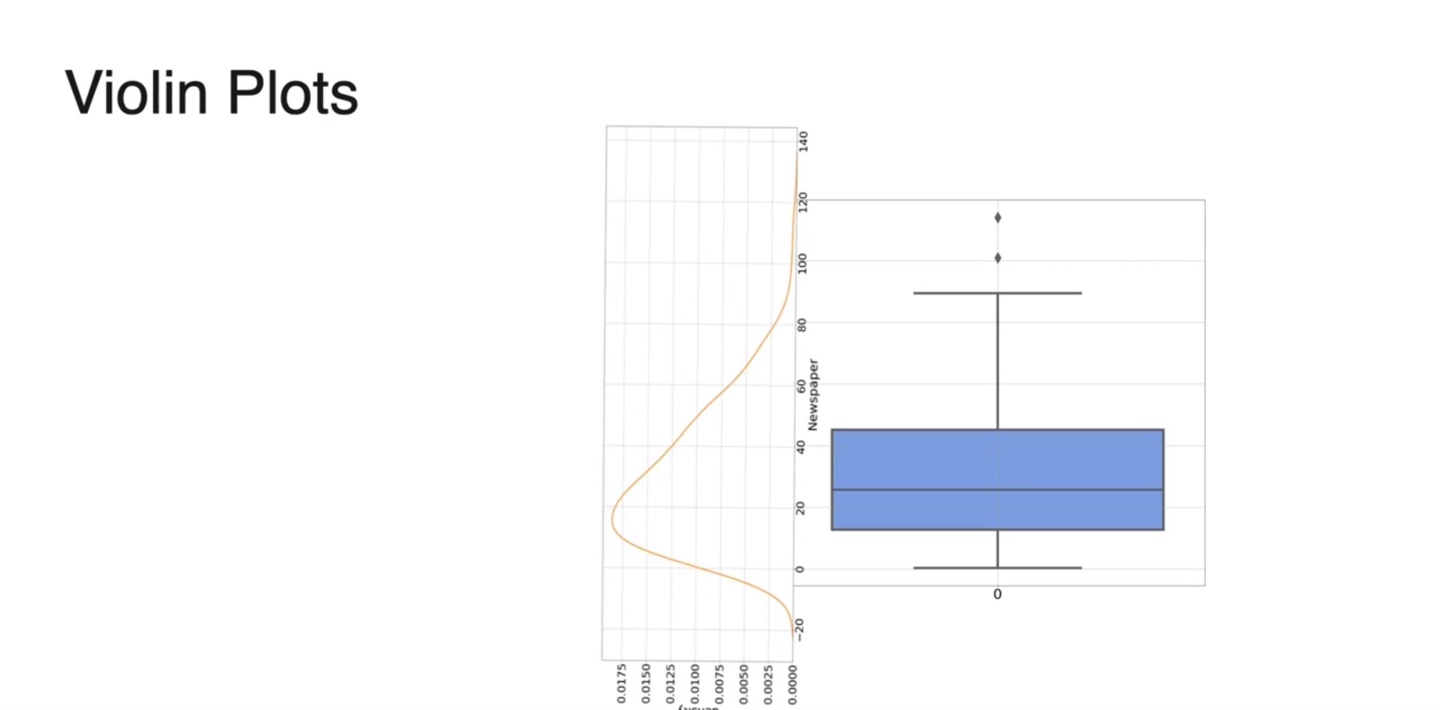
- 중앙값(median), KDE curve, Q1, Q3, Whiskers가 모두 표현된 그래프로, 데이터 분포를 시각화할 때 매우 유용하게 쓰일 수 있다.
Visualizing data: QQ plots
-
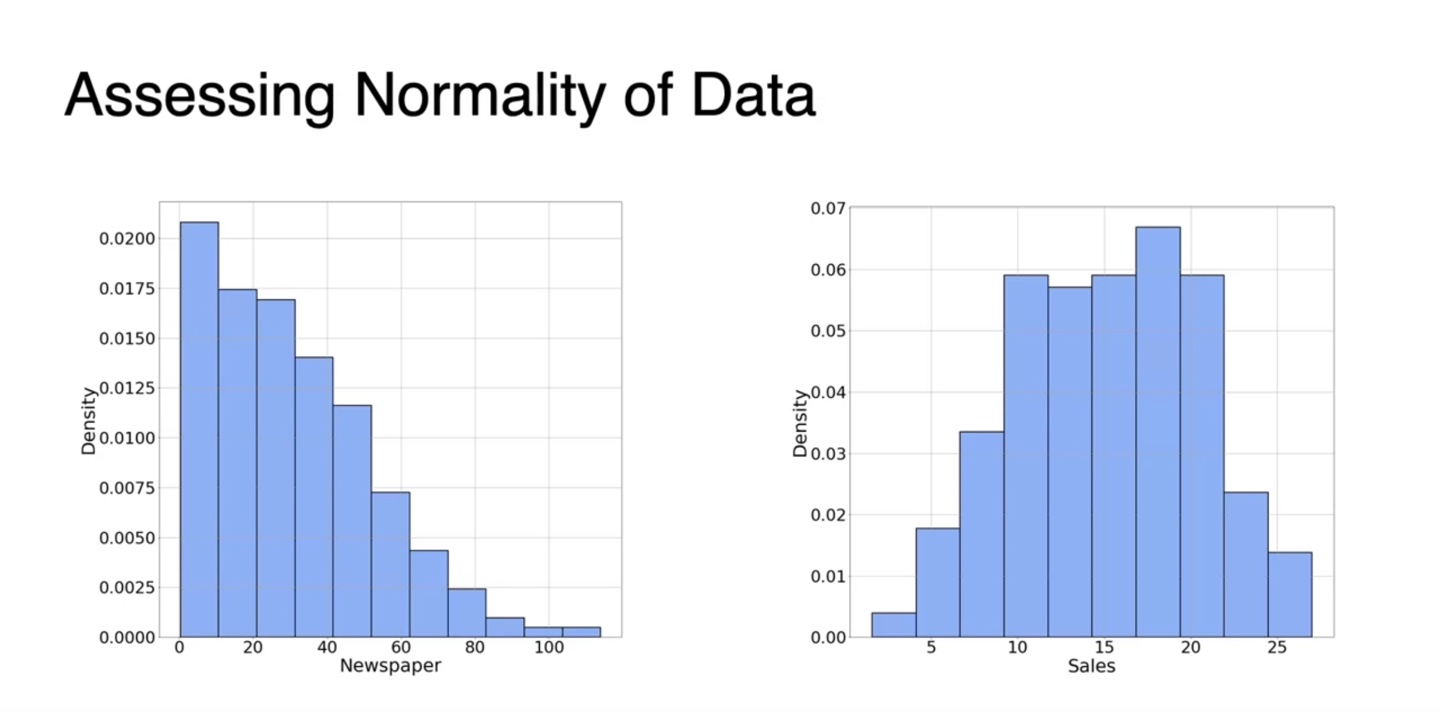
QQ plot은 분포가 normal distribution인지 아닌지에 관해 알려줄 수 있는 그래프다.
-
Linear regression이나 Logistic regression, Gaussian Naive Bayes, ... 등 일반적인 모델들은 normal distribution data를 가정하고 모델링한다.
- 따라서 normality를 확인하는 과정은 매우 유의미할 수 있다.
-

-
왼쪽의 그래프는 다소 skewed된 그래프이고 오른쪽 그래프는 normality한 형태를 띤다.
- 두 분포의 차이를 알아내기 위해 QQ plot을 정의해보자.
-
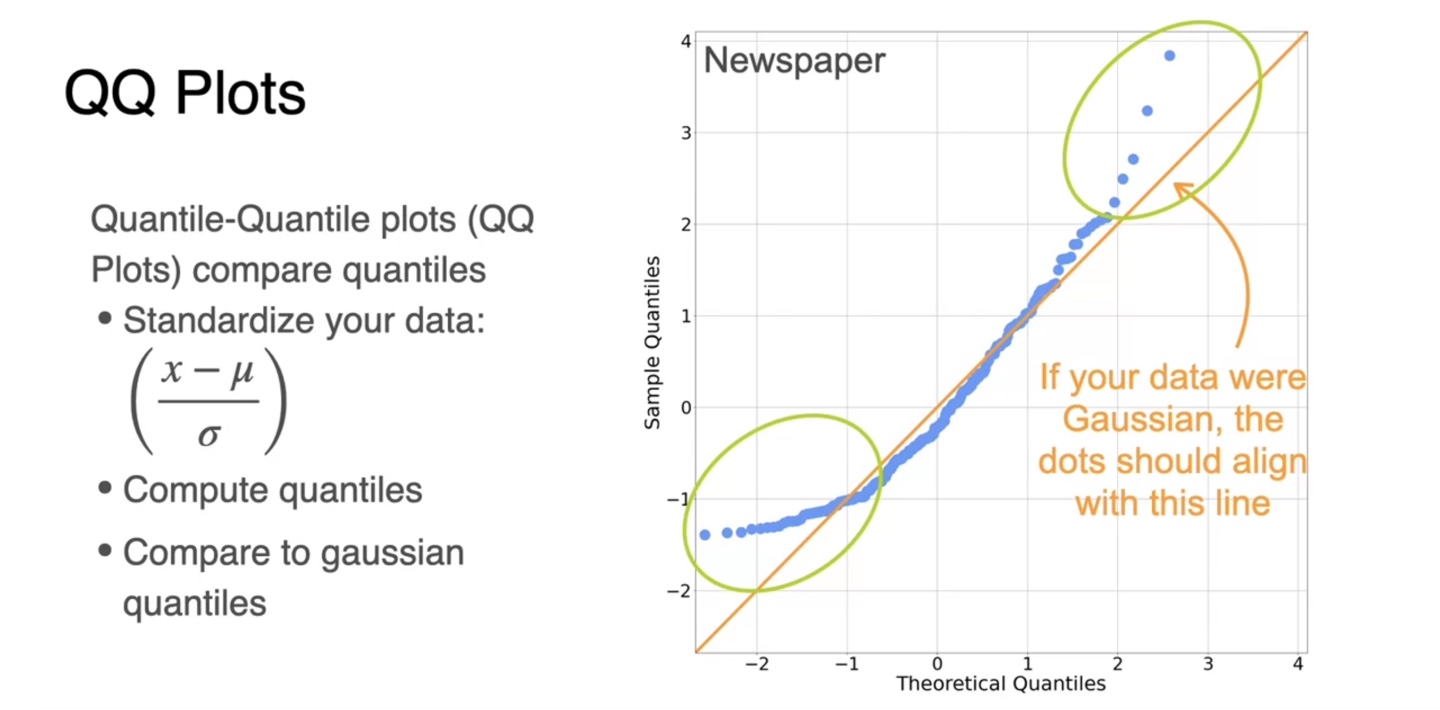
Quantile-Quantile plot은 먼저 data를 standardize하는 것부터 시작한다.
-
기존에는 25, 50%, 75%로만 quantile해서 나누었다면, 이번에는 연속적으로 잘라 quantile하여 plotting한다.
-
주황색으로 그린 선형적인 normal distribution의 quantile 분포와 비교하였을 때 벗어난 지점이 많으면 not normal, 선형적이라면 normal이라 판단한다.
-
-
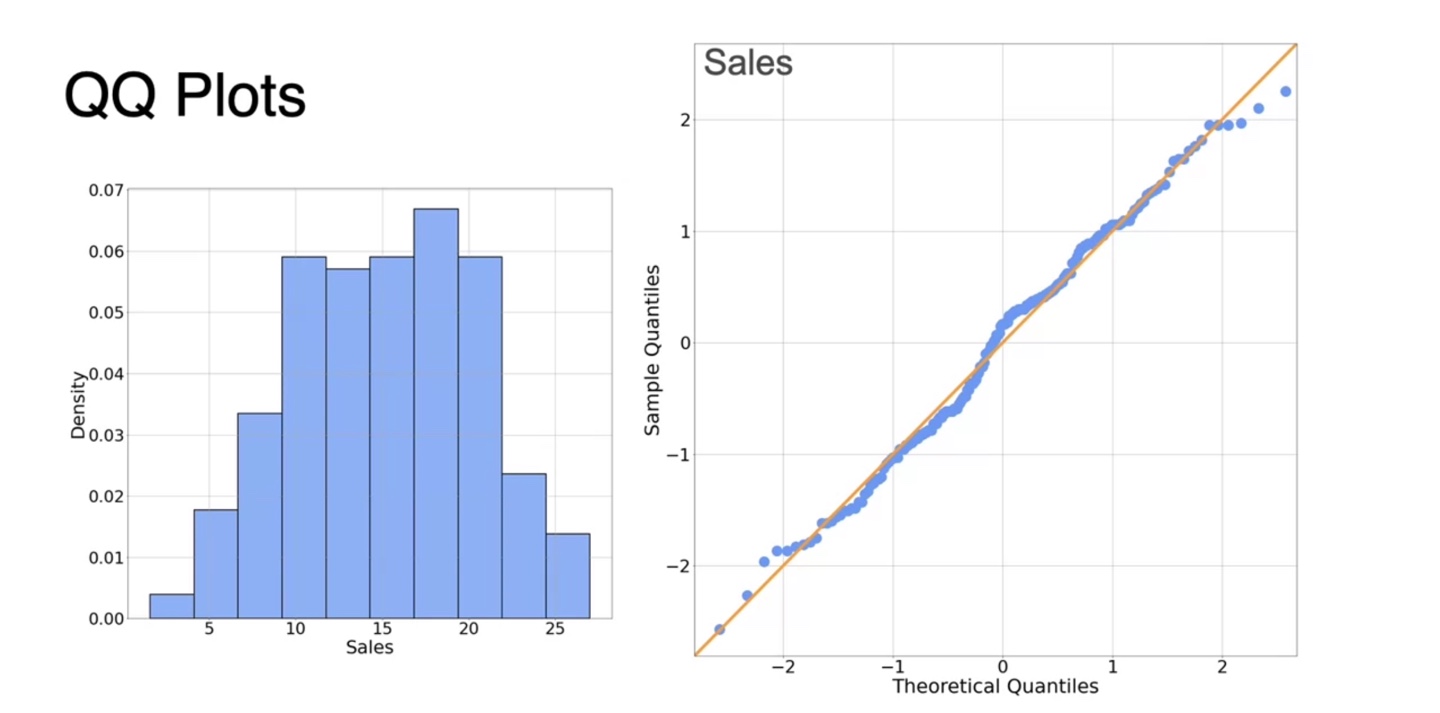
아래 그래프는 얼추 대칭적으로 보이며 이를 확인하는 방법은 QQ plot으로 가능하다.
- 아래와 같이 normal distribution의 QQ plot과 비슷하다면 normal한 분포를 따른다고 봐도 무방한 것이다.
Lesson 2 - Probability Distributions with Multiple Variables
Joint Distribution (Discrete) - Part 1
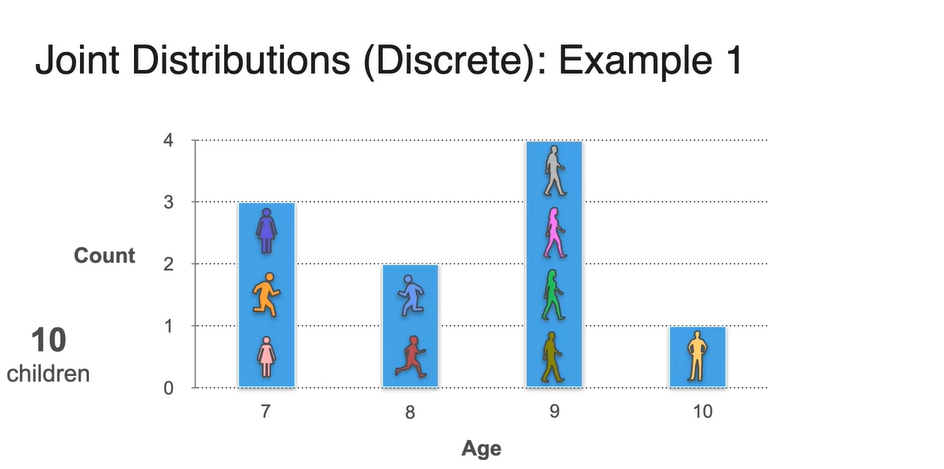
- 10명의 children의 나이를 조사하여 표로 나타내보자.

-
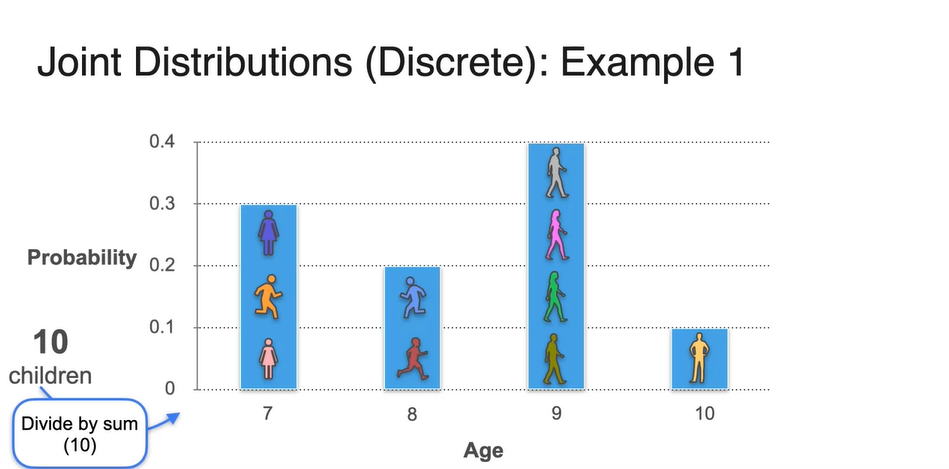
Age를 확률 변수로, 각 나이의 학생 수를 y축으로 한 Histogram으로 그려보자.
- 총 10명의 학생 수(sum)로 count를 각각 나눠주면 Probability로 표현이 가능하다.
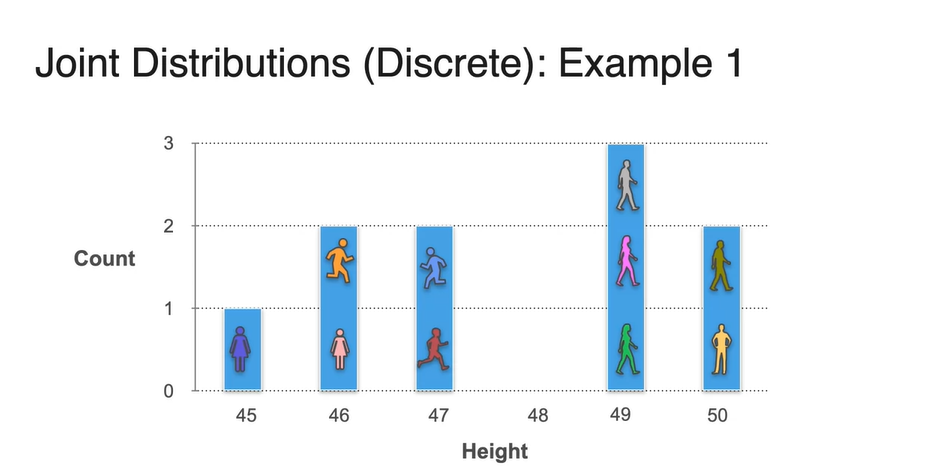
- 이들의 키(height)를 다시 한 번 조사하였더니 아래 표와 같이 나타났다고 하자.

-
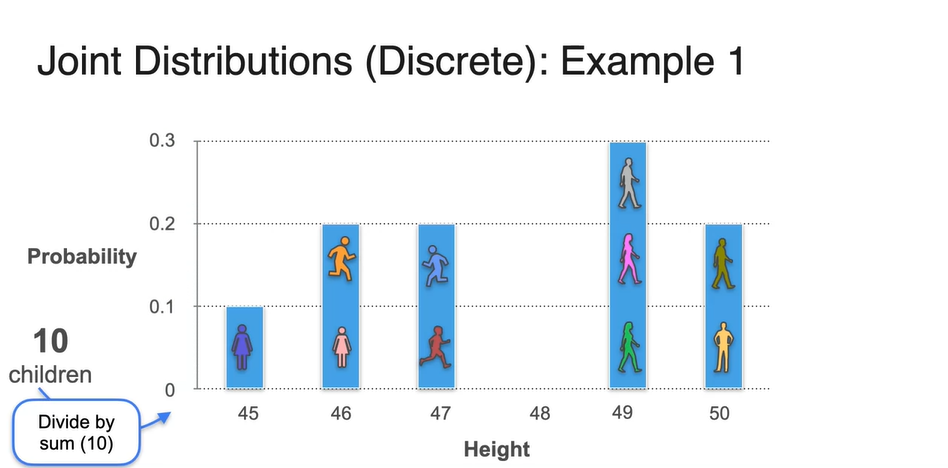
이번에는 Height를 확률 변수로 하여 각 변수에 해당되는 학생 수를 y축으로 한 histogram을 그렸다고 해보자.
- 마찬가지로 전체 학생 수 10으로 나눠주면 Probability로 표현이 가능하다.
-
그렇다면 9살이면서 49 inches의 키를 갖는 학생의 확률은 얼마일까?
- 두 그래프를 보고, 9살이자 키가 49인치인 학생은 전체 10명 중 몇 명인지 세어보라.
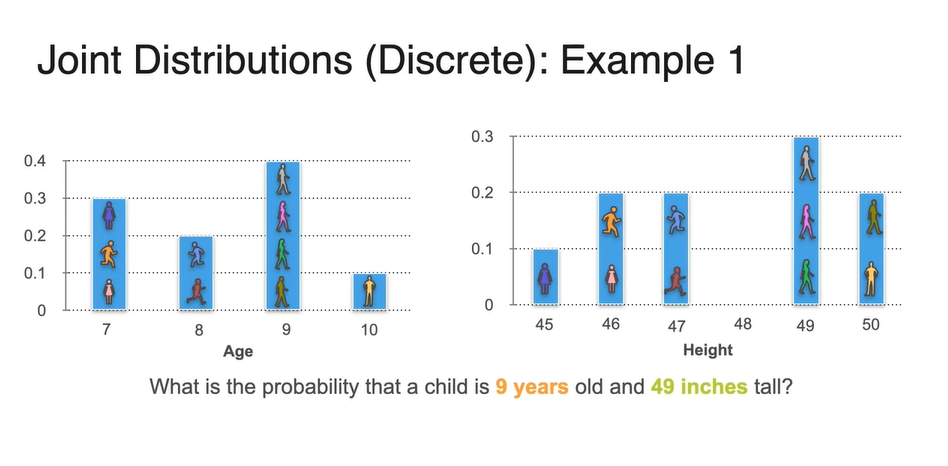
-
두 확률 변수를 모두 만족시키는 사람은 gray, pink, green 학생으로 총 3명이다.
- 따라서 확률은 임을 알 수 있고, 기호로는 혹은 로 표기한다.
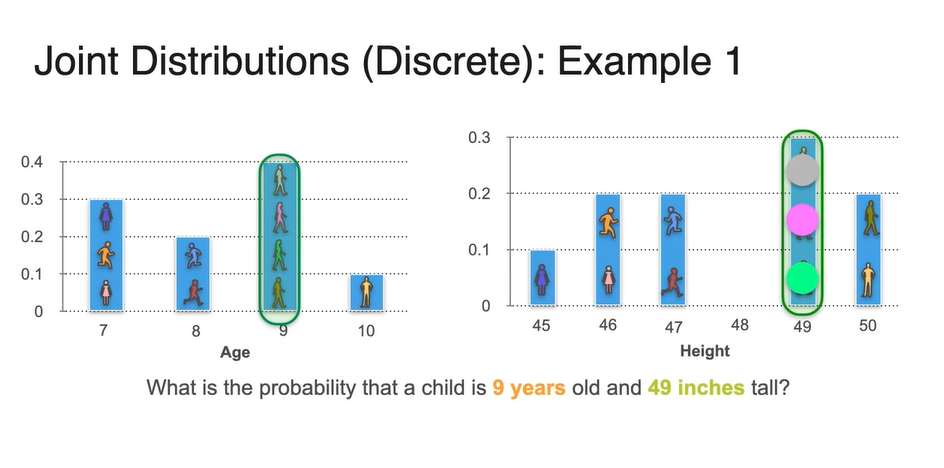
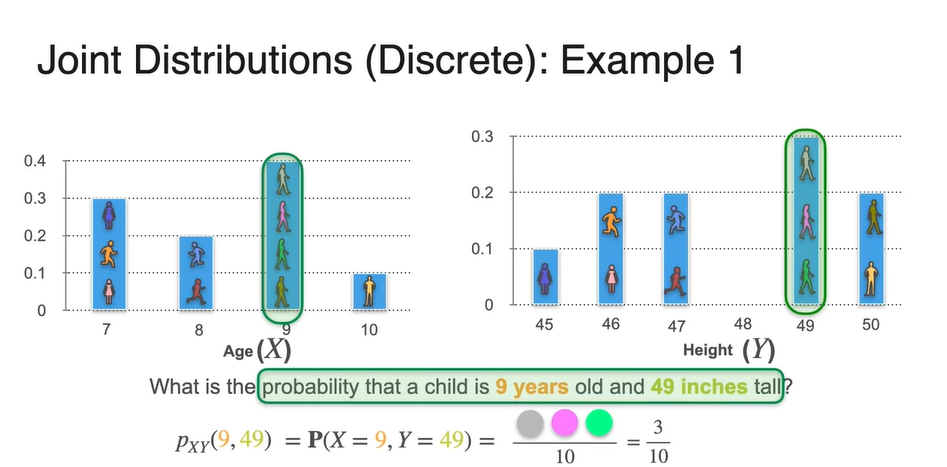
-
Joint Distribution(discrete)의 확률 표현은 로 표기한다.
- 확률 변수 가 일 때와 가 일 때의 확률을 구하고자 할 때는 를 구함으로써 알 수 있다.

-
이제, Age와 Height를 두 축으로 갖는 테이블을 만들어 학생 수를 count해보자.
-
아래와 같이 각 경우에 해당하는 학생들만 0보다 큰 값을 가지며, 해당하지 않으면 0으로 표기한다.
-
그리고 전체 학생 수 10으로 모든 값을 나눠주면 0과 1사이의 값을 갖는 확률 표현이 가능해진다.
-


-
Joint Distribution을 따르는 probability는 두 확률 변수 와 의 combinations를 모두 계산함으로써 구해진다.
-
각 변수에 공통된 경우의 수를 전체 가능한 개수로 나눈 값이 확률로 표현된다.
- 그렇기 때문에 당연하게도 테이블에 있는 모든 확률을 더했을 때 1이 나온다.
-

-
만일, 을 구하고자 한다면 과 을 만족시키는 경우의 수(확률)를 테이블에서 찾아내면 된다.
- 을 구하고자 한다면 과 을 만족시키는 경우의 수(확률)를 찾는다.


Joint Distribution (Discrete) - Part 2
-
이번에는 dice example을 다뤄보자.
-
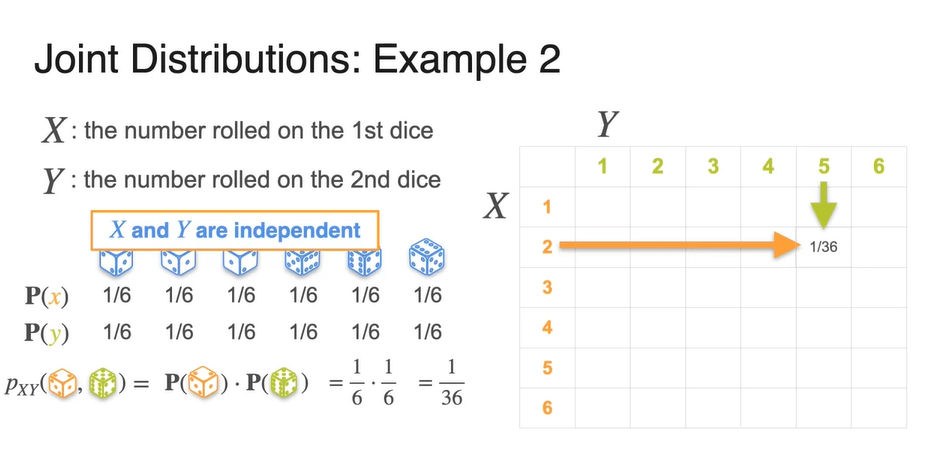
확률 변수 는 첫 번째 주사위를 던졌을 때의 number를, 확률 변수 는 두 번째 주사위를 던졌을 때의 number를 가리킨다.
- 두 변수의 각 확률은 모두 로 동일하다.
-
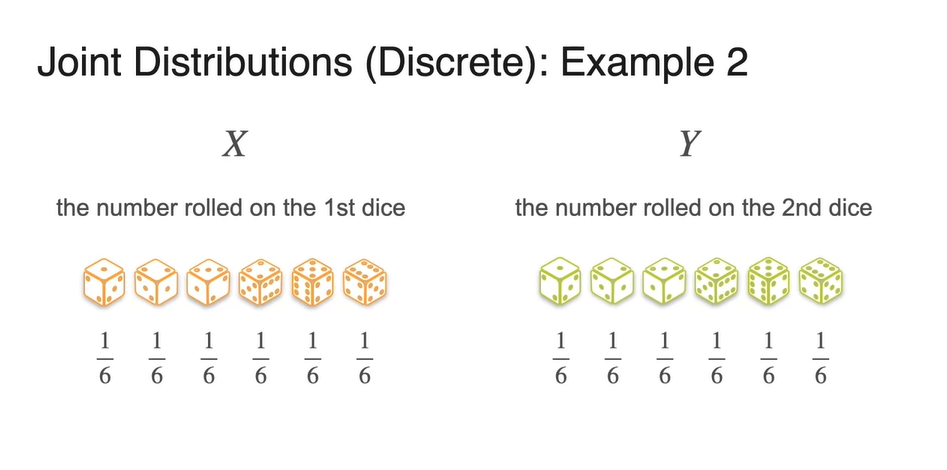
- 이를 histogram으로 표현하면 아래와 같다.

-
만약, 와 가 독립적(independent)이라고 한다면 확률은 어떻게 구해질까?
-
서로 다른 확률 변수가 독립적이라는 말은 두 분포의 경우의 수가 겹칠 일이 없다는 뜻이다.
- 즉, 두 주사위는 독립적으로 굴려지기 때문에, 아까와 같이(나이가 9살이면서 키가 46인치인 학생) 중복되어 계산될 일이 없다.
-
따라서 는 로 계산이 가능해진다.
- 두 확률을 계산해보면 으로 계산된다.
-

-
이를 일반화하면 다음과 같다.

- 이번에는 확률 변수 는 첫 번째 주사위를 굴렸을 때 나타나는 number, 확률 변수 는 두 주사위를 굴렸을 때 더해지는 값이라고 해보자.
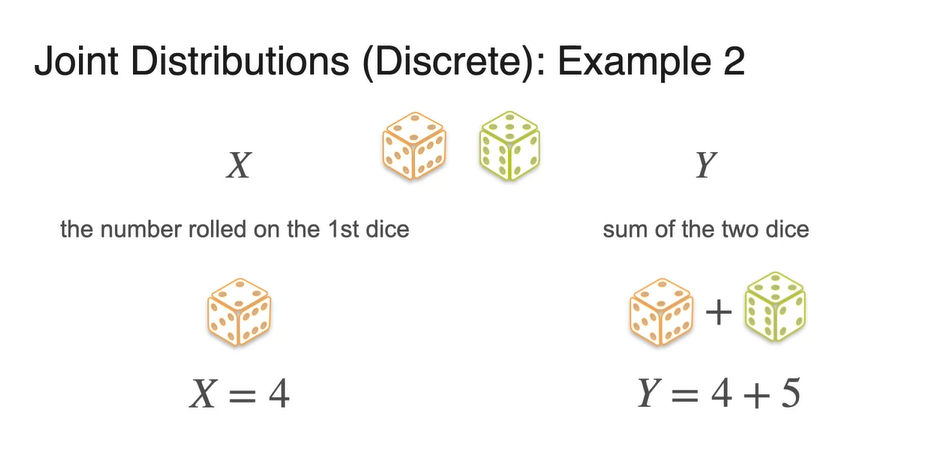
- 확률 변수 의 분포는 아까와 동일하게 모든 확률이 로 나타난다.
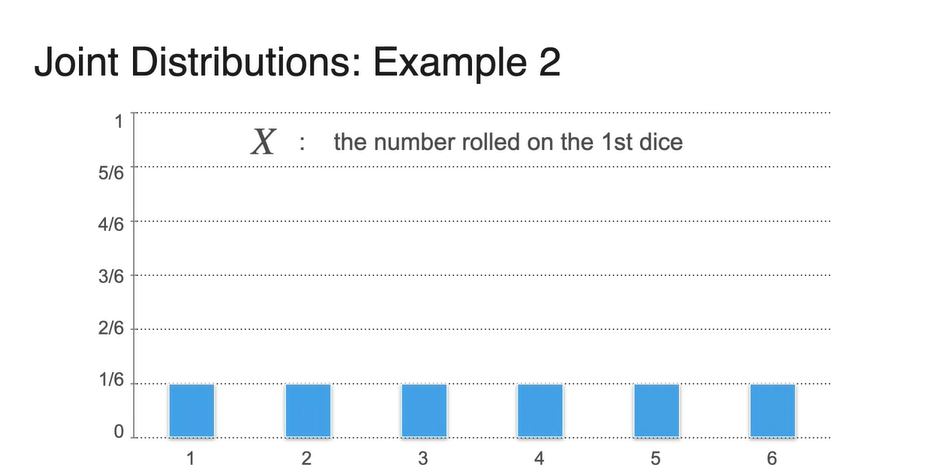
-
확률 변수 의 분포는 두 주사위의 경우의 수로 결정된다.
- 까지의 값이 아래와 같은 표로 적히며 이를 count하여 나타낸 histogram이 밑의 분포 그림과 같다.
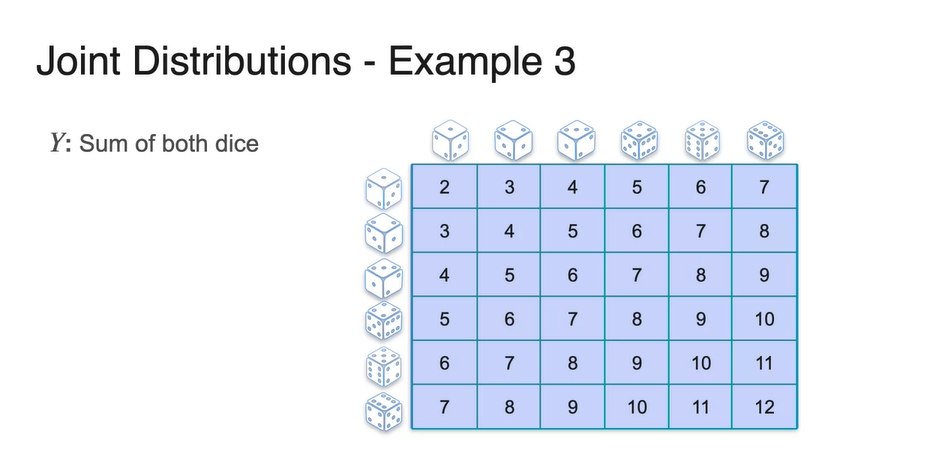

-
이제 첫 번째 주사위와 두 번째 주사위의 값이 각각 어떻게 나타났는지까지 histogram에 표시해보자.
- 이를 바탕으로 확률 변수 (num of dice 1)를 x축, 확률 변수 (sum of dice)를 y축으로 나타낸 그래프를 그려보자.
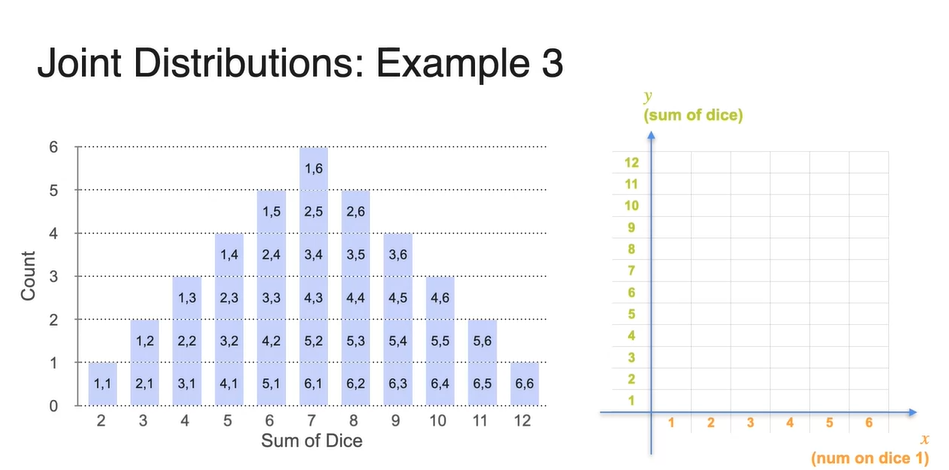
- 왼쪽에 있는 값들을 오른쪽 그래프 각 축에 맞게 표시하여, 각 경우의 수를 count하면 모두 1임을 알 수 있다.
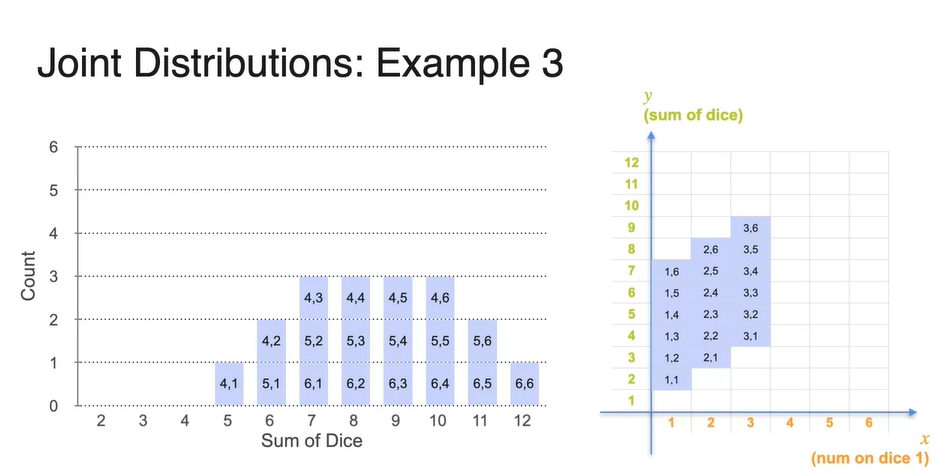
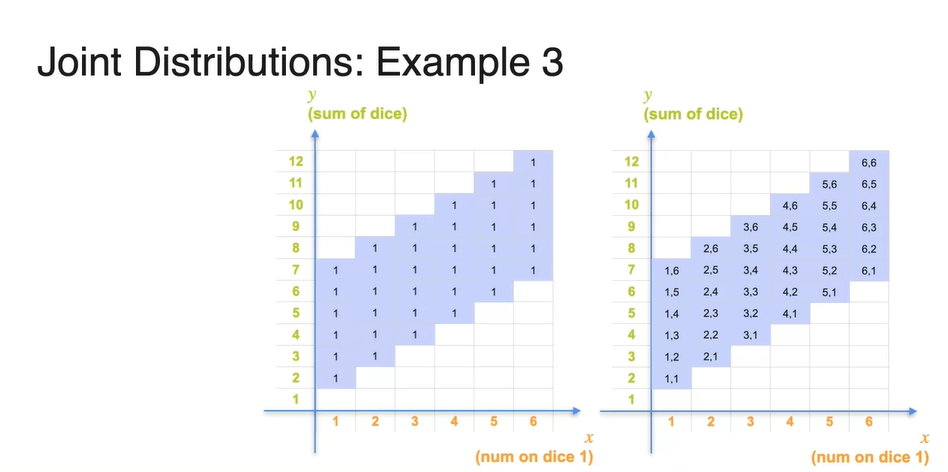
-
전체 경우의 수가 36이므로 count를 36으로 나누면 각 point들의 확률을 구할 수 있다.
- 현재 모든 경우의 수는 으로 계산된다.

- 만약, , 인 확률을 찾고자 한다면 아래와 같이 테이블을 검색하여 찾아낼 수 있다.

Joint Distribution (Continuous)
-
위에서 다루었던 예제들은 모두 discrete random variables를 다루었다.
- Continuous한 random variables를 joint하면 어떨까?

-
예를 들어 상담원이 기다린 시간을 , 고객의 만족도를 라고 해보자.
- 두 변수 모두 0-10의 interval한 변수로 나타낼 수 있기 때문에 float로 continuous하게 표현할 수 있다.

-
1000명의 고객이 상담을 받았다고 가정해보자.
-
기다린 시간에 대한 확률 변수 의 확률 분포와 만족도 의 확률 분포를 아래 그림과 같이 표현하였다.
- 의 분포는 y축을 확률 변수로, x축을 경우의 수로 나타내었다.
-
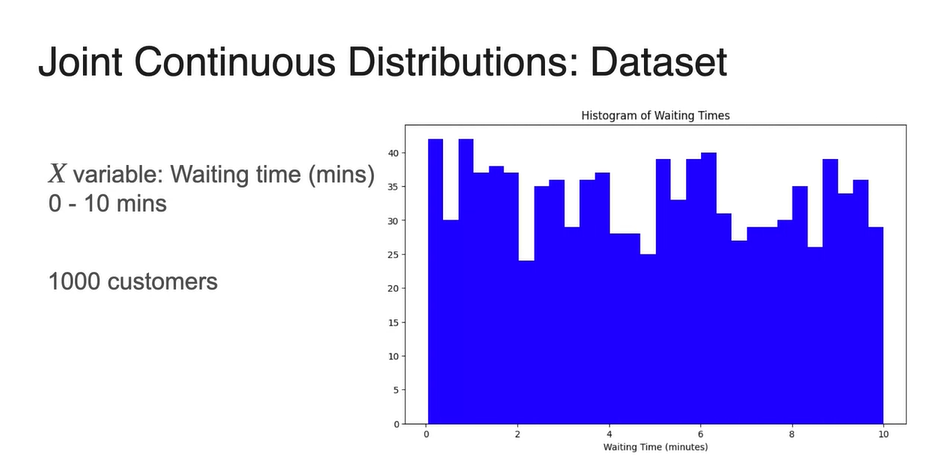
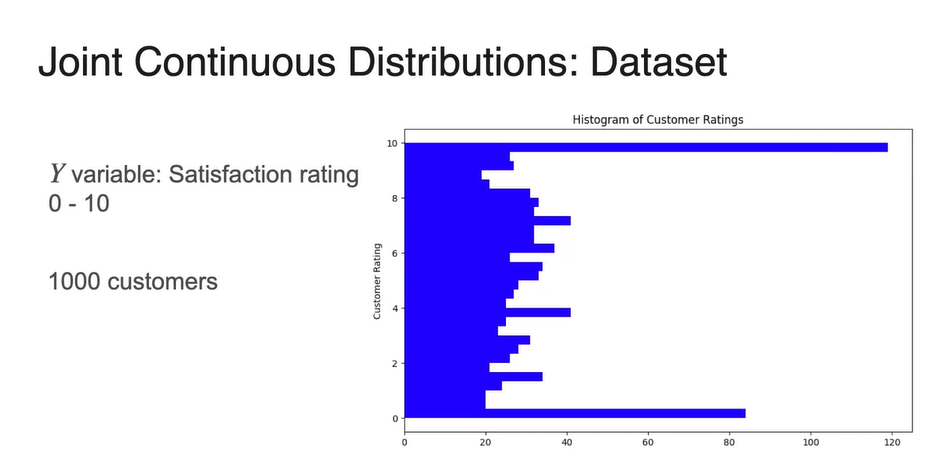
-
Continuous variable인 와 에 대한 dataset의 분포를 나타내면 아래와 같이 scatter plot으로 그려진다.
-
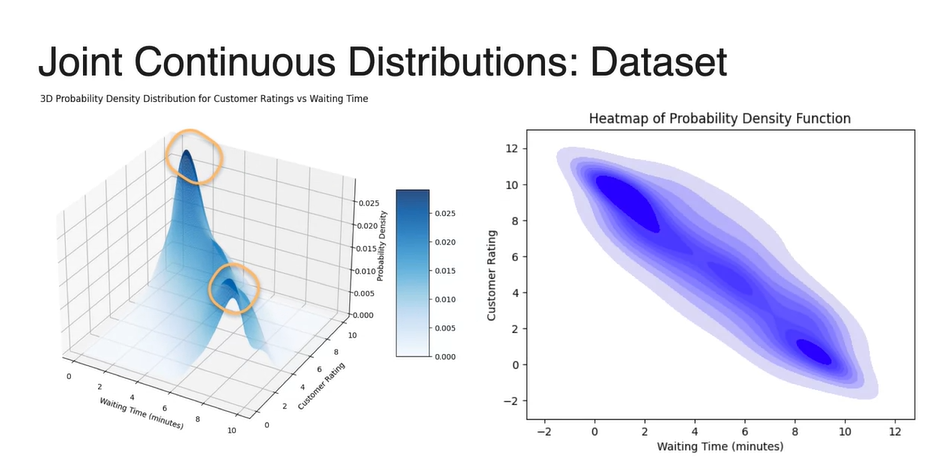
데이터 밀도를 heatmap으로 표현하면 왼쪽 위와 오른쪽 아래 값에서 큰 밀도를 갖는 것을 알 수 있다.
- 이는 기다린 시간 가 작을 때 만족도 가 높다는 것을 의미하고, 기다린 시간 가 클 때 만족도 는 낮다는 것을 의미한다. (반비례)
-
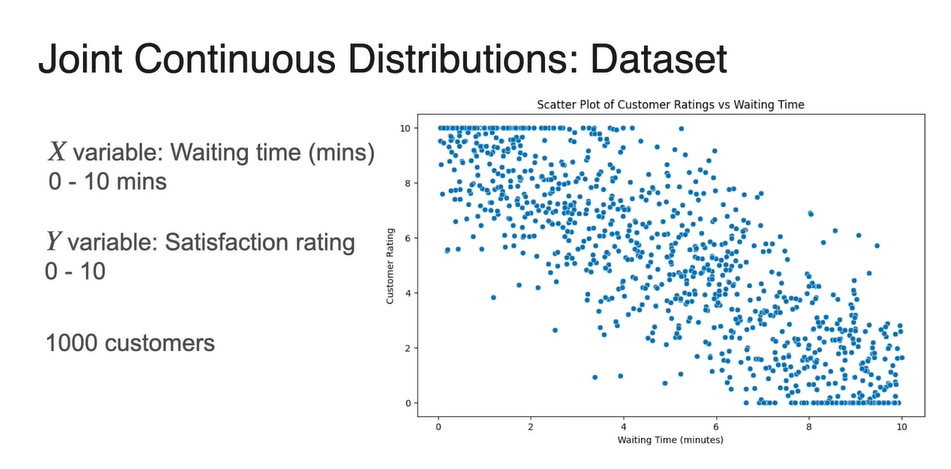
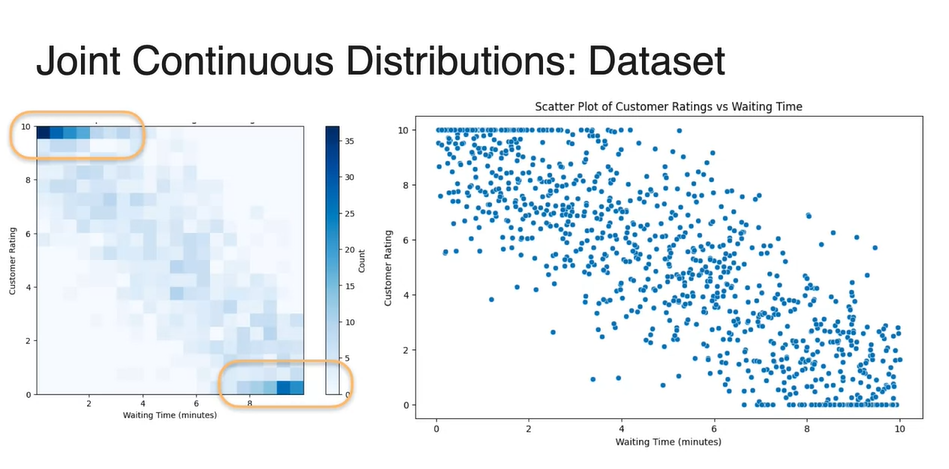
-
Probability Density Function(PDF)를 heatmap으로 표현해 보았을 때의 그래프도 왼쪽 위와 오른쪽 아래 끝 값에서 큰 밀도를 가진다. (노란 박스)
- 이를 3차원 그래프로 나타내, z축의 value가 dataset count(probability)라고 한다면 마찬가지로 양쪽 끝 값에서 높은 value를 갖는다. (노란 박스)
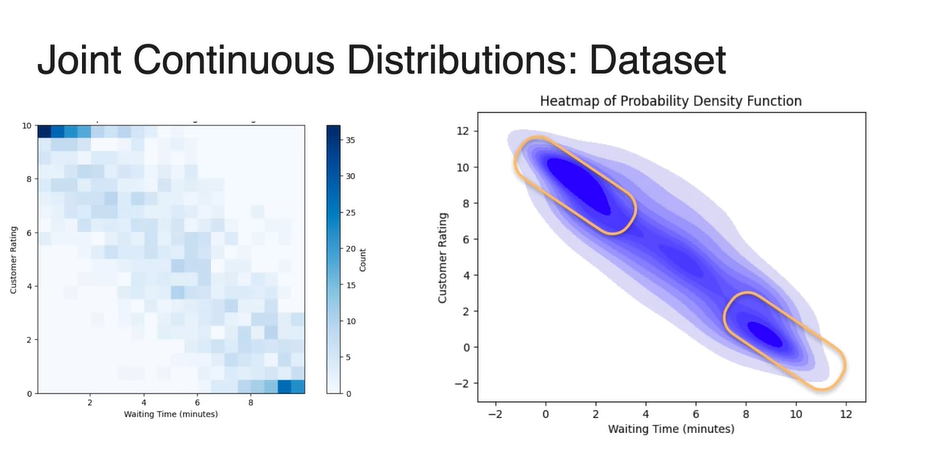
-
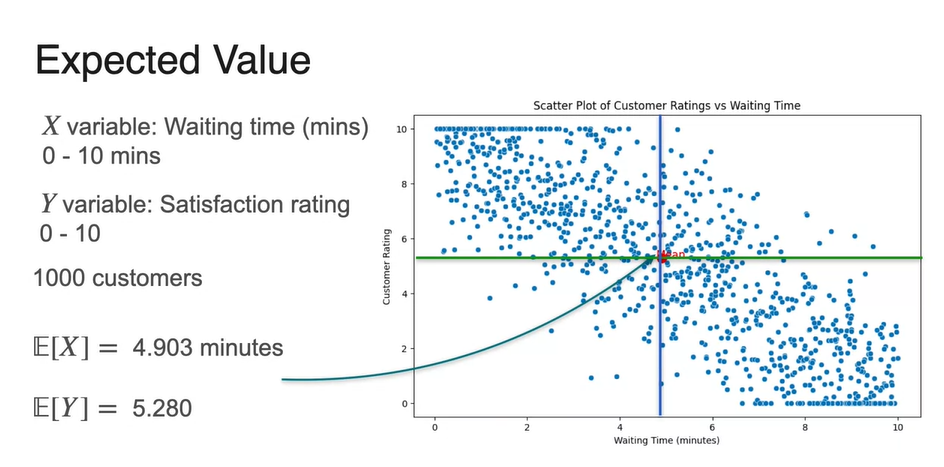
Expected Value 즉, 두 확률 변수의 독립적인 기댓값은 scatter plot의 각 축을 기준으로 각각 평균내어 구할 수 있다.
- 위 예제에서는 x축 기준 평균 가 4.903min으로, y축 기준 평균 가 5.280으로 계산되었다.
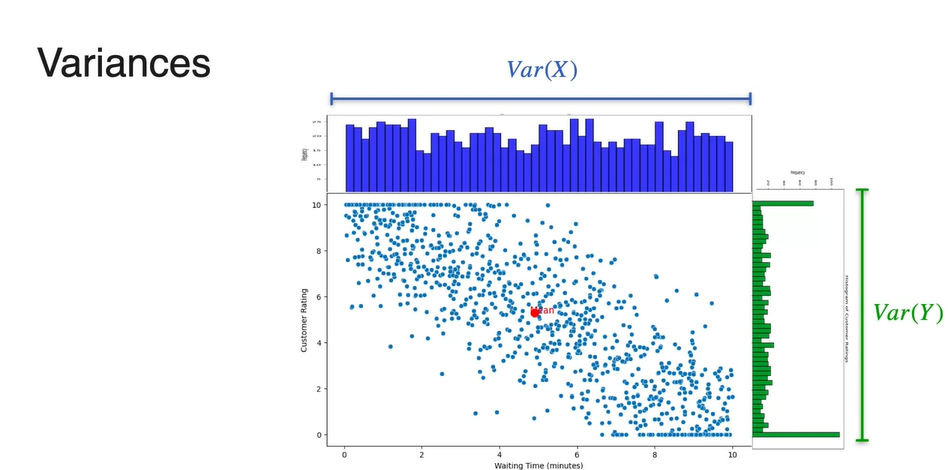
- Variance 또한 확률 변수 의 분포 따로, 확률 변수 의 분포 따로 구할 수 있다.
-
이므로 각 와 의 기댓값(expected value)를 구함으로써 계산한다.
- 확률 변수 또한 로 계산되므로 와 의 기댓값(expected value)를 구함으로써 계산한다.
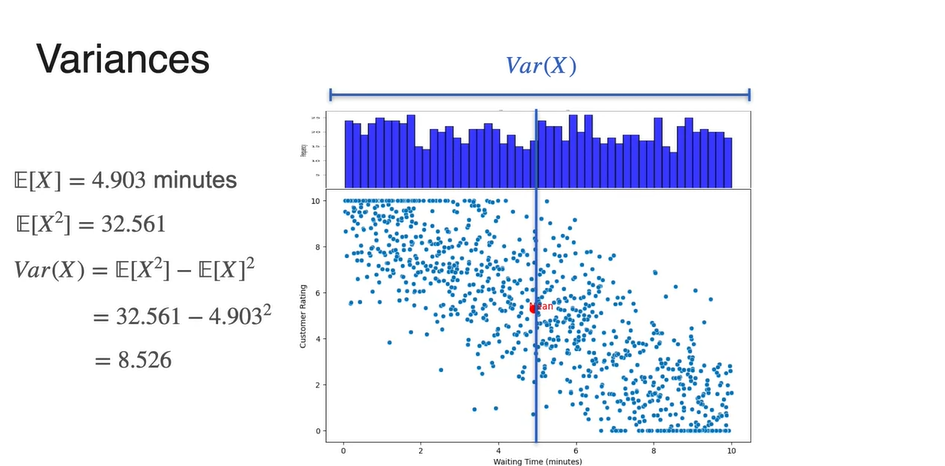
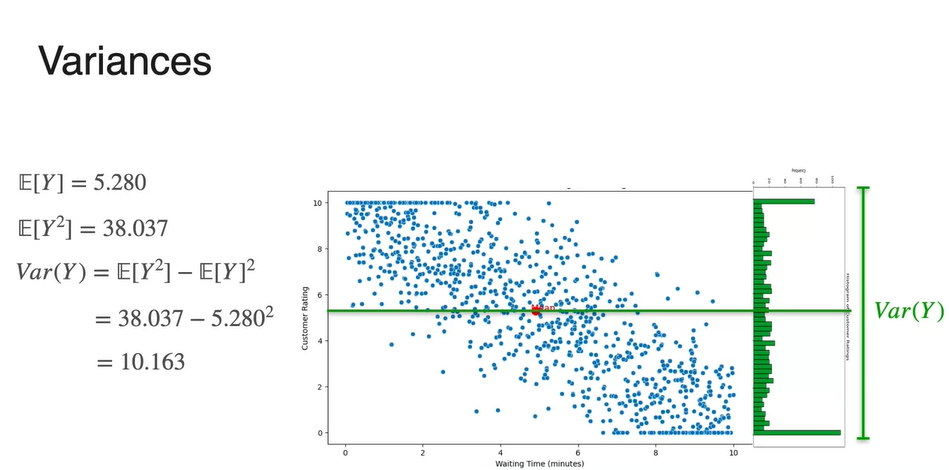
- 최종적으로 구해낸 와 는 8.526과 10.163이다.
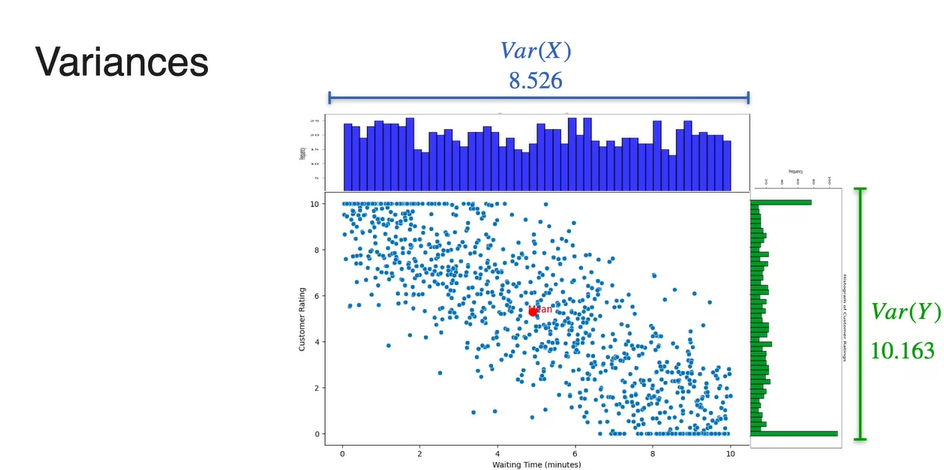
Quiz
What is the difference between preparing a joint distribution for discrete versus continuous variables?
- Discrete joint distributions assign probabilities to individual outcomes, while continuous joint distributions assign probabilities to ranges or intervals of values.
- Discrete joint distributions have a countable or finite number of possible outcomes, while continuous joint distributions have an uncountably infinite number of possible outcomes.
- Continuous joint distributions are typically represented by scatter plots, while discrete joint distributions are represented by bar charts.
Marginal and Conditional Distribution
-
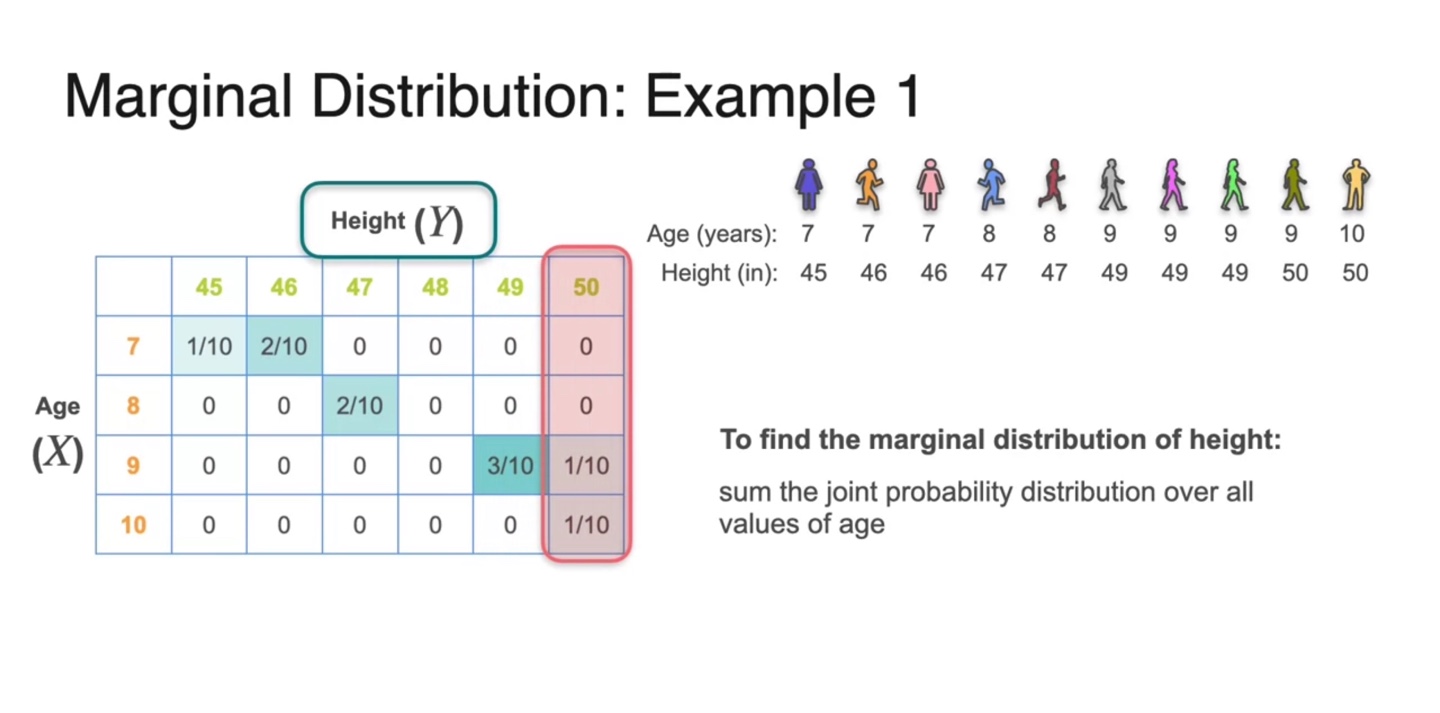
Age()와 Height()를 확률 변수로 갖는 예제를 통해 Marginal Distribution에 대해 알아보자.
- Height()에 대한 Marginal Distribution은 joint probability에서 모든 Age()에 대한 확률을 더함으로써 구해낼 수 있다.
-
만약 인 확률을 구하고자 한다면 를 구하면 된다.
- 즉, 확률 변수 가 50일 때에 해당하는 모든 variables()의 확률을 더해주면 된다.

-
마찬가지로 인 확률을 구하고자 한다면 를 구하면 된다.
- 즉, 확률 변수 가 7일 때에 해당하는 모든 variables()의 확률을 더해주면 된다.

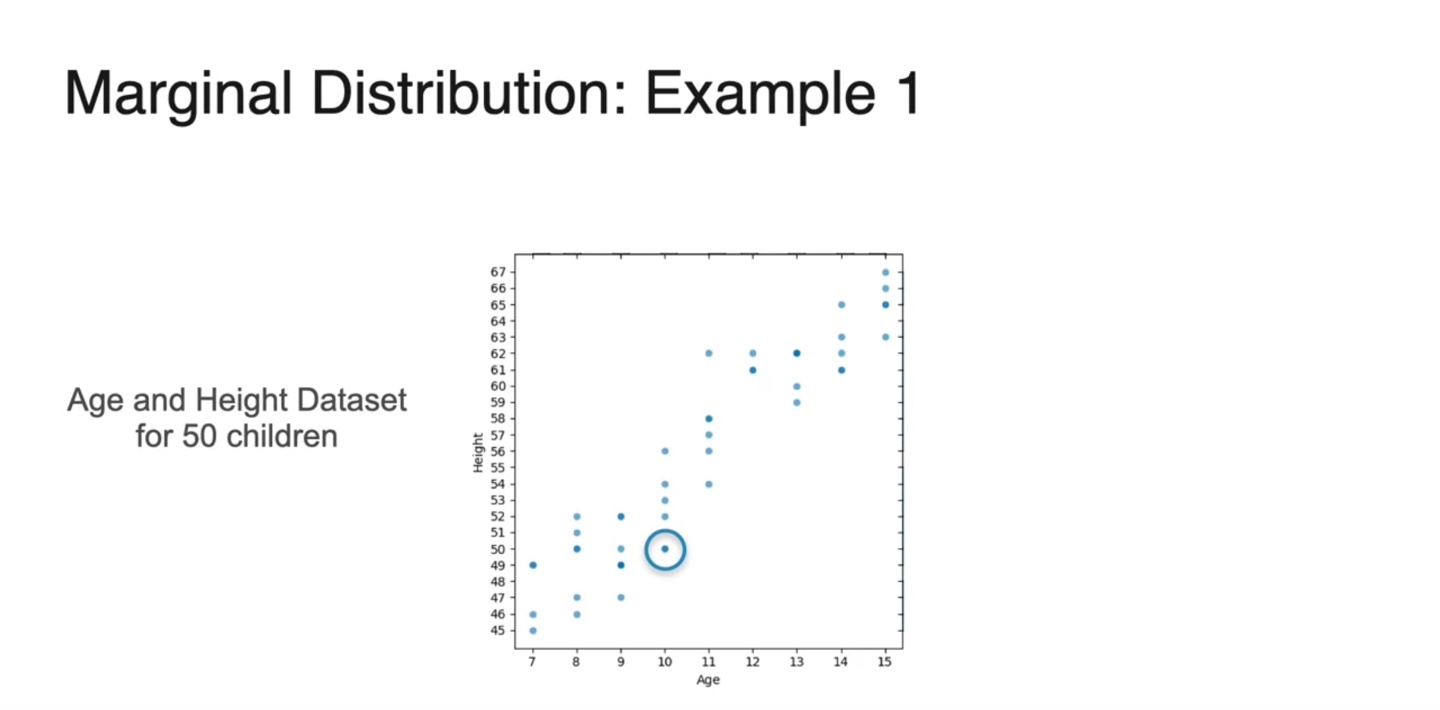
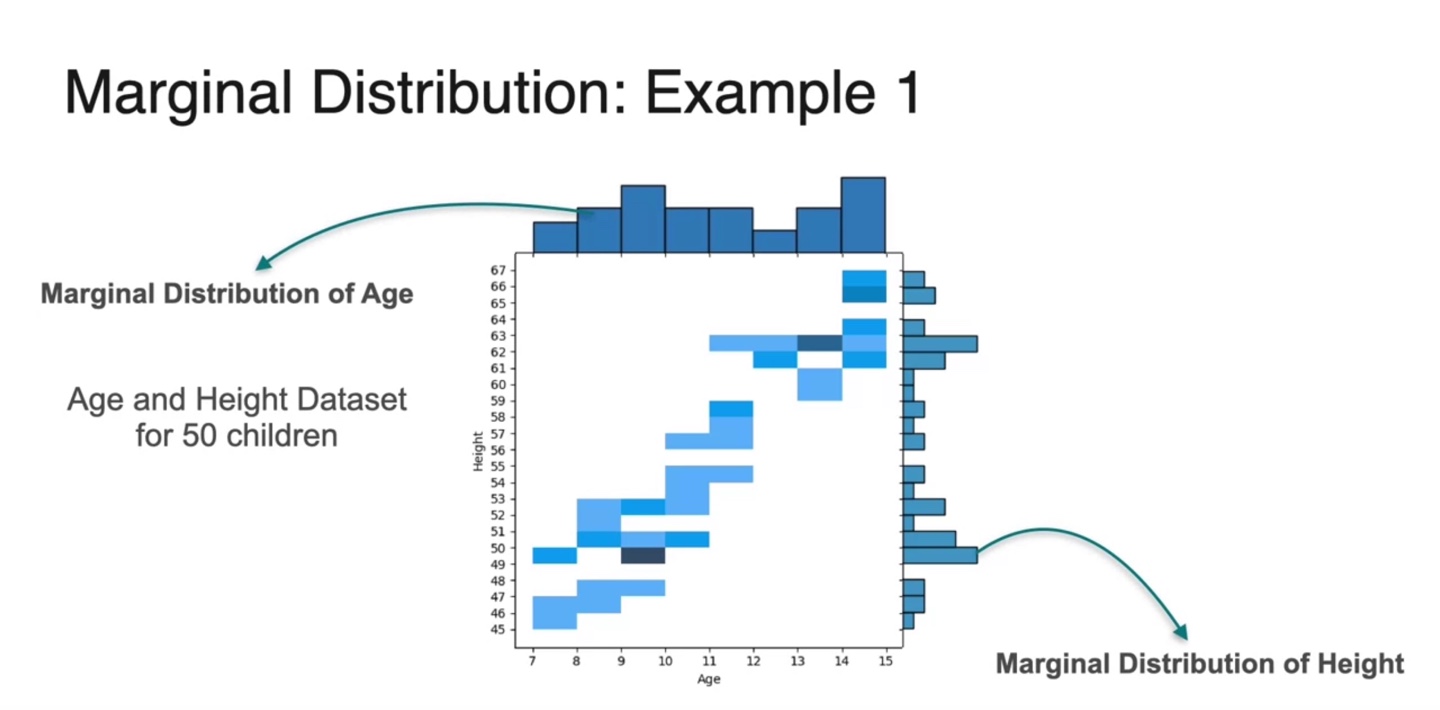
- 50명의 학생들의 Age와 Height dataset을 scatter plot 하면 아래와 같이 나타난다.
-
만일 Marginal Distribuion을 구하고자 한다면 각 축을 기준으로 probabilities를 더하여 bar chart화 하면 된다.
- 위 예제에서는 Marginal Dist. of Age와 Marginal Dist. of Height가 각각 구해진다.
-
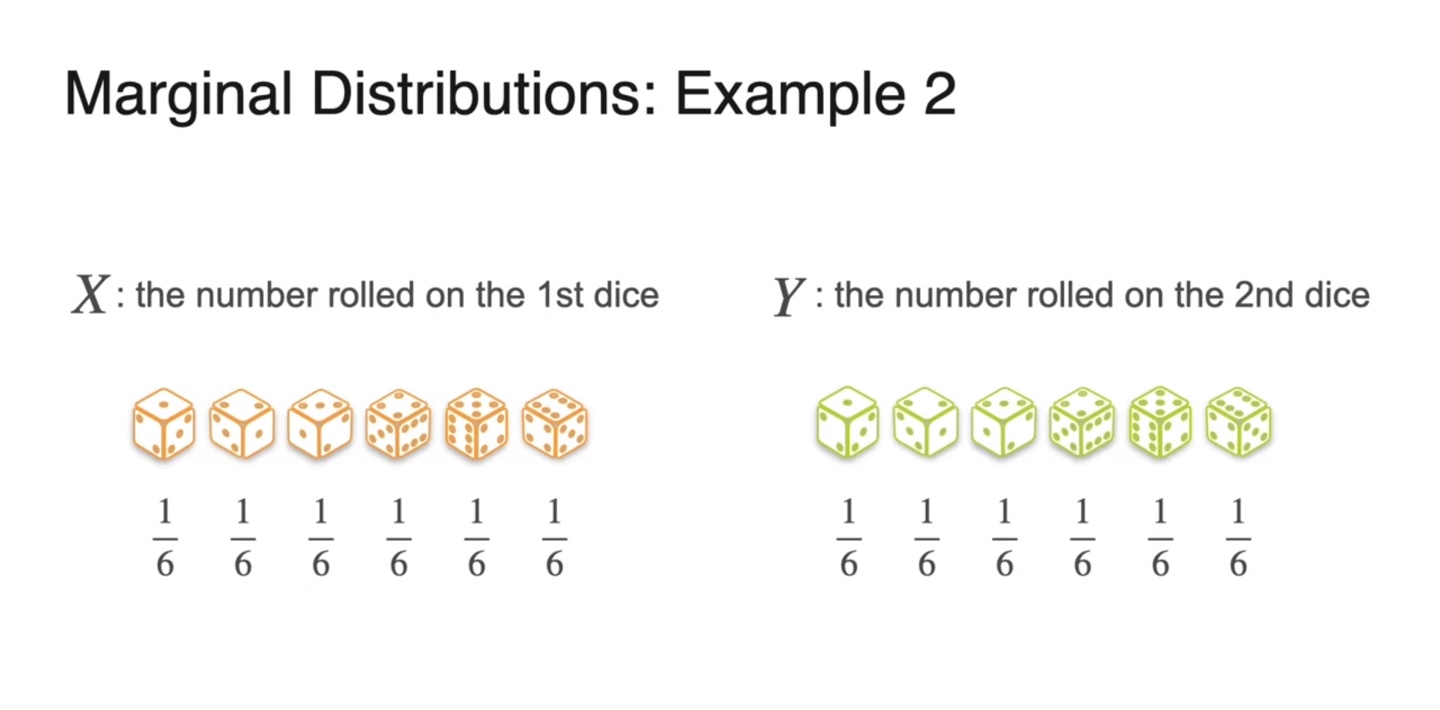
이번에는 1번 주사위를 굴렸을 때의 number를 확률 변수 , 2번 주사위를 굴렸을 때의 number를 확률 변수 로 설정해보자.
- 각 number의 확률은 모두 동일하게(uniformaly) 의 확률을 갖는다.
-
이제 Joint distribution을 통해 각 변수 와 의 Marginal distribution을 구해보자.
-
두 변수는 독립적이므로 각각의 조합을 통해 얻어진 joint distribution의 probability는 모두 이었다.
- 이를 각 변수 와 로 projection 내려 probabilities를 모두 합하면 의 uniform 분포가 얻어진다.
-

-
이번에는 1번 주사위를 굴렸을 때의 number를 확률 변수 , 2번 주사위까지 굴린 뒤 1번과 2번 주사위 numbers의 합을 확률 변수 로 설정해보자.
- 이제는 두 변수가 독립적이지 않다.

-
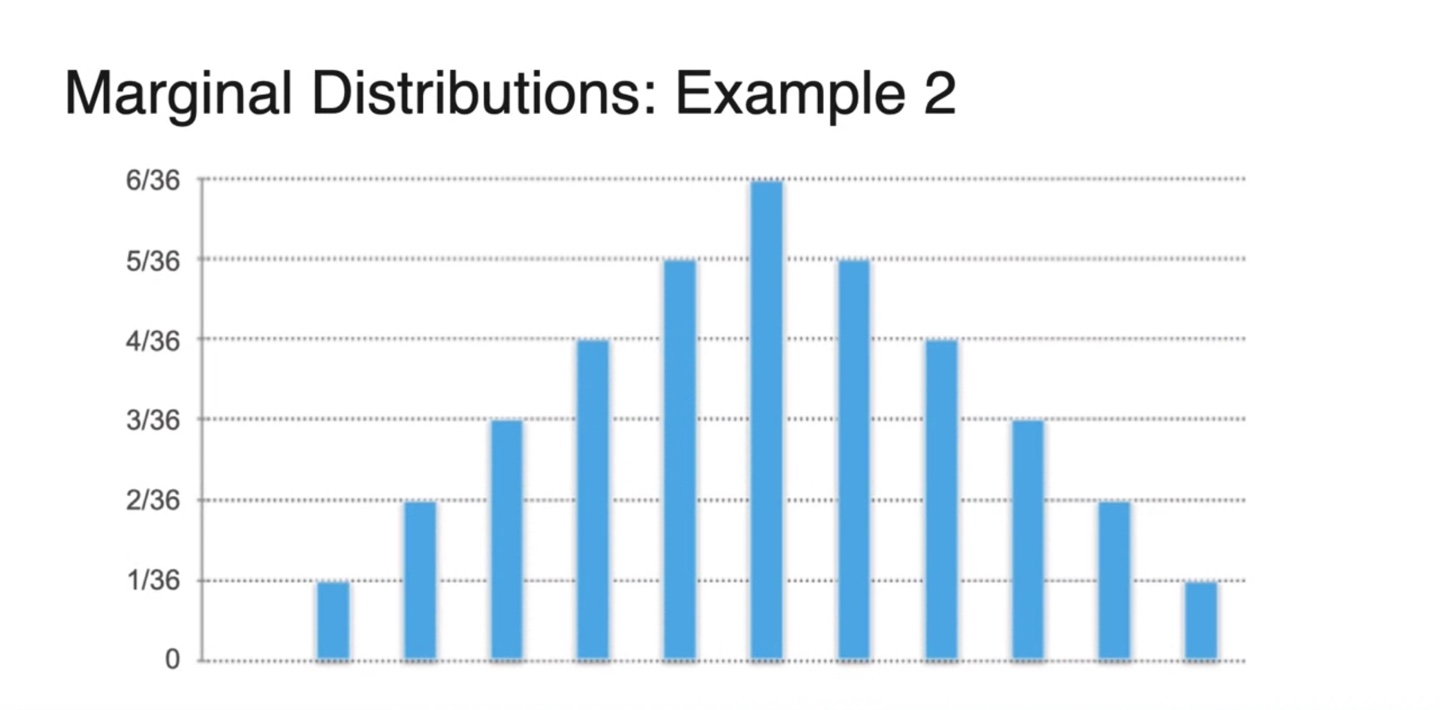
확률 변수 의 Marginal distribution은 기존 Joint distribution을 y축 기준으로 projection 내려 구해지는 모든 probabilities를 합한 값이다.
- 즉, 확률 변수 의 분포를 무시하여 얻어지는 만의 확률이다.

-
이 예제는 discrete random variables에 대한 marginal distribution을 구하는 과정이다.
- 당연하게도 한 확률 변수에 대한 모든 확률의 합은 1이어야 한다. (아래 bar들의 면적의 합 = 1)
-
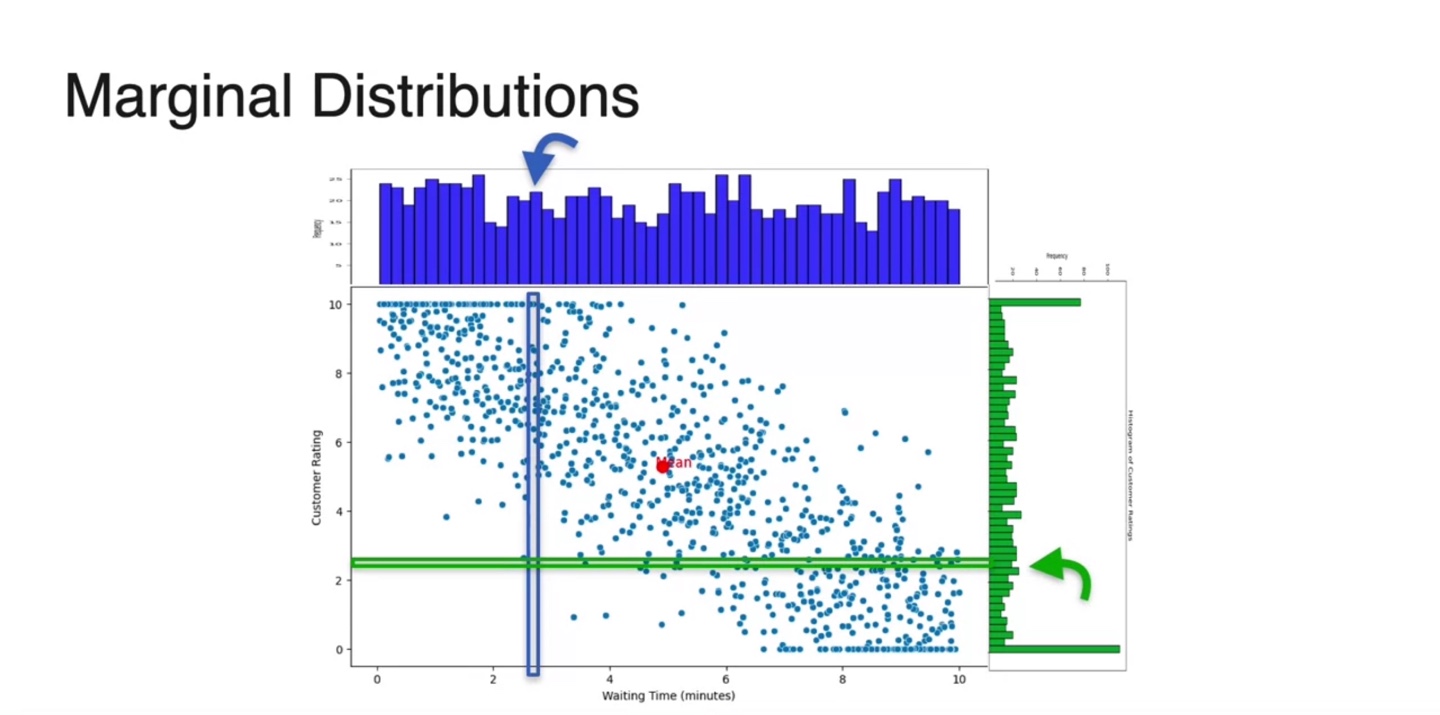
Continous random variables의 joint distribution은 아래와 같은 scatter plot으로 그려진다.
- 이 또한 마찬가지로 각 축(확률 변수)을 기준으로 projection내려 얻어지는 probabilities를 모두 더하여 histogram화 한다.
-
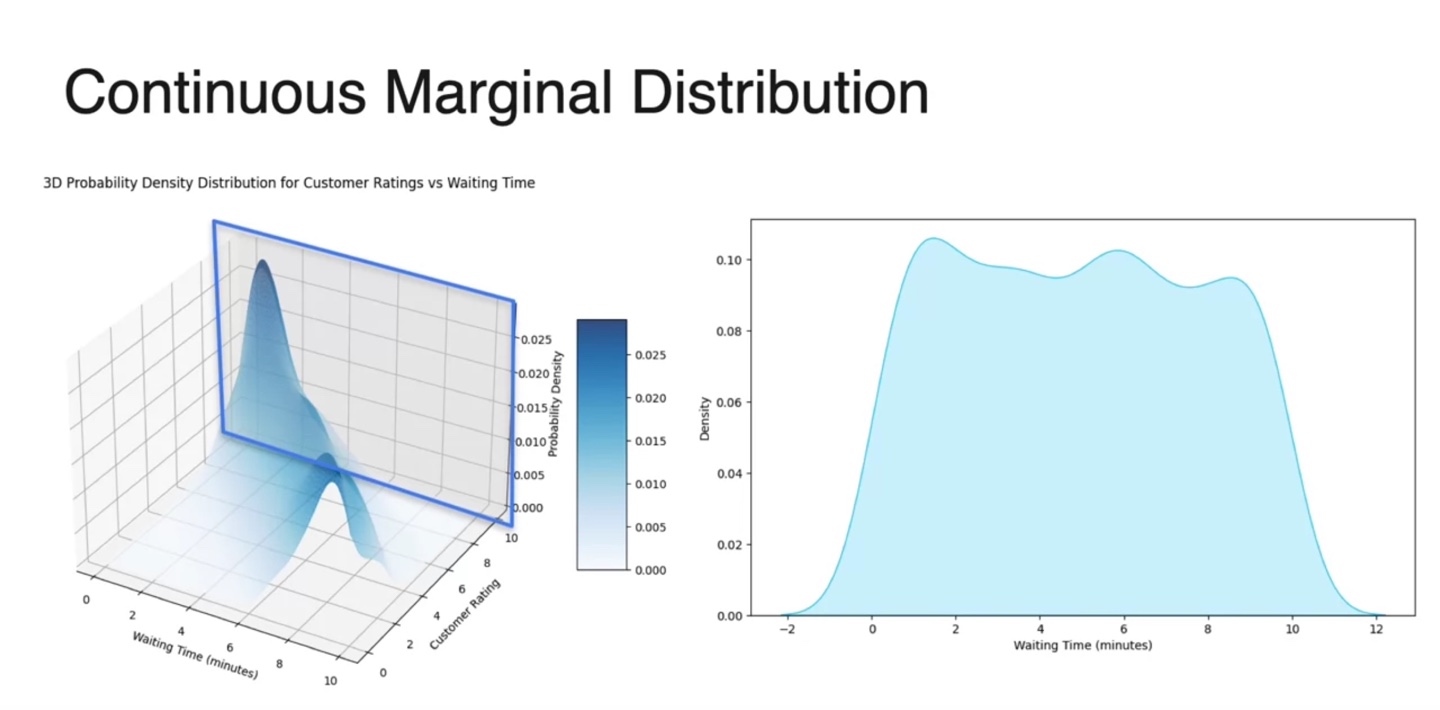
3차원 Probability Density Ditribution(PDF)에서 Marginal distribution을 구하고자 한다면, 2차원 projection을 내려 plotting하면 된다.
-
Waiting Time()의 marginal 분포는 Customal Rating() 변수를 무시하고 얻어지는 모든 probabilities의 합이다.
- 따라서 축을 없앤 아래 네모칸 2차원 평면이 Marginal Dist. of Waiting Time()이다. (not normalizing yet)
-
Conditional Distribution
-
Age()와 Height() 예제를 통해 Conditional Distribution에 대해 알아보자.
- 만약 age가 9인 친구들의 height 분포를 알고 싶다면 어떻게 해야할까?

-
수식으로는 의 확률 분포를 알고자 한다고 표현할 수 있다.
- 즉, 인 확률 분포를 알고 싶은 것이므로 테이블을 아래와 같이 잘라 얻어낼 수 있다.

-
그러나 전체 확률의 합이 1을 만족하지 못하므로 row sum으로 각 값을 나눠주어 normalizing한다.
-
만약 일 때 가 49인 값을 찾고자 한다면 를 계산한다.
-
이전에 배웠던 Baysian probability 공식에 의해 로 계산되는 것을 알 수 있다.
-
이 때 가 나타내는 값이 normalizing에 쓰이는 row sum이고, 이를 통해 확률을 계산하면 이다.
-
-

-
Discrete Conditianal Distribution을 일반화하면 로 표현한다.
- 이 때 이 Conditional PDF, 이 Joint PDF, 이 Marginal PDF다.

-
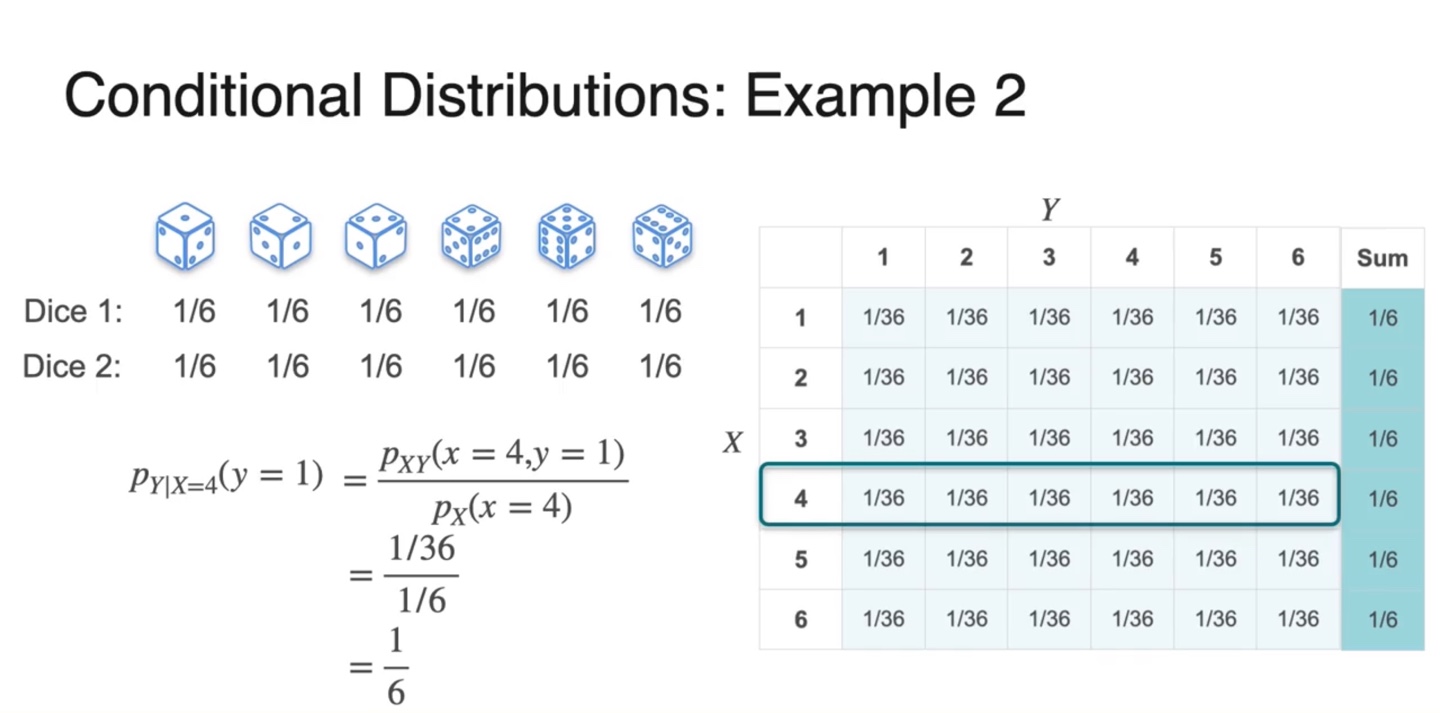
두 주사위의 number를 확률 변수로 갖는 예제에서 Conditional distribution을 구해보자.
- , joint/marginal 이다.
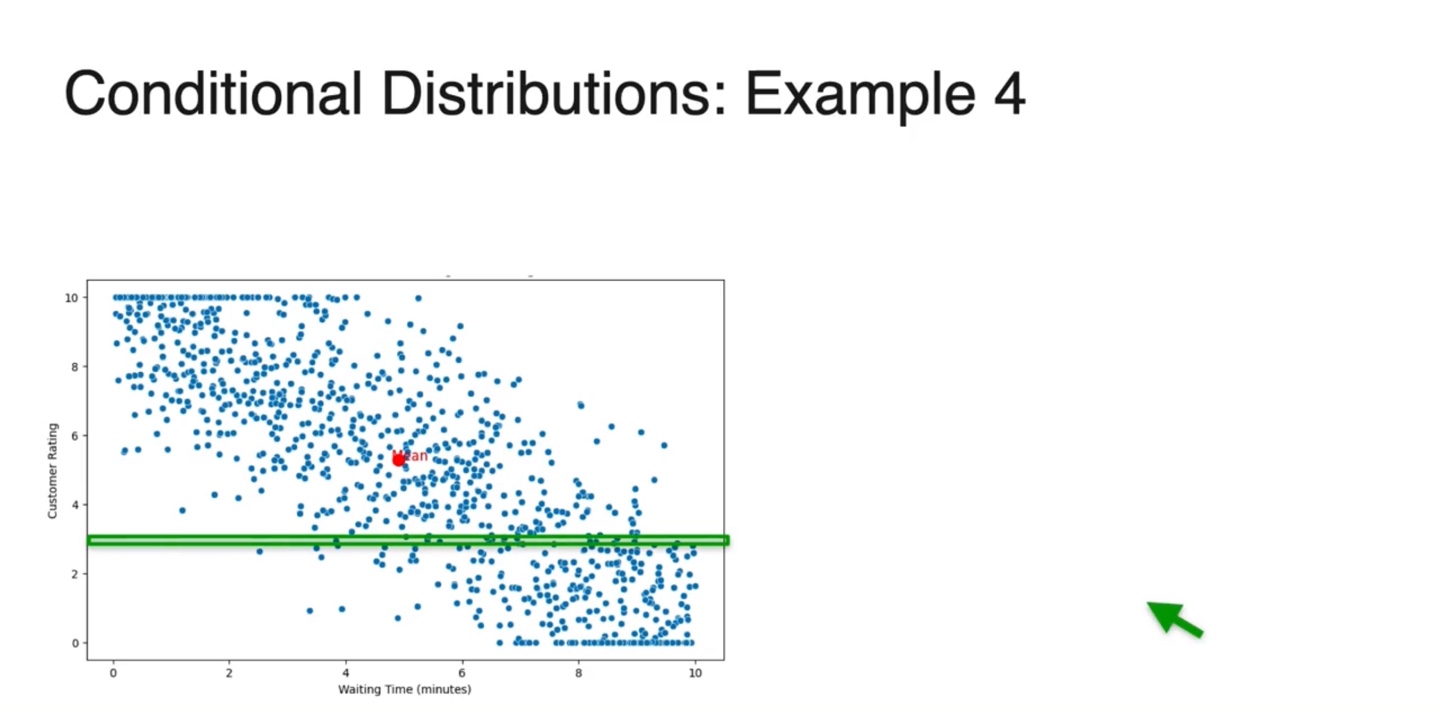
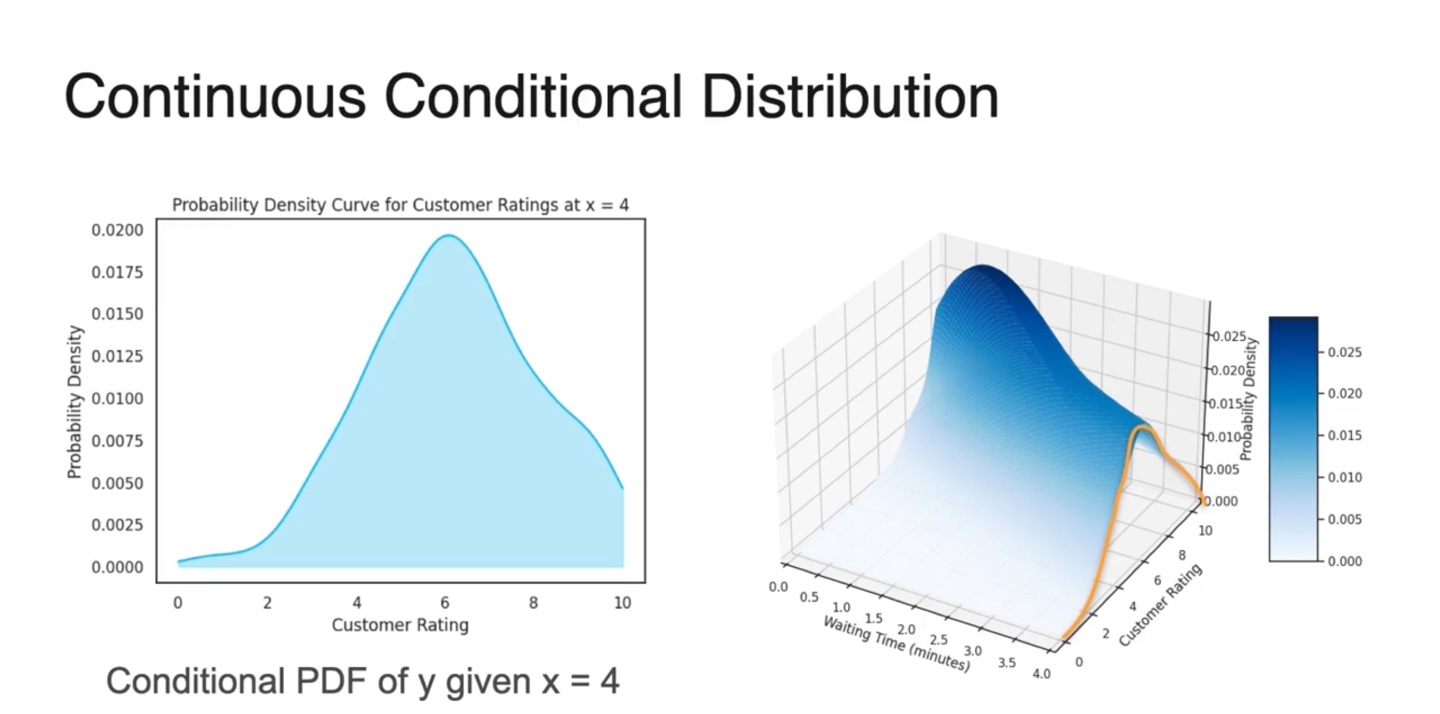
- Continuous Conditional Distribution은 아래와 같은 scatter plot의 한 축을 기준으로 수직선화하여 얻을 수 있다.
- 3차원 분포에서 conditional distribution을 구하고자 한다면 Waiting Time() 확률 변수의 constant값(현재 4)을 기준으로 cutting한다.
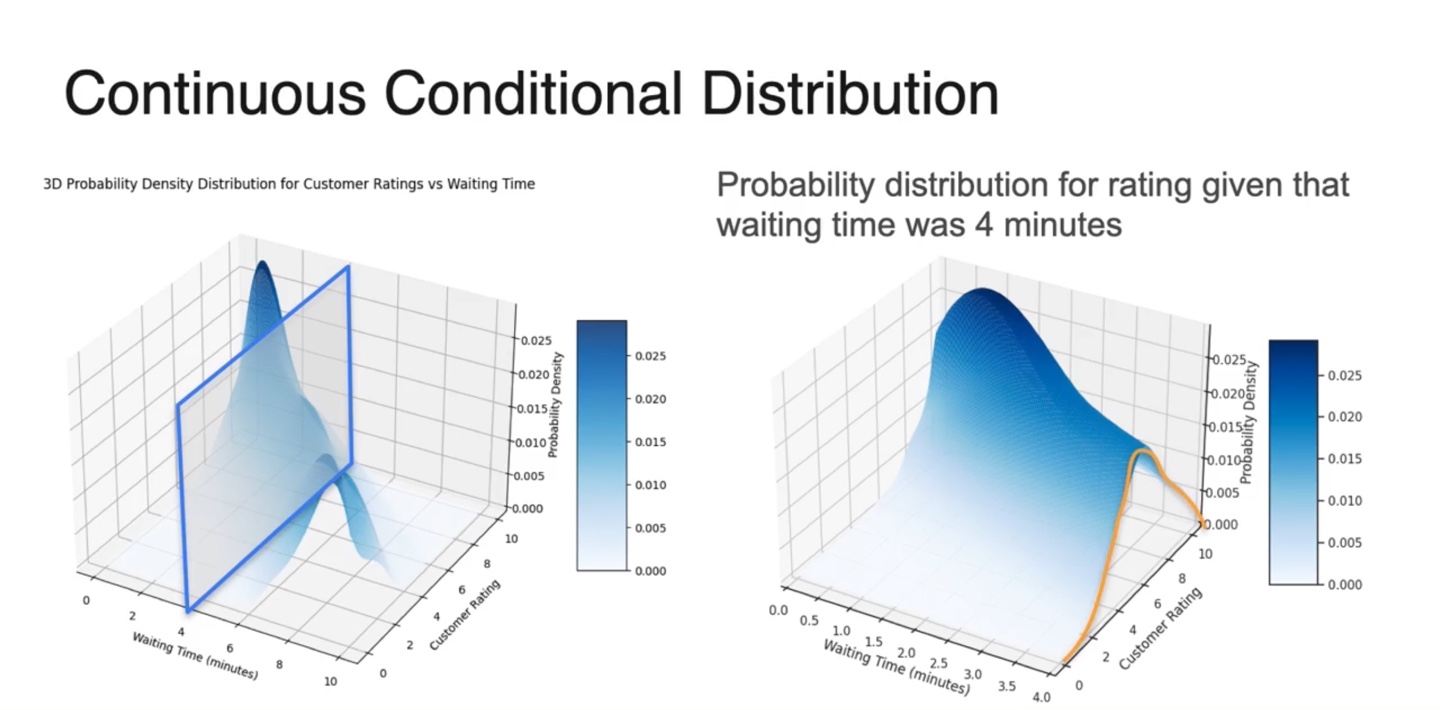
- 이 때 얻어진 2차원 분포 (노란선)가 바로 conditional distribution이다.
-
Continuous Conditianal Distribution을 일반화하면 로 표현한다.
- 이 때 이 Conditional PDF, 이 Joint PDF, 이 Marginal PDF다.

Covariance of a Dataset
-
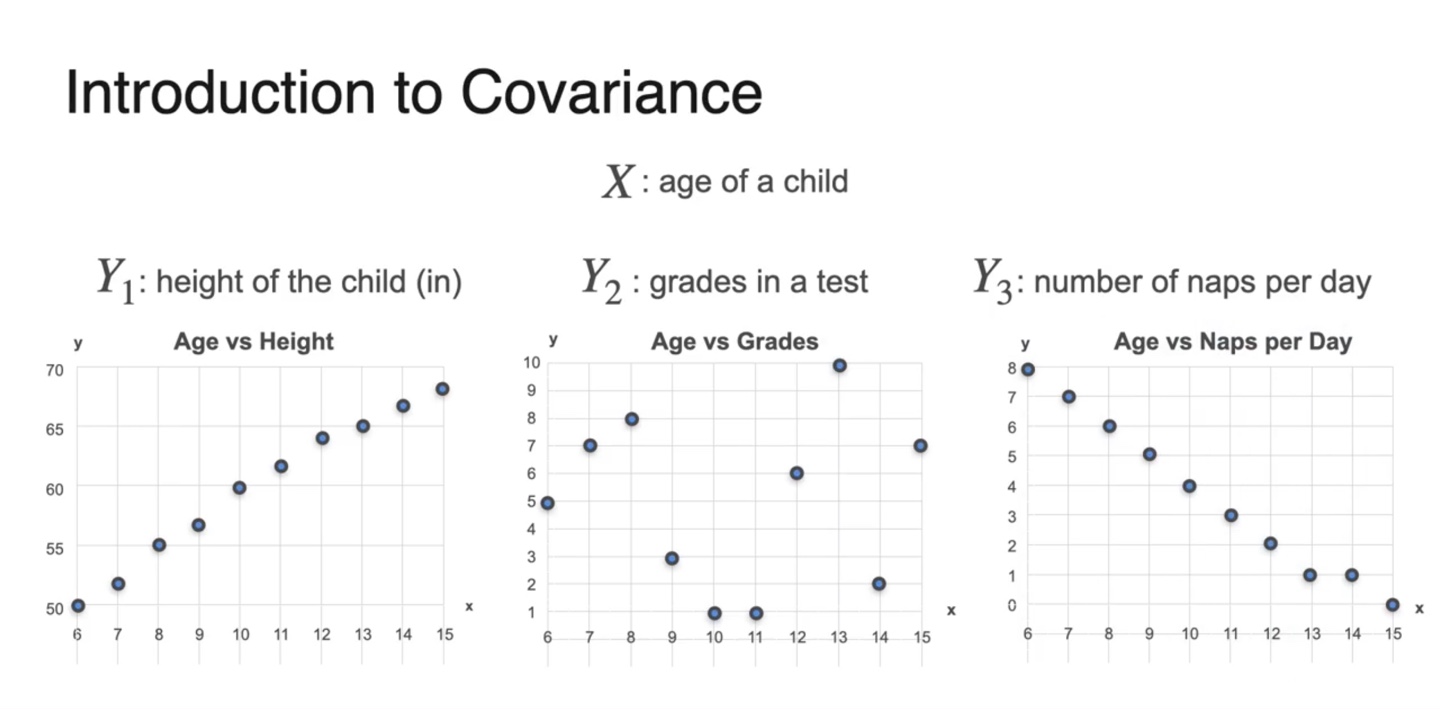
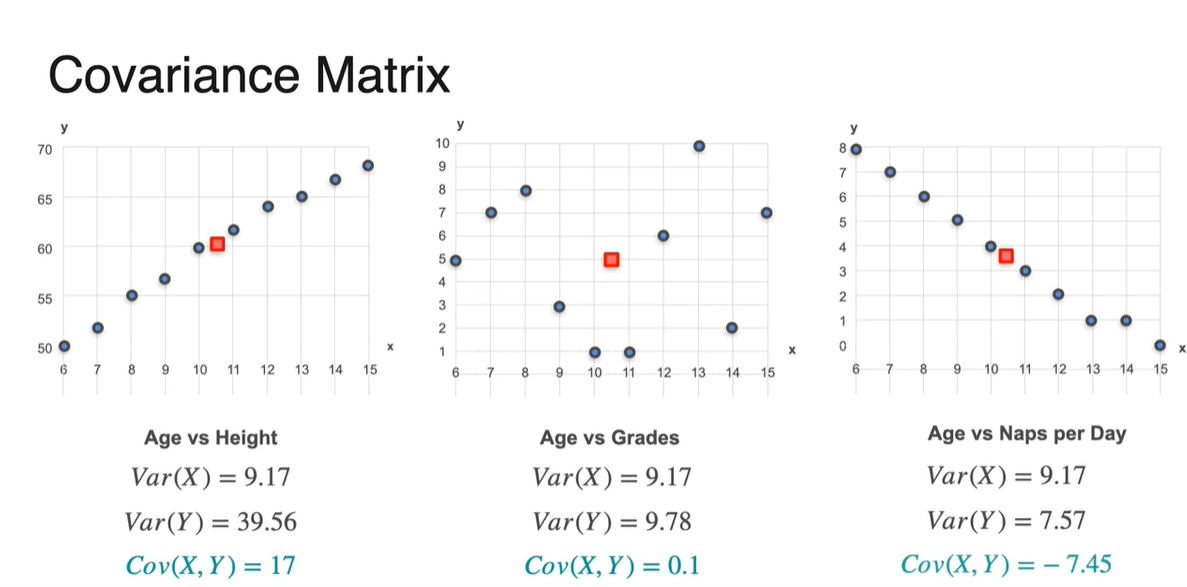
만일 학생들의 나이(age)를 확률 변수 로, 키(height)를 , 성적(grades)을 라 하자.
- variables와 의 관계를 비교할 수 는 방법이 있을까?

-
Scatter plot으로 나타내면 아래와 같이 그래프가 그려진다.
- 각 변수들은 어떤 관계를 가질지 그래프 모양을 바탕으로 추측해보자.
-
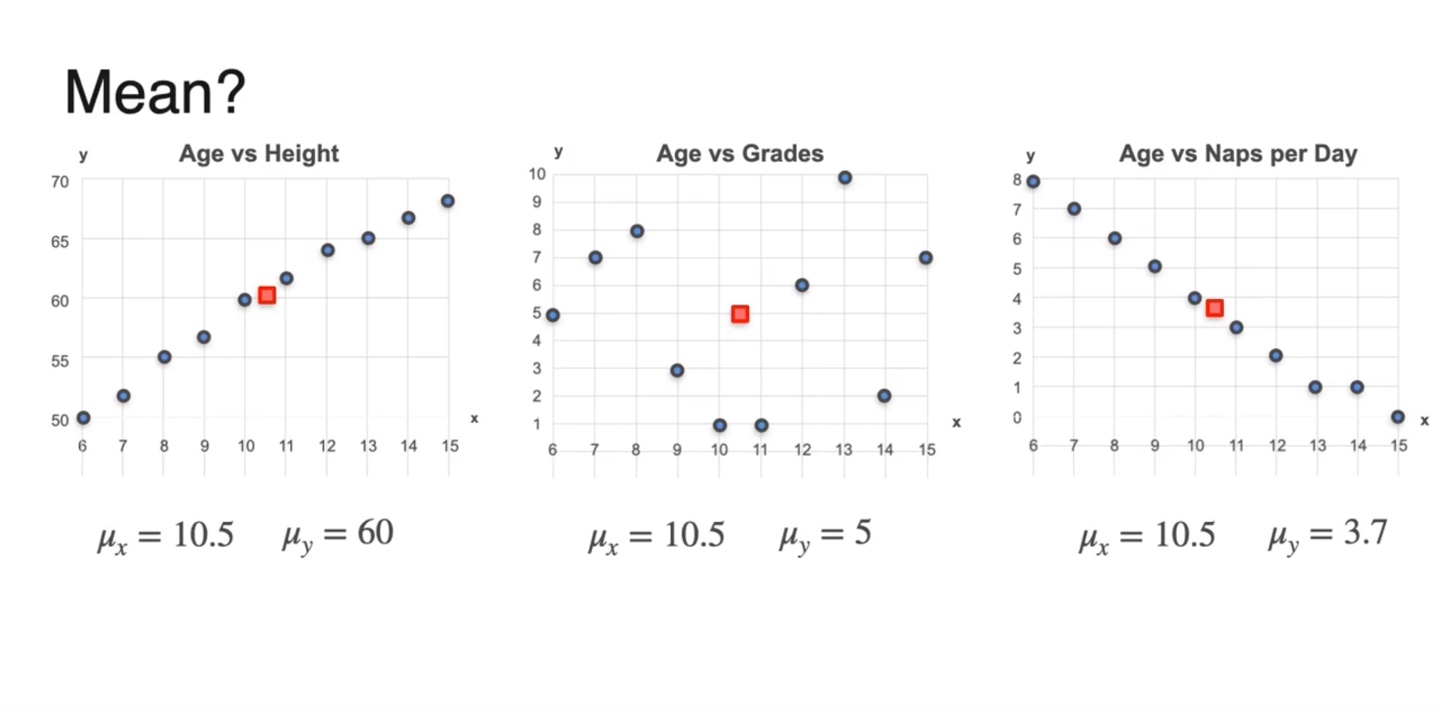
두 변수 와 variables의 평균(mean)을 구하여 빨간 점에 나타내었다.
- 는 같은 변수이기 때문에 expected value가 10.5로 동일하다.
-
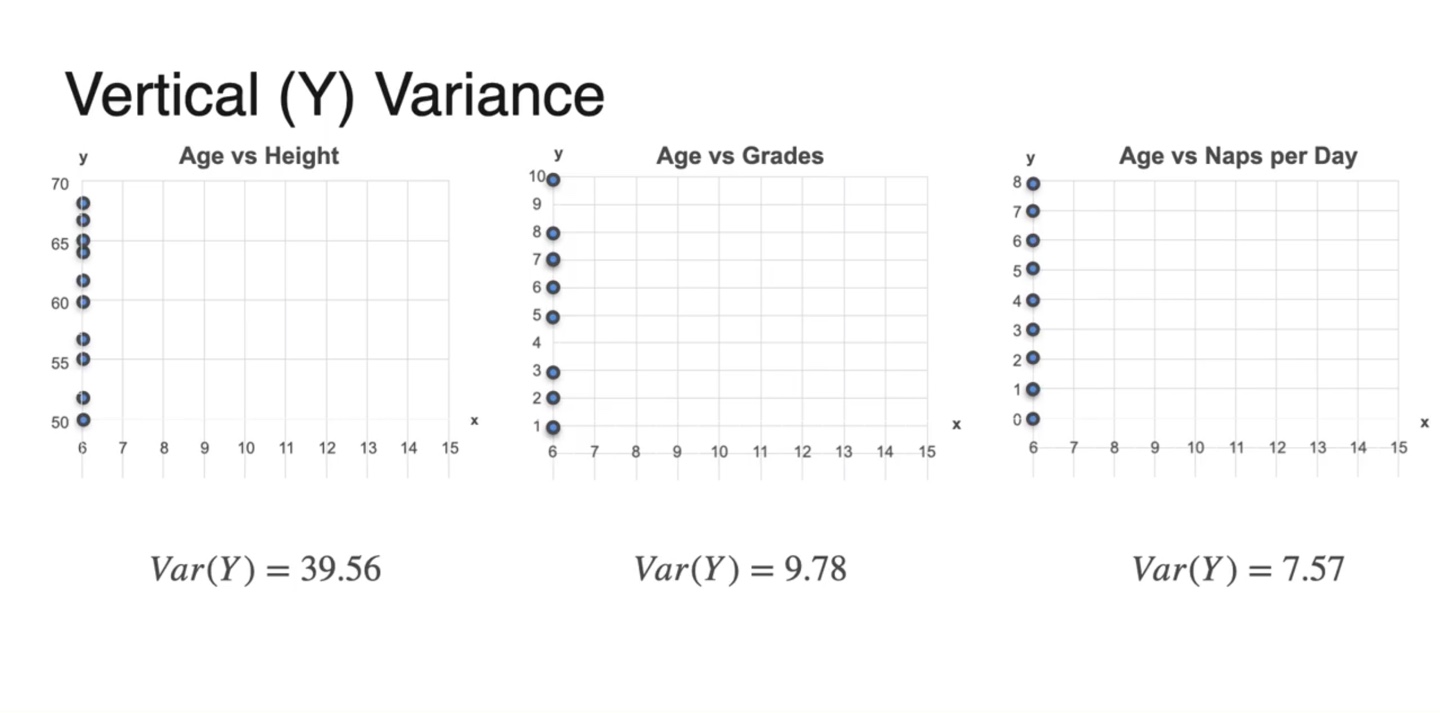
의 Variance는 marginal distribution을 통해 시각화할 수 있다.
- Height의 variance가 제일 크며 grades, naps per day 순이다.
-
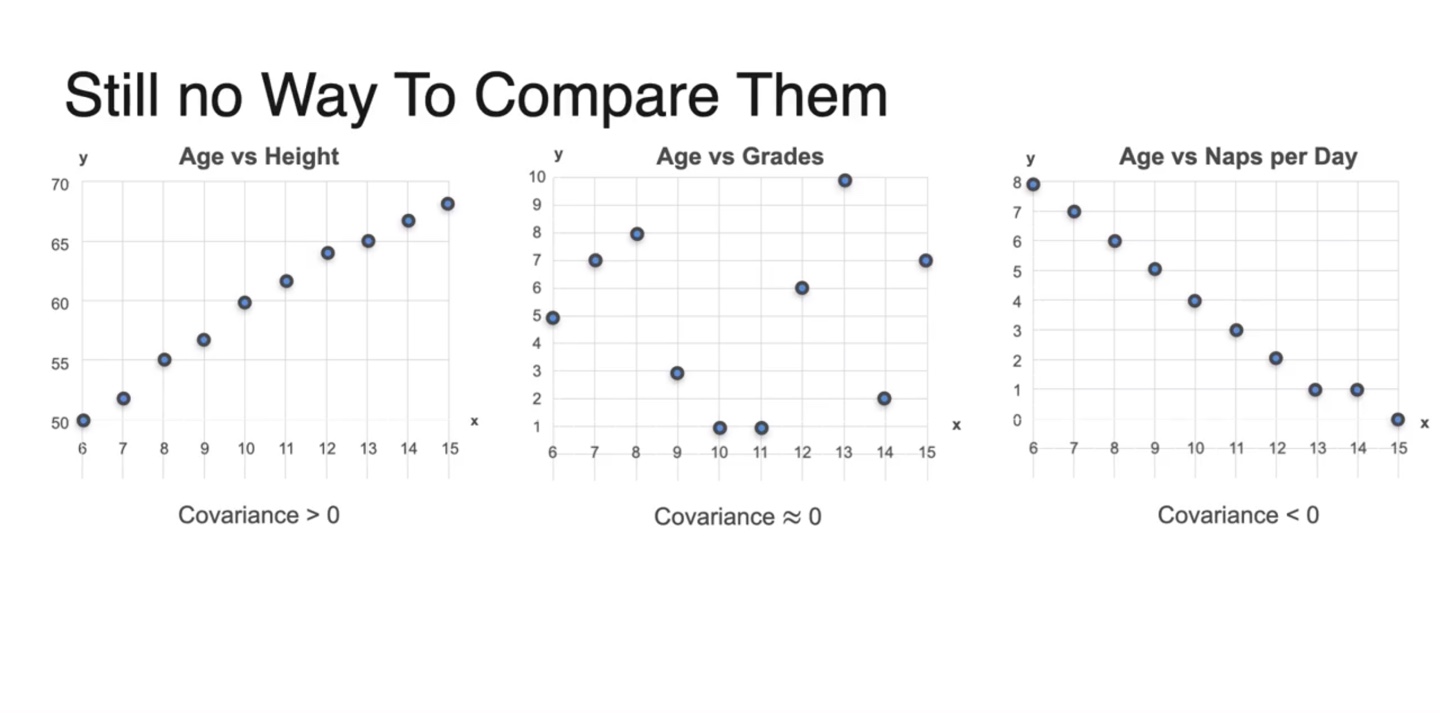
이제 Covariance를 통해 비교해보자.
- 결론부터 말하자면 age와 height는 covariance가 +를, grades는 0에 가깝고, naps per day는 -의 covariance를 갖는다.
- 본격적으로 Covariance를 구하기 위해서는 아래 두 steps를 거쳐 구해져야 한다.
- 결론부터 말하자면 age와 height는 covariance가 +를, grades는 0에 가깝고, naps per day는 -의 covariance를 갖는다.
-
첫 번째 step은 모든 데이터셋을 평균이 0, 분산이 1인 범위로 normalizing한다.
- 데이터 축의 중앙값이 (0, 0)이 되게끔 만드는 것이다.
-
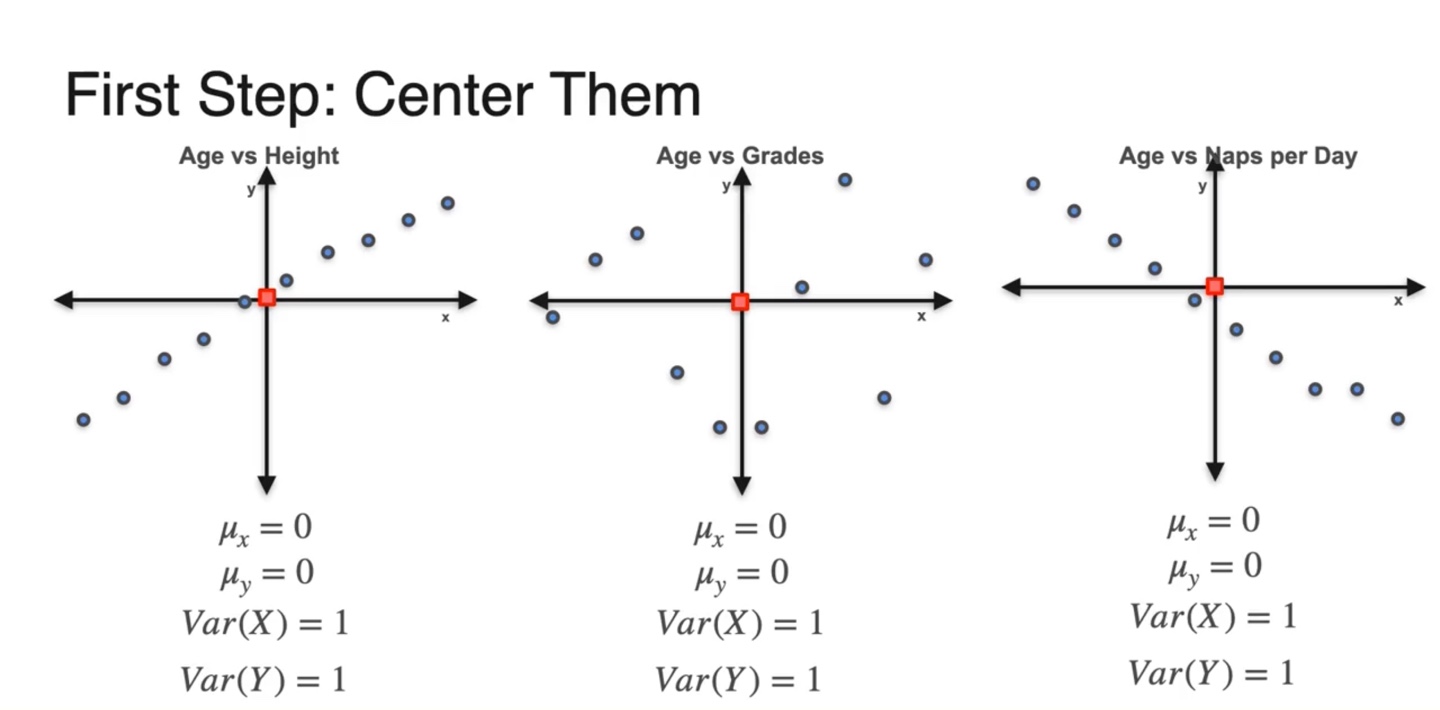
두 번째 step은 데이터를 모두 오른쪽으로 swipping한다.
-
직관적으로 해석하자면 age와 height의 분포는 증가하는 변화를 가지며 age와 naps per day의 분포는 감소하는 변화를 가진다.
- 그에 비해 age와 grades의 분포는 증가도 감소도 아닌 변화를 가진다.
-
-
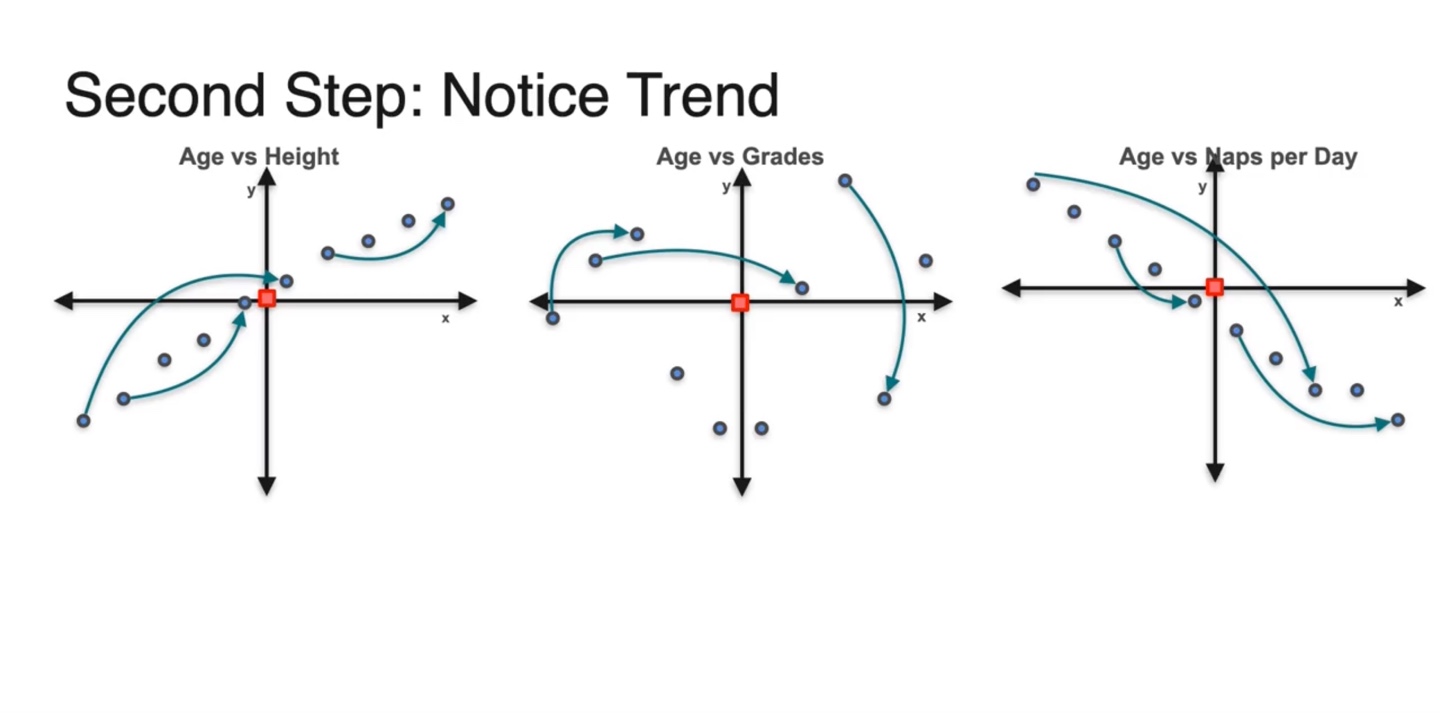
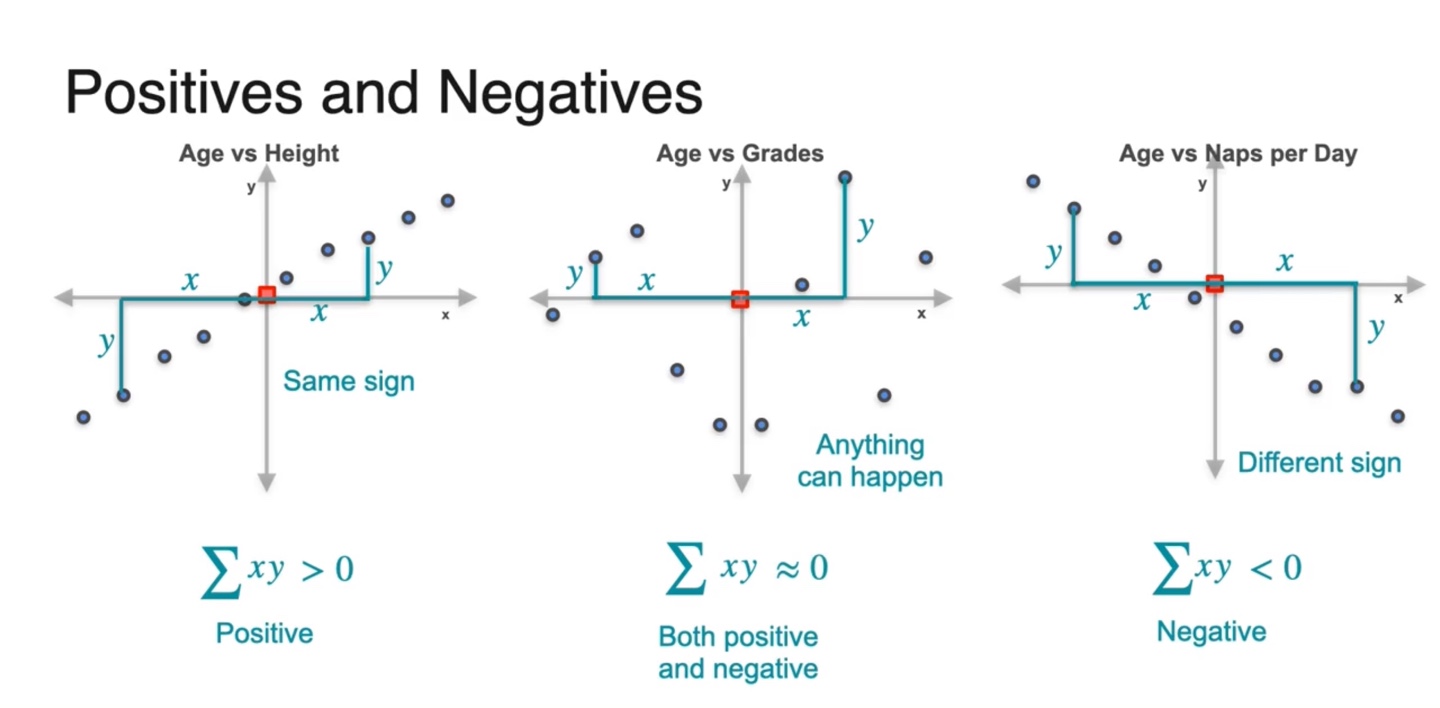
즉, 중심으로부터 떨어진 확률 변수 와 의 변화량이 same sign을 가지기도 하고, different sign을 가지기도 하며, 어떠한 경향성도 없는 값을 가지기도 한다.
- 각 데이터 샘플들의 변화량 와 의 곱이 양수인 것과 음수인 것, 그 무엇도 아닌 것으로 차이가 나타난 것이다!
-
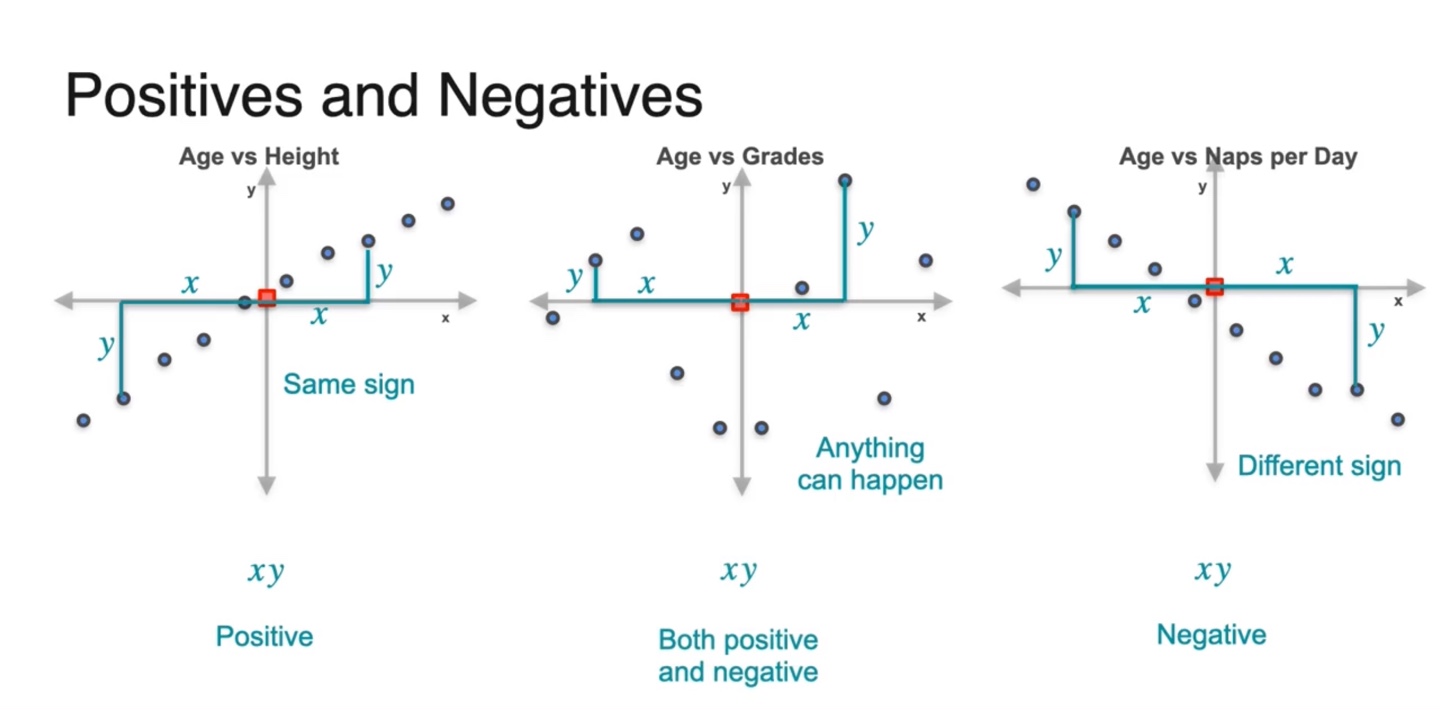
모든 데이터 샘플들의 평균으로부터의 변화량을 곱하여 전부 더해보자.
-
그러면 이러한 값들의 경우의 수는 세 가지로 나뉜다.
- Positive , None , Negative
-
-
Covariance는 모든 데이터 샘플들의 평균으로부터의 차이를 더해서 평균낸 값이다.
- , ... 정확하게는 으로 나타낸다.
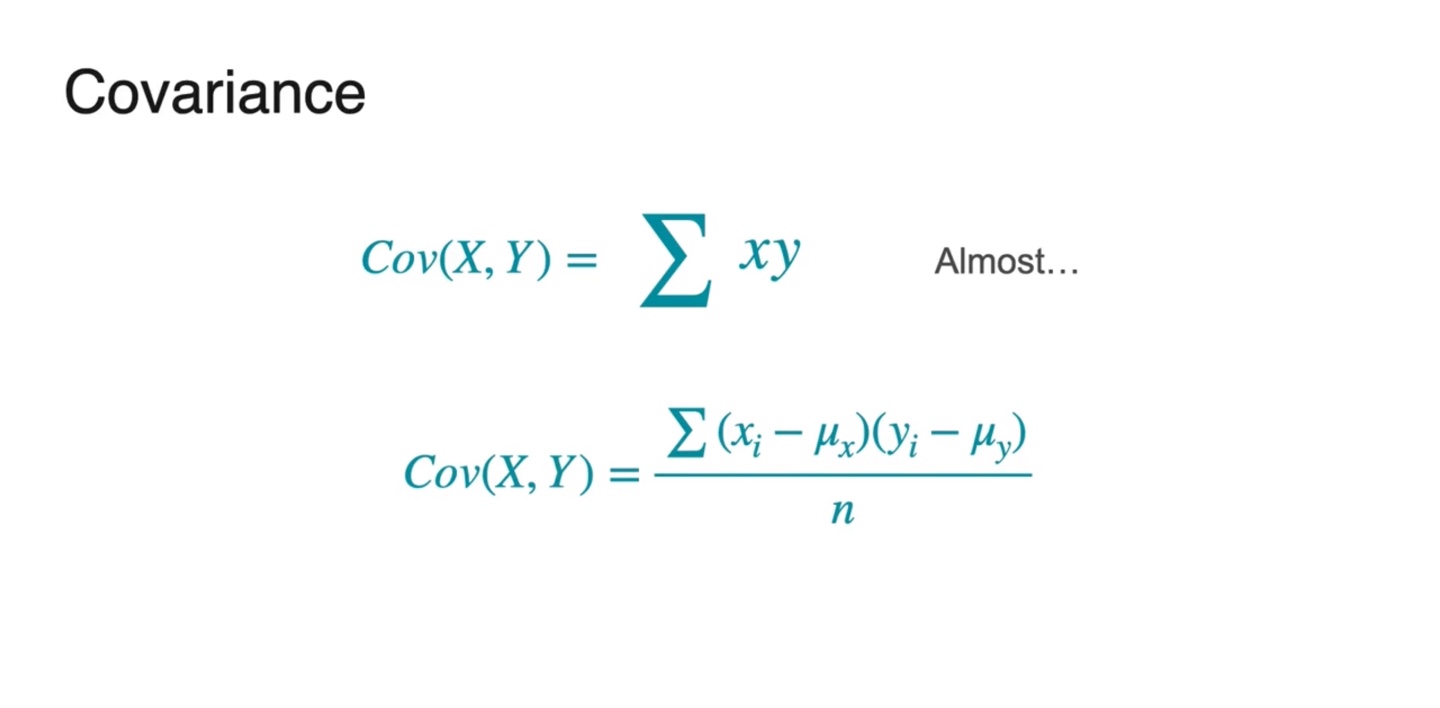
-
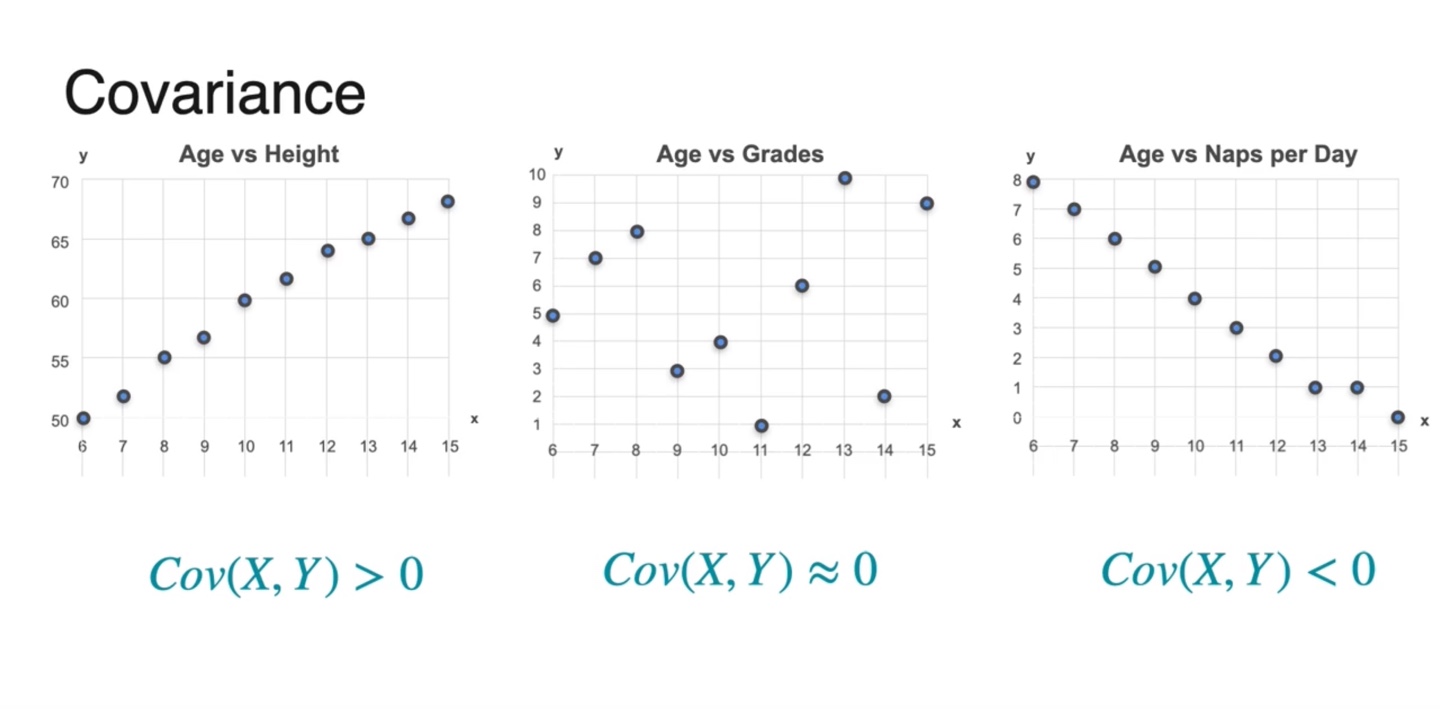
즉, 의 부호에 따라 데이터 샘플의 분포 경향성이 달라진다.
- 면 양의 상관관계, 이면 음의 상관관계, 이면 어떠한 관계도 가지지 않는 관계임을 알 수 있다.
-
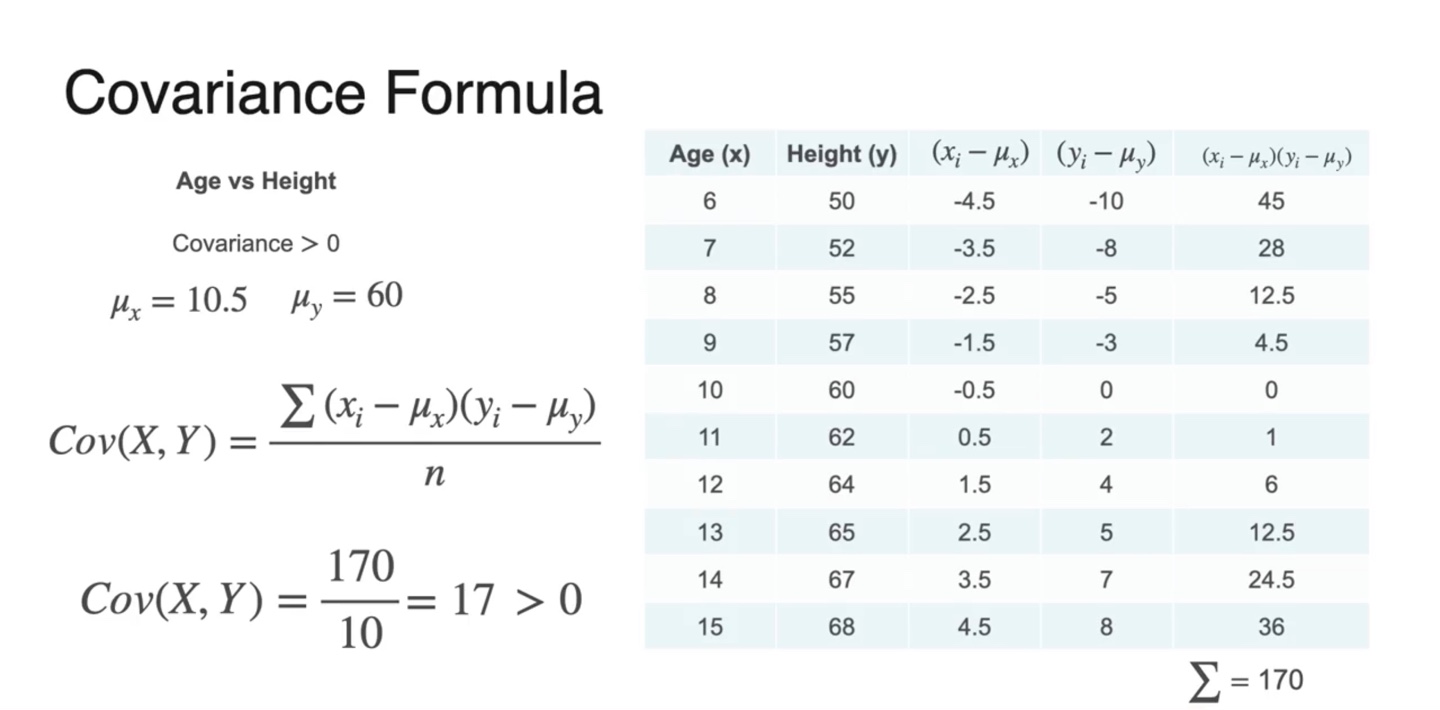
몇 가지 샘플들의 실제 Covariance 계산은 아래와 같이 한다.
-
와 를 구해 곱하고 전체 샘플의 수 으로 나눈 결과가 아래와 같다.
- 와 , 인 경우의 수, 총 세 가지 경우의 수가 있다.
-
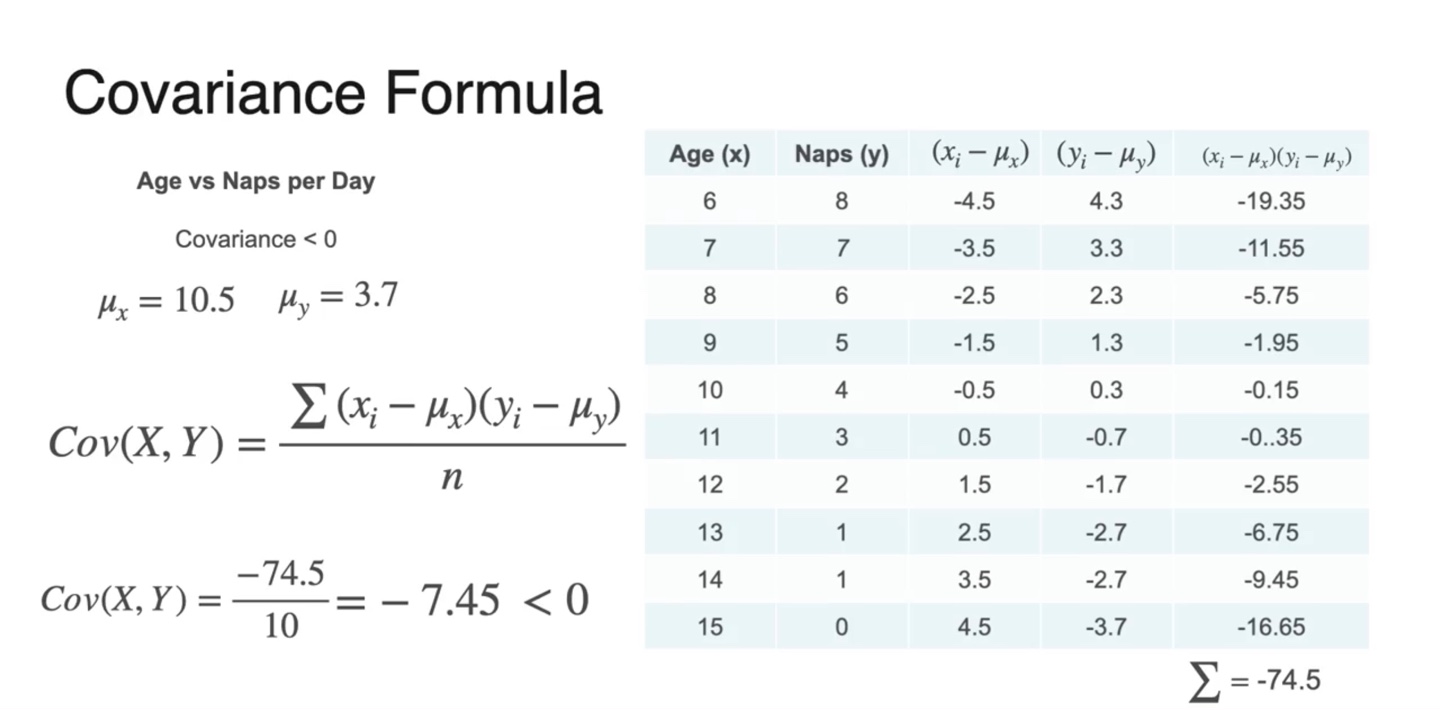
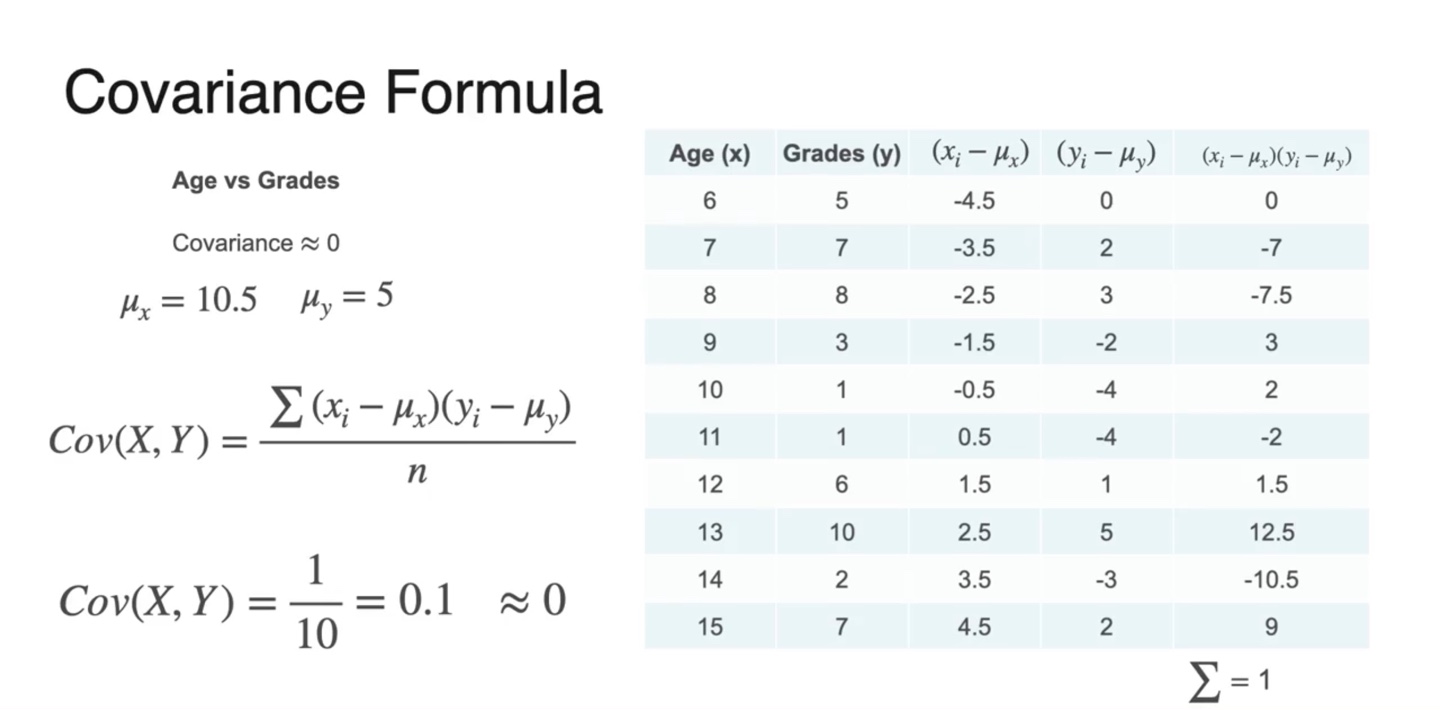
-
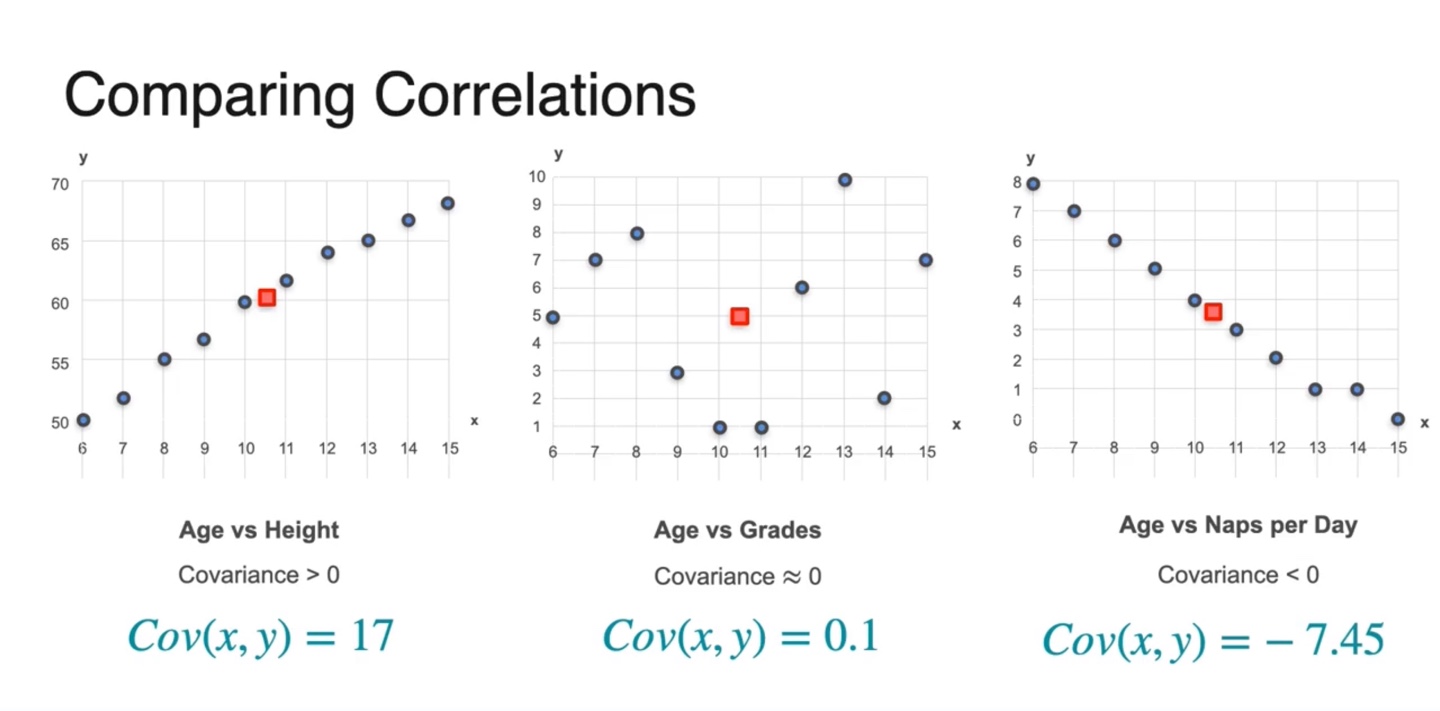
즉, Covariance는 Correlation을 정량적으로 결정해주는 값이다.
- 양수면 비례관계, 음수면 반비례관계, 0에 가깝다면 아무런 관계를 가지지 않는다고 판단하면 된다.
Covariance of a Probability Distribution
-
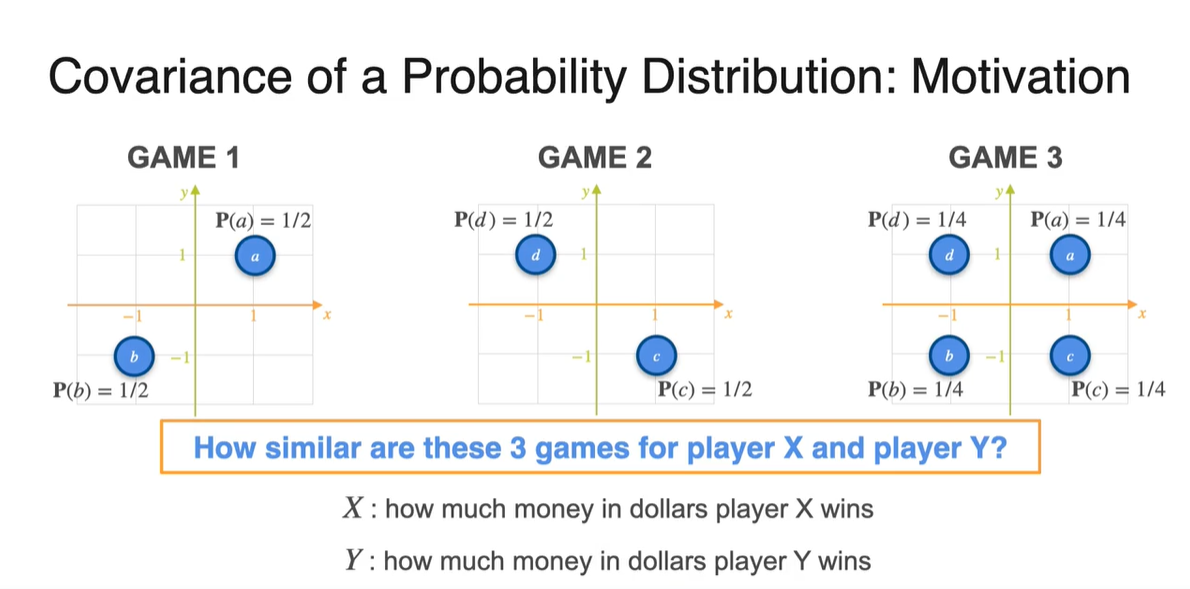
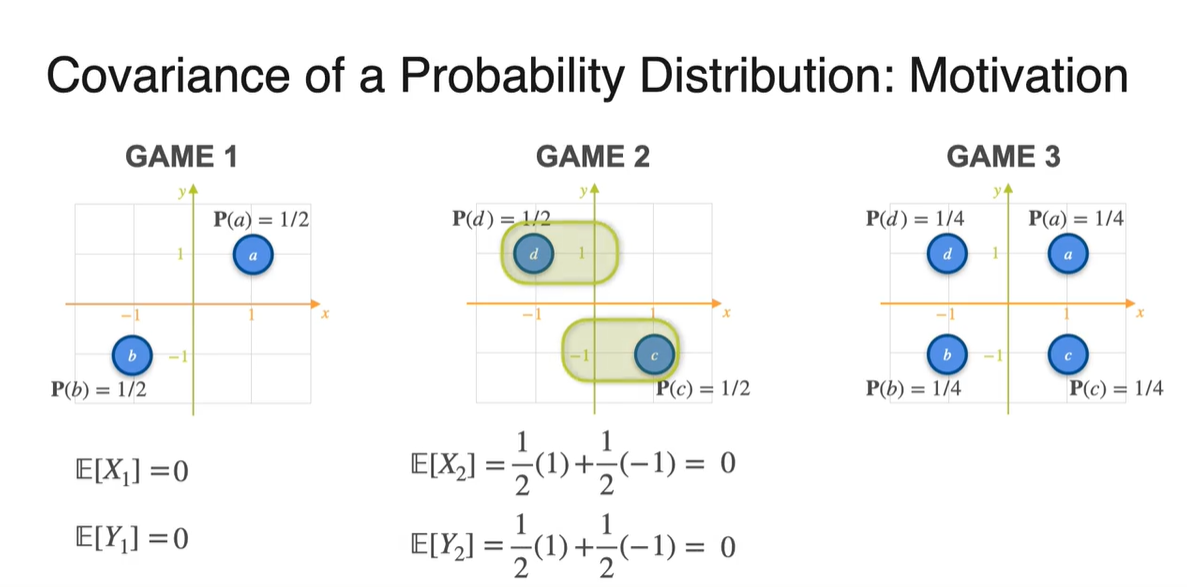
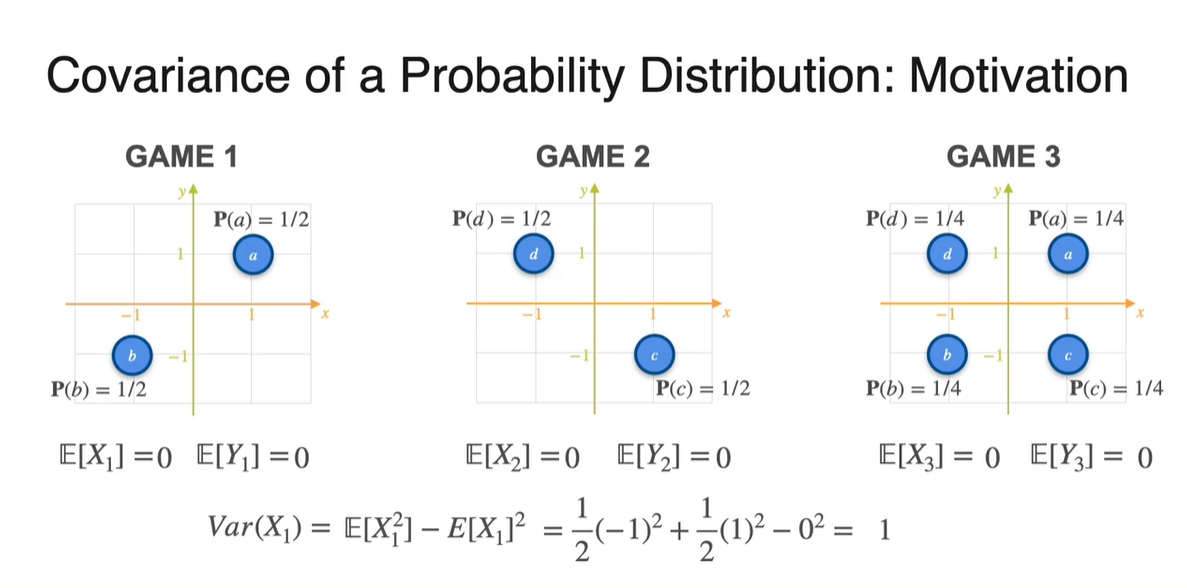
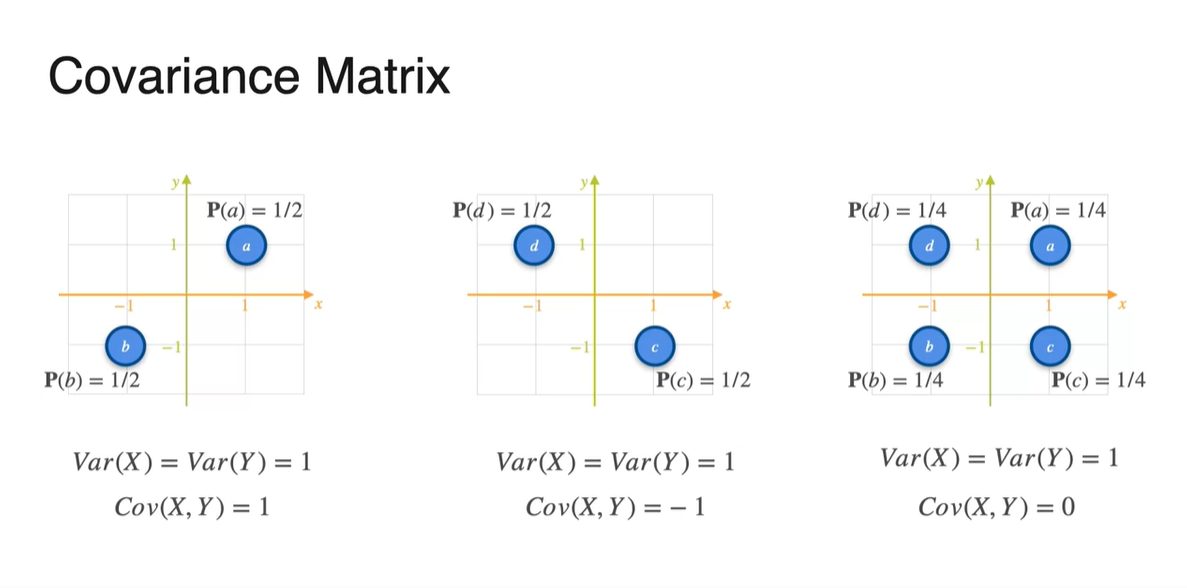
아래와 같은 Game 1, 2, 3의 분포가 주어졌을 때 Covariance를 구해보자.
- 각 경우의 수에 대해 Uniform distribution으로 확률이 주어져 있다.
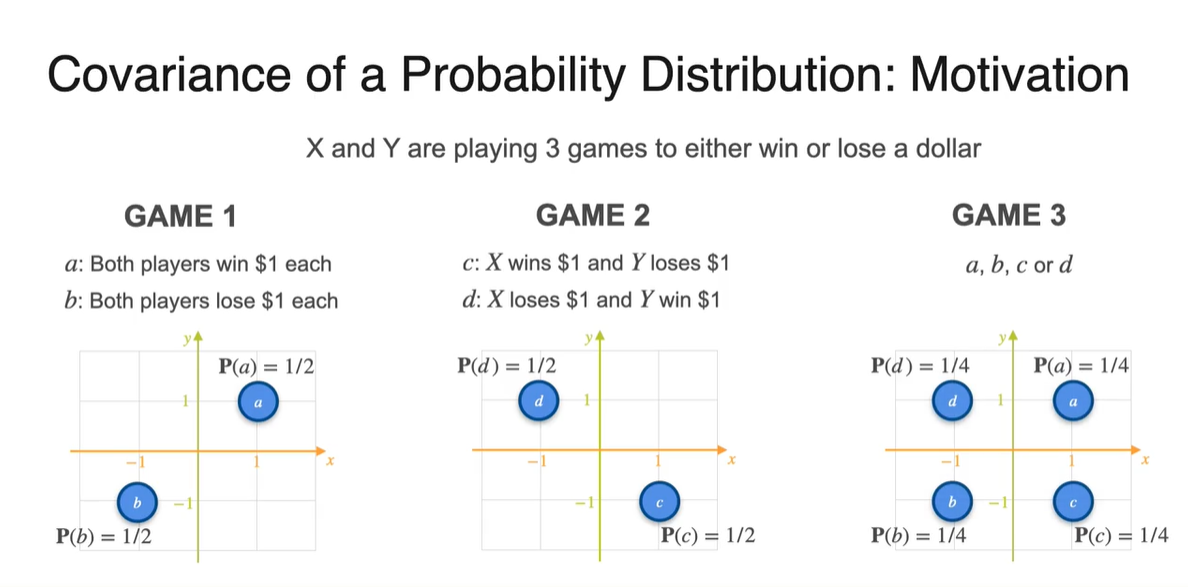
-
는 Player 가 얻게 될 돈이고, 는 Player 가 얻게 될 돈이다.
- 아래 세 가지 분포의 상황에서 Player 와 Player 의 유사성을 어떻게 표현할 수 있을까?
-
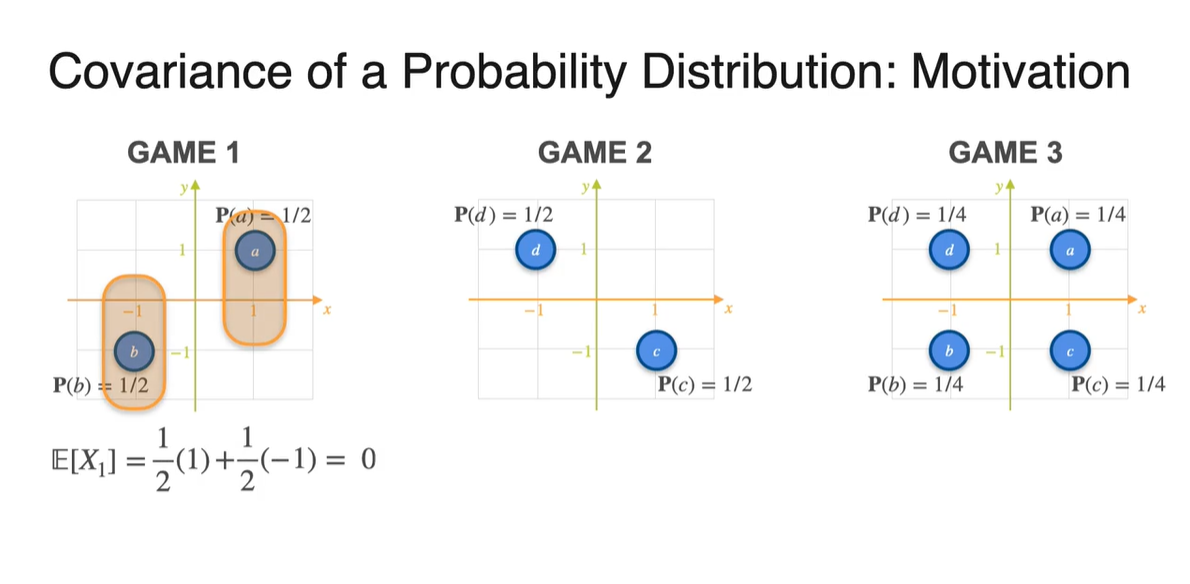
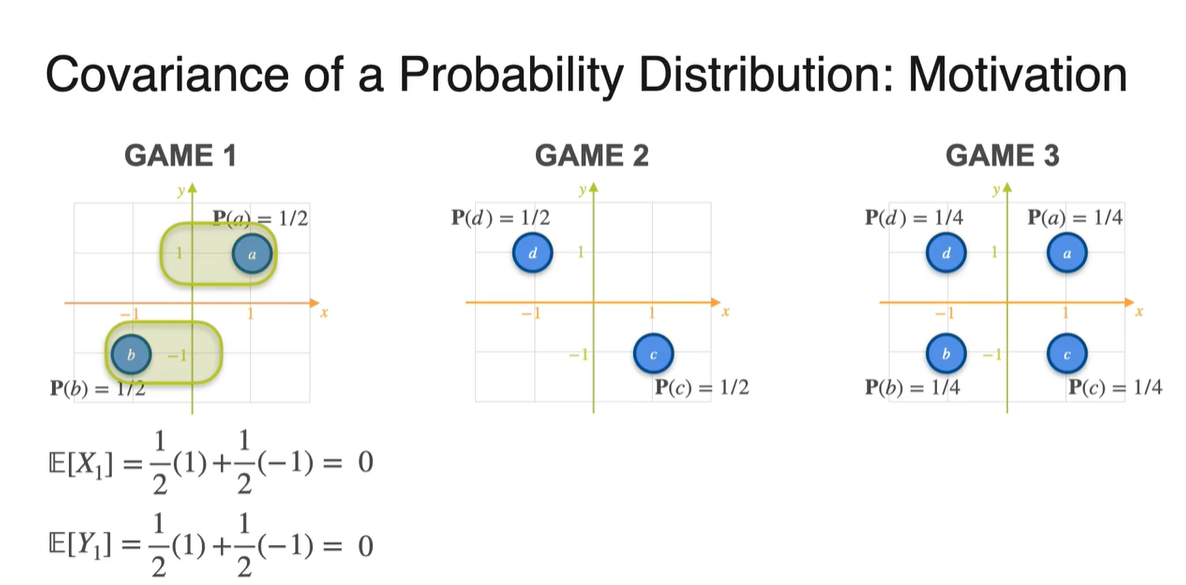
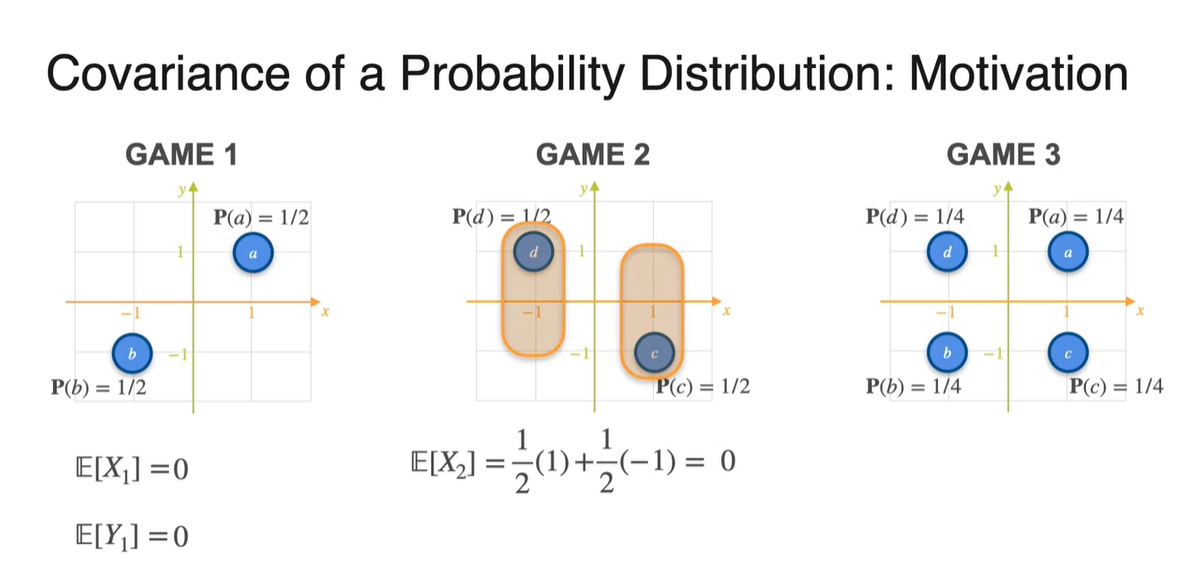
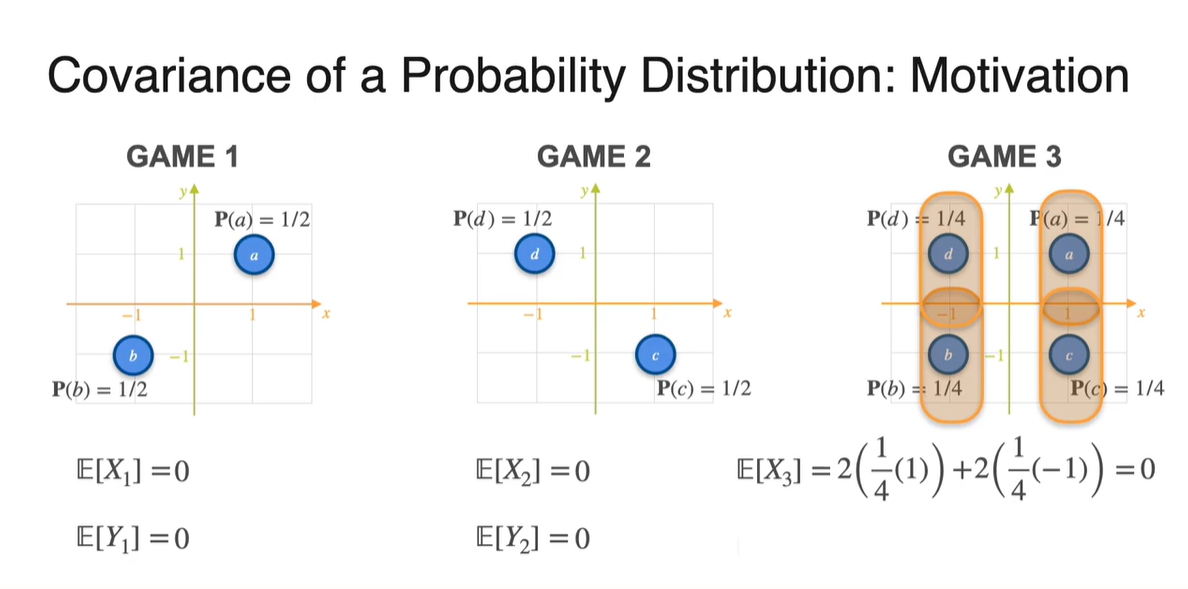
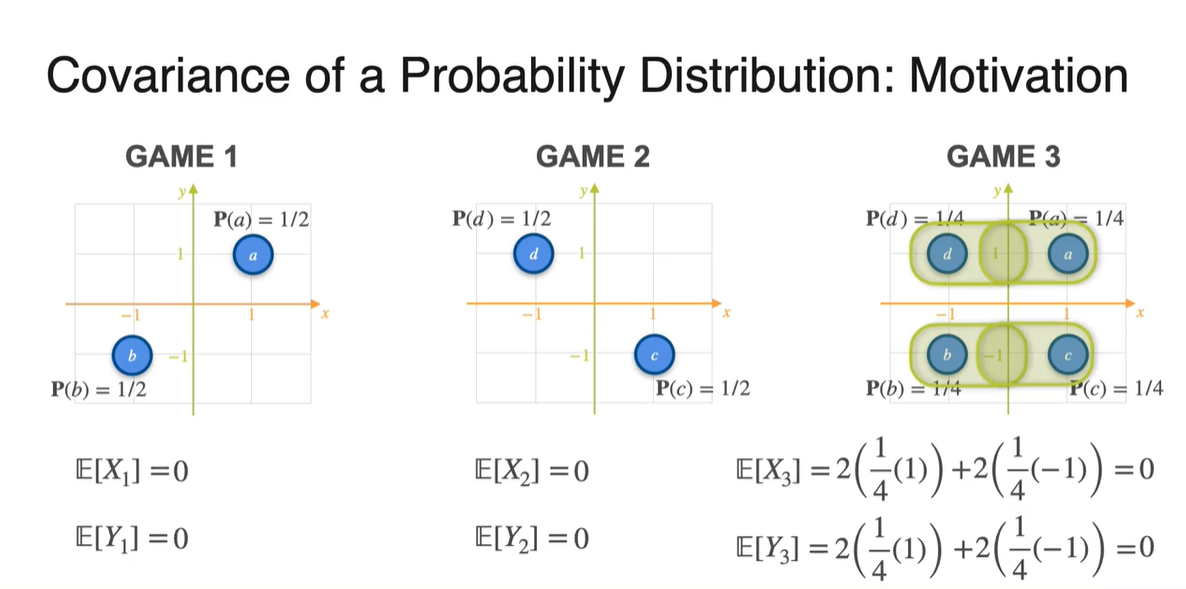
Probability가 주어진 분포의 expected value는 확률과 확률 변수의 곱을 더한 값으로 계산한다.
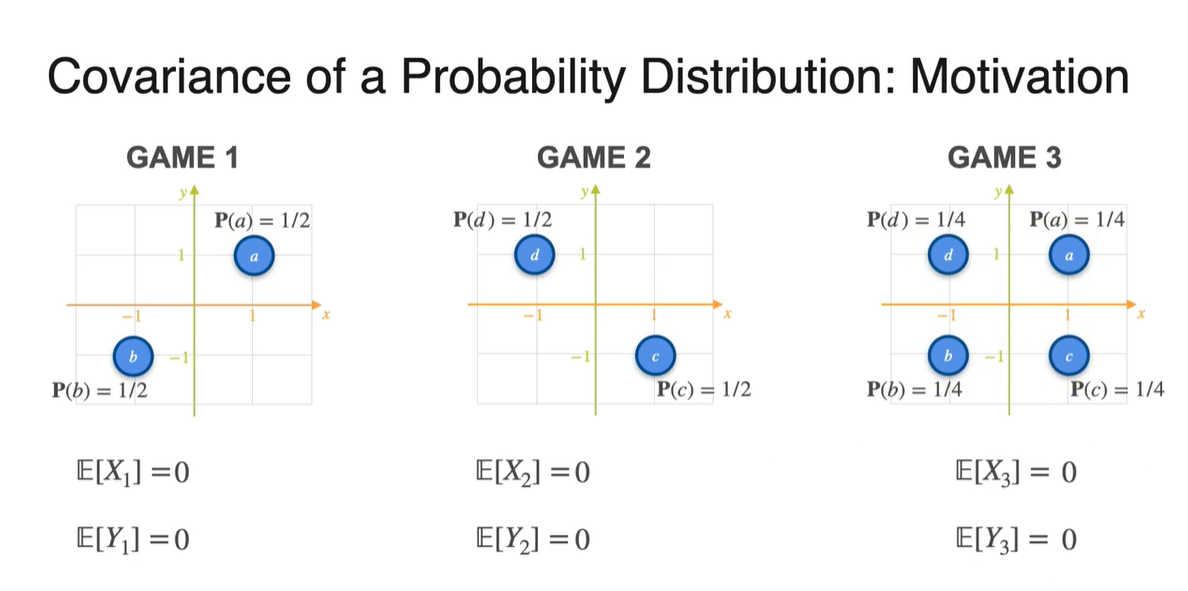
- Game 1, 2, 3의 기댓값을 확률과 확률 변수를 통해 계산하면 모두 0이 나온다.
-
Variance를 구해보면 어떨까?
- 첫 번째 game의 variance는 과 를 통해 계산한 결과 1로 계산되었다.
-
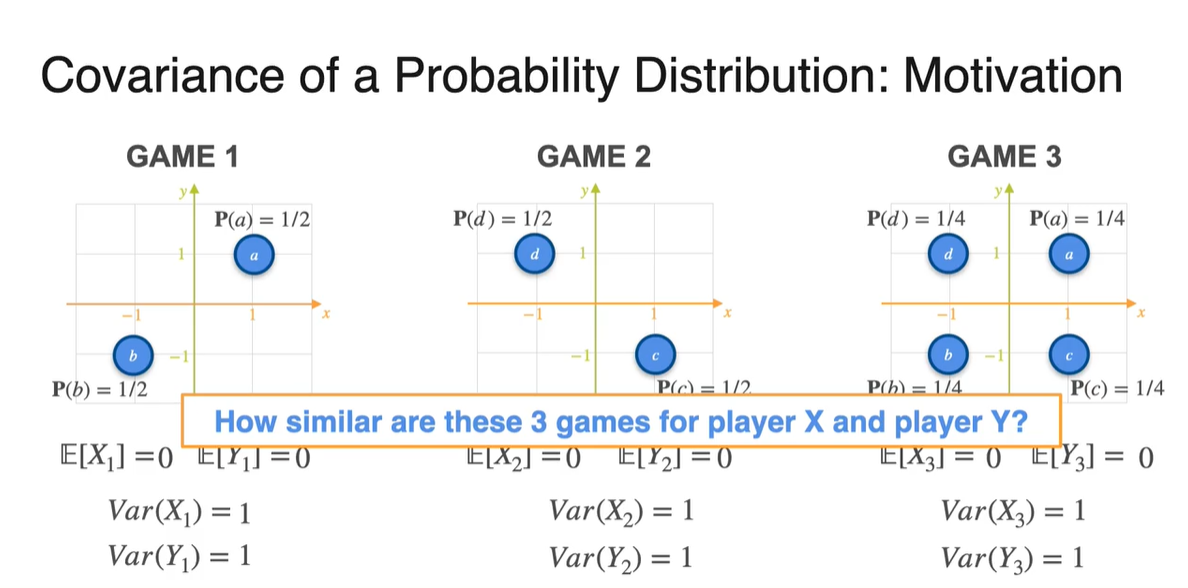
마찬가지로 Game 2와 3의 variance를 구해보면 모두 1로 나타난다.
- 그렇다면 도대체 두 확률 변수의 유사성을 무엇으로 증명해야 하는 것일까?
-
정답은 Covariance에 있다.
- 수식으로는 으로 표현한다.

-
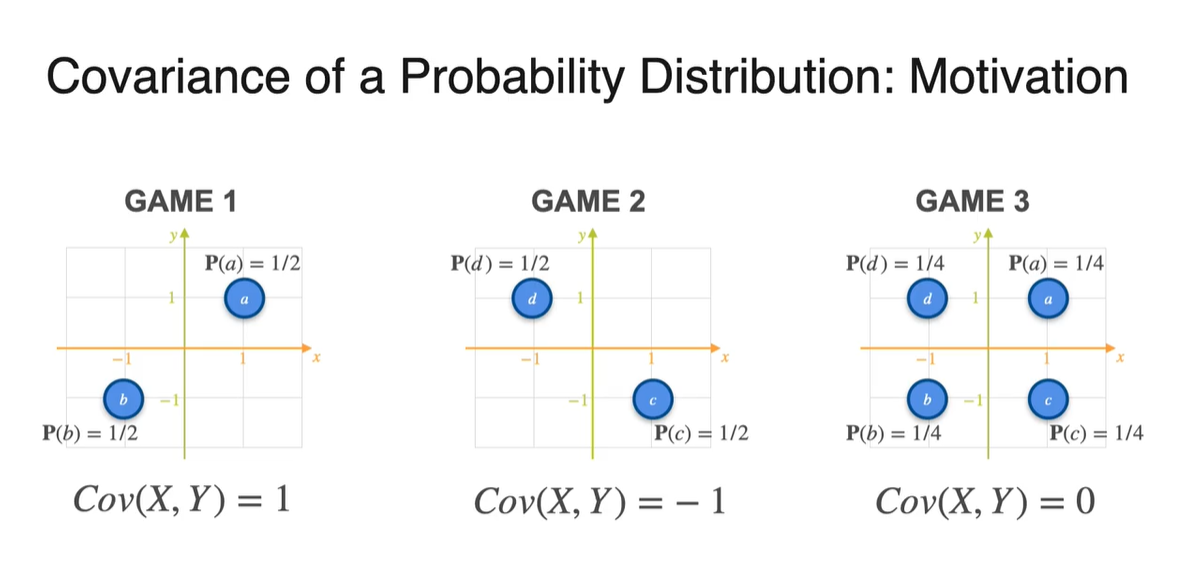
Game 1의 와 를 구해 두 값의 곱을 모두 더하면 2가 나온다.
- 이를 전체 데이터 샘플 수 2로 나누면 Covariance는 1로 얻어진다.

-
Game 2의 와 를 구해 두 값의 곱을 모두 더하면 -2가 나온다.
- 이를 전체 데이터 샘플 수 2로 나누면 Covariance는 -1로 얻어진다.

-
Game 2의 와 를 구해 두 값의 곱을 모두 더하면 0이 나온다.
- 이를 전체 데이터 샘플 수 4로 나누면 Covariance는 0으로 얻어진다.

- 정리하면 아래와 같은 분포의 covariance가 각각 1, -1, 0으로 계산된 것이다.
-
만약 새로운 Game 4와 같은, 확률이 고르지 않은 unequal probability일 때는 어떨까?
- Expectation 즉, 기댓값이 확률 weight에 영향을 받아 0에서 로 변하였음을 알 수 있다.

-
이를 바탕으로 Variance : 를 계산하면 0.806이 계산된다.
- 마찬가지로 기존 1에서 조금 벗어난 value가 얻어진다.

- 그렇다면 는 어떻게 계산될까?

-
확률 분포가 uniform distribution, equal probabilities였다면 각 변수의 평균과의 차이를 모두 더하여 으로 나눈 값으로 계산한다.
-
만약 unequal probabilities를 가지는 분포라면, joint probability(weight)까지도 고려하여 곱한 뒤 summation하여 나타낸다.
-

-
와 , 그리고 와 를 구한 뒤 Covariance를 구해보자.
- 계산 결과 0.806으로, 양수의 값을 가진다는 점을 알 수 있다.

-
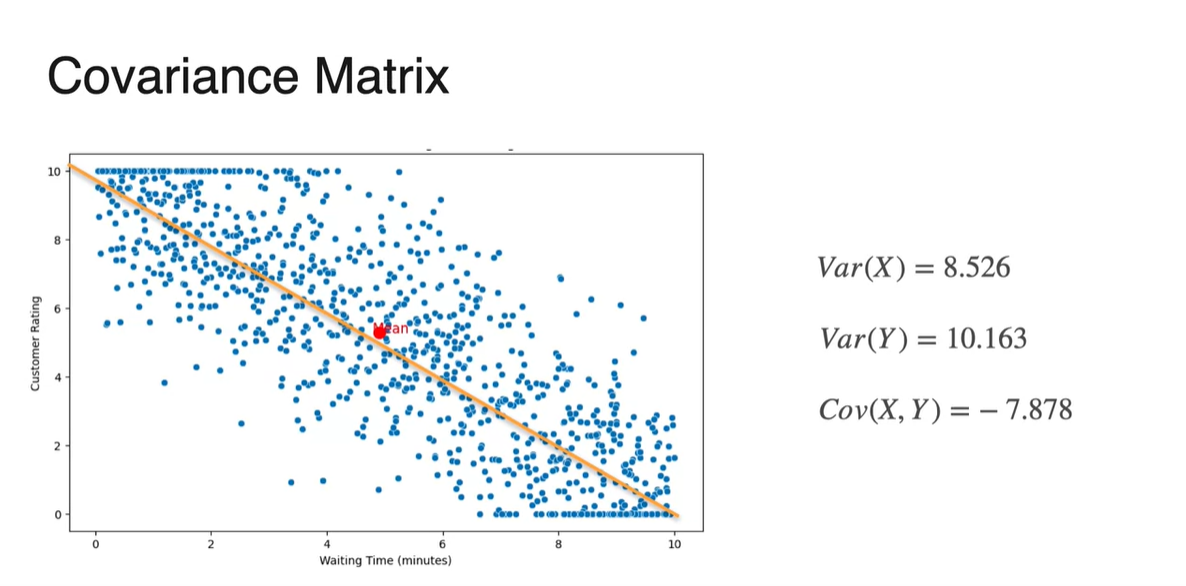
아래와 같은 분포의 Covariance 부호는 무엇일까?
- 직접 계산해보면 Covariance가 음수임을 알 수 있으며, 그래프 모양만 보아도 반비례 관계를 가진다는 것을 알아낼 수 있다.
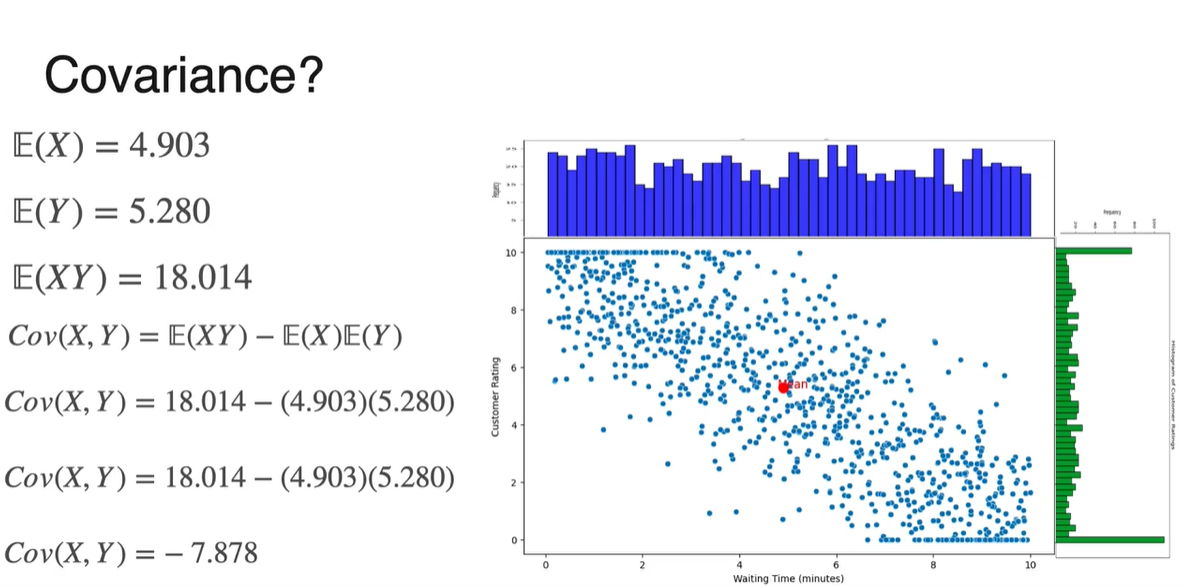
- 이를 통해 Joint Continuous Distribution에서의 Covariance를 구함으로써, 상관관계를 정의내릴 수 있음을 알게 되었다.

Covariance Matrix
-
우리는 아래와 같은 두 가지 예제들을 통해 의 부호에 따른 분포의 관계를 정의내릴 수 있었다.
- Covariance가 +면 양의 상관관계를, -면 음의 상관관계를, 0에 가깝다면 그 무엇도 아님을 말이다.
-
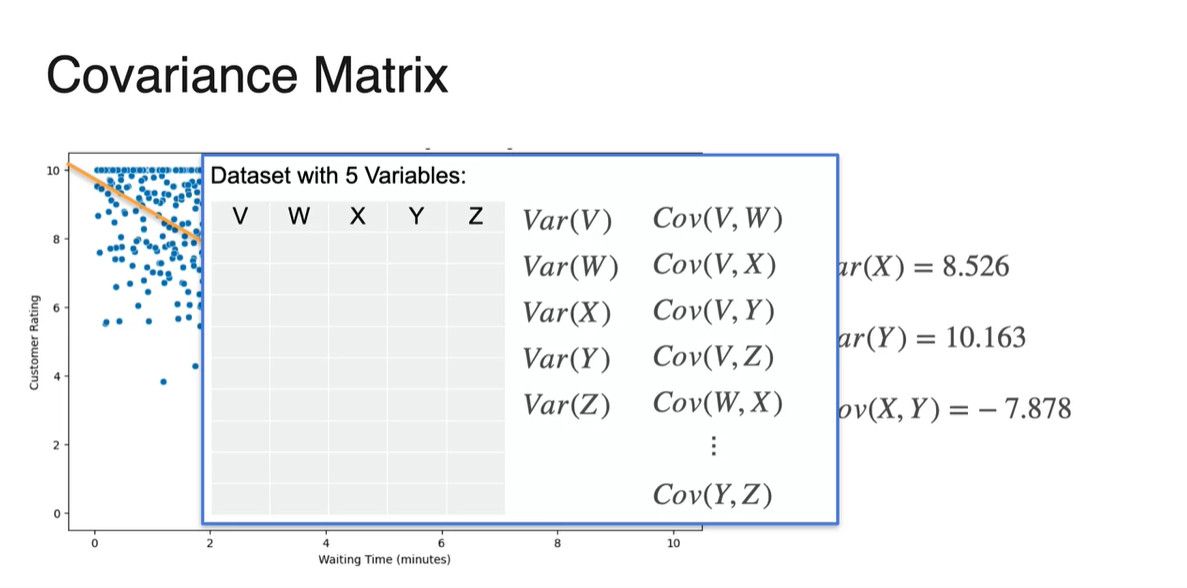
만약 5개의 random variables를 다룬다면 그 관계를 어떻게 정의내릴 수 있을까?
- 아마도 두 변수 조합의 Covariance를 구하여 통합해야 할 것이다.
-
확률 변수가 와 로 2가지일 때, Covariance matrix는 다음과 같이 쌓아진다.
-
Diagonal 항은 독립 변수의 Variance, 다른 항은 Covariance다.
- 와 는 같으므로 symmetric한 성질을 가진다.
-
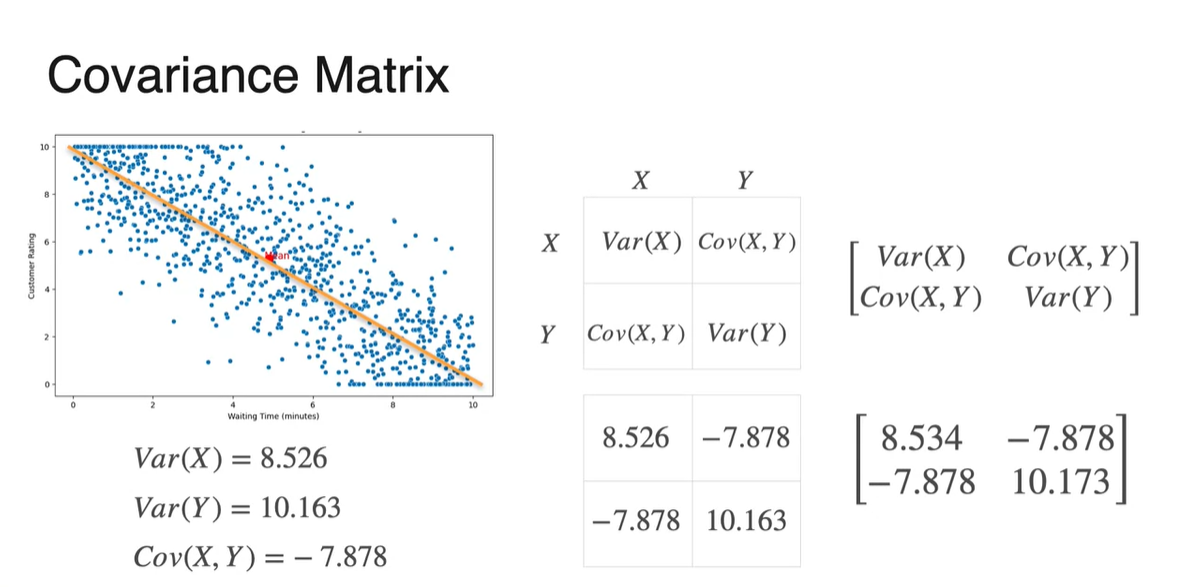
- 위 예제에서 다룬 Covariance matrix를 계산한 것이다.
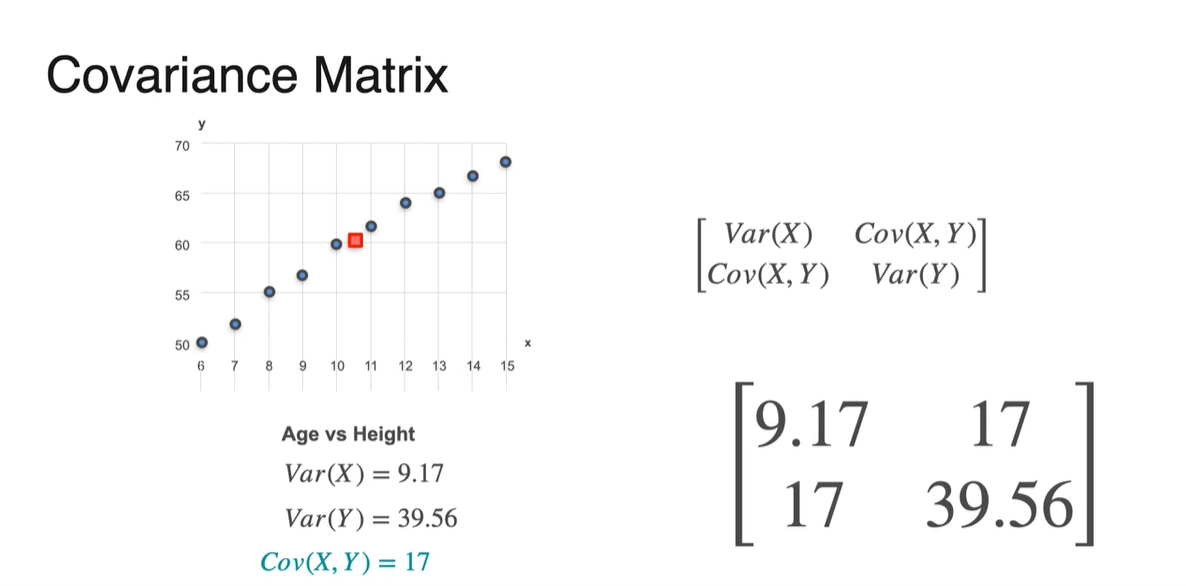
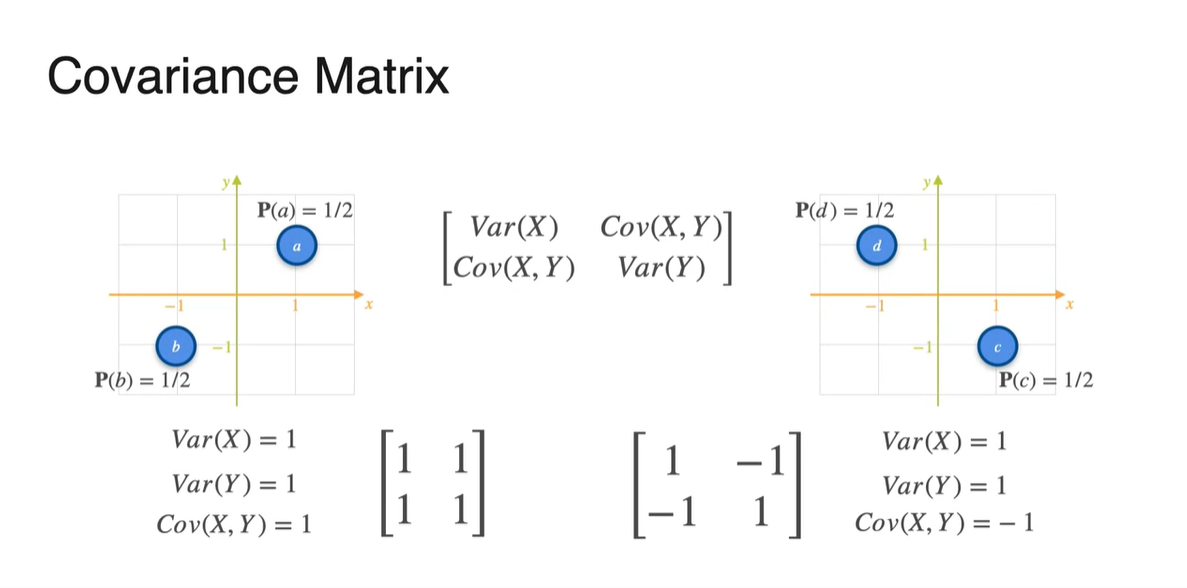
-
만약 3개 확률 변수의 Covariance matrix를 구하고자 한다면 다음과 같은 값들을 계산하면 된다.
- , , 가 있으므로 가능한 조합은 , , 가 있다.

-
5개의 변수를 갖는 Covariance matrix도 마찬가지다.
- 두 변수의 조합으로 Covariance를 계산하여 matrix 형태로 쌓아준다.

- Covariance matrix는 로 표기하며, 공분산 행렬이라 불릴 것이다.

Correlation Coefficient
-
지금까지 우리는 Covariance의 부호만을 가지고 상관관계를 확인하였다.
- Covariance가 음수라면 반비례, 양수라면 비례 관계를 가진다고 정리할 수 있다.
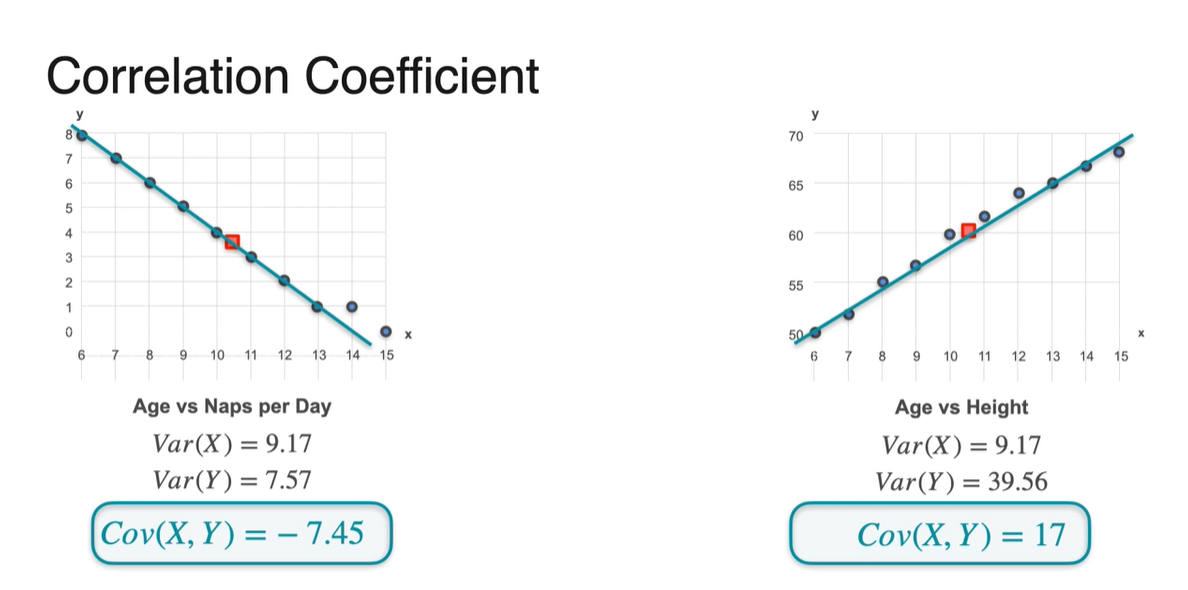
-
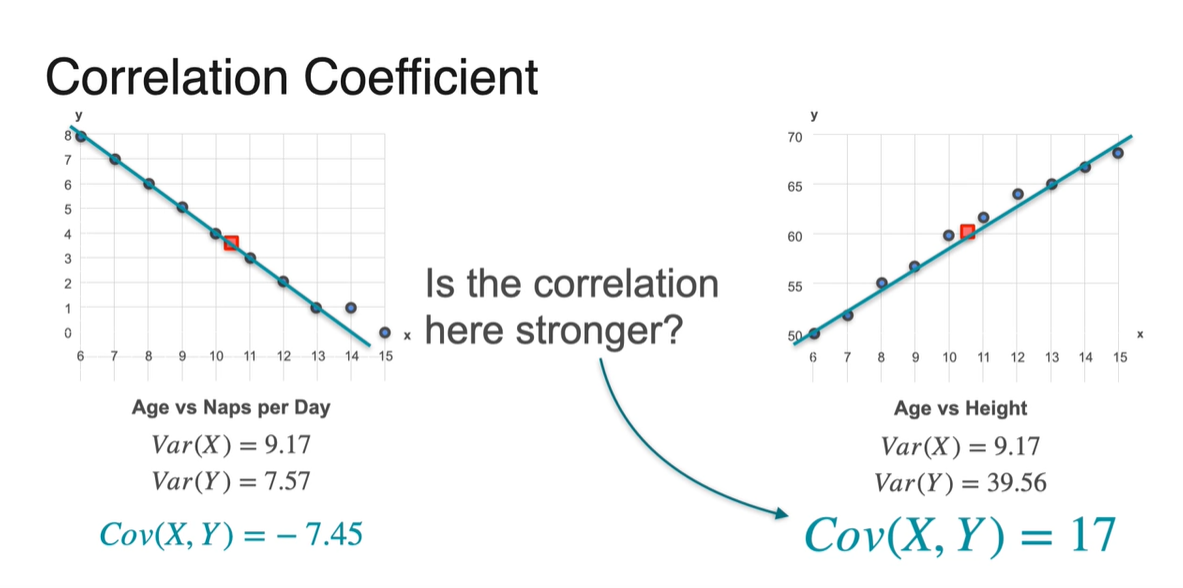
그런데 이 때, Covariance 값이 더 크다고 해서 strong correlation을 가진다고 말할 수 있을까?
- 지금과 같이 normalizing되어 있지 않은 상황이라면 "그렇지 않다"가 정답이다.
-
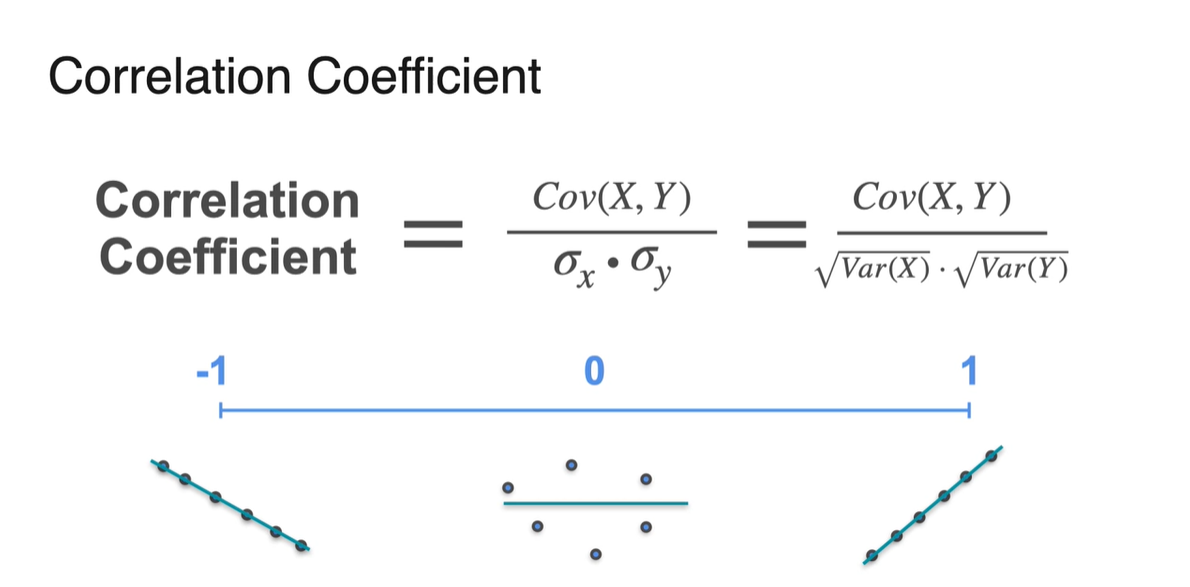
Correlation Coefficient는 양 극간의 상관관계의 치우침 정도를 -1에서부터 1까지의 값으로 나타내는 값이라 정의내릴 수 있다.
- -1에 가까우면 음의 상관관계, +1에 가까우면 양의 상관관계를 뚜렷하게 가진다고 말할 수 있다.

-
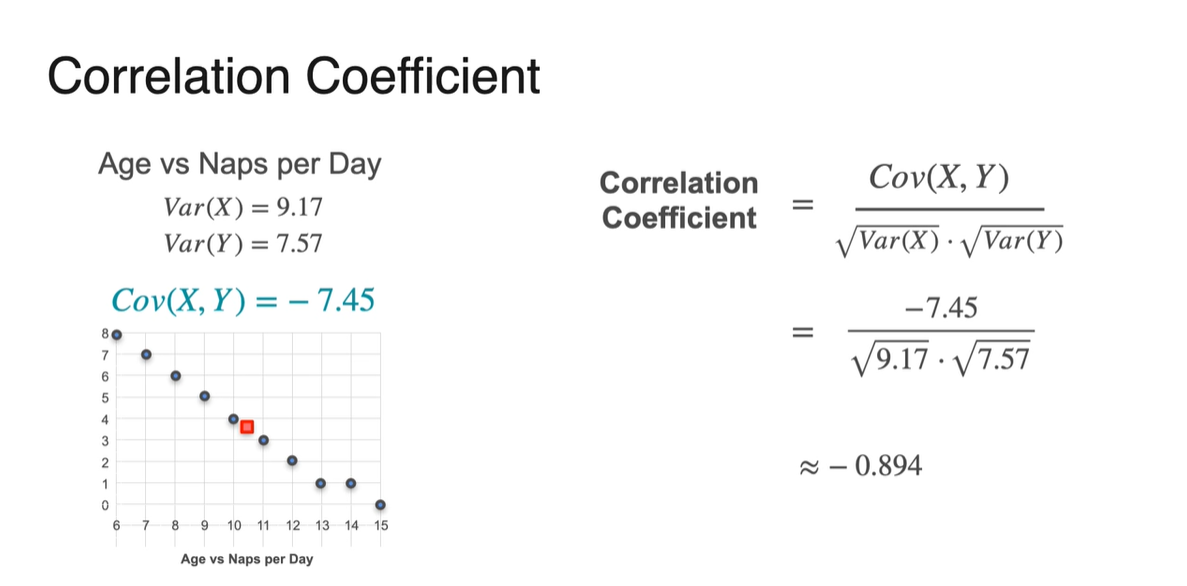
기존 Covariance를 normalizing하는 방법은 두 변수의 standard deviation(표준 편차)로 나눠주는 것이다.
- Correlation Coefficient의 정의는 다.

-
이제 위 예제의 Covariance로 Correlation Coefficient를 계산해보자.
- 처음 Covariance가 -7.45였던 값은 -0.894로 변환되었으며, 17이었던 값은 0.893으로 변환되었다.
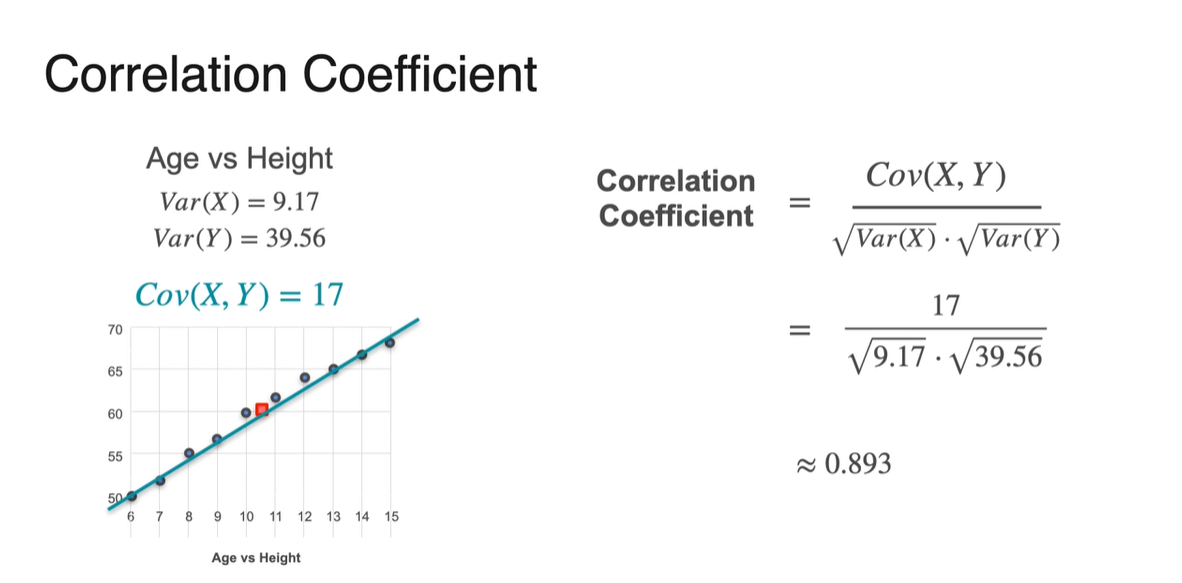
- -1에 가까운 -0.894는 음의 상관관계를, +1에 가까운 0.893은 양의 상관관계를 가진다는 것을 알아낼 수 있었다.
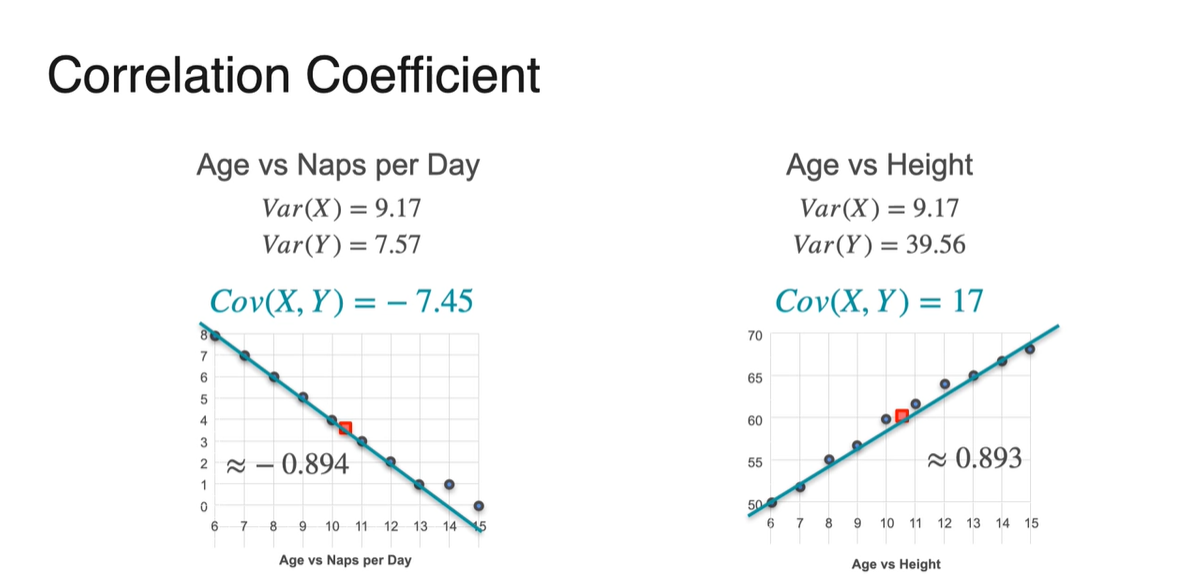
-
Covariance가 0.1이었던 예제의 Correlation Coefficient는 0.01로 변환되었다.
- 즉, 0에 가까운 값이므로 아무런 상관관계가 없다고 판단해도 좋다.
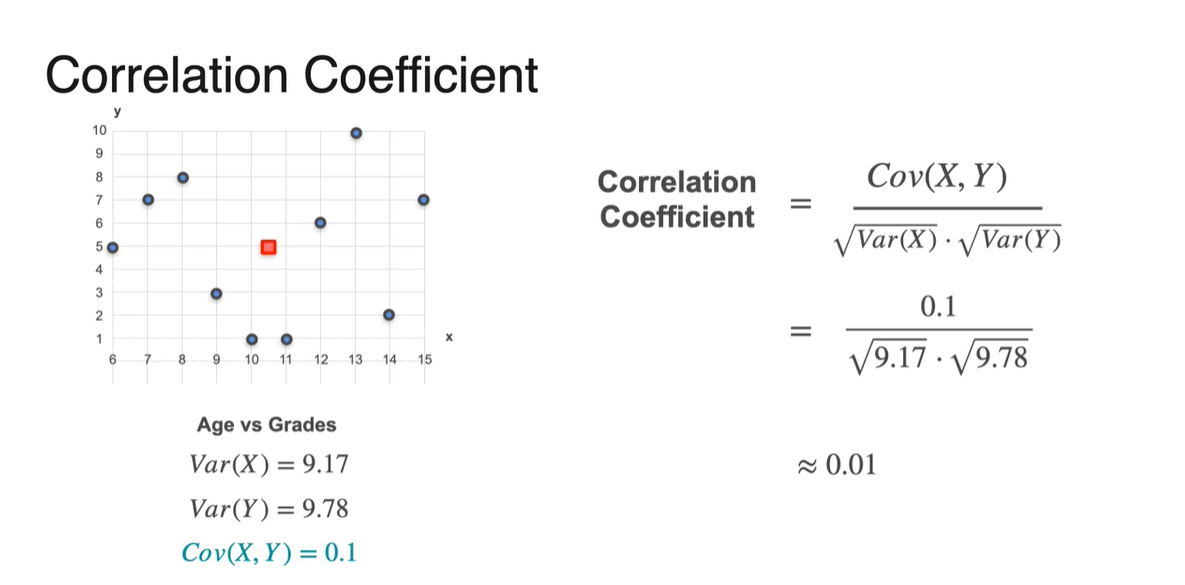
-
Continuous variable에서의 Correlation도 마찬가지다.
- Covariance와 표준편차 를 통해 Correlation을 계산하면 분포의 경향성을 파악할 수 있게 된다.
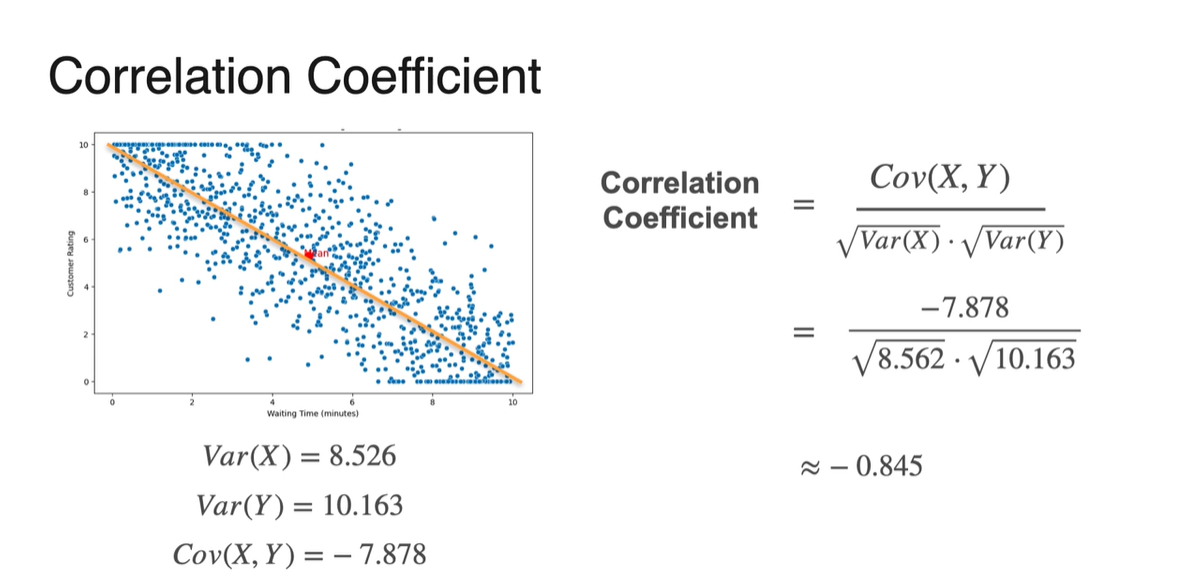
-
Correlation Coefficient의 정의와 범위는 아래와 같다.
Multivariate Gaussian Distribution
-
Single variable 에 대한 normal distribution PDF는 아래와 같은 수식으로 전개되었다.
-
- : center of the bell
- : spread of the bell
-
만약 random variables가 처럼 여러 개로 늘어난다면 PDF는 어떻게 결정될까?
-
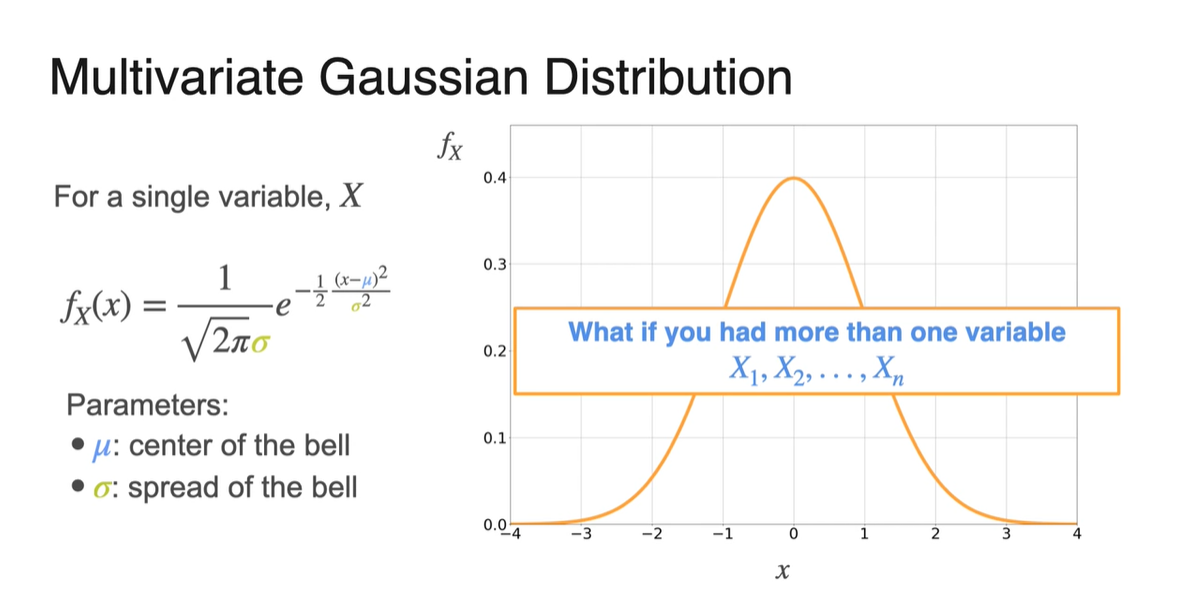
-
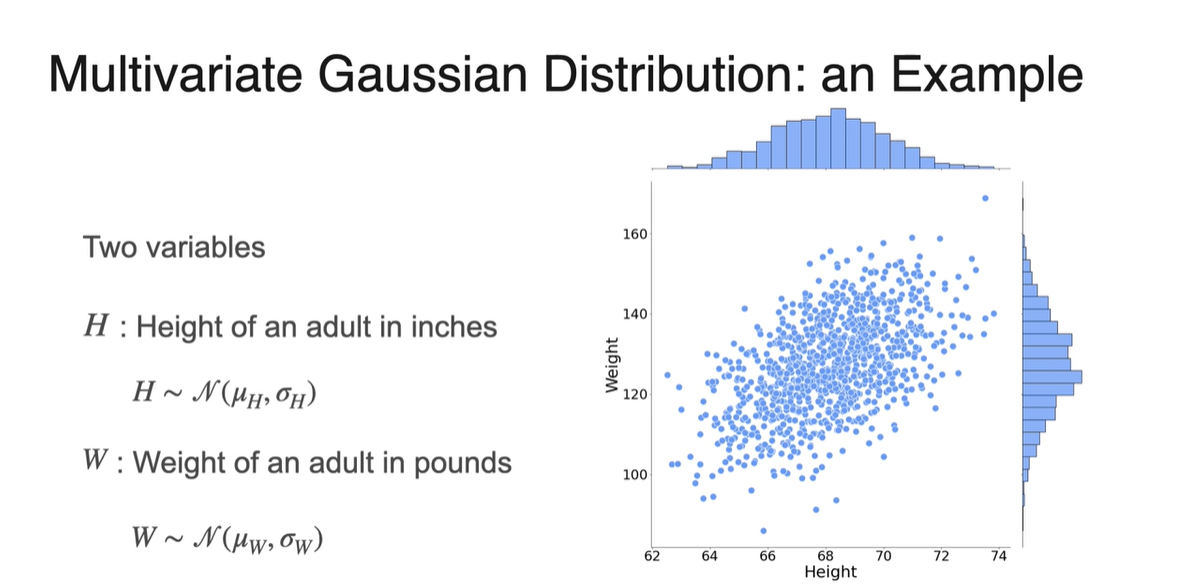
Height와 Weight로 나뉜 2개의 variables 분포가 아래와 같이 scatter plot으로 그려진다고 하자.
-
각 변수의 Marginal distribution을 그려보면 Normal distribution을 따른다.
- ,
-
-
만약 와 가 independent하다면, PDF는 두 독립된 PDF의 곱으로 나타내질 수 있다.
-
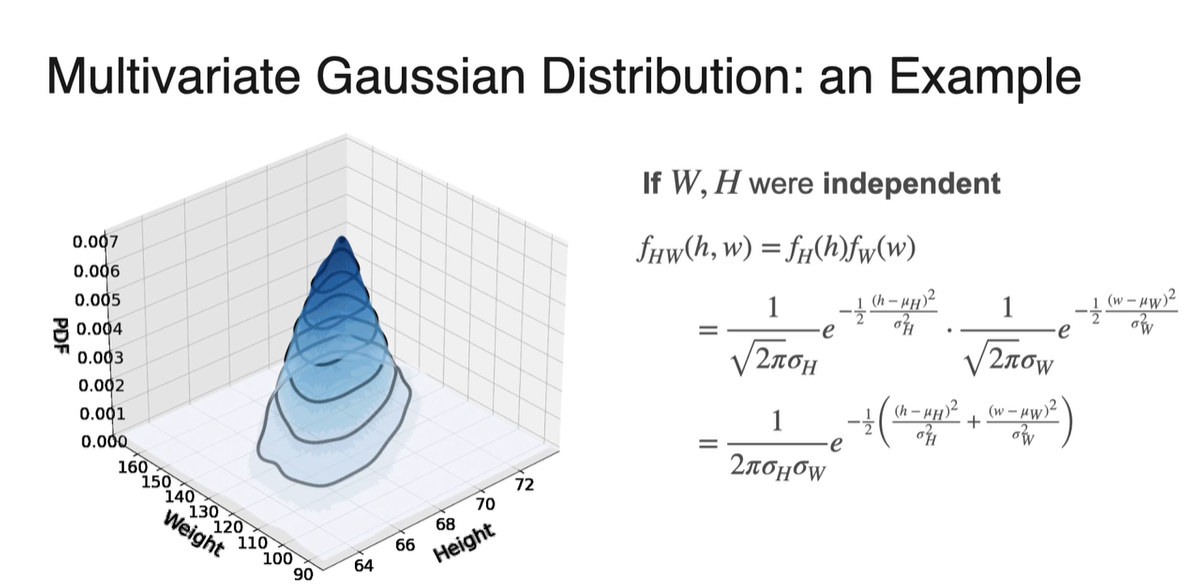
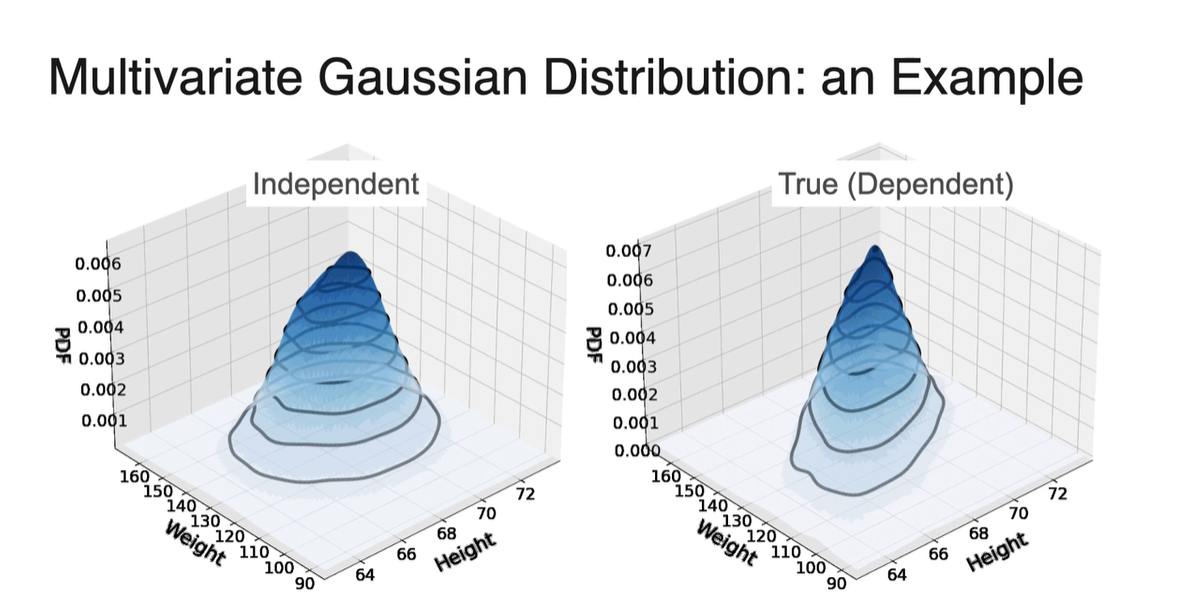
- 두 변수가 independent하다면 왼쪽 그래프와 같이 symmetric한 성질을 가지고, dependent하다면 다소 홀쭉한 분포를 갖게 된다.
-
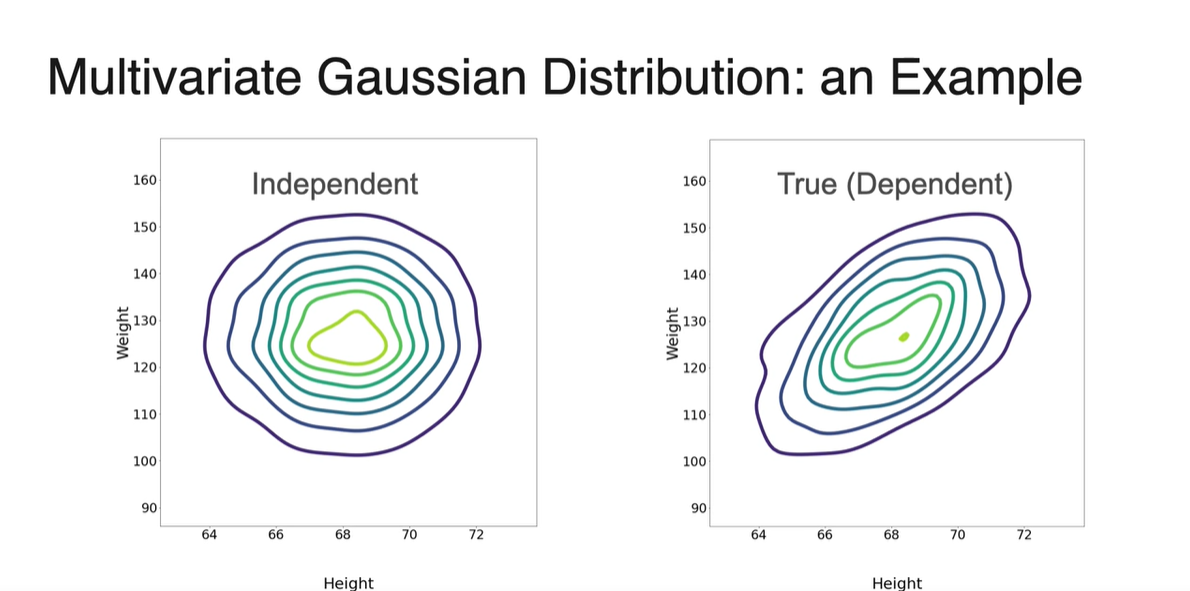
등고선 그래프를 나타내면 아래와 같이 차이가 극명하게 나타난다.
- 두 Normal distribution을 가지는 분포가 서로 independent하다면 multivariate distribution이 symmetric하고, dependent하다면 양 또는 음의 경향성을 갖게 된다.
-
Multivarite Gaussian distribution을 행렬로 표현해보자.
-
먼저 Joint PDF의 는 로 표현된 F-2 norm의 제곱값과 같다.
- 즉, 벡터의 transpose인 와 의 dot product 값이다.
-
또한, 와 는 벡터와 벡터의 차이로 표현할 수 있다.
-
마지막으로 는 으로 diagonal 원소만 살아남기 때문에 diagonal matrix로 분해가 가능하다.
-


-
는 Covariance matrix()를 나타낸다.
-
의 곱은 의 determinant다.
-
벡터는 각 변수의 평균 벡터를 나타낸다.
-

-
만약 두 변수가 independent하다면 아래와 같은 수식으로 Joint PDF를 정의내릴 수 있다.

-
와 , 행렬 표현으로 치환하면 아래와 같다.

-
만약 두 변수가 서로 dependent하다면 아래와 같은 간단한 수식으로는 표현이 불가능하다.
- Covariance인 가 diagonal하지 않고 까지도 고려해주어야 하기 때문이다.

-
확률 변수가 개인 PDF는 아래와 같은 행렬로 표현이 가능하다.
- 각 변수들은 벡터를 나타내며 covariance 는 n by n matrix꼴을 가진다.

-
Univariate variable을 갖는 PDF는 scalar 값의 mean과 variance로 표현이 가능했다.
- 2개 이상의 dependent variables나 multivariate variables를 갖는 PDF는 vector나 matrix 의 mean과 variance로 표현해야만 한다.

