Monte Carlo Methods for Prediction & Control

Introduction to Monte Carlo Methods

What is Monte Carlo?

• Monte Carlo methods에 대해 알아보자.

• 이번 강의에서는 Monte-Carlo methods를 통해 value function을 estimate하는 방법에 대해 알아보겠다.

• Dynamic Programming은 environment의 transition probabilities를 알 때 적용할 수 있는 method라고 할 수 있다.

  • 그러나 날씨 예측과 같은 문제는 transition probabilities를 알지 못하기 때문에 다른 방법으로 풀어야 한다.

• 이러한 계산(computation)은 매우 지루하고 소모적인 과정이라고 할 수 있다.

• Monte Carlo methods는 큰 수로 random sampling한 sample set에 대하여 평균낸 값으로 value를 estimate하는 방법론이다.

  • 아래와 같은 variables들로 선정된 samples의 average를 구해보니 41.57의 결과가 나왔다.

• Monte Carlo methods는 samples로 average낸 policy evaluation을 구하는 것으로부터 출발한다.

• 이후 episodic tasks를 반복해가며 State-Action-Reward-State-Action을 취한다.

  • 그러면 여러 sample의 평균치들이 점점 expected value로 수렴해가는 것을 알 수 있다.

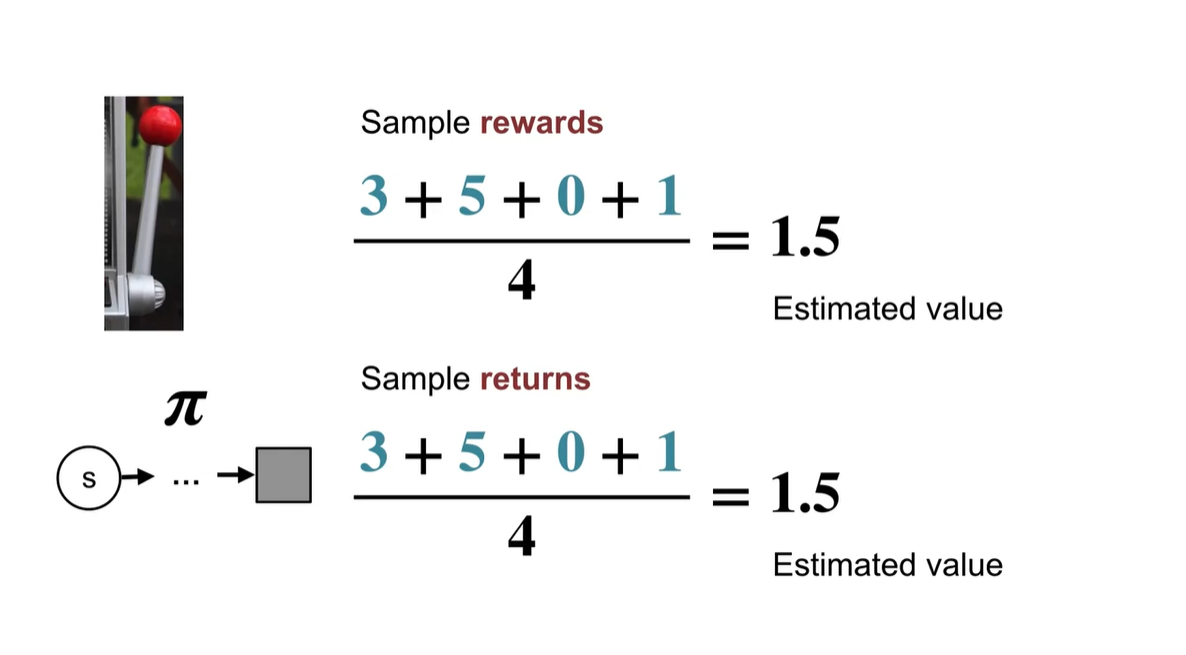
• 이전에 우리가 했던 K-armed Bandit problem이 Monte-Carlo methods와 같은 맥락이라고 볼 수 있다.

  • 4개의 samples로 rewards의 기댓값을 계산한다는 것은 policy $\pi$를 따르는 action-state를 반복하여 얻어낸 rewards의 평균치를 계산하는 것과 같다.

• MC prediction 알고리즘의 코드는 아래와 같다.

  • Loop를 돌며 S→A→R→S→A를 선택하고, 한 episode step에서 return을 업데이트 한다.

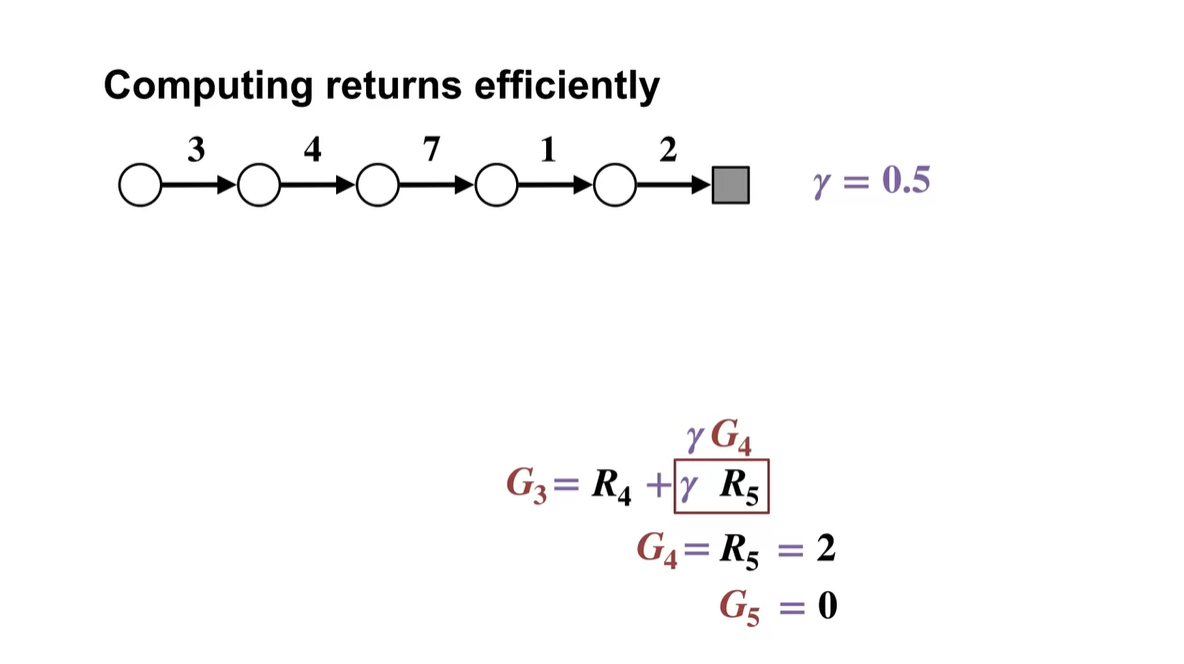
• 3→4→7→1→2의 reward를 return으로 얻는 방법은 아래와 같이 전개될 수 있다.

  • $G_5$의 episode state에서 얻어진 reward는 $G_4$와의 합으로, $G_4$는 $G_3$와의 합으로, ... 이런 식으로 $G_0$까지 backward로 구한다.

• 이를 $\gamma$와 reward $R$로 전개해 표현하면 아래와 같아진다.

  • $G$를 벗겨 $R$로 표현하면 한 episode에서의 reward는 이전 rewards를 모두 더해 return으로 얻어낸다는 것을 알 수 있다.

• MC prediction에서 return을 정의하는 방법은 다음과 같이 $G$를 0으로 initialize하는 것으로부터 출발한다.

  • 이전 time step $T-1, T-2, ... 0$에서의 return을 $\gamma$항까지 적용하여 모두 더한 return이 $G_t$로 업데이트 된다.

• Summary

Using Monte Carlo for Prediction

• Monte Carlo for Prediction에 대해 알아보자.

• 이번 강의에서는 Monte Carlo prediction을 활용하여, policy내에서의 value function을 estimate하는 방법에 대해 알아보도록 하겠다.

• Blackjack 게임은 21의 수를 초과하지 않고 딜러보다 21에 가까우면 이기는 게임이다.

  • Ace는 11과 1로 선택할 수 있으며, player가 21에 도달할 경우 게임은 player의 승리로 끝나게 된다.

    • 반면 21을 초과할 경우 곧바로 게임이 끝나고 딜러의 승리로 기록된다.

• 이 게임은 Undiscounted MDP(감쇠되지 않는)로 매번 episode에 도달할 수 있는 system이다.

  • Reward와 Action, States, 그리고 Policy 각각의 역할이 아래 설명과 같다.

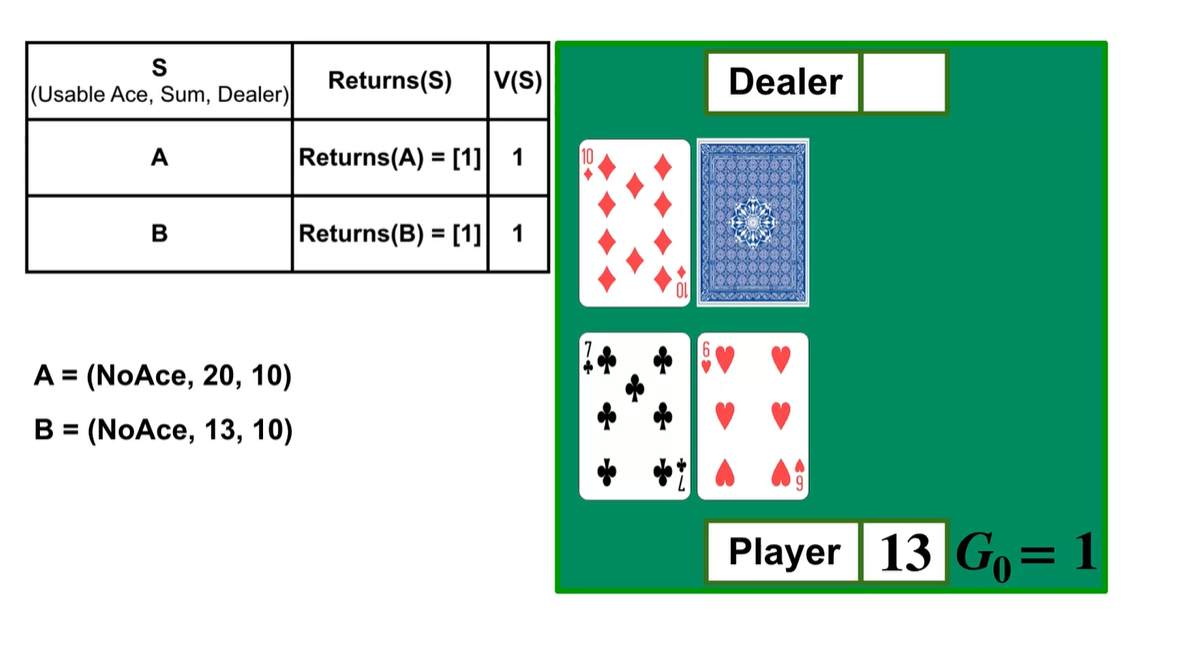
• 만약 player가 13의 숫자를 가지는 상황에서 한 장을 더 뽑아 20을 만족했다고 해보자.

  • 이 때 dealer가 23의 숫자를 가지는 state로 도달하게 되어 player가 이겼다면 Reward 1을 받는다.

• 방금 전 상황을 되돌려(Backward) 보자.

  • (No Ace, Sum=20, Dealer=10)인 상황에서 얻은 episode reward는 1로 기록된다.

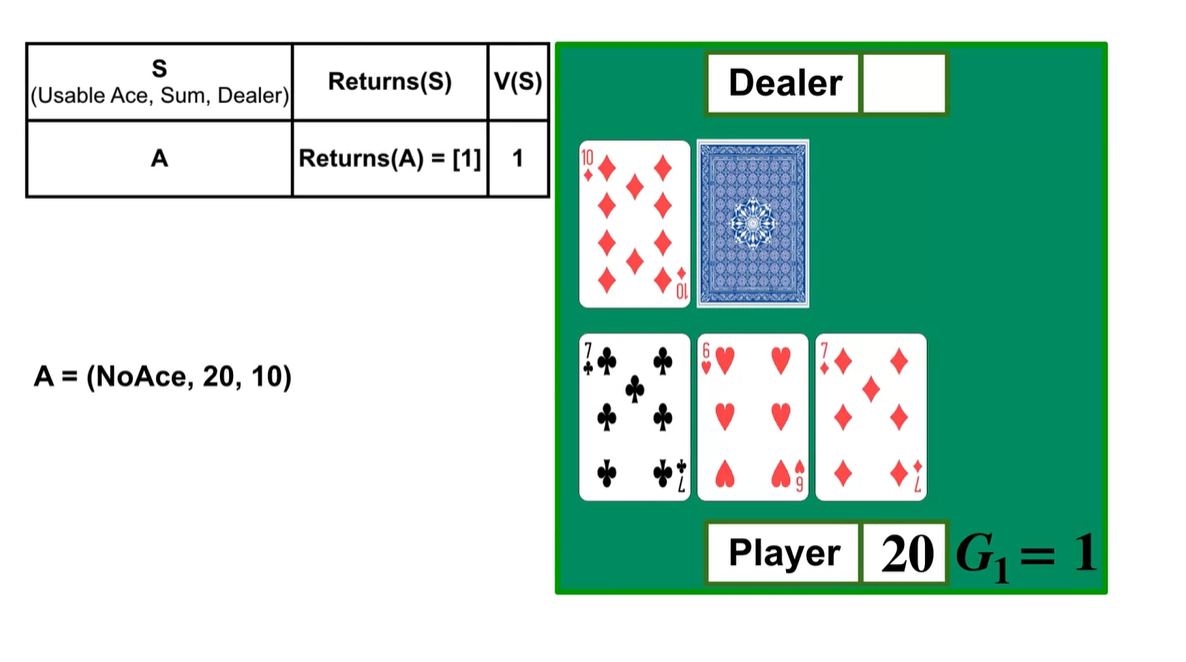
• 그 이전의 상황에서 취했던 action은 (No Ace, Sum=13, Dealer=10)이며, 이 또한 Reward 1을 받은 episode임은 동일하다.

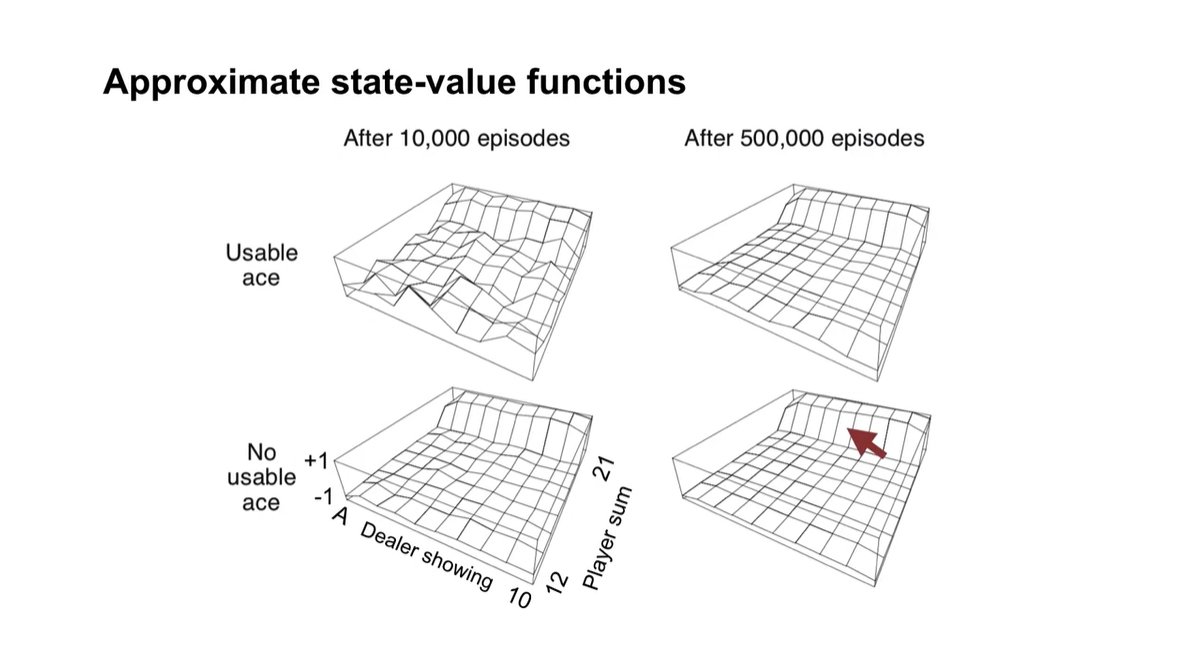
• 10,000번의 episodes를 경험하여 추정한 state-value functions의 surface와 500,000번의 surface가 아래와 같다.

  • 주목할 만한 점은 Ace를 사용할 수 있을 때의 surface가 그렇지 않을 때의 surface보다 좀 더 dynamic하다는 점이다.

  • 그리고 player sum이 21에 가까울수록 value 값이 높아지며 episodes가 많을수록 stable한 곡면을 갖는다.

• Monte Carlo learning이 암시하는 바는 다음과 같다.

  • 우리는 Monte Carlo Prediction을 통해 매 순간 다른 states를 경험하며 independently하게 value를 estimate할 수 있다.

    • 이는 더이상 MDP size 문제로 인해 computation problem을 겪을 필요가 없다는 말이다.

• Summary

Monte Carlo for Control

Using Monte Carlo for Action Values

• Action-value의 관점에서 Monte Carlo를 사용해보자.

• 이번 강의에서는 Monte Carlo methods를 활용하여 action-value를 estimate해 보고, exploration을 유지하는 것의 중요성에 대해 다뤄보려고 한다.

• 무수히 많은 sample의 estimated average는 expected value인 $v_{\pi}$에 가까워진다고 했었다.

• 이제 해당 state에서의 action까지 취하도록 하여 action-value를 추산한 결과도 마찬가지임을 보이려 한다.

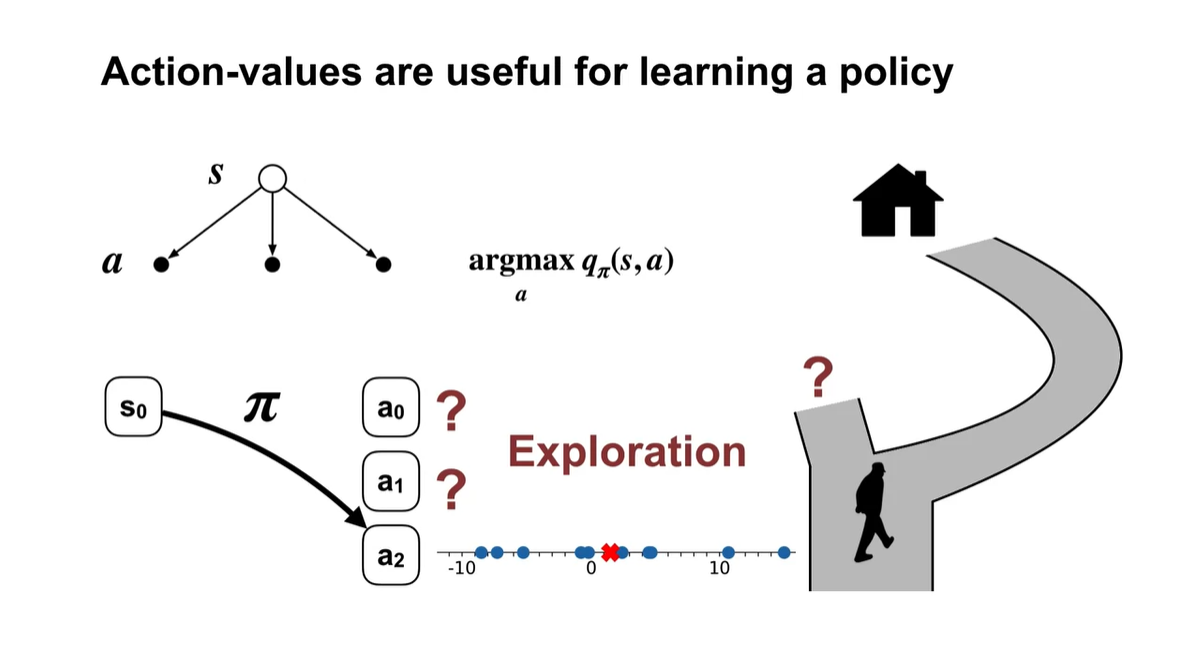
• Action-values를 argmax하여 action을 선택하다 보면 policy를 learning하기에 아주 유용한 방법일 수 있다.

  • 지금 당장 집을 가기 위해 매일 다니던 길을 선택하면 최단 거리임을 보장할 수가 없다.

    • 따라서 새로운 action을 취하는 exploration은 필수로 필요한 과정일지도 모른다.

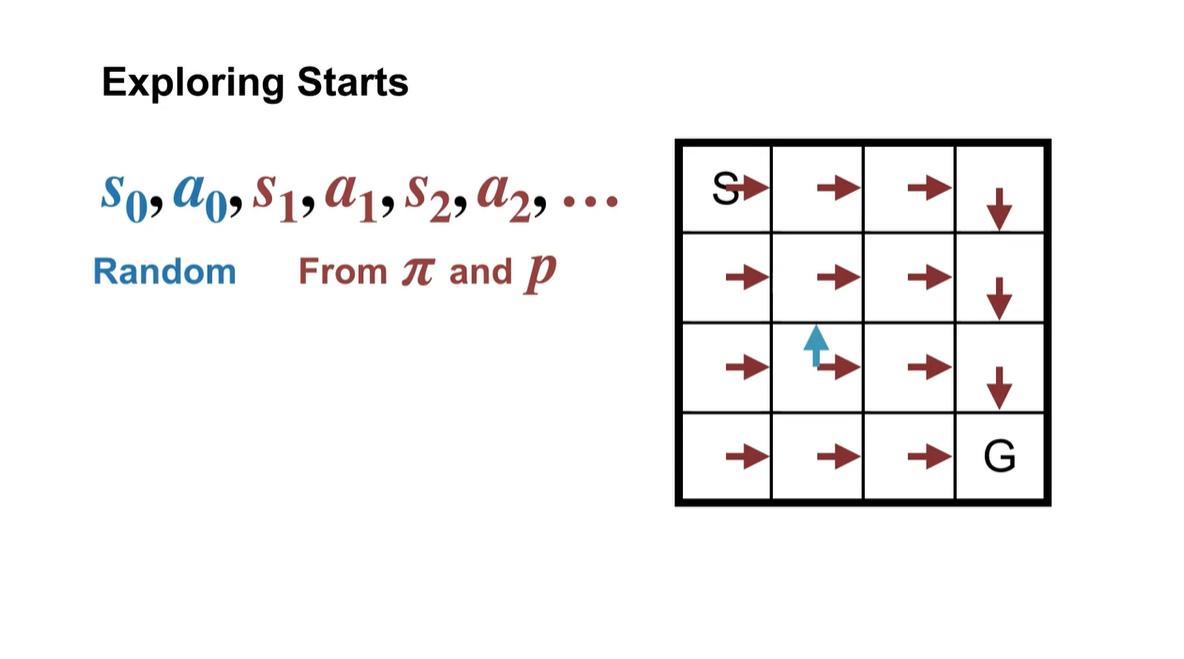
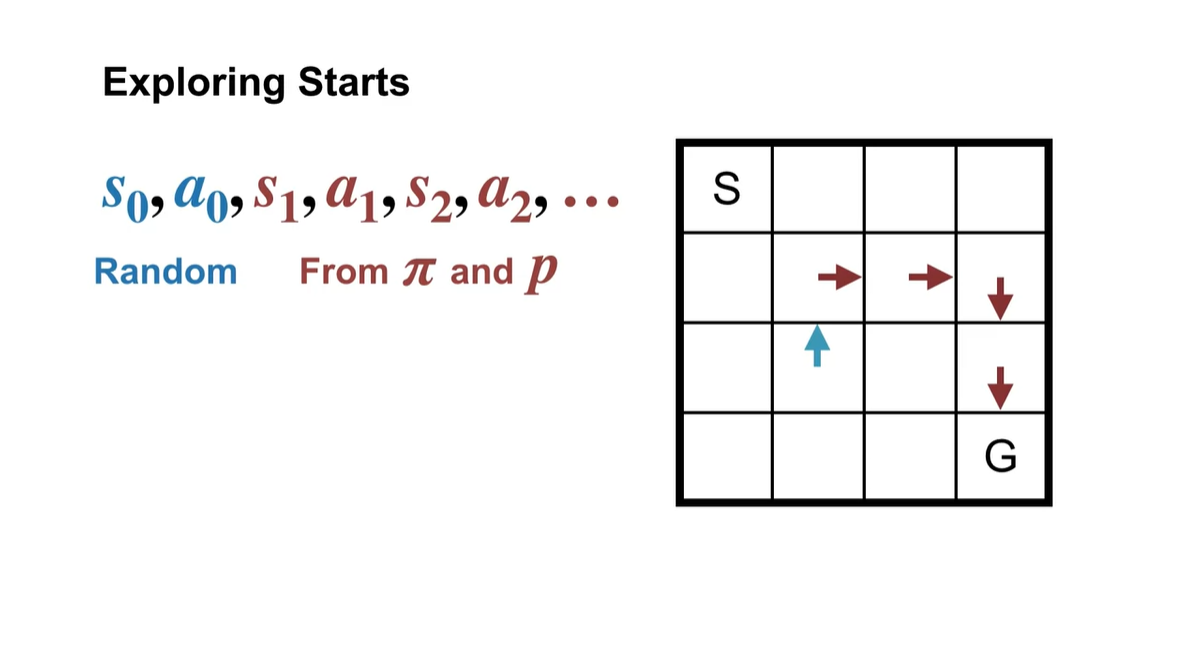
• 이를 테면 갈색으로 표시된 policy를 따르는 board판이 존재한다고 해보자.

  • Initial state 와 initial action인 $s_0$, $a_0$를 파란색이 존재하는 위치와 방향으로 선택한다면 그 다음 state 및 action은 어떻게 변화할까?

• 다음과 같이 board의 기존 policy를 따르는 방향대로 흘러갈 것이다.

  • 이러한 상황 자체가 하나의 episode 역할을 하는 것이다.

• Summary

Using Monte Carlo methods for generalized policy iteration

• 이제 Monte Carlo mathods를 사용한 generalized policy iteration을 정의해보자.

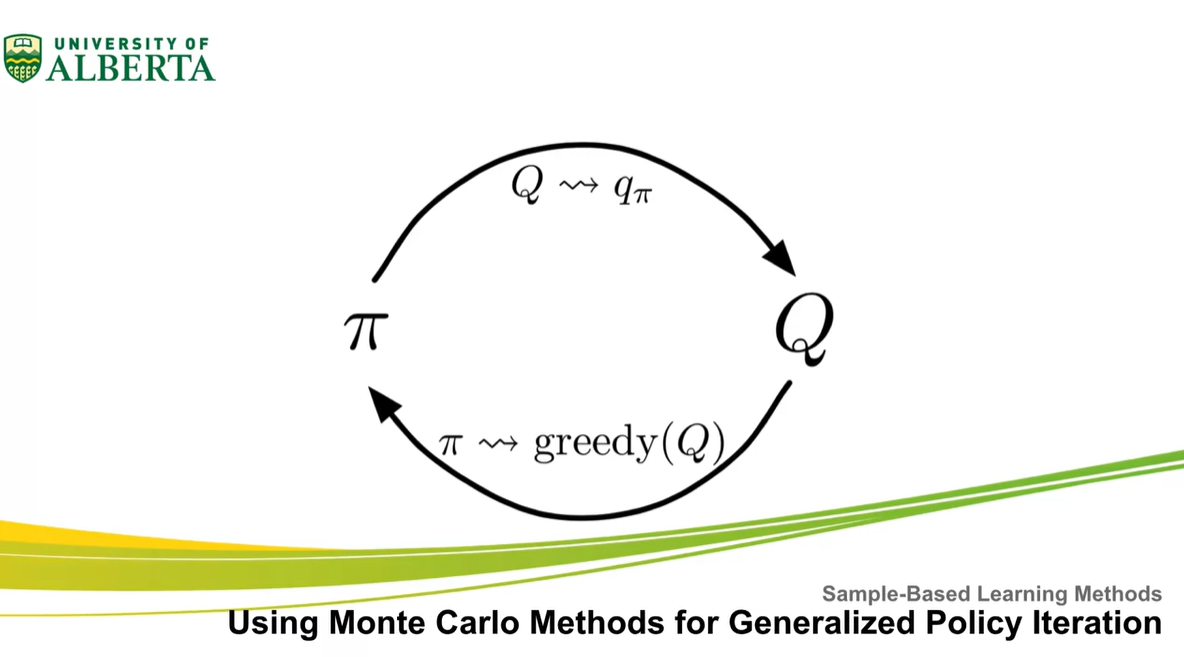
• 이번 강의에서는 Monte Carlo mathods를 활용한 generalized policy iteration 알고리즘에 대해 다룬다.

• Generalized policy iteration은 k번째 action-value를 argmax 취하여, k+1번째에서의 policy $\pi$를 improve하는 과정을 말한다.

  • 이 때 optimal value & optimal policy로 향하도록 하는 policy & value evaluation을 Monte Carlo Prediction으로 수행하는 것이다.

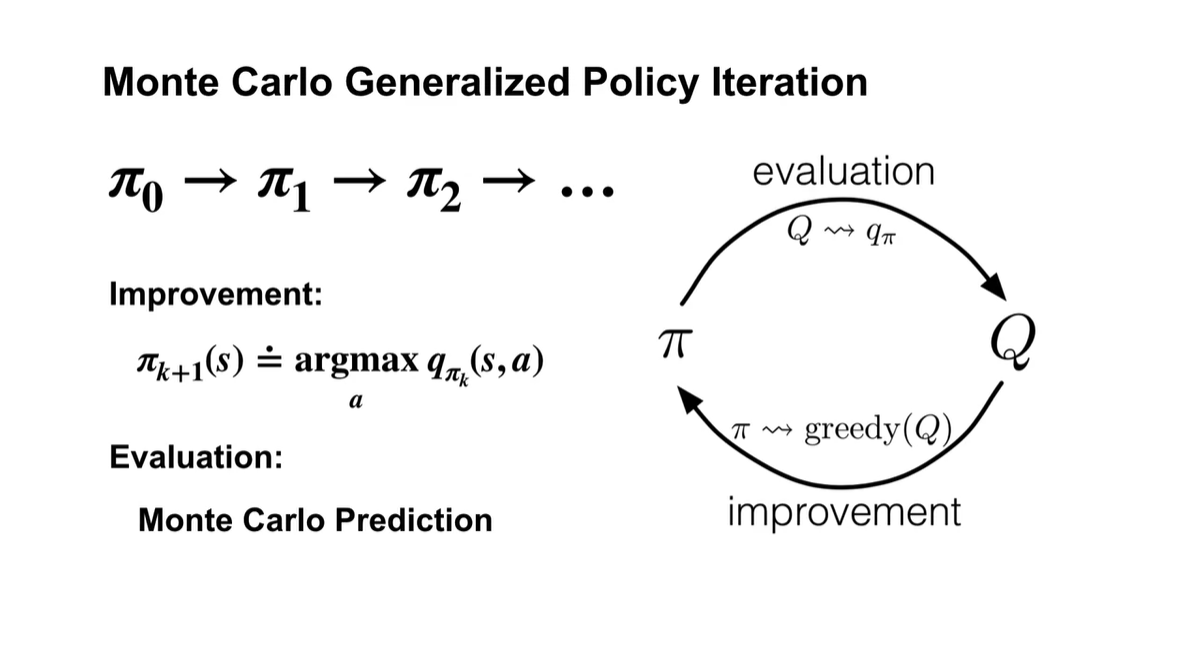
• 매 순간 value 및 policy가 optimal을 향할 수 없기에, 적절한 sampling으로 계산한 경험적 가치를 통해 업데이트 하는 방법론인 것 같다.

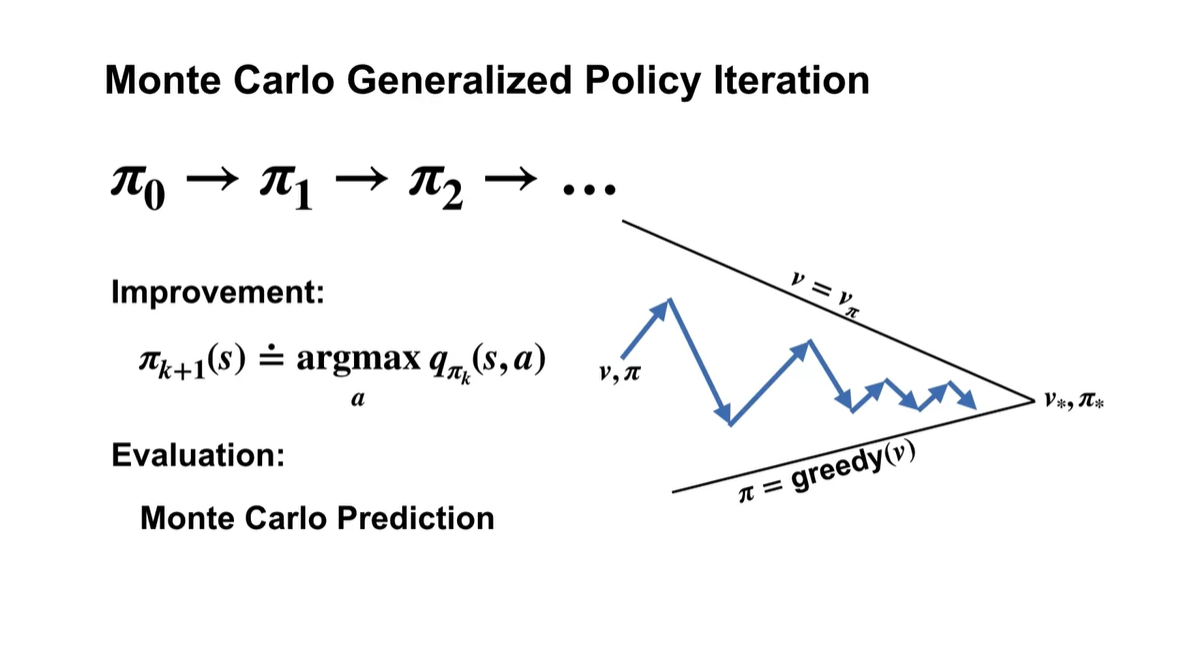
• 이 알고리즘의 전체적인 로직은 아래와 같다.

  • Random하게 initial state $s_0$와 $a_0$를 sampling하는 과정이 특징적인 부분에 해당한다.

• Summary

Solving the Blackjack Example

• Blackjack Example을 푸는 방법에 대해 생각해보자.

• 이번 강의에서는 exploration starts를 활용하여 blackjack과 같은 MDP 문제를 푸는 과정에 대해 알아보려 한다.

• 현재 player는 13의 결과값을 가지고, dealer는 8의 결과를 가지고 있다.

  • 이 상태에서 Hit(한 장 더)과 Stick(건너뜀) 중 하나의 action을 취하여 episode를 이어가 보자.

• 21에 더 가까워지기 위해 Hit을 선택하였더니 player의 최종 점수가 20으로 업데이트 되었다.

• 이제 dealer의 차례가 되어 카드를 한 장 뽑았더니 dealer가 22의 값을 갖게 되었다.

  • Player가 21에 더 가까우면서 dealer가 21을 초과하는 값이 되어버렸기 때문에, 게임은 즉시 player의 손을 들어주며 종료된다.

• 이제 다시 backward로 향하며 value를 역으로 계산해 나가 보자.

  • Player가 20인 상황에서 Stick을 선택했기 때문에 게임을 이길 수 있었으므로 Stick 선택지에 Reward 1를 적는다.

• Player가 13인 상황에서는 Hit을 선택했기 때문에 게임을 (전체적으로) 이길 수 있었으므로 Hit 선택지에 Reward 1을 적는다.

  • Greedy action이 Hit인 상황인 것이다.

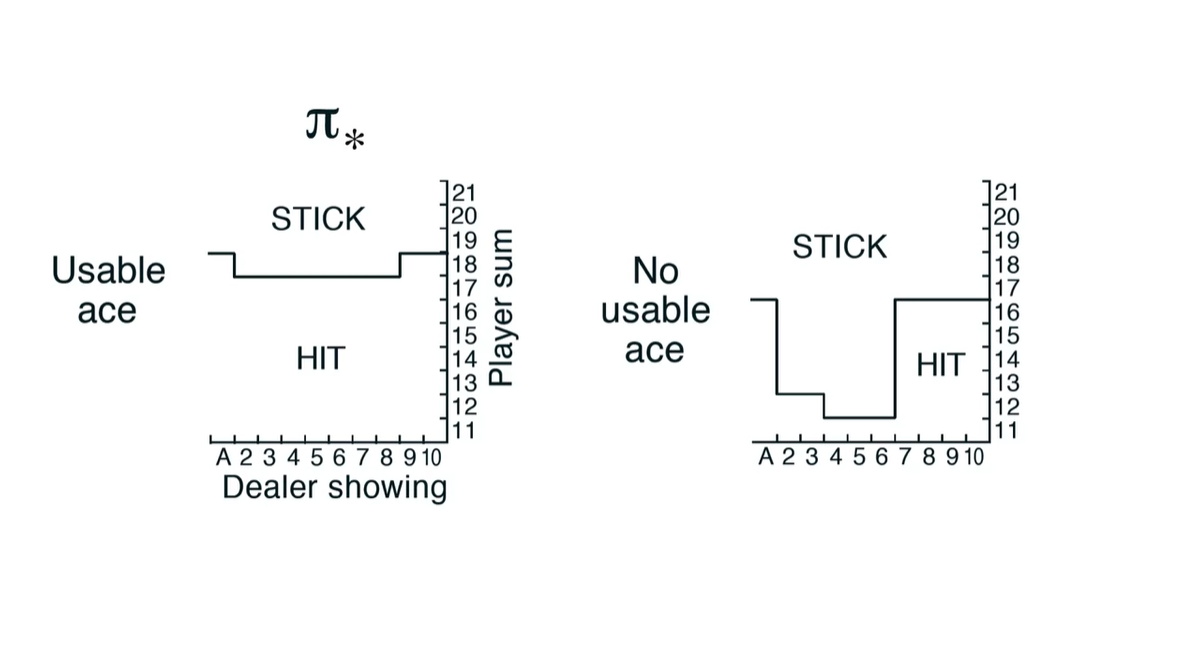
• Ace를 사용할 수 있는 상황과 그럴 수 없는 상황에서의 action 선택지로 policy를 유추해보자.

  • Ace가 존재하는 상황에서는 Hit 선택지의 action probability 가중치가 그렇지 않을 때의 상황에 비해 높다.

    • 즉, Ace가 11 혹은 1의 값으로 대체될 수 있다는 경우의 수가 어느 정도 Hit 선택지의 자신감을 심어준 것인가..?

• Summary

Exploration Methods for Monte Carlo

Epsilon-soft policies

• Epsilon-soft policies에 대하여 알아보자.

• 이번 강의에서는 exploring을 수행하기 위한 시작 지점을 현실에서는 알아낼 수 없다는 점에 대해 주목한다.

  • Monte Carlo control에서 exploration을 어떻게든 수행하기 위한 alternative method인 $\epsilon$-soft policy 방법론에 대해 알아보도록 하자.

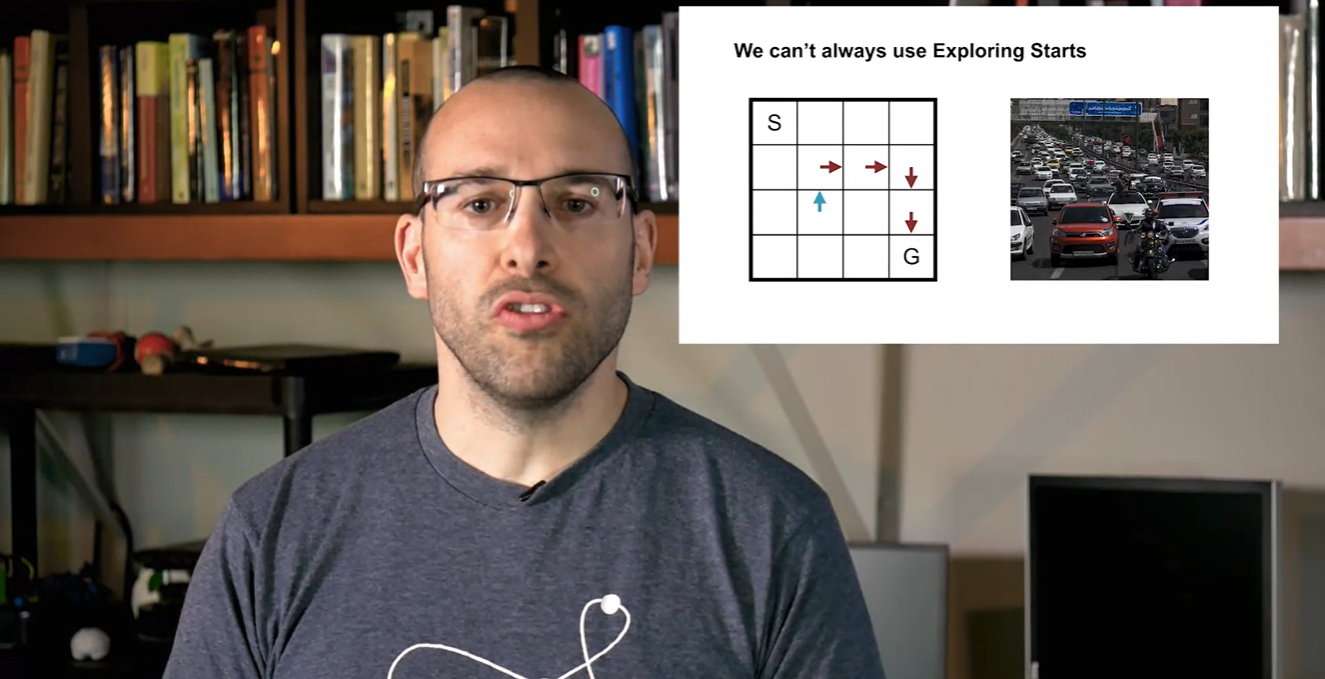
• 위에서 보았던 board판 내에서의 움직임은 Start 지점을 initialize하여 exploration할 수 있는 MC control이었다.

  • 그러나 driving car에서의 상황과 같은 현실 세계에서의 문제들은 시작 지점을 설정하기가 매우 어렵다.

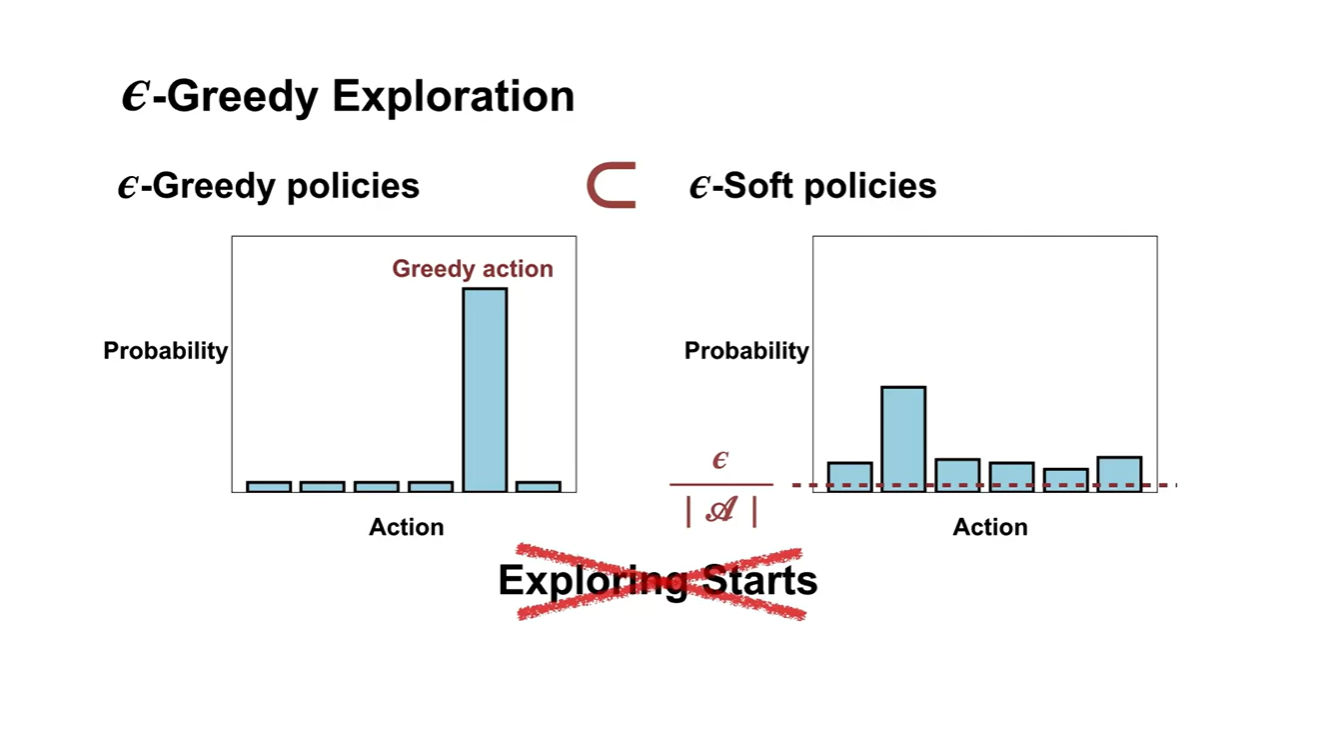
• 그래서 나온 방법론이 바로 $\epsilon$-Soft policies control이다.

  • Exploring starts를 설정하지 못할 때 사용되는 방법론으로, 지금까지 greedy하게 선택했던 방법론이 $\epsilon$-Soft policies에 포함된다고 보면 된다.

• $\epsilon$-Soft policies에서는 policy $\pi$를 stochastic하게 바라본다.

  • Action에 대한 선택지를 $\epsilon$값을 설정하여 미세하게 더 탐색할 수 있도록 말이다.

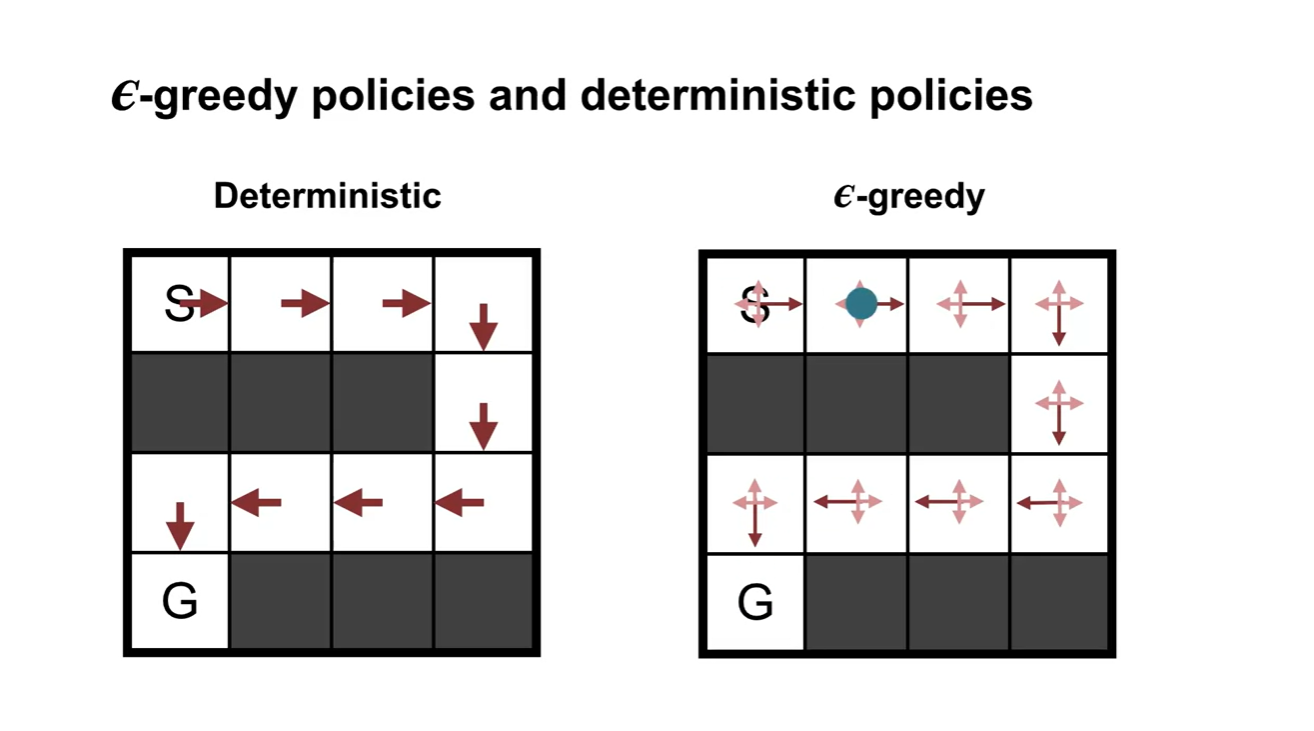
• 기존 Deterministic한 방법론과 $\epsilon$-greedy 방법론의 차이는 아래와 같다.

  • Deterministic은 policy 경로가 매우 hard하게 정해져있는 반면, $\epsilon$-greedy는 $\epsilon$만큼의 미세 조정으로 다른 경로로 갔다가 돌아오기도 하는 선택을 하도록 만든다.

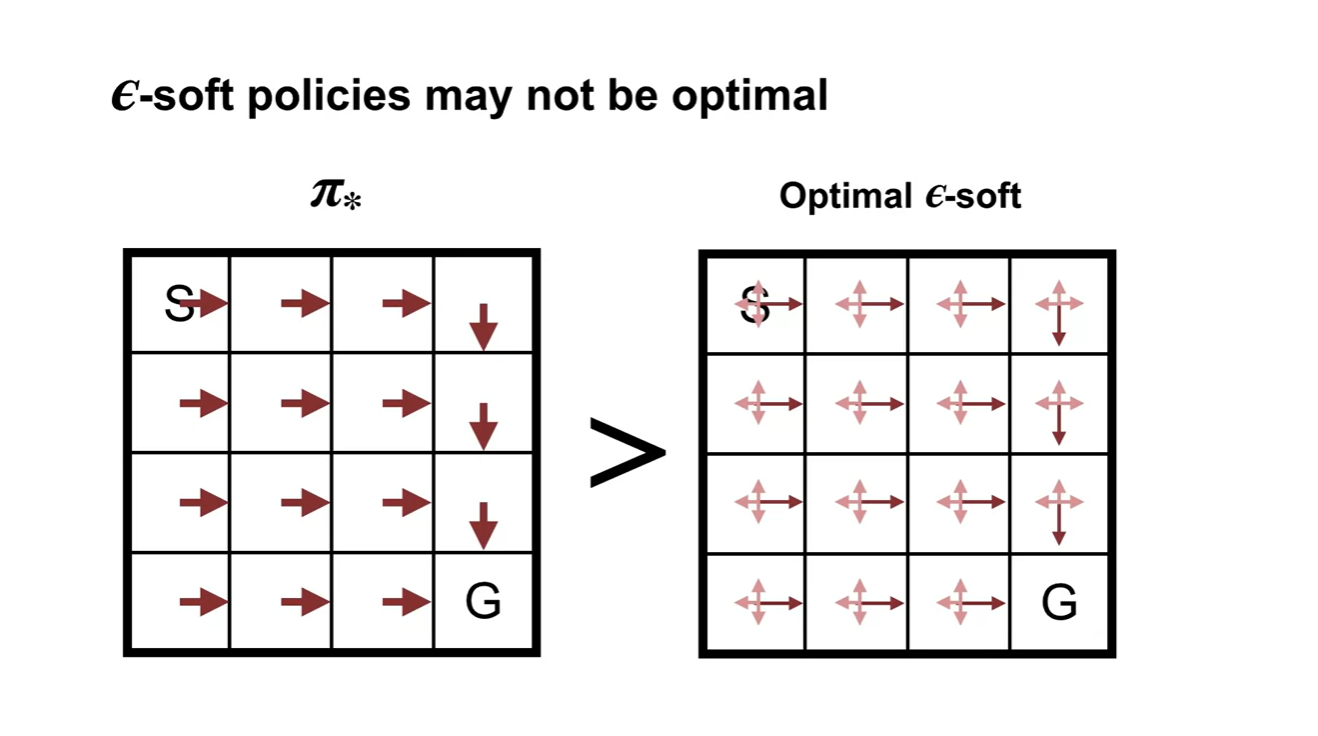
• $\epsilon$-Soft policies를 따르는 optimal policy는 기존 optimal policy $\pi_{*}$에 비해 soft하다.

  • 실제 optimal policy가 아닐 수도 있으나, exploration의 관점에서는 선택지를 확률적으로 더욱 넓힐 수 있다는 장점이 존재한다.

• $\epsilon$-Soft policies를 따르는 MC control의 알고리즘이다.

  • $\pi$에 distribution을 initialize하여 할당하고, $\epsilon$값에 따라 적절히 다른 선택을 하도록 유도하는 알고리즘이다.

• Summary

Off-policy Learning for Prediction

Why does off-policy learning matter?

• 이번에는 off-policy learning과 on-policy learning에 대해 비교 및 정리한다.

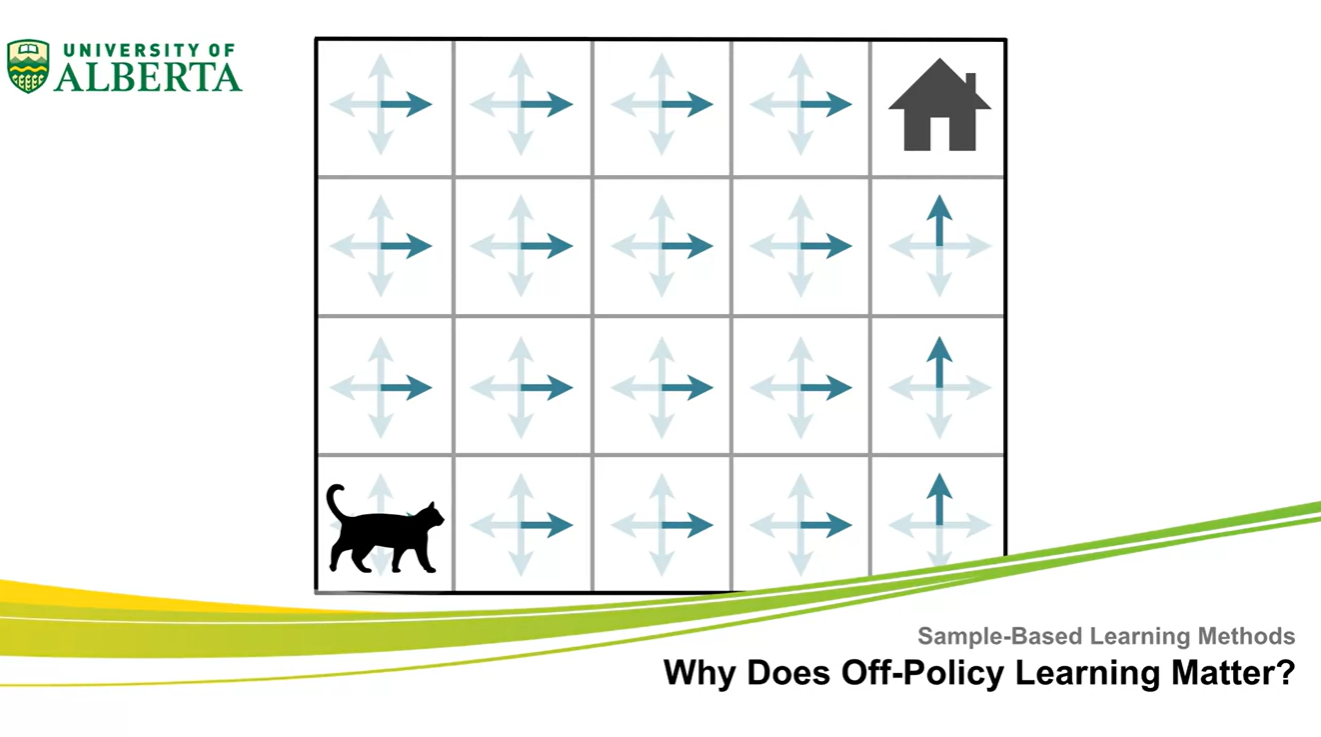
• 이번 강의에서는 off-policy learning을 이해하고, target policy와 behavior policy에 대해 구분짓게 될 것이다.

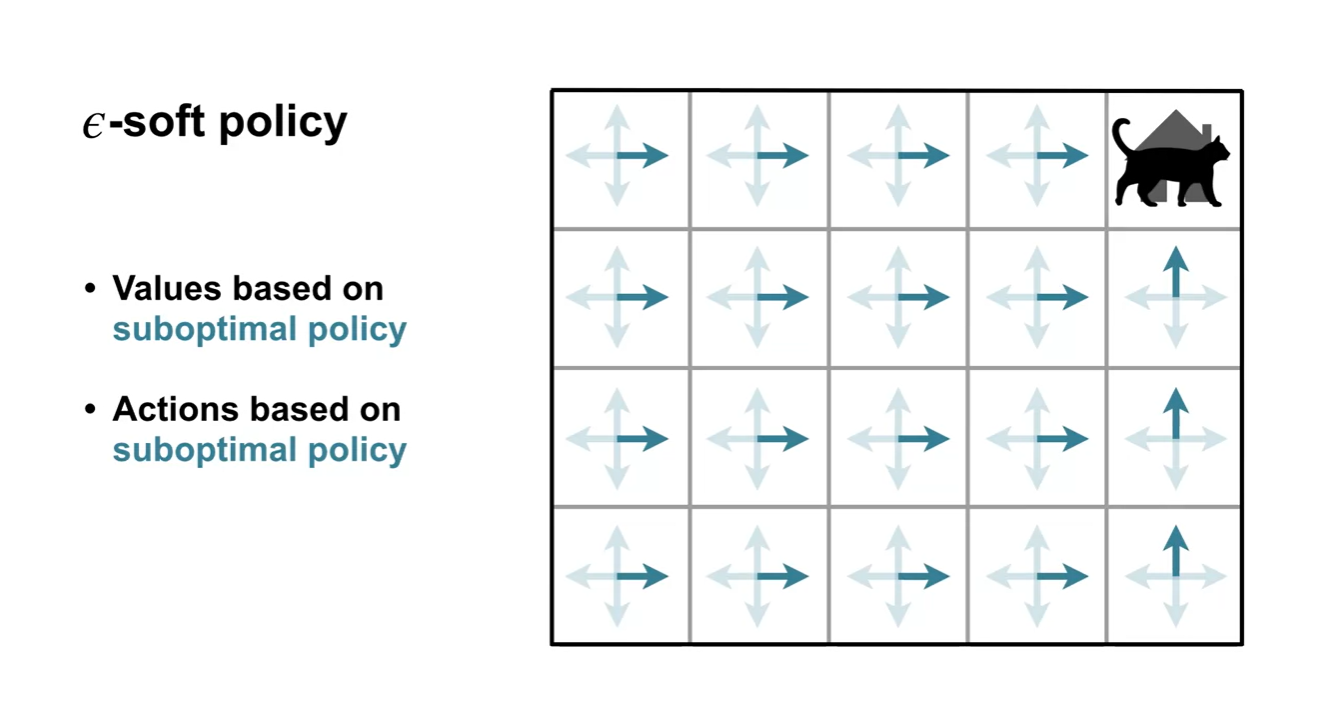
• $\epsilon$-soft policy는 suboptimal policy를 따르는 Values와 Actions를 활용한다.

  • 따라서 최적의 정책(optimal policy)이 아니라는 단점이 존재한다.

• 지금까지 배웠던 내용은 사실 On-policy를 따르는 방법론에 대해 소개한 것이다.

  • On-policy는 optimal policy를 찾기 위해 value function을 이용하여 evaluation하고 improve(by selected action)하는 과정이었다.

  • Off-policy는 "다른" policy를 따를 때 생성되는 데이터를 통해 policy를 학습한다는 점에서 차이를 갖는다.

    • 즉, uniform distribution policy 내에서 action을 random하게 선택하도록 하여 optimal policy를 찾는 방법론이라 볼 수 있다.

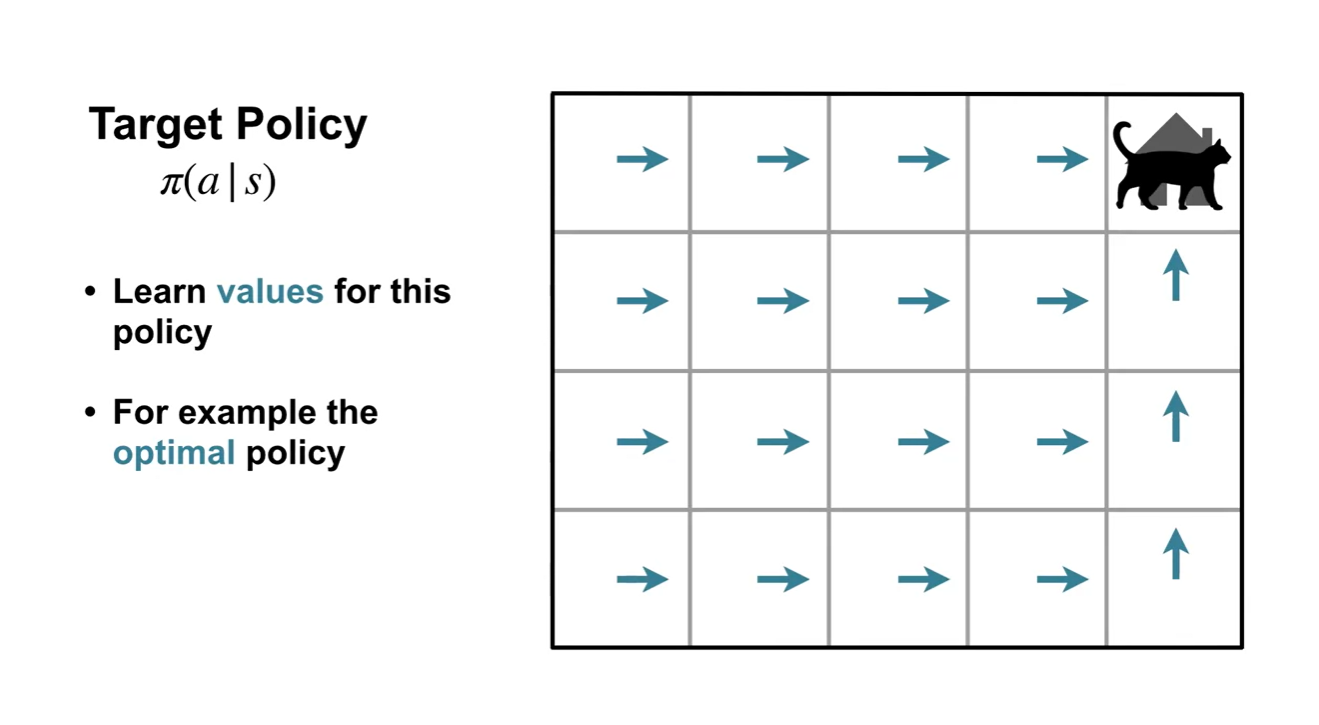
• Target policy $\pi(a|s)$는 Agent가 학습하는 policy를 대상으로 한다.

  • Agent가 학습하는 value function은 대상 policy를 기반으로 한다.

    • 예를 들어, Agent가 action을 선택하는 데 사용하는 optimal policy를 말할 수 있다.

• Behavior policy $b(a|s)$는 Agent가 action을 선택하도록 하는 역할을 한다.

  • Exploratory policy 즉, uniform distribution을 따르는 policy로 설정할 수 있다.

• Target policy는 Agent가 경험하는 경로가 매우 한정적이다.

  • Behavior policy를 따르도록 하면 훨씬 더 많은 경로를 경험하도록 함으로써 exploration을 촉진한다는 점에서 차이가 있다.

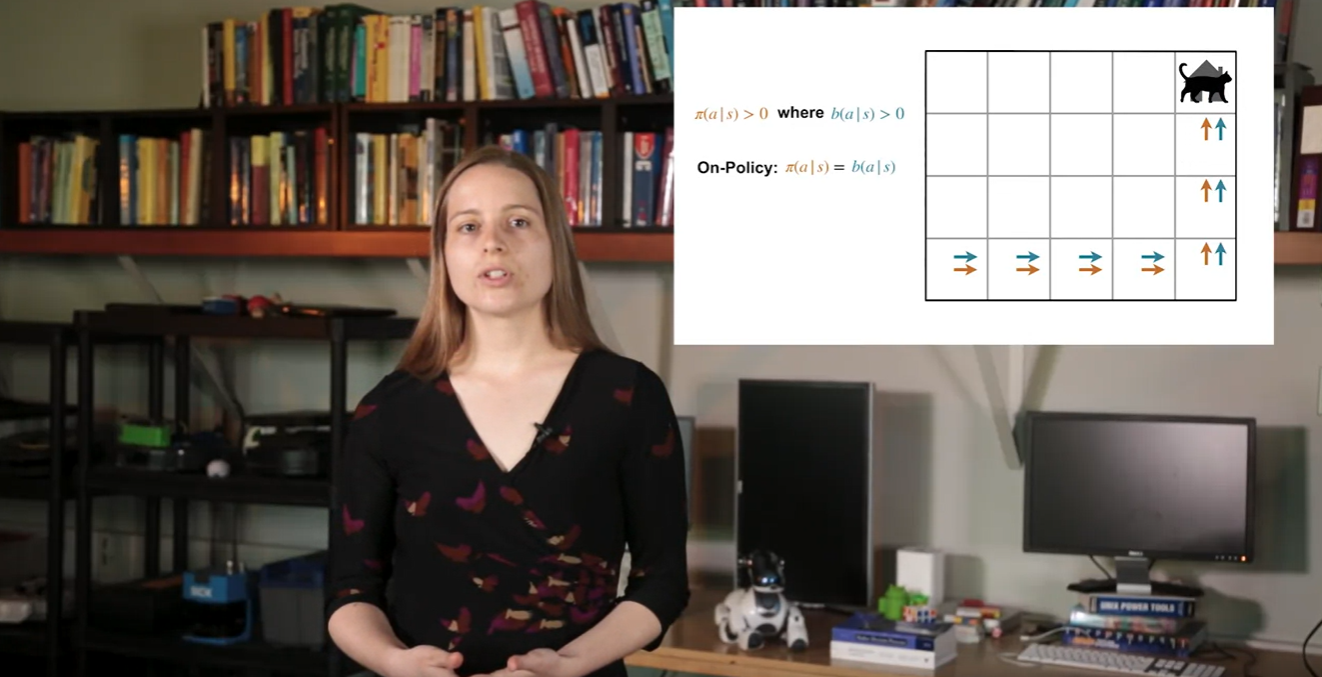
• $\pi(a|s)$는 어떠한 state가 주어진 상황에서, 어떠한 action을 선택할지 대상 policy 내에서 선택할 확률을 말한다.

  • $b(a|s)$는 어떠한 state가 주어진 상황에서 해당 action을 선택할 확률을 말한다.

• 만약 On-policy라면 $\pi(a|s)$와 $b(a|s)$는 같은 경로를 따르게 된다.

  • Off-policy 관점에서는 이를 엄격한 일반화로 본다.

• Summary

Importance Sampling

• Importance Sampling에 대해 알아보자.

• 이번 강의에서는 expected value of distribution을 추정하기 위해 different distribution인 sample distribution을 활용하는 방법의 타당성에 대하여 유도할 예정이다.

• 만약 sample $x$가 $b$를 따른다고 하고, expected value의 estimation이 $\mathbb E_{\pi} [X]$라고 하자.

  • Sample average $b$는 target distribution을 추정하는 데에 큰 역할을 하게 된다.

• $\mathbb E_{\pi} [X]$는 $\displaystyle \sum_{x \in X} x \pi(x)$를 구하는 과정이다.

  • $\displaystyle \sum_{x \in X} x \pi(x) \frac{b(x)}{b(x)} = \sum_{x \in X} x \frac{\pi(x)}{b(x)} b(x)$

    • $\displaystyle \frac{\pi(x)}{b(x)}$ 항이 바로 Importance sampling ratio다.
    • $\rho(x)$로 대체하겠다.

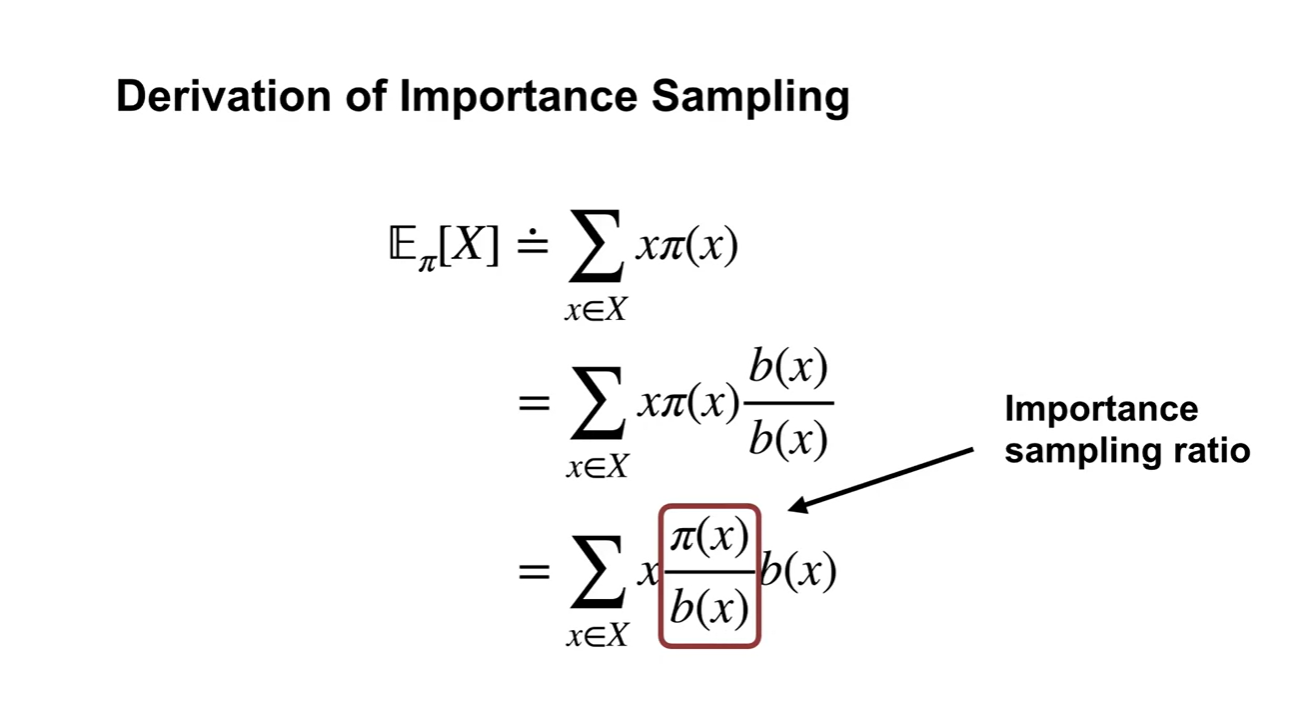
• 이로써 우리는 $\pi$를 따르는 실제 expected value를 sample space를 표현하는 $b$에 대한 expected value로 변형시켜 표현할 수 있게 되었다.

  • 기댓값의 정의에 의해 $\mathbb E_{\pi}[X]$는 $\mathbb E_{b}[X\rho(X)]$가 되었다.

• Data를 통해 Expected value를 계산하는 과정은 매우 간단하다.

  • n개의 samples가 존재한다면 $\displaystyle \frac{1}{n} \sum_{i=1}^{n} x_i \rho(x_i)$로 average 표현함으로써 기댓값을 계산하면 된다.

• 이 때 $\rho(x)$는 $\displaystyle \frac{\pi(x)}{b(x)}$임을 알아두자.

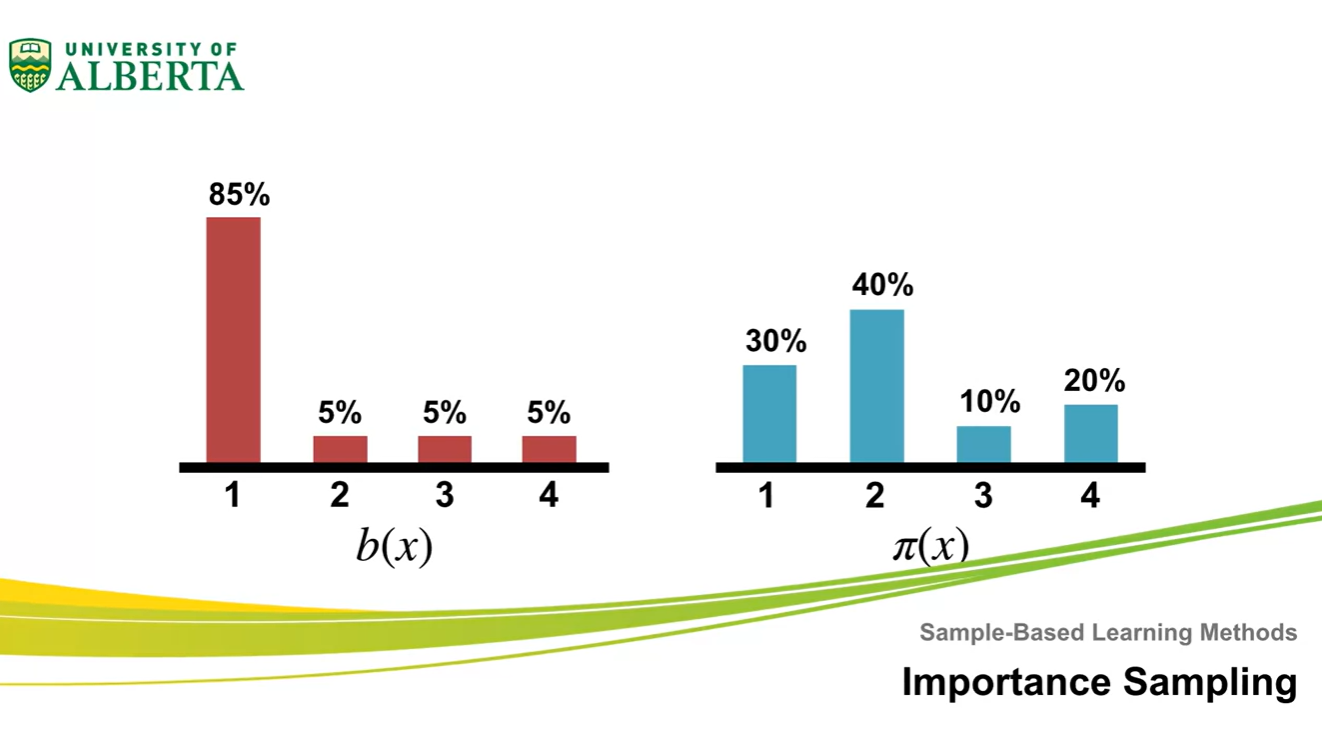
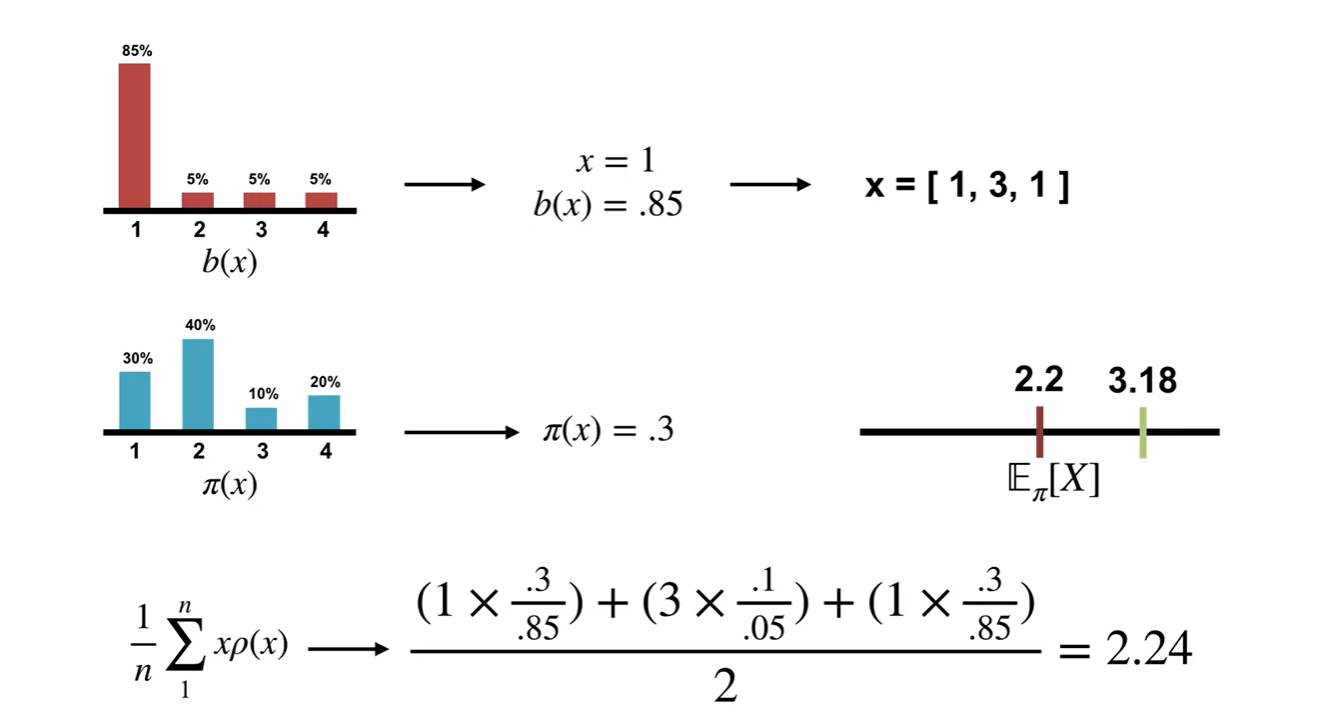
• 아래와 같은 $b$와 $\pi$ distribution이 존재한다고 해보자.

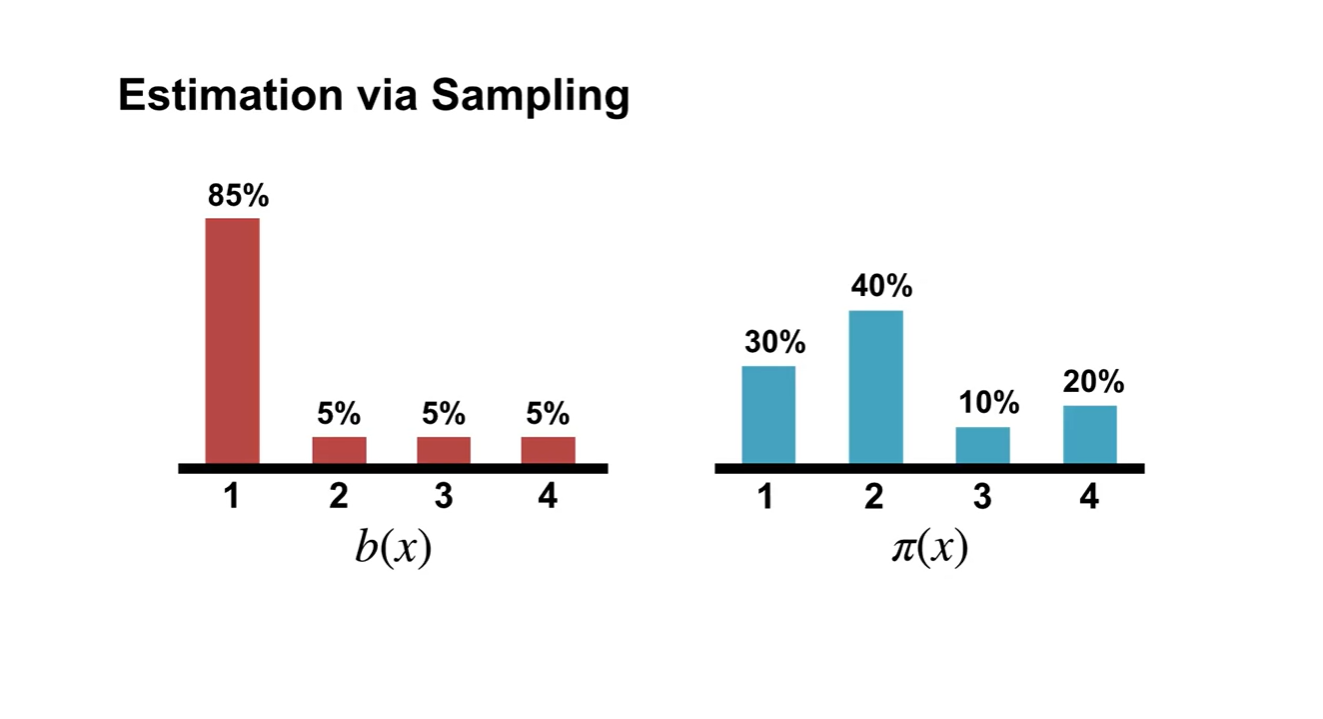
• 실제 Expected value는 갈색으로 표시된 $\mathbb E_{\pi}[X] = 2.2$ 지점이다.

  • Sample space인 $b(x)$ distribution에서 random variable $x=1$을 뽑았다고 가정하여 ratio에 따른 기댓값을 계산해 보았다.

    • $\displaystyle \frac{1}{n} \sum_{1}^{n} x \rho(x) = 1 \times \frac{.3}{.85} = 0.35$를 초록색으로 표시하였다.

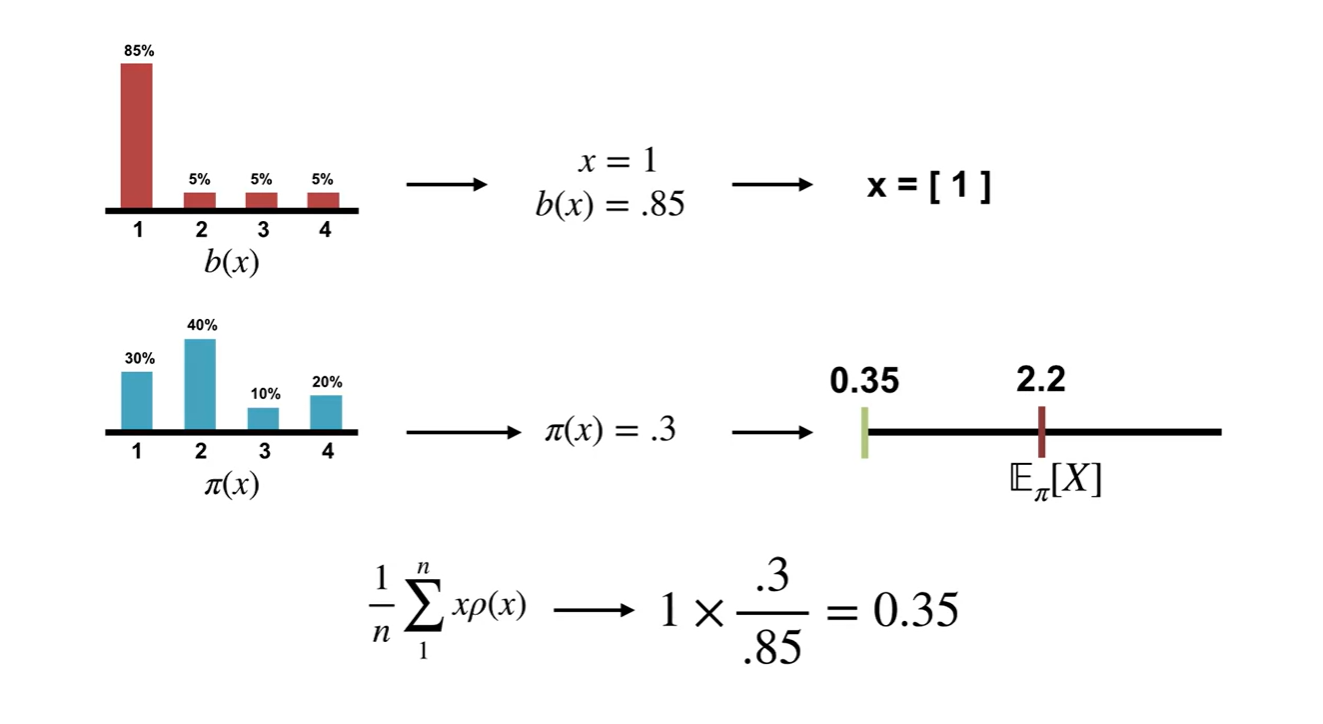
• 그 다음 random variable $x=3$이 뽑혔다고 가정해보자.

  • Samples의 기댓값을 계산하면 $\displaystyle \frac{1}{n} \sum_{1}^{n} x \rho(x) = \frac{(1 \times \frac{.3}{.85}) + (3 \times \frac{.1}{.05})}{2} = 3.18$이다.

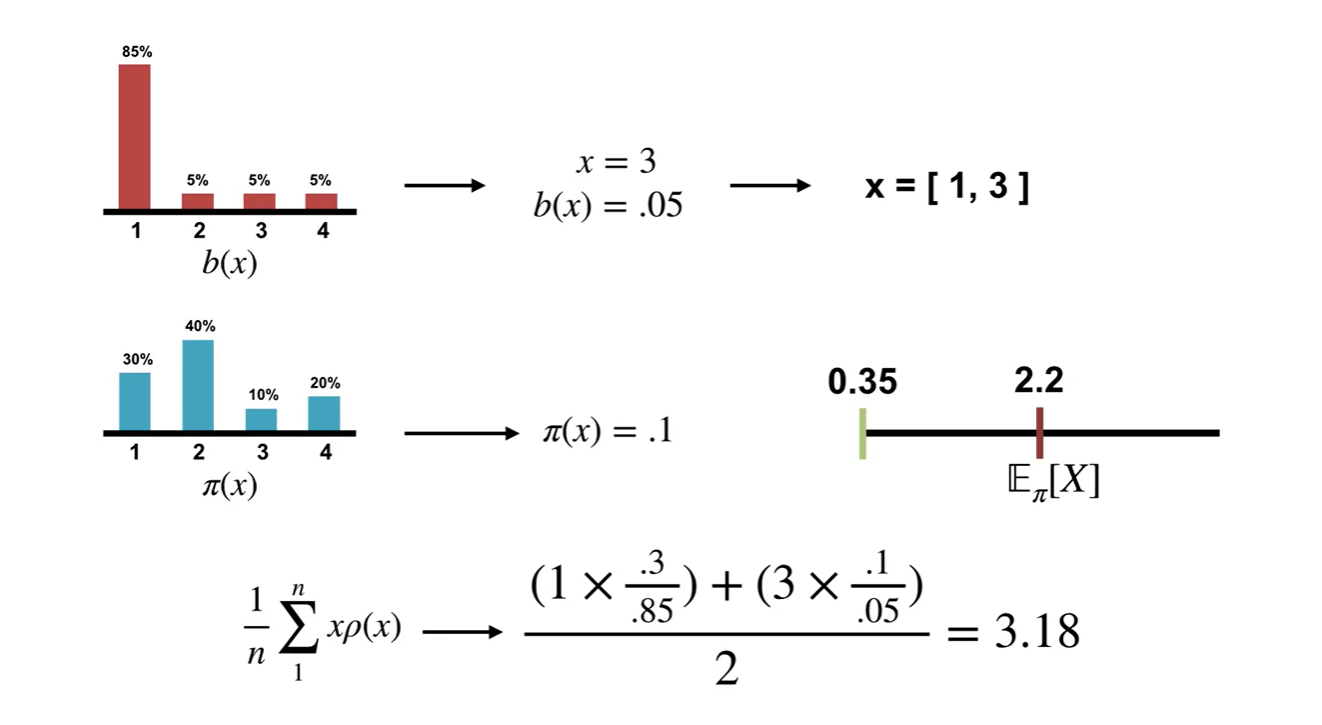
• 또 다음 random variable $x=1$이 뽑혔다.

  • 기댓값을 계산하면 $\displaystyle \frac{1}{n} \sum_{1}^{n} x \rho(x) = \frac{(1 \times \frac{.3}{.85}) + (3 \times \frac{.1}{.05}) + (1 \times \frac{.3}{.85})}{3} = 2.24$이다.

    • 이로써 $\pi$에서의 기대치를 꽤 잘 추정할 수 있게 되었다.

• Summary

Off-Policy Monte Carlo Prediction

• Off-Policy Monte Carlo Prediction에 대해 알아보자.

• 이번 강의에서는 정확한 returns를 계산하기 위해 importance sampling을 어떻게 사용할 수 있을 것인지에 대해 이해한다.

  • 또한 Off-policy learning을 위해 Monte Carlo prediction argorithm을 수정하여 정리할 것이다.

• Monte Carlo prediction은 다음과 같은 세 가지 색상의 경로로 움직이는 returns를 averaging하는 것을 말한다.

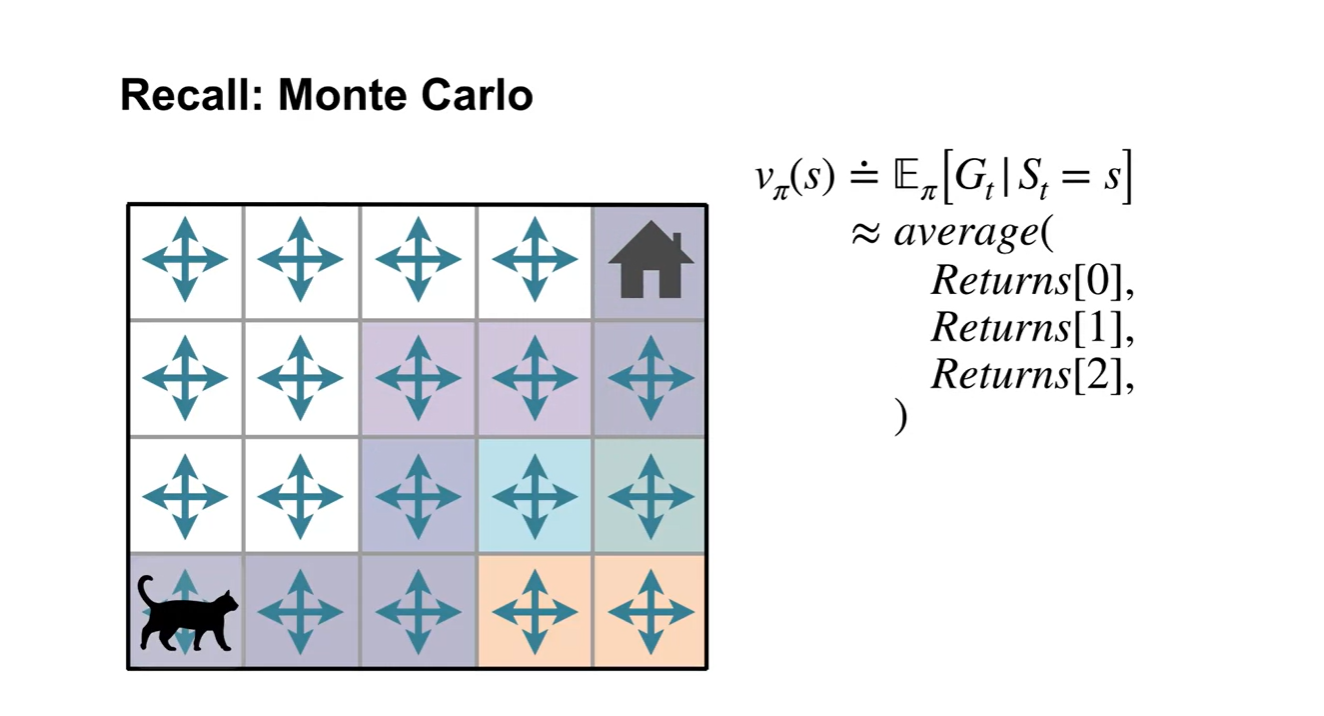
• 그러나 위에서 얻은 returns는 모두 $b$ space에서 sampling된 것이기 때문에 엄연히 말하자면 $v_{\pi}$와 같다고 말할 수는 없다.

  • Importance sampling에서 다루었듯이 $b$ space에서 sampling된 $\rho$값을 고려하여 기댓값을 계산하여야 한다.

• $\rho$값은 under $\pi$ / under $b$ ratio를 말한다.

  • Expected value는 $\mathbb E_b[\rho G_t | S_t=s]$로 계산한다.

• Actions는 behavior $b$에 대해 sampling되었다.

  • 기존 Policy 수식은 $S_t$, $A_t$가 주어졌을 때 그 다음 states, actions의 상황에 놓일 확률을 모델링한다.

• Behavior $b$에 관한 chain-rule로 풀어서 정리하면 다음과 같이 전개된다.

  • $b(A_t|S_t)p(S_{t+1}|S_t,A_t)b(A_{t+1}|S_{t+1})p(S_{t+2}|S_{t+1},A_{t+1}), ...$

    $\rightarrow \displaystyle \Pi_{k=t}^{T-1} b(A_k|S_k) p(S_{k+1}|S_t, A_t)$

• 우리가 구하고 싶은 $\rho$는 under $\pi$ / under $b$로 정의한다.

  • 이 값은 $\displaystyle \frac{\Pi_{k=t}^{T-1} \pi(A_k|S_k) p(S_{k+1}|S_t, A_t)}{\Pi_{k=t}^{T-1} b(A_k|S_k) p(S_{k+1}|S_t, A_t)}$로 정리할 수 있고,

    약분하면 $\displaystyle \frac{\Pi_{k=t}^{T-1} \pi(A_k|S_k)}{\Pi_{k=t}^{T-1} b(A_k|S_k)}$로 표현된다.

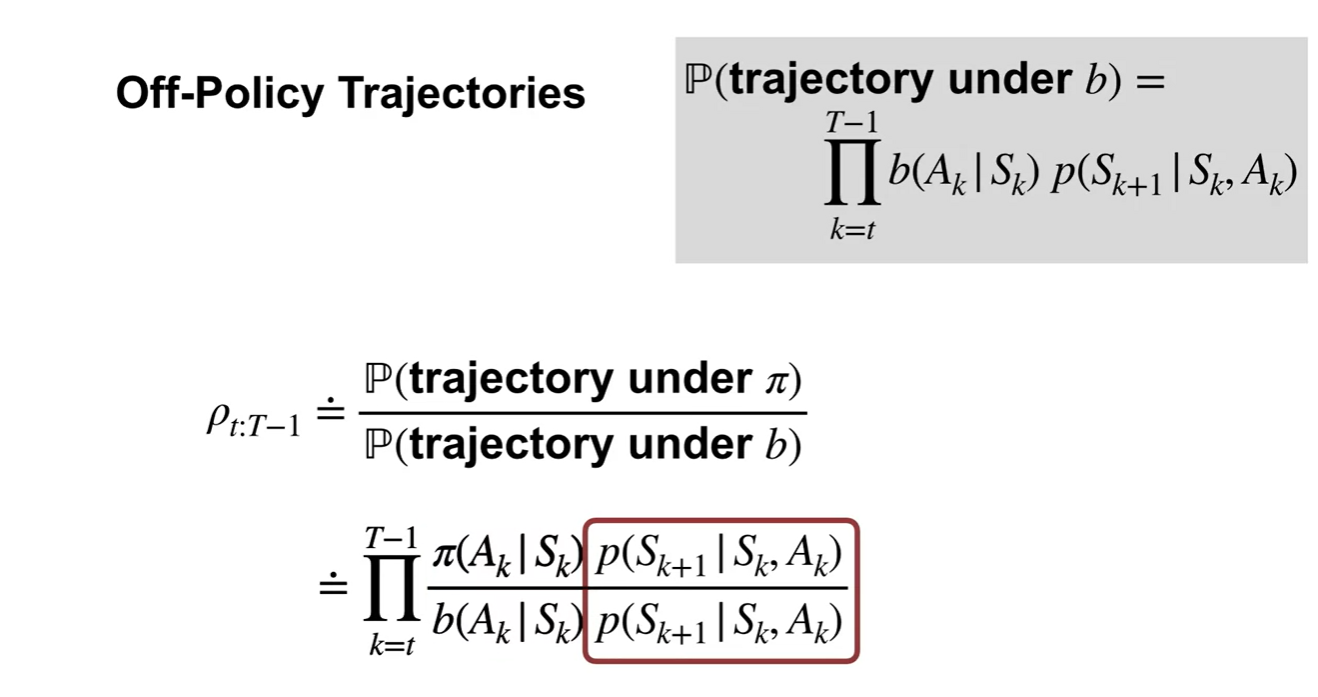
• 따라서 Off-Policy Trajectories는 $\displaystyle \frac{\Pi_{k=t}^{T-1} \pi(A_k|S_k)}{\Pi_{k=t}^{T-1} b(A_k|S_k)}$로 최종적으로 나타낸다.

• 이는 behavior $b$에 대하여 sampling된 데이터의 기댓값이라 말할 수 있다.

  • $\mathbb E_b [\rho_{t:T-1}G_t|S_t=s] = v_{\pi}(s)$

• 기존 MC prediction에서의 value estimation은 아래와 같은 알고리즘으로 구현되어 있다.

  • $G \leftarrow \gamma G + R_{t+1}$

• Off-policy MC prediction 알고리즘은 sample space와 real space의 ratio를 고려한 $W$값까지 함께 returns 값에 추가시킨다.

  • $G \leftarrow \gamma WG + R_{t+1}$

  • $W \leftarrow W \displaystyle \frac{\pi(A_t|S_t)}{b(A_t|S_t)}$

• $\rho_{t:T-1}$를 incremental하게 계산하는 방법은 다음과 같이, 가장 최근의 과거로부터 initial $t$까지의 값을 곱해주는 과정으로 전개된다.

  • $W_{t+1} \leftarrow W_t \rho_t$

• Summary

---

• 출처 : [Coursera] Reinforcement Learning Specialization