Temporal Difference Learning Methods for Prediction

Introduction to Temporal Difference Learning

What is Temporal Difference (TD) learning?

• Temporal Difference(TD) learning에 대해 배워보도록 하자.

• 이번 강의에서는 TD learning의 정의와 TD(0) 알고리즘에 대해 이해해 볼 예정이다.

• 기존 value estimation은 최종 return $G_t$를 통해 업데이트 되었다.

  • $V(S_t) \leftarrow V(S_t) + \alpha(G_t - V(S_t))$

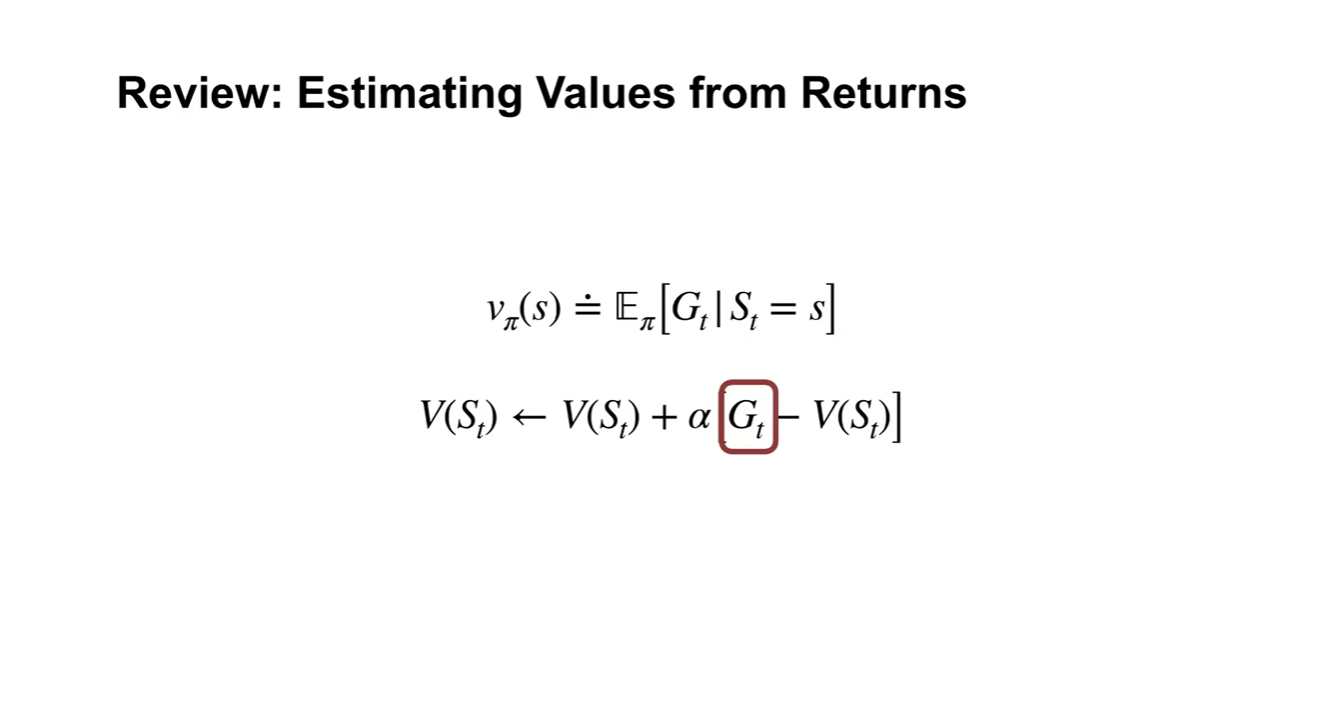
• Boosttrapping하여 전개하면 $t+1$ 시점에서의 return $G_{t+1}$로 연속된 수식이 정리된다.

  • $v_{\pi}(s) = R_{t+1} + \gamma v_{\pi}(S_{t+1})$

• TD learning은 최종 return인 $G_t$를 통해 업데이트하는 것이 아니라, 바로 다음 state에서의 value인 $R_{t+1} + \gamma v_{\pi}(S_{t+1})$를 return으로 참조하여 업데이트 한다.

• $R_{t+1} + \gamma v_{\pi}(S_{t+1})$를 $\delta_t$로 치환하면 해당 time step에서 얻어진 바로 다음 state에서의 return과의 차이로 해석할 수 있다.

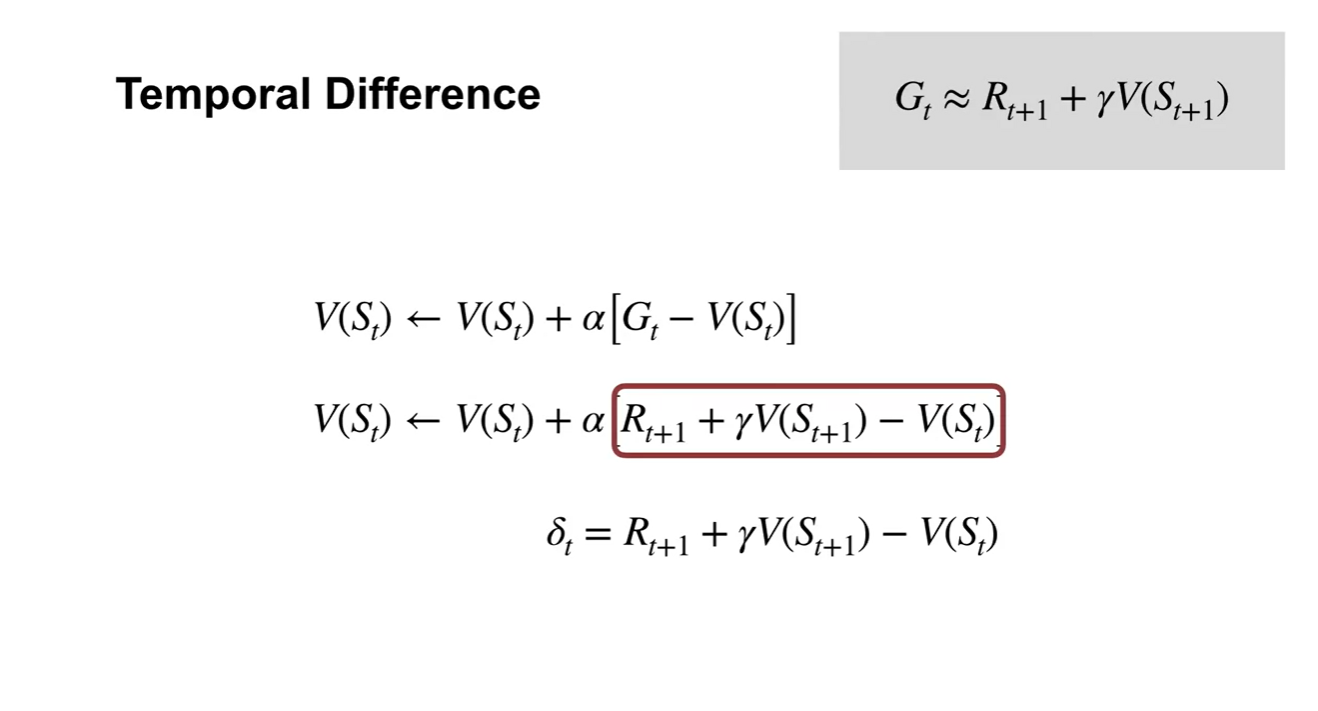
• 아래 그림의 애니메이션 상에서는 $V_{\pi}(S_{t+1})$가 실제 expected value인 $\mathbb E_{\pi}[G|S=s_{t+1}]$에 점점 가까워지는 것을 볼 수 있다.

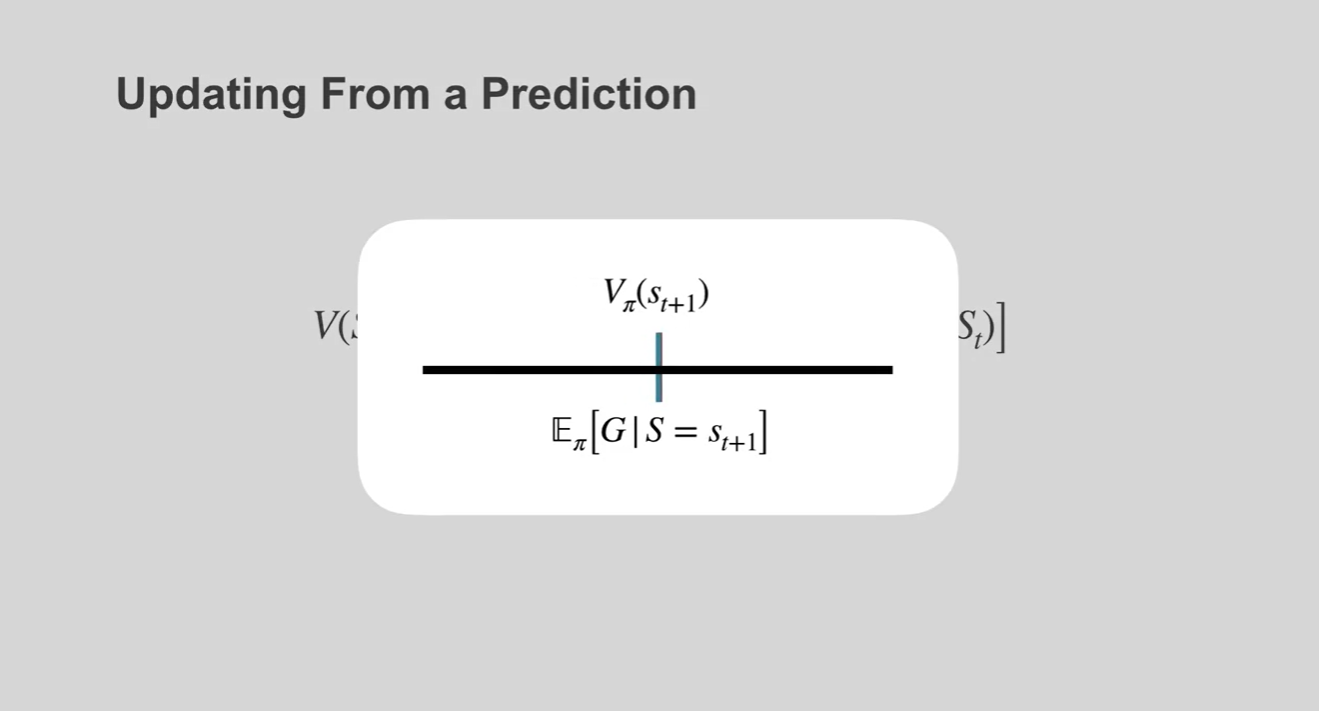
• DP 알고리즘은 environment 내에서 갈 수 있는 모든 경우의 수를 계산해 value를 업데이트 하였다.

  • TD 알고리즘은 바로 다음 state에서의 value와의 차이를 통해 업데이트 한다는 점이 다르다.

• 1-Step TD는 1번의 State, Action 뒤에 얻게 되는 Reward, new State로 업데이트 된다.

• 이러한 알고리즘을 TD(0)라고 한다.

  • 뒤에서 다루겠지만 parameter로 설정되는 TD($\lambda$)에서의 $\lambda$가 0일 때의 상황을 가리킨다.

    • $\lambda$는 얼마나 먼 미래까지 고려할 것인지를 결정하는 parameter라는 점만 알아두자.

• Summary

Advantages of TD

The advantages of temporal difference learning

• TD의 이점이 무엇인지 알아보자.

• 이번 강의에서는 online TD learning의 이점에 대해 이해하고 DP, MC와의 차이점을 비교해보도록 하자.

• Driving Home example을 생각해보자.

  • 회사로부터 차를 타고 출발해 집으로 가는 상황을 가정해보는 것이다.

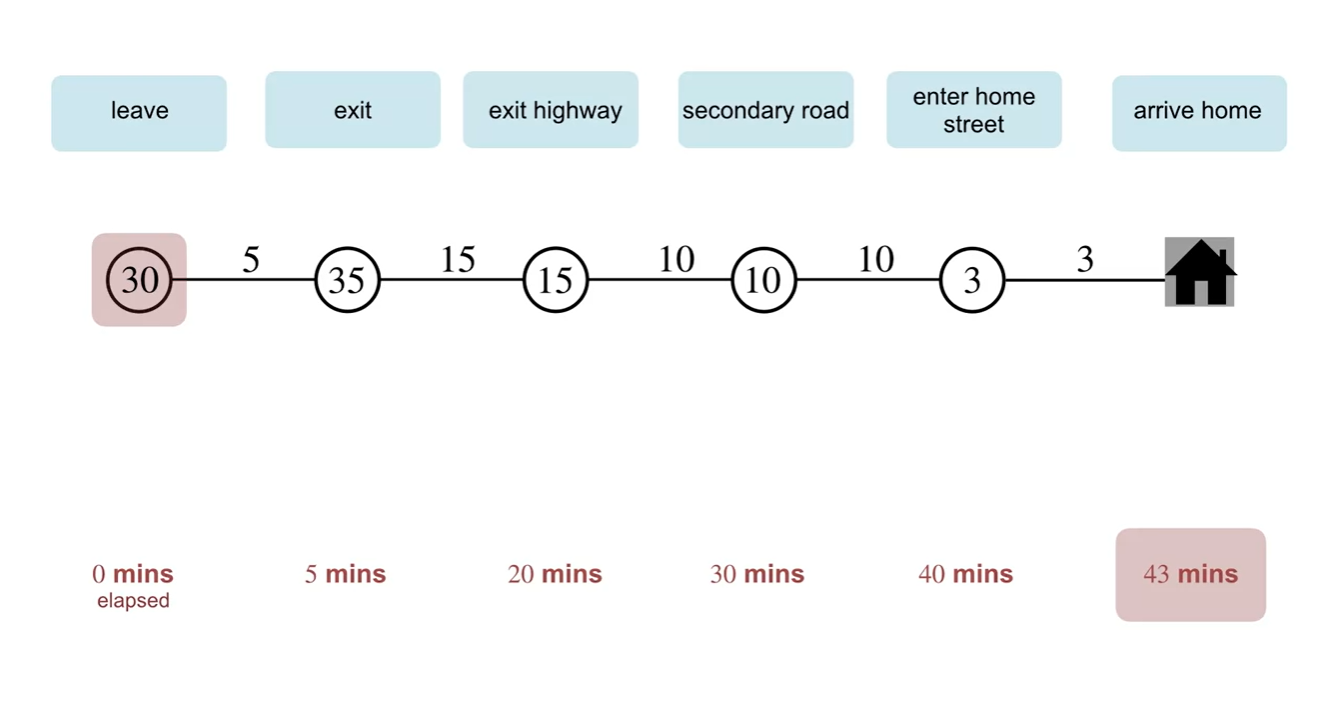
• 노드에는 각 State에 놓인 Agent가 예상하는 도착 시간이 적혀 있고, 간선에는 각 state로 이동했을 시 발생하는 실제 걸린 시간을 Reward로 설정한다.

  • 아래 빨간색으로 적힌 시간은 첫 state에서부터 걸린 시간을 총합하여 나타낸 값이다.

    • 해석하자면 회사에서 leave한 순간부터 Agent는 30분 뒤 집에 도착할 것이라 예상했으나, episode가 끝나고 난 뒤 총 43분이 걸렸음을 알게 된 것이다.

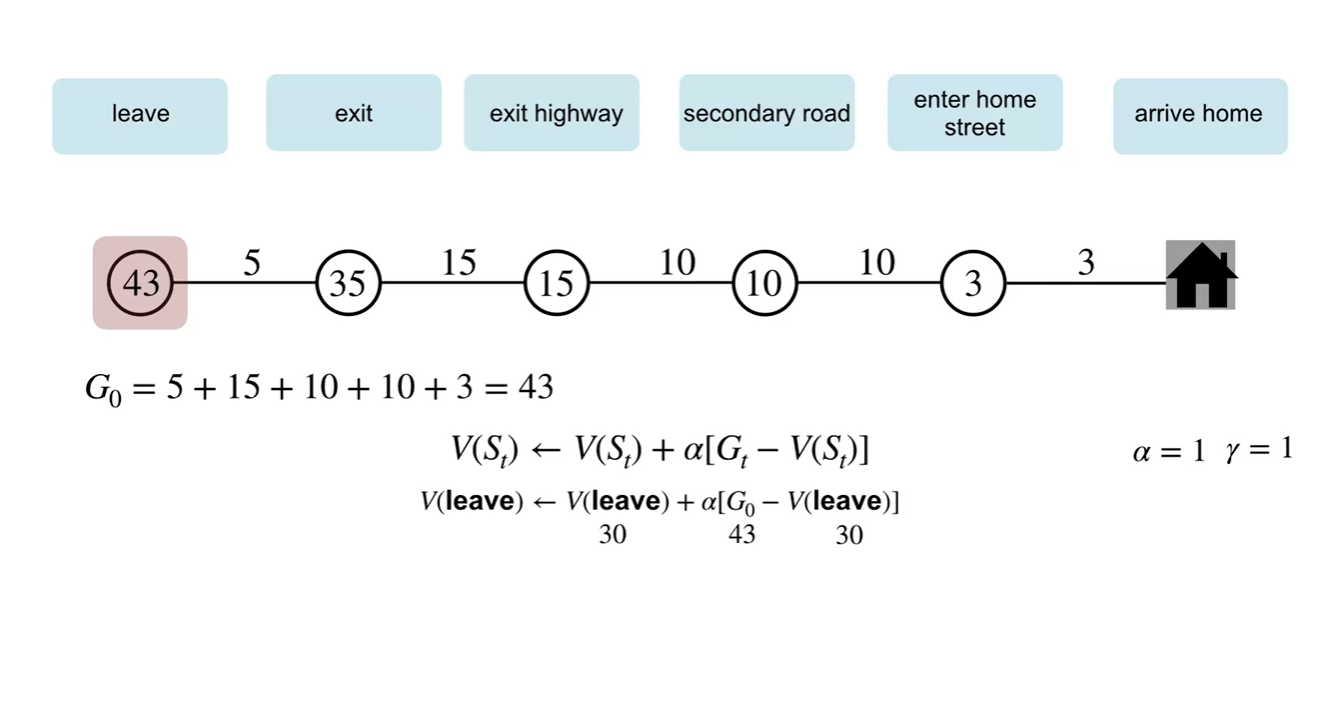
• MC 방식으로 업데이트하는 과정을 살펴보자.

  • 최종 return인 $G_0$는 43분이며, $G_0$와 각 state에서의 value를 빼서 업데이트 하는 과정을 볼 수 있다.

    • 이 때, 감쇠 상수 $\alpha$와 $\gamma$는 각각 1로 설정한다.

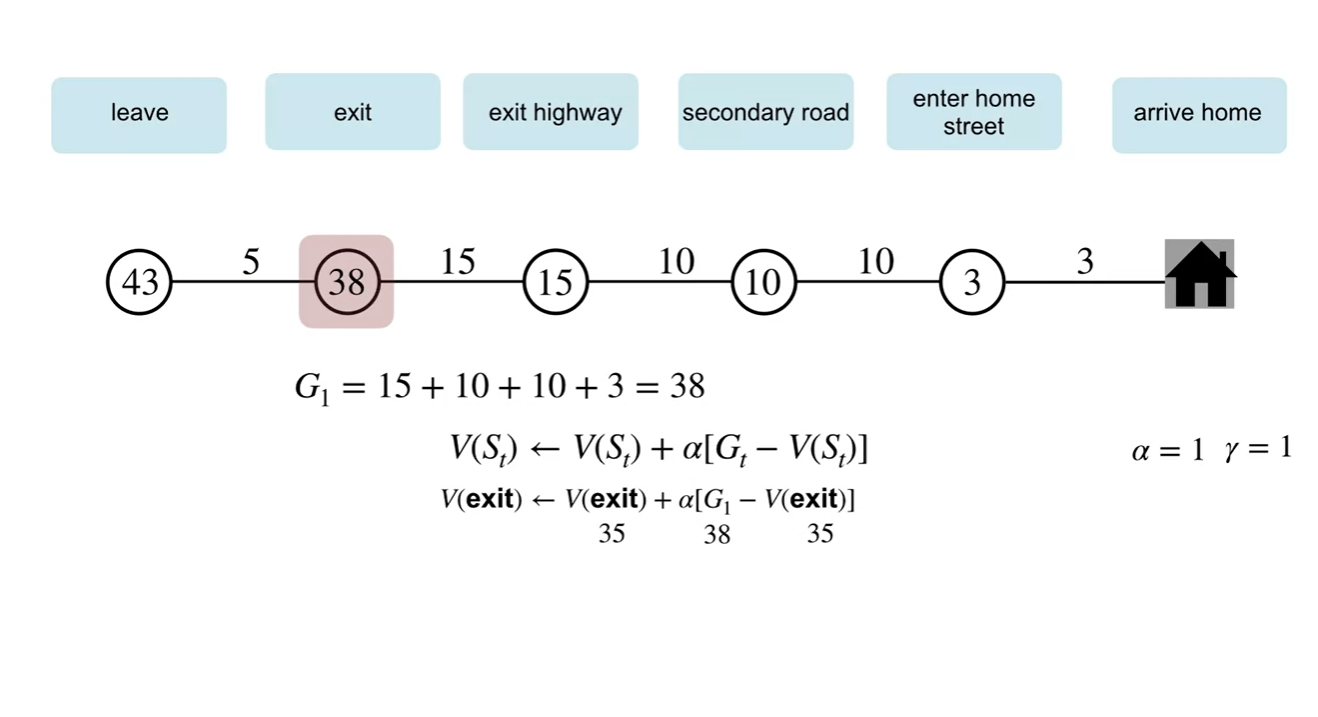
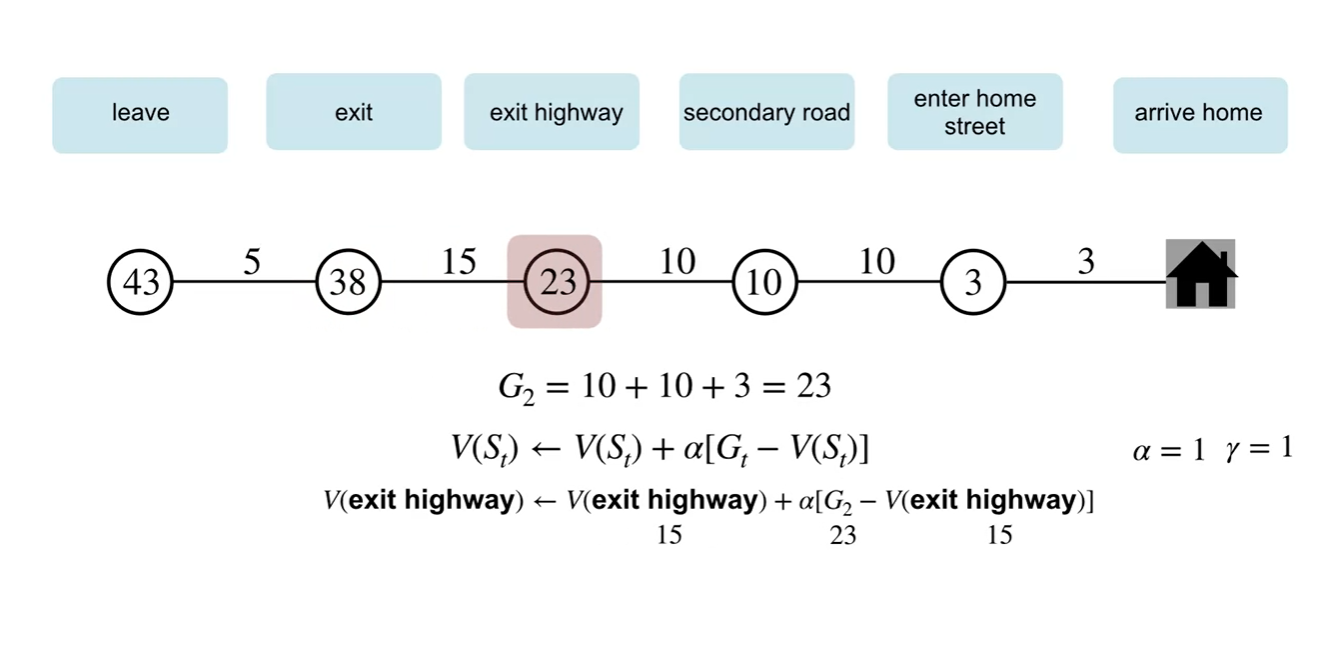
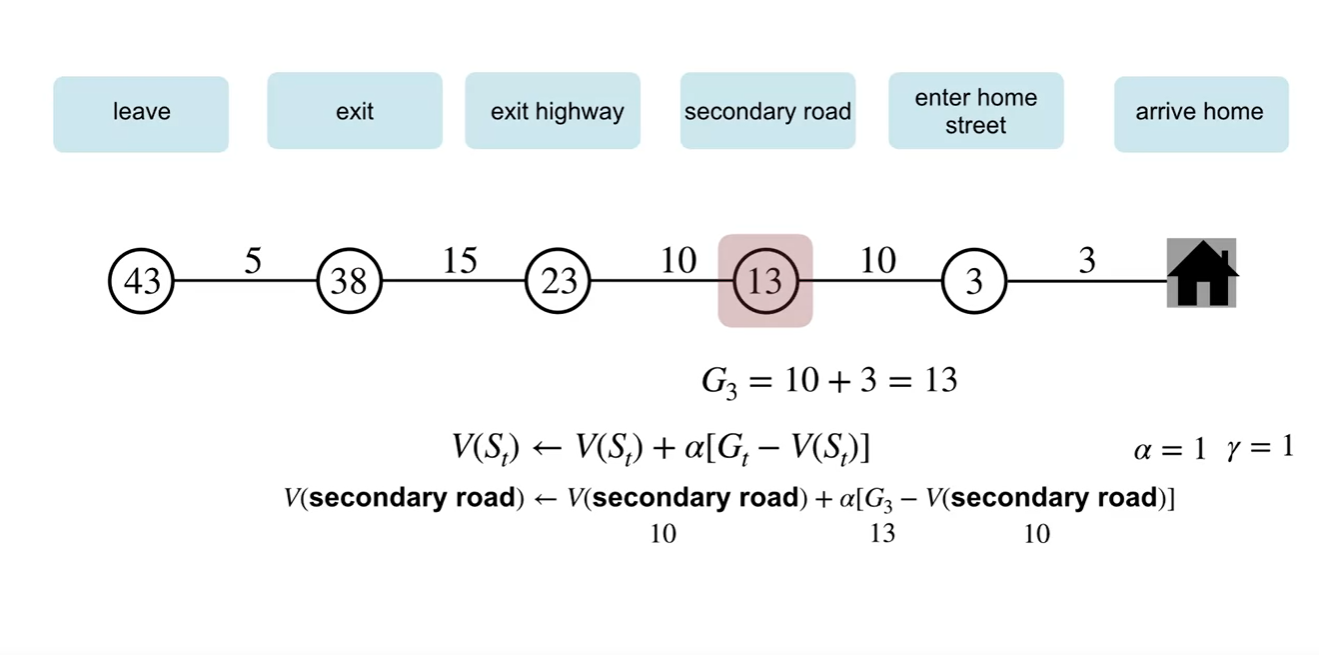
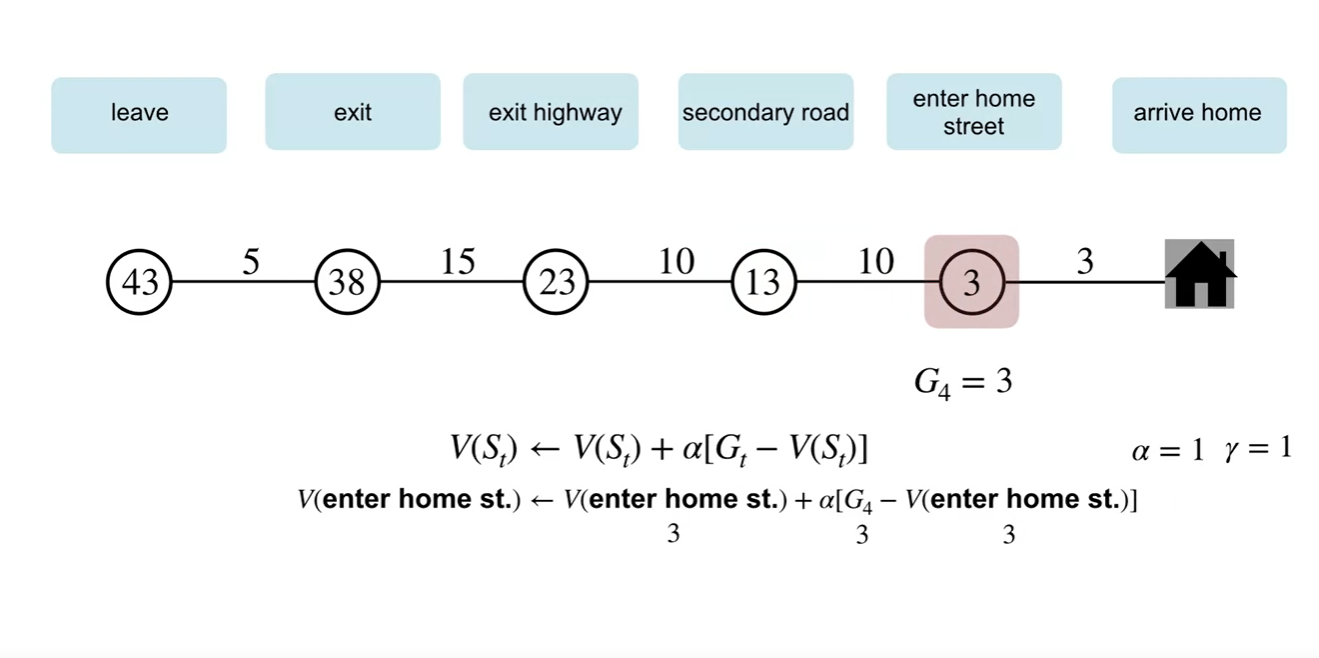
• MC 방법은 episode가 끝나기까지 기다렸다가 learning(updating)을 시작해야 한다는 특징이 있다.

• TD 방식으로 업데이트하는 과정을 살펴보자.

  • 바로 다음 state에서의 reward와 value를 이용하여 업데이트 하는 과정을 볼 수 있다.

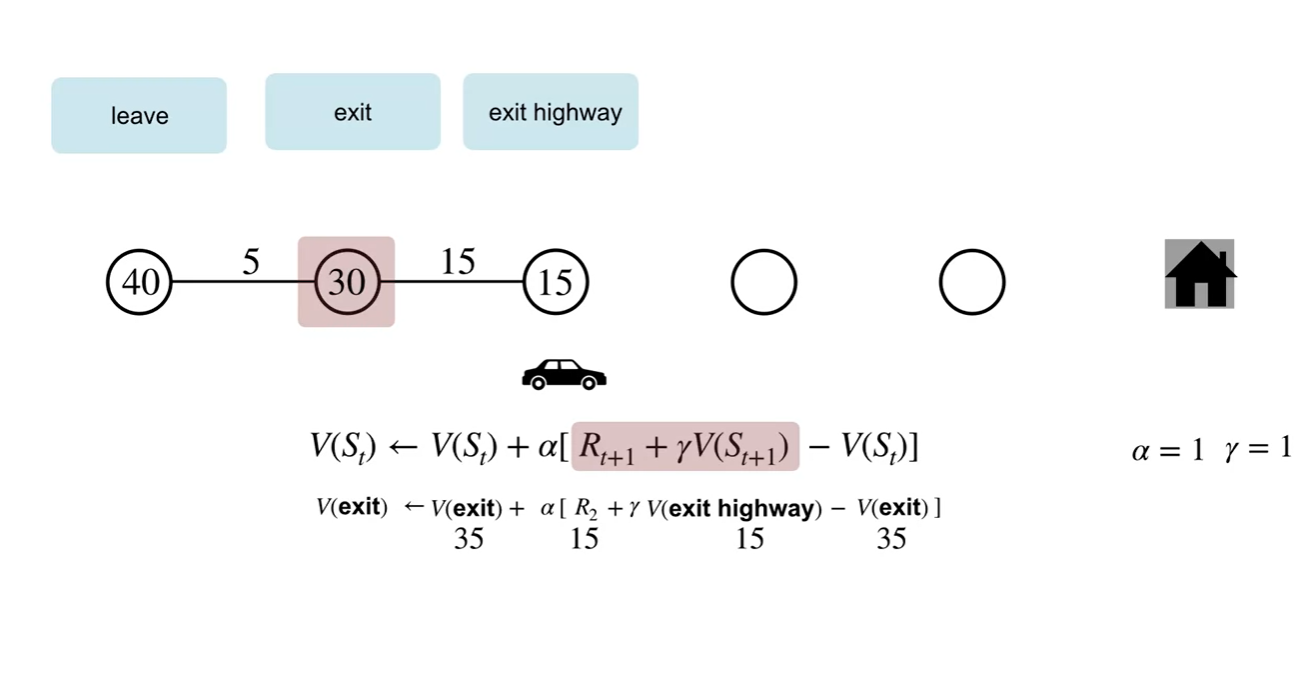
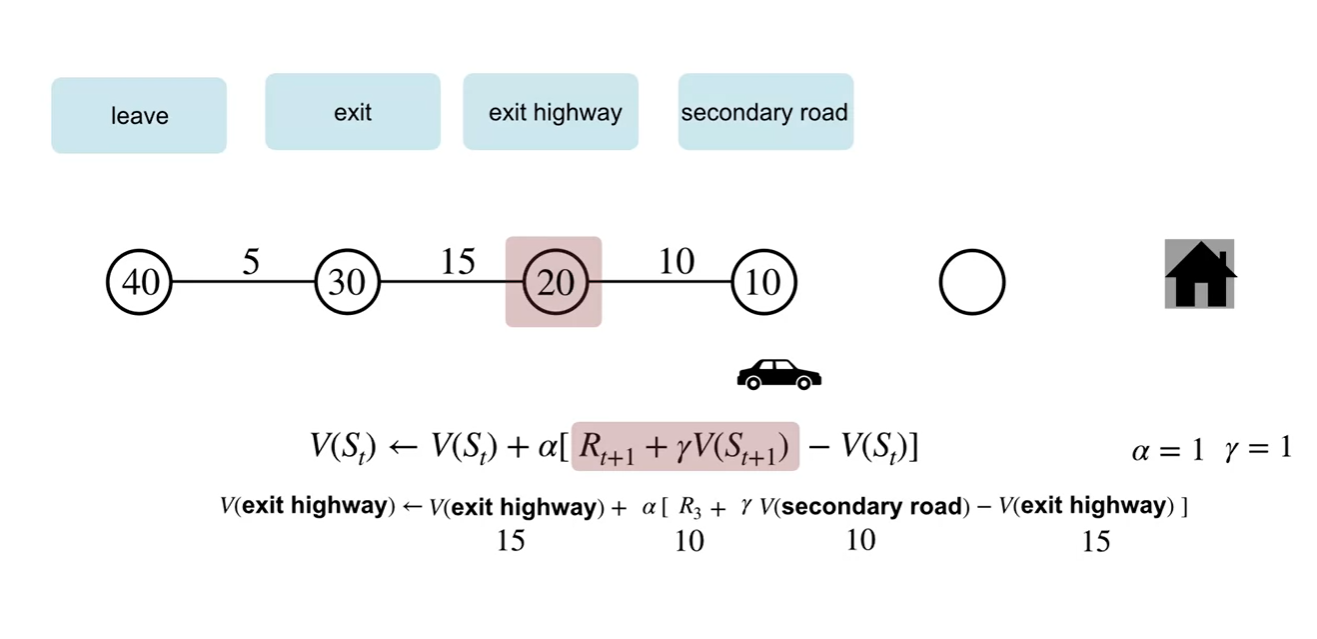
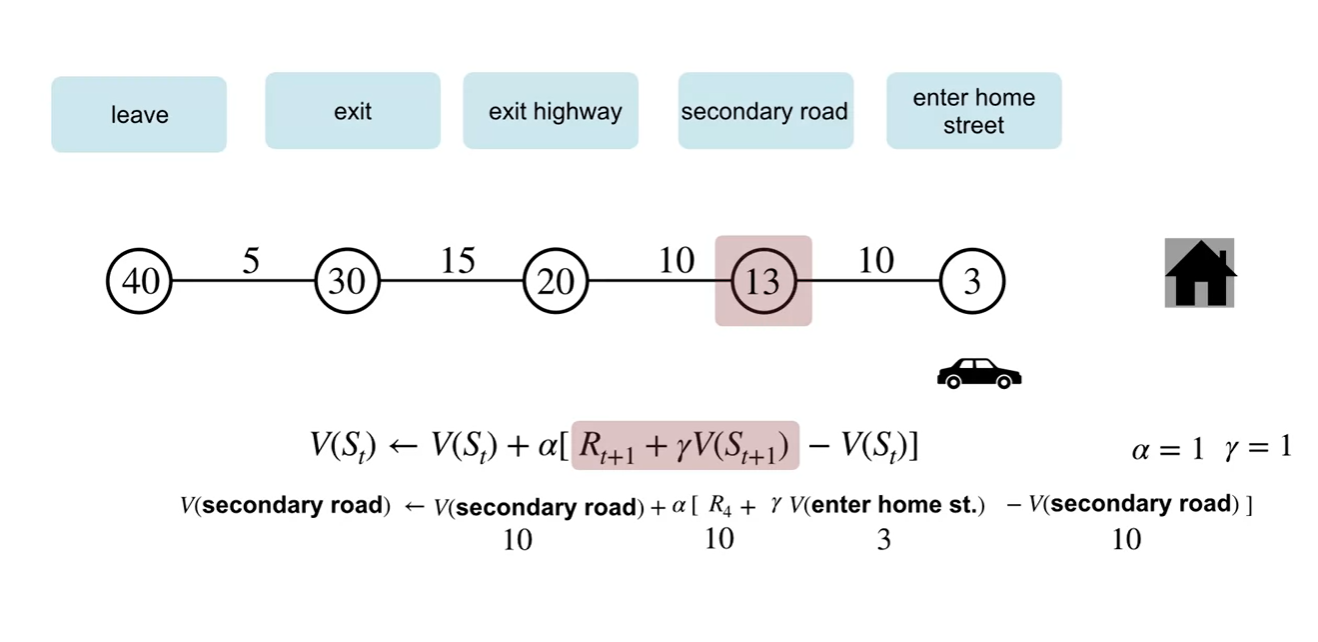
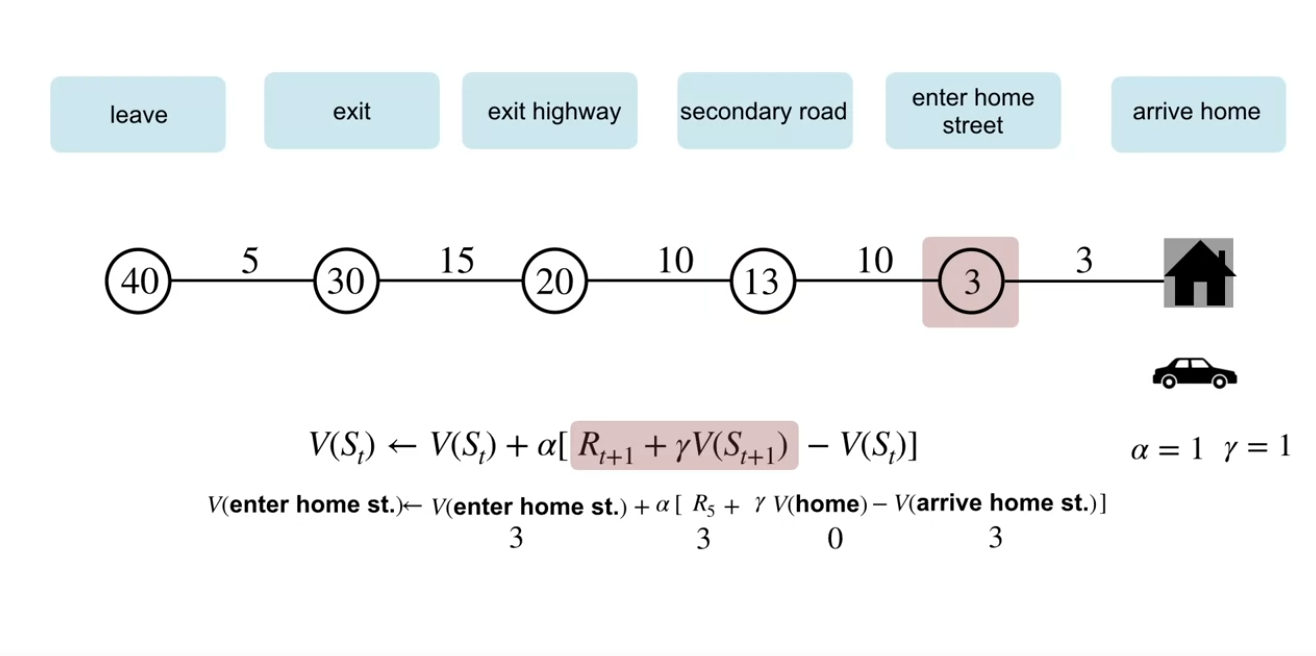
• Episode가 끝날 때까지 기다리지 않고돌 learning을 진행할 수 있다는 점에서 차이를 가진다.

  • 따라서 online learning이 가능하다고 말할 수 있다.

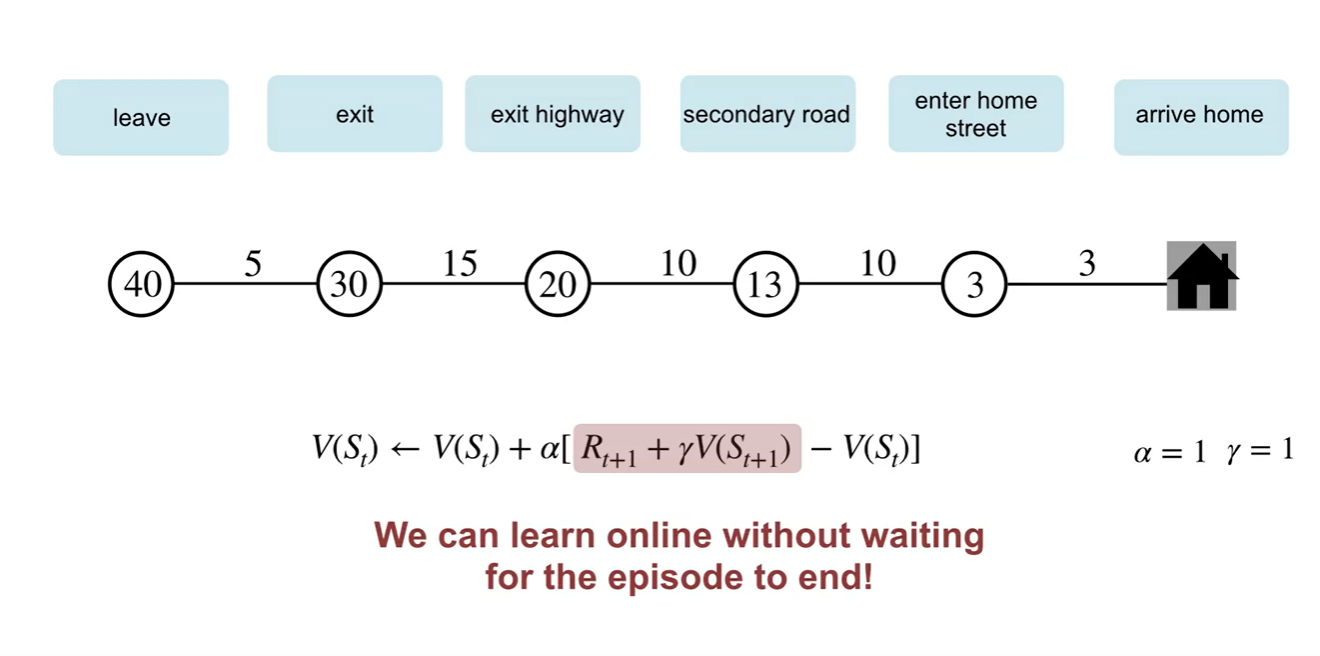
• Summary

Comparing TD and Monte Carlo

• TD와 MC 방법을 비교해보자.

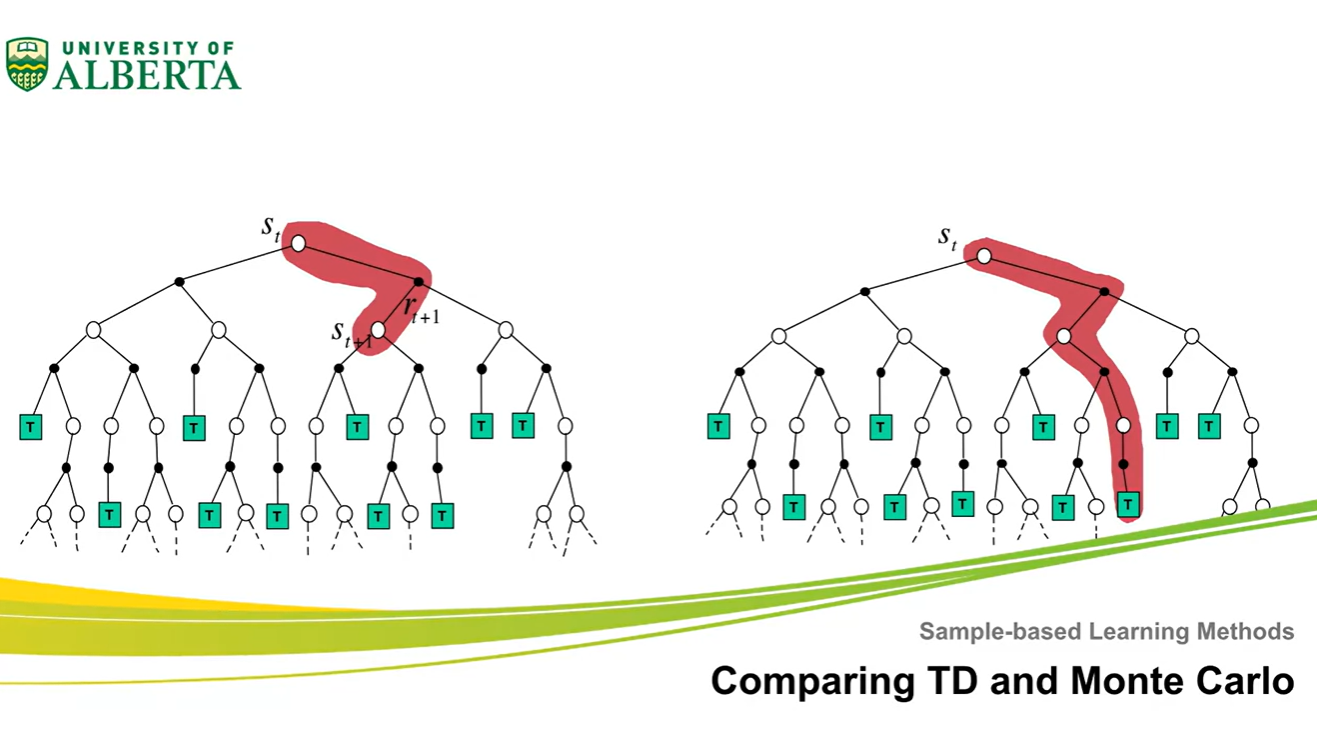
• 이번 강의에서는 TD learning의 강력한 이점에 대해 알아볼 예정이다.

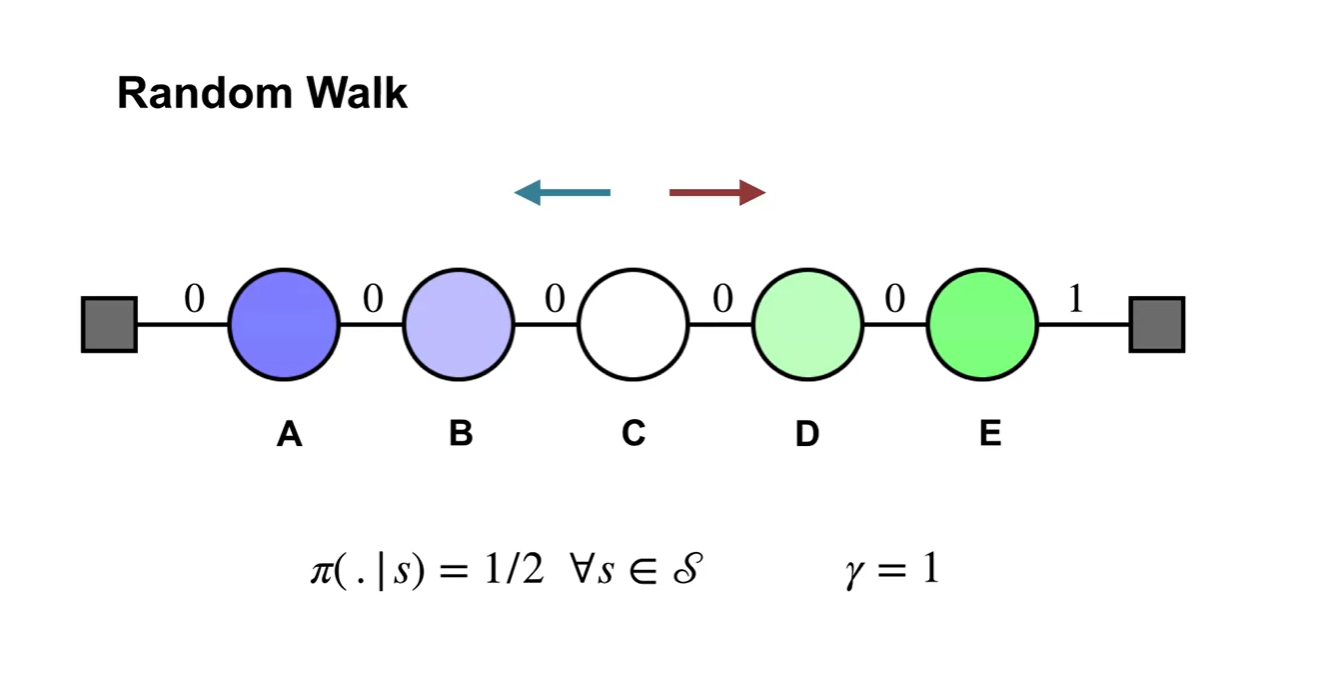
• Random walk example에 대해 다뤄보자.

  • Policy $\pi$는 1/2의 확률 분포를 가지며 $\gamma$는 1로 가정한다.

    • 맨 오른쪽 간선을 제외하고는 모두 reward가 0이며 최종 목적지인 맨 오른쪽 state로 향해 가도록 learning하는 system임을 알 수 있다.

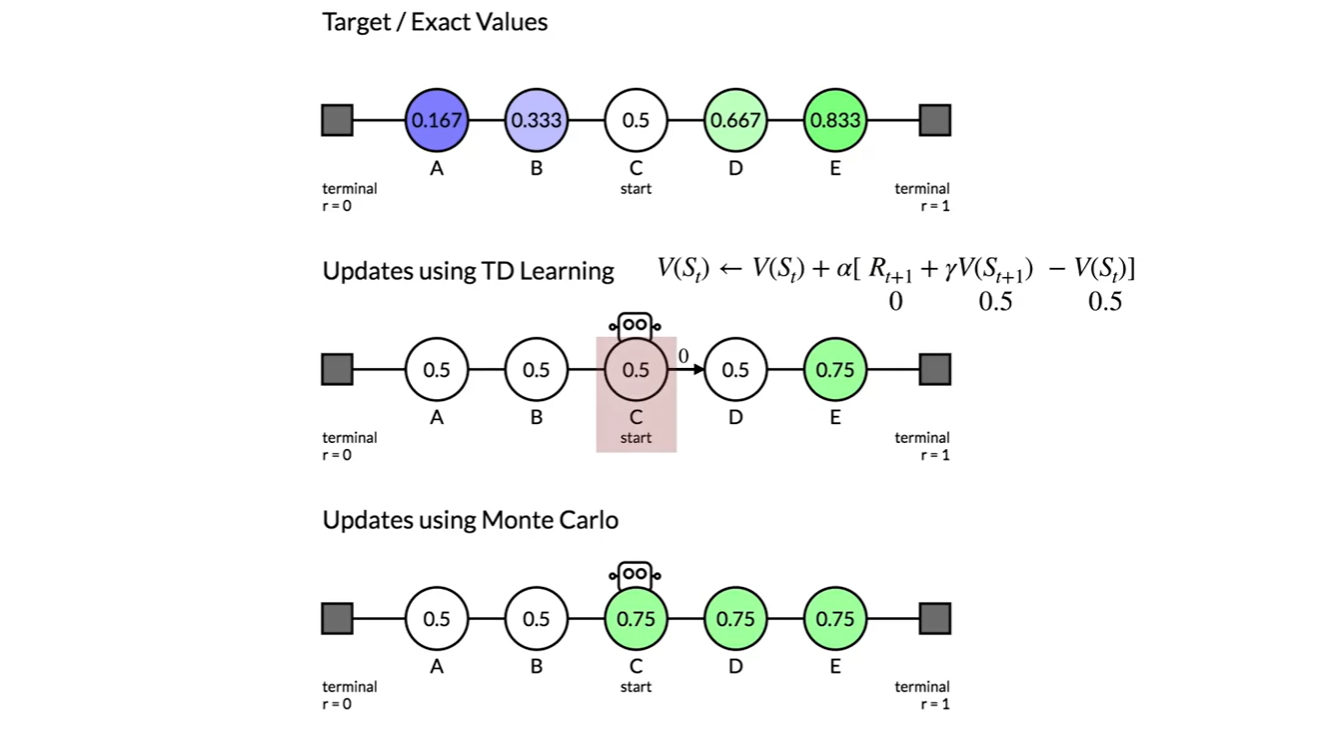
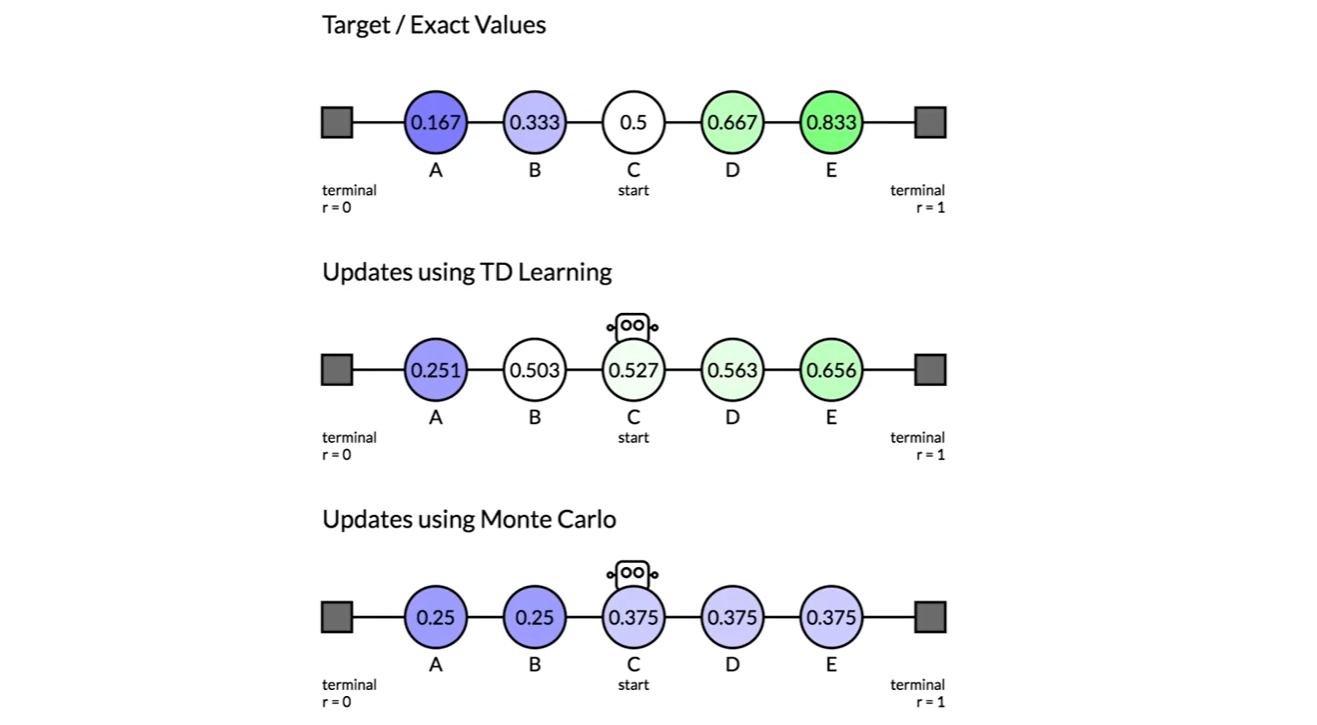
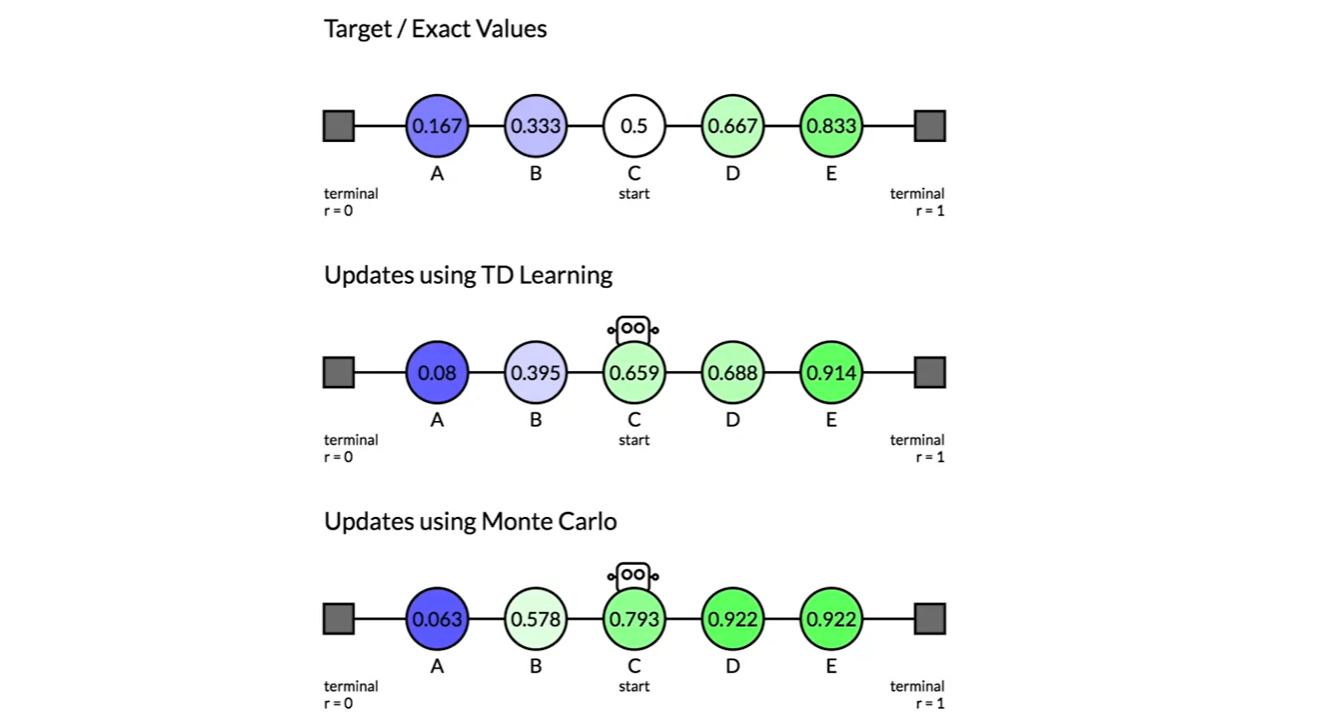
• 아래 그림이 TD learning과 MC learning의 차이를 명확하게 보여준다.

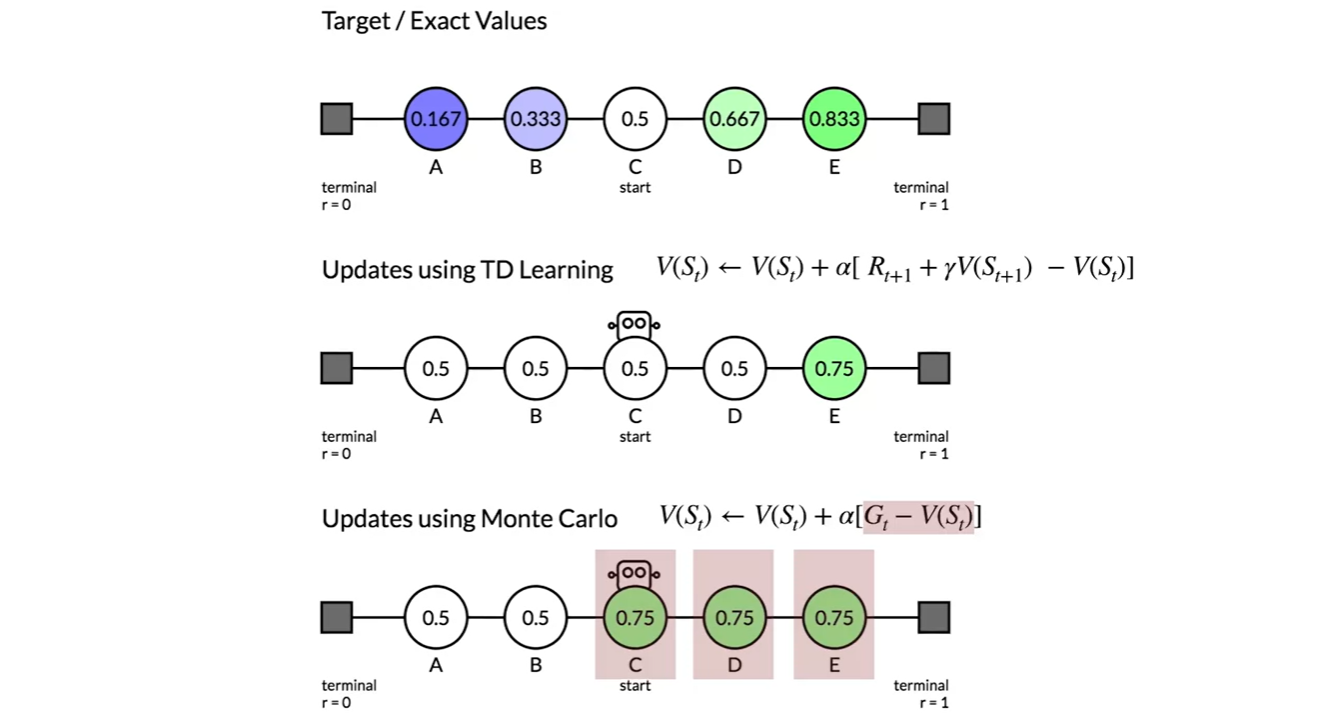
  • C state에서 출발하여 맨 오른쪽 state에 도달하는 end of episode를 겪고나면, TD는 E state value만 0.75로 업데이트 되지만 MC는 C, D, E state 모두 업데이트 된다.

    • 이후로도 TD는 $R_{t+1} + \gamma V(S_{t+1})$에 집중하며, MC는 $G_t$에 집중한다는 것을 알 수 있다.

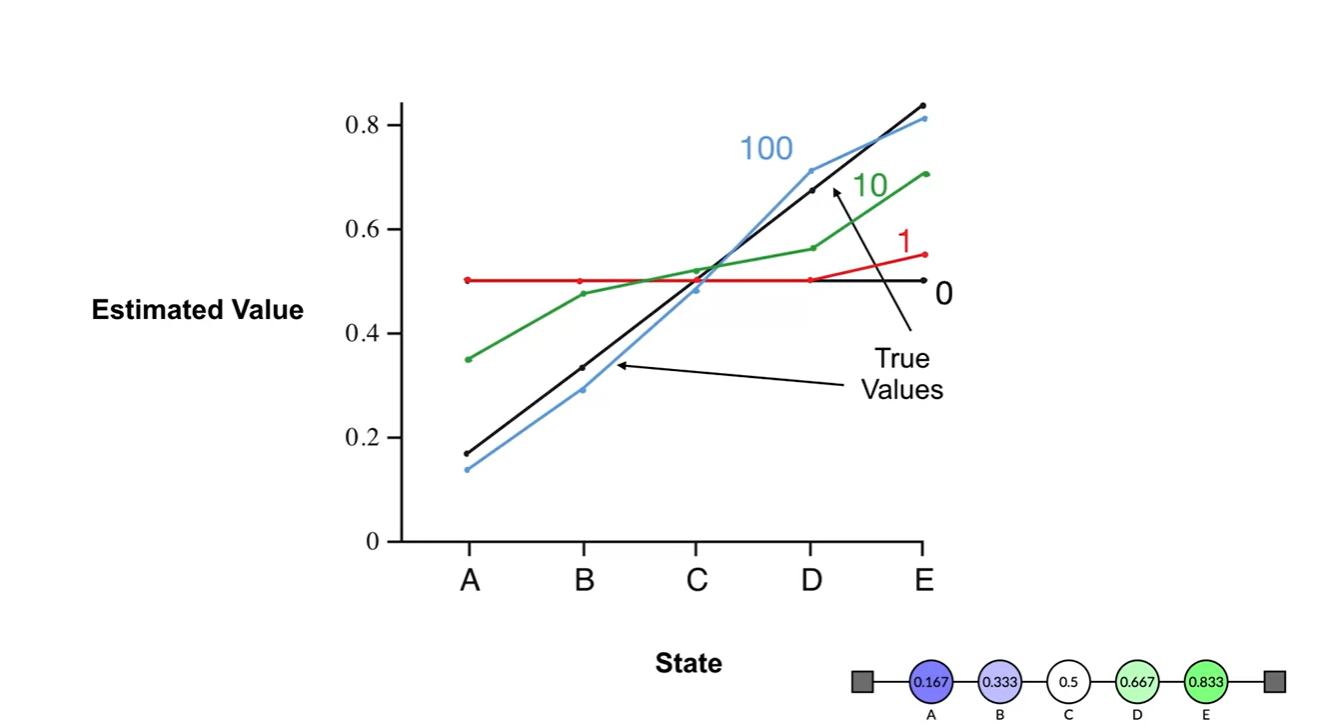
• 어떠한 learning도 이루어지지 않았을 때의 state-value는 빨간색 선과 같다.

  • 10번, 100번의 learning으로 value를 업데이트하고 나면 E state 쪽으로의 value가 선형적으로 증가하게 됨을 알 수 있다.

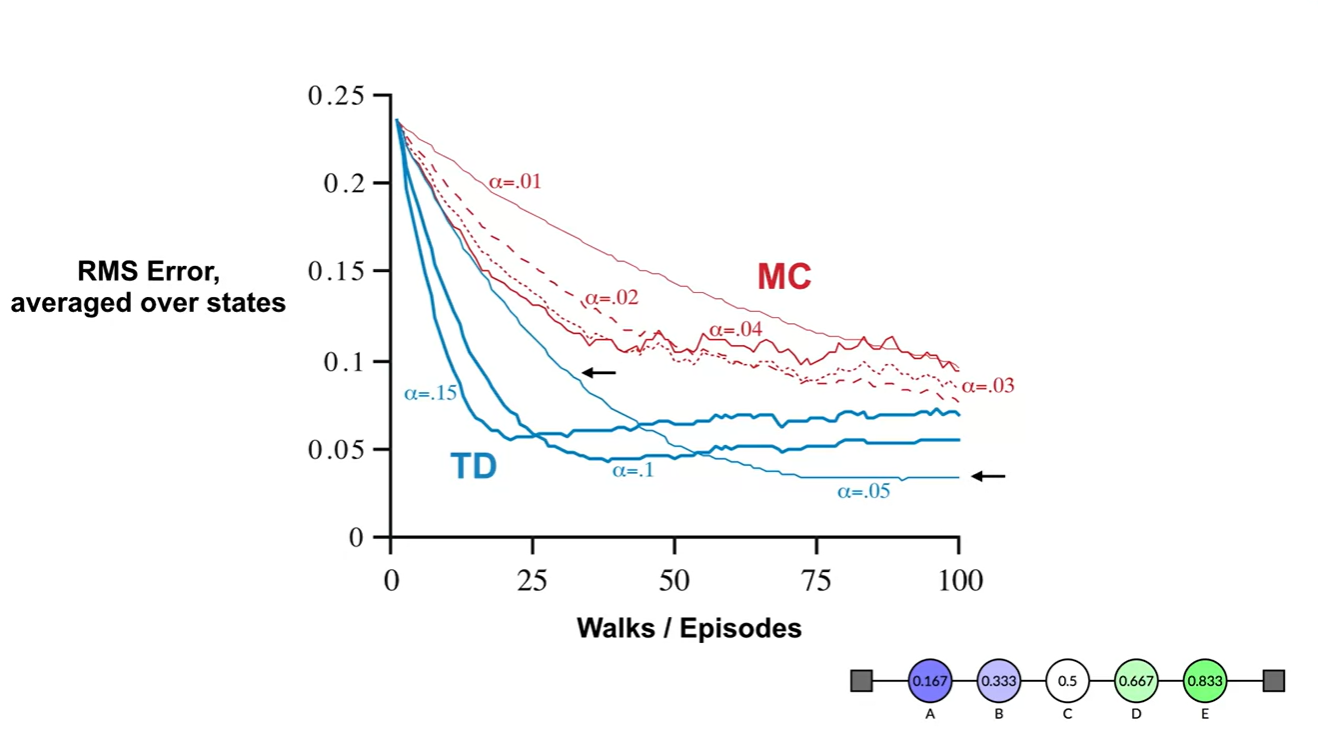
• MC와 TD의 수렴 속도 차이는 아래와 같이 보여진다.

  • TD가 MD보다 훨찐 빠른 속도로 수렴한다는 점에서 큰 이점을 가진다.

• Summary

---

• 출처 : [Coursera] Reinforcement Learning Specialization