Tips

깃허브

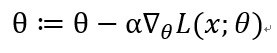
MLE (Maximum Likelihood Estimation)

Likelihood: 우리말로 하면 가능도 또는 우도이며, 확률의 반대 개념

• 확률: 확률분포가 주어졌을 때, 해당 관측값이 나올 확률
  고정값은 확률분포
• 가능도: 관측값이 주어졌을 때, 이 관측값이 어떤 확률분포로부터 나왔는지에 대한 확률
  고정값은 관측값 X

최대 가능도 추정(Maximum Likelihood Estimation, MLE):
각 관측값 X에 대한 총 가능도(=모든 가능도의 곱)가 최대가 되게 하는 확률분포(강의에서는 확률분포 함수의 parameter)를 찾는 것
이때, 임의의 확률분포를 가정해야 함

출처

최대가 되는 Local Maximum을 찾기 위해선 Gradient ascent를 수행하고,
최소가 되는 Local Minimum을 찾기 위해선 Gradient descent를 수행함

Overfitting

그러나 MLE는 그 데이터를 가장 잘 설명하는 확률 분포 함수를 찾다 보니
Overfitting이 숙명적으로 따르게 됨

해결 방법?

분포가 비슷하도록 훈련 set과 테스트 set을 나눠서
실제 훈련 후, 해당 훈련이 얼마나 잘 학습되었는지 검증함.

• 훈련 set에 대해 overfitting된다면 테스트 set에서 좋은 성능을 내지 못할 것.
• Development set은 더 나아가서 테스트 셋에 대해서도 overfitting되었는지를 확인할 수 있음
  

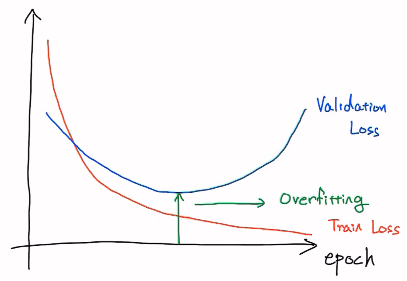
이외에도 Overfitting을 방지하는 방법

• 데이터를 많이 모음
• feature(어떤 분포를 잘 설명하는 특징)을 적게 사용
• Regularization

Regularization의 방법

• Early Stopping : Validation Loss가 최소가 되는 지점
• Reducing Network Size : (딥러닝에 한함) neural network의 사이즈를 줄여서 학습할 수 있는 양을 줄임 (웨지감자)
• weight decay : neural network weight 파라미터의 크기를 제한함
  (너무 커지면 쉽게 오르내리락하는 그래프가 만들어질 수 있음)
• Dropout
• Batch Normalization

DNN(Deep Neural Network)을 훈련시키는 과정

• Neural network architecture를 설계함 (input, output, layer 등)
• 모델이 Overfitting되었는지를 확인하며 훈련시킴
  Overfitting될 때? validation set의 loss가 높아지지만, traning set의 loss는 낮아질 때
  Overfitting되지 않는다면 -> 모델 사이즈를 늘림 (중간에 있는 layer들을 deeper and wider)
  Overfitting된다면 -> Regularization 추가 (Drop-out 또는 Batch-Normalization)
• 2번 방법을 반복

데이터 전처리

데이터 전처리를 통해 데이터를 미리 학습하기 쉽도록 바꿔 줌
여기에서는 Standardization(정규분포화)를 사용함

mu = x_train.mean(dim=0) # 평균
sigma = x_train.std(dim=0) # 표준편차
norm_x_train = (x_train - mu) / sigma

최종 구현 코드

class MultivariateLinearRegressionModel(nn.Module):
    def __init__(self):
        super().__init__()
        self.linear = nn.Linear(3, 1)

    def forward(self, x):
        return self.linear(x)

def train_with_regularization(model, optimizer, x_train, y_train):
    nb_epochs = 20
    for epoch in range(nb_epochs):

        # H(x) 계산
        prediction = model(x_train)

        # cost 계산
        cost = F.mse_loss(prediction, y_train)

        # l2 norm 계산
        l2_reg = 0
        for param in model.parameters():
            l2_reg += torch.norm(param)

        cost += l2_reg

        # cost로 H(x) 개선
        optimizer.zero_grad()
        cost.backward()
        optimizer.step()

        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch + 1, nb_epochs, cost.item()
        ))
        
x_train = torch.FloatTensor([[73, 80, 75],
                             [93, 88, 93],
                             [89, 91, 90],
                             [96, 98, 100],
                             [73, 66, 70]])
y_train = torch.FloatTensor([[152], [185], [180], [196], [142]])

mu = x_train.mean(dim=0) # 평균
sigma = x_train.std(dim=0) # 표준편차
norm_x_train = (x_train - mu) / sigma

model = MultivariateLinearRegressionModel()
optimizer = optim.SGD(model.parameters(), lr=0.1)
train_with_regularization(model, optimizer, norm_x_train, y_train)

근데 아직 L2 norm에 대해서 잘 모르기도 하고... test 함수가 제대로 작동하지 않는다... ㅎㅎ
일단 test 관련해서도 코드를 아래에 적음

x_test = torch.FloatTensor([[75, 82, 59], [100, 88, 97], [79, 65, 80]])
y_test = torch.LongTensor([[144], [186], [160]]) # 임의로 한번 넣어 봄

def test(model, optimizer, x_test, y_test):
    prediction = model(x_test)
    predicted_classes = prediction.max(1)[1]
    correct_count = (predicted_classes == y_test).sum().item()
    cost = F.cross_entropy(prediction, torch.FloatTensor(y_test))

    print('Accuracy: {}% Cost: {:.6f}'.format(
         correct_count / len(y_test) * 100, cost.item()
    ))