이진 트리 (Binary Tree)
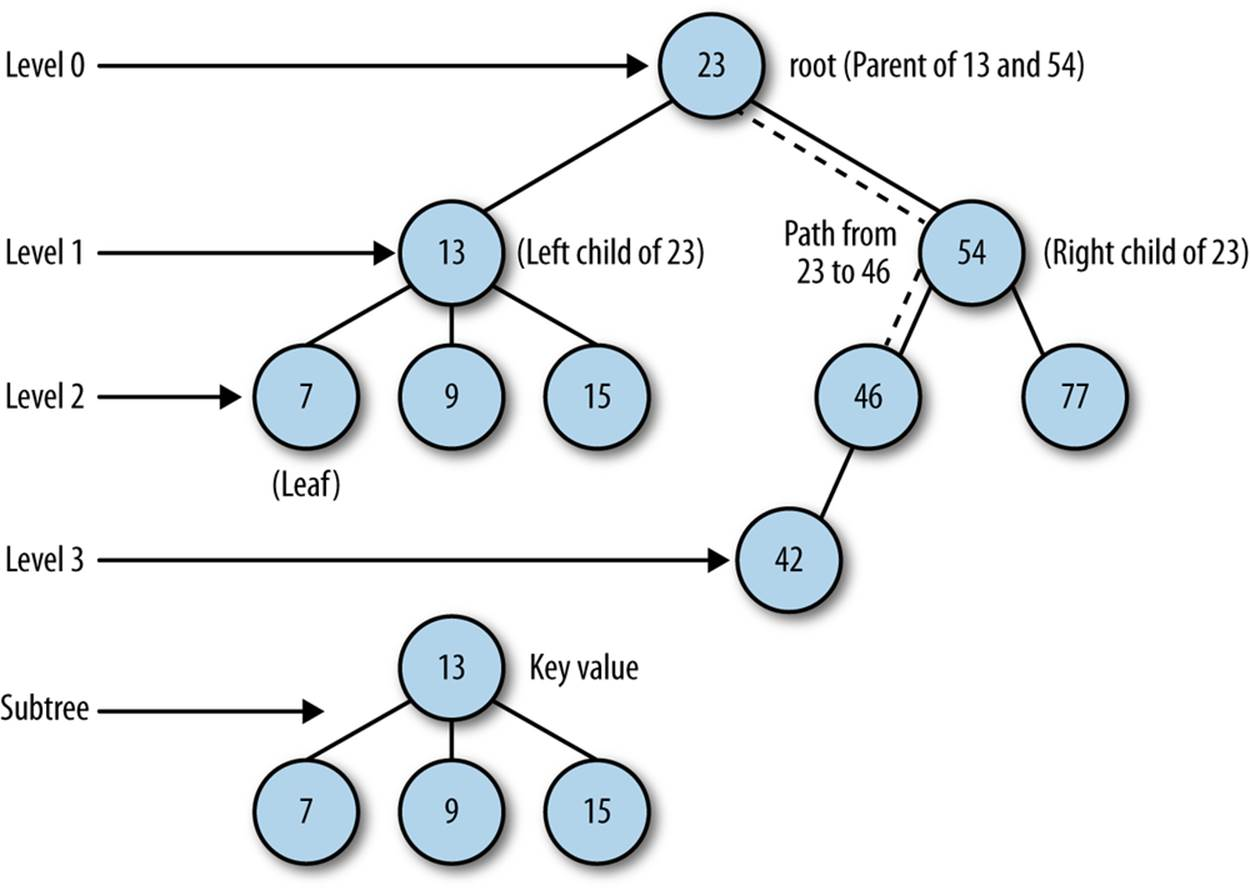
이진 트리(Binary Tree)의 성질
- 각 부모노드는, 최대 두 개까지의 자식 노드를 가짐.
- Root에서부터 다른 노드로 가는 path는 unique함.
높이가 h인 Binary Tree의 최대 레벨은 l=h-1 (높이-1까지의 레벨을 가짐!)
또한, 높이가 h인 Binary Tree는, 최대 2^h - 1만큼의 노드를 가진다
Binary Search Tree (BST)
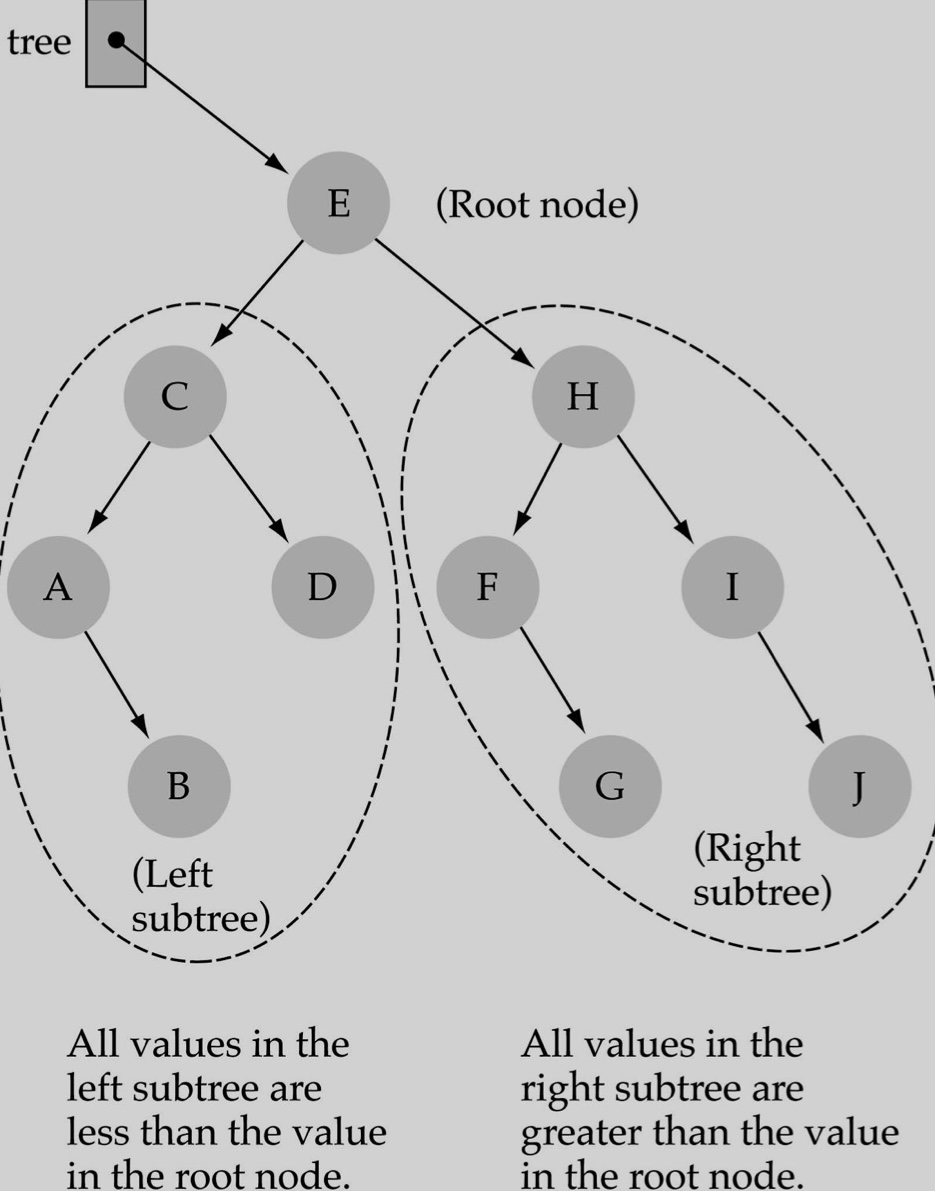
Binary Search Tree를 이용하기 위해선,
왼쪽 서브트리 모두 부모노드보다 작은 값이며
오른쪽 서브트리는 부모노드보다 큰 값들인
특수한 이진트리를 이용함.
Binary Search Tree의 방법
- Root에서부터 시작
- 찾으려는 아이템의 값과, Root의 값을 비교함.
- 비교한 값이 동일하다면 검색에 성공함
동일하지 않다면, leaf node로 내려가 검색을 계속 진행 - 찾으려는 값이 Root보다 작다면, left subtree에서 검색을 진행함.
- 찾으려는 값이 Root보다 크다면, right subtree에서 검색을 진행함.
- subtree의 루트에서부터 2-6을 다시 진행.
=> 순차적으로 검색하는 방법은 O(n)만큼의 시간이 소요되는 반면
이진트리를 이용한 검색은 최대 O(log n)만큼의 시간이 소요됨!
Binary Tree의 종류
Full Binary Tree
가장 말단의 모든 leaf들이 동일 레벨을 가지며
leaf가 아닌 다른 노드들은 모두 자식을 두 개씩 갖는 트리
Complete Binary Tree (완전이진트리)
마지막 레벨을 제외하고 모든 레벨이 완전히 채워진 트리
마지막 레벨은 왼쪽 노드부터 채워져야 함
Binary Tree의 삽입
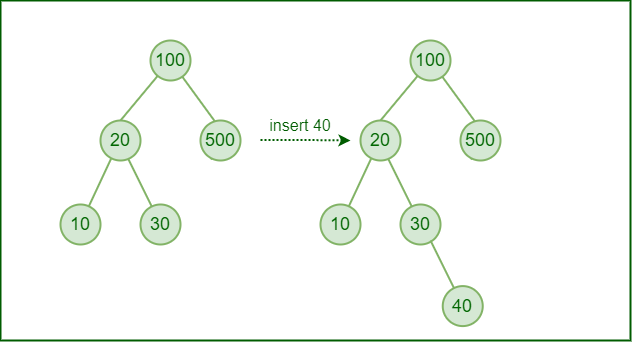
넣으려는 아이템의 값을 root에서부터 비교해 가며 아래로 내려간다.
root보다 작으면 왼쪽 서브트리로, root보다 크면 오른쪽 서브트리로 내려가서
더 내려갈 곳이 없을 때까지 반복한 후, 아이템을 삽입한다.
Binary Tree의 삭제
노드를 삭제할 땐, 세 가지 경우가 존재한다.
- leaf 노드 삭제
- 두 개의 자식을 가진 노드 삭제
- 하나의 자식을 가진 노드 삭제
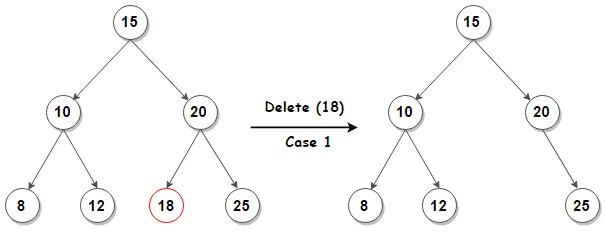
1의 경우엔, 그냥 지우면 됨.
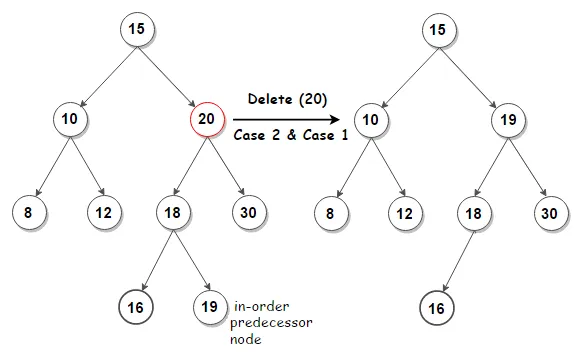
2의 경우엔, inorder successor(오른쪽 서브트리에서 가장 작은 값) 또는 inorder predecessor(왼쪽 서브트리에서 가장 큰 값)을 찾아서, 해당 값을 대체함.
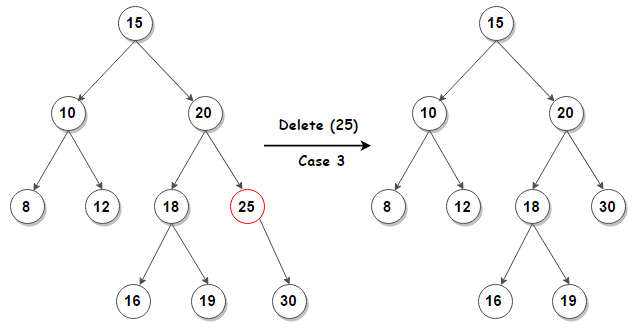
3의 경우, 해당 노드를 지우고, 자식이 그 자리를 대체함.
Preorder(전위) / Inorder(중위) / Postorder(후위)
트리 순회의 방법 세 가지
-
Preorder traversal
root -> left subtree -> right subtree
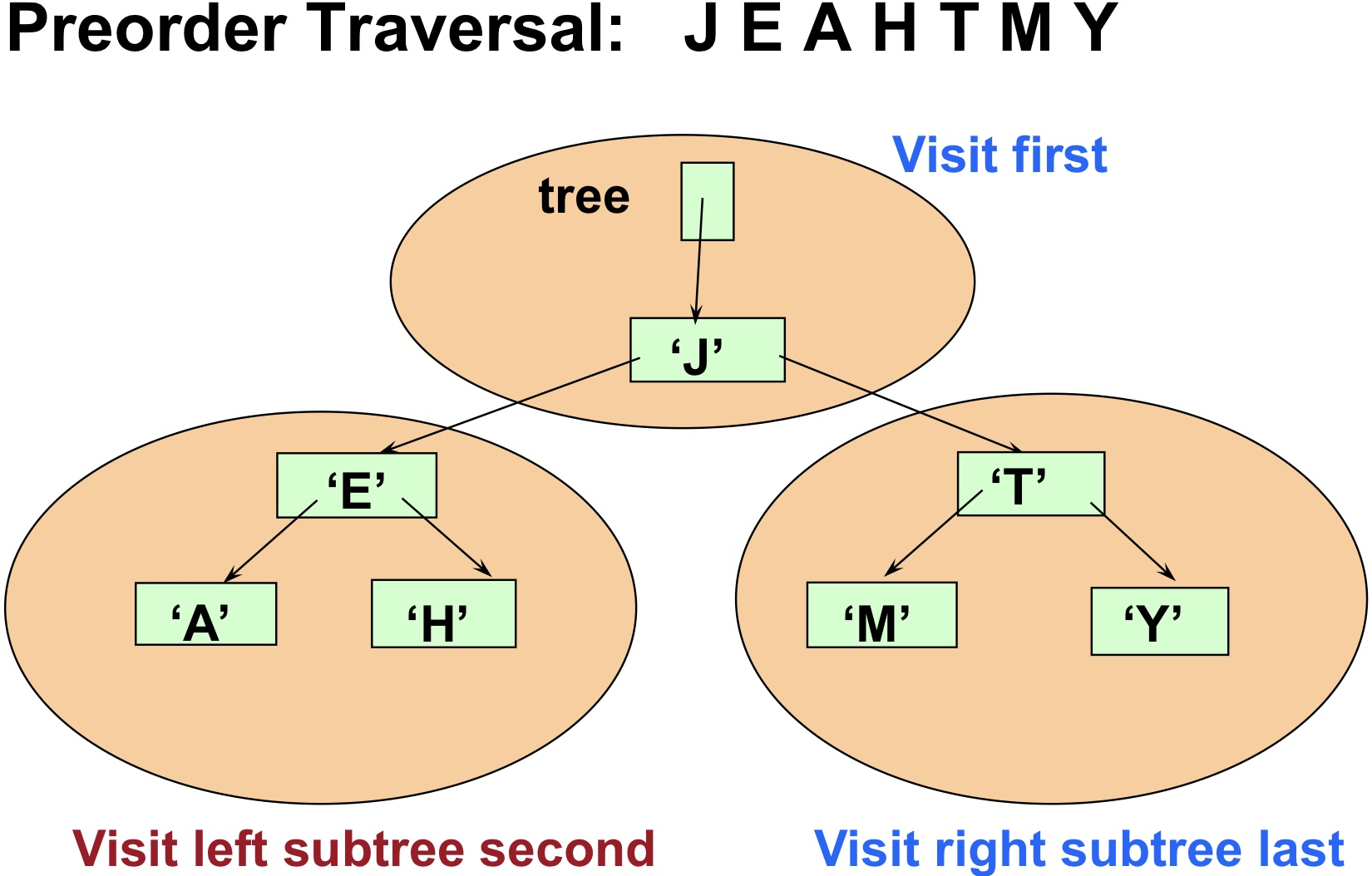
-
Inorder traversal
left subtree -> root -> right subtree
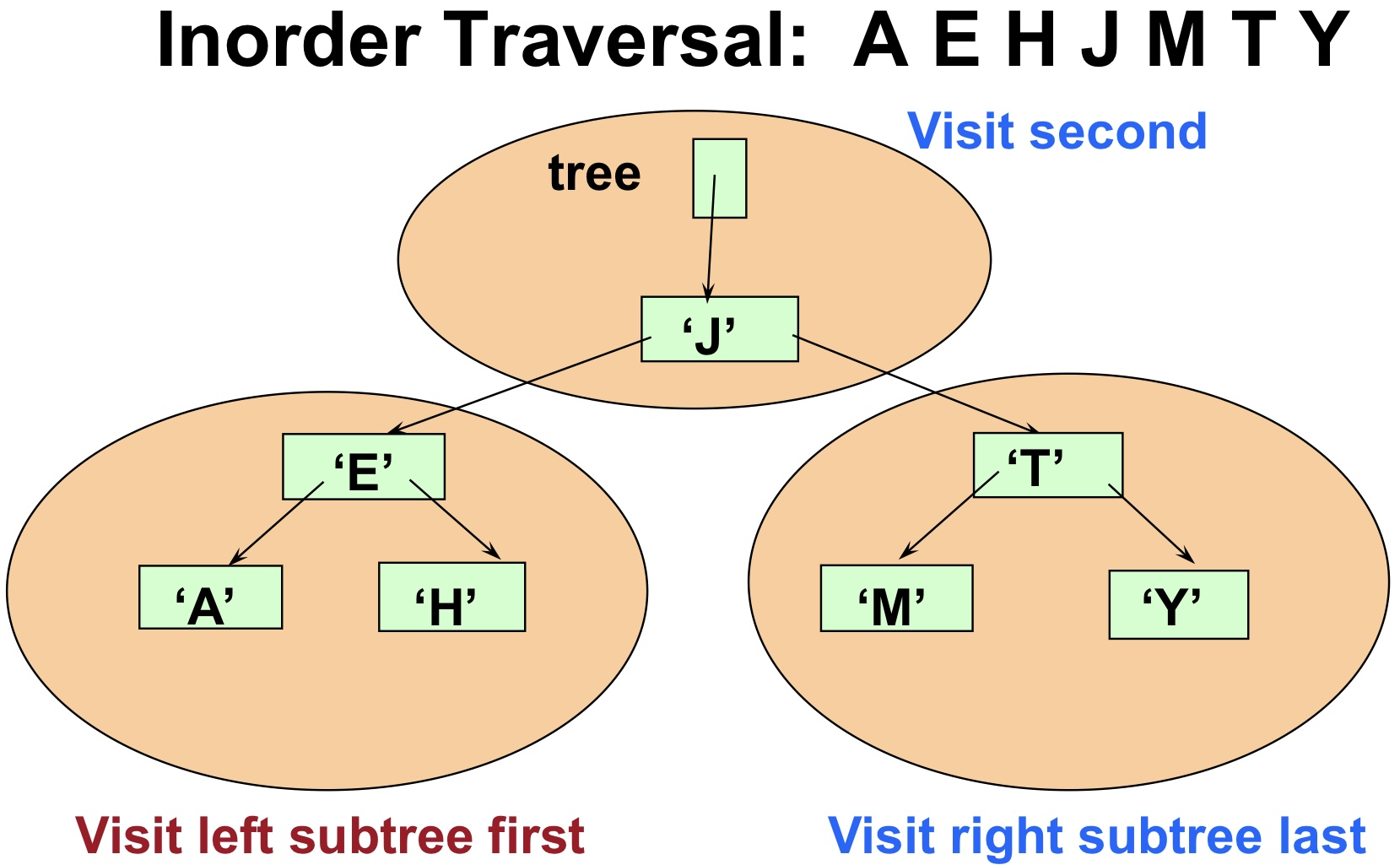
-
Postorder traversal
left subtree -> right subtree -> root
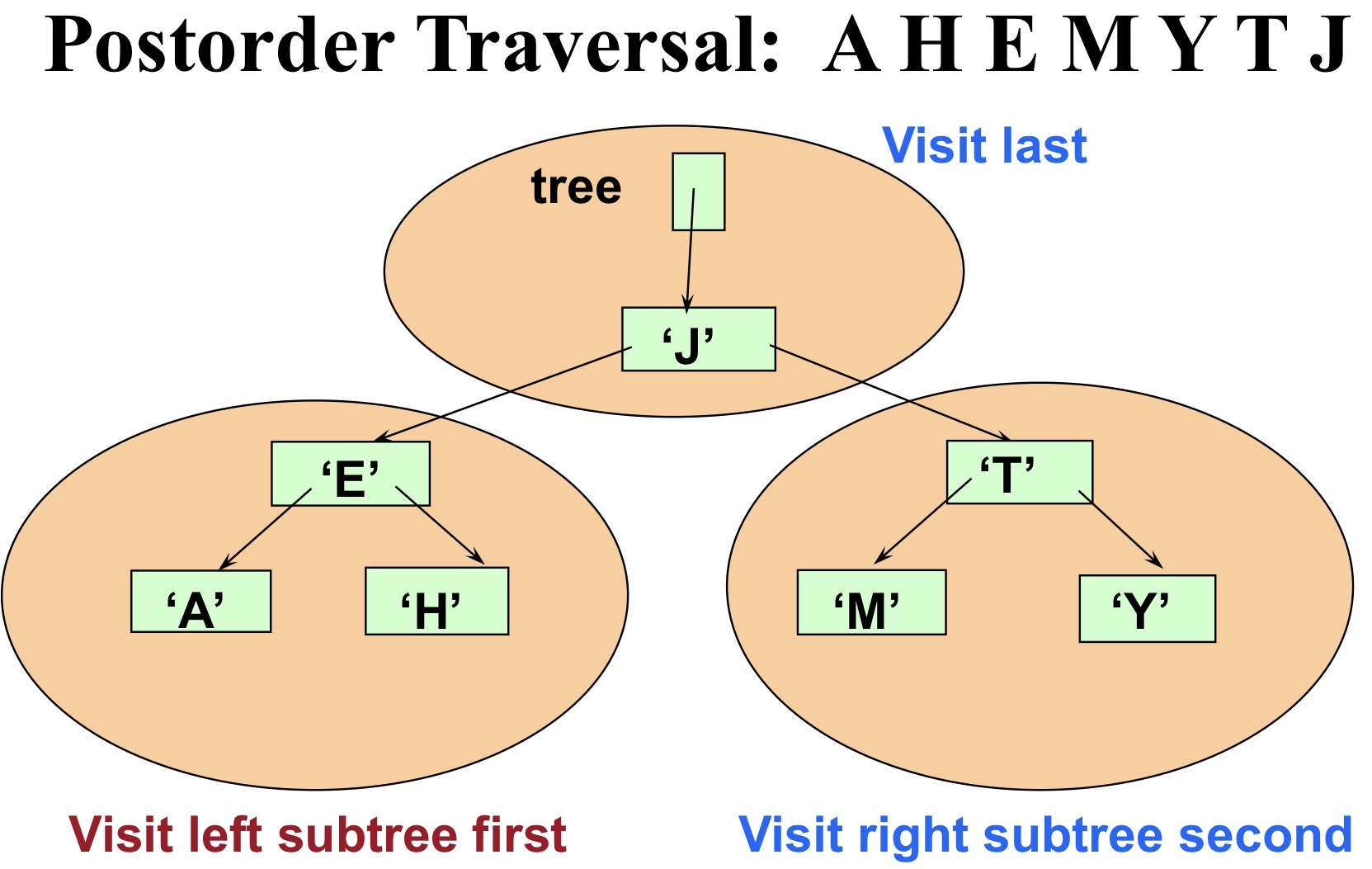
구현
추가 예정... 왜 에러가 뜨는 거지
참고
