경사하강법(Gradient Descent)

최적화(Optimization)

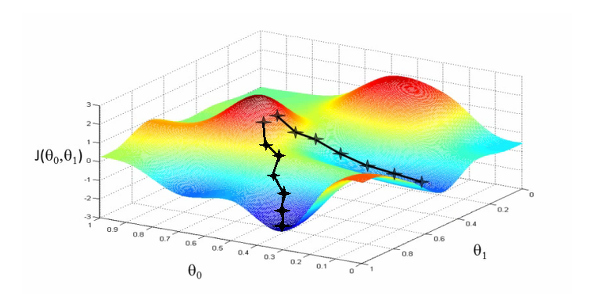
• 현재 위치에서 내리막 방향으로 조금씩 이동하면서, 손실함수가 최소가 되는 파라미터 조합을 찾는 과정
• Global minimum/local minimum->Global minimum을 찾아야 함
  

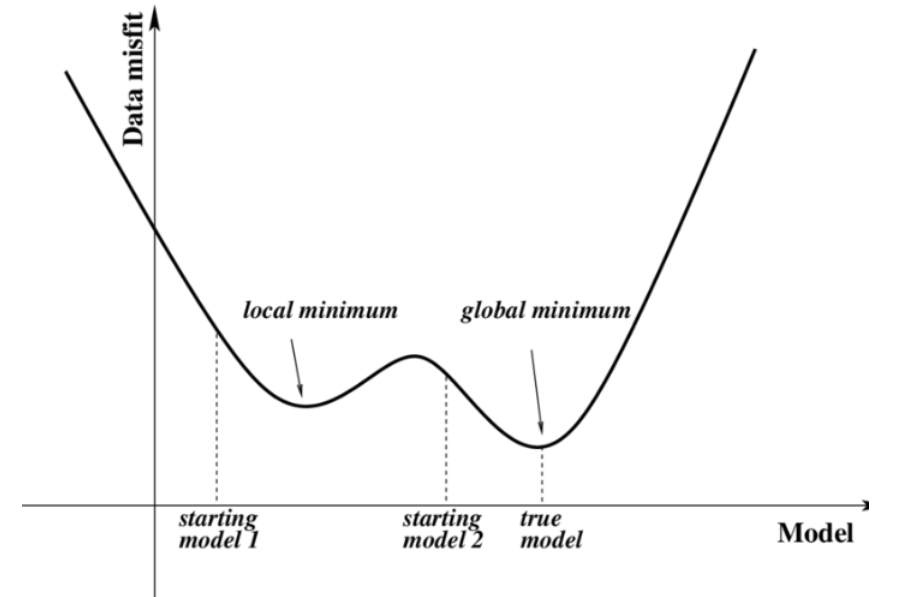
경사하강법(Gradient Descent Method)

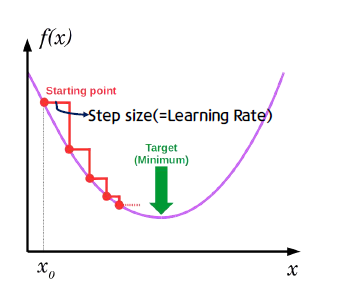
• 경사가 가장 가파른 바향으로 이동을 하면서 최소점을 찾는 것
• 모델의 parameter들을 θ (->W,b)라고 했을 때, Loss function J(θ)의 최소화를 찾기 위해 파라미터의 기울기(gradient) ∇θJ(θ) (즉, dW와 db)를 이용하는 방법
• Gradient Descent Algorithm

경사하강법 수식
W=W−αdW
b=b−αdb
α : learning rate

Gradient Descent Algorithm은 한 iteration에서 다룰 데이터 크기에 따라 세가지로 나눌 수 있음

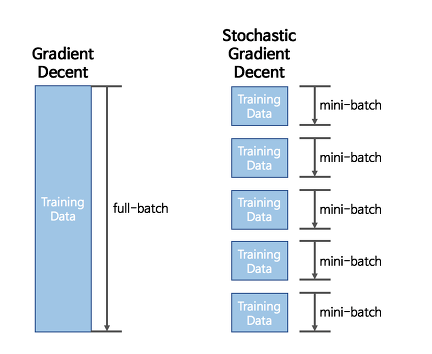
1) Batch Gradient Desencet (BGD)

• 기본적인 gradient descent임
• batch가 전체 데이터 셋으로 생각!
• 학습에 이용하는 모든 데이터에 대한 error를 구하고 기울기를 한 번만 계산하여 가중치를 덥데이트하는 방법
• 장점은,
  - 전제 데이터에 대해서 업데이트가 한 번에 이루어지므로 업데이트 횟수 자체는 적음
  • 전제 데이터에 대해 error gradient 계산하므로 optimal로 수렴이 안정적
• 단점은,
  - 한 번의 업데이트에 모든 학습 데이터 셋을 사용하므로 계산 자체는 오래 걸림
  • Local optimal 에 수렴할 경우 탈출하기 어려울 수 있음

2) Stochastic Gradient Descent (SGD)

• 확률적으로 가중치를 갱신하는 방법
• 학습 데이터 중 무작위로 1개의 데이터를 선택한 후에 error와 기울기를 구하고 가중치를 업데이트함
• 장점은,
  - 실제 모든 데이터에 대해 gradient 계산하는 것보다 연산 시간이 단축
  - shotting이 일어나기 때문에 local minimum에 빠질 위험이 적음
• 단점은,
  - Global Optimum을 찾지 못할 가능성이 있음
  • 다른 알고리즘에 비해 속도가 느림

3) Mini-batch Gradient Descent (MGD)

• 대부분의 학습에서 사용하는 방법
• 여러 개의 데이터 포인트를 샘플링해서 gradient를 계산
• 한 번 학습을 할 때 설정했던 batch_size 만큼의 이미지만 추출해서 error을 계산하고 기울기 값을 구한 후 가중치를 업데이트함
• 예를 들어, 100개의 학습 데이터가 있고 batch_size=10일 때, 한 번 학습을 할 때(1 iter) 10개의 이미지를 사용해서 학습하고 이 과정을 10번 반복하면 1 epoch임
• 장점은,
  - 한 번에 고려하는 데이터가 SGD에 비해 많아지므로 보다 정확도가 높음
  • 모든 데이터를 한 번에 고려해서 계산하는 것이 아니므로 (Batch) Gradient Descent보다 더 효율적임
• 단점은,
  - SGD 보다 상대적으로 메모리 사용이 많음
  

후에 더 많은 Optimization 알고리즘을 추가하겠습니다!

참고자료

https://daebaq27.tistory.com/35
https://ganghee-lee.tistory.com/24
https://aoc55.tistory.com/48