손실함수(Loss Function)
- 비용함수(Cost Function)라고도 함
- 신경망 학습에서 최적의 매개변수 값을 탐색하기 위해 사용하는 지표는 손실함수->신경망 성능이 좋은 지 나쁜 지 나타냄
- 예측 값과 실제 값의 차이를 loss 라고 하며, loss를 줄이는 방향으로 신경망 학습이 진행
- 통계학적 모델은 회귀(regression)와 분류(classification) 2가지로 나뉘는 데 손실함수도 그에 따라 2가지로 나뉨
손실함수를 지표로 사용하는 이유
기계 학습의 궁극적인 목적은 높은 정확도를 이끌어내는 매개변수(가중치와 편향) 값을 찾는 것->왜 정확도 지표가 아닌 손실함수 지표를 사용할까?
- 정확도를 지표로 삼는다면, 예를 들어 100장의 훈련 데이터 중 40장만 올바르게 인식했을 때 정확도는 40%이다. 가중치 매개변수의 값을 조금 바꾼다고 해도 정확도는 그대로 40%임->매개변수를 약간만 조정해도 정확도가 개선되지 않고 40.0112%와 같은 연속적인 변화보다는 41%,42%처럼 불연속적인 값으로 변경됨
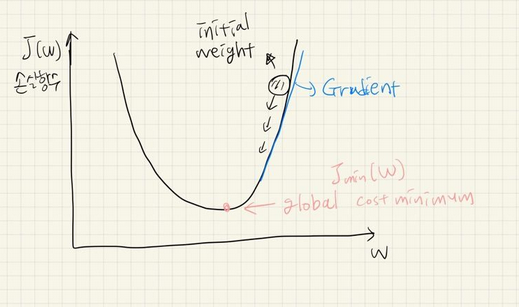
- 신경망 학습에서는 최적의 매개변수를 탐색할 때, 손실 함수의 값을 가능한 작게 하는 매개변수 값을 찾음는다. gradient를 계산하고, 이를 이용해 매개변수의 값을 서서히 갱신하는 과정을 반복함->만약 gradient 값이 음수라면 매개변수를 양의 방향으로 변화시키고, gradient 값이 양수라면 매개변수를 음의 방향으로 변화 시켜 손실함수의 값을 줄임. 그러다가 gradient 값이 0 이 되면 매개변수의 갱신은 멈춤
- So, 연속적인 값으로 변하는 지표인 손실함수를 사용!
회귀에 쓰이는 손실함수
1) MAE(Mean Absolute Error)
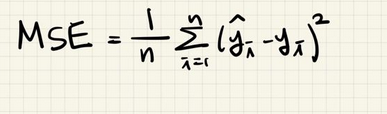
- n : 데이터의 개수
- y_hat : 예측된 값
- y : 실제 값- 예측 값과 실제 값의 차이를 절대값 취하고 평균화
- 오차에 동일한 가중치를 부여
- 이상치에 대해 강건 ROBUST 하기 때문에 이상치에 영향을 덜 받음
- So, 약간의 이상치가 있는 경우 그 이상치의 영향을 적게 받으면서 모델을 만들고자 할 때 사용
2) MSE(Mean Squaared Error)

- n : 데이터의 개수
- y_hat : 예측된 값
- y : 실제 값- 예측 값과 실제 값의 차이를 제곱해 평균화
- 이상치에 대해 민감
3) RMSE(Root Mean Squared Error)
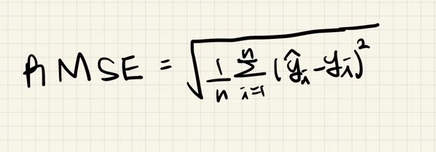
- n : 데이터의 개수
- y_hat : 예측된 값
- y : 실제 값- MSE 값에 루트를 씌운 값
- MSE 는 실제 오류 평균보다 더 커지는 특성이 있는데 MSE의 이런 단점을 어느정도 보완
- MAE 대신에 RMSE를 많이 사용->큰 오류값 차이에 대해서 크게 패널티를 주는 이점이 있기 때문(이상치에 덜 민감)
- 모델 학습 시 이상치에 가중치를 부여하고자 한다면, RMSE를 채택
분류에 쓰이는 손실함수
Cross Entropy Error
- 분류(Classification) 문제에서 성능을 측정할 때 사용하는 손실함수
- softmax값을 토대로 구함->후에 블로그에서 더 자세히 다룰 예정

- 현실 분류 문제에서는 정답이 있다고 가정(분류할 때 관찰하는 것이 100% 정답존재)
- ont-hot encoding 된 벡터로 나타냄
- 실제 이미지가 0.2일 확률로 고양이 일 리 없다->그 이미지가 고양이라고 사람이 정답을 정의했기 때문
참고링크
https://ce-notepad.tistory.com/8
https://jysden.medium.com/%EC%96%B8%EC%A0%9C-mse-mae-rmse%EB%A5%BC-%EC%82%AC%EC%9A%A9%ED%95%98%EB%8A%94%EA%B0%80-c473bd831c62
