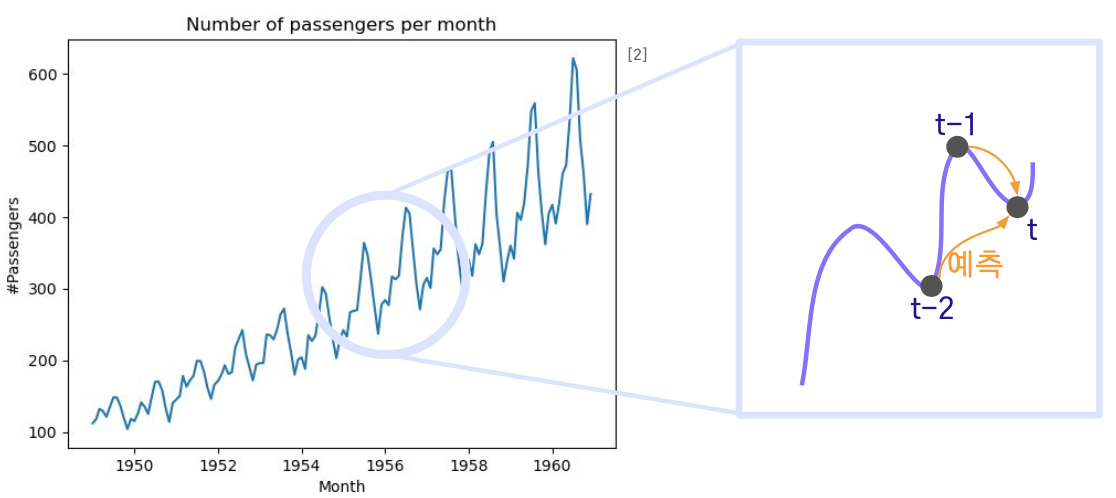
시계열 데이터의 특성

시계열 데이터와 순차적 데이터

시계열 데이터

시간 순서로 관측된 일련의 데이터.
일반적으로 동일한 시간간격마다 측정된 값들의 시퀀스.

• 매일 아침 9시 서울의 기온

순차적 데이터

어떠한 순서를 가지는 데이터로, 순서가 바뀌면 의미를 잃는다.

• 텍스트 데이터
• 유전체(DNA) 데이터
• 시계열 데이터 전체를 포함

시계열 데이터의 구성성분

불규칙 성분 (Irregular Component)

시간에 따른 규칙적인 움직임과 무관한, 랜덤한 원인에 의한 변동.
예측이 불가능한 노이즈 성분으로 이해할 수 있다.

규칙 성분 (Systematic or Regular Component)

시간에 따른 데이터의 변동 중에서, 시간에 따라 보이는 데이터의 패턴이나 경향성에 의해 설명될 수 있는, 예측 가능한 변동 성분

규칙 성분은 다시

• 추세(Trend)
• 계절성(Seasonality)
• 순환성(Cycle)의 세가지 성분으로 나누어볼 수 있다.

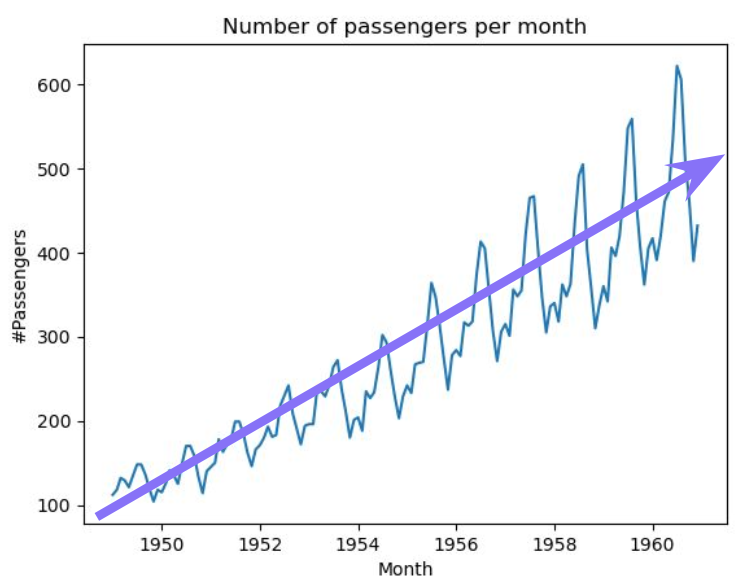
추세(trend)

데이터가 단기적으로는 증감하며 변화하더라도 장기적으로 점차 증가하거나 점차 감소하는 등의 방향성을 보이는 것

계절성(seasonality)

계절에 따른 변화처럼 일정하게, 정기적으로 데이터가 변화하는 것

• 성수기/비수기에 따른 비행기 탑승객 수
• 평일/주말에 따른 식당의 손님 수
• 낮과 밤의 기온, 조수 간만의 차
• 서울의 월별 강수량

순환성(cycle)

데이터가 주기적으로 변화하기는 하지만, 일정하지 않은 주기로 변화하는 것

• 2~7년 주기로 번갈아 발생하는 엘니뇨와 라니냐 현상에 따른 수온변화
• 대략 11년을 주기로 증가와 감소를 반복하는 태양 흑점의 개수

시계열 데이터의 특성

기술적 분석(Descriptive Analysis)

과거의 데이터를 이해하기 위한 분석과정. 데이터가 가진 패턴,
추세, 주기성 등의 규칙적인 정보를 파악해 데이터의 기본 구조와 패턴을 이해하고, 이상치를 탐지하거나 데이터의 일반적인 행동을 설명

예측적 분석 (Predictive Analysis)

미래의 데이터를 예측하기 위해 과거 데이터의 분석하는 것. 미래의 트렌드, 변동성 등을 예측하고, 비즈니스 전략을 수립하거나 의사결정을 지원하기 위해 쓰인다.

시계열 예측

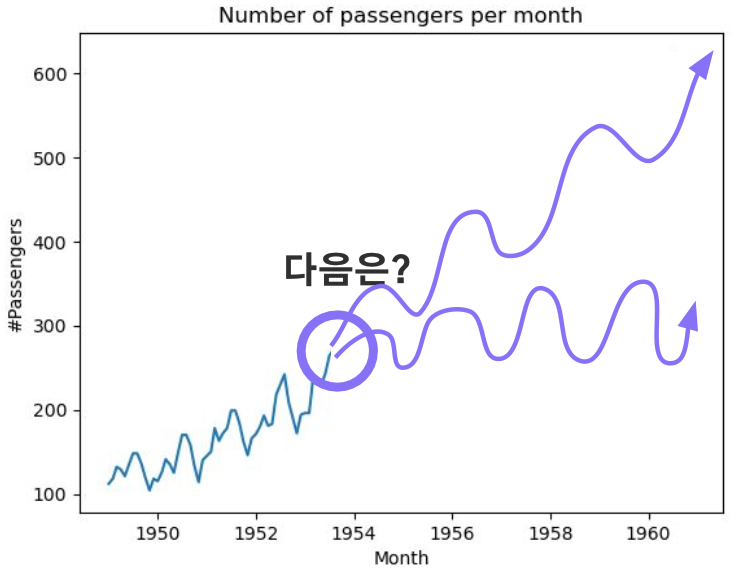
시계열 데이터로부터 데이터를 예측하는 것은
기본적으로 과거가 미래에 영향을 주기 때문에 가능하다.
일반적으로 머신러닝에 쓰이는 데이터와는 달리 서로 다른 시점의 데이터가 서로 독립이 아니므로, 독립항등분포(IID) 가정이 성립하지 않는다.

독립 항등 분포(Independent and Identically Distributed)

어떤 확률변수들이 같은 확률분포로부터 생성된 독립적인 샘플이라면 각 변수가 IID(Independent and Identically Distributed; 독립항등분포)이라고 한다.
머신러닝에서 다루는 대부분의 모델이 IID를 가정하므로 IID를 가정하지 못하는 데이터의 경우 추가적인 고려가 필요

• (gambler’s paradox) 주사위 하나를 굴려 어떤 눈이 나올지 맞히면 건 돈의 5배를 받는 도박이 있다. 방금전까지 10번 연속으로 3이 나왔다면, 이번에는 어디에 베팅할 것인가?
• 내일 비가 올 확률을 예측하는 모델을 만든다고 할 때, 10일 연속으로 비가 왔다면 내일도 비가 온다고 예측해야할까?

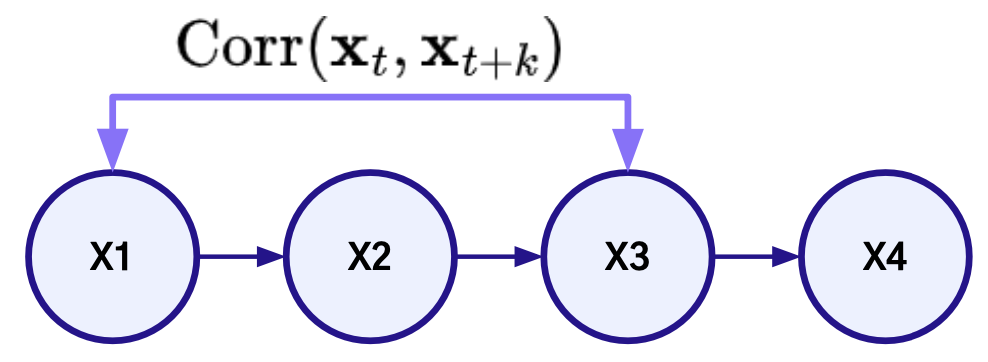
자기 상관(Autocorrelation)

한 시계열 내에서 자기자신과 다른 시점과의 상관관계
t 시점과 시차 k 이후인 t+k 시점 데이터의 상관계수로 측정

• 시차 1의 자기상관이 높으면 오늘의 데이터는 어제의 데이터가 가장 잘 설명한다는 의미

마르코프 속성(Markov property)

랜덤 프로세스의 미래 상태에 대한 조건부 확률 분포(과거 및 현재 값 모두에 대한 조건부)가 현재 상태에만 의존하는 것

• 마르코프 속성을 가정하고 예측 모델링하면 마르코프 모델
• 마르코프 속성을 만족하는 이산시간 랜덤 프로세스를 마르코프 체인
• 현재 상태가 이전 1개 상태만이 아닌 n개 상태에만 의존하면 n차 마르코프 속성이라 한다.

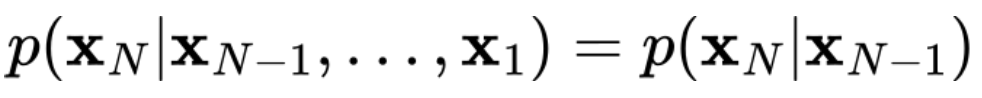
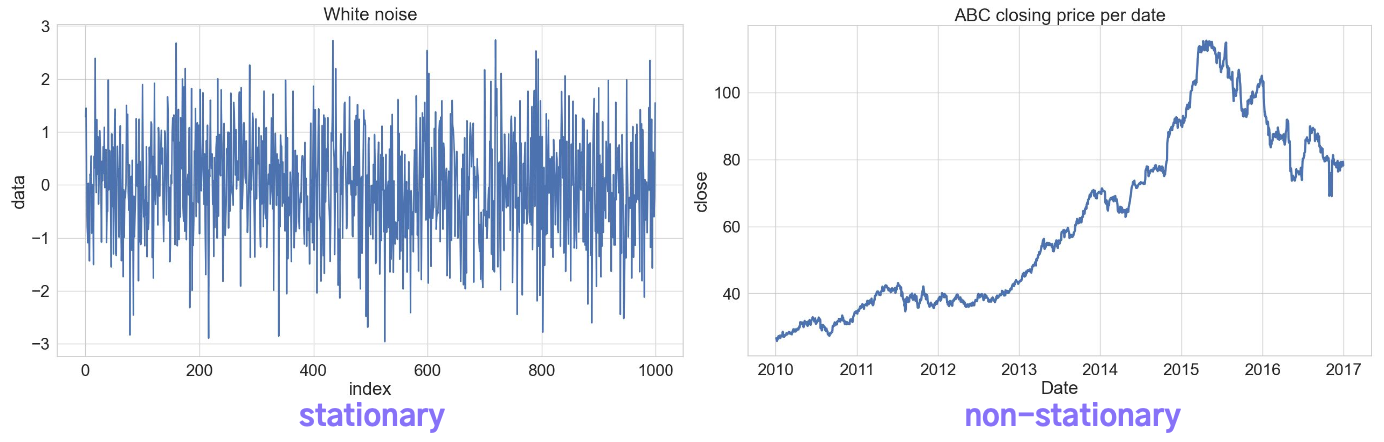
시계열의 정상성(Stationarity)

정상성(stationary) 데이터는 데이터를 생성하는 분포가 시간에 따라 변하지 않고 동일하게 유지되는 것. 비정상성(non-stationary) 데이터는 반대로 생성 분포 자체가 시간이 지남에 따라서 변화하는 것.

• 화이트노이즈: 정상적
• 주식의 가격: 비정상적

시계열 데이터 모델링 방법론

시계열 데이터의 분석방법

시계열 데이터는 non-IID와 같은 여러 특성에 주의해 분석을 수행해야한다.

• 정상성 검정(stationarity test)을 이용하여 데이터의 정상성 여부를 먼저 판단하고,
• 데이터를 정상적 데이터로 전처리(분해) 한 뒤,
• 이를 이용하여 모델을 구성
  평균이 일정하도록, 분산 및 공분산에 연속적인(시점 t에 의존하는) 상관성이 없도록 변환한다.

적용 분야에 따른 두 가지 접근법

• 시계열의 진동수를 활용한 분석:
  • 푸리에(Fourier) 분석
  • 스펙트럼 밀도(Spectrum Density) 분석
  • 웨이브렛(Wavelet) 분석
• 시간에 따른 변화를 분석
  • 자기회귀모델(Autoregressive model)
  • 이동평균(Moving Average)
  • 추세(trend)분석
  • 성분분해(decomposition) 등등

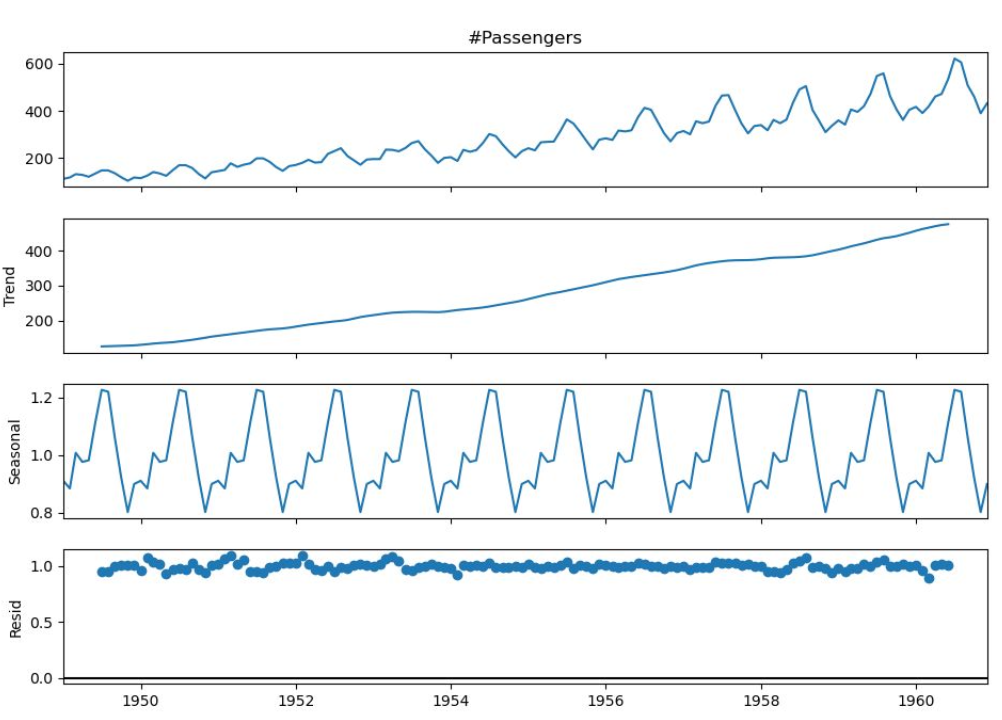
시계열 데이터의 분해

시계열데이터를 각 성분으로 분해하여 예측이나 계절성에 따른 변화를 조정하는데 활용한다.

• 주어진 시계열을 계절성, 추세와 불규칙 성분으로 분해하는 계절성 분해(Seasonal Decomposition)
  

이동평균과 자기회귀 모델

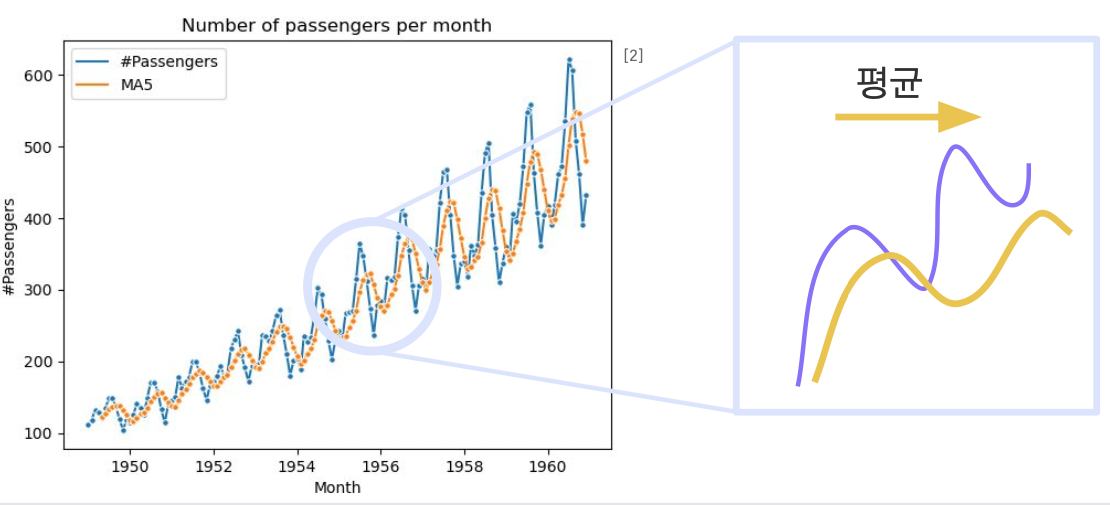
이동 평균 모델 (Moving Average model)

p 기간 안의 시계열 데이터를 평균하여 시간 t의 추세-주기를 측정
시계열 데이터에서 단기적인 변동을 smoothing하여 제거하고, 장기적인 추세를 더 잘 확인할 수 있다.

• 5일간 데이터가 2, 5, 1, 9, 11순으로 변화했다면, 다음 값에 대한 예측은 p=2에서 10으로, p=5일 때는 5.4

자기회귀 모델 (Auto-Regressive model)

시계열의 특정 스텝(t)을 예측하기 위해, 일정 스텝 수(p) 만큼의 과거 데이터들(t-p 부터 t-1까지)을 입력값으로 선형회귀모델을 학습하는 방식