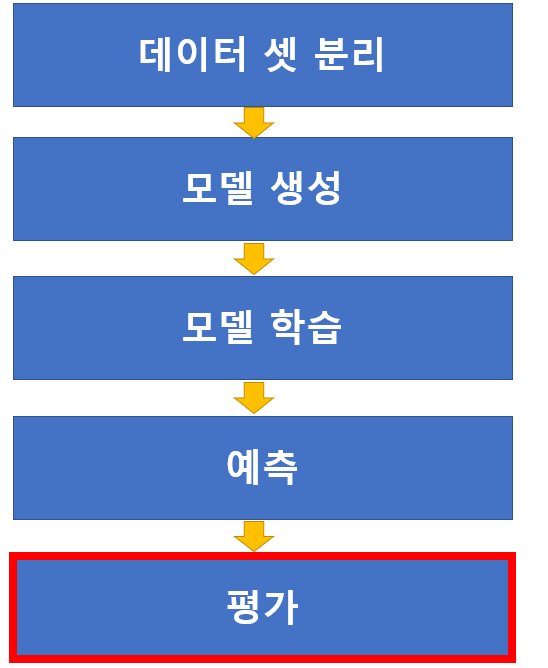
모델평가

- 모델의 성능을 평가하고 평가결과에 따라 프로세스를 다시 반복한다.
##과정
데이터 셋 분리 -> 모델 생성 -> 모델 학습 -> 예측 -> 평가
scikit-learn 평가함수 모듈
- sklearn.metrics모듈을 통해 평가함수 모듈을 제공한다.
평가방법(분류 / 회귀)
-
분류 평가 지표
- 정확도(Accuracy)
- 정밀도(Precision)
- 재현률(Recall)
- F1점수(F1 Score)
- PR Curve, AP score
- ROC,AUC score
-
회귀 평가 지표
- MSE (Mean Squared Error)
- RMSE (Root Mean Squared Error)
- 𝑅2 (결정계수)

분류(Classification)평가 지표
- 다중 분류 (Multi class classification)
- Target이 여러개의 클래스 중 하나를 분류한다.
- 이진 분류 (Binary classification)
- 어떤 항목이 맞는지 아닌지 분류
- 이진 분류 양성(Positive)과 음성(Negative)
- 양성(Positive): 찾는 대상 / 보통 1로 표현
- 음성(Negative): 찾는 대상이 아닌 것 / 보통 0으로 표현
- 정확도 (Accuracy)
- 대표적인 분류의 평가 지표=> 전체 예측 한것 중 맞게 예측한 비율로 평가
방법
accuracy_score(정답, 모델예측값)
Accuracy 평가지표의 문제
- 이진분류의 경우 양성(Positive)에 대한 지표만 확인할 수 없다.
다시말해 음성(Negative)에 대한 지표만 확인 할 수 없다는 것.
why?
전체 중 몇개가 맞았는지에 대한 지표이지 양성에 대한 지표가 무엇인지 음성에 대한 지표가 아니기때문이다. (따로따로 알 수 없음) - 불균형 데이터의 경우 정확한 평가지표가 될 수 없다.
why?
예를들어, 양성과 음성의 비율이 1:9인 경우 모두 음성이라고 하면 정확도는 90%가 된다.
MNIST Data set
- 손글씨 숫자 데이터 셋(이미지 데이터 셋)
- 사이킷런에서 제공하는 이미지 사이즈
- image size: 8 X 8
- 원본 데이터는 28 X 28 크기로 train 60,000장, test 10,000 장을 제공
# mnist 데이터 셋 로드 및 확인
from sklearn.datasets import load_digits # 데이터셋 저장된 라이브러리
import numpy as np
import matplotlib.pyplot as plot # 시각화용
mnist = load_digits() # 데이터 셋 로드
mnist.keys() # 키값 확인
# 결과
dict_keys(['data', 'target', 'frame', 'feature_names', 'target_names', 'images', 'DESCR'])load_digits() 함수는 숫자 데이터 세트인 MNIST를 불러와서, MNIST 데이터 세트에 해당하는 여러 정보들이 딕셔너리 타입으로 담겨 있다. 이 함수에서 반환하는 각각의 데이터 타입들은 다음과 같다.
- data : 각 이미지의 픽셀값을 나타내는 feature data
- target : 각 이미지에 대한 정답 클래스(0~9)를 나타내는 target data입니다.
- images : data를 이미지 형태로 나타낸 값
- feature_names : data의 feature 이름
- target_names : target의 이름
- DESCR : 데이터 세트와 관련된 설명
위 코드에서 X 변수에는 data 값을, y 변수에는 target 값을 담고 있다. 나머지 변수들은 본 데이터를 다룰 때 비교적 사용 빈도가 적다,
X,y = mnist['data'],mnist['target']
X.shape,y.shape, type(X),type(y)
# 결과
((1797, 64), (1797,), numpy.ndarray, numpy.ndarray)
np.unique(y, return_counts=True) # 고유한 원소와 원소의 갯수
# 결과
(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
array([178, 182, 177, 183, 181, 182, 181, 179, 174, 180]))
X[0].shape # 첫번째 사진 (64, )
X[0]
# 결과
array([ 0., 0., 5., 13., 9., 1., 0., 0., 0., 0., 13., 15., 10.,
15., 5., 0., 0., 3., 15., 2., 0., 11., 8., 0., 0., 4.,
12., 0., 0., 8., 8., 0., 0., 5., 8., 0., 0., 9., 8.,
0., 0., 4., 11., 0., 1., 12., 7., 0., 0., 2., 14., 5.,
10., 12., 0., 0., 0., 0., 6., 13., 10., 0., 0., 0.])
X[0].reshape(8, 8) # 8x8로 변경
# 결과
array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])
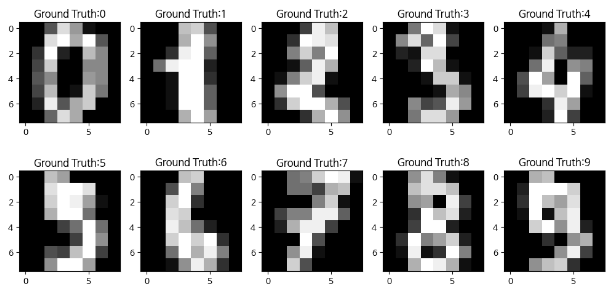
plot.imshow(X[0].reshape(8,8), cmap='Greys')
plot.title(str(y[0]))
plot.show()
# 결과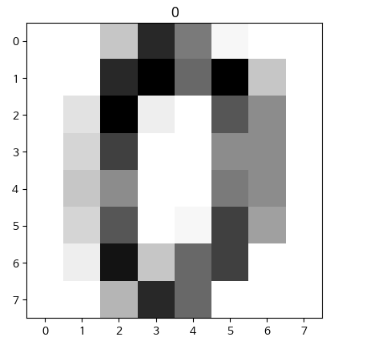
plot.figure(figsize=(10,5))
for i in range(10):
plot.subplot(2, 5, i+1)
plot.imshow(X[i].reshape(8,8), cmap="gray")
plot.title(f"Ground Truth:{y[i]}")
plot.tight_layout()
plot.show()
# 결과혼동 행렬 (Confusion Marix)
-
실제 값(정답)과 예측한 것을 표로 만든 평가표이다.
언제사용?
=> 분류의 예측결과가 몇개나 맞고 틀렸는지 확인 시 사용 -
함수: confusion_matrix(정답, 모델예측값)
-
결과의 0번축: 실제 class, 1번 축: 예측 class
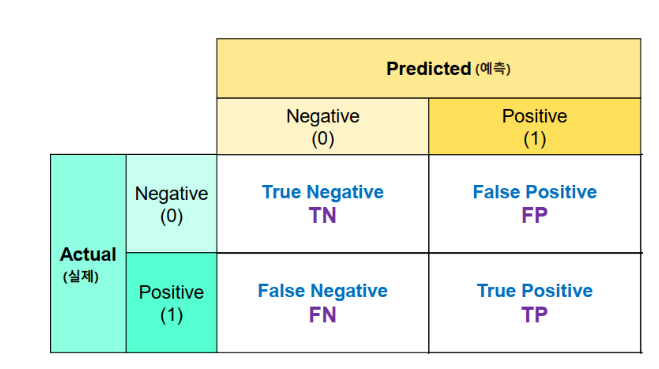
-
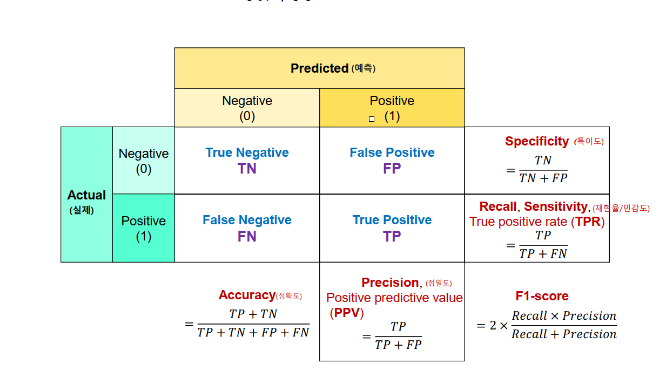
TP(True Positive)
=> 양성으로 예측했는데 맞은 개수
TN(True Negative)
=> 음성으로 예측했는데 맞은 개수
FP(False Positive)
=> 양성으로 예측했는데 틀린 개수
음성을 양성으로 예측
FN(False Negative)
=> 음성으로 예측했는데 틀린 개수
양성을 음성으로 예측
예)
[[20, 6],
[4, 40]]
각각 예측한 개수
이진 분류 평가지표
- Accuracy (정확도)
- 전체 데이터 중 맞게 예측한 비율
- Accuracy (정확도)는 이진분류 뿐아니라 모든 분류의 기본 평가방식
양성(Positive) 예측력 측정 평가지표
-
Recall/Sensitivity(재현율/민감도)
=> 실제 Positive(양성)인 것 중에 Positive(양성)로 예측 한 것의 비율
ex) 스팸메일이야? -> 응 스펨이야(1) / 아니야 (0)
-> 스팸 메일 중 스팸메일로 예측한 비율 -
Precision(정밀도)
=> Positive(양성)으로 예측 한 것 중 실제 Positive(양성)인 비율
ex) 스펨메일일거야 -> 응 스펨이야(1) / 아니야 (0)
-> 스팸메일로 예측한 것 중 스팸메일의 비율 -
F1 점수
- 정밀도와 재현율의 조화평균 점수
- 정밀도와 재현율은 반비례관계이다.
- recall과 precision이 비슷할 수록 높은 값을 가진다.
- F1 score이 높다는 것은 recall과 precision이 한쪽으로 치우쳐져있지 않고 둘다 좋다고 판단할 수 있는 근거
음성(Negative) 예측력 측정 평가지표
-
Specificity(특이도)
=> 실제 Negative(음성)인 것들 중 Negative(음성)으로 맞게 예측 한 것의 비율
-
Fall out(위양성률)
=> 실제 Negative(음성)인 것들 중 Positive(양성)으로 잘못 예측한 것의 비율
=> 1 - 특이도
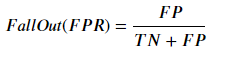
# Dummy 모델 혼동핼렬
# dummy model: 진짜 모델이 아니라 모델을 흉내낸 모델을 말한다.
# Target Label중 무조건 최빈값으로 예측하는 모델을 정의한다.
import matplotlib.pyplot as plt
from sklearn.metrics import (confusion_matrix,
ConfusionMatrixDisplay,
recall_score,
accuracy_score,
precision_score,
f1_score)
# 혼동행렬 생성
result_cm_1 = confusion_matrix(y_train, pred_train)
result_cm_1
# 결과
array([[1212, 0],
[ 135, 0]])
result_cm_2 = confusion_matrix(y_test, pred_test)
result_cm_2
# 결과
array([[405, 0],
[ 45, 0]])# 각 행렬 시각화
plt.figure(figsize=(4,4))
ax = plt.gca()
disp = ConfusionMatrixDisplay(result_cm_1,
display_labels=["Not 9", "9"])
disp.plot(cmap="Blues", ax=ax)
plt.title("Train set ConfusionMatrix")
plt.show()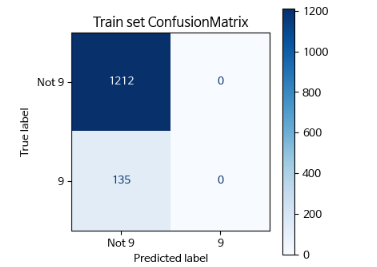
plt.figure(figsize=(4,4))
ax = plt.gca()
disp2 = ConfusionMatrixDisplay(result_cm_2, display_labels=['0~8', '9'])
disp2.plot(cmap='Reds', ax=ax)
plt.title("Test set ConfusionMatrix")
plt.show()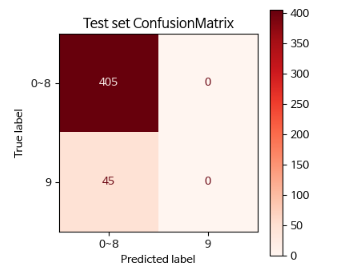
# dummy 모델 Accuracy, Recall, Precision, F1-Score
print("Accuracy") # 정확도
accuracy_score(y_train, pred_train), accuracy_score(y_test, pred_test)
# 결과
Accuracy
(0.8997772828507795, 0.9)
print("Recall") # 재현률
recall_score(y_train, pred_train), recall_score(y_test, pred_test)
# 결과
Recall
(0.0, 0.0)
print("Precision") # 정밀도
precision_score(y_train, pred_train), precision_score(y_test, pred_test)
# 결과
Precision
(0.0, 0.0)
print("f1-score")
f1_score(y_train, pred_train), f1_score(y_test, pred_test)
# 결과
f1-score
(0.0, 0.0)classification_report()
- Accuracy와 각 class가 Positive일 때의 recall, precision, f1-score를 한번에 보여주는 함수이다.
from sklearn.metrics import classification_report
result = classification_report(y_train, pred_train_tree)
print(type(result)) # result가 문자열이므로 print해서 봐야한다.
print(result)
# 결과
2]
0초
from sklearn.metrics import classification_report
result = classification_report(y_train, pred_train_tree)
print(type(result)) # result가 문자열이므로 print해서 봐야한다.
print(result)
<class 'str'>
precision recall f1-score support
0 0.98 0.96 0.97 1212
1 0.71 0.80 0.75 135
accuracy 0.95 1347
macro avg 0.84 0.88 0.86 1347
weighted avg 0.95 0.95 0.95 1347재현율과 정밀도의 관계
-
이진분류의 경우 Precision(정밀도)가 중요한 경우와 Recall(재현율)이 중요한 업무가 있다.
-
재현율이 더 중요한 경우
- 실제 Positive 데이터를 Negative 로 잘못 판단하면 업무상 큰 영향이 있는 경우
- FN(False Negative)를 낮추는데 점
-
정밀도가 더 중요한 경우
- 실제 Negative 데이터를 Positive 로 잘못 판단하면 업무상 큰 영향이 있는 경우
- FP(False Positive)를 낮추는데 초점
Positive(1)일 확률에 대한 임계값(Threshold) 변경을 통한 재현율, 정밀도 변환
- 재현율과 정밀도는 반비례 관계이므로 이 둘의 적절한 비율을 찾아야한다.
- 임계값 (Threshold)
- 모델이 분류 Label을 결정할 때 기준이 되는 확률 기준값
- 정밀도나 재현율을 특히 강조해야 하는 상황일 경우 임계값 변경을 통해 평가 수치를 올릴 수있다
- 단 극단적으로 임계점을 올리나가 낮춰서 한쪽의 점수를 높이면X

임계값 변경에 따른 정밀도와 재현율 변화관계
<정리>
- 임계값을 낮추면 재현율은 올라가고 정밀도는 낮아진다.
- 임계값을 높이면 재현율은 낮아지고 정밀도는 올라간다.
- 임계값을 변화시켰을때 재현율과 정밀도는 반비례 관계를 가진다.
- 임계값을 변화시켰을때 재현율과 위양성율(Fall-Out/FPR)은 비례 관계를 가진다.
임계값에 따른 recall,precision 변화
분류 모델의 추론 메소드
model.predict(X)
* 추론한 X의 class를 반환model.predict_proba(X)
*추론한 X의 class별 확률을 반환임계값 변화에 따른 recall/precision 확인
- precisionrecall_curve(y정답, positive_예측확률) 이용
- 반환값: Tuple
from sklearn.metrics import precision_recall_curve
result = precision_recall_curve(y_test, pos_test_tree) # (정답, 모델이 추론한 양성의 확률)
type(result), len(result)
# 결과
(tuple, 3)
precision_list, recall_list, thresh_list = result # 튜플대입
precision_list.shape, recall_list.shape, thresh_list.shape
# 결과
((8,), (8,), (7,))
thresh_list = np.append(thresh_list, 1) # thresh_list에 1을 추가.
thresh_list
# 결과
array([0.00826446, 0.01304348, 0.03389831, 0.04 , 0.14925373,
0.54545455, 0.75 , 1. ])
# 전체확인해보기
print("idx. prec, recall, thresh")
for idx, (p, r, t) in enumerate(zip(precision_list, recall_list, thresh_list)):
print(f"{idx}. {p:.4f}, {r:.4f}, {t:.4f}")
# 결과
idx. prec, recall, thresh
0. 0.1000, 1.0000, 0.0083
1. 0.1076, 0.9778, 0.0130
2. 0.4318, 0.8444, 0.0339
3. 0.5139, 0.8222, 0.0400
4. 0.5606, 0.8222, 0.1493
5. 0.7556, 0.7556, 0.5455
6. 0.8235, 0.6222, 0.7500
7. 1.0000, 0.0000, 1.0000# 시각화
import matplotlib.pyplot as plt
plt.plot(thresh_list, precision_list, marker='.', label="정밀도")
plt.plot(thresh_list, recall_list, marker='.', label="재현율")
plt.legend()
plt.grid(True)
plt.show()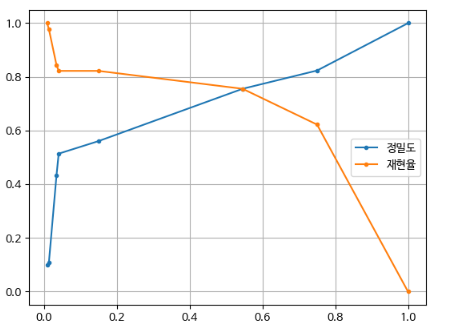
임계값 변경 후처리를 통한 recall/precision 변경
# 기본 임계값
from metrics import print_metrics_classification
# threshold=0.5일때 결과.
pred_test = tree.predict(X_test) #추론
print_metrics_classification(y_test, pred_test, title="threhold: 0.5")
# 결과
================threhold: 0.5===============
정확도: 0.9511111111111111
재현율: 0.7555555555555555
정밀도: 0.7555555555555555
F1: 0.7555555555555555
# 임계점을 내리기
thresh = 0.1
pred_test_01 = np.where(pos_test_tree > thresh, 1, 0) # 1일 확률이 0.1 초과면 1로 아니면 0으로 추론.
print_metrics_classification(y_test, pred_test_01)
# 결과
정확도: 0.9177777777777778
재현율: 0.8222222222222222
정밀도: 0.5606060606060606
F1: 0.6666666666666666
# 임계점을 올려기
thresh = 0.6
pred_test_06 = np.where(pos_test_tree > thresh, 1, 0)
print_metrics_classification(y_test, pred_test_06)
# 결과
정확도: 0.9488888888888889
재현율: 0.6222222222222222
정밀도: 0.8235294117647058
F1: 0.7088607594936709정밀도와 재현율을 평가하는 또다른 함수
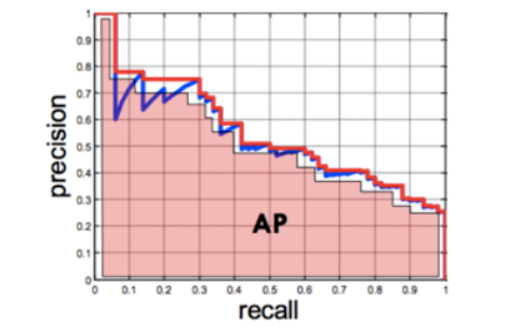
PR Curve(Precision Recall Curve-정밀도 재현율 곡선)와 AP Score(Average Precision Score)
-
이진분류의 평가지표 중 하나
-
재현율이 변화할 때 정밀도가 어떻게 변화하는지 평가
-
Precision과 Recall 값들을 이용해 모델을 평가하는 것으로 모델의 Positive에 대한 성능의 강건함(robust)를 평가
-
X축에 재현율, Y축에 정밀도
-
임계값이 1 → 0 변화할때 두 값의 변화를 선그래프로 나타낸다.
-
AP Score
- PR Curve의 성능평가 지표를 하나의 점수(숫자)로 평가
- PR Curve의 선아래 면적을 계산한 값으로 높을 수록 성능이 우수
from sklearn.metrics import (precision_recall_curve, # threshold 변화에 따른, recall/precision
PrecisionRecallDisplay, # PR Curve(계단모양 나타내는)를 그리는 클래스
average_precision_score) # AP Score 계산 함수.
## DecisionTree
ap_score = average_precision_score(y_test, pos_test_tree)
#recall, precision, threshold값들 조회
precision_list1, recall_list1, _ = precision_recall_curve(y_test, pos_test_tree) # 필요없는 경우 _로 표현 가능
disp_tree = PrecisionRecallDisplay(precision_list1, # precision(정밀도)
recall_list1, # recall(재현율)
average_precision=ap_score, # ap score
estimator_name="DecsionTree") # 범례(Legend)에 표시될 Label.
disp_tree.plot()
plt.title('DecisionTree Testset PR Curve')
plt.show() 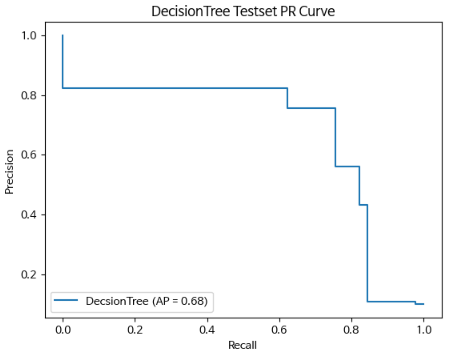
# AP score
ap_score = average_precision_score(y_test, pos_test_tree) # (y정답, positive확률)
ap_score
# 결과
0.6766948888666132### RandomForest
ap_score_rfc = average_precision_score(y_test, pos_test_rfc) # (y정답, positive확률)
#recall, precision, threshold값들 조회
precision_list2, recall_list2, _ = precision_recall_curve(y_test, pos_test_rfc)
disp_rfc = PrecisionRecallDisplay(precision_list2,
recall_list2,
average_precision=ap_score_rfc,
estimator_name="RandomForest")
disp_rfc.plot()
plt.title('RandomForest Testset PR Curve')
plt.show()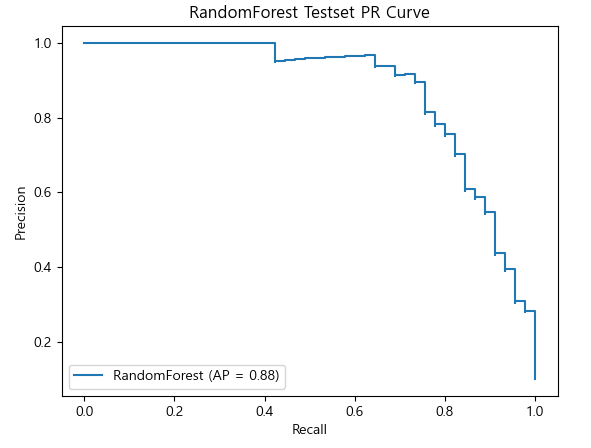
# DecisionTree와 RandomForest의 PR Curve를 하나의 Axes(subplot)에 display
ax = plt.gca()
disp_tree = PrecisionRecallDisplay(precision_list1,
recall_list1,
average_precision=ap_score,
estimator_name="DecisionTree")
disp_rfc = PrecisionRecallDisplay(precision_list2,
recall_list2,
average_precision=ap_score_rfc,
estimator_name="RandomForest")
# plot이 같은 axes를 지정.
disp_tree.plot(ax=ax)
disp_rfc.plot(ax=ax)
plt.title("Precision Recall Curve")
plt.show()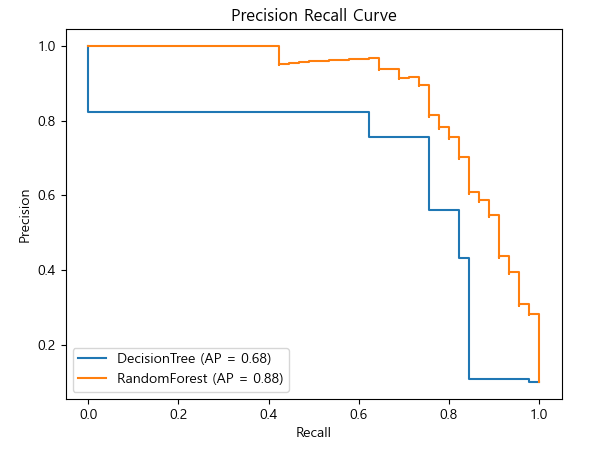
위양성률과 재현률과의 상관관계
ROC curve(Receiver Operating Characteristic Curve)와 AUC(Area Under the Curve) score
-
FPR(False Positive Rate-위양성율)
- 실제 음성중 양성으로 잘못 예측한 비율
- 납을 수록 좋다
-
TPR(True Positive Rate-재현율/민감도)
- 실제 양성중 양성으로 맞게 예측한 비율
- 높을 수록 좋다
=> Positive의 임계값을 변경할 경우 FPR과 TPR(recall)은 비례해서 변화한다.
-
ROC Curve
-
이진분류의 성능 평가 지표 중 하나
-
FPR 변화할 때 TPR이 어떻게 변하는 지를 평가
-
FPR을 X축, TPR을 Y축
-
임계값이 1 → 0 변화할때 두 값의 변화를 선그래프로 그린다.
-
Positive(양성), Negative(음성) 에 대한 모델의 성능의 강건함(robust)을 평가
-
AUC Score
-
ROC Curve의 결과를 점수화(수치화) 하는 함수로 ROC Curve 아래쪽 면적을 계산
-
0 ~ 1 사이 실수로 나오며 클수록 좋다
-
AUC 점수기준
1.0 ~ 0.9 : 아주 좋음
0.9 ~ 0.8 : 좋음
0.8 ~ 0.7 : 괜찮은 모델
0.7 ~ 0.6 : 의미는 있으나 좋은 모델은 아님
0.6 ~ 0.5 : 좋지 않은 모델
-
선 아래의 면적이 넓은 곡선이 나올 수록 좋은 모델이다.
-
roccurve(y값, Pos예측확률) : FPR, TPR, Thresholds (임계치)
-
rocauc_score(y값, Pos예측확률) : AUC 점수 반환
-
RocCurveDisplay: 시각화
-
-
-
ROC Curve/ROC-AUC score
- 이진분류에서 양성클래스 탐지와 음성클래스 탐지의 중요도가 비슷할 때 사용(개고양이 분류)
-
Precision Recall Curve/AP Score
- 양성클래스 탐지가 음성클래스 탐지의 중요도보다 높을 경우 사용(암환자 진단)
from sklearn.metrics import roc_curve, RocCurveDisplay, roc_auc_score
import pandas as pd
fpr_list1, tpr_list1, thresh_list1 = roc_curve(y_test, pos_test_tree)# (y정답, pos확률)
fpr_list1.shape, tpr_list1.shape, thresh_list1.shape
df = pd.DataFrame({
"임계값":thresh_list1,
"FPR":fpr_list1,
"TPR-Recall":tpr_list1
})
df # 1.75는 그냥 상징적인 큰값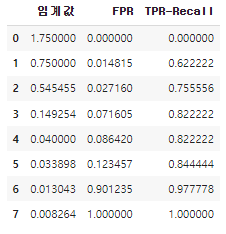
plt.plot(df['FPR'], df['TPR-Recall'])
plt.show()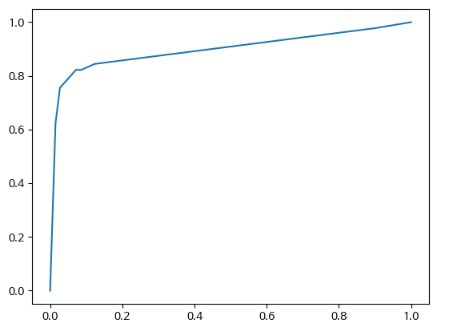
auc = roc_auc_score(y_test, pos_test_tree) # (정답, pos확률)
print(auc)
# 결과
auc = roc_auc_score(y_test, pos_test_tree) # (정답, pos확률)
print(auc)
0.8975308641975308disp_tree = RocCurveDisplay(fpr=fpr_list1, # 위양성률
tpr=tpr_list1, #재현율
roc_auc=auc, # roc-auc 점수 계산한 값
estimator_name="DecisionTree") # 범례에 출력될 Label 값
disp_tree.plot()
plt.show()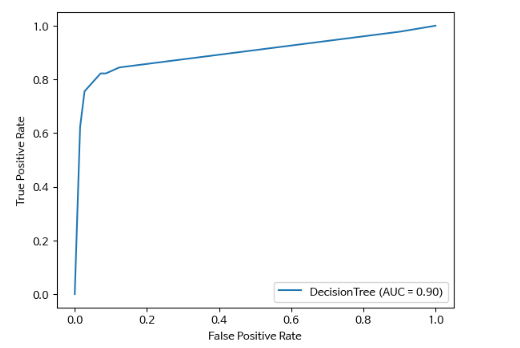
# decisiontree, random forest 의 roc 커브 시각화
ax = plt.gca()
fpr1, tpr1, _ = roc_curve(y_test, pos_test_tree)
fpr2, tpr2, _ = roc_curve(y_test, pos_test_rfc)
auc_tree = roc_auc_score(y_test, pos_test_tree)
auc_rfc = roc_auc_score(y_test, pos_test_rfc)
disp_tree = RocCurveDisplay(fpr=fpr1, tpr=tpr1, roc_auc=auc_tree, estimator_name="Tree")
disp_rfc = RocCurveDisplay(fpr=fpr2, tpr=tpr2, roc_auc=auc_rfc, estimator_name="RF")
disp_tree.plot(ax=ax)
disp_rfc.plot(ax=ax)
plt.title("Roc 커브 - Test set")
plt.show()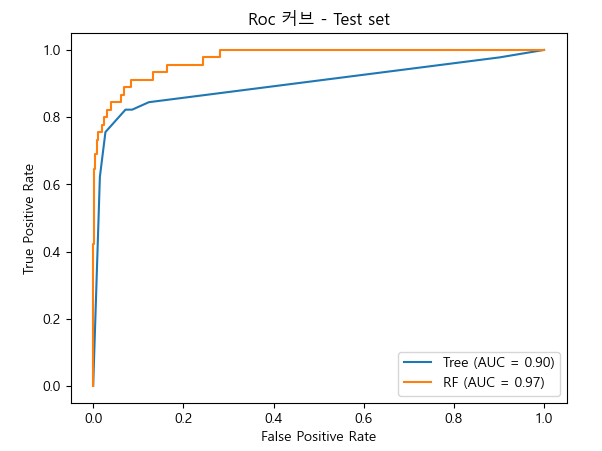
회귀(Regression) 평가지표
- 예측할 값(Target)이 연속형(continuous) 데이터인 지도 학습(Supervised Learning)
회귀의 주요 평가 지표
- MSE (Mean Squared Error)
- 실제 값과 예측값의 차를 제곱해 평균 낸 것.
- scikit-learn 평가함수: mean_squared_error() 사용
- 교차검증시 지정할 문자열: 'neg_mean_squared_error'
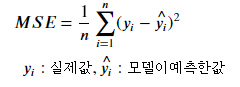
-
RMSE (Root Mean Squared Error)
-
MSE는 오차의 제곱한 값이므로 실제 오차의 평균보다 큰 값이 나온다. MSE의 제곱근이 RMSE
-
mean_squared_error() 의 squared=False로 설정해서 계산
or
MSE를 구한 뒤 np.sqrt()로 제곱근을 구한다.
-
교차검증시 지정할 문자열:'neg_root_mean_squared_error'
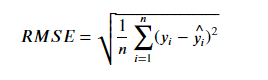
-
- 𝑅2 (R square, 결정계수)
결정계수는 회귀모델에서 Feature(독립변수)들이 Target(종속변수)를 얼마나 설명하는지를 나타내는 평가지표
평균으로 예측했을 때 오차(총오차) 보다 모델을 사용했을 때 얼마 만큼 더 좋은 성능을 내는지를 비율로 나타낸 값으로 계산
1에 가까울 수록 좋은 모델
scikit-learn 평가함수: r2_score()
* 교차검증시 지정할 문자열: 'r2'
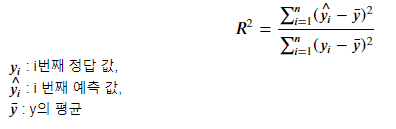
Dataset 생성 함수
- make_regression(): 회귀 문제를 위한 dummy dataset 생성
- make_classification(): 분류 문제를 위한 dummy dataset 생성
Noise란
- 같은 Feature를 가진 데이터포인트가 다른 label을 가지는 이유를 Noise(노이즈)라고 한다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression # 내가 원하는 데이터 셋을 만들어주는 것.(가상의데이터셋을 내가 만들겠다.)
X, y = make_regression(n_samples=1000, # 데이터포인트 개수
n_features=1, # feature(컬럼)의 개수 # (1000,1)
n_informative=1, # label(y)에 영향을 주는 feature의 개수. n.features와 같거나 작은 정수를 설정.
noise=30, # 모델이 찾을 수 없는 값의 범위. 0~30사이의 랜덤실수 값을 생성된 y에 더한다. ==> 인정할 수 있는 오차의 범위.
random_state=0
)
X.shape, y.shape
# 결과
((1000, 1), (1000,))plt.scatter(X, y, alpha=0.3)
plt.show()
np.corrcoef(X.flatten(), y) # 상관관계를 표현
# 결과
array([[1. , 0.93856218],
[0.93856218, 1. ]])상관관계
- 양수: 양의 상관관계 -> 선형적인 비례관계
- 음수: 음의 상관관계 -> 선형적인 반비례관계
- 값의 범위: -1 ~ 1사이의 값이 나온다.
- 절대값 기준으로 1에 가까울 수록 선형적 상관관계가 강하다.
- 0에 가까울 수록 관계가 적다.