선형회귀(Linear regression)
- 선형회귀(Linear regression)
- 완전 쉽게 말하자면 일차항들을 쭉 더한것이다.
- 각 Feature들에 가중치(Weight)를 곱하고 편향(bias)를 더해 예측 결과를 출력한다.
그런데 우리는 얼만큼의 가중치(Weight)를 곱해야 하는지,편향(bias)를 더해야하는지 모르기 때문에 학습을 통해 찾아야한다.
그래서
Weight와 bias가 학습대상 Parameter가 된다.
식은 아래와 같다.
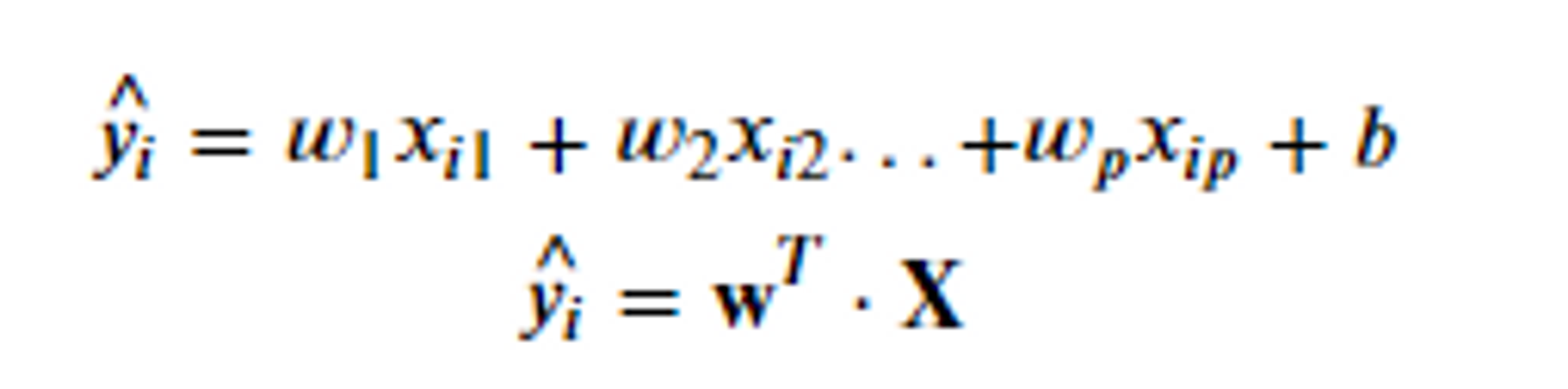
1번째 식과 w를 전치 시킨 2번째는 동일한 것을 구하는 것이다.
전체적으로 선형회귀를 하는 방식은 위와같다.
선형회귀의 종류에 대하여 알아보자.
- 선형회귀 종류
- LinearRegression Model
- RidgeRegression Model
- LassoRegression Model
첫번째
-
LinearRegression Model
-
가장 기본적인 선형회귀 모델이다.
-
각 Feature에 가중치의 합으로 y값을 추론한다.
(위에서 설명한 방식) -
데이터 전처리 방법
- 선형회귀 모델 사용시 전처리 방법에 대해 알아보자.
- 범주형 Feature 경우
- One Hot Encoding
- 연속형 Feature 경우
- Feature Scaling을 통해서 각 컬럼들의 값의 단위를 맞춰준다.
- StandardScaler를 사용할 때 성능이 더 잘나오는 경향이 있다.
-
<예제를 통해 확실하게 이해하기>
# 1. 데이터셋 로드 및 분리
from dataset import get_boston_dataset
X_train, X_test, y_train, y_test = get_boston_dataset() 데이터 셋: 379 rows × 13 columns
우리는 13가지의 속성을 가지고 집값을 예측할 것이다.
# 2.전처리
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler() # 객체 생성
X_train_scaled = scaler.fit_transform(X_train) # train set으로 학습 + 변환
X_test_scaled = scaler.transform(X_test) # Test set: train set으로 학습한 scaler이용해 변환.
# 3. 모델링
from sklearn.linear_model import LinearRegression # 선형회귀모델
lr = LinearRegression() # 객체생성 # 애는 하이퍼파라미터(넘겨주는 값)이 따로 존재하지 않다.
lr.fit(X_train_scaled, y_train) # 학습
# weight조회: 각 feature들에 곱할 가중치들을 조회할 수 있다.
# Feature가 13개 이므로 각각의 Feature에 얼마의 가중치를 곱했는지 알 수 있다.
lr.coef_
# 음수가 나왔다 => 집값을 떨어뜨리는 feature이다. # 양수가 나왔다 => 집값을 올리는 feature이다.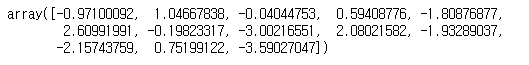
# bias조회: 모든 값이 0일때 출력값
lr.intercept_22.608707124010557
여기까지 weight와 bias를 구했다.
그럼 밑에서 사용할 Conficient의 부호에 대하여 설명하겠다.
- Conficient의 부호
weight가 - 양수: Feature가 1 증가할때 y(집값)도 weight만큼 증가
- 음수: Feature가 1 증가할때 y(집값)도 weight만큼 감소
=> 절대값 기준으로 0에 가까울 수록 집값에 영향을 주지 않고 0에서 멀어질 수록 집값에 영향을 많이 주는 Feature인 것을 알 수 있다.
# Train dataset에 대한 선형회귀 추정결과 모델을 이용해 추론
pred_train2 = lr.predict(X_train_scaled)
pred_train2.shape(379,)
pred_train2[:13]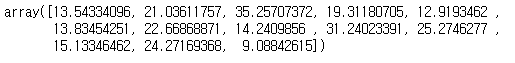
=> 추론한 y의 값을 알 수 있다.
그럼 이제 전처리도 하고 모델링도했으니 평가를 해보자.
pred_train = lr.predict(X_train_scaled)
pred_test = lr.predict(X_test_scaled)
from metrics import print_metrics_regression
print_metrics_regression(y_train, pred_train, "train set")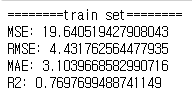
pred_test = lr.predict(X_test_scaled)
print_metrics_regression(y_test, pred_test, "test set")
=> test set의 성능이 더 좋은 것을 확인 할 수 있다.
LinearRegression(선형대수)도 복잡도를 조정할 수 있다.
규제 (Regularization)
- 선형 회귀 모델에서 과대적합(Overfitting) 문제를 해결하기 위해 가중치(회귀계수)에 페널티 값을 적용한다.
⇒ 페널티 값을 준다는 것은 가중치를 0에 가까운 값을 준다는 것이다.- 규제 (Regularization) 을 통해 Feature들에 곱해지는 가중치가 커지지 않도록 제한한다.
- LinearRegression의 규제는 학습 시 계산하는 오차를 키워서 모델이 오차를 줄이기 위해 가중치를 0에 가까운 값으로 만들도록 하는 방식을 사용
=> ⇒ 다시한번 말하자면 입력데이터의 Feature들이 너무 많은 경우 Overfitting이 발생하다.
but
- 규제를 조정하는 Regularization 클래스 모델은 따로 있다. (Ridge / Lasso)
- 규제의 종류
- L1 규제 (Lasso)
- L2 규제 (Ridge)
- 즉 모델이 추정한 값과 정답 간의 최소한의 오차를 찾는 다는 것이다.
오차를 어떻게 구하는데?
-
손실함수(Loss Function): 모델의 예측한 값과 실제값 사이의 차이를 정의하는 함수로 모델이 학습할 때 사용된다. ⇒ 오차를 계산해주는 것이 손실함수 이다.
-
Lasso Regression (L1 규제)
- w들을 모두더하는데 각 w들에 절댓값을 한다.
- |w| + |w|
- Lasso 회귀의 상대적으로 덜 중요한 특성의 가중치를 0으로 만들어 자동으로 Feature Selection이 된다.
-
Ridge Regression (L2 규제)
- 손실함수(loss function)에 규제항으로
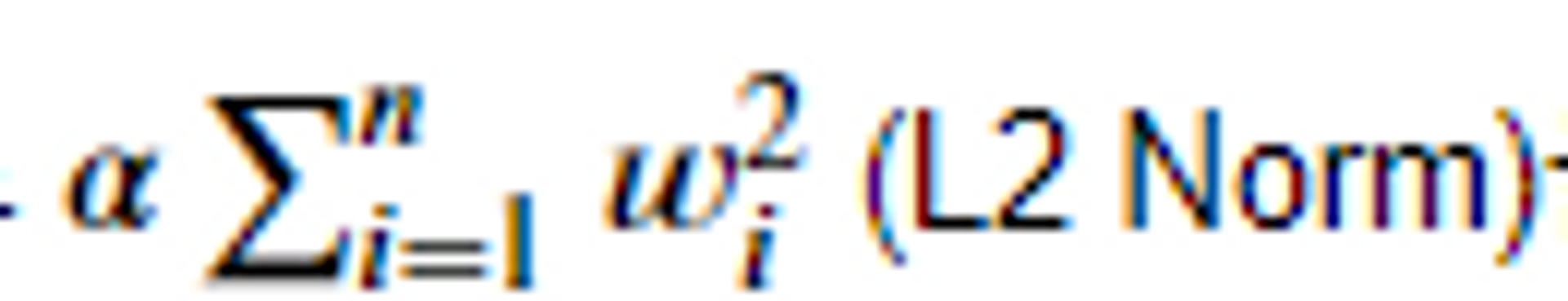
을 더해준다.
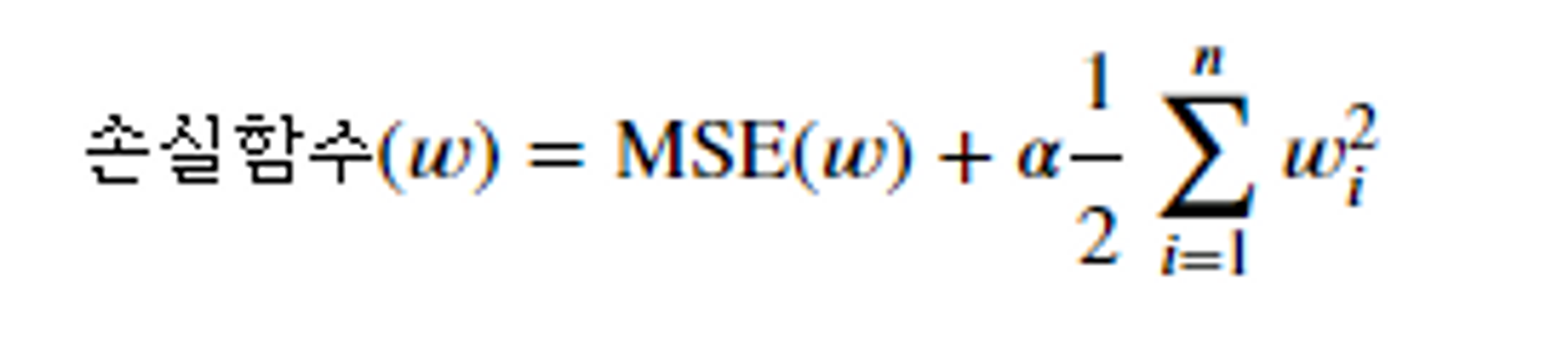
- 손실함수(loss function)에 규제항으로
⇒ 가중치가 커지면 오차가 커지므로
MSE를 계산한 후 + 무언인가를 한다. → 가중치가 커지면 오차가 커지므로 weight를 더해준다. 그런데 이것을 제곱을 하여 모두 더해 준다. (w)제곱+(w)제곱 → 그리고 앞의 a 이것이 내가 조정해주는 하이퍼파라미터이다. → a를 0점대로 주면 규제가 약해지고 1이상으로 주면 규제가 강해진다.
- 𝛼=0에 가까울수록 규제가 약해진다.
(더한거 다쓰지 않고 0.1%만 사용하겠다.- 규제 약하게한것)
<정리>
- LinearRegression : MSE만 계산
- Lasso Regression (L1 규제) : MSE + w들 각각 절댓값의 합
- Ridge Regression (L2 규제): MSE + (alpa:내가 규제하는 파라미터)*(w들 각각 제곱한 값)
<Ridge Regression (L2 규제) 를 예제를 통해 테스트 해보자>
from sklearn.linear_model import Ridge, Lasso
alpha = 1
ridge = Ridge(alpha=alpha, random_state=0) # alpha: 규제강도이다. default값은 1이다.
ridge.fit(X_train_scaled, y_train)
print_metrics_regression(y_train, ridge.predict(X_train_scaled))
print("=========================")
print_metrics_regression(y_test, ridge.predict(X_test_scaled))
# weight 조회
ridge.coef_
# baias 조회
ridge.intercept_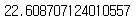
import pandas as pd
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100, 500, 1000]
# alpha 의 변화에 따른 weight의 변화를 저장할 DataFrame
coef_df = pd.DataFrame() # weight (coef) 저장
bias_list = [] # baias (intercept_) 저장
for alpha in alpha_list:
ridge = Ridge(alpha=alpha, random_state=0)
ridge.fit(X_train_scaled, y_train)
# weight와 bias 저장
coef_df[f"alpha: {alpha}"] = ridge.coef_
bias_list.append(ridge.intercept_)
print(f"-------------{alpha}---------------")
# print_metrics_regression(y_train, ridge.predict(X_train_scaled), "train")
print_metrics_regression(y_test, ridge.predict(X_test_scaled), "test")
bias_list # 변하지 않음
coef_df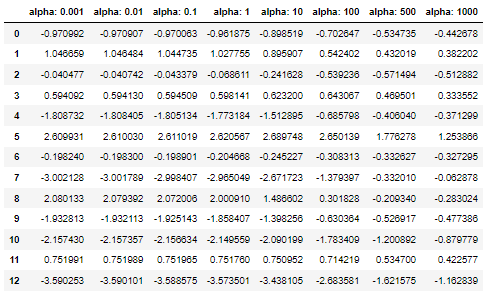
<Lasso Regression (L1 규제) 를 예제를 통해 테스트 해보자>
alpha_list2 = [0.001, 0.01, 0.1, 1, 5, 10]
coef_df2 = pd.DataFrame()
bias_list2 = []
for alpha in alpha_list2:
lasso = Lasso(alpha=alpha, random_state=0)
lasso.fit(X_train_scaled, y_train)
coef_df2[f'alpha: {alpha}'] = lasso.coef_
bias_list2.append(lasso.intercept_)
print(f"alphaL {alpha}-----------------------")
# print_metrics_regression(y_train, lasso.predict(X_train_scaled), "train")
print_metrics_regression(y_test, lasso.predict(X_test_scaled), "test")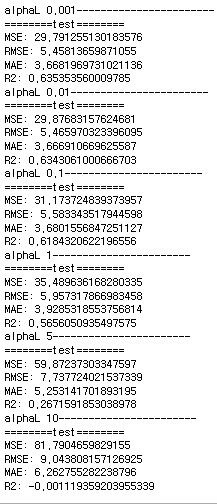
bias_list2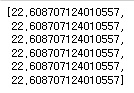
coef_df2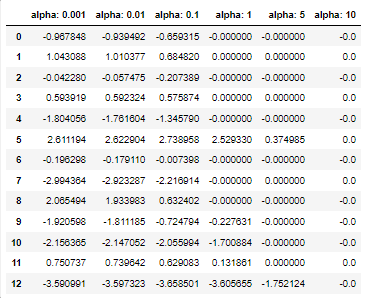
<마무리>
- 일반적으로 선형회귀의 경우 어느정도 규제가 있는 경우가 성능이 좋다.
- 기본적으로 Ridge를 사용한다.
- Target에 영향을 주는 Feature가 몇 개뿐일 경우 특성의 가중치를 0으로 만들어 주는 Lasso 사용한다.