Neural Machine Translation by Jointly Learning to Align and Translate 논문 리뷰

본 페이지에서는 Neural Machine Translation by Jointly Learning to Align and Translate의 등장배경과 특징에 대해서 말하고자 합니다.

---

1. Intro

최근에 NLP 분야에서 많은 모델들이 나오고 성능도 많이 좋아졌다.

대부분의 NLP 모델에서는 Encoder-Decoder 형식의 구조를 많이 사용했는데 그중에서도 원천 문장을 고정된 길이의 벡터로 만들어 이를 Decoder에서 번역을 생성하는데 주로 사용하였다.

이러한 방식이 성능을 많이 올려준 것은 사실이나 고정된 길이의 벡터로 만드는 것은 성능 향상에 큰 병목을 발생시킨다.

그 이유는 시간이 지날 수록 고정된 길이에 여러 단어의 정보를 압축해내야 하기에 정보의 손실이 많이 발생하기 때문이다.

다음의 사진으로 간단한 예로 들면 다음과 같습니다.

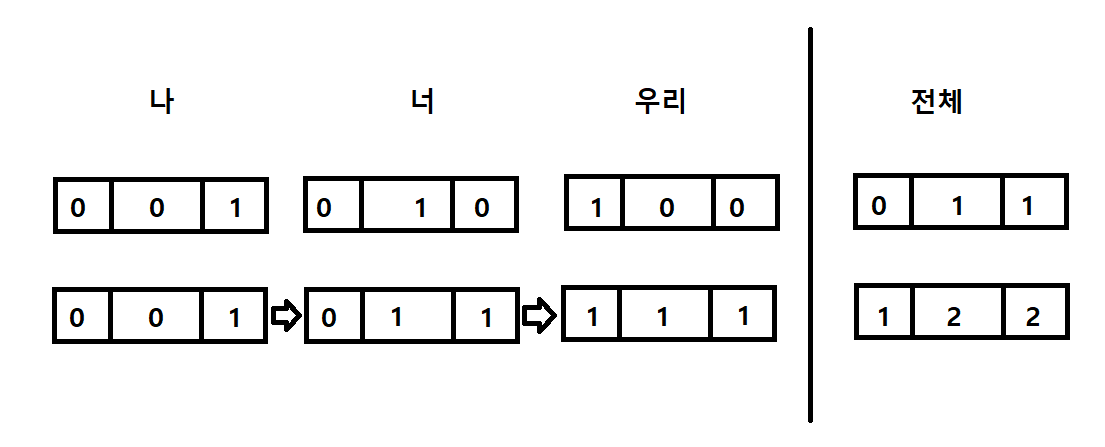
처음에 단어가 "나 너 우리" 라는 문장에 세 단어가 있고 각 단어가 길이가 3인 벡터로 다음과 같이 [0,0,1] , [0,1,0] , [1,0,0] 으로 변환됐다 하고 이를 시간이 지나면서 간단한 합으로 나타낸다고 하자

세번째 단어까지는 벡터를 보며 어떤 단어들이 있다고 확실히 말할 수 있다.

이때 네번째 '전체'라는 단어가 주어질 때 이 단어가 [0,1,1]로 변환 하고 이를 벡터에 반영을 하면 [1,2,2]가 되어 이제는 '나'라는 단어만을 확실히 알 수 있고 나머지 단어에 대한 정보를 확실히 알 수 없게 되었다.

실제로는 더더욱 복잡하게 작동하지만 어느정도 감만 잡고 가면 될 것 같다.

이러한 이유 때문에 장문에서의 번역 성능이 크게 떨어지는 경우가 발생한다.

이를 해결하기 위해서 예측하려는 목표 단어와 전체 원천 문장 내의 단어들 사이의 관계를 판단하고 이를 이용하는 방식을 제안한다.

---

2. RNN

기존의 일반적인 RNN은 Encoder를 통해 단방향으로 입력 문장에 대해서 하나의 고정길이 벡터를 얻어냈다. 이 고정된 길이의 벡터를 Context vector(문맥 벡터)라고 한다.

Decoder는 이 고정 길이 벡터를 활용해 한 시점의 특정 단어에 대한 확률을 얻어내 단어를 출력한다.

2.1 Original RNN

기존의 RNN 구조의 식은 다음과 같다.

$(1) h_t = f(x_t,h_{t-1})$

$c = q({h_1,...,h_T}) = h_T$

위 식에서 $h_t$ 는 각 순간의 은닉층의 상태의 벡터를 의미하고 c는 은닉층의 상태들을 통해 얻어낸 고정된 길이의 벡터이다. f와 q는 비선형 함수를 의미한다.

RNN의 Decoder에서 특정 문장을 번역하는 과정을 식으로 나타내면 다음과 같다.

식 (2)는 전체 출력 문장에 대한 확률 값이고 식 (3)은 각각의 출력 문장에 대한 조건부 확률값이다.

RNN의 학습에는 식 (2)를 최대화 하는 방향으로 학습을 시킨다.

식 (3)을 보면 현재 시점에서 출력 단어에 대한 확률값을 구하는데 이전 출력과 현재의 은닉층 상태와 문맥 벡터를 통해 출력할 단어들의 확률값을 구한다.

이때 g는 비선형 함수이다. yt는 출력 결과고 st는 RNN의 은닉층 상태를 말한다.

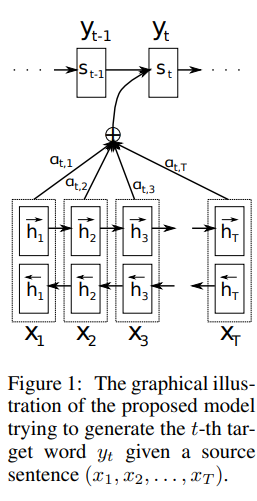
3 RNN with Attention Mechanism

기존의 방식과는 다르게 본 논문에서는 Encoder를 통해 입력 문장을 양방향으로 읽고 Decoder 부분은 이전 은닉층의 정보를 활용하고 출력할 단어를 입력 문장 내의 모든 단어들과의 연관성을 고려해 출력한다.

3.1 Decoder

위의 식 (2)를 기반으로 새로운 식을 정의하면 다음과 같다.

여기서 문맥 벡터 C는 각 시점의 y에 대해서 달라진다.

문맥 벡터 ci 는 annotation들의 sequence(h1,...,htx)에 의해 결정된다.

각각의 annotation인 hi는 전체 입력 sequence에 대한 정보를 담고 있다. 그 중 i번 째 단어에 강하게 집중(focus)하게 된다.

이때 식 (6) 은 Softmax 함수이다.

$e_{ij}$ 는 출력할 시점 i의 단어가 j번째 입력과 얼마나 잘 매치가 되는지를 의미 한다. 즉,유사도가 높다면 해당 $e_{ij}$ 값이 크다는 것을 의미한다.

$s_{i-1}, h_j$는 각각 Decoder의 i-1번째 은닉층 상태와 Encoder의 i번째 은닉층 상태이다.

이때 함수 $a$라는 함수를 학습시켜 출력할 단어와 입력 문장의 단어들과의 연관성을 찾도록 학습시키면 된다.

이때 본 논문에서 $\alpha_{ij}$ 는 변역될 문장 $y_i$가 원천 문장 $x_j$와 연관된 확률이라고 한다.

그러면 i번째 문맥 벡터 $c_i$는 출력될 단어가 원천 문장의 어느 단어와 가장 큰 연관성을 가지고 있는지 알 수 있게 해준다.

확률 $a_{ij}$는 연관 에너지(assosiated energy) $e_{ij}$와 동일한 말이다.

이러한 연관 에너지는 출력 $y_i$와 은닉상태 $s_i$를 출력할 때 $h_j,s_{i-1}$의 중요도를 반영한다. 이를 통해 Decoder에서 attention 메커니즘을 구현한다.

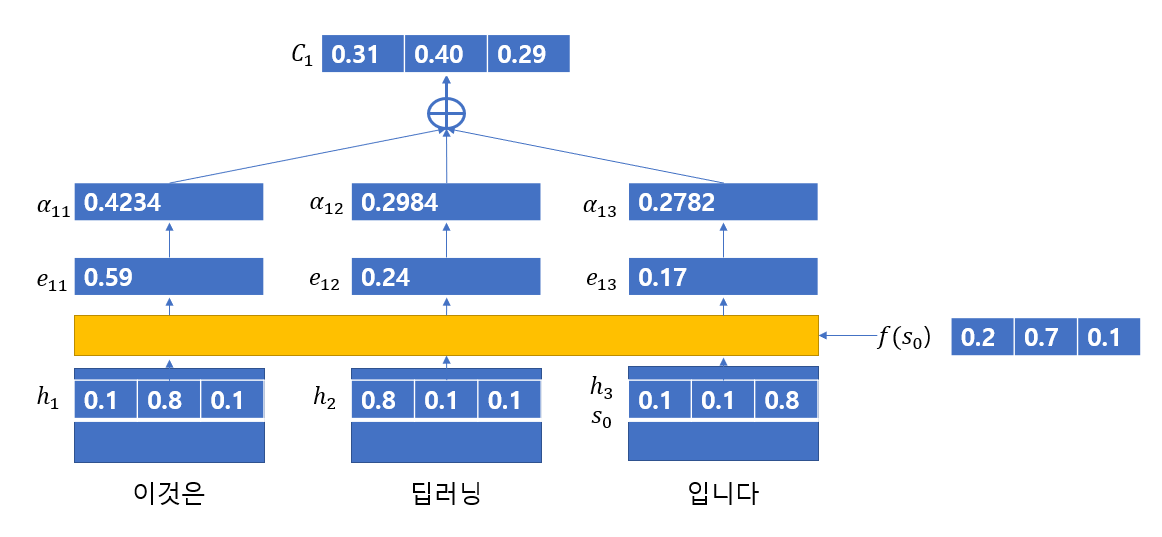
다음의 사진으로 "이것은 딥러닝 입니다"를 영어로 번역하는 동작과정을 살펴보면 다음과 같다.

이때 $a(s_{i-1},h_j)$는 다음과 같다고 가정한다.

우선 $c_i$ 값을 구하는 과정을 살펴보면 다음과 같다.

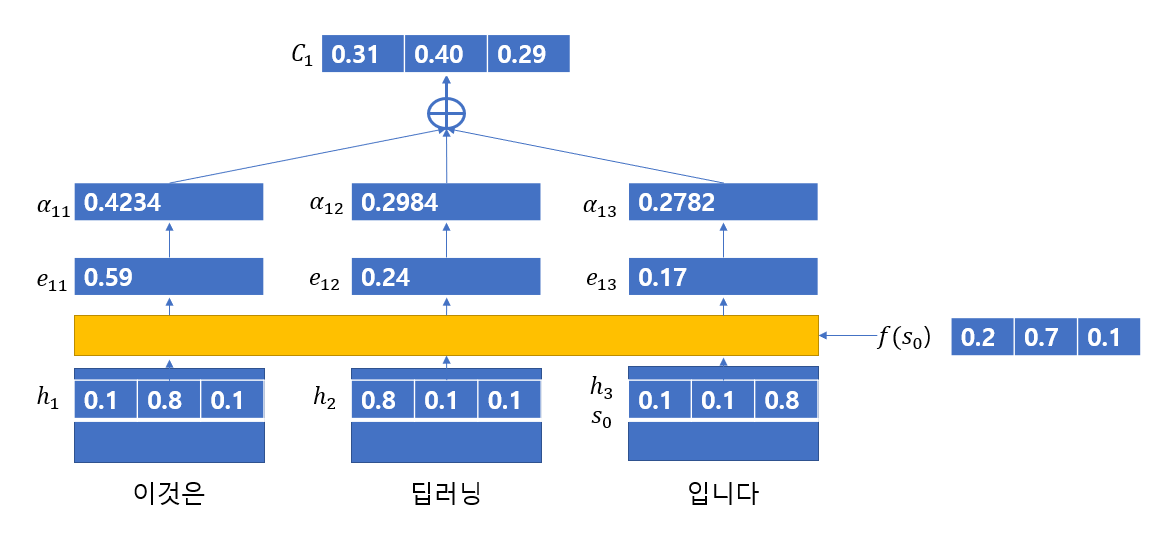
1. Encoder의 각 단어로부터 은닉 상태($h_i$)를 얻는다.

2. 이전 Decoder의 은닉 상태(여기서는 마지막 Encoder의 은닉 상태)를 특정 연산을 통해 $f(s_0)$ 를 얻어낸다.

3. $f(s_0) \times h_j$연산을 하여 각 벡터의 내적값을 구한 뒤 이를 softmax함수에 적용해 $\alpha$ 값을 구한다.

4. 이 $\sum_{j=1}^3a_{1j}h_j$ 연산을 통해 $C_1$값을 구한다.

이를 행렬곱 연산으로 간단히 나타내면 다음과 같다.

과정 1,2,3

과정 4

이렇게 얻어낸 $s_0,y_0,c_1$ 값을 통해 현재 디코더의 은닉 상태 $s_1$을 만들어낸다.

이때 출력 단어는 $s_1,y_0,c_1$을 모두 활용해 출력 단어에 대한 확률 값을 구하여 적절한 단어를 출력한다.

특히 과정 1,2,3,4를 통해 매출력마다 입력 sequence의 모든 단어들을 확인하기 때문에 Intro에서 말한 단점들을 보완할 수 있었다.

3.1 Encoder : Bidirectional RNN

기존의 RNN은 입력 Sequnce에 대해서 정방향($x_1,...,x_t$)으로만 단어들을 읽었다.

본 논문에서 제안한 모델은 이전 단어들만 하나의 고정 벡터로 압축(summarize)하는 것이 아닌 다음의 단어들도 요약하고자 했다.

Bidirectional RNN(BiRNN)은 Foward RNN와 Backward RNN으로 이루어져있다.

Foward RNN($\overrightarrow{f}$)은 정방향($x_1,...,x_t$)으로 단어를 읽어들이며 Forward 은닉 상태($\overrightarrow{h_1}$,...,$\overrightarrow{h_t}$)를 만들어내고 Backward RNN($\overleftarrow{f}$)은 역방향 ($x_1,...,x_t$)으로 단어를 읽어 Backward 은닉 상태($\overleftarrow{h_1}$,...,$\overleftarrow{h_t}$)들인다.

이때 Foward,Backward 은닉 상태를 Concatenate 하여 다음의 상태들을 만든다.

$h_j = [\overrightarrow{h^T_j};\overleftarrow{h^T_j}]^T$

이를 통해 양방향에서 입력 sequence를 읽어들이기 때문에 기존과는 달리 $x_j$ 주변의 정보를 모두 활용할 수 있다.

위의 Encoder와 Decoder의 동작을 간단히 모두 나타내면 다음과 같다.

4. Perfomance

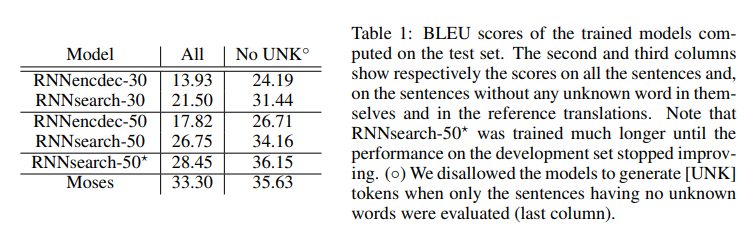
위의 그래프는 모델별 문장 길이에 따른 BLEU score를 나타낸 것이다.

RNNsearch-n은 본 논문에서 제안한 모델이고 RNNenc-n 은 기존의 RNN 구조이다.

이때 n은 입력 문장의 길이를 말한다.

특히 Attention 매커니즘을 통해 해당 출력이 어떤 입력 단어와 연관이 되어있는지 확인 할 수 있다.

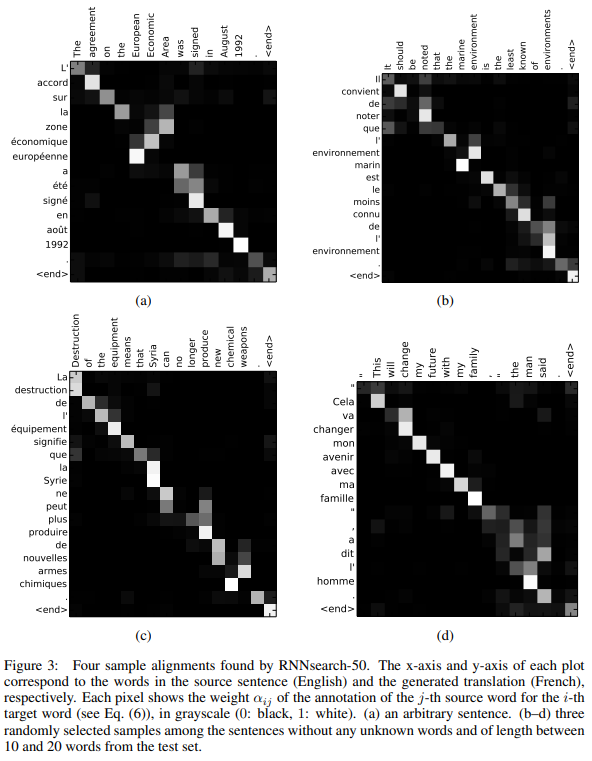
이러한 그래프를 통해 현재 해당 출력 근거에 대해서 말할 수 있다는 장점이 있다.

5. Detail of Architecture

모델의 구조는 기존의 LSTM 모델을 변형한 모델을 기반으로 Attention 메커니즘을 사용한다.

5.1 RNN

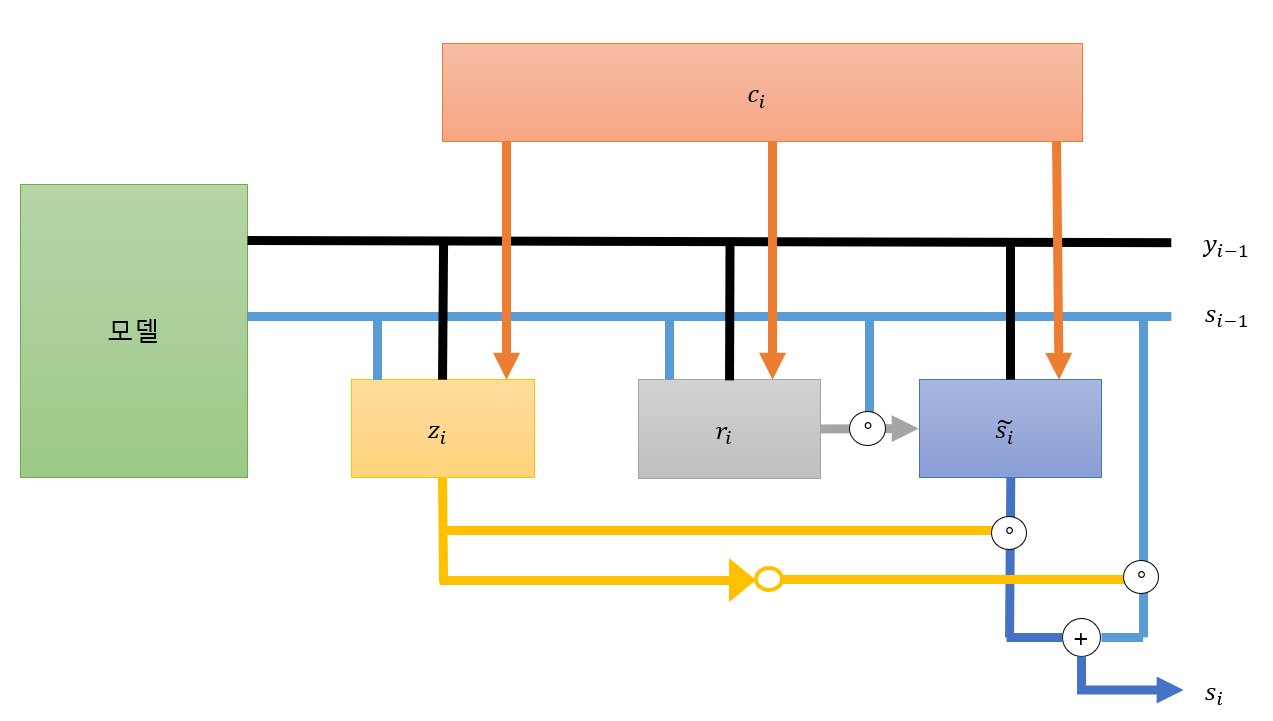
은닉상태 $s_{i}$는 다음의 식으로 계산이 된다.

이때 $\circ$는 요소간 곱셈이다. $z_i$는 아래에 상세히 다룬다.

$\tilde{s}_{i-1}$ 새로 갱신된 은닉 상태이며 계산은 다음과 같이 한다.

이때 $e(y_{i-1})\in \R^{m}$은 단어 $y_{i-1}$의 m차원으로 embbeding 한 것이고

각 Gate의 설명은 다음과 같다.

1. Update gate($z_i$) : 새로히 갱신한 은닉 상태를 얼마나 사용할지를 정함(이전 은닉상태와 새로운 은닉상태를 적절히 혼합)

2. Reset gate($r_i$) : 새로운 은닉 상태를 갱신하는 중에 이전의 상태를 얼마나 활용하는지를 정한다.

이때 $\sigma$는 simoid 함수이다.

이를 그림으로 나타내면 다음과 같다.

이때 각 Gate에서 사용하는 가중치들은 모두 다르다.

또한 은닉층에 대해 여러 겹의 레이어를 쌓아서 출력을 내며 하나의 출력값을 내기 위해 softmax 함수를 적용하여 출력 확률값을 얻어낸다.

위의 방식은 Decoder에서 사용되는 방식이며 만약 Encoder에서 사용하는 경우에는 다음과 같이 식을 변경한다.

1. $s$대신 $h$로 표기한다.(단 h는 Foward,Backward를 신경쓴다.)
2. $y_{i-1}$대신 $x_i$를 사용한다.
3. 문맥벡터 $C_rc_i$를 사용하지 않고 사용하면 된다.

5.2 Alignment Model

입력 문장의 길이가 $T_x$이고 출력 문장의 길이가 $T_y$라고 한다면 모델의 연산은 $T_x \times T_y$번 진행하게 된다.

연산량이 많아지게 되는 경우 모델이 무거워지므로 연산량을 줄이기 위해 다음의 식과 같이 Alignment model을 정의한다.

$W_a \in \R^{n' \times n}, U_a \in \R^{n' \times 2n}, v_a \in \R^{n'}$ 이고 각각은 가중치 행렬이다

이때 $U_a h_j$는 $i$에 상관 없이 작동하므로 연산량을 줄이기 위해 이전에 계산한 값을 사용한다.

5.3 Dimension

이 절은 각 가중치 행렬과 입출력 단어 임베딩의 차원의 수를 살펴보겠다.

원천 문장의 입력 벡터를 표현하면 다음과 같다.

$\bold x = (x_1,...,x_{T_x}), x_i \in \R^{K_x}$

출력 문장의 입력 벡터를 표현하면 다음과 같다.

$\bold y = (y_1,...,y_{T_y}), y_i \in \R^{K_y}$

$K_x,K_y$는 각각 번역 과정에서 입출력 언어에 해당하는 단어장의 크기이고 $T_x,T_y$는 각각 입출력 문장의 길이를 의미한다.

가중치 행렬이 들어가는 식은 다음과 같다.

이때 input은 Encoder의 경우 입력 단어이고 Decoder에서는 이전 Decoder 블록의 출력 단어이다.

$e$는 입력단어에 대한 임베딩 행렬으로 $e \in \R^{m\times T_x,m\times T_y}$이다.

$W \in \R^{n \times m},U \in \R^{n \times n},C \in \R^{n \times 2n}$이다.

이때 $n$은 은닉 상태의 벡터의 크기이며 $m$은 입력 단어를 임베딩한 차원의 크기이다.

이때 $C_r \in \R^{n \times 2n}$ 에서 $2n$인 이유는 $h_i$들을 통해 문맥 벡터 $c_i$를 만들어 내는데 $h_i = [\overrightarrow{h}_i,\overleftarrow{h}_i]$ 이다. ${h}_i$에서 각각은 $n$크기의 벡터를 가지고 있기 때문에 $2n$인 것이다.

---