PyTorch 독립 레이어 만들기(Grad 끊기)

먼저 문제에 대한 배경을 먼저 읽고 와주세요

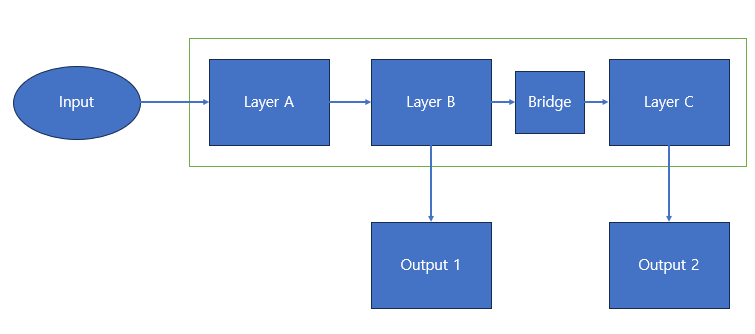
독립 레이어

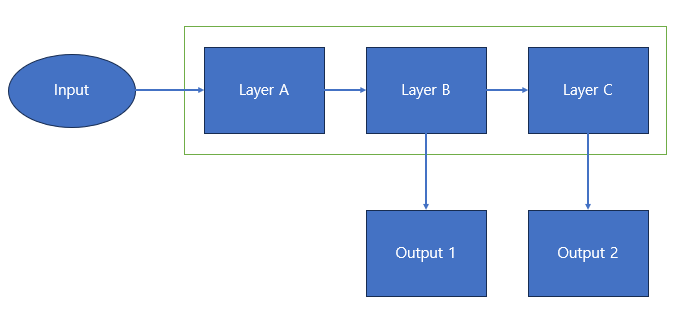
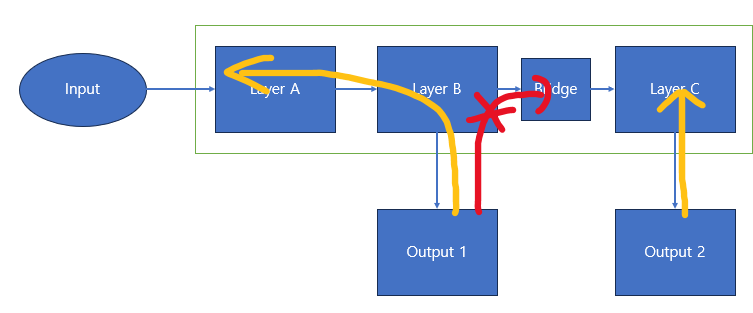
위와 같은 구조의 모델이 있다고 할 때 Layer B가 학습이 완료되어야지 C가 정상적인 학습이 진행된다고 할 때 문제점은 다음과 같다.

• Output 2의 Loss로 인한 Gradient가 Layer A,B에 모두 흐르게 되어 이전 레이어들의 최적 상태를 변경하여 학습이 원활하지 않게 됨

이를 해결하기 위해 Layer C의 Gradient를 B로 흐르지 않게 끊어주는 역할이 필요함을 느꼈고 다음의 사진에서 Bridge가 그 역할을 해줌

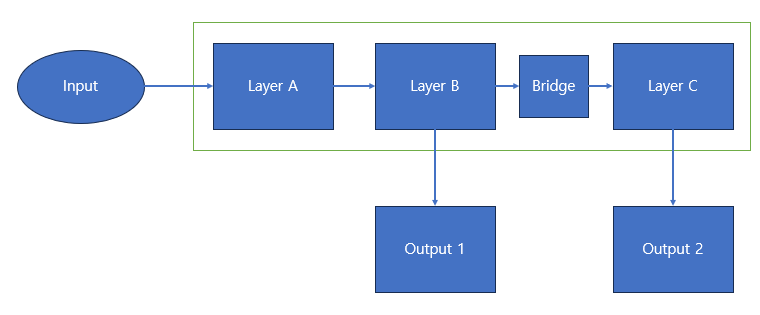
How?

그렇다면 Bridge의 구현은 어떻게 할까?

hidden_unit = 2
class test(nn.Module):
    def __init__(self):
        super(test, self).__init__()
        self.layerA = nn.Linear(hidden_unit, hidden_unit)
        self.layerB = nn.Linear(hidden_unit, hidden_unit)
        self.layerC = nn.Linear(hidden_unit, hidden_unit)
            
    def forward(self, x):
        a = self.layerA(x)
        b = self.layerB(x)
        c = self.layerC(b.detach()) #bridge를 b.detach()로 구현한다.
        
        return b,c

정말 간단하게 구현이 가능하다.

그러면 실제 Gradient의 흐름을 통해 파라미터의 변화를 보기 위해서 다음과 같이 코드를 작성한다.

def checkgradflow(bridge=True,m=0,hidden_unit = 2): #mode는 BackPropagation 위치 (0:B, 1:C, 2:BC둘다)
	#실험을 위한 Randomness 시드 고정
    seed = 1000
    deterministic = True

    random.seed(seed)
    np.random.seed(seed)
    torch.manual_seed(seed)
    torch.cuda.manual_seed_all(seed)
    if deterministic:
        torch.backends.cudnn.deterministic = True
        torch.backends.cudnn.benchmark = False

    # 모델 정의
    class test(nn.Module):
        def __init__(self):
            super(test, self).__init__()
            self.layerA = nn.Linear(hidden_unit, hidden_unit)
            self.layerB = nn.Linear(hidden_unit, hidden_unit)
            self.layerC = nn.Linear(hidden_unit, hidden_unit)
                
        def forward(self, x):
            a = self.layerA(x)
            b = self.layerB(x)

            if (bridge): #Bridge 구조 사용시 
                c = self.layerC(b.detach())
            else:
                c = self.layerC(b)
                
            return b,c
    
    #모델,손실함수,입출력 선언
    model = test()
    input_data = torch.randn(hidden_unit)
    label_1 = torch.zeros(hidden_unit)
    label_2 = torch.ones(hidden_unit)
    optim = torch.optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
    criterion = nn.MSELoss()
    

    optim.zero_grad()

    output1, output2 = model(input_data)

    if m == 0:
        loss = criterion(output1 , label_1)
    elif m == 1:
        loss = criterion(output2 , label_2)
    else :
        loss = criterion(output1 , label_1) + criterion(output2 , label_2)

    loss.backward()

    optim.step()

    print(model.layerA.weight)
    print(model.layerB.weight)
    print(model.layerC.weight)

실험 결과

Bridge,Mode	Layer A	Layer B	Layer C
원본	[[-0.2561, 0.1606],[-0.0823, -0.3422]]	[[-0.0834, -0.1905],[-0.2072, 0.1374]]	[[-0.1108, -0.5298],[ 0.2571, -0.6263]]
False,0	[[-0.2561,0.1606],[-0.0825,-0.3420]]	[[-0.0844,-0.1900],[-0.2067,0.1371]]	[[-0.1108,-0.5298],[0.2571,-0.6263]]
False,1	[[-0.2551,0.1597],[-0.0833,-0.3413]]	[[-0.0851,-0.1896],[-0.2002,0.1335]]	[[-0.1124,-0.5290],[0.2533,-0.6245]]
False,2	[[-0.2551,0.1597],[-0.0835,-0.3412]]	[[-0.0861,-0.1890],[-0.1997,0.1333]]	[[-0.1124,-0.5290],[0.2533,-0.6245]]
True,0	[[-0.2561,0.1606],[-0.0825,-0.3420]]	[[-0.0844,-0.1900],[-0.2067,0.1371]]	[[-0.1108,-0.5298],[0.2571,-0.6263]]
True,1	[[-0.2561,0.1606],[-0.0823,-0.3422]]	[[-0.0834,-0.1905],[-0.2072,0.1374]]	[[-0.1124,-0.5290],[0.2533,-0.6245]]
True,2	[[-0.2561,0.1606],[-0.0825,-0.3420]]	[[-0.0844,-0.1900],[-0.2067,0.1371]]	[[-0.1124,-0.5290],[0.2533,-0.6245]]

위 표에서 원본 행은 Back Propagation 하기 전 각 레이어의 가중치 입니다.

Mode는 Loss계산 위치입니다. (0:B, 1:C, 2:B,C)

Bridge가 False인 부분을 보고 분석하면 다음과 같습니다.

• Mode 0 : B에서 BackPropagation을 진행하여 A,B의 가중치는 업데이트 되었지만 C의 가중치는 변화하지 않았습니다.
• Mode 1 : C에서 BackPropagation을 진행하여 A,B,C의 가중치가 모두 업데이트 되었습니다.
• Mode 2 : B,C에서 BackPropagation을 진행하여 A,B,C의 가중치가 모두 업데이트 되었으며 A와 B의 가중치가 Mode 1보다 더 많이 업데이트 되었습니다.(중첩)

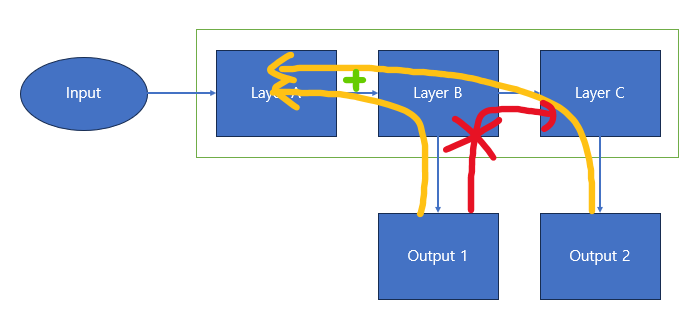
위의 분석을 통해 BackPropagation은 중첩이 되며 거꾸로 흐를 뿐 B->C로 영향은 주지 않음을 알 수 있습니다.

Bridge가 False인 부분을 보고 분석하면 다음과 같습니다.

• Mode 0 : B에서 BackPropagation을 진행하여 A,B의 가중치는 업데이트 되었지만 C의 가중치는 변화하지 않았습니다.
• Mode 1 : C에서 BackPropagation을 진행하여 C의 가중치만 업데이트 되었습니다.
• Mode 2 : B,C에서 BackPropagation을 진행하여 A,B,C의 가중치가 모두 업데이트 되었으며 A와 는 (False,0)일때와 동일하게 업데이트 되었으며 C는 Bride(True,0)일때와 동일하게 업데이 트되었습니다.

즉, 이 결과를 보면 Bridge가 존재하는 경우에 Layer C는 독립적으로 학습됨을 알 수 있습니다.

추론과정에서의 오류 발생

위의 코드로 학습을 하는 과정에서는 오류가 발생하지 않지만 간혹 다음과 같은 오류가 발생하는 경우가 있다.

RuntimeError: set_sizes_and_strides is not allowed on a Tensor created from .data or .detach().

해결 방법

c = self.layerC(b.detach()) 

위의 코드를 아래와 같이 바꾸면 된다.

with torch.no_grad():
	br = torch.zeros_like(b)
	br.set_(b)
c = self.layerC(br)

Bridge,Mode	Layer A	Layer B	Layer C
원본	[[-0.2561,0.1606],[-0.0823,-0.3422]]	[[-0.0834,-0.1905],[-0.2072,0.1374]]	[[-0.1108,-0.5298],[0.2571,-0.6263]]
False,0	[[-0.2561,0.1606],[-0.0825,-0.3420]]	[[-0.0844,-0.1900],[-0.2067,0.1371]]	[[-0.1108,-0.5298],[0.2571,-0.6263]]
False,1	[[-0.2547,0.1594],[-0.0840,-0.3407]]	[[-0.0876,-0.1882],[-0.1970,0.1317]]	[[-0.1108,-0.5298],[0.2496,-0.6227]]
False,2	[[-0.2547,0.1594],[-0.0842,-0.3405]]	[[-0.0886,-0.1877],[-0.1965,0.1315]]	[[-0.1108,-0.5298],[0.2496,-0.6227]]
True,0	[[-0.2561,0.1606],[-0.0825,-0.3420]]	[[-0.0844,-0.1900],[-0.2067,0.1371]]	[[-0.1108,-0.5298],[0.2571,-0.6263]]
True,1	[[-0.2561,0.1606],[-0.0823,-0.3422]]	[[-0.0834,-0.1905],[-0.2072,0.1374]]	[[-0.1108,-0.5298],[0.2496,-0.6227]]
True,2	[[-0.2561,0.1606],[-0.0825,-0.3420]]	[[-0.0844,-0.1900],[-0.2067,0.1371]]	[[-0.1108,-0.5298],[0.2496,-0.6227]]

값만 다를 뿐 결과는 이전 방법과 동일하다.