Machine Learning

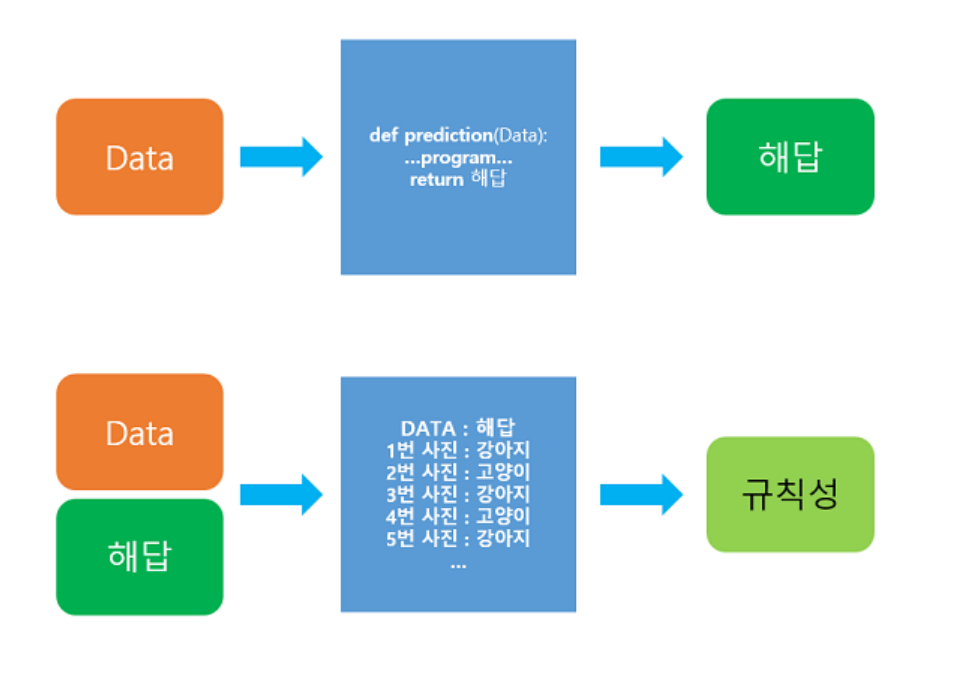
글의 순서가 좀 잘못 된 것 같다. 사실 머신러닝과 딥러닝은 별개의 개념이 아니라 머신 러닝 속에 딥러닝이 있는 상위-하위 개념이다. 그리고 머신러닝과 딥러닝은 AI의 하위 개념이다. 정리해보면 AI>ML>DL인 것이다.GDSC에서 DL의 멤버가 되었기 때문에 DL을

이미 정해진(인간이 컴퓨터에게 학습시킨) 레이블이 있는 데이터를 학습하는 것으로, 대표적으로 분류 문제와 회귀 문제가 있다.분류: 로지스틱 회귀법(선형 회귀 방식을 분류 모델에 적용하므로 회귀가 아니다), KNN, 서포트 벡터 머신(SVM), 의사 결정 트리 등이 있

머신러닝은 무작정 데이터를 넣고 학습시키고 평가하는 것이 아니라, 준비된 데이터 셋을 우선 훈련(Training)용과 평가(Testing)용으로 나누는데, 이때 훈련용 데이터 셋의 비중을 더 크게 두고, 훈련용 데이터 셋은 또 훈련용과 검증(Validation)용 데이

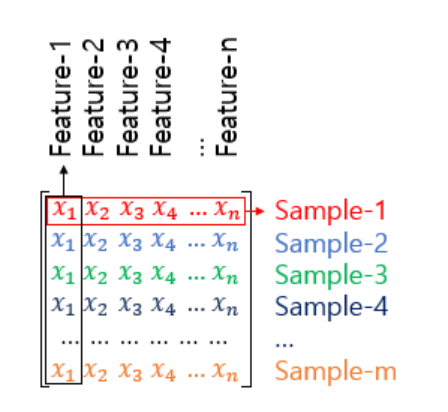
머신러닝에서는 맞춘 문제/전체 문제=정확도 라고 하는데, 이 정확도만 가지고는 맞춘 문제와 틀린 문제의 세부사항을 알 수가 없다. 세부 사항을 알아야 틀린 문제의 원인을 파악하고 수정을 할 수 있는데, 정확도만 갖고는 판단을 할 수 없으니 혼동 행렬이라는 개념을 사용한

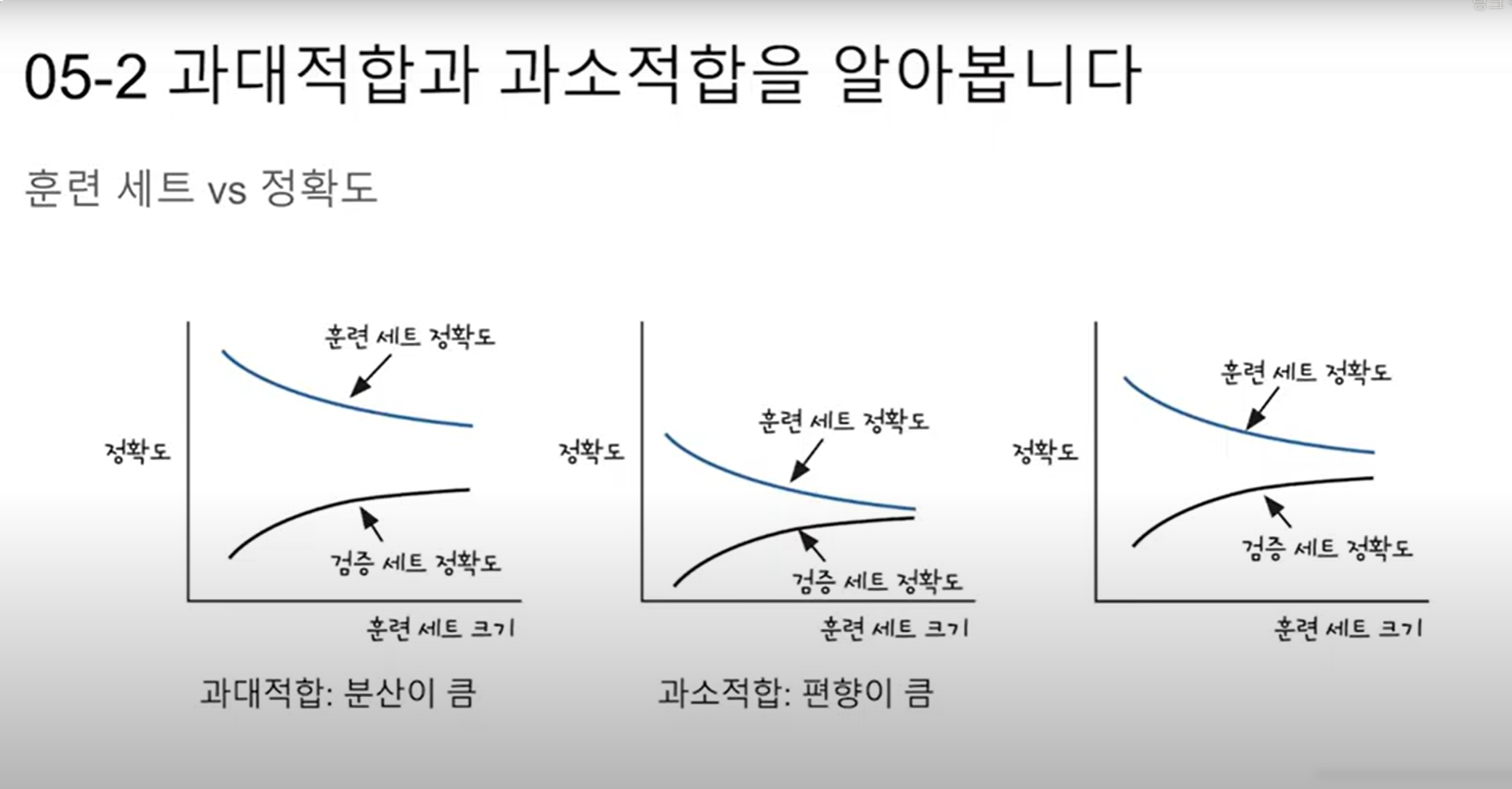
머신 러닝에서 과적합(Overfitting)이란 훈련 데이터를 과하게 학습한 경우를 말한다. 머신 러닝 모델이 학습에 사용하는 훈련 데이터는 극히 일부의 데이터이다. 그런데 이 훈련 데이터만 너무 과하게 학습한 나머지 테스트 데이터, 그리고 실제 서비스에 적용해 보았을

머신러닝은 데이터 수집, 전처리, 피처추출, 학습, 검증(학습과 검증은 이전 게시글에서 다룬 바 있다)의 5단계 과정을 거쳐 이루어진다.데이터를 수집하는 것은 알겠는데, 전처리가 왜 필요하냐? 그것은 우리가 수집한 데이터는 날것의 데이터이기 때문에, 이것을 무작정 때려

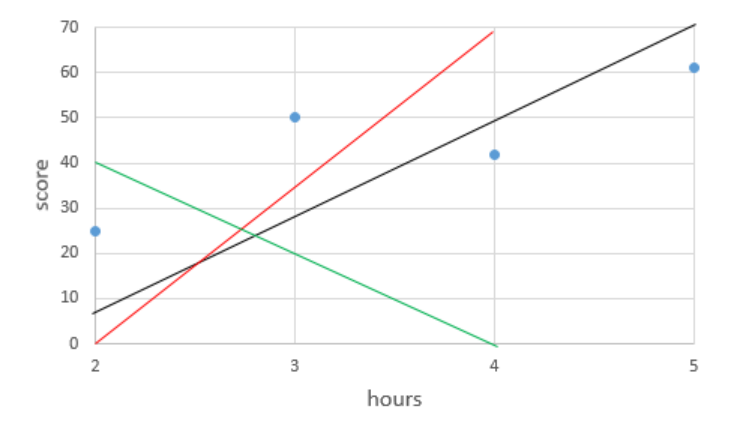
본격적으로 머신러닝의 메커니즘을 이해하러 가보자.딥러닝은 머신러닝의 하위 개념이라 이 선형 회귀, 그리고 나중에 후술할 로지스틱 회귀 등 똑같이 원리가 적용되므로 반드시 알아둘 필요가 있다.시험 공부하는 시간을 늘리면 늘릴 수록 성적이 잘 나옵니다. 하루에 걷는 횟수를

비용함수에 대해 공부하기 전에, 목적함수와 비용함수, 손실함수 용어가혼용되어 쓰이고 있다는 것을 알았고 더 조사해 본 결과 엄밀히 따지면 다르다는 것을 알게 되어 더 정리해 보고자 글을 쓰게 되었다.목적함수(Objective Function)목적 함수는 말그대로 어떠한

이전 게시글에 비용함수, 손실함수, 목적함수에 대해 다뤘는데, 이번에는 저번 게시글에 언급했듯 비용함수, 그중에서도 MSE에 대해 정리하고자 한다. MSE란 무엇인가 Mean Squared Error의 약자로, 평균 제곱 오차라는 뜻이다. 그러니까 수식으로 나타내면

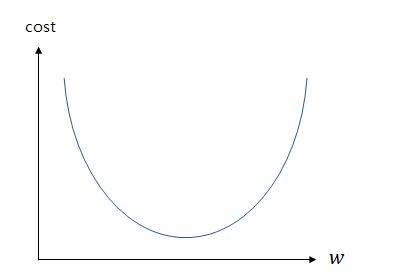
선형 회귀를 포함한 기계 학습은 결국 비용 함수를 최소화하는 매개 변수인 x와 y을 찾는 것이 목적이다. 이때 사용되는 알고리즘을 최적화 알고리즘(Optimizer)이라고 한다.지난 게시글을 보면 알 수 있듯, 기울기가 너무 커져도, 기울기가 너무 작아져 음수가 되어도

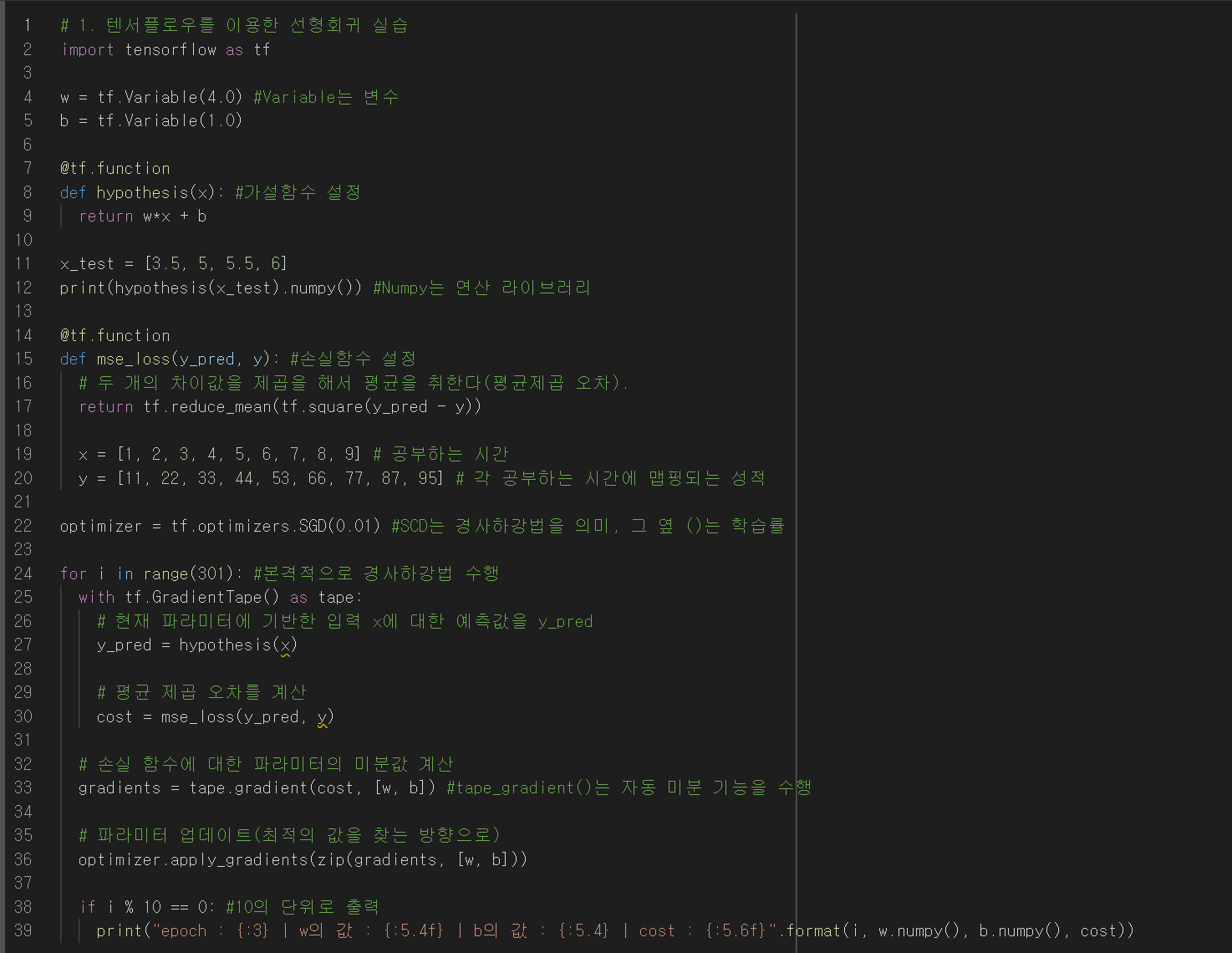
이 코드는 제가 학습하면서 참고했던 https://wikidocs.net/111472 예제 코드임을 밝힙니다.오타가 났다! SGD인데! 참고로 Stochastic Gradient Descent: 배치가 1인 경사 하강법(확률적 경사하강법)이라는 뜻인데, 배치는

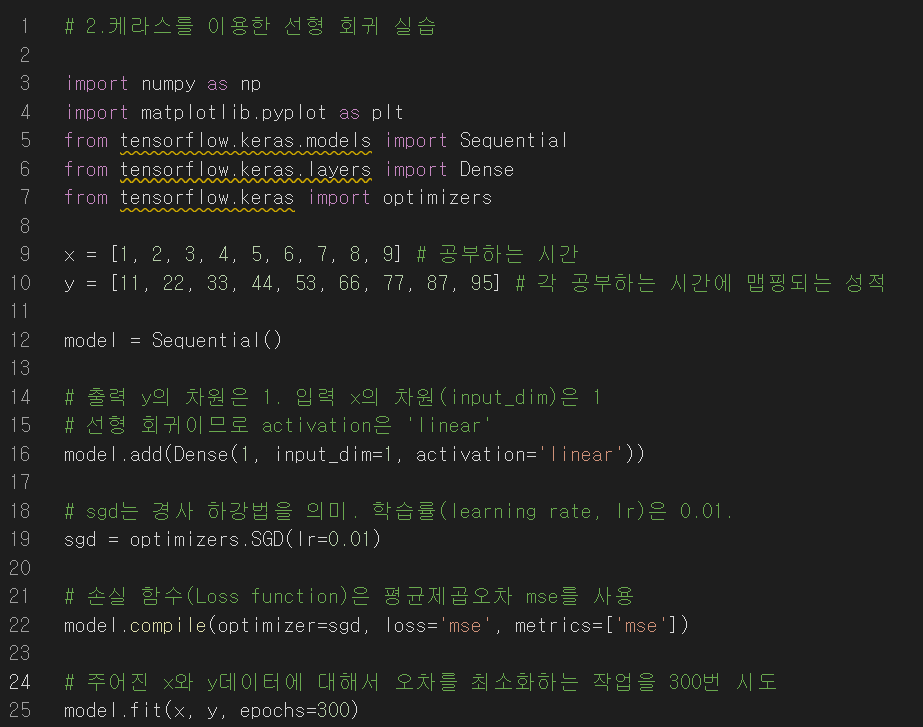
이 코드는 제가 학습하면서 참고했던 https://wikidocs.net/111472 예제 코드임을 밝힙니다앞서 텐서플로우를 이용한 선형회귀 코드 실습을 해 보았는데,사실 훨씬 더 간결하게 코드를 작성할 수 있다. 바로 케라스라는 라이브러리를 통해서이다. 사실

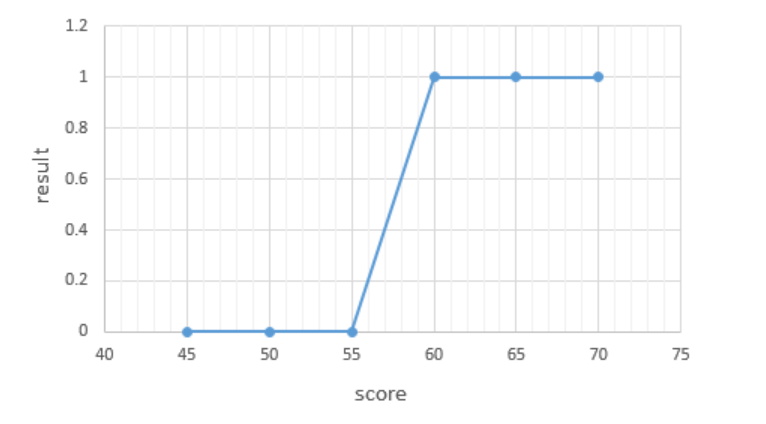
본 게시글의 코드는 https://wikidocs.net/22881 를 참고했음을 밝힙니다.선형 회귀 알고리즘이 공부한 시간에 따라 변하는 성적, 역까지의 거리에 따라 달라지는 집값 등의 수치를 분석하고 예측하는 알고리즘이었다면, 로지스틱 회귀는 점수가 주어질