본격적으로 머신러닝의 메커니즘을 이해하러 가보자.
딥러닝은 머신러닝의 하위 개념이라 이 선형 회귀, 그리고 나중에 후술할 로지스틱 회귀 등 똑같이 원리가 적용되므로 반드시 알아둘 필요가 있다.
시험 공부하는 시간을 늘리면 늘릴 수록 성적이 잘 나온다, 집의 평수가 클수록 매매 가격은 비싸진다 등의 어떤 변수(수치)의 값에 따라서 특정 변수의 값이 영향을 받고 있다고 볼 수 있다. 대표적으로 1차함수의 식을 생각해 보면, y=ax+b(선형 회귀에서는 a대신 w가 쓰인다)와 같은 형태에서 x는 독립적으로 변할 수 있으므로 독립 변수, y는 x에 따라 종속적으로 값이 결정되므로 종속 변수라고 한다. 선형 회귀는 바로 이 x와 y의 선형 관계를 모델링하는 것이다. 이 때 x, 즉 독립 변수가 1개라고 한다면 단순 선형 회귀, 그 이상이라면 다중 선형 회귀라고 한다. 상술했던 집의 가격은 집의 평수 뿐만 아니라 언제 지어졌는지, 방 개수는 몇개인지, 지하철 역과의 거리는 몇인지 등 다양한 요소에 따라 결정되므로, x도 여러개이다. 이런 경우 다중 선형 회귀를 이용할 수 있다.
더 직관적으로 이해하기 위해, 하나의 예시를 가져왔다.
출처ㅣhttps://wikidocs.net/21670
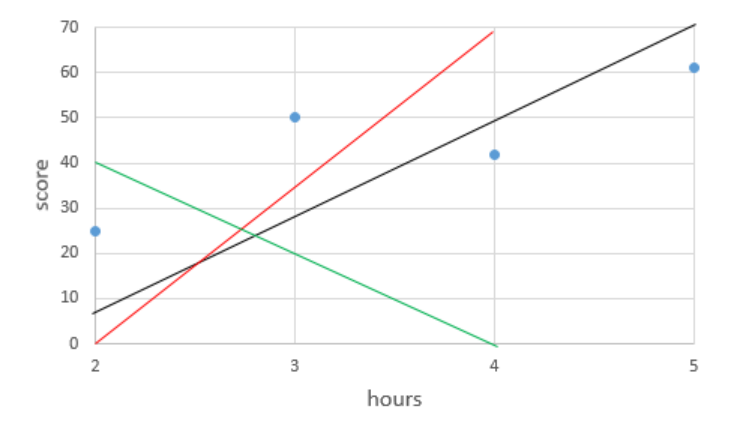
위 그림을 보면 점과 선이 여러개 그려져 있다. x값은 hours뿐이므로 단순 선형 회귀의 예시이다. 얼마나 공부했느냐에 따라 점수가 달라지는지, hours와 score의 관계를 가장 잘 나타내 줄 만한 직선을 찾아내는 게 바로 선형 회귀이다.
머신러닝에서는 x와 y의 관계를 유추하기 위해 H(x)=wx+b와 같은 식을 세우는데, 이러한 식을 가설이라고 한다. H는 가설(Hypothesis)의 약자이다.
이 직선은 결국 w와 b값에 따라 결정되는 것이므로, 적절한 직선을 찾아내는, 즉 적절한 w값과 b값을 찾아내는 것이 선형 회귀에서 해야 할 일이 되는 것이다.
적절한 w와 b를 찾았다면, 위 그림에 나타나 있지 않는 6시간, 7시간 혹은 그 이상의 공부를 했을 때 대략 점수가 어느 정도가 나올 것인지 예측할 수 있게 될 것이다.
