최적화 알고리즘

선형 회귀를 포함한 기계 학습은 결국 비용 함수를 최소화하는 매개 변수인 x와 y을 찾는 것이 목적이다. 이때 사용되는 알고리즘을 최적화 알고리즘(Optimizer)이라고 한다.

- 경사하강법

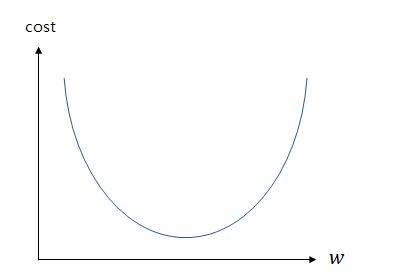
지난 게시글을 보면 알 수 있듯, 기울기가 너무 커져도, 기울기가 너무 작아져 음수가 되어도 오차는 커진다. 이 오차와 기울기의 관계를 그래프로 나타냈을 때,

출처ㅣhttps://wikidocs.net/21670

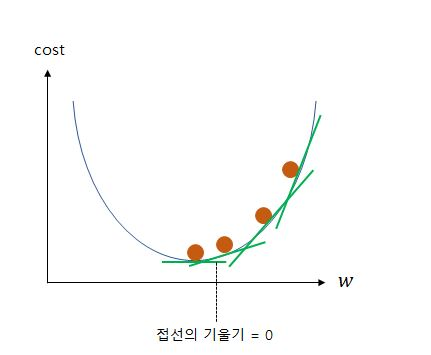
비용함수의 값 cost가 가장 낮은 지점은 그래프에서 보면 알다시피 기울기가 0이 되는 지점이다. 바로 이 지점이 우리가 도달해야 할 지점인 것이다. 그리고 그 지점의 w의 값이 우리가 찾는 최적의 w값이 될 것이다. 이 지점보다 위에 있다면 무조건 손실이 그보다 커질 것이다. 따라서 경사를 하강하며 점차 아래로 내려오도록 하여, 최적의 w값에 가까워지도록 하는 것이다. 아래 그림처럼 말이다.

출처ㅣhttps://wikidocs.net/21670
바로 이것을 경사하강법이라고 한다. 경사하강법은 최적화 알고리즘 중에 하나이다. 선형 회귀에서는 경사하강법이 회적화 알고리즘으로 자주 사용된다.

접선의 기울기가 0, 즉 미분값이 0이 되게 하는 값. 그것을 알기 위해 당연히 미분을 해야 한다. 일반적인 공식을 생각해보면 w와 b라는 두개의 매개변수(parameter)가 있기 때문에, 어느 한 쪽만 미분하는 편미분을 이용한다. 기울기는 w와 마찬가지이므로 w에 대해 편미분을 하면 δcost(w)/δw가 될 것이다.
그런데 여기서 끝나는 것이 아니다. 우리는 편미분에서 끝날 게 아니라 이 값을 0에 가깝게 만들어줘야 한다. 그렇게 하기 위해 다음의 공식을 이용한다.

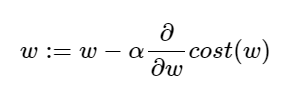
현재 w값에서, 현재 w에서의 접선의 기울기와 학습률을 곱한 값을 뺀 값을, 새로운 w의 값으로 한다는 것을 의미한다.
왜 이러한 식이 도출되었는가를 이해하려면 다음의 그래프를 보자.

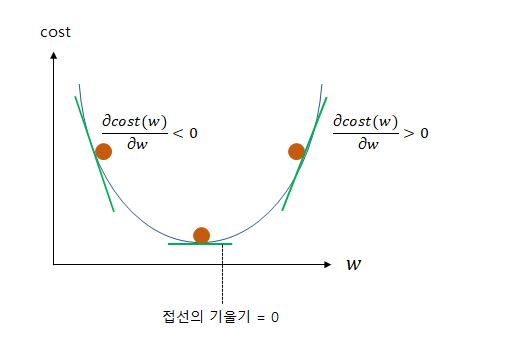
상술하기 이전에, 알파 값은 학습률(Learning rate)라는 것인데, 이는 딥러닝 챕터에서 자세히 상술할 터이니 여기서는 신경쓰지 않도록 한다.

w에 대해 미분한 값이 음수라면, 위 공식에 대입해 보았을 때 (-)*(-)가 되고 이는 결국 +가 되는 것이다. 따라서 w는 증가하여 현재 위치보다 오른쪽, 즉 -에서 0에 가까워지는 방향으로 이동할 것이다.
반대로 w대 대해 미분한 값이 양수라면, w값이 감소, +에서 0에 가까워지는 방향으로 이동하므로, 결과적으로 둘 다 모두 접선의 기울기가 0, 즉 cost값이 최소가 되는 값을 찾게 되는 것이다.
실제로 경사하강법은 w뿐 아니라 b에도 적용이 되어 둘 다 경사하강법을 통해 최적의 값을 찾아가게 된다.