[논문 리뷰] Learning the Graphical Structure of Electronic Health Records with Graph Convolutional Transformer (AAAI, 2019)

딥린이·2023년 4월 4일

Artificial Intelligence Data Science Deep Learning Medical AI Natural language processing ehr graph neural network paper-review transformer

Overview

이번에 리뷰할 논문은 카이스트 인공지능 대학원 최윤재 교수님이 작성하신 Learning the Graphical Structure of Electronic Health Records with Graph Convolutional Transformer이라는 논문이다. 이 논문은 의료 분야에서 사용하는 EHR 데이터를 그래프 인공 신경망과 Transformer라는 자연어 처리의 혁신적 모델을 결합하여 분석한 논문이라고 할 수 있다.

Background

Eletronic Health Reocords (EHR, 전자 건강 기록)

본 논문을 리뷰하기에 앞서 필요한 사전 지식에 대해 말해보도록 하겠다.
이 논문에서는 EHR이라는 데이터를 다룬다. 이 데이터는 환자의 방문 날짜 및 진단, 치료 등의 환자에 대한 전반적인 진료 데이터가 Real World의 자연어 형태로 기록이 되어있는 데이터이다.

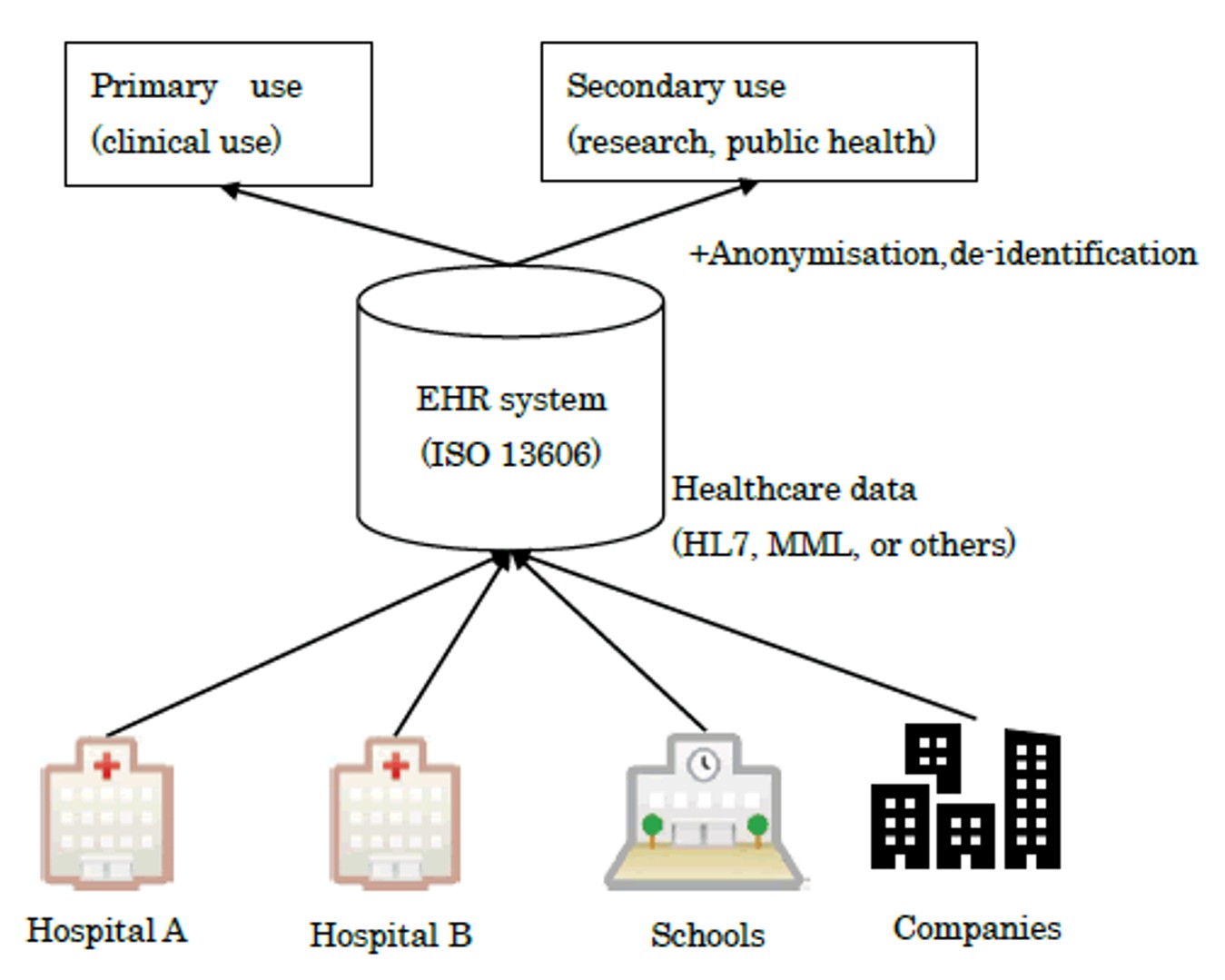위의 사진을 보듯이 EHR 데이터는 각 병원과 학교 회사 등에서 환자들에 대한 정보를 수집 및 통합하여 EHR system을 통해 관리하게 된다. 환자의 전체적인 정보와 흡연, 음주 등의 생활 습관 및 질병 이력이 구조화되어있어 환자의 이후 질병 패턴을 예측하는데 중요한 정보가 될 수 있다. 앞으로 전반적인 구조가 담긴 EHR 데이터를 encounter로 정의하도록 하겠다.

Graph Convolutional Networks (GCN, 그래프 합성곱 신경망)

다음은 논문에서 주력으로 다루는 GCN에 대해 간단히 이야기 해보도록 하겠다. GCN은 그래프 기반의 데이터를 처리하기 위한 딥러닝 방법론이다. 그래프의 각 각의 노드와 그들의 이웃 노드 간의 정보를 공유하고, 그래프의 구조에서 숨겨진 패턴을 학습하여 노드별 특성을 업데이트한다.

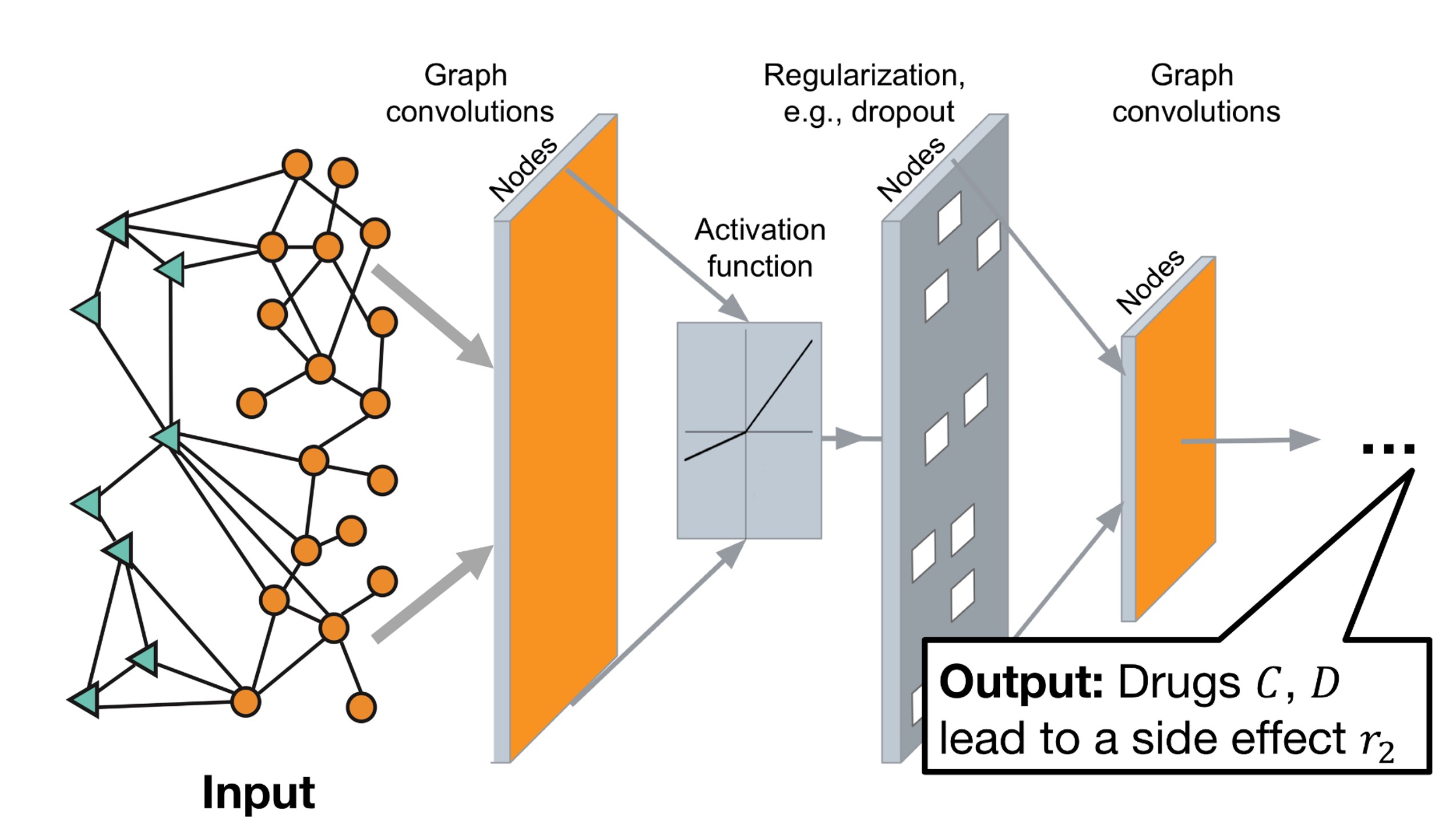위의 그림은 GCN의 전반적인 구조이다. Input으로 Graph가 들어가게 되고 이 그래프는 각각 Convolution → Activation → Regularization → Convolution의 순서대로 진행된 후 최종 Output을 내보낸다. 이런 GCN은 데이터가 구조가 잘 잡혀있다면, 데이터상의 숨겨진 구조 정보를 잘 찾아낸다는 장점이 있다.

Transformer

이 논문에서는 GCN과 Transformer의 장점을 합쳐서 새로운 모델을 제안한다. 그렇기에 Transformer를 한번 짚고 넘어가도록 하겠다. Transformer란 Attention 기반의 모델로 문장 속 단어들 간의 관계를 잘 이해하도록 설계된 모델이다.
다음은 각각 Scaled dot-product Attention의 구조이다.

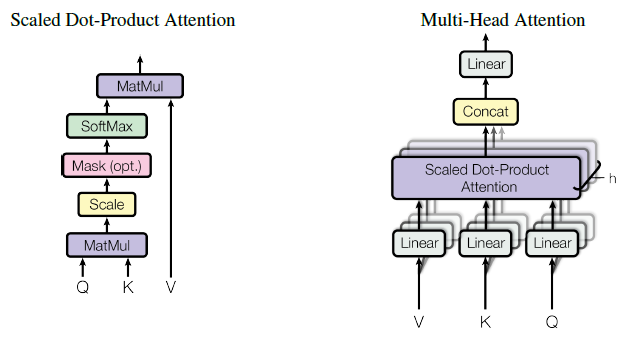Transformer는 각각 Query, Key Value라는 이름의 행렬이 있다. 이는 Q, K, V 라는 이름으로 단어 벡터를 행으로 가지는 문장 행렬이다. Q와 K 행렬의 내적을 통해 Attention Score를 구하고, Attention 분포를 구한 뒤 이를 모든 V 벡터를 가중합 하여 Attention 값 또는 Context Vector를 구하게 되고 이를 모든 Q에 대해서 반복한다.

지금까지 논문에 대한 Background를 모두 설명했다. 이제 부터 본 논문에 대해 리뷰를 시작하도록 하겠다.

Introduction

기존의 연구에서는 EHR system에서 수집된 대규모 의료 기록은 진단 예측, 의료 개념 표현 학습, 해석 가능한 예측과 같은 다양한 작업에서 높은 성능을 보였다. 이를 통해 EHR은 진단 코드, 검사 결과, 진료 등 심지어 환자 자체를 효과적으로 표현하는 방법을 배우는 것이 EHR 관련 작업을 수행하는데에 필수적이라고 볼 수 있다.

EHR 데이터는 보통 계층적 그래프로 표현될 수 있는 관계형 데이터 베이스에 저장되어진다. 그러나 현재까지의 일반적인 처리 방법은 데이터를 bag-of-features로 처리하였다. 이는 의사의 결정 과정을 반영하는 그래프의 구조를 무시하게되어진다.

다음의 그림을 통해 예시를 들 수 있다.

그림의 그래프 구조를 bag-of-features로 처리 시 Benzonatate라는 치료가 Cough에 의해 내려진 구조이지만 이를 무시하게 될 수 있다는 것이다. 즉, 기존의 방법을 사용할 시 정보 손실을 일으킬 수 있다는 것이다. 그에 따라 이 논문은 아래의 3가지 Contribution을 내세웠다.

본 연구는 EHR 데이터의 숨겨진 구조와 지도학습의 예측 작업의 공동 학습을 성공적으로 수행한 최초의 연구이다.
Attention Mask와 Conditional probability 기반 규제 형태의 prior knowledge를 활용하여 Self-attention을 Guide하고, EHR의 숨겨진 구조를 학습하도록 Transformer에 독창적인 구조적 수정을 제안한다.
GCT는 합성 데이터셋과 공개된 EHR 데이터셋에서의 모든 예측 작업에서 모든 Baseline 모델들을 능가하여, EHR 데이터에 대한 효과적인 일반적인 표현 학습 알고리즘 으로서의 잠재력을 보여준다.

이 Contribution들에 집중하며 리뷰해보도록 하겠다.

Method

Electronic Health Records as a Graph

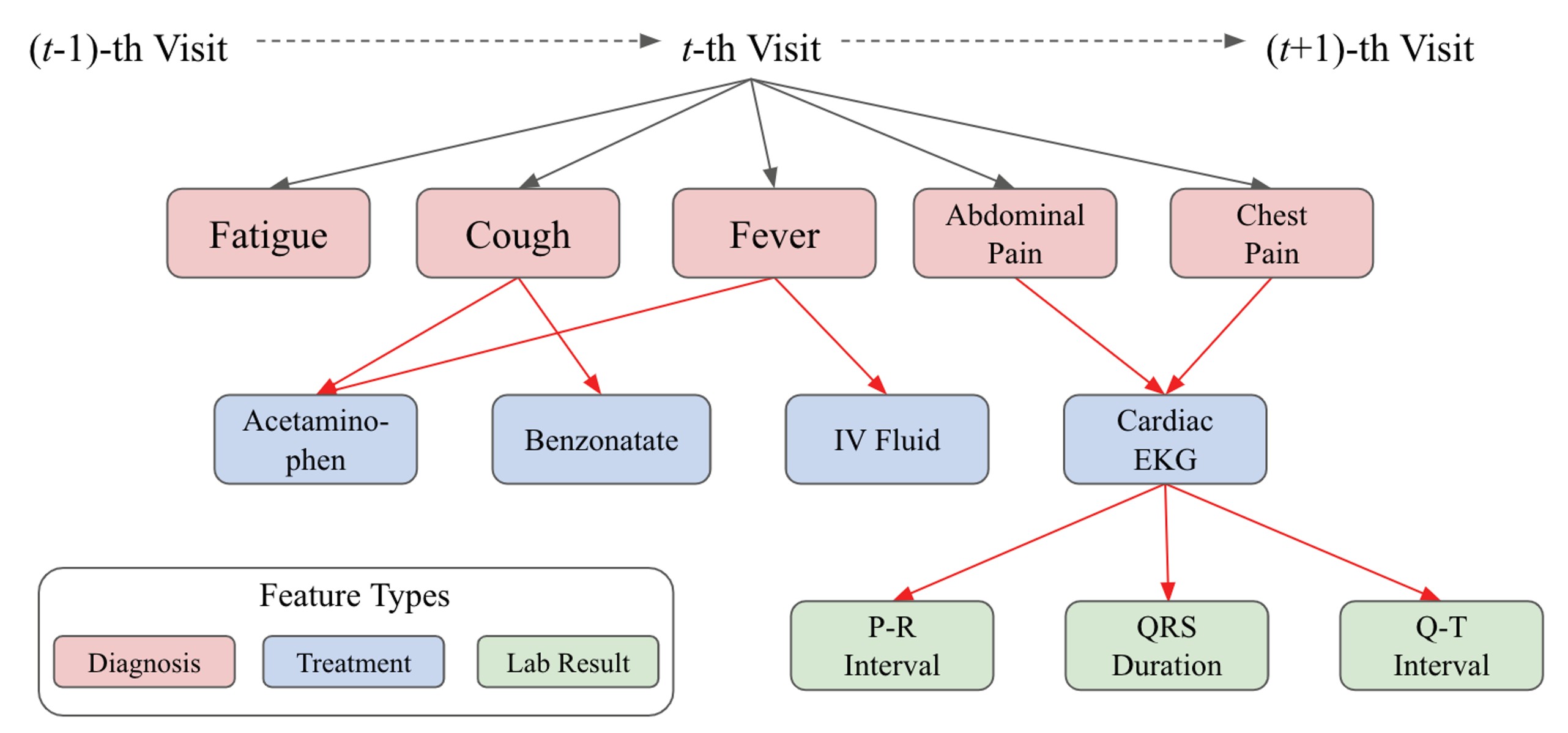
Figure.1: 전자 건강 기록의 그래픽 구조이다. 방문은 여러 유형의 특징으로 구성되며, 그 연결 (빨간색 edge)은 의사 결정 과정을 반영

Figure.1에 나타난 대로, $t$ 번째 방문 $V(t)$ 는 맨 위의 방문 노드 $v(t)$ 으로 부터 내려오기 시작한다. 그 아래에는 진단(Diagnosis) 노드 $d_{1}^{(t)},...,d_{\vert d^{t}\vert}^{(t)}$ 가 있으며, 이는 일련의 치료(Treatment) 노드 $m_{1}^{(t)},...,m_{\vert m^{t}\vert}^{(t)}$ 을 만들게 되는데 이때 아래첨자로 있는 $\vert d^{(t)}\vert, \vert r^{(t)}\vert$ 은 각각 $V(t)$ 에서 진단 및 치료의 코드 수를 나타낸다. 또한 일부 치료는 연속 값(혈압)또는 binary 값(양/음성 알레르기 반응)과 연관된 검사 결과(Lab Result) 노드 $r_{1}^{(t)},...,r_{\vert r^{t}\vert}^{(t)}$ 이 생성되며, 이후에 설명에선 방문 횟수를 나타내는 $t$ 를 생략하고 진행하도록 하겠다.

이 논문의 큰 맥락은 다음과 같다.

만약 모든 노드들이 특정 잠재 공간에서 표현이 가능하다면 $\vert d\vert + \vert m\vert + \vert r\vert$ 개의 노드로 이루어진 encounter로 볼 수 있다.
후에 나오는 인접행렬 $A$ 는 EHR의 구조를 표현하는 행렬이다. 또한 $d_{i}, m_{i}, r_{i}$ 를 의미하는 통합 용어로 $c_{i}$ 를 사용한다.
만약 $c_{i}$ 와 $A$ 가 함께 있을 경우 Graph Network를 사용하여 방문 표현 $v$ 를 도출해낸다.
구조정보 $A$ 가 없을 경우 Transformer의 feed-forward network를 사용하여 $v$ 를 도출해낸다.
위의 과정들은 기본적으로 모든 노드 표현 $c_{i}$ 를 합산하고 어떤 잠재공간으로 투영하는 과정이다.

Transformer and Graph Networks

이 논문에서는 한가지의 문제점을 둔다. 구조정보 $A$ 가 없더라도, 진단 및 치료를 요청할 때 의사가 어떤 결정을 내렸는지 명백히 존재한다는 점을 감안하면 $V$ 를 $c_{i}$ 의 bag-of-node로 취급하는 것은 각 노드 간의 상호작용을 고려하지 않을 수 있다는 문제점이다.

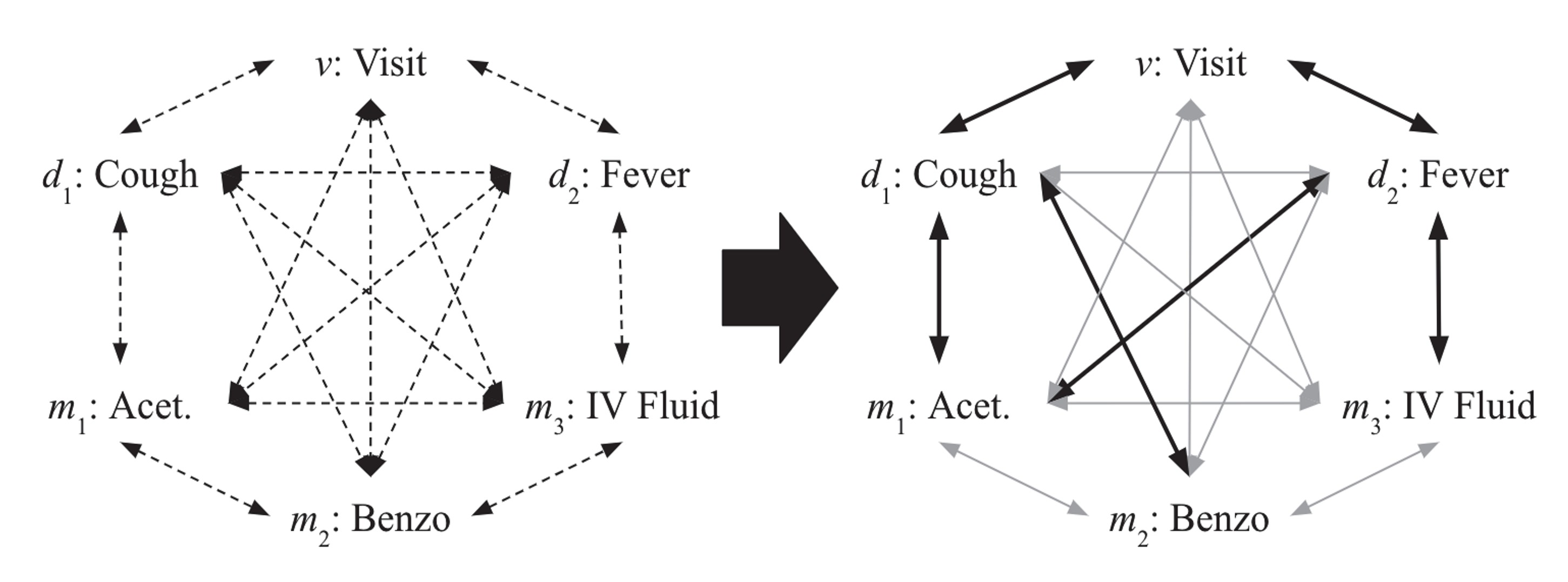
그렇다면 $A$ 가 없을 때 어떻게 기본 구조를 활용할 것지에 대한 해결 방법으론 다음 Figure.2와 같은 방법을 제시하였다.

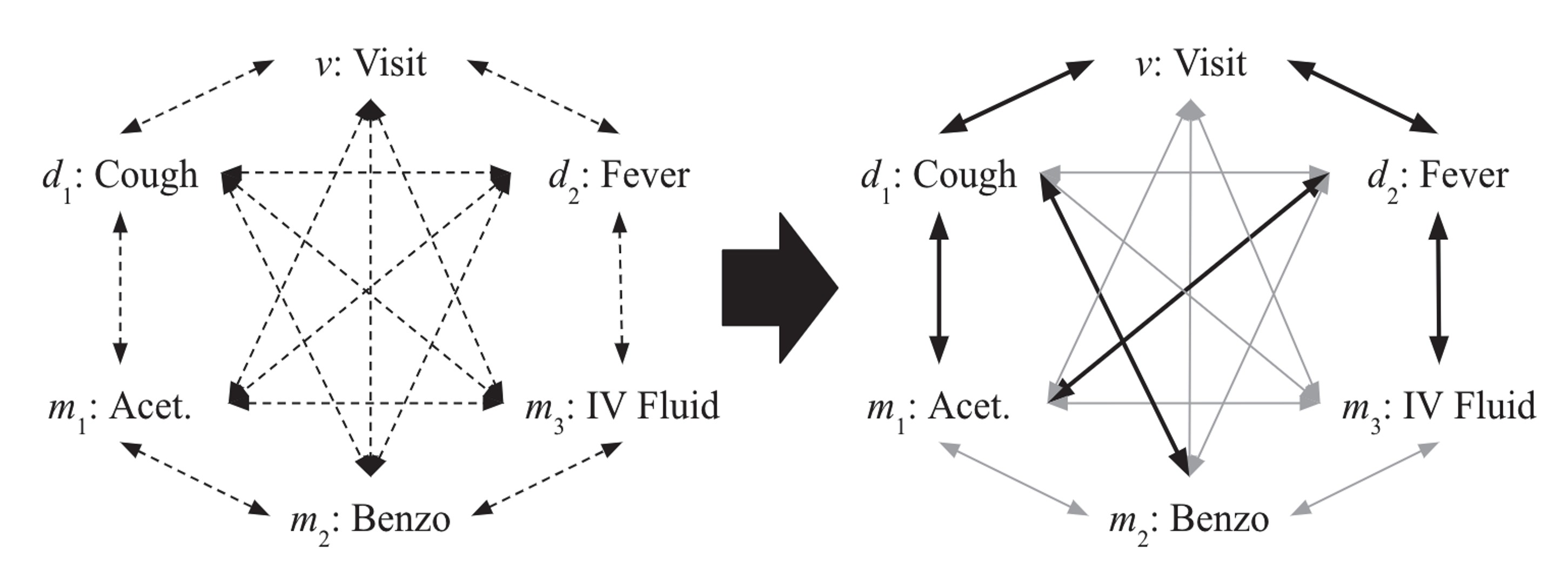Figure.2: encounter의 잠재적 구조 학습 학습의 진행에 따라 오른쪽의 구조와 같이 변한다.

Figure.2에서 알 수 있듯이 encounter의 각 노드들을 학습 시작시에는 모두 연결해 놓은 상태로 진행하게 된다. 이때 Transformer의 self-attention을 이용하여 구조를 학습해 나가며 각 노드별로 의미있는 연결에는 더 강한 edge를 의미가 없는 연결에는 약한 edge를 주는 방식으로 학습을 진행하게된다.

이 부분을 저자는 2개의 Case로 나누어 설명하였으나, 앞서 식에 사용되는 기호들의 Notation을 짚고 넘어가도록 하겠다.

기호	설명
$\tilde{A}$	구조 정보를 가진 인접 행렬(addjency matrix) A와 그래프 상에서 self-connection을 포함한 행렬
$\tilde{D}$	$\tilde{A}$ 의 대각선 노드 차수 행렬
$C^{(j)}, W^{(j)}$	각 $j$ 번째 convolution 노드 임베딩과 학습 가능한 parameter
$MLP^{(j)}$	$j$ 번째 convolution의 Multi-layer perceptron으로, 자체적으로 학습 가능한 parameter 지님
$Q^{(j)}, K^{(j)}, V^{(j)}$	Transformer의 Query, Key, Value

Case A: 구조 정보 $A$ 를 알고 있기 때문에 Graph Convolution Network (GCN)을 사용할 수 있다. 이 경우 아래의 GCN 계산 식을 가지고 연산을 진행한다.
$C^{(j)}=MLP^{(j)}(\tilde{D}^{-1}\tilde{A}C^{(j-1)}W^{(j)}) \quad\quad\quad\quad\quad (1)$
이 식은 $j$ 번째 층에서 $C^{(j)}$ 는 이전 층의 $C^{(j-1)}$ 에 Weight Matrix $W^{(j)}$ 를 곱한 후 $\tilde{A}$ 와 대각선 노드 차수 행렬의 역행렬인 $\tilde{D}^{-1}$ 을 곱하여 그래프의 구조를 적용한 다음 $MLP$ 를 통과 시켜 현재 층의 $j$ 번째 층의 $C^{(j)}$ 를 얻게 된다. 이 과정은 그래프의 구조를 고려하여 인접한 노드의 정보를 집계하고, 비선형 함수를 적용하여 각 층에서 노드의 새로운 representation을 학습하는 것으로 이해할 수 있다.

이 GCN의 식을 이용하여 구조 정보 $A$ 가 주어진 encounter의 경우 숨겨진 구조를 파악하여 학습을 진행할 수 있다.
Case B: 구조정보 $A$ 를 모르기 때문에 Transformer를 사용하여 Single-head attention을 갖는 encoder를 사용한다. 이를 위해 아래의 Transformer의 Scaled Dot-Production의 식을 사용하게 된다.
$C^{(j)}=MLP^{(j)}(\mathrm{softmax}({Q^{(j)}K^{(j)T}\over\sqrt{d}})V^{(j)}) \quad\quad\quad\quad\quad (2)$
위의 식은 Transformer의 Attention Mecahnism에서 사용되어진다. 먼저 $Q^{(j)}$ 와 $K^{(j)}$ 행렬 간의 내적을 수행한 후 이를 차원 $d$ 의 제곱근으로 나누어 scaling을 진행한다. 이렇게 scaling된 내적 결과에 softmax함수를 적용시켜 Attention Weight를 구하게 된다. 이 Weight를 $V^{(j)}$ 에 곱하여 Attention 출력값을 얻게 되고, 이 출력을 $MLP$ 에 통과 시켜 최종 출력값을 계산하게 된다. 이 과정은 입력간의 상대적인 중요도를 계산하여 정보를 집중시키는 역할을 한다.

위의 식1과 식2를 고려해보면, 정규화된 인접행렬 $\tilde{D}^{-1}\tilde{A}$ 와 attention map $\mathrm{softmax}({Q^{(j)}K^{(j)T}\over\sqrt{d}})$ , 그리고 노드 임베딩 $C^{(j-1)}W^{(j)}$ 과 값 벡터 $C^{(j-1)}W^{(j)}_{V}$ 모두 정보를 통합하거나 전파하는 기능을 수행한다. 또한 두 경우 모두 임베딩과 값 벡터를 곱하여 정보를 처리하므로 두 행렬 $\tilde{D}^{-1}\tilde{A}$ 와 $\mathrm{softmax}({Q^{(j)}K^{(j)T}\over\sqrt{d}})$ 가 상응관계에 있다고 볼 수 있다.

이에 따라 저자는 GCN은 Attention Mechanism을 알려진 인접 행렬로 대체한 Transformer의 특수한 경우로 볼 수 있으며, 반대로 Transformer는 전체적으로 연결된 노드를 가정하고 학습 중 연결된 강도를 학습하는 Graph 임베딩 알고리즘으로 볼 수 있다고 주장하였다.

Graph Convolutional Transformer

저자는 각 케이스에 대해 GCN과 Transformer를 복합적으로 사용하는 방법을 제시했으니 이에 대한 한계로 Transformer가 숨겨진 encounter의 구조를 학습할 수 있는 가능성은 있으나, 단 한개의 정보도 없이 의미 있는 연결을 만들어 내는 것을 Transformer의 Attention이 모든 feature들에 대소해 진행되고 있는 것을 보고 확인하였다. 이를 해결하기 위해 다음의 2가지의 요소를 활용하였다.

EHR 데이터의 특성
feature간의 Conditional Probaility

EHR 데이터 상에서 encounter 기록에서 일부 연결이 허용되지 않는 다는 사실을 관찰하였다. 아래의 그림에서 예시를 살펴볼 수 있다.

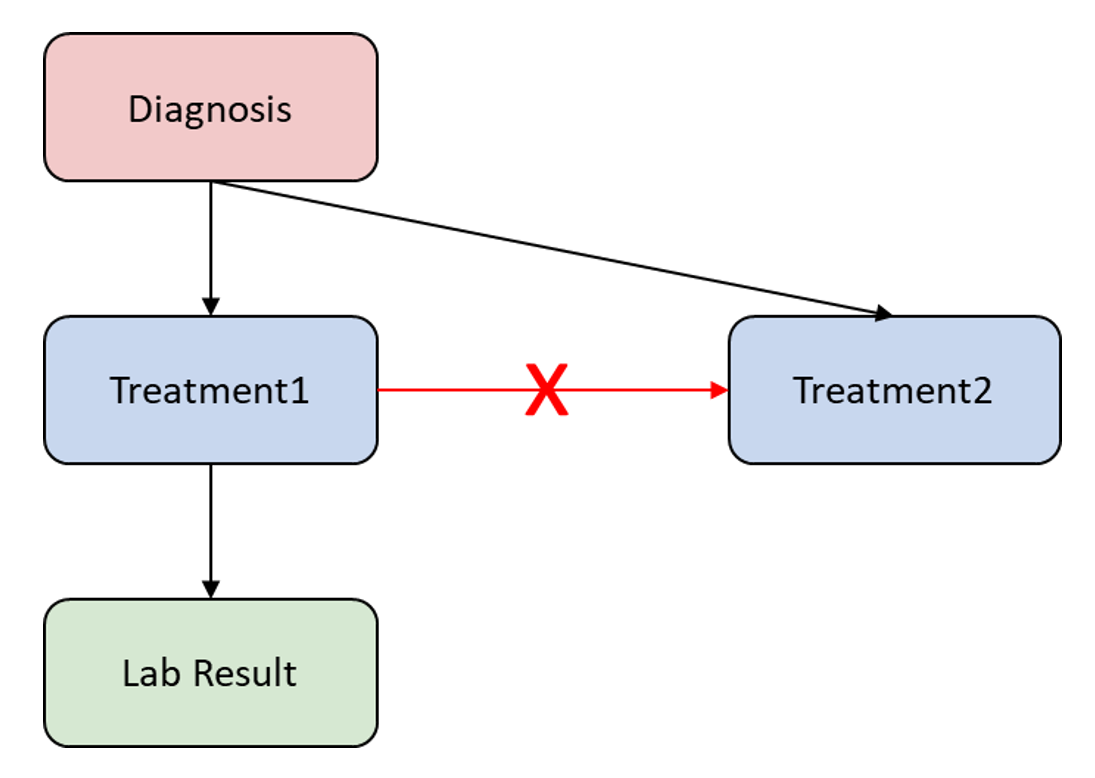위의 그림에서는 각 진단 노드는 서로 다른 치료 노드에 연결될 수 있고, 치료 노드는 반응 노드에 연결 될 수 있다. 그러나 치료 노드끼리는 연결 될 수 없는 구조를 가지고 있다는 것을 확인할 수 있다.

이러한 관찰을 기반으로 Attention 생성 단계에서 사용될 마스크 $M$ 을 만들 수 있으며, 이 $M$ 은 연결 허용 여부에 따라 값을 가지게 된다.

또한 Transformer가 Attention을 잘 가지게 하기 위해 학습 초기에 각 노드간의 연결 강도를 Conditional Probability를 이용하여 학습할 수 있도록 하였다.

Conditional Probability는 feature간의 잠재적 연결을 결정하는데 유용하게 쓰일 수 있다.

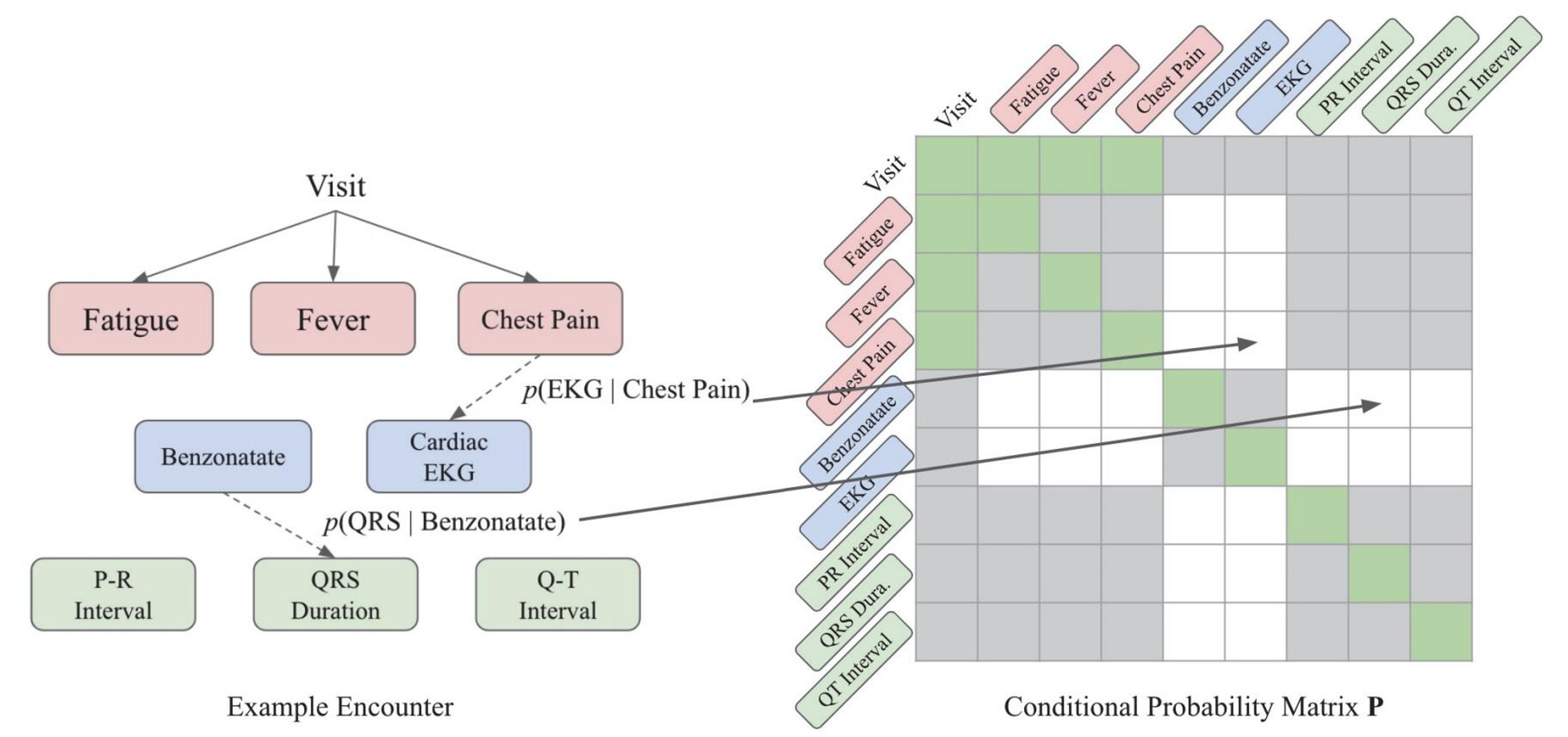Figure.3: encounter에기초한 조건부 확률 행렬 𝑃 생성되며, 회색 셀은 연결이 허용되지 않는 0의 확률 값을 가지며, 녹섹셀은 연결이 보장되어있는 셀, 흰색 셀에는 Conditional Probability의 값이 할당되어진다.

예를 들어 Figure.3과 같이 가슴 통증, 발열과 같은 진단 노드 및 EKG라는 치료 노드가 주어졌을 때 구조 정보가 없다면, 어떤 진단이 EKG를 요청하는 지 알 수 없다. 그러나 Conditional Probability을 사용하여 $p(\mathrm{EKG}|\mathrm{Chest\,Pain}) > p(\mathrm{EKG}|\mathrm{Fever})$ 라는 Conditional Probability간의 값을 비교하여 더 큰 값으로 연결 강도를 정할 수 있다면, 어떤 진단이 해당 치료를 결정하는지 구조를 알 수 있게된다.

이러한 방식으로 각각 진단 코드, 치료 코드, 반응 코드에 대해 $p(m|d), p(d|m), p(r|m), p(m|r)$ 을 계산 후 encounter 기록이 주어질 시에 Conditional Probability 행렬 $P$ 가 생성되어진다. 이때 $P$ 는 각 행의 합이 1이 되도록 정규화 0에서 1사이 값으로 정규화 되어있으며, GCT의 attention, 마스크 $M$ 과 Conditional Probability 행렬 $P$ 는 모두 같은 크기의 행렬로 연산이 진행되어진다.

저자는 주어진 $M$ 과 $P$ 를 사용하여 GCT가 가능한 한 정확한 그래프 구조를 복원하도록 학습하며 주어진 예측 작업을 해결하는데 도움이 되는 새로운 connection을 학습할 수 있게 하기 위해 다음의 공식을 사용하였다.

\hat{A}^{(j)} := \mathrm{softmax}({Q^{(j)}K^{(j)T}\over\sqrt{d}} + M)\quad\quad\quad\quad\quad (3)

이 식은 기존의 Attention 행렬에 마스크 $M$ 을 추가한 식으로 가능한 연결에 대한 attention만 고려하여 불필요한 계산을 하지 않는다. 이를 통해 다음과 같은 self attention을 제안하였다.

C^{(j)}=MLP^{(j)}(PC^{(j-1)}W_{V}^{(j)})\text{\;when\;} j=1,\\ C^{(j)}=MLP^{(j)}(\hat{A}C^{(j-1)}W_{V}^{(j)})\text{\;when\;} j>1

첫번째 GCT block에서는 Conditional Probability $P$ 를 사용하며, 이후의 block에서는 마스크되어진 $\hat{A}$ 를 이용하여 self-attention mechanism을 사용하여 노드의 특징을 업데이트 하게 된다.

이렇게 제안된 공식을 통해 모델을 업데이트 하기 위한 Loss 함수가 새로 정의가 되었다.

L_{reg}^{(j)}=D_{KL}(P\Vert\hat{A}^{(j)})\text{\;when\;}j=1,\\ L_{reg}^{(j)}=D_{KL}(\hat{A}^{(j-1)}\Vert\hat{A}^{(j)})\text{\;when\;}j>1\\ L = L_{pred}+\lambda\sum_{j}L_{reg}^{(j)}\quad\quad\quad\quad\quad (4)

위으 식은 $KL$ 발산 방법에서 아이디어를 얻어온 방법이다 $KL$ 발산이란 두 확률 분포 $A$ 와 $B$ 가 주어질때, $KL$ 발산은 $A$ 와 $B$ 가 얼마나 다른지를 나타내는 지표이다. 이 방법을 이용하여 GCT가 $P$ 에서 크게 벗어나지 않고, 오히려 $P$ 를 점진적으로 개선해나가며 attention이 그 자체로 확률 분포가 되게한다. 또한 $j$ 번째 block이 $j-1$ 번째 block의 attention 분포와 크게 벗어날 시 loss를 크게 내보내 업데이트를 진행한다.

Experiments

실험을 위해 데이터셋은 Sythetic의 합성 데이터와 eICU 데이터셋을 사용하였다.

Synthetic Encounter Record

현재 공개되어진 EHR 데이터 중 구조 정보를 포함하는 데이터가 존재하지 않았다. 그렇기 때문에 본 논문에서는 GCT의 EHR 데이터와 같은 방문-진단-치료-검사 결과의 계층 구조를 가진 합성 데이터를 생성하였다. 또한 실제 EHR 데이터 테스트를 위해 2014년부터 2015년 사이의 미국 여러 지역에서 수집된 중환자실 기록으로 구축된 데이터를 사용하였다.

데이터의 분포는 위의 Table과 같으며 Sythetic 데이터셋은 합성 데이터인 만큼 각 노드별 수가 일정하지만 eICU 데이터셋은 일정하지 않은 것을 볼 수 있다.

Baseline Models

본 논문에서는 5가지의 Baseline Model을 사용하였다.

$GCN$ : 기본적인 Graph Convolution Network
$GCN_P$ : 행렬 $A$ 대신 Conditional Probability 행렬 $P$ 를 사용
$GCN_{random}$ : 행렬 $A$ 대신 random하게 normalized된 행렬 사용
$Shallow$ : 일반적인 단층의 feed-forward network
$Deep$ : 다층의 feed-forward network

Prediction Tasks

실험에 사용된 데이터셋은 각각 Train : Validation : Test = 8 : 1 : 1로 구성하였으며, 5개의 Task를 진행하였다.

Graph reconstruction (Synthetic dataset) & Diagnosis-Treatment classification (Synthetic dataset)

Graph reconstruction: $N$ 개의 특성을 가진 encounter가 주여졌을 때, 모델은 $N$ 개의 특성 임베딩 $c$ 를 학습하여 그래프 재구성을 수행한다.
Diagnosis-Treatment classification: 특정 진단 코드( $d_{1}$ 및 $d_{2}$ )와 치료 코드( $m_{1}$ ) 간의 연결이 있는 encounter에 레이블을 할당하여 모델이 진단과 치료코드 간의 실제 연결 구조를 학습하도록 하며, encounter에 각각의 코드가 존재하는지의 여부에 의존하여 점수를 얻지 못하도록 제한하였다.

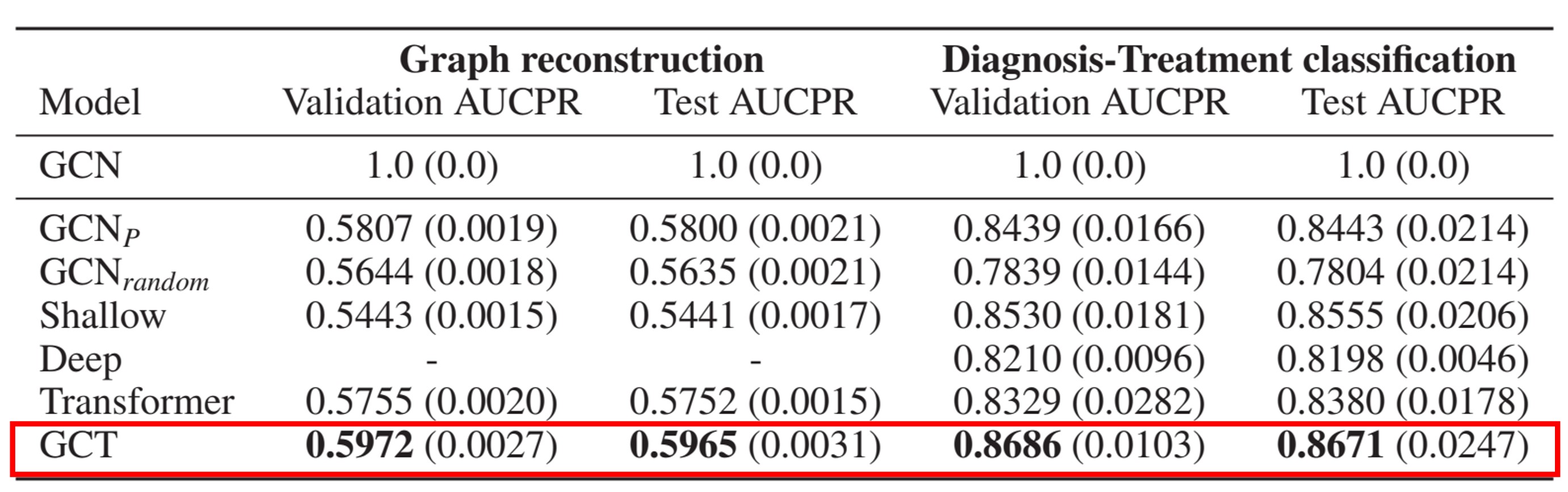
Baseline의 모델보다 GCT가 각 Task에서 약 2~3%의 성능 향상을 이뤄낸 것을 볼 수 있다. 또한 이 Task에서 평가 metric을 AUCPR을 사용하였다 이는 Precision과 Recall에 대해 ROC-curve 곡선의 면적을 재는 것으로 Recall의 결과를 더 잘 반영하기 위해 사용한다.

Masked diagnosis code prediction (Synthetic dataset & eICU dataset)

Masked diagnosis code prediction: ecounter가 주어진 경우, 무작위로 선택된 진단 코드 $d_{i}$ 를 마스크 시킨 후 마스크된 코드의 임베딩을 학습하여 실제 코드를 예측한다.

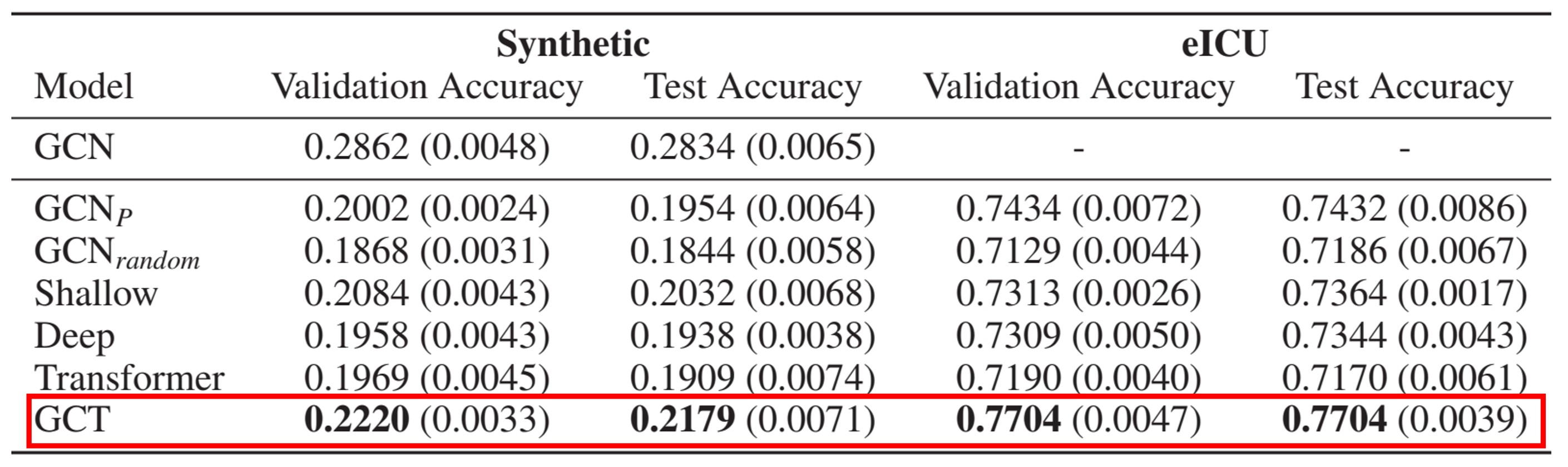
합성 데이터 셋에서 약 22%로 높은 성능은 아니지만 Baseline모델에 비해 잘 나온 것을 볼 수 있으며 실제 EHR 데이터셋에서도 77%의 성능으로 다른 모델에 비해 약 4%의 성능향상을 이루어냈다.

Readmission prediction (eICU dataset) & Mortality prediction (eICU dataset)

Readmission prediction: encounter가 주어진 경우 visit 임베딩 $v$ 를 학습하여 환자의 중환자실 재입원을 예측한다.
Mortality prediction: encounter가 주어진 경우 visi 임베딩 $v$ 를 학습하여 중환자실 입원중 환자의 사망을 예측한다.

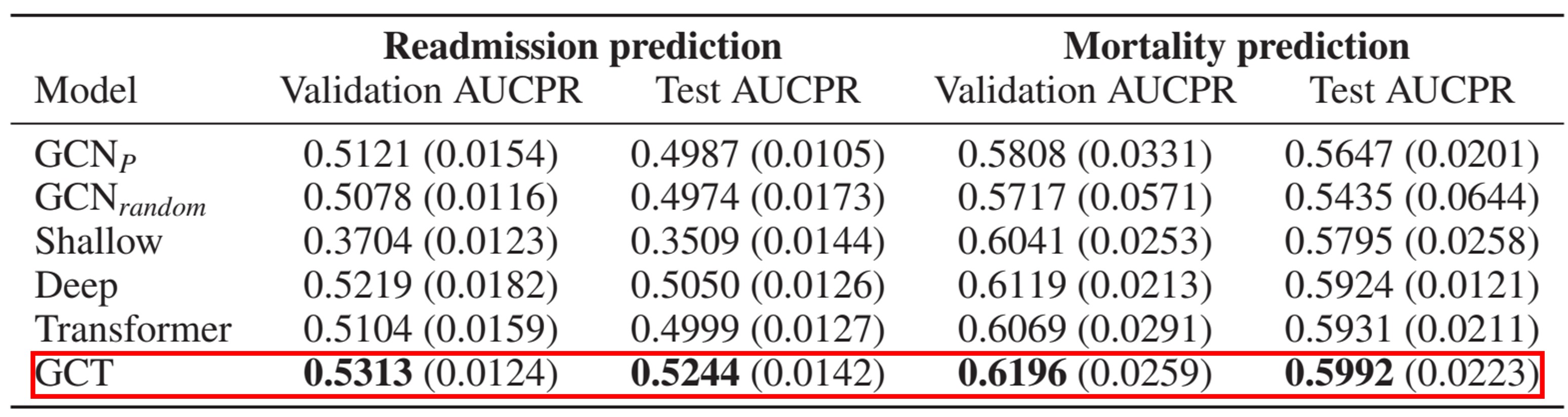
각각의 Task에서 약 53%, 약 61%의 높은 성능은 아니지만 Baseline 모델보다 미세하게 더 높게 나온 것을 볼 수 있다.

Evaluating the Learned Encounter Structure

Graph reconstruction task에서 Transformer와 GCT의 학습된 구조를 분석하여 두 모델이 얼마나 구조 정보를 잘 학습하였는지 평가한 것으로 각각 $KL$ 발산 값과 Entropy가 낮을 수록 학습이 잘된 모델이다.

Table에서 알 수 있듯 Transformer는 GCT가 대부분 더 작은 값을 내보냈고, $GCN_{P}$ 와 비교했을 때 더 낮은 값을 내보내거나 비슷한 값을 내보내는 것을 볼 수 있다.

Attention Behavior Visualization

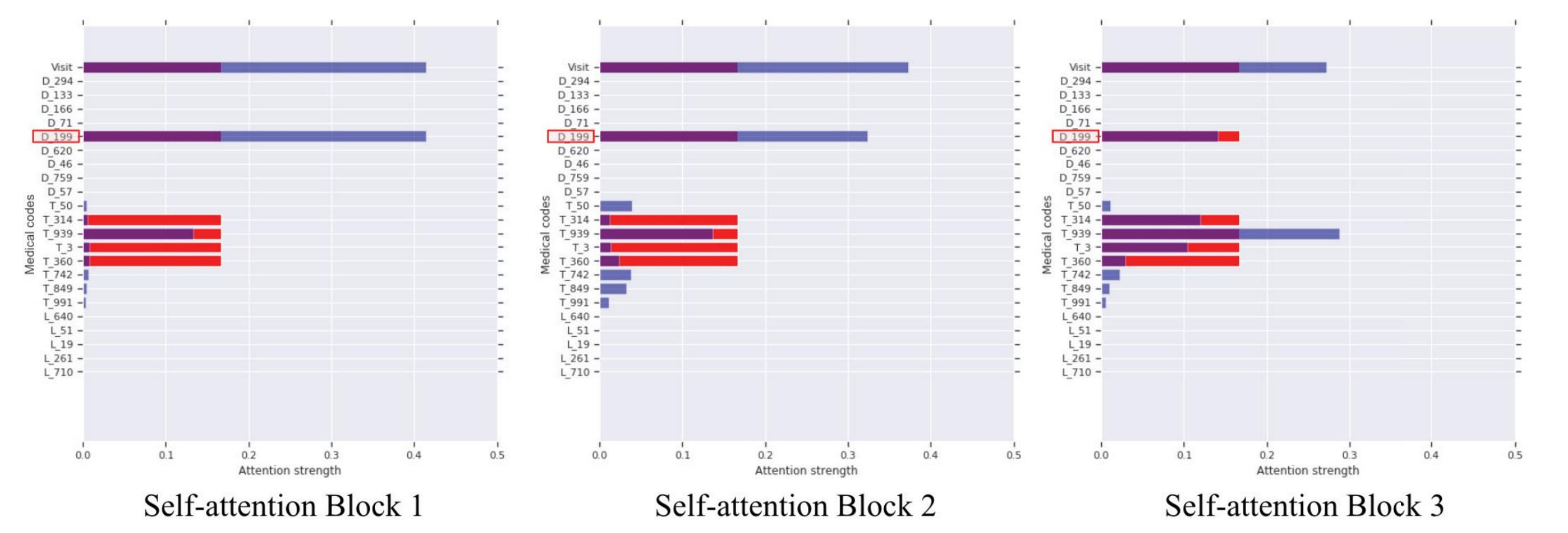
위의 Attention Figure는 모델의 각 Self-attention block별로 Attention score를 시각화한 것이다. Figure의 Blue bar는 D_199 진단 코드가 다른 모든 코드에 주어진 Attention score이며, Red bar는 Conditional probability 기반의 Attention score이다. 마지막으로 Purple bar는 실제 EHR의 관계를 수치화한 것이다.

Block 1에서는 T_50부터 T_991까지의 모든 코드에 아주 미세하게 모델이 Attention을 진행하였고 이에 Conditional probability를 통해 T_314부터 T_360까지의 코드에 보정을 진행하였으며, 점차 Block을 거칠 수록 T_939의 코드에 모델이 Attention을 하며, Conditioanl Probability 행렬 $P$ 에서 벗어나지 않고 학습이 되고 있는 것을 볼 수 있다.

Conclusion

이 논문의 Conclusion은 다음과 같이 3가지로 나눌 수 있다.

GCT는 완전한 진료 구조 정보가 필요한 이전의 최첨단 방법의 문제를 해결하였다.
GCT는 합성 데이터와 공개 EHR 데이터셋에서 기준 모델을 능가하여, 일반적인 EHR 모델링 알고리즘으로서의 잠재력을 보여주었다.
GCT와 RNN을 결합하여 심부전 진단 예측이나 예기치 않은 응급실 입원 예측과 같은 환자 수준 예측 작업을 수행하면서, 의학적으로 더 의미 있는 패턴을 학습하도록 attention mechanism을 개선할 수 있다.

이상으로 논문 리뷰를 마치도록 한다.

딥린이

파이토치 어린이 코린이 입니다

2개의 댓글

케로베르스

2023년 4월 4일

와오,,,,, 딥린이님이 아니라 딥문가로 이름 바꾸셔야겠어요!!
내용 잘 보고 갑니당🤗

1개의 답글