Support Vector Machine

• 선형인 비선형 분류, 회귀, 이상치 탐색에도 사용할 수 있는 머신러닝 방법론
• 딥러닝 이전 시대까지 널리 사용된 방법론
• 복잡한 분류 문제를 잘 해결, 상대적으로 작거나 중간 크기를 가진 데이터에 적합
• 최적화 모형으로 모델링 후 최적의 분류 경계 탐색
• 두 클래스 사이에 가장 넓이가 큰 분류 경계선을 찾기 때문에 Large margin classification 이라고도 함
• Support Vector라고 하는 것은 각각의 클래스에서 분류 경계선을 지지하는 관측치들을 Support Vector라고 함
  
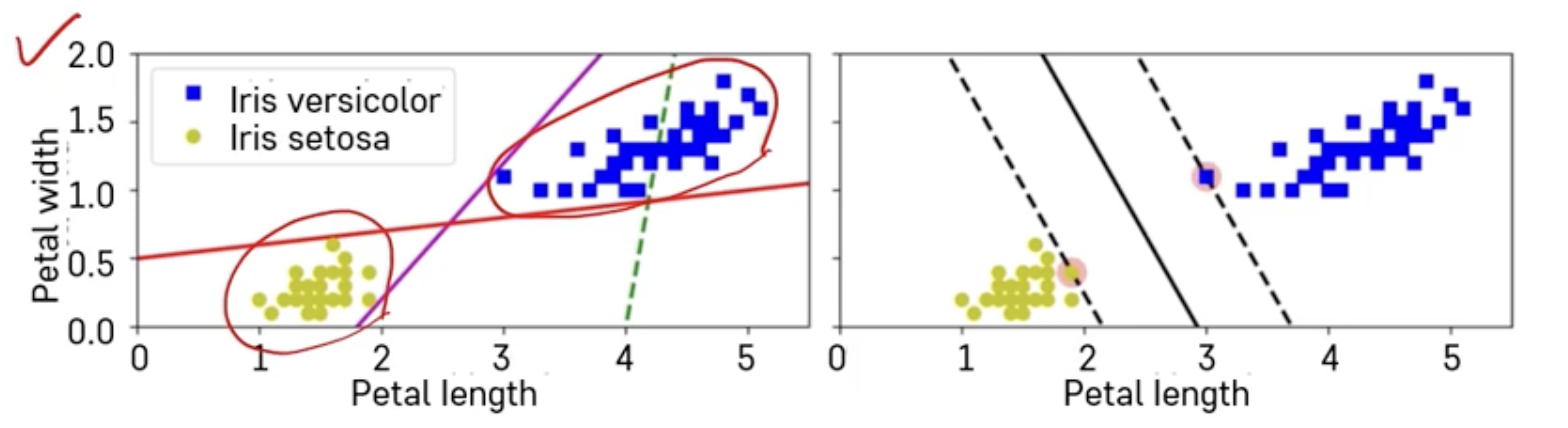
  ➡️ 노랑색 - 파랑색 분류
  ➡️ Generalization (일반화)
  ➡️ Validation Error

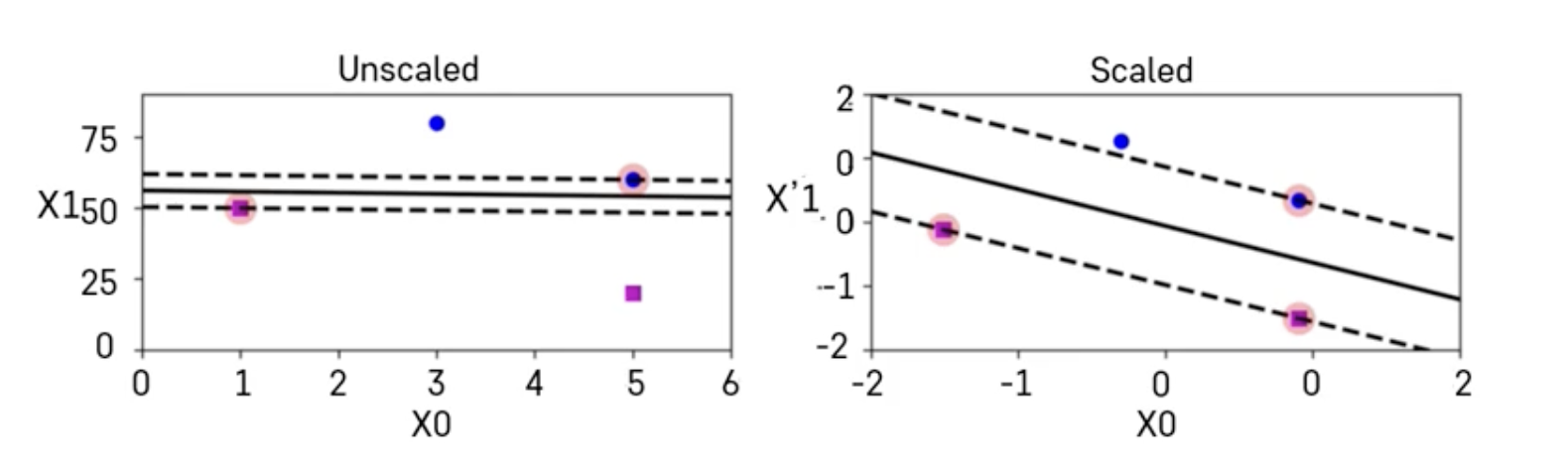
• SVM은 스케일에 민감하기 때문에 변수들 간의 스케일을 잘 맞추는 것이 중요
• Sklearn의 StandardScaler를 사용하면 스케일을 잘 맞출 수 있음
  

Hard Margin vs Soft Margin

• Hard Margin : 두 클래스가 하나의 선으로 완벽하게 나눠지는 경우에만 적용 가능

• Soft Margin : 일부 샘플들이 분류 경계선의 분류 결과에 반하는 경우를 일정 수준 허용하는 방법
  
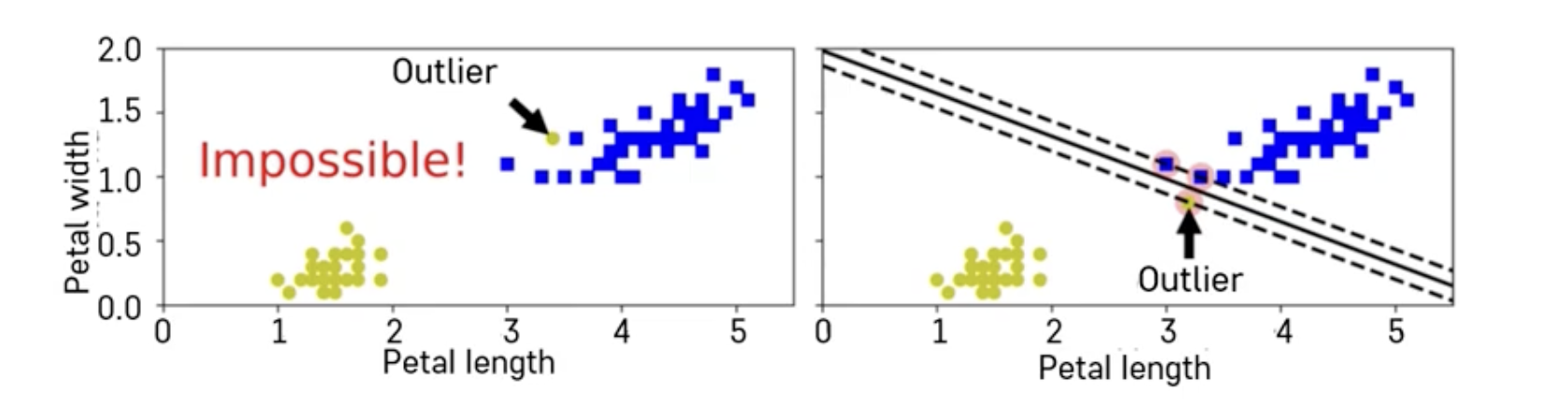
  ➡️ 첫번째 사진으로는 분류 경계선 불가능
  ➡️ soft margin 주로 사용 (일정수준 분류 경계선 넘어가는 경우에만 허용 가능)

• C 페널티 파라미터로 조정 (SVM-Hyperparameter)
  
  ➡️ 왼쪽 사진 : 패널티 작게 줌, margin 넓음, train error 커질 수 있음
  ➡️ 오른쪽 사진 : 패널티 크게 줌, margin 좁음, train error 줄어들 수 있음

=> 적절한 trade-off 필요함

Hard Margin Optimization

margin 계산

Soft margin Optimization

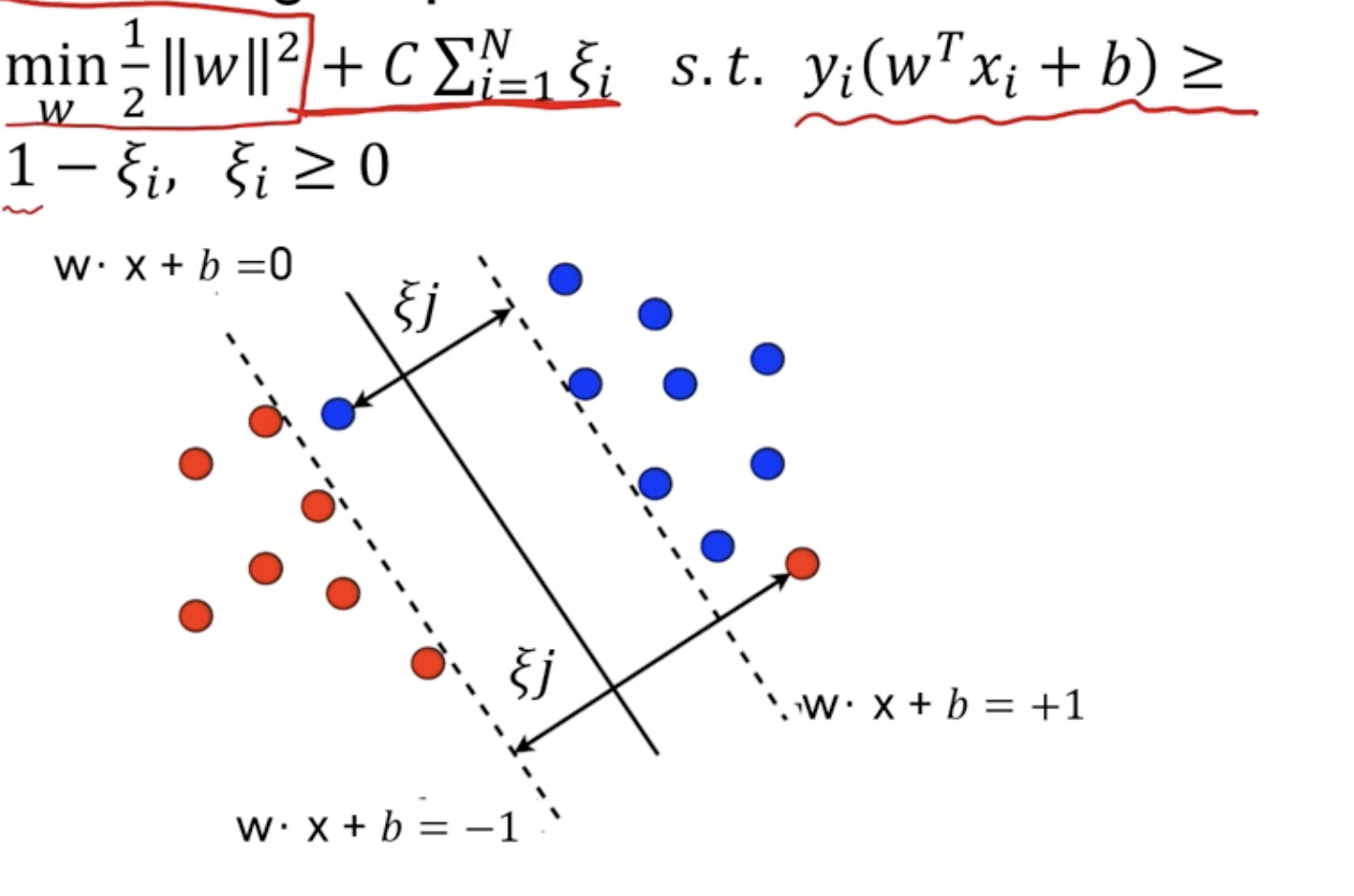
SVM Prediction

• Classifier ( 분류 경계선 )
  

Nonlinear SVM Classification

• 기본적인 아이디어 : 다항식 변수들을 추가함으로써 직선으로 분류할 수 있는 형태로 데이터 만들기
  
  

Polynominal Kernel

: 다항식의 차수를 조절할 수 있는 효율적인 계산 방법

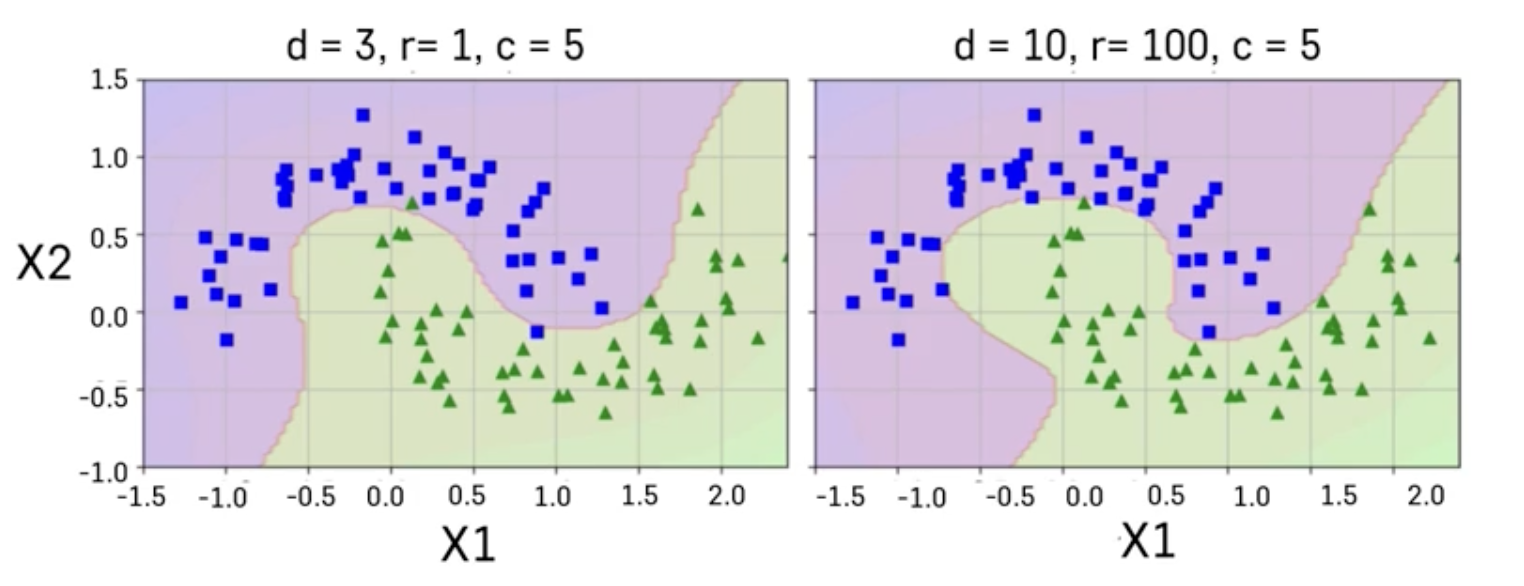
Gaussian RBF Kernel

: 무한대 차수를 갖는 다항식으로 차원을 확장시키는 효과
(gamma - 고차항 차수에 대한 가중 정도)

SVM Regression

: 선형회귀식을 중심으로 이와 평행한 오차 한계선을 가정하고 오차한계선 너비가 최대가 되면서 오차 한계선을 넘어가는 관측치들에 패널티를 부여하는 방식으로 선형 회귀식 추정

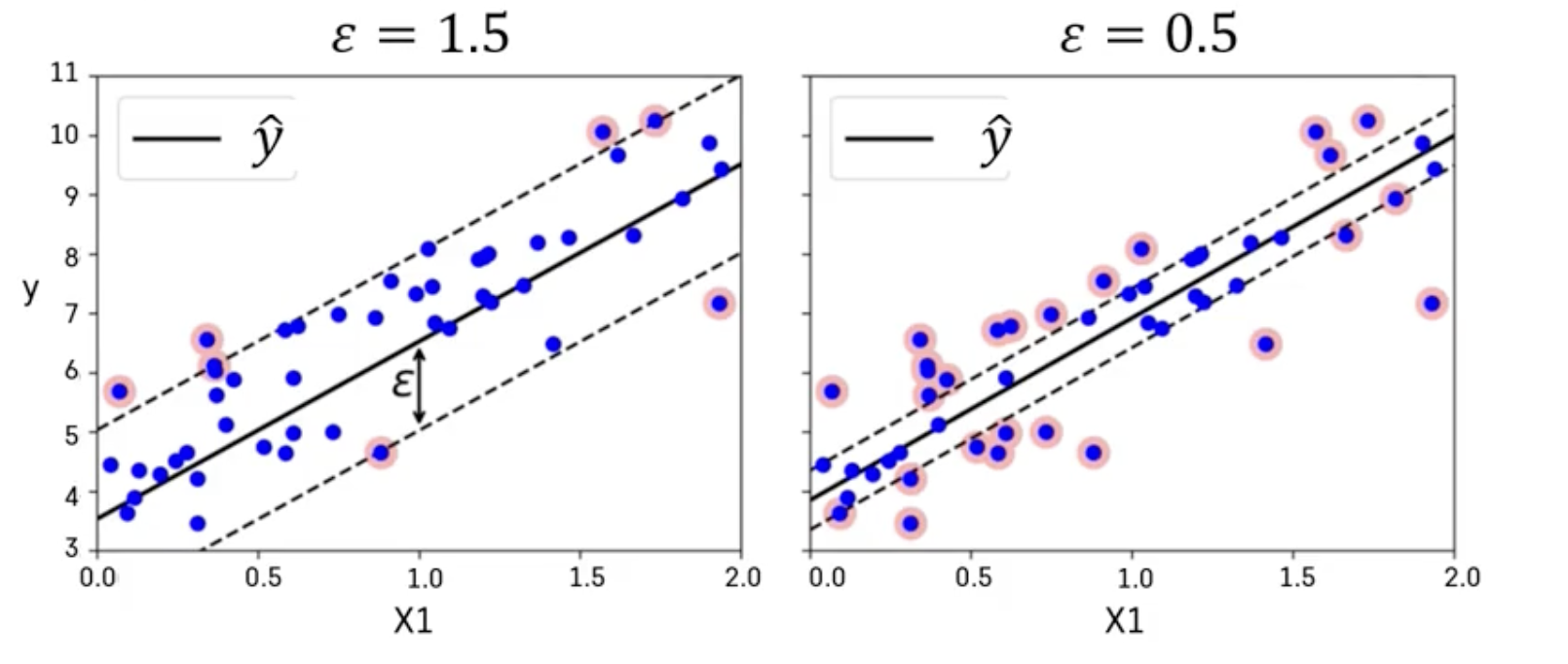
• SVM Classification 모델과 같이 다항식 변수항을 추가하는 개념을 도입함으로써 비선형적인 회귀 모형을 적합할 수 있음

reference : K-MOOC 실습으로 배우는 머신러닝