1. 다중선형 회귀분석

import statsmodels.api as sm

model = sm.OLS(endog = Y, exog = X).fit()
model.summary()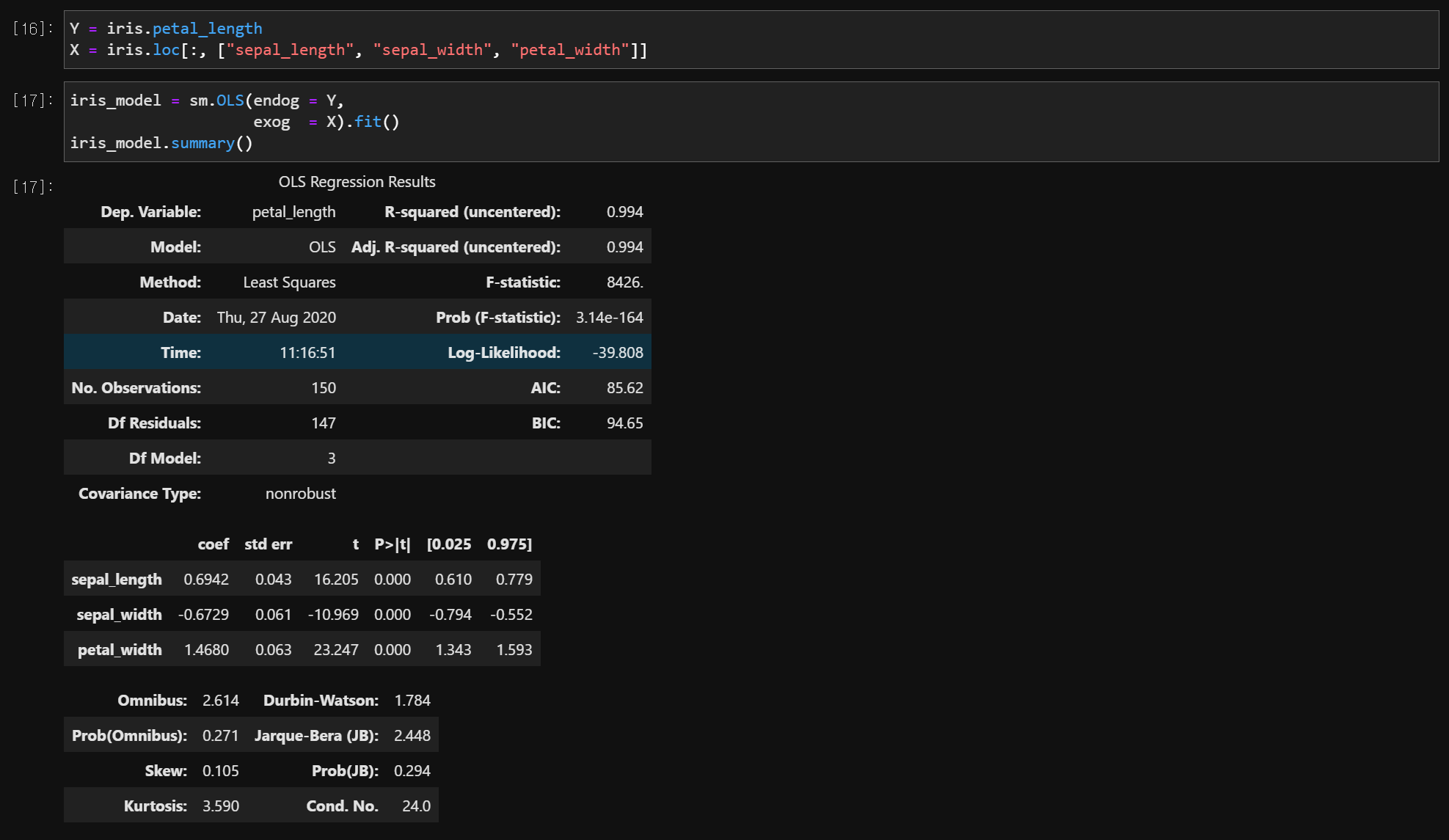

1) 회귀모형은 타당한가?

• 귀무가설 : 회귀모형은 타당하지 않다.
• 대립가설 : 회귀모형은 타당하다.

결과

• F-statistic : 검정통계량 = 8426.
• Prob (F-statistic) : P-value = 3.14e-164
• 유의확률이 0.000이므로 유의수준 0.05에서 회귀모형은 통계적으로 유의하게 타당한 것으로 나타났다.

2) X는 Y에게 유의한 영향을 주는가?

• 귀무가설 : X는 Y에게 영향을 주지 않는다. (beta1 == 0 or beta2 == 0)
• 대립가설 : X는 Y에게 영향을 준다. (beta1 != 0 or beta2 != 0)

결과

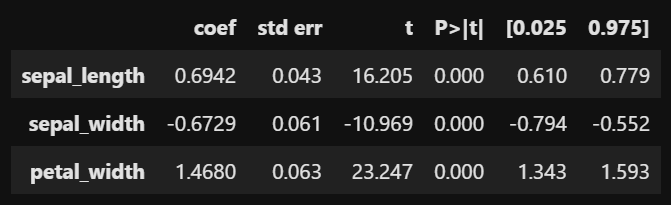
• speal_length : P-value = 0.000 -> 유의한 영향을 준다.
• sepal_width : P-value = 0.000 -> 유의한 영향을 준다.
• petal_width : P-value = 0.000 -> 유의한 영향을 준다.

3) X는 Y에게 어떤 영향을 주는가?

• 회귀계수의 값이 크면 X가 Y에게 많은 영향을 준다.
• 회귀계수의 값이 작으면 X가 Y에게 작은 영향을 준다.
• 회귀계수의 부호가 +이면 X가 Y를 증가시키는 영향을 준다.
• 회귀계수의 부호가 -이면 X가 Y를 감소시키는 영향을 준다.

결과

• speal_length : coef = 0.694
  : 꽃받침의 길이는 꽃받침의 너비와 꽃잎의 너비가 고정되어 있을 때, 꽃받침의 길이가 1cm 증가하면 꽃잎의 길이를 약 0.694cm 정도 증가
• speal_width : coef = -0.673
  : 꽃받침의 너비는 꽃받침의 길이와 꽃잎의 너비가 고정되어 있을 때, 꽃받침의 너비가 1cm 증가하면 꽃잎의 길이를 약 0.673cm 정도 감소
• petal_width : coef = 1.468
  : 꽃잎의 너비는 꽃받침의 길이와 꽃받침의 너비가 고정되어 있을 때, 꽃잎의 너비가 1cm 증가하면 꽃잎의 길이를 약 1.468cm 정도 증가

4) 회귀모형의 설명력 or X들의 설명력

• Y의 다름(변동)을 회귀모형이 얼마나 설명하고 있는가?
• Y의 다름(변동)을 X가 얼마나 설명하고 있는가?

결과

• R-squared (uncentered) = 0.994
• Adj. R-squared (uncentered) = 0.994
• 회귀모형이 Y의 변동을 약 99.4% 정도 설명하고 있다.

  수정된 결정계수는 Y에게 유의한 X가 모형에 들어올 때는 결정계수가 증가하고 Y에게 유의하지 않은 X가 모형에 들어올 때는 결정계수가 증가하지 않도록 조치를 한 것임

MSE

from sklearn.metrics import mean_squared_error

mean_squared_error(y_true = , y_pred = )

• 회귀 모델의 적합도를 나타내는 척도로 0에 가까울 수록 적합도가 높음

5) 예측 (Prediction)

model.predict(exog = X)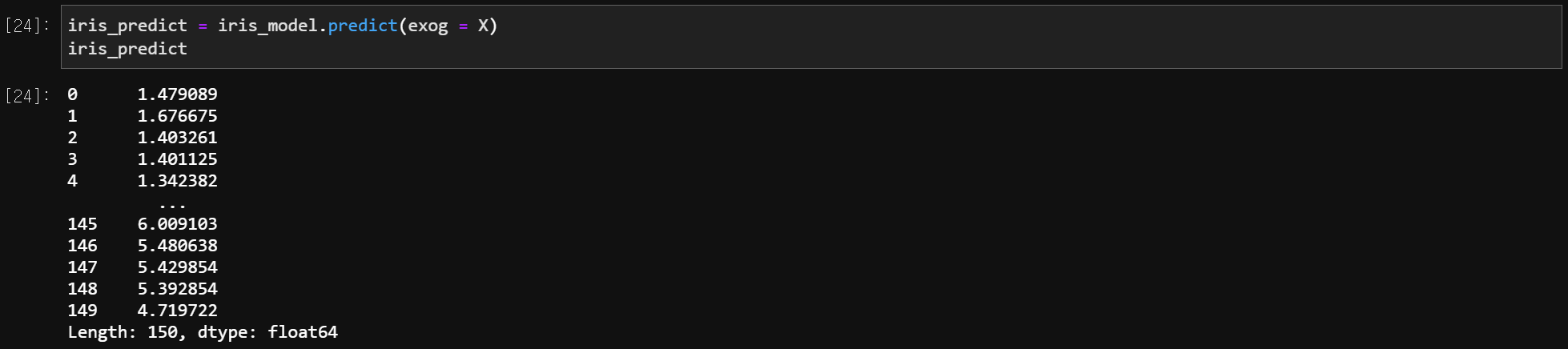

2. 회귀모형의 진단 or 가정

1) 다중공선성 (Multicolinearity)

# VIF (Variance Inflation Factor)

from statsmodels.stats.outliers_influence import variance_inflation_factor

VIF             = pd.DataFrame()
VIF['VIF']      = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
VIF['Variable'] = X.columns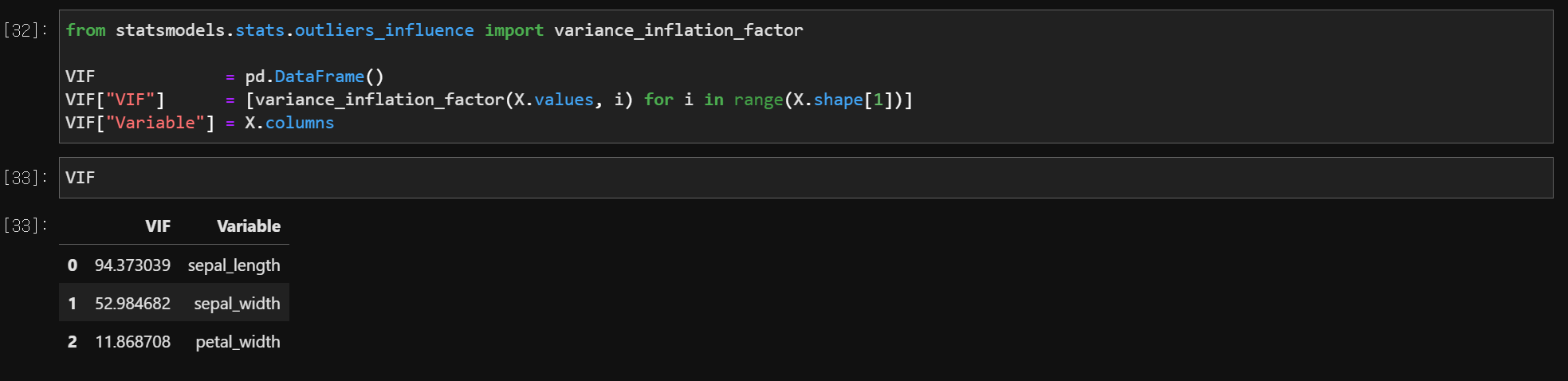

결과

• VIF 값이 10 이상이기 때문에 독립변수들을 바꿔 넣어가면서 유의미한 값을 도출해야 함

2) 표준화된 회귀계수

from scipy.stats.mstats import zscore

model = sm.OLS(endog = zscore(Y), exog = zscore(x)).fit()
model.summary()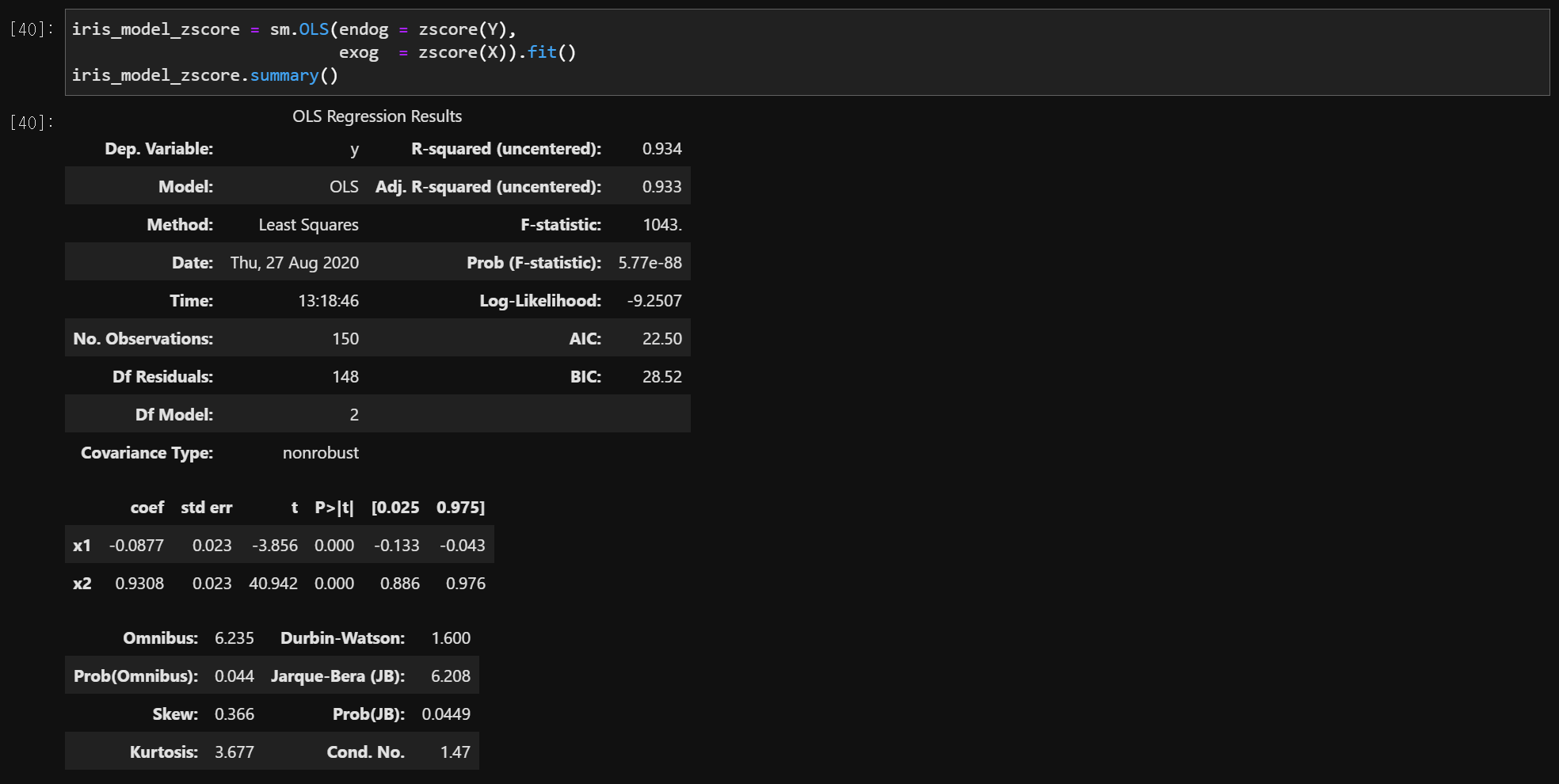

3) 더미변수

dummy_data = pandas.get_dummies
data = data.join(dummy_data)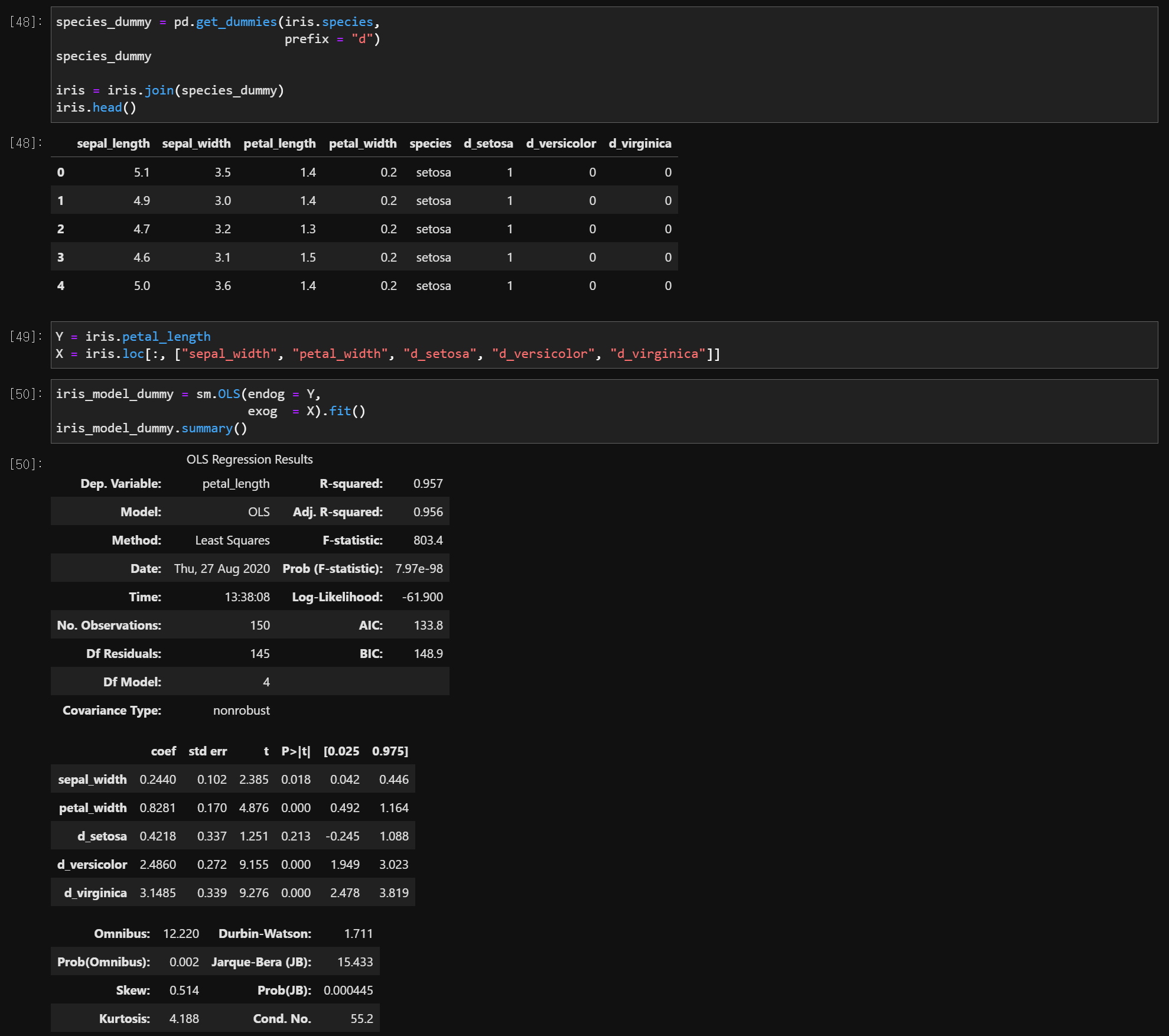

4) 오차의 정규성 가정

• 귀무가설 : 정규분포를 따른다.
• 대립가설 : 정규분포를 따르지 않는다.
• Jarque-Bera Normality test
• Jarque-Bera (JB) = 6.208
• Prob (JB) = 0.0449
• 유의확률이 0.0449이므로 유의수준 0.05에서 정규성 가정이 깨짐

5) 오차의 독립성 가정

• 귀무가설 : 독립이다.
• 대립가설 : 독립이 아니다.
• Durbin-Watson = 1.600
• DW 값이 2에 가까우므로 오차들은 독립이다.

  DW 값이 2에 가까우면 오차들은 독립
  DW 값이 0에 가까우면 독립 X, 양의 자기상관 O
  DW 값이 4에 가까우면 독립 X, 음의 자기상관 O

# 참고
import statsmodels.stats as sms

sms.durbin_watson(residuals)

6) 회귀모형의 유의성 검정

• 귀무가설 : 유의하지 않다.
• 대립가설 : 유의하다.
• 독립변수들을 회귀모형에 적용했을 때, 회귀모형의 유의성 검정
• Omnibus = 6.235
• Prob(Omnibus) = 0.044
• 유의확률이 0.044이므로 유의수준 0.05에서 독립변수들을 적용했을 때, 통계적으로 유의하다.

3. 변수선택 방법

from mlxtend.feature_selection import SequentialFeatureSelector as sfs
from sklearn.linear_model import LinearRegression

variable = sfs(LinearRegression(),
           k_features = , # number of features to select, 'best'도 가능
           forward    = True or False, # False = backward
           floating   = , # adds a conditional exclusion/inclusion if Ture
           scoring    = , # 'accuracy for sklearn classifiers
                          # 'r2' for sklearn regressors
           cv         = ).fit(X, Y) # cv = cross validation, default = 5

result.k_feature_names_