Optimization (최적화)

학습에 있어서 중요한 것은 틀리지 않은 방향으로 학습하는 것.

loss function의 최솟값을 찾는 것이 학습의 목표.

최솟값을 찾아가는 과정 : 최적화(optimization)
이 과정을 행하는 알고리즘 : 최적화 알고리즘(optimizer).

Objective vs Loss vs Cost
Objective function : 학습을 통해 최적화시키려는 함수.
Loss function : single input에 대한 $y$와 $\hat{y}$ 사이의 오차를 계산하는 함수.
Cost function : entire input에 대해서 오차를 계산하는 함수.

즉, Objective ftn > Loss ftn > Cost ftn

---

---

Gradient Descent

경사(Gradient)가 가파른 방향으로 이동하여 최솟값을 찾는 알고리즘.
목적함수 $J(\theta)$의 최소화.

$\theta_{t+1}=\theta_t-\eta\times\nabla_{\theta} J(\theta)$ where $\eta$ is a learning rate.

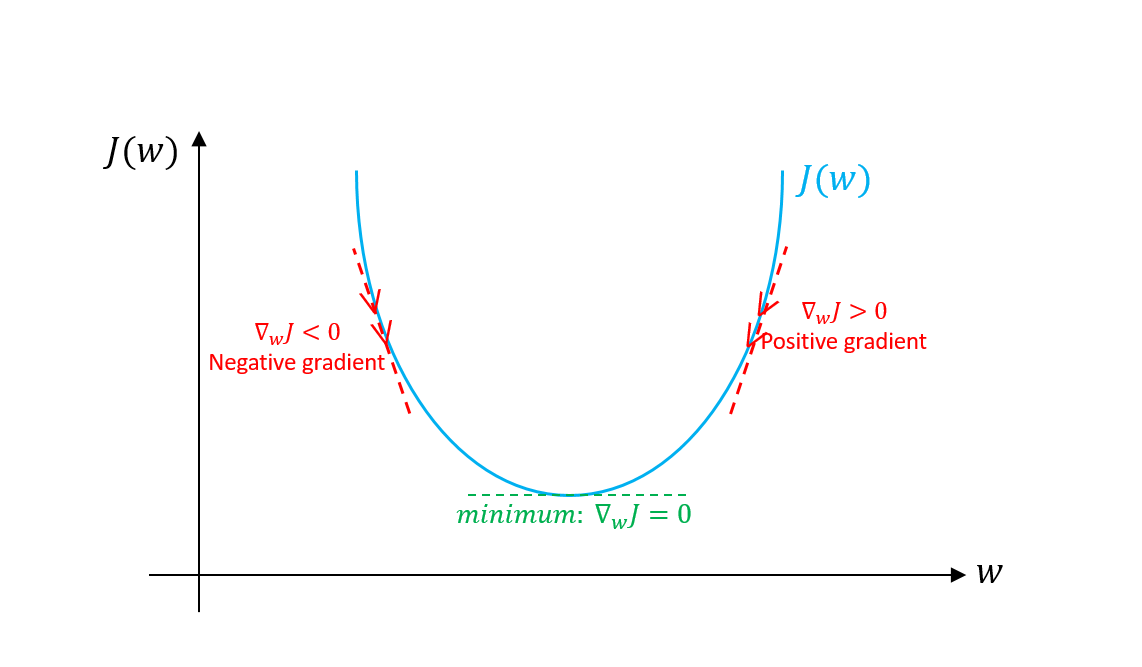
Gradient $\nabla_{\theta}J(\theta)$를 빼줌으로써 최솟값을 찾음.

Learning rate $\eta$
$\eta$가 작다면 수렴 속도가 느려짐.
$\eta$가 크다면 minimum을 지나쳐버릴 수 있고 발산할 수도 있음.

1) Batch Gradient Descent (BGD)

전체 학습 데이터를 하나의 batch로 묶어 학습.
전체 data set에 대한 error의 평균을 구하여 Gradient 계산.

장점
업데이트 횟수가 적음. (1 epoch당 1회 업데이트)
안정적인 수렴.

단점
학습이 오래 걸림.
local minimum에 빠지기 쉬움.

2) Stochastic Gradient Descent (SGD)

전체 학습 데이터 중 단 하나의 데이터를 이용하여 학습.
전체 data set 중 랜덤하게 하나의 데이터를 학습하므로 확률적.

장점
적은 데이터로 학습 가능.
1회 학습이 빠름.
local minimum에 잘 빠지지 않음.

단점
불안정적인 수렴.
saddle Point에서 학습 종료.

3) Mini-batch Gradient Descent (MGD)

BGD와 SGD의 절충안.
전체 학습 데이터를 batch size개로 나누어 학습.

장점
계산량이 BGD보다 적으므로 학습이 상대적으로 빠름.
SGD에 비해 정확도가 높음.
local minimum을 어느정도 피할 수 있음.

Mini-batch size
전체 데이터 크기를 n
1) Mini-batch size = n : Batch Gradient Descent
2) Mini-batch size = 1 : Stochastic Gradient Descent
3) Mini-batch size < m : Mini-batch Gradient Descent

---

Momentum

SGD의 gradient descent의 이동 과정에서 '관성' 부여.
과거의 이동 과정을 기억하여 추가적 이동.

$m_t=\gamma m_{t-1}+\eta\nabla_{\theta_{t}}J(\theta_{t})$, $\gamma∈(0,1)$

$∴\theta_{t+1}=\theta_t-m_t$
($\gamma$는 gradient가 0일 경우, 서서히 줄어드는 역할. 주로 $0.9$.)

장점
관성을 이용하여 local minimum이나 saddle point에서 벗어남.

단점
overshooting.
$\theta$ 이외에도 과거의 관성을 저장해야하므로 메모리가 두 배 필요.

---

Nesterov Accelerated Gradient (NAG)

Momentum 방식을 기초로 하되, 미래를 먼저 보고 현재의 관성을 조절하여 학습.
overshooting을 막기 위해 미래를 먼저 가서 overshooting된 만큼 조절.

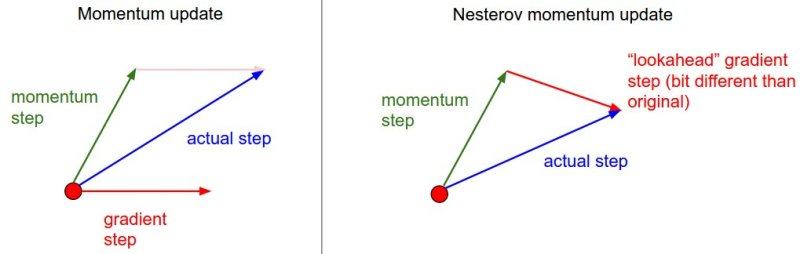
Momentum Update
momentum step ($\gamma m_{t-1}$)과 gradient step ($\eta\nabla_{\theta_{t}}J(\theta_{t})$)의 독립적 합산.

NAG Update
momentum step ($\gamma m_{t-1}$)을 먼저 이동한 후, 그 위치에서의 gradient step ($\eta\nabla_{\theta_{t}}J(\theta_{t}-\gamma m_{t-1})$)만큼 이동.

Why $\eta\nabla_{\theta_{t}}J(\theta_{t}-\gamma m_{t-1})$ ?
$\theta_{t+1}=\theta_t-m_t$ (미래)의 위치에서 gradient 계산.
$m_t$를 알지 못하므로 $\gamma m_{t-1}$ 사용.
즉, $\theta_t-\gamma m_{t-1}$.

$m_t=\gamma m_{t-1}+\eta\nabla_{\theta_{t}}J(\theta_{t}-\gamma m_{t-1})$, $\gamma∈(0,1)$

$∴\theta_{t+1}=\theta_t-m_t$

장점
관성에만 의존하지 않고 momentum 방향으로 이동한 후, 방향을 결정.

---

AdaGrad (Adaptive Gradient)

SGD, Momentum, NAG는 모든 params에 동일한 learning rate 적용.
이는 sparse한 경우 비효율적.
⇒ params의 이전 gradient를 저장.
⇒ 각 params에 따라 step size를 다르게 함.

$\theta_{t,i}$ : $t$번째 step의 $i$번 param
$g_{t,i}=\nabla_{\theta_t}J(\theta_{t,i})$
$G_{t,i}=g_{1,i}^2+g_{2,i}^2+\ ···\ +g_{t,i}^2$ (곡면의 변화량)

$∴\theta_{t+1,i}=\theta_{t,i}-$$\eta\over(G_{t,i}+\epsilon)^{1/2}$$g_{t,i}$

변화 ($g_{t,i}$)가 적음 ⇔ $G_{t,i}$↓ ⇔ step size↑
변화 ($g_{t,i}$)가 큼 ⇔ $G_{t,i}$↑ ⇔ step size↓

단점
$t$가 증가할수록 $G_{t,i}$도 증가하므로, step size가 작아져서 learning rate가 소실.

---

RMSProp

Adagrad의 경우 learning rate 소실.
⇒ $G_{t,i}$를 지수 가중 이동평균으로 대체 (hyper param $\beta$).
⇒ learning rate가 소실되지 않으며, 상대적인 크기 유지.

$E[g^2]_t=\beta E[g^2]_{t-1}+(1-\beta)g_t^2$
($E[g^2]_t$는 $G_t$의 가중 이동 평균; 최근 곡면의 변화량)

$∴\theta_{t+1}=\theta_t-$$\eta\over(E[g^2]_t+\epsilon)^{1/2}$$g_t$

지수 가중 이동평균
$E[g^2]_t=\beta E[g^2]_{t-1}+(1-\beta)g_t^2$ ($\beta$는 주로 $0.9$)
$=\beta^{t-1}E[g^2]_1+(1-\beta)(g_t^2+\beta g_{t-1}^2+\ ···\ +\beta^{t-1}g_1^2)$
최근 변화 ($g_t^2$)는 많이 반영, 오래된 변화 ($\beta^{t-1}g_1^2$)는 적게 반영.

변화 ($g_t$)가 적음 ⇔ $E[g^2]_t$↓ ⇔ step size↑
변화 ($g_t$)가 큼 ⇔ $E[g^2]_t$↑ ⇔ step size↓

단점
초기 경로의 편향 문제

---

Adam (Adaptive Moment Estimation)

Adam = Momentum (관성) + RMSProp (최근 곡면의 변화량)
즉, $E[g]_t$ (Momentum)과 $E[g^2]_t$ (RMSProp) 업데이트.

Moment
확률변수 $X$의 $n$차 moment : $E[X^n]$

moment 값은 모수이므로 추정 (estimation)해야함.

$m_t=\beta_1m_{t-1}+(1-\beta_1)g_t$ (gradient의 1차 moment)
$v_t=\beta_2v_{t-1}+(1-\beta_2)g_t^2$ (gradient의 2차 moment)

$∴\theta_{t+1}=\theta_t-$$\eta\over(v_t+\epsilon)^{1/2}$$m_t$
이는 학습 초기에 가중치들이 0으로 편향되는 경향.

Why?
$m_0=v_0=0$
$v_1$이 작아지면서 $\theta_1$은 출발 지점 $\theta_0$과 멀어짐.

편향을 보정하기 위해,
$\hat{m_t}=$$m_t\over1-\beta_1^t$, $\hat{v_t}=$$v_t\over1-\beta_2^t$ ($\beta_1=0.9,\beta_2=0.99$ 사용)

$∴\theta_{t+1}=\theta_t-$$\eta\over(\hat{v_t}+\epsilon)^{1/2}$$\hat{m_t}$

---

NAdam (Nesterov-accelerated Adaptive Memoment Adam)

NAdam = Nag + Adam

Nag 변형
$m_t=\gamma m_{t-1}+\eta\nabla_{\theta_t}J(\theta_t)$

$∴\theta_{t+1}=\theta_t-(\gamma m_t+\eta\nabla_{\theta_t}J(\theta_t))$
$∴\theta_{t+1}=\theta_t-m_{t+1}$

Adam 업데이트
$\theta_{t+1}=\theta_t-$$\eta\over(\hat{v_t}+\epsilon)^{1/2}$$(\beta_1\hat{m_t}+$$(1-\beta_1)g_t\over1-\beta_1^t$$)$

---

Reference
[DL] 최적화 알고리즘 - SGD, Momentum, Nesterov momentum, AdaGrad
[DL] 최적화 알고리즘 - RMSProp, Adam
[딥러닝] 딥러닝 최적화 알고리즘 알고 쓰자. 딥러닝 옵티마이저(optimizer) 총정리
Gradient Descent Optimization Algorithms 정리