0. Saturation(포화)

더 이상 변하지 않는 상태.
Back-propagation 시, 가중치가 업데이트 되지 않음.
즉, Vanishing Gradient.

---

1. Sigmoid 함수

$f(x)=(1+e^{-x})^{-1}$
$df/dx=(1+e^{-x})^{-1}\times(1-(1+e^{-x})^{-1})$

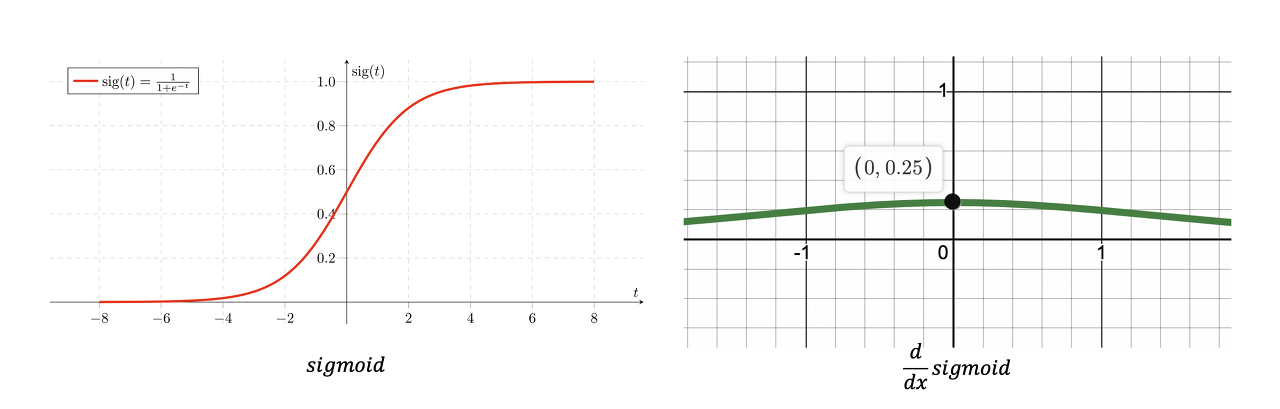
1) Saturation

$x→\infin$ or $x→-\infin$, $df/dx→0$
Back-propagation 시, Gradient가 매우 작아짐.
즉, Vanishing Gradient.

2) Not Zero-centered

그래프의 중심이 $(0,0)$이 아님.

Back-propagation 시, $∂L/∂w=∂L/∂f\times∂f/∂w$
Input : $∂f/∂w=x$ (이전 layer의 output이므로 양수)
즉, $∂L/∂w$와 $∂L/∂f$는 부호가 같음.
zig zag path에 의해 비효율적인 학습.

3) Exponential

exponential 연산은 비용이 많이 들고, 근사값 계산으로 인해 error가 높음.

---

2. tanh

$tanh(x)=(e^x-e^{-x})/(e^x+e^{-x})$

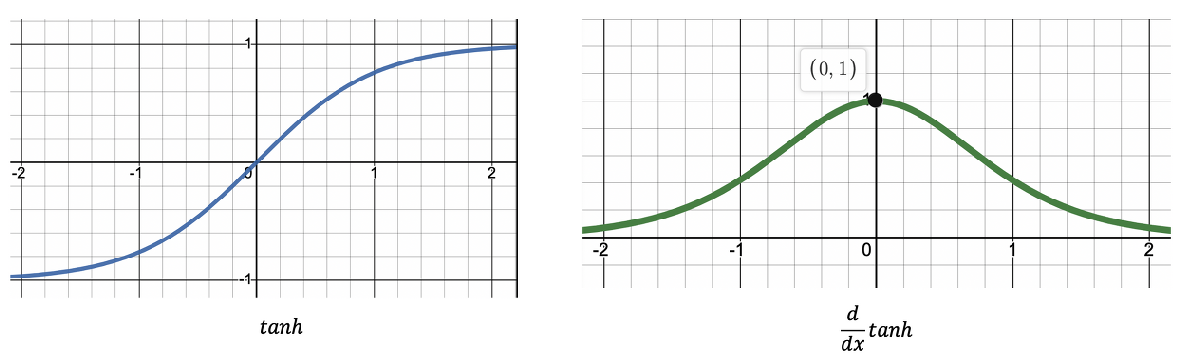
1) Saturation

$x→\infin$ or $x→-\infin$, $df/dx→0$
Back-propagation 시, sigmoid보다는 덜 하지만 Gradient가 매우 작아짐.
즉, Vanishing Gradient.

2) Exponential

여전히 exponential 연산 존재.

---

3. ReLU

$f(x)=max(0,x)$

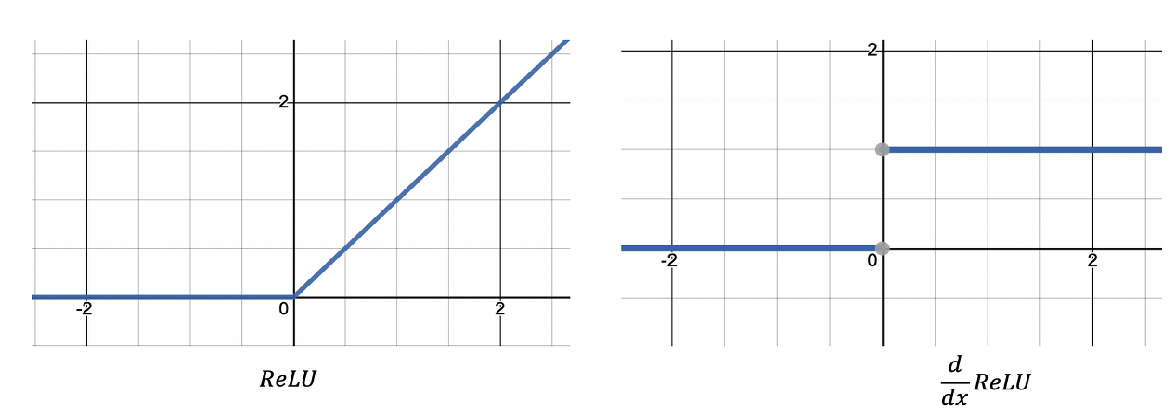
1) Saturation

$x>0$일 때, saturated 하지 않지만
$x<0$일 때는 saturated함.

2) Not Zero-centered

그래프의 중심이 $(0,0)$이 아님.
zig zag path에 의한 비효율적인 학습.

3) Max

기존의 exponential 함수에서 max 함수로 바뀌면서 연산 단순화.

4) Dead-ReLU

---

Reference
[AI] AlexNet (2) - ReLU nonlinearity
[딥러닝] 기울기 소실(Vanishing Gradient)의 의미와 해결방법
[CS231n] Lecture 6. Training Neural Networks I