독립성 검정
분류변수에 대한 검정 중 가장 빈번하게 사용됩니다. 한 모집단에서 두 개의 분류변수가 서로 독립적으로 움직이는지 확인 하기 위해 사용하는 분석법입니다.
2개의 분류변수 혹은 범주변수가 주어진 경우, 관련성을 알아보기 위해서 표로 요약
-> 각 범주변수의 범주값을 가로와 세로에 나열해 교차
-> 교차되는 곳의 관측 도수를 세어서 요약한 표 (교차표,분할표,이원분류표)
table() 함수 또는 xtabs() 함수 이용
카이제곱 검정
한 모집단에서 두 범주형 변수의 관련성 확인을 위해 교차표 또는 분할표로 먼저 요약 후에 이용
동질성 검정
모집단의 범주형 변수가 가지는 분포의 차이 확인
한 모집단에서 두 분류의 변수 관계를 관측
<->
독립성 검정
모집단의 각 행과 열의 변수가 가지는 범주가 나열되어 교차하는 곳에 관찰도수를 카운트
여러 모집단에서 한 분류변수를 측정
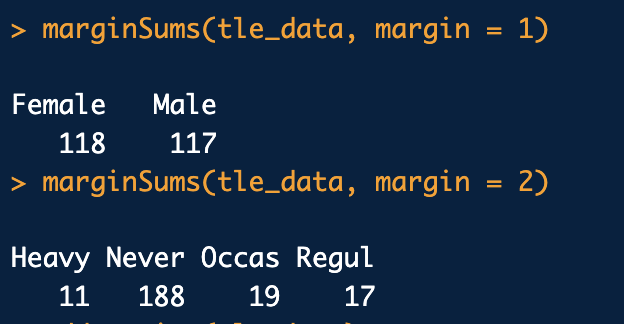
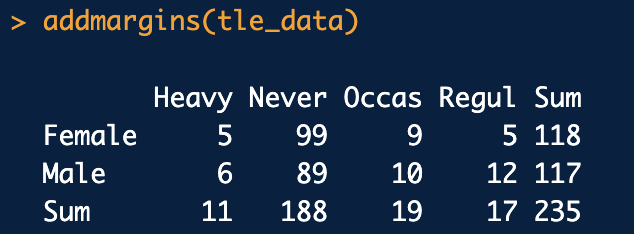
addmargins(tle_data)
행, 열 합계 추가
상관분석
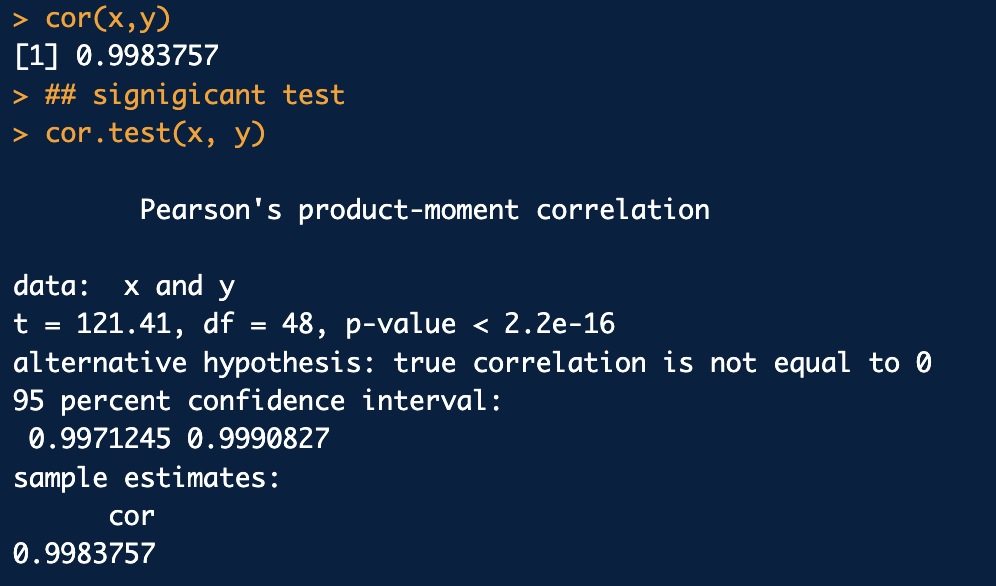
pearson 상관분석 -> 두 변수의 선형성을 본다
두 변수가 모두 수치형 변수인 경우 일반적으로 pearson의 상관계수를 계산합니다.
pearson 상관계수는 대표본이거나 각 변수의 모집단분포가 정규분포인 경우(Xi, Yi)와 같은 순서쌍으로 주어집니다.
표본상관계수를 가지고 모상관계수에 대한 가설검정을 할 수 있음
t분포를 이용하여 유의확룰를 계산 했을 때 유의수준 a보다 작으면 귀무가설 기각
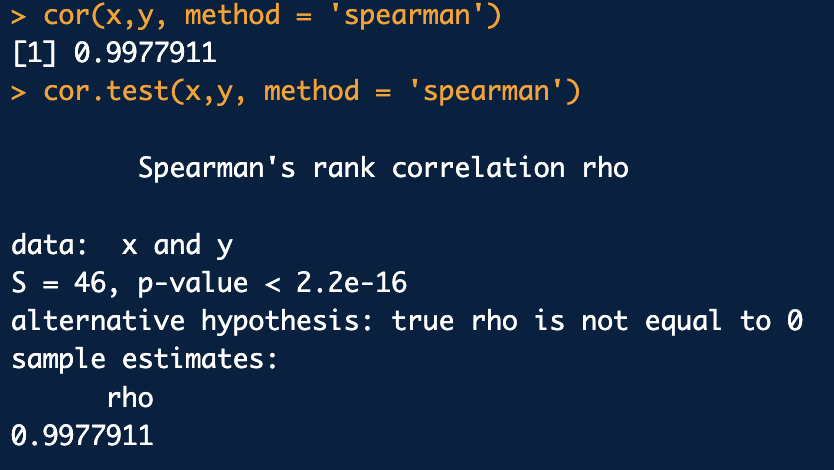
비모수적 상관계수
소표본인데 변수의 분초가 정규분포라고 할 수 없을 때, 각 변수의 순위를 가지고 순위에 대한 pearson 상관계수를 구하는 공식으로 계산
유의성 검정은 pearson의 상관과는 달리 비모수적 검정에 의해 실시함
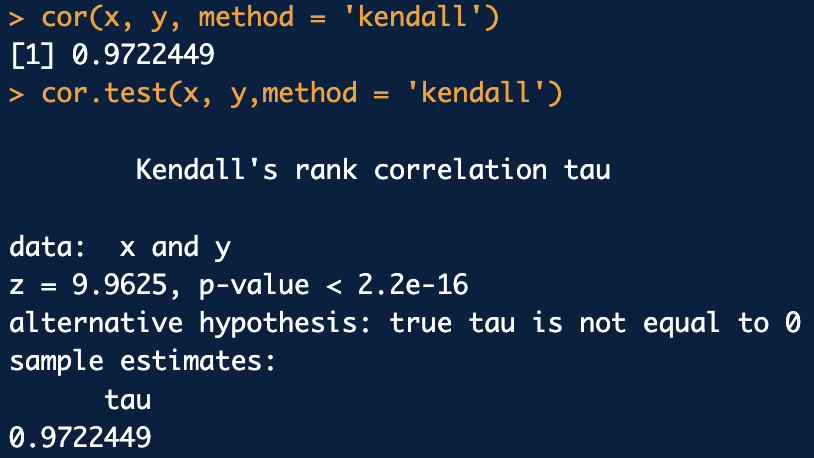
kendal의 타우 -> 두 변수의 순위에 대한 선형성을 본다
spearman 순위상관계수처럼 두 변수 사이의 연관성을 나타내는 비모수적 방법
pearson
spearman
kendal
pairs() 을 통해 산점도 행렬을 그릴 수 있다
pairs( ~ Price + Weight + MPG.city + Length, data = Cars93)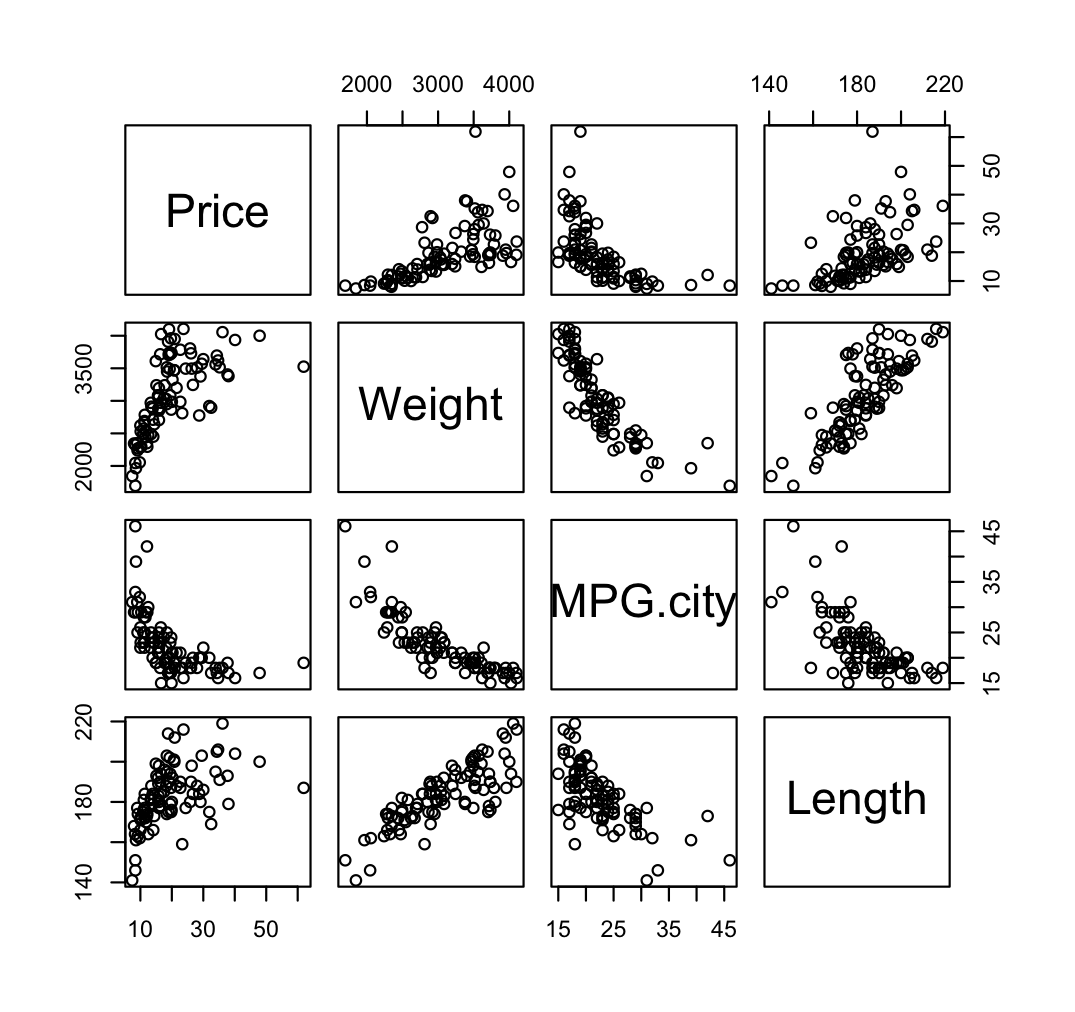
회귀모형
하나의 종속변수를 여러 개의 독립변수가 설명한다고 보는 통계적 모형
회귀모형 설정
선형회귀모형
-> 종속변수 Y가 독립변수들의 선형 함수로 표현
비선형회귀모형
-> 종속변수 Y가 독립변수들의 비선형 함수로 표현
예) 지수함수, 로그함수
종속변수와 독립변수 사이의 선형적인 관계 또는 비선형적인 관계가 있는지 확인할 수 있습니다.
단순회귀모형
독립변수가 한개
다중선형회귀모형
독립변수가 두 개 이상
- 출처 통계청 통계교육원