반복측정 분산분석

반복측정 분산분석

반복요인만 있는 경우

한 개의 요인이 있고 요인이 시간처럼 반복요인이라고 하면, 수치형 종속변수를 측정할 때 한 시험대상은 반복되는 시간마다 종속변수를 관측하게 됨

K명의 실험대상자가 총 r번의 반복마다 종속변수를 측정하여 반복마다가 차이가 있는지 알아볼 경우

반복 요인과 요인 1개가 있는 경우

한 개의 요인 (실험집단, 처리집단)이 있고, 다른 요인은 시간처럼 반복요인이라고 할 경우
-> 수치형 종속변수를 측정할 때 한 시험대상은 반복되는 시간마다 요인간 종속변수를 관측

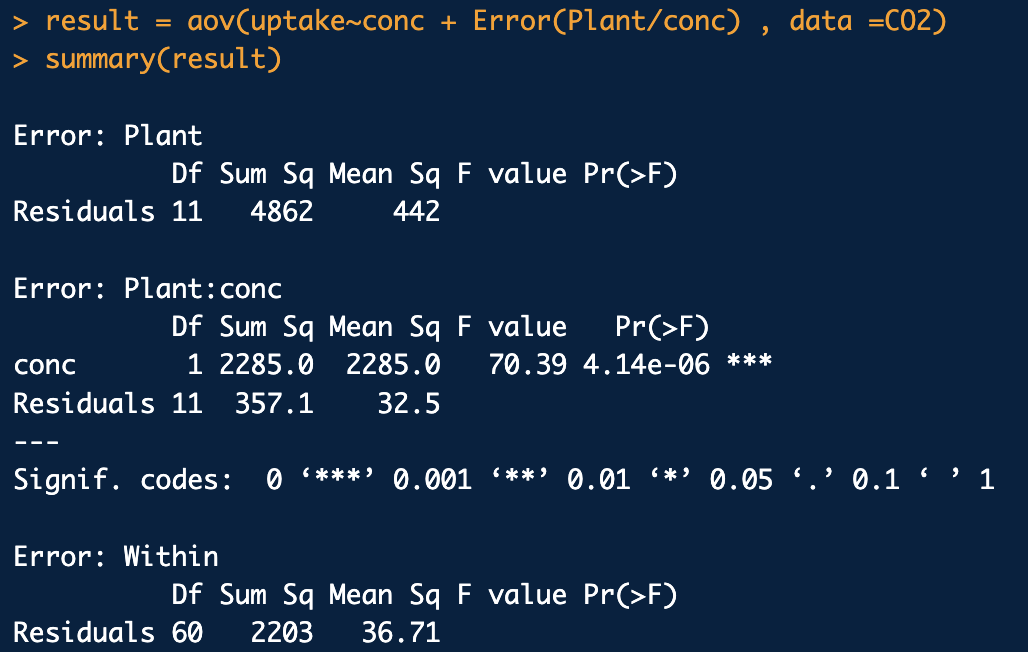
conc factor는 반복측정되므로 오차항에 Error(Plant/conc)로 넣어줘야 함

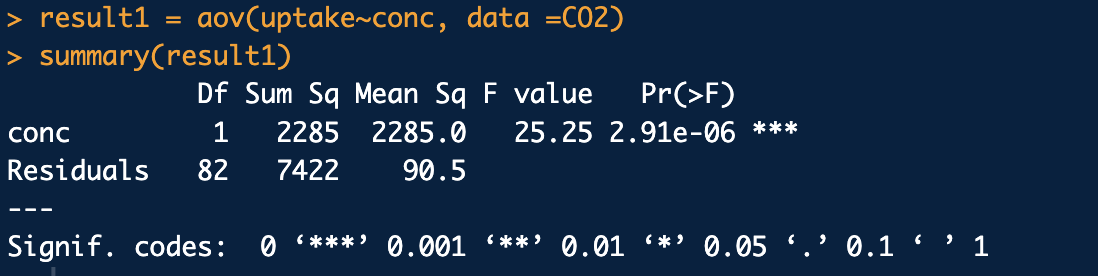
C1-way anova와 차이: MSE = 90.5인 반면, 위의 반복측정분산분석에서는 32.5로 반복측정의 MSE가 더 작으므로 conc의 유의성 검정에서 F값이 더 크므로 검정력이 높아짐

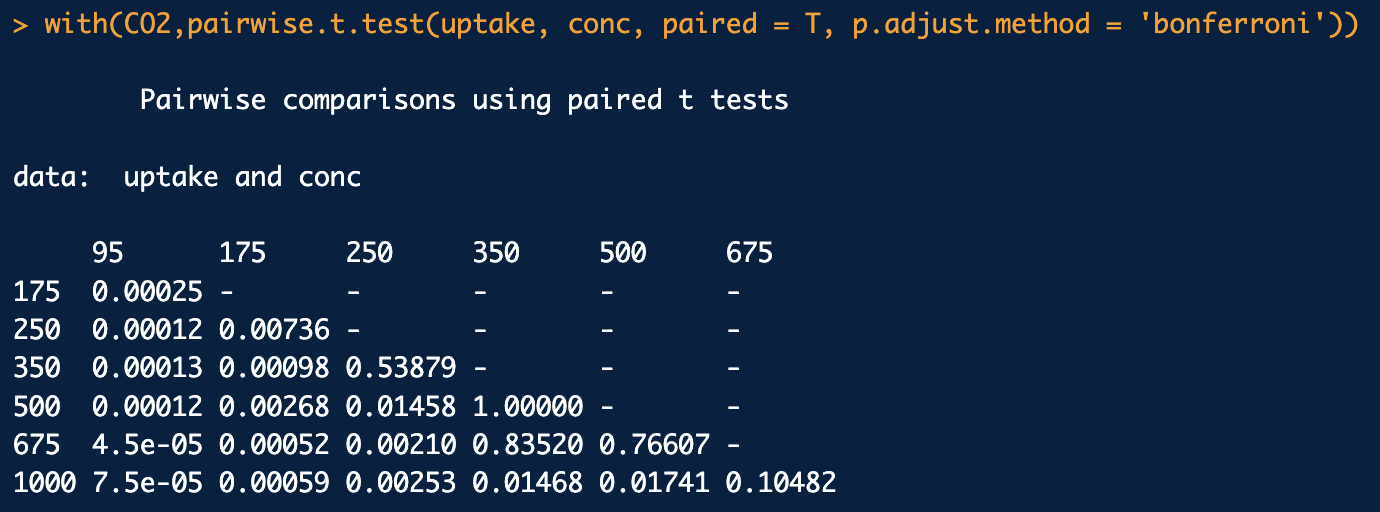
pairwise.t.test() -> 사후 분석

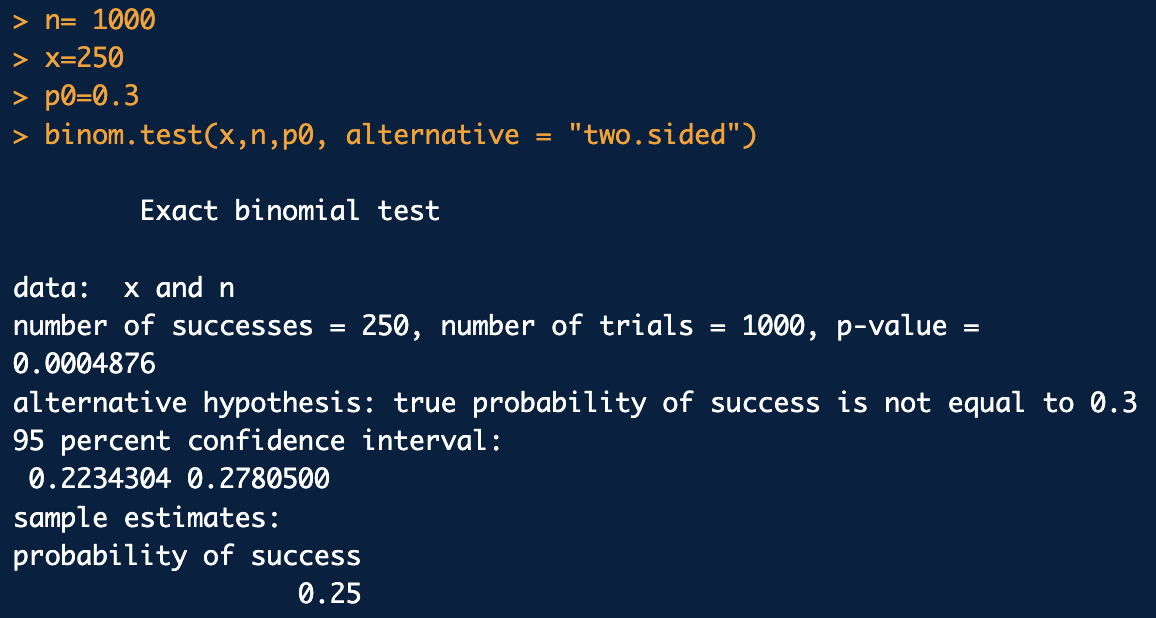
binom.test()함수

이항분포를 이용할 떄

binom.test(x=관측도수, n=표본수, p=p0(귀무가설 모비율), alternative = '대립가설종류')

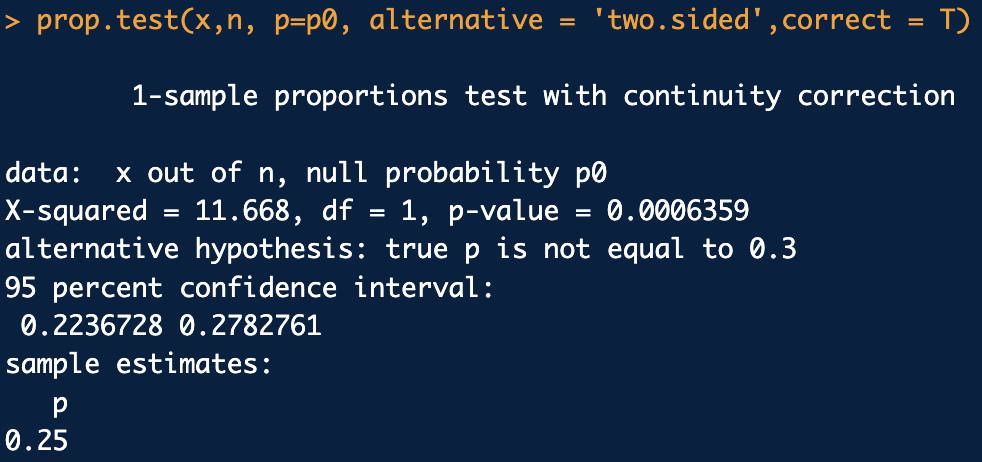
prop.test()함수

이항분포의 정규근사 이용
prop.test(x=관측도수, n=표본수, p=p0(귀무가설 모비율), alternative = '대립가설종류', corret=T)

단일 분류변수에 대한 검정

한 모집단에서 단일 분류변수가 특정 분포를 가지는지에 대한 적합성 검정이라고도 합니다.
분류변수의 범주별 비율이 다를 수도 있고 또 같은 분포를 가질 수도 있음
-> 귀무가설에서 설정하기에 따라 다름
한 모집단에서 단일 분류변수 X는 k개의 범주값을 가지며, 주어진 표본 n개의 자료로부터 관측도수는 다음과 같음
관측도수와 기대도수를 가지고 검정통계량을 생각 할 수 있다.
검정통계량의 분포가 카이제곱 분포를 따르기 때문에 카이제곱 검정한 범주형 변수에 분포에 대한 접합성 검정은 카이제곱 분포를 이용할 수 있다.
검정통계량의 값을 이용해서 유의 확률을 계산 할 수 있다.
관측도수와 기대도수의 차이가 적으면 0에 가까울 것이고 차이가 많을수록 값이 커지게 되어 대립가설을 받아들이게 되므로 오른쪽으로 길게 됩니다.

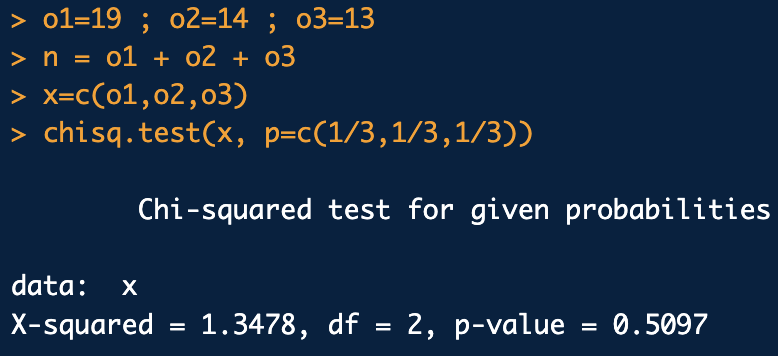
chisq.test()함수

chisq.test(x=범주별관측도수, p=범주별 비율)
chisq.test(x=범주별관측도수, p=범주별 비율,rescale.p,correct)

두 모집단에 대한 단일 분류변수에 대한 검정

두 모집단에 대해서 단일변수의 분포가 동일한지를 알아보는 것을 동질성 검정이라고 합니다.
표본을 뽑을 때 모집단이 2개이기 때문에 서로 다른 모집단에서 각각 동일한 분류변수를 관측하는 것이 차이가 있습니다.
동절성 검정은 한 변수는 모집단을 나타내고 다른 변수는 단일 분류변수를 나타냅니다.

• 출처 통계청 통계교육원