Linear classifiers

Blog 목적

지금까지 CV의 역사 그리고 CV의 핵심 요소 중에 하나로 불리는 Image Classification에 대해서 설명을 드렸습니다.

이번 블로그에선 Neural Network의 기초를 이루는 단순하지만 핵심인 Linear Classifier의 여러 가지 종류와 문제점에 대해서 알아보겠습니다.

모든 사진 출처 : 링크텍스트

---

Linear classifier

*위의 그림처럼 여러 개의 linear classifier들이 쌓여서 하나의 큰 Neural Network를 만듭니다.

Parametric Approach

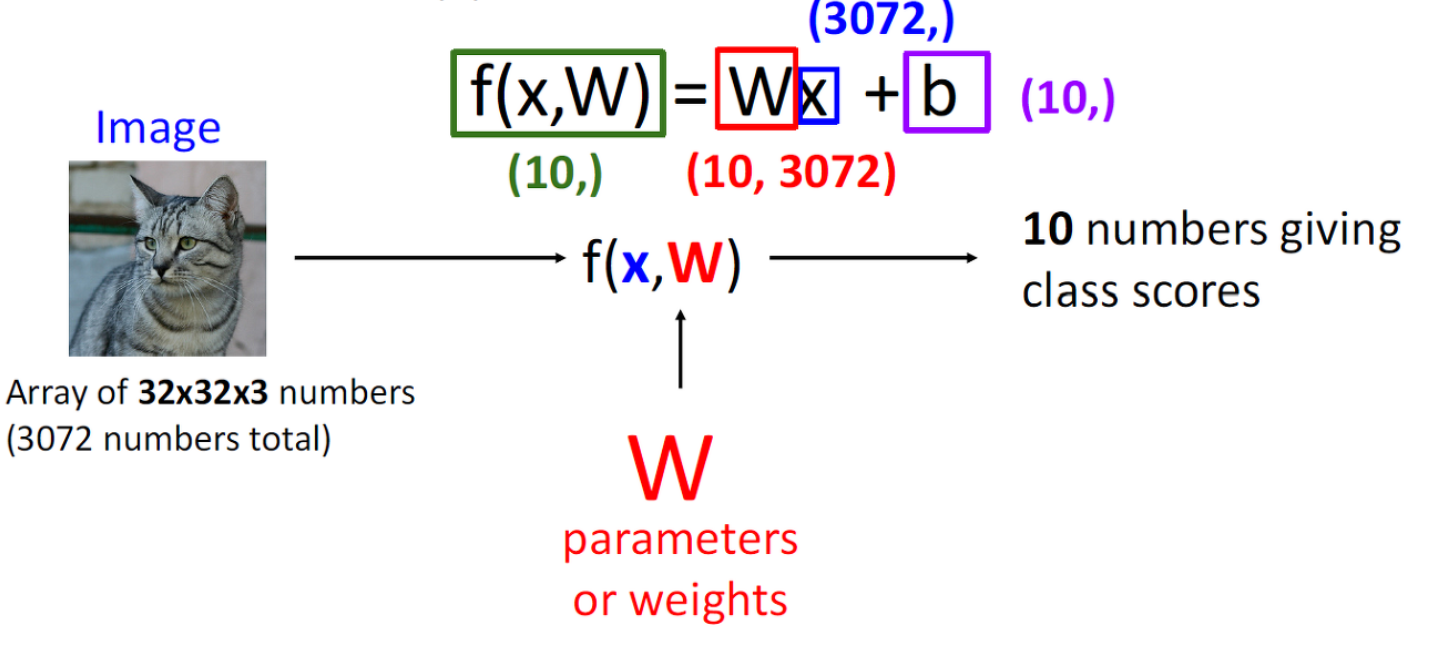
• K-Nearest Neighbor(KNN)은 input Image만 분류 과정에서 활용했지만, Linear Classifier에서는 x(input Image)와 함께 W(parameter weights)가 활용됩니다

• Parametric Approach를 함수 f(x, W)로 표현할 수 있어서, 이 함수의 출력 값은 분류하고 싶은 대상의 가짓수만큼 나오게 됩니다.

  *(EX: CIFAR10의 경우, 10개의 class score가 출력)

• f(x, W) = Wx + b

  • b(bias)는 offset을 뜻하며 생략 가능합니다.

  • Wx는 2차원 Parameter 행렬 W와 입력 이미지를 변환하여 만든 1차원 벡터 x 사이의 행렬곱을 나타냅니다.

    *1차원 벡터 x는 이미지의 spatial structure는 변환 과정에서 잃어버린 상태이다.

    EX) 32 x 32 x 3 -> 3072 x 1

*사진으로 보는 예시

---

Linear Classifier를 이해하는 관점들

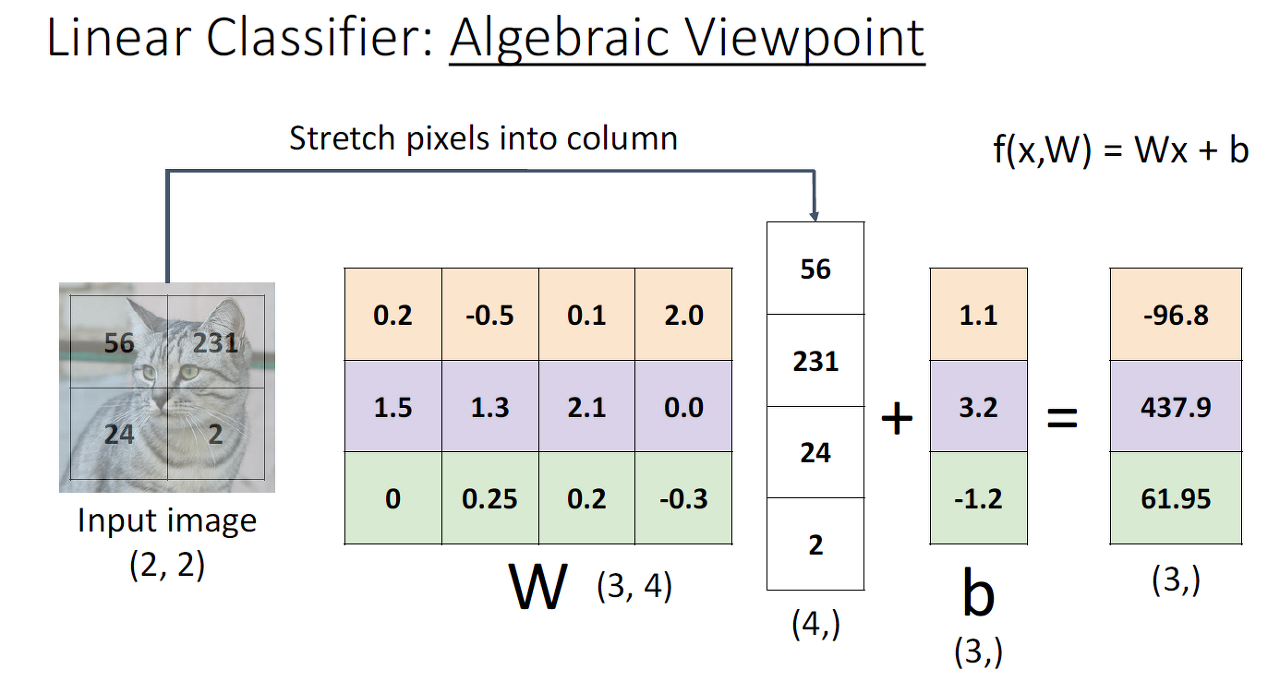
Algebraic Viewpoint

Linear Classifier를 단순히 행렬과 벡터의 곱에 b(offset) 벡터를 더한 것을 말합니다.

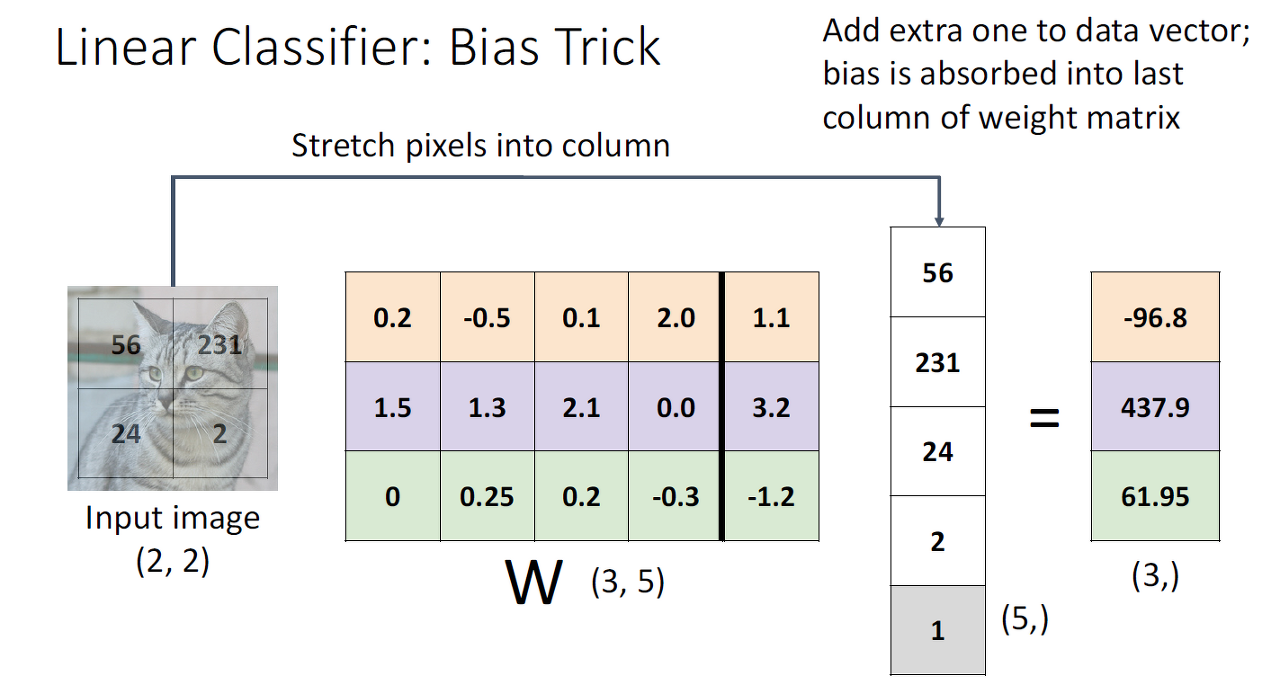
Bias Trick

• Bias Trick는 b를 weight의 마지멱 열로 더해서, data vector의 마지막 원소로 1을 추가하므로, b(offeset)을 더 추가적으로 하지 않고 곱하기만 하여도 간단한 계산이 가능합니다.

  
  

• 이 방식은 장단점이 있는데, 장점은 1차원 벡터에서는 유용한 것이고 단점은 ConvNet등과 같이 복잡한 경우 사용하기 어렵고 weight와 bias가 서로 다른 방식으로 regularize 혹은 initialize를 한 경우에는 적용이 되지 않는 어려움을 갖게 됩니다.

Predictions are Linear

• 신기한 점은 Linear classifier의 결과가 Linear한 결과를 나타내는 것입니다.(이름값을 한다는 점이요)

• 추가적으로, linearity로 인해 분류 결과는 달라질 가능성이 있으나 적절하게 손실함수(loss function)을 사용하는 방법을 통해서 대처가 가능합니다.

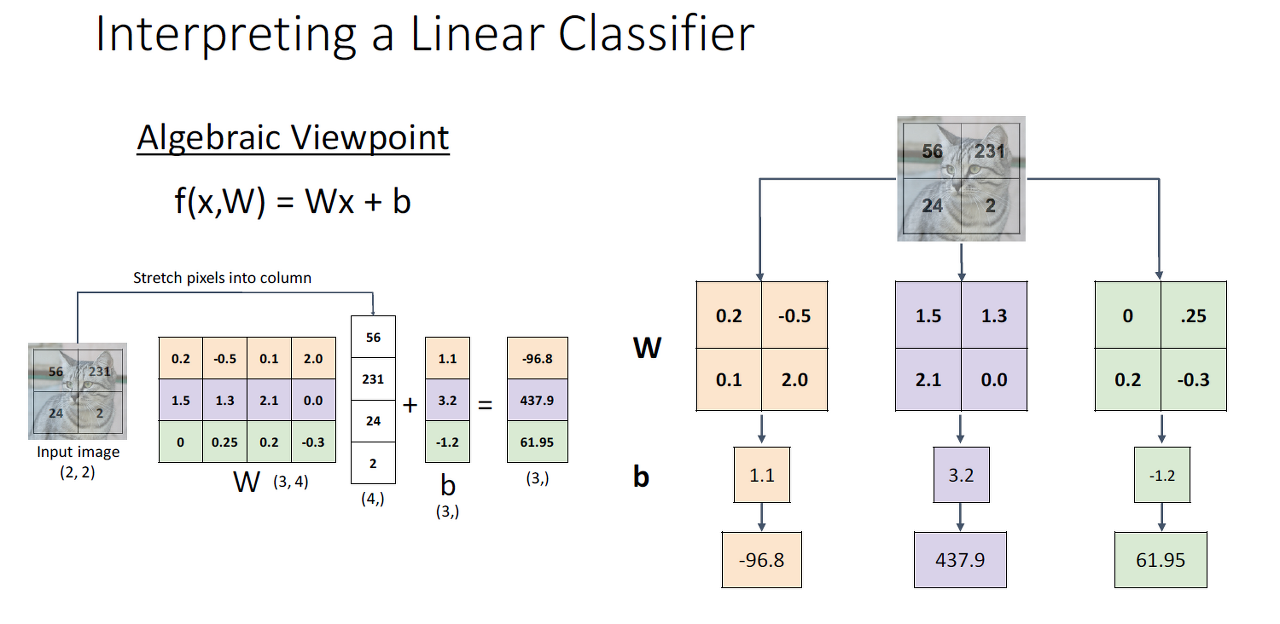
Visual Viewpoint

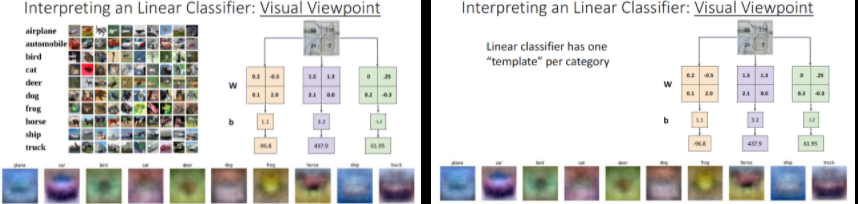
• Visual Viewpoint는 weight의 각 행을 입력 이미지의 크기로 변환하고 및 이미지와 내적을 하고, weight의 각 행에 대응하는 b를 더해주는 것입니다.

• 즉, classifier이 weight를 학습하는 것으로 category에 있는 하나의 이미지 탬플릿을 학습하는 것입니다.

• Linear classifier이 Context Cue에 많은 영향을 받습니다.

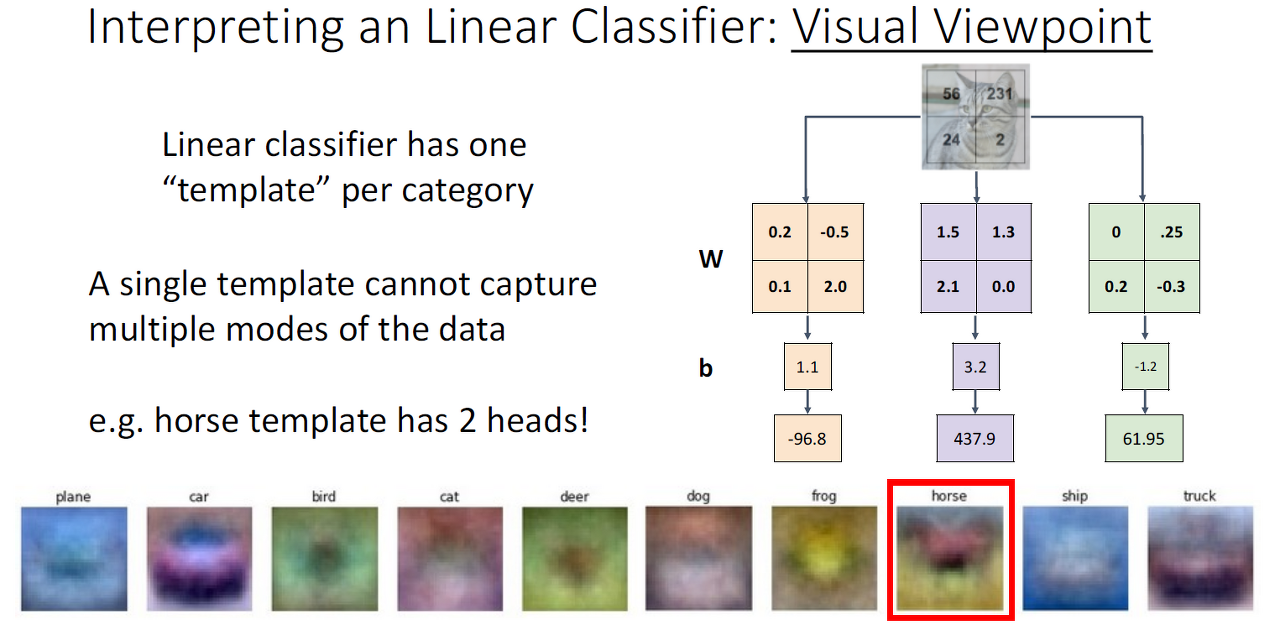
• Linear classifier는 category 당 1개의 탬플릿만 학습 가능하나 이미지 내의 물체가 항상 같지는 않기에 Mode Splitting문제를 이해할 수 있습니다.

Geometric Viewpoint

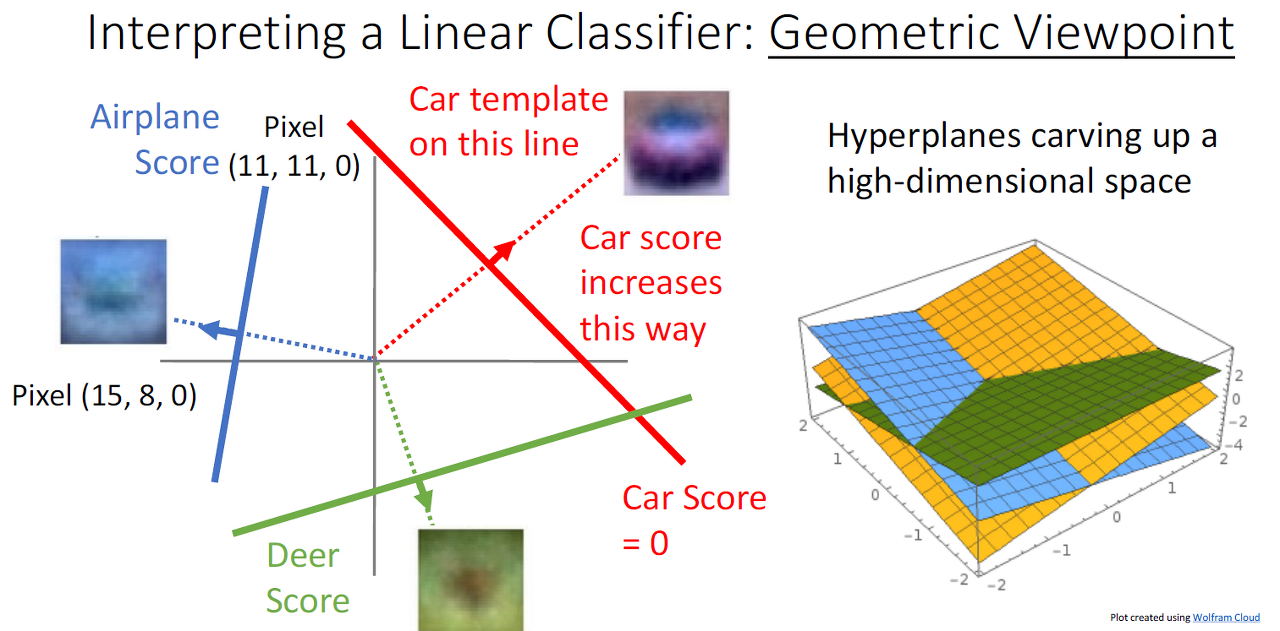
• 이미지는 고차원 유클리드 공간에서 존재합니다.

  
  

• Category는 각 1개의 초평면이 존재하고 이것이 이미지를 2등분한다고 봅니다.

  *초평면: 3차원 공간 속의 평면

  
  

  해결 방법

  Feature Transforms

  

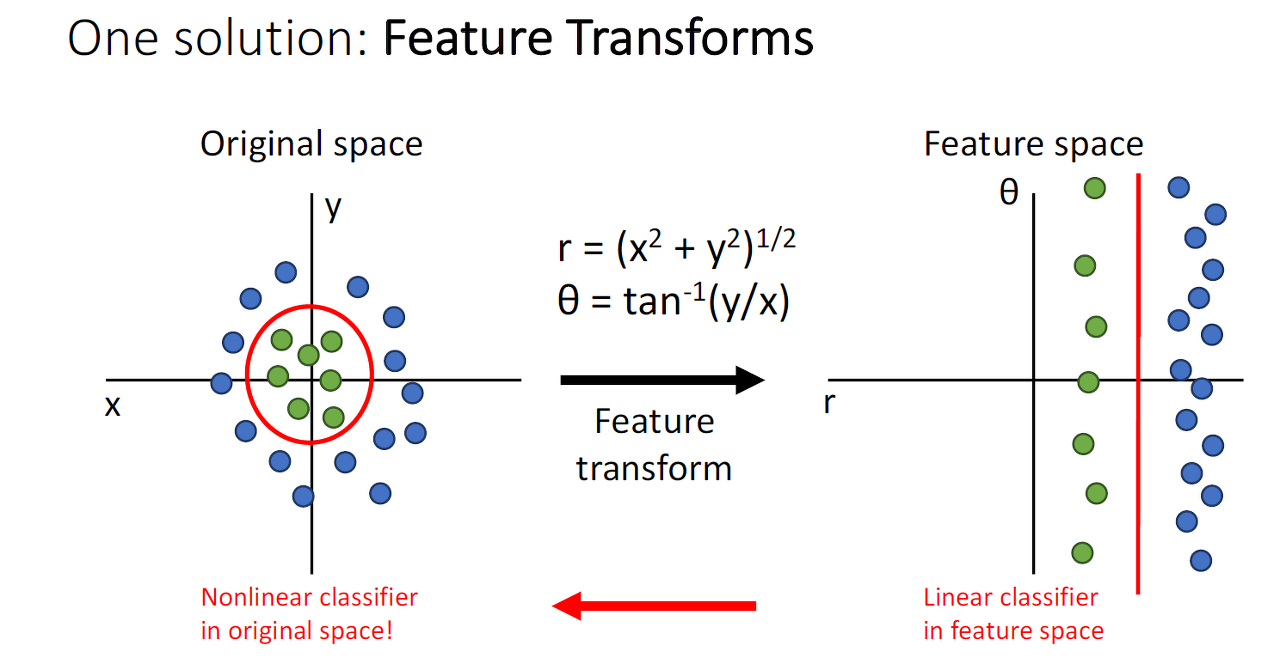
그림처럼 특성을 변형시키는 것으로 Geometric viewpoint나 visual point의 문제를 해결은 할 수 있으나 고차원 데이터에서는 더 많은 조건들을 고려해서 사용해야합니다.

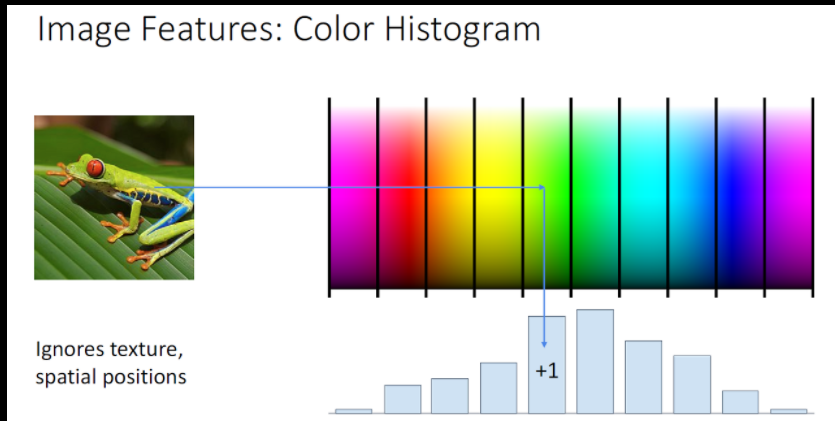
대표적인 예시로, Color Histogram로 색상의 빈도를 통해 히스토그램 그래프를 만들어서 이미지를 분석합니다. 이를 통해 기존의 이미지 속 객체 각도 혹은 위치가 달라지는 문제를 해결할 수 있게 됩니다.

또 다른 예시는 Histogram of Oriented Gradients(HoG)는 local edge를 통해서 이미지 분석을 합니다.

마지막으로, 가장 구현이 간단한 Bag of Words(Data Driven)이 있는데 학습 데이터의 각 이미지 별로 randomly하게 patch를 추출하고 각 patch들에 클러스터링을 한 후에 군집을 이루는 codebook(with visual word)을 만듭니다.

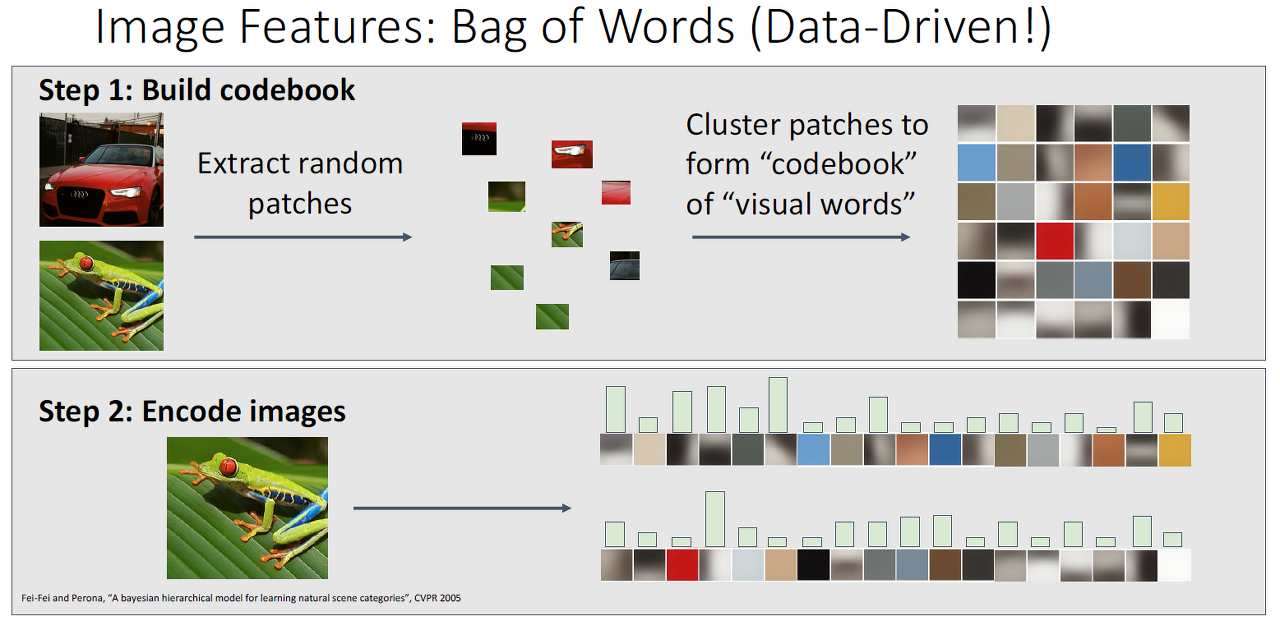
마지막으로, 학습이 끝난 후에 이미지를 입력으로 받으면 어느 정도 visual word가 있는지 히스토그램을 통해 분석합니다.

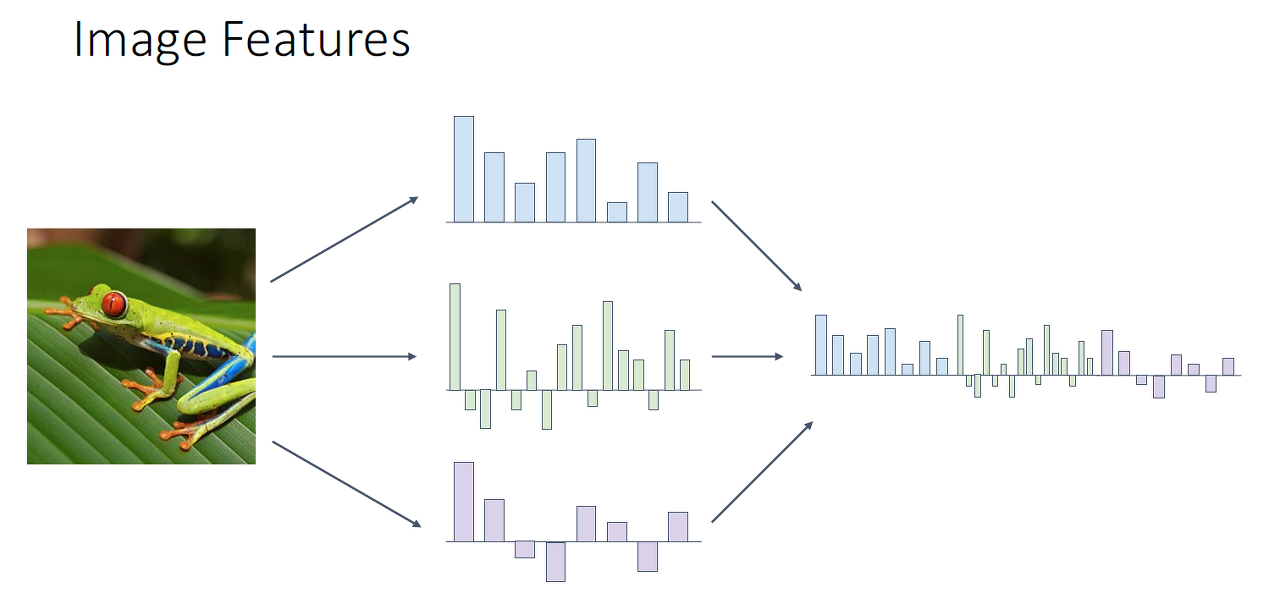
총 정리

고차원 공간에서의 Linear classifier를 3차원임을 완전히 이해하기는 어렵지만, 최소한 Linear Classifier의 장점과 단점에 대해 이해 정도는 할 수 있다고 생각합니다.

---

Linear Classifier의 한계

Hard Cases

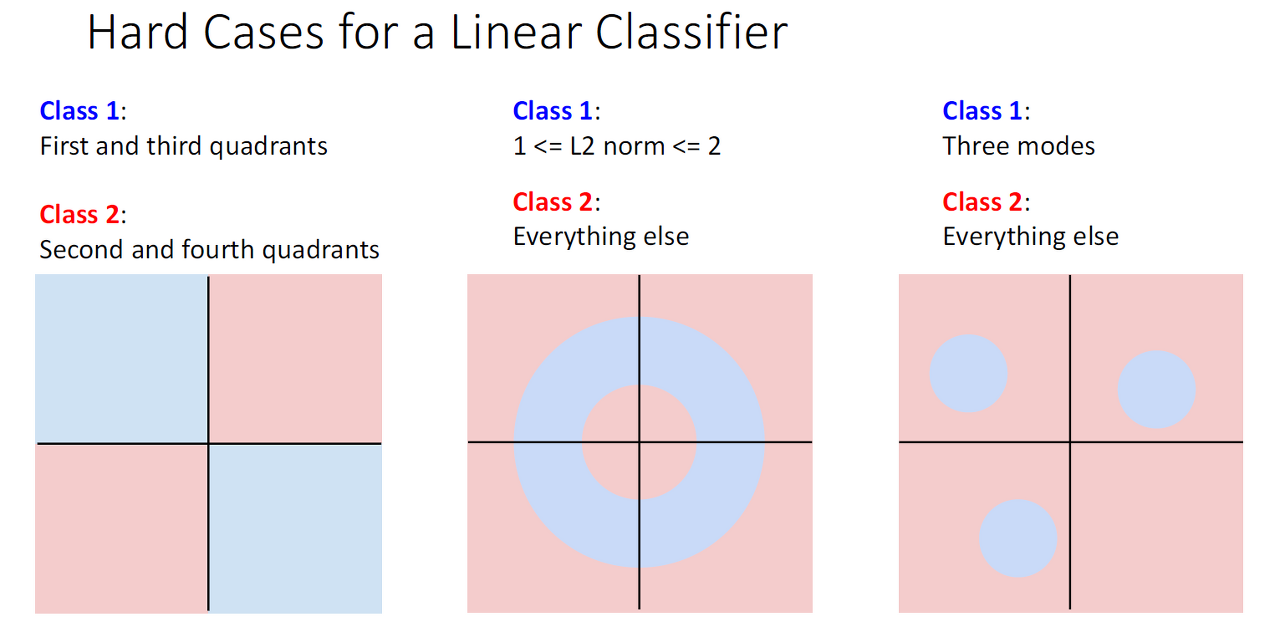
사진의 경우들은 1개의 직선으로 두 개의 클래스를 제대로 분류할 수 없기에 Linear classifier을 사용할 수 없습니다.

XOR

위의 사진은 Perceptron에서 XOR연산을 제대로 수행하지 못하는 것을 보여주는 것입니다.

*Geometric viewpoint

W(weight): Linear classifier의 핵심

알다시피 Linear classifier에서 W를 이용하면 class score를 구할 수 있고 이를 통해서 분류를 하므로 W는 핵심입니다.

---

Loss Function

Loss function은 현재의 클래스를 분류하는 분류기가 좋은 성능을 보여주는지를 알려주는 척도로, 출력값을 loss라 하고 loss와 classifier은 반비례합니다.

왜냐하면, loss가 낮을 수록 classifier의 성능이 좋은 것을 의미합니다.

물론, Loss에 마이너스를 붙이면 loss와 classifier은 비례합니다.

loss는 항상 작아지는 방향으로 W가 학습이 됩니다.

Multiclass SVM Loss

SVM Loss, Loss가 다른 class의 class score와 정답 클래스의 score의 차가 margin보다 크면 0, 아니면 차이에 margin을 더합니다

*보통 margin =1

아래의 사진은 Multiclass SVM Loss의 예시입니다.

추가적으로, SVM Loss의 특징에 대해서 설명합니다.

• margin이 크면, class score가 바뀌더라도 loss가 0이면 계속 0이 됩니다.(by max())

• max연산을 사용하기에 최솟값은 0이고 최댓값은 무한합니다.

• score가 무작위로 나와도 가우시안 분포를 따르게 되면 각 score의 차의 합은 0에 근접하게 됩니다. 그러므로, Loss = (C-1) margin이라는 식이 나옵니다.(C= 클래스 수)

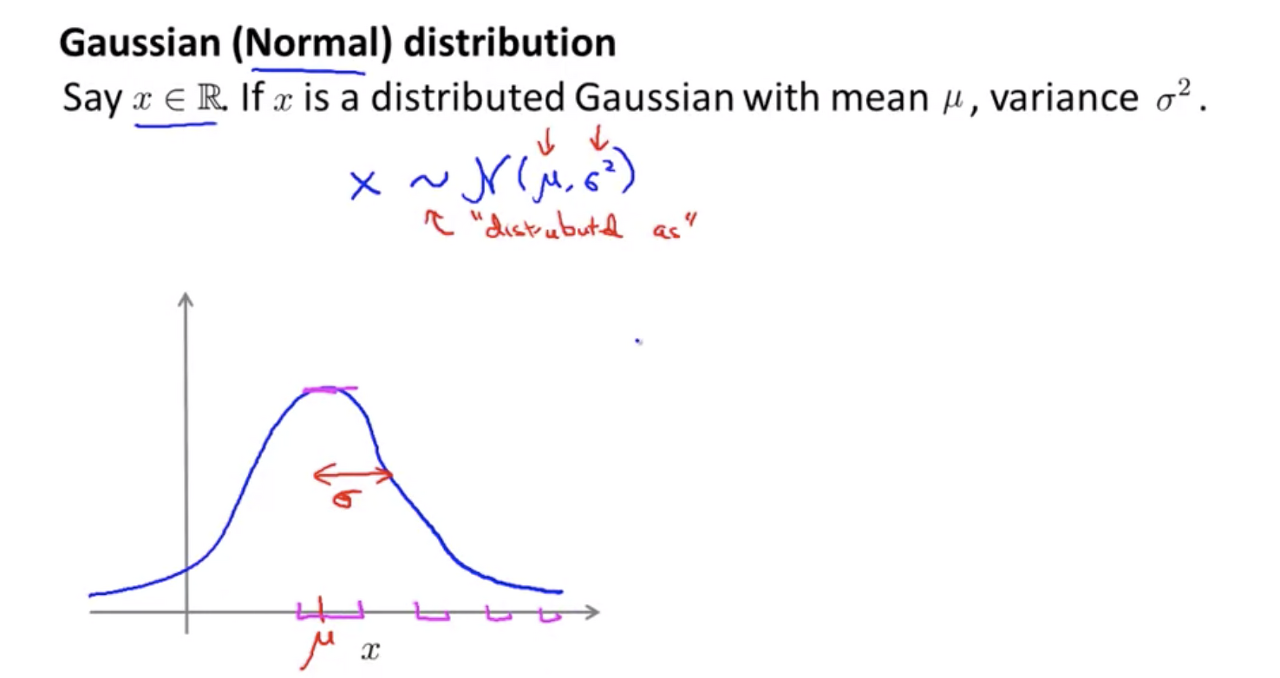
이미지 출처:링크텍스트

• Sum대신 mean을 사용하더라도 loss는 달라지겠지만 결과는 동일합니다.

• Sum대신 제곱을 취하면 선형성을 잃기에 loss도 달라지고 결과도 달라집니다.

• W는 유일한 것이 아니고 여러 개입니다.

Regularization

간단하게 Regularization을 설명해보면, 정의는 모델의 오버피팅을 방지하는 방법입니다.

Linear classifier에서 사용을 할 때는 data loss + regularization(with lambda:hyperparameter)을 추가하여 사용을 합니다.

다양한 regularization중 linear classifier에서는 주로 Dropout, batch normalization이 사용됩니다.

실제로는 overfitting뿐만 아니라 다양한 효과가 있고 이제 그것들을 알아봅니다.

Expressing Preferences

• L1 regularization은 각각의 feature들이 서로 연관이 되기에 특정 feature를 고르기 어려운 경우에 사용이되고, 그 결과 하나의 feature에 weight가 몰립니다.

• L2 regularization은 각각의 feature들이 서로 연관이 되기에 특정 feature를 고르기 어려운 경우에 사용이되고, 그 결과 모든 feature의 weight가 균등합니다.

Prefer Simpler Models

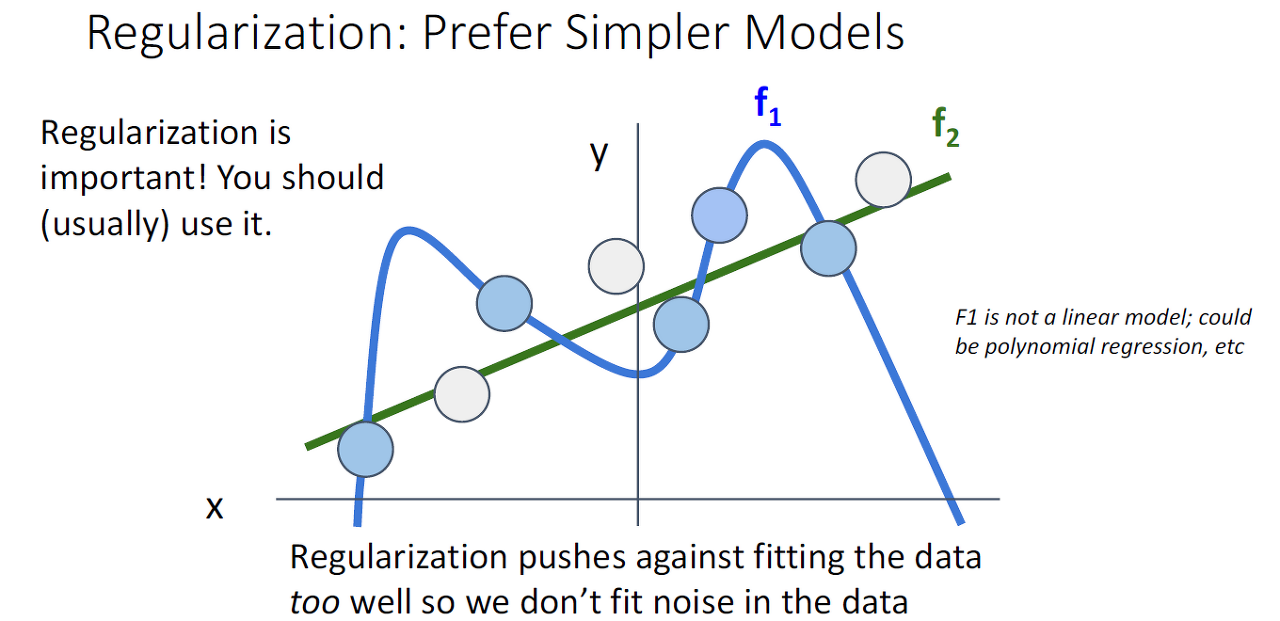
그림을 설명하면, f1은 학습 데이터(파란색)에 적합한 모델이고 f2는 그렇지 않습니다.

그렇기에 학습이 되지 않은 데이터(회색)이 들어오면 f2가 f1보다 대응을 잘할겁니다.

실제 데이터의 수가 학습 데이터(파란색) > 예측 데이터(회색)인 경우는 많지 않으므로
학습 데이터에 적합한 모델(f1)보다 여러 데이터에 유연한 대체가 가능한 모델(f2)가 필요합니다.

Cross-Entropy Loss(Multinomial Logistic Regression, 두 가지 확률 비교)

이 Loss는 raw classifier score를 확률로 활용하기 위한 방식으로 Softmax function을 사용합니다.

Softmax는 일반적인 max함수처럼 최댓값이 1 혹은 0으로 극단적이지 않는 함수입니다.

*process of raw classifier score to get probabilities

추가적으로, Cross-Entropy Loss의 특징에 대해 설명해드립니다.

• min loss: 0에 수렴, max loss: + inifinity

• score가 가우시안 분포를 따르면 log(C)입니다.

SVM Loss 와 Cross-Entropy Loss 차이점 정리

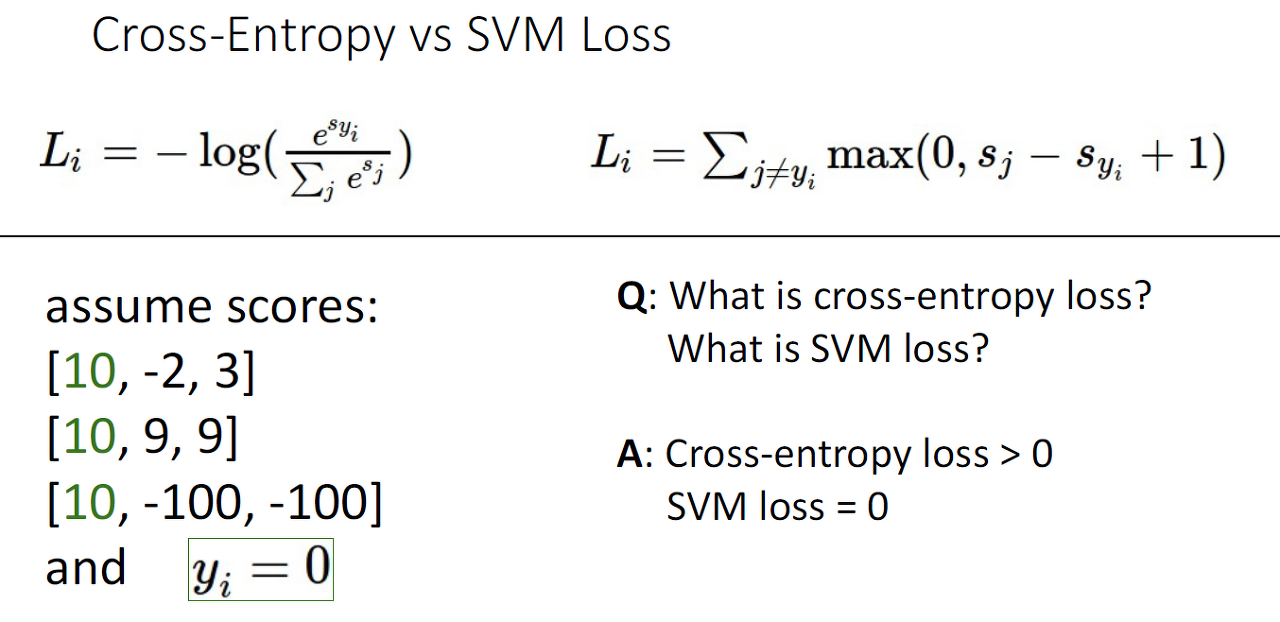
• SVM Loss는 score가 margin 1이상이기에 0입니다.

• Cross-Entropy는 0보다 큽니다.

• Score의 변동 시, SVM Loss는 margin과 score차이가 존재하므로 없습니다.

• Score의 변동 시, Cross-entropy는 변할 겁니다.

• correct class score * 2, Cross- Entropy loss는 감소합니다.

• correct class score * 2, SVM Loss는 Margin과 score의 차이가 점점 커지므로 0입니다.(max함수)

  이제, Linear classifier이 끝났고 다음에는 Optimization블로그로 만나뵙겠습니다.