Blog목적
이번 블로그에서는 최적화에 대해서 알아보겠습니다.
Linear classifier에서 w를 최적으로 찾는 방식에 대해서 알아보도록 하겠습니다.
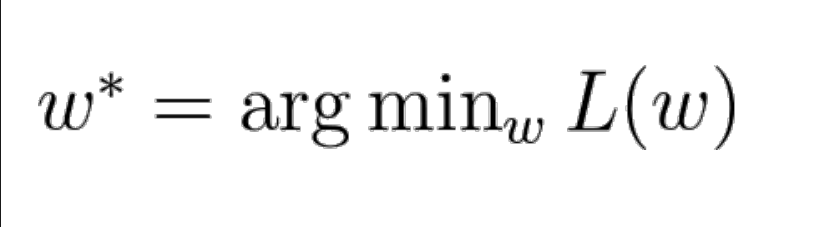
이미지 출처: 링크텍스트
Optimization
이미지 출처: 링크텍스트
- Optimization은 최적의 w를 찾는 것이 아닌 loss를 최소화하는 w를 찾는 것입니다.
- 목적함수의 함수값(최댓값, 최솟값)을 최적화 시키는 파라미터를 찾는 것입니다.
ex) 카메라 초점거리 찾기. 사람의 관절 움직임 관찰하는 모델링,...등등
How to change W
Random Search
-
기준없이 무작위하게 W를 변경하는 것입니다.
-
Loss의 개선 여부로 W를 갱신합니다.
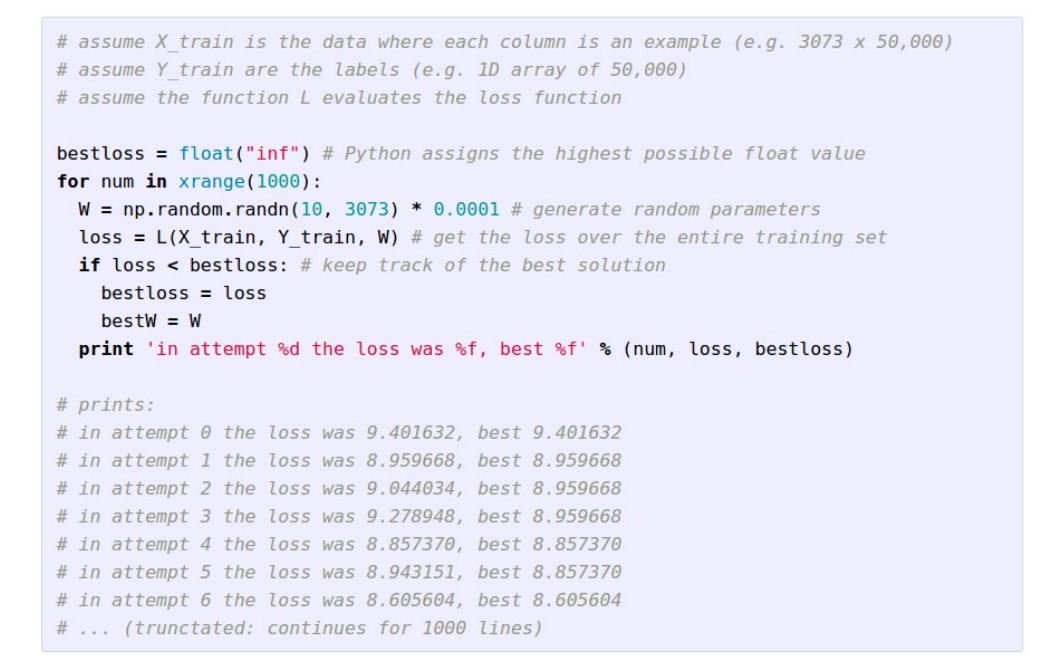
- CIFAR 10으로 실험했을 때 15.5%라는 좋지 않은 결과를 냅니다.

- 즉, Bad Idea입니다.
Flow the slope
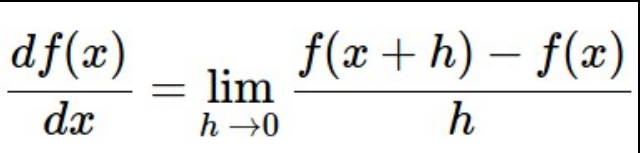
-
손실함수를 따라서 최적의 W를 찾는 방법입니다.
-
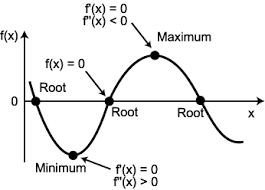
손실함수가 1차원이면 도함수를 이용하면 됩니다.
-
손실함수가 1차원이 아니면 gradient를 이용합니다.
-
gradient는 각 차원을 따르는 백터입니다.
-
slope의 방향은 각 gradient의 방향을 내적한 것입니다.
-
steepest descent의 방향은 negative gradient입니다.
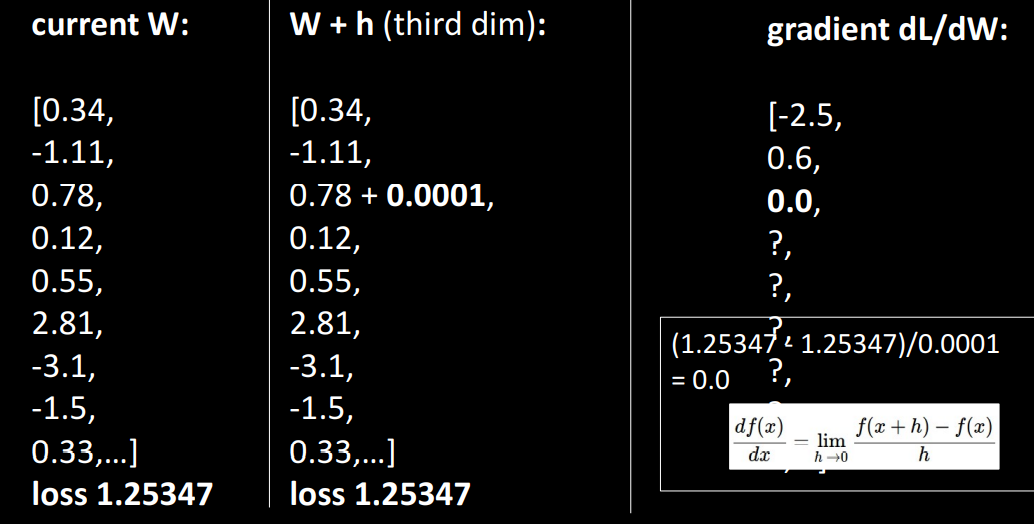
Numeric Gradient

-
Gradient를 구하는 방법입니다.
-
벡터 W에서 요소를 1개씩 번갈아서 각 요소에 대응하는 gradient를 구할 수 있게 됩니다.
-
계산 횟수가 W의 크기에 비례하기에 W가 크면 좋지 않은 성능을 보입니다.
Analytic Gradient

- 미분을 이용하여 gradient를 구합니다.

- 정확하지만 복잡하여 구현 실수가 일어납니다.
총 정리
-
Numeric gradient: 근접성, 느림, 쓰기 편함
-
Analytic gradient: 정확함, 빠름, error-prone
-
Analytic gradient개발 시 구현의 실수가 있는지를 확인하기 위해 Numeric Gradient를 사용하여 gradient check를 합니다.


Gradient Descent

Graient descent는 gradient를 활용해서 더 작은 loss를 갖는 w를 찾는 방식입니다.
Hyperparameter
-
W(weight) 초기화
-
W를 찾는 횟수
-
step 시 이동할 거리(learning rate), lr이 높으면 최적의 W를 빨리 찾지만 overshoot문제가 생기고 lr이 낮으면 오래 걸립니다.
즉, W의 변화량과 gradient는 비례 관계입니다.
Batch Gradient Descent
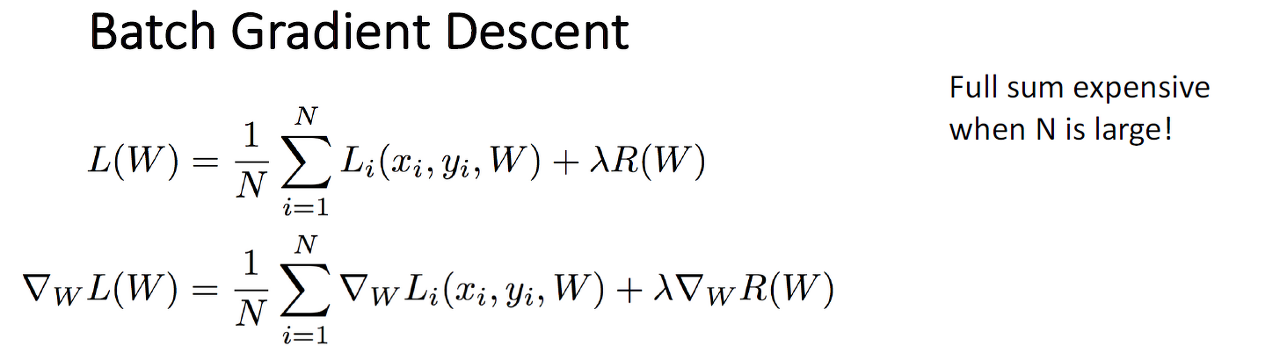
사실 loss가 데이터의 합으로 이루어지는 것처럼 gradient도 데이터의 합으로 있기에 데이터가 많을 수록 비용이 증가합니다.
SGD(Stochastic Gradient Descent)
말했다시피, 많은 수록 비용이 증가하므로 gradient descent를 변형시켜서 사용하는데 그중 대표적인 것이 SGD입니다.

SGD는 데이터에 대해 Gradient와 Loss를 구하는 것에 집중하지 않고 적은 수의 데이터로 구합니다. (* 적은 수의 데이터: minibatch, size:32,64,128)
표본 데이터를 통해서 Gradient와 Loss를 구하므로, 표본 데이터의 분포를 설정할 때 전체 데이터와 유사해야합니다.
즉, 손실함수의 기울기를 계산하여서 이 기울기 값에 학습률(Learning Rate)을 계산 값을 통해서 기존의 가중치 값을 갱신합니다.
- Code
class SGD:
def init(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]출처: https://sacko.tistory.com/42 [데이터 분석하는 문과생, 싸코]
Hyperparameter
-
minibatch
- batch size: minibatch의 크기, GPU의 메모리 크기가 허용하는 한 가장 큰 게 좋습니다
- Data sampling: 데이터 선정 방식, ranking이나 prediction에서 중요합니다.

Problems
Overshoot
기울기가 과하게 진동하면서 더 많은 step이 소요되는 것을 말합니다.
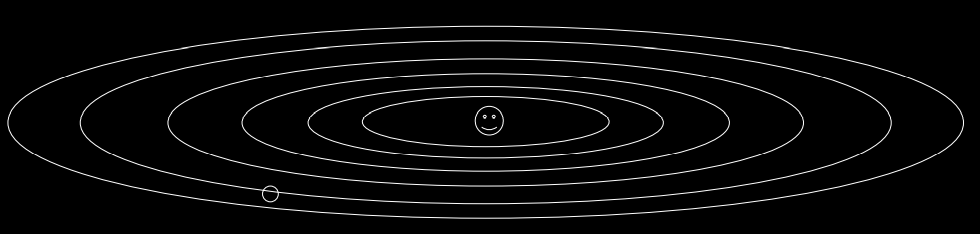
Local Minimum
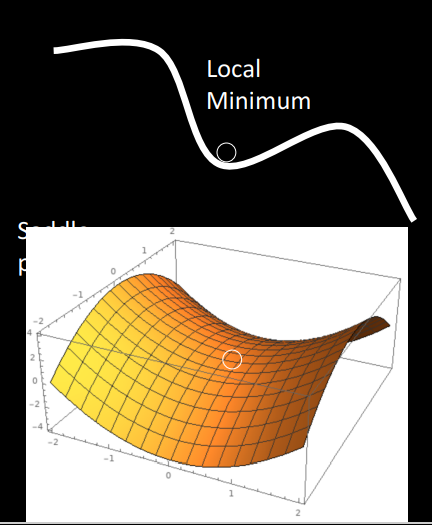
Local minima 문제는 에러를 최소화시키는 최적의 파라미터를 찾는 문제로 위의 그림처럼 hole에 빠져서 global minimum을 찾기 힘들게 되는 문제입니다.
hole은 gradient =0 인 saddle point에 위치하는 점으로 학습이 지연이 됩니다.
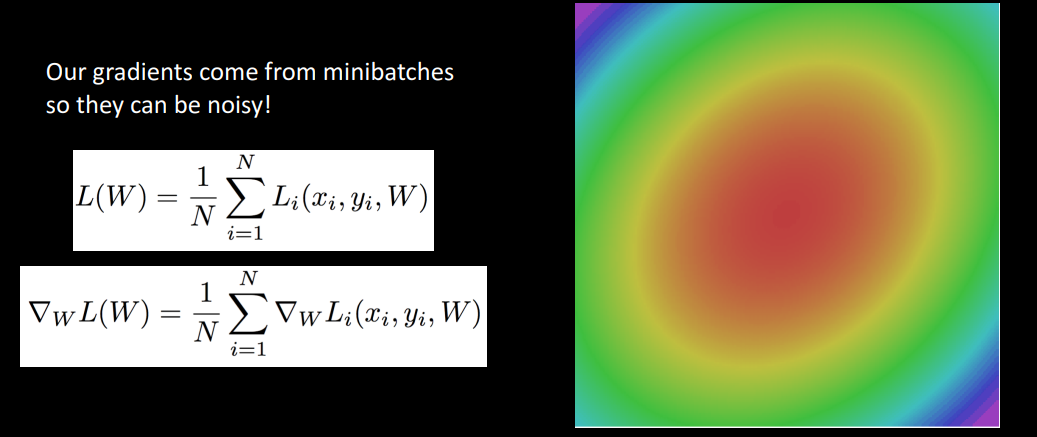
Noise
SGD는 적은 데이터로만 학습을 진행하므로 손실함수의 가중치의 방향이 항상 LOSS를 따르면 좋겠지만 노이즈가 껴서 그렇지 않은 경우도 당연히 있습니다.
SGD + Momentum

-
step의 정보를 반영하여 velocity와 gradient가 합쳐서 다음이 정해집니다.
-
딥러닝 모델에 잘 쓰입니다.
-
Momentum은 SGD의 진행 추세(관성)입니다.
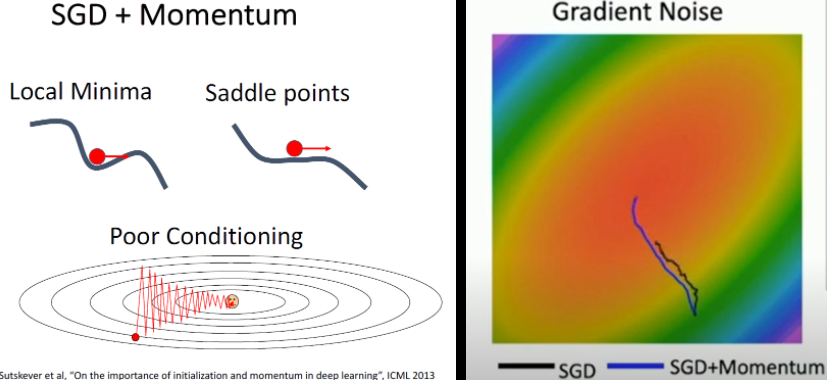
관성으로 인해 W가 local minimum or saddle point문제가 생겨도 탈출할 수 있고 기울기가 지그재그로 움직이게 되는 것도 완화해줍니다.
-
decay rate: hyperparameter로 비율 감소의 의미를 나타냅니다.
-
정헤진 form보다는 상황에 따라 바뀔 수 있답니다.
Nesterov Momentum
- 현재 위치에서 속도만큼 이동하는 동시에 gradient를 이용하여 다음 step을 정합니다.
- 직관적으로 사용하면 사용범위가 넓지 않아서 변형해서 적용을 많이 합니다.

Momentum Code
class Momentum:
def init(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] 출처: https://sacko.tistory.com/42 [데이터 분석하는 문과생, 싸코]
AdaGrad

AdaGrad는 Adaptive Gradient의 줄임말로서 지금까지 많이 변화한 매개변수는 적게 변화하도록, 반대로 적게 변화한 매개변수는 많이 변화하도록 learning late의 값을 조절하는 개념을 기존의 SGD에 적용한 것입니다. -위키백과-
-
Gradient가 크면 step size가 작아집니다.(큰 값으로 나누기 때문입니다.)
-
Gradient가 작으면 step size가 커집니다.(작은 값으로 나누기 때문입니다.)
-
무수한 진동이 일어나는 문제를 완화시킵니다.
-
주의할 점은 step이 많이 진행될수록 grad_squared가 커지기에 GD가 멈추게 됩니다.
- Code
class AdaGrad:
def init(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)출처: https://sacko.tistory.com/42 [데이터 분석하는 문과생, 싸코]
RMSProp(AdaGrad 개선)
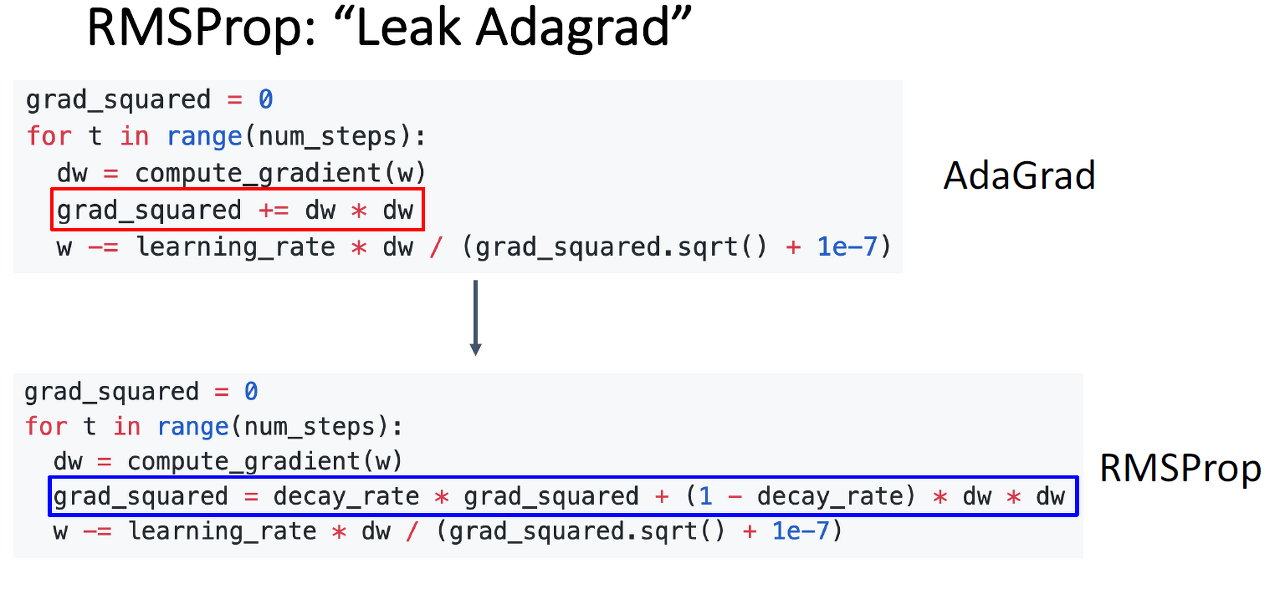
RMSProp는 새로운 기울기의 정보만 반영하도록 해서 학습률이 크게 떨어지게 되어 0에 수렴하는 것을 방지합니다.
overshoot 완화
RMSProp는 step size가 점점 줄어들기에 기존의 SGD+ Momentum보다 덜합니다.

Adam

- Adaptive Moment Estimation의 줄임말로 SGD + Momentum and RMSProp의 장점을 합친 방식입니다.
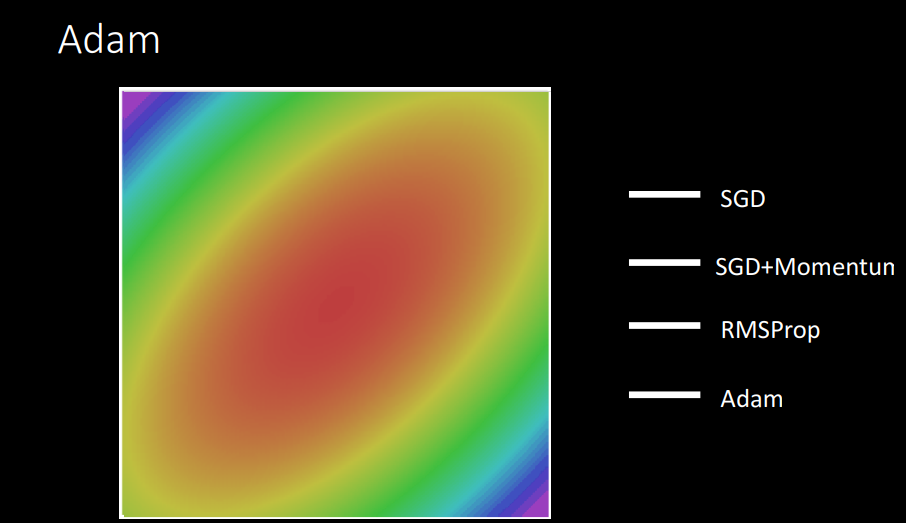
Hyperparameter
-
beta1=0.9
-
beta2는 1의 가까울 수록 t=0이 되어 step size가 커지므로 Bias correction을 추가하여 사용한다.
-
lr = 1e-3 , 5e-4, 1e-4
표를 이용한 총 정리