활성화함수

선형과 비선형

1. 선형

• 성질

--> T(0) =0. 모든 x,y는 V공간에 속하고 c는 실수에 대한 다음 식과 동치.

• T(cx+y) = cT(x) + T(y) # 선형인지 아닌지 판단.

• T(x-y) = T(x) - T(y)

  

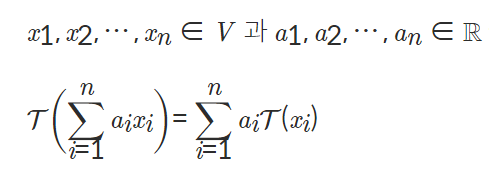
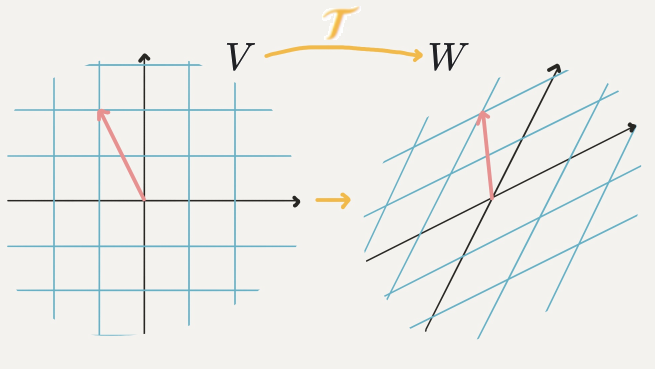
• 1-1. 선형 변환

: 선형이라는 공간적 규칙을 잘 지키면서 V공간상의 벡터를 W공간 상의 벡터로 바꿔줌

1-2. 합성함수

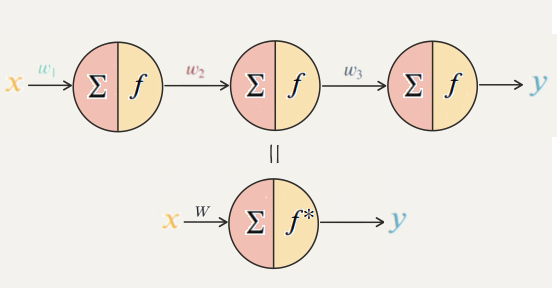
: 선형함수를 합성해도 그 합성함수는 선형함수입니다.

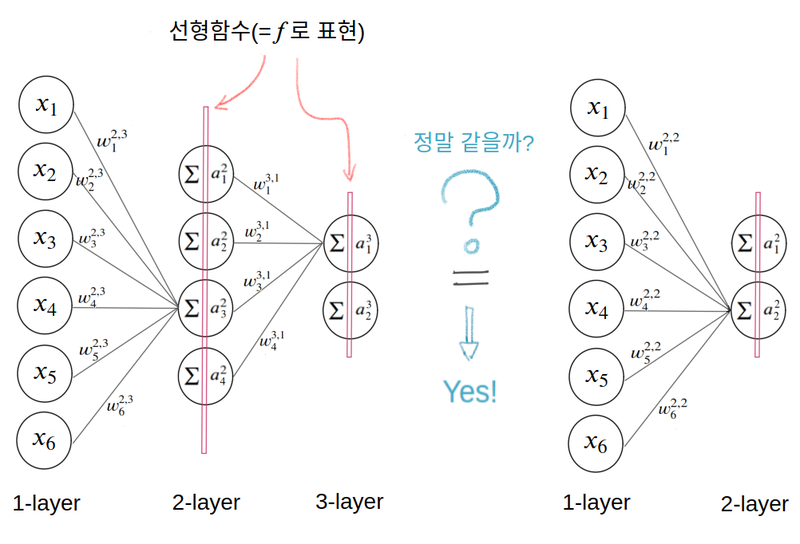
: 그러므로 3개의 노드를 1개로 줄여 표현해도 상관 없다.(그렇기에 아무리 레이어를 쌓아도 깊어지는 게 아니라 그저 한 개를 쓰는 것과 다름이 없는 것이다.)

2. 비선형

• 정의: 선형이 아닌 함수

• 특징:

  	- 딥러닝 모델의 표현력 향상시킴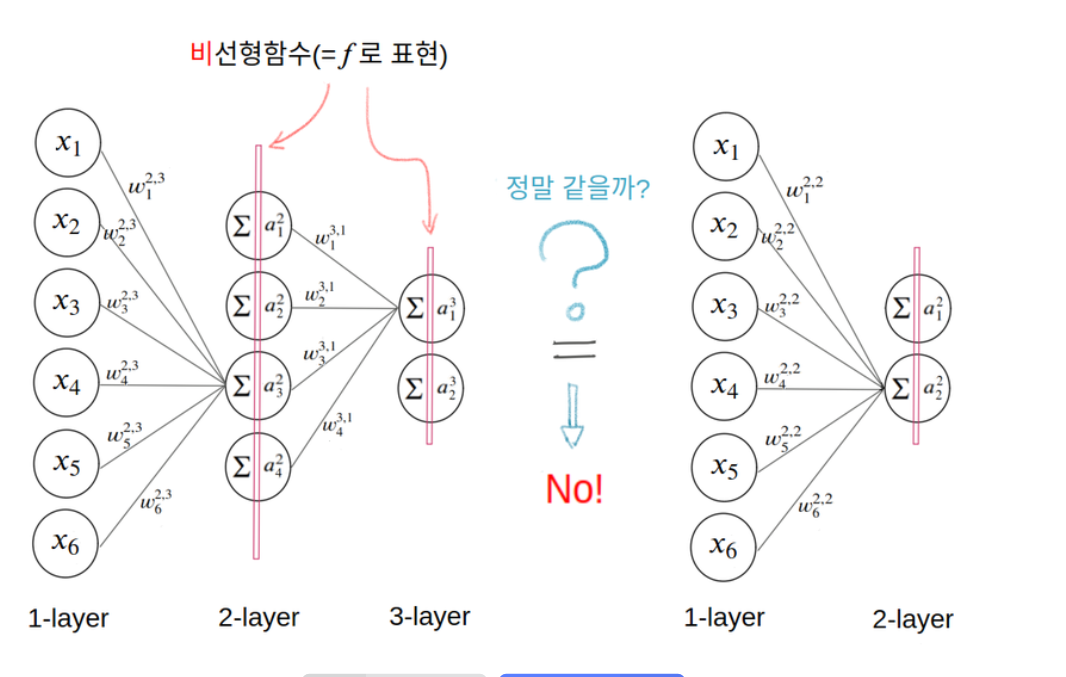

  

  • 합성함수로 표현시 선형처럼 갖지 않고 다르다.

활성화

• 특징

  	- 딥러닝 모델의  표현력 향상(representation capacity)

  --> 선형 데이터뿐만 아니라 비선형 데이터에도 표현 가능.
  

함수의 종류

이진 계단 함수(Binary step function)

• 공식:

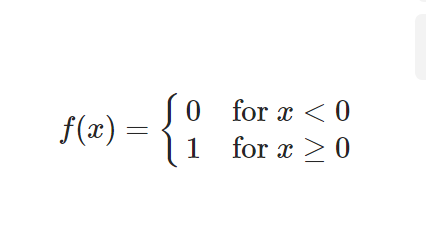
• 정의: 입력 값 > 특정 임계점 --> 1 / 입력 값 <= 특정 임계점 -> 0

• 특징:

  	- 단층 퍼셉트론에 잘 쓰인다.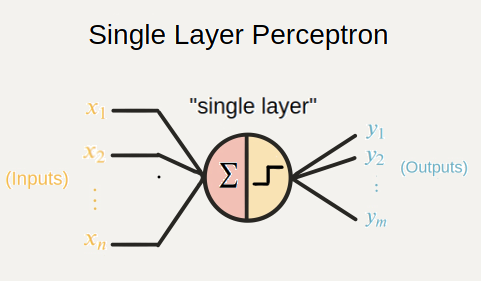

  

  • And gate 와 Or gate표현 가능(진리 값을 하나의 선으로 구분 가능)

    

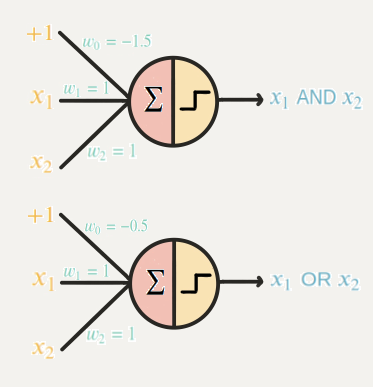
  • 최적의 가중치가 하나로 정해지지 않아 훈련할 때마다 그래프의 모양이 다름.

• 한계1 : XOR gate 구현 불가(진리 값을 하나의 선으로 구분이 불가능하다)

• 해결책: MLP모델을 이용한다

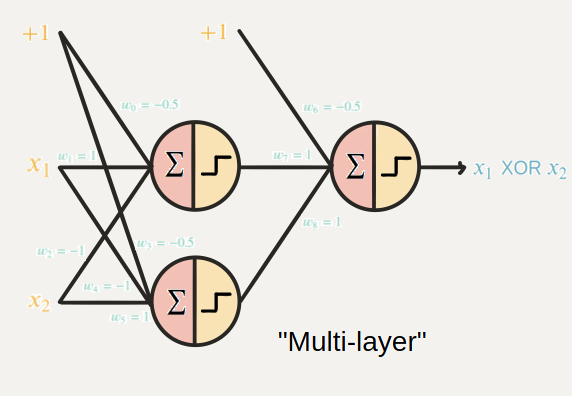
• 한계2 : 역전파 알고리즘을 사용하지 못한다.

  	- 0인 값에선 미분이 불가

  • 0인 부분을 제외하고 미분해도 미분값은 0
  • 위의 두 가지로 인해 가중치 업데이트 불가

• 한계3 : 다중 출력할 수 없다.

Code

링크텍스트

선형 활성화 함수(Linear activation function)

링크텍스트

• 정의: 선형인 활성화 함수이다

• 특징:

  	- 다중 출력이 가능
    
  	- 이진 분류 뿐만 아니라 다중 분류도 가능하다.

  • 미분이 가능하여 역전파 알고리즘 사용 가능

  • 치역은 실수 전체이다.

  • 선형적으로 구분 가능한 문제 해결(And gate와 Or gate가능)

    

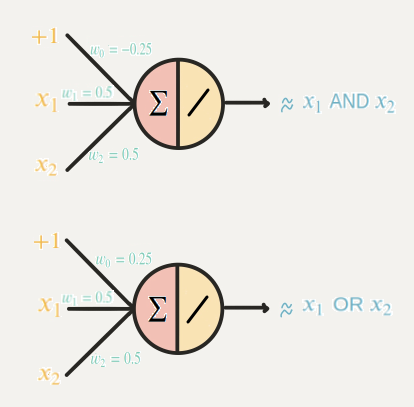
• 한계:

  	- 정확한 값 예측은 못함

  • XOR gate 구현 불가
  • 비선형성을 지닌 데이터 예측 불가

비선형 활성화 함수(Non - linear activation function)

함수들의 구현 CODE

링크텍스트

• 정의: 활성화 문제점들을 해결하기 위해 만들어진 함수

• 특징:

  	1. 역전파 알고리즘 사용 가능

  2. 다중 출력 가능
  3. 비선형적 특성을 지닌 데이터 예측 가능

  시그모이드(sigmoid 혹은 logistic)

  

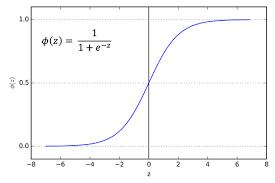
• 미분

  

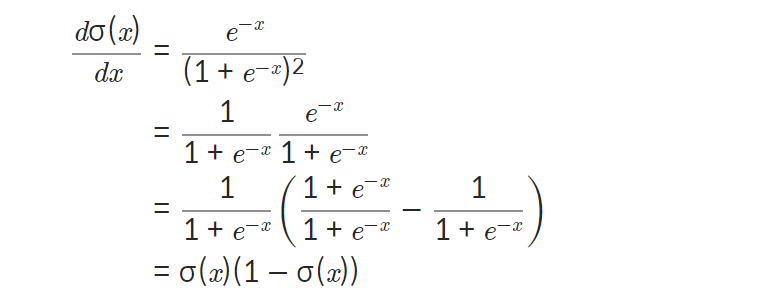
• 단점

  	- 포화 문제: 0 또는 1에 몰림
  
  --> gradient가 0에 가까워진다. - > 역전파 시, 가중치 업데이트가 일어나지 않는다

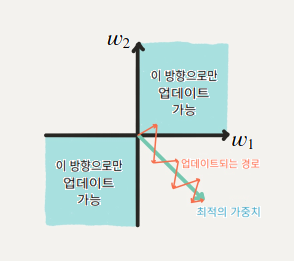
  • 시그모이드 함수의 출력: 0이 중심이 아님( 훈련 시간이 오래 걸림)

    

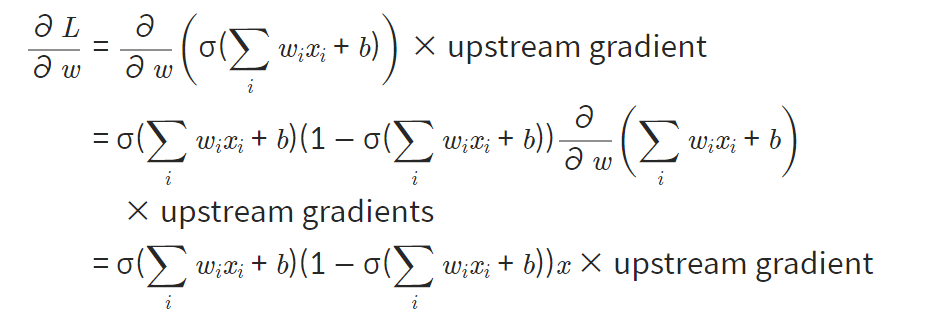
  --> 입력 값이 모두 양수가 되면 upstream gradient가 결정이 되는데 이 gradient의 부호에 따라 이 노드의 가중치는 모두 양의 방향으로 업데이트 되거나 음의 방향으로 업데이트가ㄷ 된다. 즉 한 쪽으로 몰리기 때문에 최적값을 향해 업데이트되는 것보다 느리다.
  

• 수치 미분과 해석 미분의 차이

  	- 수치 미분: 우리가 알고 배운 미분.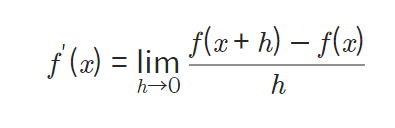

  

  • 해석 미분: 종이와 펜을 이용해 논리적으로 전개하여 푸는 것

• And gate, Or gate, Xor gate 구현

  	- sigmoid를 이용하여 Xor gate가 구현이 가능된다.

  • layer 추가로 Xor gate가 구현이 가능함

  Softmax

• 사진을 구분하고 분류하는 문제에 주로 쓰임.

• 각 class의 확률을 구할 때 쓰임

• 모든 class의 확률을 다 더하면 1이다.

• 모델의 마지막 layer에 활용됨

  하이퍼볼릭 탄젠트

  

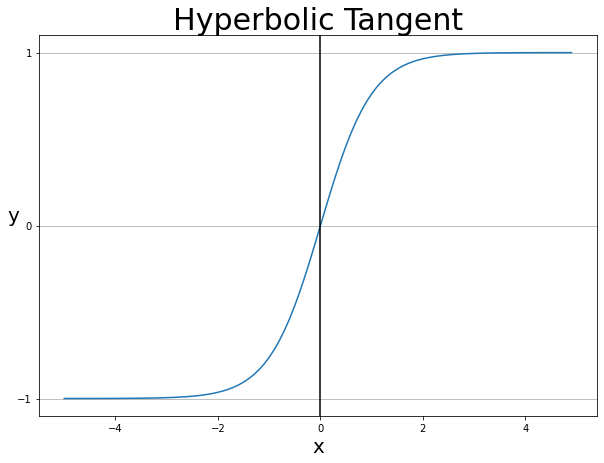
• 쌍곡선 함수

• 0이 중심이다

• 속도가 빠름

• 미분

  :

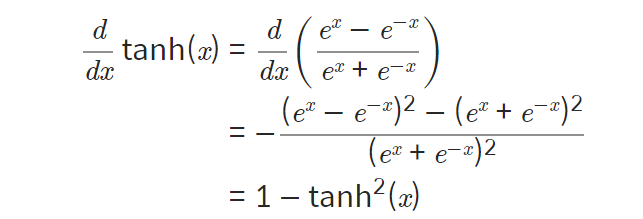
• 시그모이드로도 표현이 가능

  

  

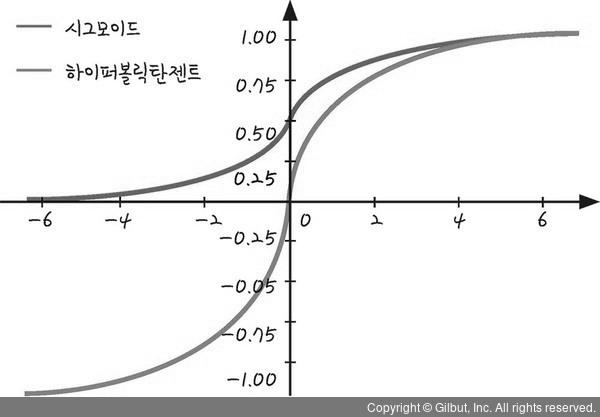
• 단점: 포화문제가 가능하다( -1 OR 1)

  ReLU

  

• 높은 비용의 연산을 사용하지 않으므로 처리 속도가 빠르다

• 0을 제외한 구간에서 미분이 가능하다

  

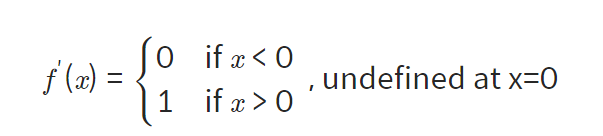
• 병렬 쌓기가 잘된다.

• 단점

  - 0이 중심아니어서 포화문제가 일어날 수 있다

  • Dying ReLU: 비활성화되면서 출력을 0으로만 함.

  단점 극복

1. Leaky ReLU

• 정의: Dying ReLU해결

  

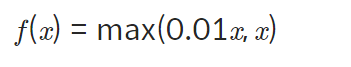
• 0을 출력하던 부분을 작은 음수 값으로 만든다.

2. PReLU

• 정의: 새로운 파라미터를 추가하여 0미만일 때의 기울기가 되도록 훈련시킴

  

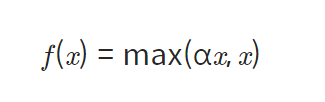
  3.ELU

• 정의: ReLU의 모든 장점과 Dying ReLU문제 해결한 활성화 함수

  

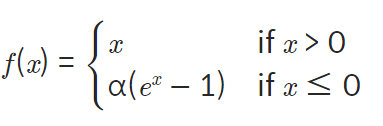
• 미분:

  

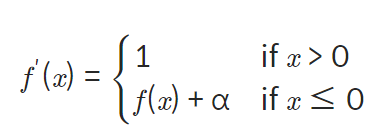
• 단점: exponential 연산이 들어가게 되어 계산 비용이 높아짐