나만봄 - CNN이 뭐야

오늘도 ChatGPT에게 먼저 질문했다.
이제는 답변을 정리해서 쓰기로 했다.
좋은 답을 내놓긴 하지만 장황하게 대답하는 경우가 많아서.

Q. What is CNN in Deep Learning?

• CNNs are inspired by the visual cortex of animals, which is responsible for processing visual information.
• They consist of multiple convolutional layers that extract features from the input images.
• The output of each convolutional layer is passed through a non-linear activation function.
• Pooling layers are often used to reduce the spatial dimensionality of the feature maps.

Q. What is the biggest change in CNN compared to earlier neural network architectures?

• The use of convolutional layers, which allows for the automatic extraction of relevant features from images
  • traditional neural networks used fully connected layers, which required the input data to be flattened into a 1-dimensional vector, losing the spatial information in the process. This made it difficult to handle images and other high-dimensional data
• which apply a set of filters to the input image, extracting features such as edges, corners, and textures
• can learn increasingly complex features and relationships in the data
• allowing for higher accuracy and faster training times

Q. What do convolutional layers do in CNN?

• their purpose is to automatically extract relevant features from the input image.
• consists of a set of filters (also called kernels or weights), each of which is a small matrix that is applied to a specific region of the input image
  • The filter slides across the input image, computing the dot product between itself and the region of the image it is currently positioned over

---

재정리 해보자.

• 이전 다층신경망(MLP)은 각 뉴런들이 선형 모델과 활성함수로 모두 연결된(Fully-Connected) 구조.
  $h_{i} = \sigma(\sum^p_{j=1} W_{i}x_{j})$
  • $\sigma$ : 활성함수(Activation Function)
  • $W_{i}$ : 가중치(Weignt) 행렬
  • 각 성분 $h_{i}$에 대응하는 가중치 행렬 $W_{i}$이 필요하다.
    • $i$가 바뀌면 가중치도 바뀐다.

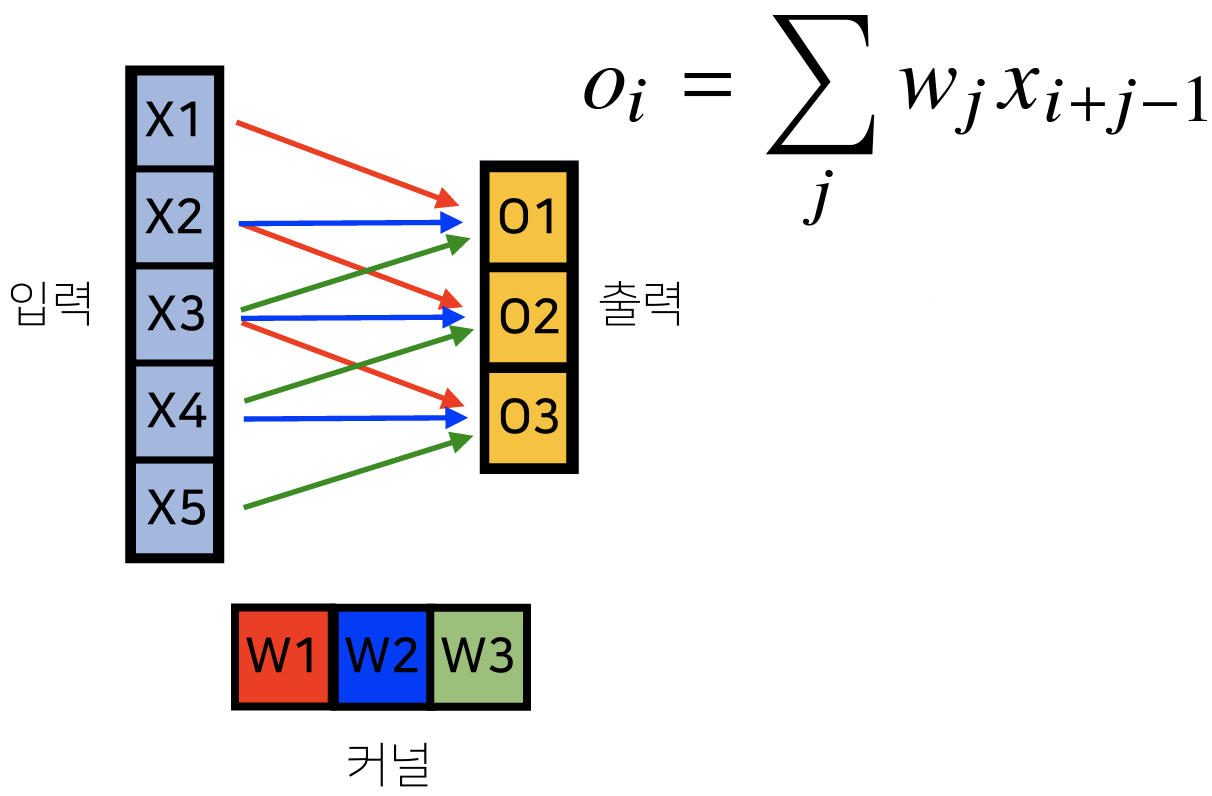
• Convolution 연산은 커널(Kernel)을 입력 벡터 상에서 움직이며 선형 모델, 활성 함수가 적용된다.

  $h_{i} = \sigma (\sum^k_{j=1} V_{j}x_{i+j-1})$
  • $k$ : 커널 사이즈
  • $V$ : 가중치 행렬
  • 모든 $i$에 적용되는 커널은 $V$로 같고 커널의 사이즈만큼 x상에서 이동하며 적용된다.

• 수학적 의미는 신호(signal)를 커널을 이용해 국소적으로 증폭 또는 감소시켜 정보 추출, 필터링 하는 것.

• 1차원뿐만 아니라 다양한 차원에서 계산가능하다.

• 정의역 내에서 움직여도 변하지 않고(Translation Invariant) 국소적으로(Local) 적용

• f: 커널, g: 입력

  • 오직 입력에 해당하는 값만 바뀌고 커널은 그대로 유지한다.
    $[f*g](i,j) = \sum_{p,q}f(p,q)g(i+p,j+q)$

• 입력크기 $(H,W)$ 커널 크기 $(K_{h},K_{w})$, 출력 크기 $(O_{H},O_{W})$
  → $O_{H} = H -K_{H} + 1$, $O_{W} = H -K_{W} + 1$

• 채널이 여러 개인 경우 커널의 채널 수와 입력의 채널 수가 같아야 한다.

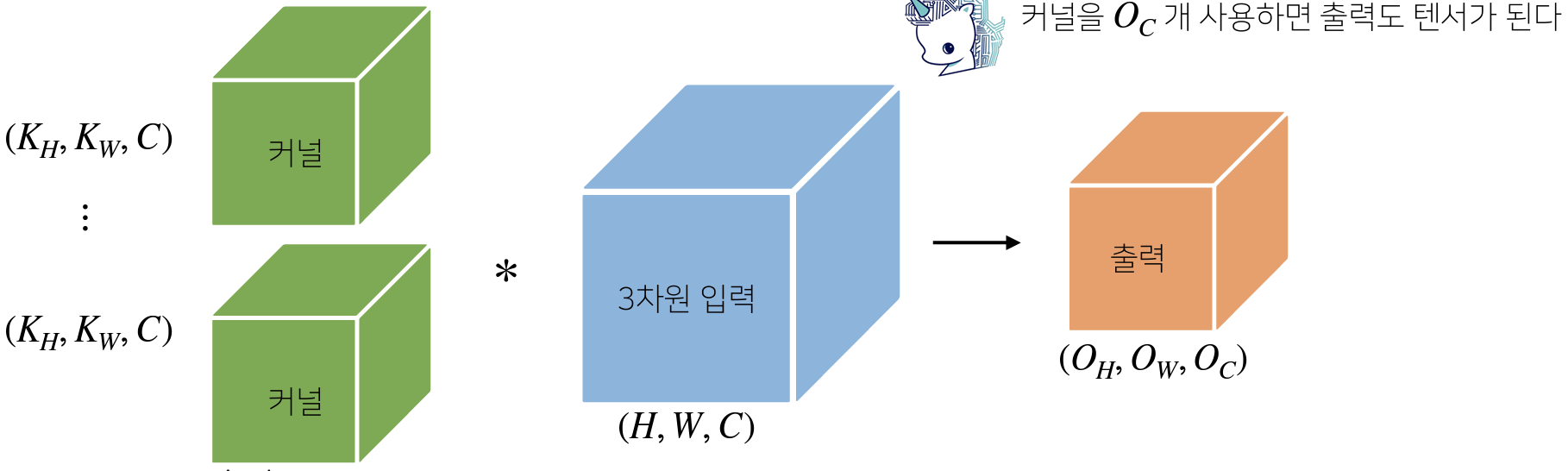
  • 이 때, 3차원 부터 행렬이 아니라 텐서(Tensor)라고 부른다.
    

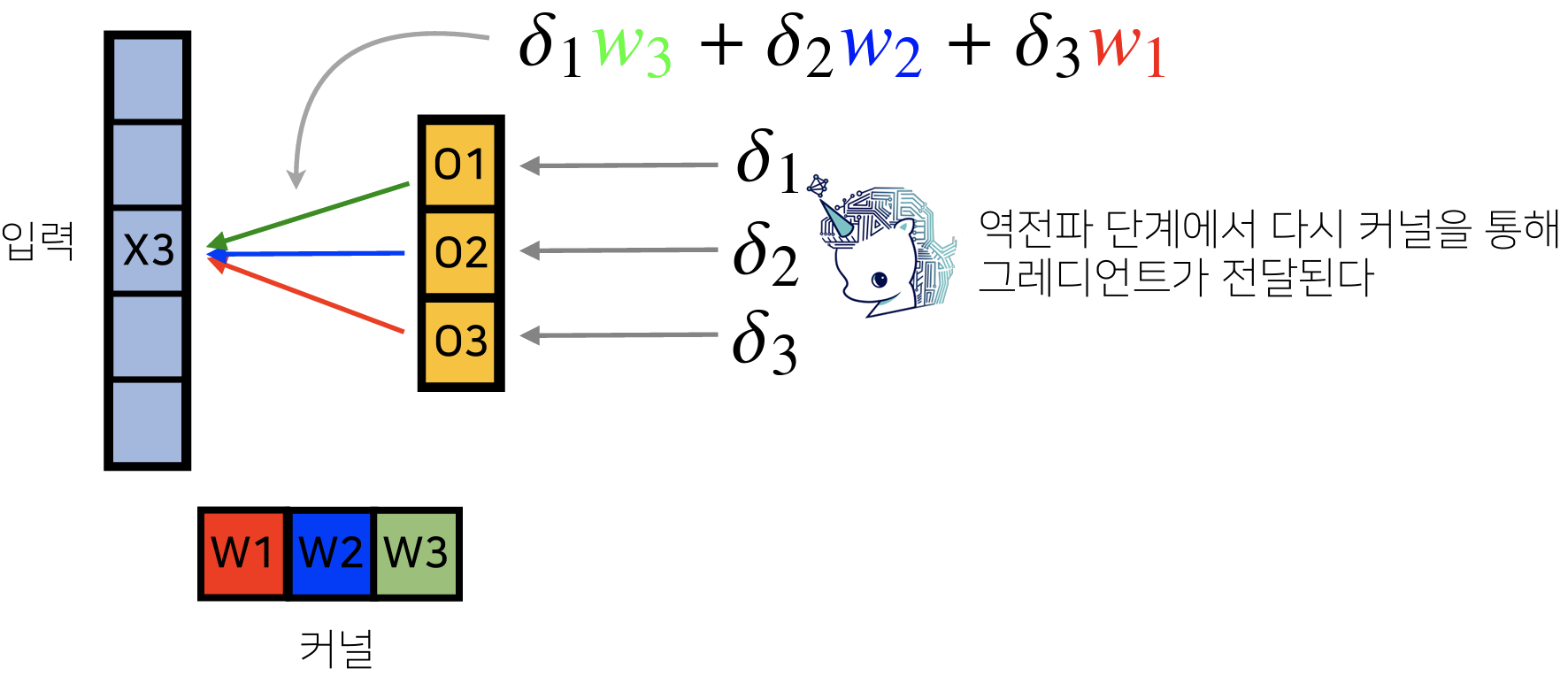
• 커널이 모든 입력에 공통 적용되기 때문에 역전파 계산할 때도 convolution 연산을 한다. (Discrete 일 때도 성립한다.)

• $o_{i} = \sum_{j}w_{j}x_{i+j-1}$
  • $o_{1} = x_{1}w_{1} +x_{2}w_{2}+ x_{3}w_{3}$
  • $o_{2} = x_{2}w_{1} +x_{3}w_{2}+ x_{4}w_{3}$
  • $o_{3} = x_{3}w_{1} +x_{4}w_{2}+ x_{5}w_{3}$
• $\delta_{1}$→ $o_{1}$, $\delta_{2}$ → $o_{}$, $\delta_{3}$ → $o_{3}$
  각 $\delta$는 미분값.

---

위에선 수학적으로 접근했다면
이제는 단순하게 정리해보겠다.

• CNN은 convolution layer, pooling layer, and fully connected layer로 구성된다.

  • Convolution and pooling : feature extraction
    -> Convolution Layer에서는
    Kernel이 Input을 Stride만큼 옆으로 가며 Feature를 뽑는다.
  • Fully connected layer: decision making (e.g., classification)

• EX)

  • 5x5x3 Kernel 1개가 32x32x3 image를 읽으면 28x2x1 feature가 된다.
  • 32x32x3 image를 5x5x3 kernel 4개 28x28x4 feature가 된다.

• Stride : Kernel의 step size를 결정한다.

  • 1이면 1픽셀, 2면 2픽셀을 움직이고 그에 따라 output size가 감소한다.
  • 큰 값의 Stride를 사용하면 Output feature의 Spatial Dimensions을 줄여 computational complexity를 줄이고 Overfitting을 방지할 수있지만 정보의 손실 또한 발생한다.

• Padding : Input의 spatial dimensions을 보존하기 위해 사용한다.

  • Kernel이 Input을 Sliding 할 때 가장자리에 있는 픽셀은 비교적 잘 반영되지 않는다.
    또한 Input에 비해 Output의 크기가 무조건 감소한다.
  • 이를 방지하기 위해 Convolution 연산 전에 Input 테두리에 추가적인 pixel을 더한다.
  • 이러면 데이터의 축소도 막고 edge pixel도 활용할 수 있다.
    

• Parameters 수 계산해보기

  • Input : W = 40, H = 50, C = 128 / Output: W = 40, H = 50, C = 64 / 3x3 Kernel, Padding = 1 ,Stride = 1
    일 때, Parameters의 개수는?
    -> $3*3*128*64 = 73,728$
    
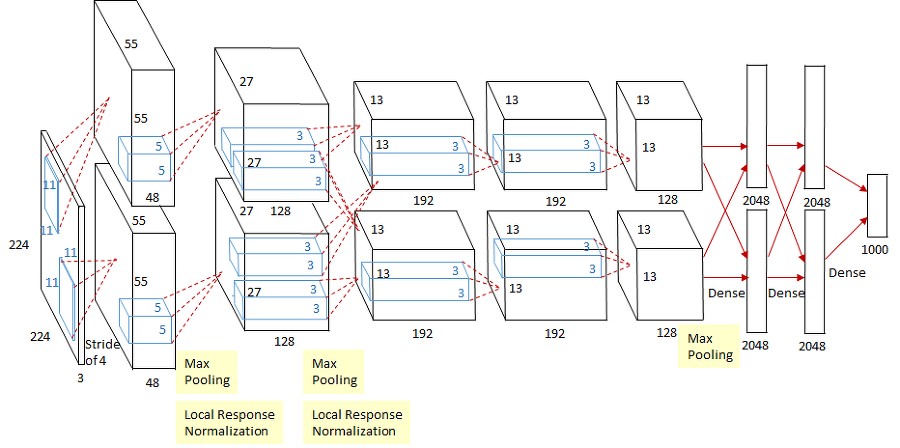
  • AlexNet
    1. $11*11*3*48*2$
    2. $5*5*48*128$
    3. $3*3*128*2*192*2$
    4. $3*3*192*192*2$
       ...

---

참고 자료

• AI Tech 교육 자료
• CS213n 강의 자료
• https://towardsai.net/p/l/introduction-to-pooling-layers-in-cnn