Calculus Backgrounds

Roh's warehouse·2025년 9월 21일

Optimization in Learning

목록 보기
2/8

Matrix Derivatives

Types of Matrix Derivative

TypeScalar yyVector y\mathbf{y} (m×1)(m\times 1)Matrix Y\mathbf{Y} (m×n)(m\times n)
Scalar xx∂y∂x\frac{\partial y}{\partial x}∂y∂x\frac{\partial\mathbf{y}}{\partial x}: (m×1)(m\times 1)∂Y∂x\frac{\partial \mathbf{Y}}{\partial x}: (m×n)(m\times n)
Vector x\mathbf{x} (n×1)(n\times 1)∂y∂x\frac{\partial y}{\partial \mathbf{x}}: (1×n)(1\times n)∂y∂x\frac{\partial \mathbf{y}}{\partial \mathbf{x}}: (m×n)(m\times n)
Matrix X\mathbf{X} (p×q)(p\times q)∂y∂X\frac{\partial y}{\partial \mathbf{X}}: (p×q)(p\times q)

Dimension을 주의할 것!

Gradient and Hessian

  • ∇f(x)\nabla f(x) = the gradient of ff
    • The transpose of the first derivatives of ff
∇f(x):=[∂f∂x1⋮∂f∂xn]=(∂f∂x)T∈Rn×1\nabla f(x) := \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \vdots \\ \frac{\partial f}{\partial x_n} \end{bmatrix} = \left( \frac{\partial f}{\partial \mathbf{x}} \right)^T \in \mathbb{R}^{n\times 1}
  • ∇2f(x)\nabla^2 f(x) = the Hessian of ff
    • The matrix of second partial derivatives of ff
    • The Hessian is a symmetric matrix
∇2f(x):=[∂2f∂x12∂2f∂x1∂x2…∂2f∂x1∂xn∂2f∂x2∂x1∂2f∂x22…∂2f∂x2∂xn⋮⋮⋱⋮∂2f∂xn∂x1∂2f∂xn∂x2…∂2f∂xn2]∈Rn×n\nabla^2 f(x) := \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \dots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \dots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \dots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix} \in \mathbb{R}^{n\times n}

Jacobian and Matrix Derivative

  • Jacobian when x∈Rn,y∈Rm\mathbf{x} \in \mathbb{R}^n, \mathbf{y} \in \mathbb{R}^m
J:=∂y∂x=[∂y1∂x1∂y1∂x2…∂y1∂xn∂y2∂x1∂y2∂x2…∂y2∂xn⋮⋮⋱⋮∂ym∂x1∂ym∂x2…∂ym∂xn]∈Rm×nJ := \frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} & \dots & \frac{\partial y_1}{\partial x_n} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} & \dots & \frac{\partial y_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \frac{\partial y_m}{\partial x_2} & \dots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \in \mathbb{R}^{m\times n}
  • Matrix derivative when X∈Rp×q,Y∈Rm×n,z∈R\mathbf{X} \in \mathbb{R}^{p\times q}, \mathbf{Y} \in \mathbb{R}^{m \times n}, z \in \mathbb{R}
∂z∂X=[∂z∂x11∂z∂x12…∂z∂x1q∂z∂x21∂z∂x22…∂z∂x2q⋮⋮⋱⋮∂z∂xp1∂z∂xp2…∂z∂xpq],∂Y∂z=[∂y11∂z∂y12∂z…∂y1n∂z∂y21∂z∂y22∂z…∂y2n∂z⋮⋮⋱⋮∂ym1∂z∂ym2∂z…∂ymn∂z],\frac{\partial z}{\partial \mathbf{X}} = \begin{bmatrix} \frac{\partial z}{\partial x_{11}} & \frac{\partial z}{\partial x_{12}} & \dots & \frac{\partial z}{\partial x_{1q}} \\ \frac{\partial z}{\partial x_{21}} & \frac{\partial z}{\partial x_{22}} & \dots & \frac{\partial z}{\partial x_{2q}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial z}{\partial x_{p1}} & \frac{\partial z}{\partial x_{p2}} & \dots & \frac{\partial z}{\partial x_{pq}} \end{bmatrix}, \quad \frac{\partial \mathbf{Y}}{\partial z} = \begin{bmatrix} \frac{\partial y_{11}}{\partial z} & \frac{\partial y_{12}}{\partial z} & \dots & \frac{\partial y_{1n}}{\partial z} \\ \frac{\partial y_{21}}{\partial z} & \frac{\partial y_{22}}{\partial z} & \dots & \frac{\partial y_{2n}}{\partial z} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_{m1}}{\partial z} & \frac{\partial y_{m2}}{\partial z} & \dots & \frac{\partial y_{mn}}{\partial z} \end{bmatrix},

Useful Matrix Derivative

For A∈Rn×nA \in \mathbb{R}^{n \times n},

  • ∂∂x(bTx)=∂∂x(xTb)=bT\frac{\partial}{\partial x}(b^Tx) = \frac{\partial}{\partial x}(x^Tb) = b^T

  • ∂∂x(xTx)=∂∥x∥2∂x=2xT\frac{\partial}{\partial x}(x^Tx) = \frac{\partial \|x\|^2}{\partial x} = 2x^T

  • ∂∂x(xTAx)=xT(A+AT)\frac{\partial}{\partial x}(x^TAx) = x^T(A+A^T)

    • 2xTA2x^TA if AA is symmetric.

Chain Rule

Chain Rule

Theorem: Chain Rule
When the vector xx in turn depens on another vector tt, the chain rule for the univariate function f:Rn→Rf:\mathbb{R}^n \rightarrow \mathbb{R} can be extended as follows:

df(x(t))dt=∂f∂xdxdt=∇f(x(t))Tdxdt\frac{df({\mathbf{x}(t)})}{dt} =\frac{\partial f}{\partial x} \frac{d \mathbf{x}}{d t} = \nabla f(\mathbf{x}(t))^T \frac{d \mathbf{x}}{d t}
  • If z=f(y)z=f(\mathbf{y}) and y=g(x)y=g(\mathbf{x}) where x∈Rn,y∈Rm,z∈R\mathbf{x}\in \mathbb{R}^n, \mathbf{y}\in \mathbb{R}^m, z\in \mathbb{R}, then
dzdxi=∑jdzdyjdyjdxi=∑jdyjdxidzdyj\frac{d z}{d x_i} = \sum_j \frac{d z}{d y_j}\frac{d y_j}{d x_i} = \sum_j \frac{d y_j}{d x_i}\frac{d z}{d y_j}

(gradients from all possible paths)

  • or in vector notation
dzdx=dzdydydx\frac{d z}{d \mathbf{x}} = \frac{d z}{d \mathbf{y}} \frac{d \mathbf{y}}{d \mathbf{x}}
[1×n][1×m][m×n][1\times n] \quad [1\times m] [m \times n]

Neural Net에서의 BackPropagation 기법의 기초가 된다.

Chain Rule on Level Curve

  • level curve : f(x,y)=cf(x,y)=c를 만족하는 (x,y)(x,y)의 집합.

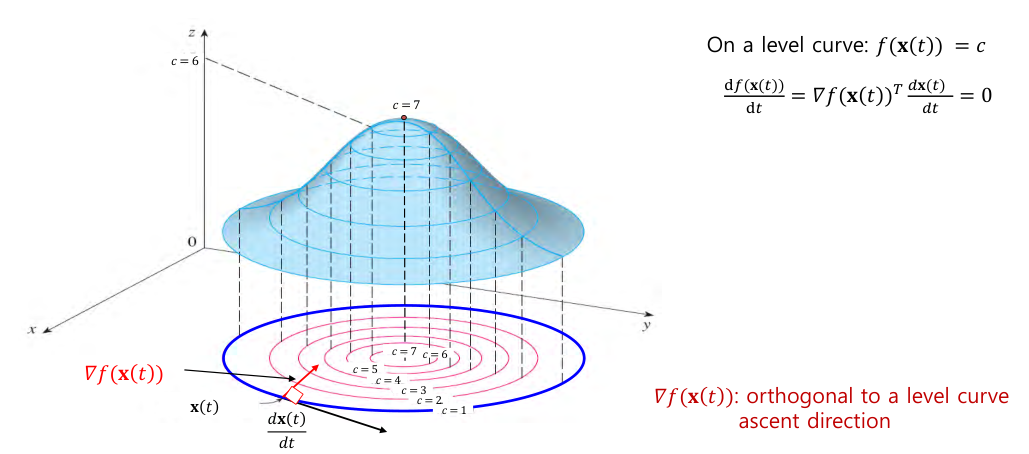
  • On level curve f(x(t))=cf(\mathbf{x}(t)) = c,
df(x(t))dt=∇f(x(t))Tdx(t)dt=0\frac{df({\mathbf{x}(t)})}{dt} = \nabla f({\mathbf{x}(t)})^T \frac{d\mathbf{x}(t)}{dt} = 0

즉, ∇f(x(t))\nabla f({\mathbf{x}(t)})는 level curve에서 수직(orthogonal)이며, ff가 증가하는 방향(ascent direction)을 가르킨다.

Directional Derivatives

  • ff is continuously differentiable and p∈Rnp \in \mathbb{R}^n, directional derivative of ff in the direction of pp is given by
D(f(x);p)=lim⁡ε→0f(x+εp)−f(x)ε=∇f(x)TpD(f(x);p) = \lim_{\varepsilon \rightarrow 0}\frac{f(x+\varepsilon p) - f(x)}{\varepsilon} = \nabla f(x)^Tp

Taylor Series Expansion

  • First order

    f(x+p)≊f(x)+∇f(x)Tpf(x+p) \approxeq f(x) + \nabla f(x)^Tp

  • Second order

    f(x+p)≊f(x)+∇f(x)Tp+12pT∇2f(x)pf(x+p) \approxeq f(x) + \nabla f(x)^Tp + \frac{1}{2}p^T\nabla ^2 f(x)p

추후 나올 일반적인 search(또는 learning) algorithm에서는 1st order expansion이면 충분하다.

Taylor Series Expansion을 통해 간단하게 ∇f(x)\nabla f(x)가 ascent direction임을 보일 수 있다.

f(x+λ∇f(x))≊f(x)+λ∇f(x)T∇f(x)=f(x)+λ∥∇f(x)∥2≥f(x)\begin{aligned} f(x+\lambda \nabla f(x)) &\approxeq f(x) + \lambda\nabla f(x)^T\nabla f(x) \\ &= f(x) + \lambda \| \nabla f(x) \|^2\\ &\ge f(x) \end{aligned}
profile
Roh's warehouse
공부랑 연구랑 생각
이전 포스트

Matrix Computation

다음 포스트

Convex Optimization

0개의 댓글