Convex Optimization

Convexity

Convex Sets

• 두 points의 convex combination 은 line segment between them.

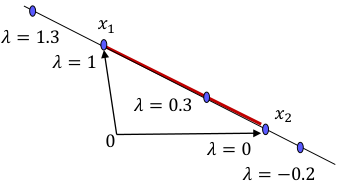
• A set $C \in \mathbb{R}^n$에 대해, $C$ 안의 임의의 두 점 $x_1, x_2$의 convex combination이 항상 $C$에 포함되면 이를 convex 하다고 한다.

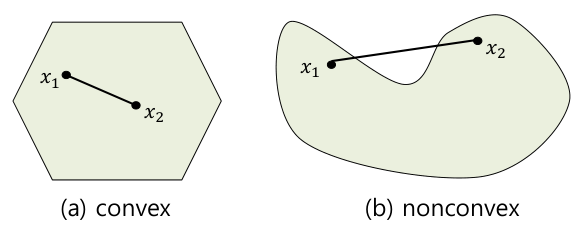
기하학적으로는 오목하게 들어간 부분이나 내부에 구멍이 없는 집합이다.

• A set $C$ 내 점들의 모든 convex combination을 $C$의 convex hull ($conv(C)$) 이라고 한다.

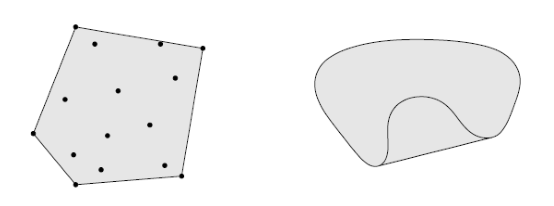
conv(C)는 집합 C를 포함하는 가장 작은 convex set이다.

Convex Functions

• Let $f:C \rightarrow \mathbb{R}$, where $C$ is a nonempty convex set in $\mathbb{R}^n$.
  The function $f$ is said to be convex on $C$ if $x_1, x_2 \in C$ with $0 \le \lambda \le 1$
  $f(\lambda x_1 + (1-\lambda)x_2) \le \lambda f(x_1) + (1-\lambda)f(x_2)$
  • concave : if $-f$ is convex on $C$.
  • strictly convex or strictly concave if the equality doesn't hold.

Convex function $f$는 domain 위의 임의의 두 점을 이은 선분이 항상 $f$ 위에 있다.

Theorem: Jensen's inequality
For a convex function $f$ and $\sum_{i=1}^k \lambda_i = 1, \lambda_i \ge 0$ $\forall i$,

$f(\sum_{i=1}^k \lambda_i x_i) \le \sum_{i=1}^k \lambda_i f(x_i)$

$\sum_{i=1}^k \lambda_i x_i$를 확률(합이 1)에서의 기댓값으로도 볼 수 있다: $f(\mathbb{E}[x])\le \mathbb{E}[f(x)]$.

Theorem: First-order conditions
Let $C$ be a nonempty open convex set in $\mathbb{R}^n$, and let $f: C \rightarrow \mathbb{R}$ be differentiable on $C$.
Then $f$ is convex if and only if for any $x,y\in C$, we have,

$f(y) \ge f(x) + \nabla f(x)^T(y-x)$

Convex function은 항상 특정 point (x,f(x))의 접선보다 크거나 같다.

Convexity and Optima

Critical Points

여기서 말하는 제약이 없는 최적화 문제 (unconstrained problem)는 최소화 문제(minimizing problem)을 말한다.

minimizing $f(x)$ over $\mathbb{R}^n$에 대해,

• If $f(x^*) \le f(x)$ for all $x\in \mathbb{R}^n$, then $x^*$ is called a global minimum.

• If $f(x^*) \le f(x)$ for all $x\in N_\varepsilon (x^*)$, then $x^*$ is called a local minimum.

• If $f$ is differentiable and $\nabla f(x^*)=0$, then $x^*$ is called a critical point of $f$.

• If $x^\ast$ is a critical point, but neither a maximum nor a minimun, then $x^\ast$ is called a saddle point.

단, critical point가 아니더라도, local maximum (또는 minimum)이 나타날 수 있다.

Convex Optimization Problem

• Convex set $C$에 대해, 함수 $f$가 $C$ 상에서 convex function이면, $\min\limits_{x\in C} f(x)$를 Convex optimization problem (CO)라고 말한다.

CO에서는 local optima가 곧 global optima라는 좋은 성질이 있다.

Theorem: Convex optimization problem
$x^*$ is a local minimum for (CO), if and only if, $x^*$ is a global minimum for (CO).

주어진 optimization 문제가 CO인지 확인하기 위해서는 우선 domain이 convex set인지 확인해야 하며, 이후 해당 set 위에서의 $f$에 대한 Hessian matrix가 SPD인지 확인해야 한다.

Theorem: Second-order conditions
Let $C$ be a nonempty open convex set in $\mathbb{R}^n$, and let $f:C\rightarrow \mathbb{R}$ be twice differentiable on $C$.
Then $f$ is convex if and only if its Hessian $\nabla^2f(x)$ is positive semidefinite for all $x \in C$.

또한, $f$의 Hessian matrix에 대한 postive definiteness 검증을 통해 $f$가 strictly convex function임을 보일 수 있다.

Lemma:
If the Hessian matrix is positive definite, then $f$ is strictly convex.
If $f$ is strictly convex and quadratic then its Hessian matrix is positive definite at each point of $C$.

참고로, 2x2 matrix $A =\left[ \begin{array}{cc} a & b \\ b & c\\ \end{array} \right]$, 의 경우 $a>0$, $ac-b^2>0$ 를 만족하면 postive definite이다.