Optimization vs Learning

Pure Optimization vs Machine Learning Training?

• Pure optimization의 목표는 매우 명확하다: optimum을 찾는 것!

  • Step 1. 문제를 mathematical formulation으로 (최대한) 나타낸다.
  • Step 2: (가능한) 최적의 optimum solution을 찾는다.

• 반면에, (machine) learning training의 경우, real optimum과 training alogrithm의 goal은 유사하지만 다르다.

  • learning에서의 optimal parameter는 수리적 optimal이 아니다. (overfitting 방지)

How Learning Differs from Pure Optimization

Machine learning은 train set이 아닌, test set에서 측정되는 performance measure를 최적화 하는 것이 목적이다. Test set은 train 과정에서 알 수 없기 때문에 intractable하다.

• 기본적으로 train이란, data의 (generating) distribution에 대해 cost function의 expectation을 최소화 하는 것을 골자로 삼는다.

즉, generating probability가 낮은 sample/data는 error가 커도 결과에 큰 영향을 미치지 않는다. (probabilitic optimization)

• Data의 distribution을 알지 못하기 때문에, train dataset을 통해 expectation의 추정값(empirical risk)을 사용한다.

• 즉, empirical risk를 최소화하기 위한 minimization 문제를 풀어야 한다. 다만, 앞서 말한대로 해당 empirical risk의 minimum이 test set performance 측면에서의 optimum이 아니다. 따라서, overfitting을 방지하기 위해 regularization term(아래 식에서 $\lambda\Omega(\theta)$)을 objective function에 더해준다.

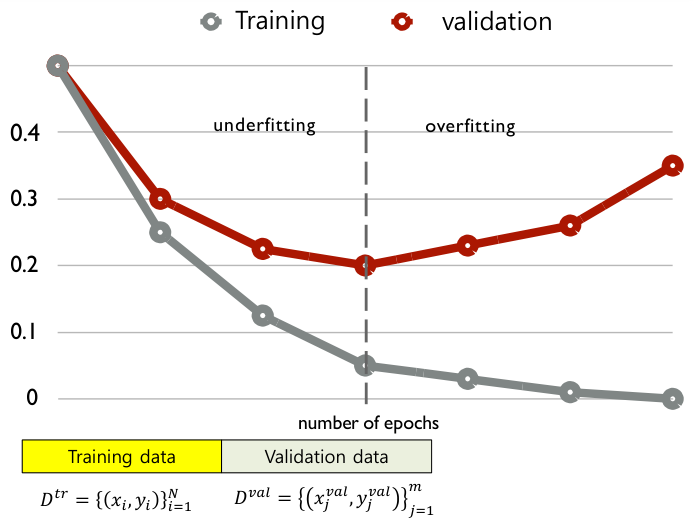
Early Stopping

Test set performance를 미리 알 수 없기에, 이를 예측하기 위해 validation error가 최소화되는 지점에서 train을 종료한다.

이렇듯 overfitting이 발생하기 시작하는 시점에 train을 멈추는 전략을 early stopping이라고 한다.