Stochastic Gradient Descent

• Remind: Calculus Backgrounds

Gradient Descent

일반적인 machine learning 방법론들은 steepest descent 방법 또는 gradient descent(GD) 방법을 통해 loss function을 최소화하는 값을 찾아간다.

이 때, gradient를 모든 training data를 활용하여 계산하는 경우, (full) batch GD라고 한다.

GD는 좋은 접근이나, 일반적으로 loss surface는 non-quadratic, highly non-convex, very high-dimensional하기 때문에, gradient를 계산하는 것조차 어렵고, 또 local minima 또는 saddle point(+ flat region)에서 멈출 확률이 높다. 또한, 모든 data의 gradient를 계산하기에는 dataset이 무척 크기에, 학습 속도가 상당히 느리다.

Stochastic Gradient Descent

GD에서의 $g_t$는 기본적으로 the law of large number를 이용하여 계산된 cost function의 gradient에 대한 approximation이다.

이 때, stochastic gradient descent(SGD)은 approximation을 더 적은 수의 sample들(minibatch)로 계산하는 방식이다.

기존 연구들을 살펴보면 minibatch는 주로 32-256개의 sample을 단위로 삼고 있는데, 실제적으로는 model의 computing 성능에 따라 결정하는 것이 적합하다.

SGD is Often Better

SGD는 당연하게도 GD보다 속도가 빠른데, 이에 더해 심지어 performance도 더 좋은 편이다.
이는 SGD가 이론적으로 GD에 비해 noisy하게 minimum으로 다가가기에 오히려 local optima에 빠지는 것을 피할 수 있기 때문이라고 생각된다.

Noisy gradients가 regularization으로 작동하는 것으로 볼 수 있다.

또한, GD는 data의 distribution보다 data 자체에 대해 최적의 값을 도출하려는 편인데 반해,
SGD는 매 instance마다 학습에 사용되는 data가 data distribution에서 새롭게 생성되는 data라고 볼 수 있으므로, GD에 비해 generalization error를 최소화하는 경향이 있다.

따라서, dataset을 minibatch로 나눌 때 minibatch 간 distribution이 유사하도록 분리하는 것이 좋기 때문에 일반적으로 나누기 전 data를 한번 섞어준다.

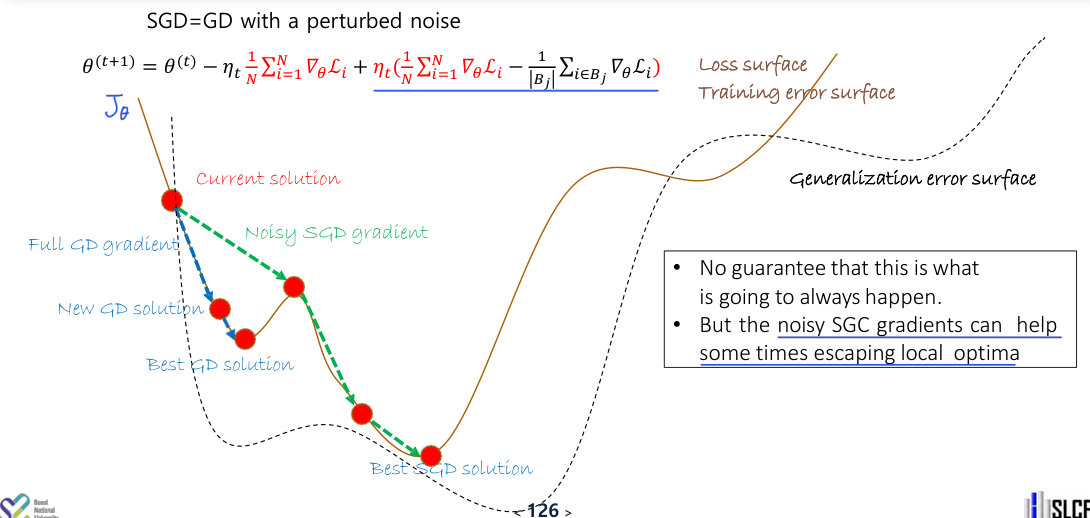
특히, 시간에 따라 변하는 dataset에 대해서는 더더욱 SGD가 적합하다. (GD는 past sample들에 대해 biased되는 경향이 강하다.)