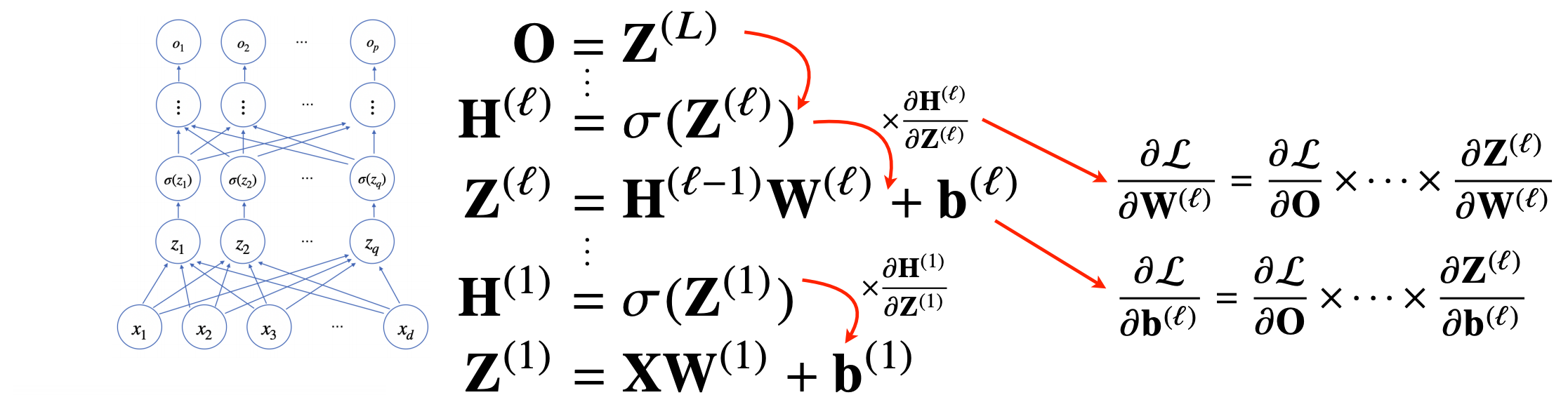[AI Basic] 비선형모델 - 신경망 이론(Neural Network, Perception) [+ MLP, Backpropagation]

Recorder·2021년 8월 3일

BoostCamp - Deep Learning Basic

목록 보기

4/5

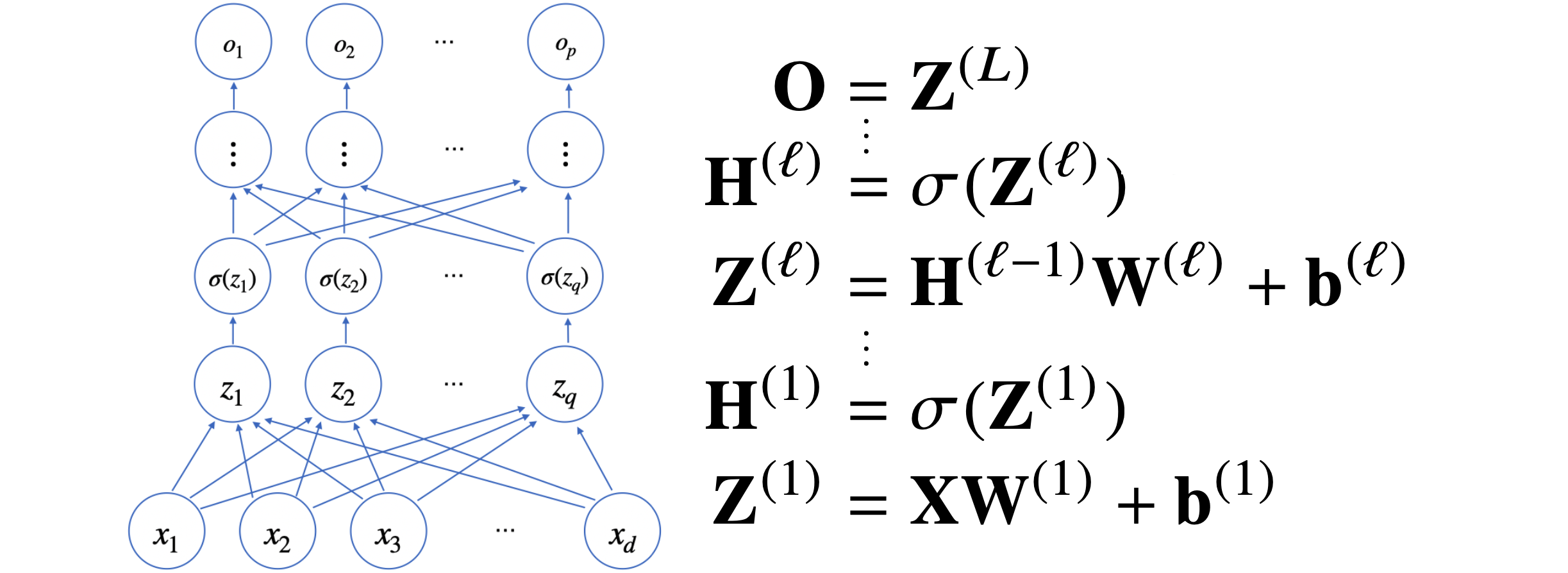
데이터를 해석하는 가장 간단한 방법은 선형모델이다. 하지만 선형 모델만으론 복잡한 데이터를 해석하기 어려운 경우가 많다.

따라서 비선형적인 방법을 이용해서, 더 다양하고 정교한 분석을 하곤 한다.

그 대표적인 방법이 신경망 이론이다. 이는 흔히 딥러닝이라고 불리는 가장 기본적인 방법이다.

1. 구성 요소

먼저 신경망 모델을 분해해보자.

신경망 모델은 비선형 모델이지만, 선형 모델과 비선형 함수들의 결합으로 이루어져있다. 선형 수식에 비선형함수를 곱해서, 비선형으로 바꿔주는 것이다.

여기선 신경망 모델에 사용되는 대표적인 수식들을 살펴보자. 아래의 수식들을 결합하여 사용하면, 하나의 신경망이 된다.

A. 선형 모델 수식

이때 사용하는 선형 모델 수식은 아래와 같다.

O = X * W + B
(n * b) (n * d) (d * p) (n * p)

X : 데이터 (수집한 데이터 그 자체)**텍스트**
W : 가중치 (데이터를 다른 벡터 공간으로 보내줌. 결과로 바꿔줌)
b : 절편 (모든 행에 일정한 값을 더해줌. 각 행이 보두 같은 값을 가짐)

식을 보면, 입력 X는 n * d, 출력 O는 n * b 로 행렬 크기가 바뀐다. 이를 통해 d가지 종류의 데이터로 b가지 종류의 정보를 얻을 수 있음을 알 수 있다. 아래의 그림과 같이 변형된다고 생각하면 된다.

이때 W가 입력을 결과 값으로 바꾸어 주는 중간 과정이다.

📂(참고) n는 항복의 개수이고, d와 b는 항목 별 요소의 수 이다.
예를 들면, 100개의 강의에 대해 각각 카테고리, 구독자수, 가격, 별점 정보를 가지고 있고, 이걸로 각 강의별 조회수와 판매량을 예측한다고 가정해보자. 이 경우 n=100, d=4, b=2이다.

선형모델에 대해 좀 더 알고 싶으면, 이 앞의 글(https://velog.io/@recoder/AI-Basic-%EC%84%A0%ED%98%95%ED%9A%8C%EA%B7%80%EB%B6%84%EC%84%9D)을 참고하자

B. 활성함수

활성함수는 비선형 함수로서, 선명 모델로 나온 출력값을 비선형 모델로 바꾸어 준다.

활성함수를 쓰지 않으면, 딥러닝은 선형 모델과 차이가 없으므로 매우 중요하다.

활성하수는 여러가지가 있다. 아래는 일반적으로 알려진 활성함수들이다.
이 중 딥러닝에선 ReLU를 기본으로 한 함수들이 많이 사용된다.

📁 ReLU를 많이 사용하는 이유
전통적으로 많이 사용하는 활성함수였던 Sigmoid와 tanh의 경우 -1~1의 값을 가지고 있다. 이로 인해 반복적으로 곱해줄 경우 값이 0에 수렴하게 된다. 즉 값이 너무 작아져서 제대로된 기능을 할 수 없게된다(소실). 이에 대안으로 고안된 함수가 ReLU이다. 물론 여전히 특정 분야(ex. RNN)에선 전통적인 함수도 많이 사용된다.

이런 활성함수는 선형모델로 계산한 결과인 잠재벡터의 각 노드에 개별적으로 적용되어 새로운 잠재벡터를 만든다.

수식으로 보면 이와 같고,

그림으로 보면 아래와 같은 구조를 가진다.

이와 같이 선형모델과 합성함수를 합성한 함수가 하나의 신경망이다.

C. Softmax 연산

위 수식들을 통해 구한 결과를 해석할 때, softmax 연산을 사용하는 경우가 많다.

소프트맥스는 모델의 출력을 확률로 해석할 수 있게 변환해주는 함수이다.
벡터가 특정 클래스에 속할 가능성을 계산하는데 사용한다.
주로 학습에만 사용되며, 추론을 할 땐 one-hot 벡터를 사용한다.

모든 결과 값에 대해, 아래의 수식을 적용해준다.

2. MLP, 다층 퍼셉트론(Multi-Layter Perceptron)

딥러닝에선 위에서 만든 신경망을 여러층 합성하여 사용하며, 이를 다층 퍼셉트론이라고 부른다.

신경망을 계산한 결과(선형분석 -> 활성함수)에 다시 선형함수를 적용하고, 활성함수를 적용하는 것이다.

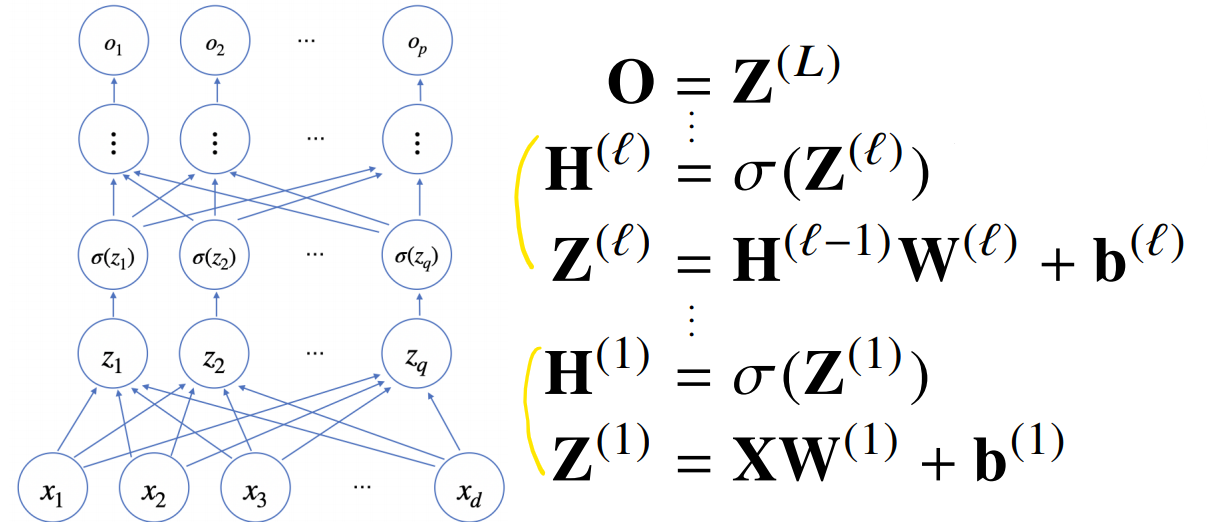
목적 함수를 근사할 땐 노드가 많아야 정확한 결과가 나온다.
하지만 만약 이 노드들을 2층으로만 모두 구현할 경우(universal approximation theorem), 속도가 느리고 효율이 떨어지게 된다.
이를 해결하기 위해 사용되는 것이 MLP이다. MLP로 층을 깊게해서, 층별 노드의 숫자를 크게 줄이면 속도가 훨씬 빨라진다. 같은 기능을 구현할 때의 노드 숫자도 크게 줄어든다.
따라서 일반적으로 2층 신경망보다 효율적이다.

3. 역전파(Backpropagation)

위에선 입력으로부터 출력을 계산하는 과정을 설명하였다.

이제 이 식을 개선시키기 위해선, 이 식으로 계산한 결과와 실제 데이터의 차이를 줄여야 한다. 즉, 손실함수(loss function)을 최소화하는 가중치행렬을 찾아야 한다.

손실함수( $L$ )를 최소화하기 위해선 경사하강법을 사용할 수 있다.
그리고 경사하강법을 이용하기 위해선 손실함수에 대한 미분값( $\frac{\partial L}{\partial W^{(l)}}$ )을 계산해야한다.

손실함수와 경사하강법에 대해 알고 싶으면 아래 링크를 함고하자!
https://velog.io/@recoder/Basic-AI-경사하강법선형회귀분석

이때 여러 층으로 구성된 복잡한 신경망을 미분하기 위해서, 역전파(Backpropagation) 알고리즘을 사용한다.

이 역전파 알고리즘을 사용하는 과정을 살펴보자.

1) 순전파(Forward Propagation) 단계에서, 단계별 미분

순전파는 입력 $X$ 에서 예측값 $\hat{y}$ 까지의 순차적인 계산을 의미한다.
앞서 MLP를 설명할 때처럼, 아래의 화살표 순서로 계산하는 것이다.

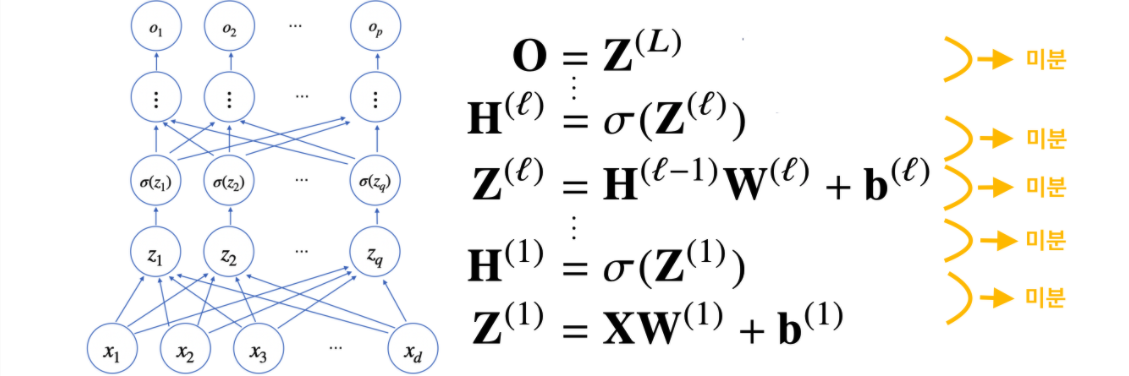
역전파 알고리즘은 기본적으로 Forward Propagation 단계에서 미리 미분 값을 활용한다.
따라서 순전파 단계에서 미분값을 미리 저장해두어야 한다.

2) 연쇄법칙(chain-rule) 기반 자동미분(auto-differentiation)

MLP는 일종의 합성함수이다. 따라서 합성함수 미분법인 연쇄법칙을 통해 미분할 수 있다.

\frac{\partial z}{\partial x} = \frac{\partial z}{\partial w} \frac{\partial w}{\partial x}

MLP에서의 과정을 살펴보면 아래와 같다.

최종 결과물 $\hat y$ (n층)을 그 아래층(n-1)으로 미분해서, n-1층을 가중치(W)를 업데이트한다. 그리고 해당 미분한 값은 아래 층으로 전달한다.
최종 결과물(n)을 n-2층으로 미분한 결과물은, (n-1층에서 전달받은 미분 값) * (n-1 층을 n-2로 미분한 값)으로 계산할 수 있다. 이를 통해 n-2층의 가중치를 업데이트 한다.
...
최종 결과물(n)을 입력(1층)으로 미분한 결과물은, (2층에서 전달받은 미분 값) * (2층을 입력으로 미분한 값)으로 계산할 수 있다. 이를 통해 1층(입력)의 가중치를 업데이트 한다.