[AI-Basic] 선형모델 - 선형회귀분석(Linear Regression)

인공지능 모델은 크게 보면 선형모델과 비선형모델로 나눌 수 있다.
말 그대로 모델의 모양이 선형인지, 아닌지를 통해 구분하는 것이다.

그림으로 보면 왼쪽이 선형모델, 오른쪽이 비선형모델이다.

현실 속 대부분의 데이터는 비선형모양을 가진다. 이로 인해 최신 딥러닝 기술에선 주로 비선형모델을 사용한다.

하지만 선형 모델의 경우 훨씬 쉽게 모델링할 수 있다는 장점이 있어서, 선형 분석이 가능한 데이터라면 비선형모델보다 훨씬 효율적으로 만들 수 있다.
또한 비선형 모델도 선형모델을 기초로 만들어진다.

이 글에선 가장 기본적인 선형분석방법인 선형회귀분석(Linear Regression)에 대해 알아보겠다.

1. 선형회귀분석이란?

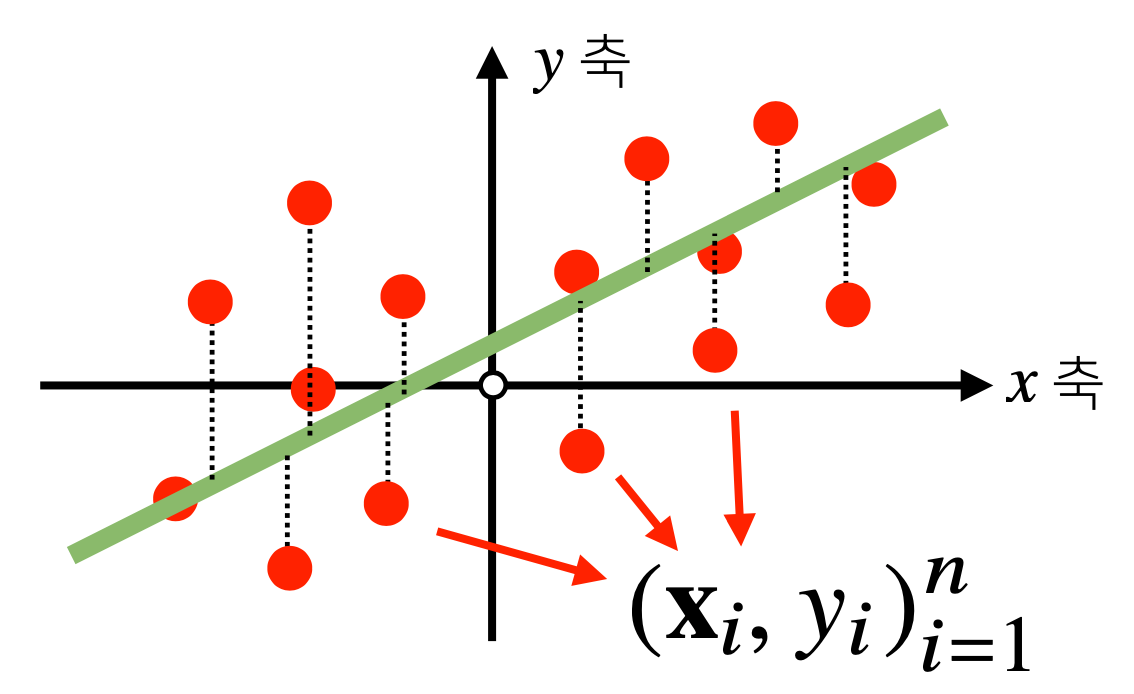
선형회귀분석은 독립변수 X와 종속변수 y의 상관관계를 선형모델(직선)로 회귀분석하는 것이다.

가장 간단한 형태로 이해해보면

이 식과 같은 형태이다. 좀 더 풀어쓰면, 아래와 같다.

x->y 로 변환하는 β를 찾는다고 생각하면 쉽다.

위 수식을 그림으로 나타내보면, (x, y) 평면에서 관계식(초록색 직선)을 찾는 것이다.

2. 목적식

여기서 수식을 통해 찾는 $\hat y$ 과 실제 데이터 y는 오차가 존재하게 된다.
모든 데이터가 이미 완벽한 직선 형태로 주어지지 않는 한, 데이터와 완벽히 일치하는 직선은 없기 때문이다.

이 오차를 최소화하는 β(선형회귀계수)를 찾을수록 정확한 회귀분석을 수행하는 것이다.

이때 $\hat y$ = Xβ이므로,

를 만드는 β를 찾아야 한다.

3. 경사하강법으로 선형회귀계수(β) 구하기

$||y - Xβ||_2$ 의 최소값을 구하기 위해, 경사하강법을 사용한다.

경사하강법에 대해 잘 모른다면, 이 앞의 글 (https://velog.io/@recoder/series/Deep-Learning)을 참고하길 바란다.

1) 위 식을 미분하기

• 편미분 전개

• 모든 항 전개

  $(- \frac{X_1^T(y-X\beta)}{n||y-X\beta||_2}, ..., - \frac{X_d^T(y-X\beta)}{n||y-X\beta||_2} )$

• 합치기

  $-\frac{X^T(y-X\beta)}{n||y-X\beta||_2}$

2) 경사하강법 적용

경사하강법에 따라, 위 미분값을 반복적으로 빼면 $||y - Xβ||_2$ 의 최소값을 구할 수 있다.

앞서 미분한 식을 여기 대입하면 아래와 같다.
이때, 미분한 식이 앞에 -가 붙은 식이므로, 경사하강법 적용 시엔 +가 된다는 점을 주의하자.

✌️ Loss Function
위 계산에선 y와 $\hat y$의 오차를 $||y - Xβ||_2$로 계산하였다.
하지만 둘의 오차를 표현하는 방식은 이 이외에도 여러가지가 있다. 그리고 오차를 계산하는 함수들을 손실함수(loss function)이라고 부른다.
이는 데이터와 구하고자 하는 값 등 요소에 따라, 적절히 선택해야 한다.
✌️ 가장 쉬운 예로는 앞에서 사용한 식을 제곱한 식($||y-X\beta||_2^2$)을 대신 사용할 수도 있다.
최소화하는 β를 찾는 것이므로 결과는 같으면서도, 식이 좀 더 간단해진다.

$\nabla _\beta||y-X\beta||_2^2 = (\partial _{β_1}||y-X\beta||_2^2, ..., \partial _{β_d}||y-X\beta||_2^2) = -\frac{2}{n} X^T(y-X\beta)$

$\beta^{(t+1)} \leftarrow \beta^{(t)} + \frac{2\lambda}{n} X^T(y-X\beta^{(t)})$

4. 알고리즘

for t in range(T):                       #종료조건을 학습 횟수로 설정(앞서처럼 eps를 설정해도 무방)
    error = y - X @ beta                 #@는 행렬곱
    grad = - transpose(X) @ error
    beta = beta - lr * grad

알고리즘은 기본적으로 이 앞 포스트에서 설명한 경사하강법 알고리즘과 동일한 방식이다.
단, 이번에는 eps이하로 가면 종료하는 대신, 학습 횟수를 설정하였다. (어느 쪽이든 상관은 없다. 단 요즘 딥러닝은 횟수를 주로 사용한다.)

예를 들면 아래와 같은 형태로 구현할 수 있다.

이와 같은 알고리즘은 학습률(lr)과 학습횟수(T)에 따라 성능이 크게 차이난다.
따라서 두 가지 요소를 잘 설정해야 한다.