[paper-review] Asymmetric Non-local Neural Networks for Semantic Segmentation

riverdeer·2021년 7월 19일
Deep LearningNon-local blocknon-localsemantic segmentation
0

Paper Review

목록 보기
17/23

Zhu, Z., Xu, M., Bai, S., Huang, T., & Bai, X. (2019). Asymmetric non-local neural networks for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 593-602).

Non-local Series

아래에서 Non-local operation에 대한 내용을 먼저 다루었습니다.
1. Non-local Neural Networks

1. Introduction

@ Long range dependency
현재 많은 연구에서 사용되고 있는 Convolution은 long range dependency를 포착하는 데 제한된 역량을 가지고 있다. 단일 convolution filter는 그 부분에 상관있는 부분을 모두 포착하는 데 receptive field의 크기가 제한적이기 때문이다.

Long range dependency - 한 부분에 대해 상관 관계를 가지는 부분은 꼭 그 부분 근처에 있을 것이란 보장은 없다. 예를 들어 한 사람이 공을 찼을 때 멀리 떨어진 공은 공의 주변의 배경보다는 멀리 떨어진 공을 찬 사람이 더 관련이 있을 것이다. 이렇게 거리적으로 멀리 떨어졌으나 그 두 요소가 가지는 상관관계를 long range dependency라 부른다.

이전의 연구들은 long range dependency를 충분히 활용하는 경우 성능이 개선될 수 있다고 말하고 있다.

@ Non-local
Non-local Neural Networks에서 non-local means라는 컴퓨터 비전에서 image denoising을 위한 filter 테크닉을 신경망과 결합해 이미지 내의 한 위치와 다른 모든 위치들 간의 상관관계를 계산했다.

(a) Non-local Neural Networks 에서 제안한 기존 Non-local block 도식, (b) 본 논문에서 제안하는 Non-local block 도식

하지만 이 Non-local operation을 거치는 과정에서 많은 컴퓨팅 비용과 GPU 메모리 점유가 필요했다. 본 논문의 저자들은 Key branch와 Value branch에서의 출력 크기가 동일하다면 non-local block의 출력 크기가 변하지 않을 것이라고 생각했다.
이에 따라 Key branch와 Value branch에서 몇 가지 대표적인 지점(SS)만 샘플링할 수 있으면 컴퓨팅 비용을 크게 줄일 수 있다고 제안한다.

Semantic segmentation과 scene parsing에서 context information 및 long range dependency를 확보하기 위한 최근 관련 연구를 리뷰한다.

@ Encoder-Decoder

  • Long et al., Noh et al.
    • FCN의 형태로 Encoder에서 bottleneck feature를 만듬.
    • 이를 deconvolution과 같은 방법으로 Decoding하여 sementic segmentation을 수행
  • Ronneberger et al.
    • U-Net.
  • Zhang et al.
    • Context Encoding Module을 도입하여 semantic 클래스 중요도를 예측.
    • 이를 기반으로 선택적으로 클래스 별 feature map을 강화하거나 약화시킴.

@ CRF
머신러닝에서 주로 context information을 포착하기 위해 frequently-used operation, Conditional Random Field (CRF)를 딥러닝에 결합하는 연구들이 있었다.

@ Different Convolutions

@ Spatial Pyramid Pooling
object detection에서 활용되던 spatial pyramid pooling에 영감을 얻어 이를 semantic segmentation에 적용하고자 하는 연구들이 있었다.

  • Chen et al.
    • DeepLab, multiple scales를 포착하기 위한 Atrous Spatial Pyramid Pooling (ASPP) layer 도입.
  • Zhao et al.
    • PSPNet
    • 서로 다른 scale의 embed context features를 반영하기 위한 Specific layer를 도입.
    • Spatial Pyramid Pooling 뒷 부분에 Specific layer 추가

@ Non-local

  • Wang et al.
    • Non-local means라는 컴퓨터 비전에서 image denoising을 위한 filter 테크닉을 신경망과 결합
    • 이미지 내의 한 위치와 다른 모든 위치들 간의 상관관계를 계산

3. Asymmetric Non-local Neural Network

3.1. Revisiting Non-local Block

여기에선 기존의 Non-local Neural Networks의 non-local operation의 설계를 다시 짚어보고 있다.

Non-local Neural Networks 에서 제안한 기존 Non-local block 도식

1.
입력 X∈RC×H×WX \in \mathcal R^{C \times H \times W}가 주어졌을 때, 1×11\times 1 convolution Wϕ,Wθ,WγW_\phi, W_\theta, W_\gamma를 통해 XX를 서로 다른 임베딩으로 변환한다.

ϕ=Wϕ(X),θ=Wθ(X),γ=Wγ(X),ϕ∈RC^×H×W,θ∈RC^×H×W,γ∈RC^×H×W\phi = W_\phi (\mathcal X), \theta = W_\theta(\mathcal X), \gamma = W_\gamma(\mathcal X),\\ \phi \in \mathcal R^{\hat C \times H \times W}, \theta \in \mathcal R^{\hat C \times H \times W}, \gamma \in \mathcal R^{\hat C \times H \times W}

C^\hat C는 변환된 임베딩의 채널 수

2.
다음으로 행렬 ϕ\phi와 θ\theta를 C^×N\hat C \times N의 사이즈로 flatten을 거치고 곱해 행렬 VV를 생성한다.
즉, ϕ∈RC^×H×W,θ∈RC^×H×W,γ∈RC^×H×W→ϕ∈RC^×N,θ∈RC^×N,γ∈RC^×N\phi \in \mathcal R^{\hat C \times H \times W}, \theta \in \mathcal R^{\hat C \times H \times W}, \gamma \in \mathcal R^{\hat C \times H \times W} \rightarrow \phi \in \mathcal R^{\hat C \times N}, \theta \in \mathcal R^{\hat C \times N}, \gamma \in \mathcal R^{\hat C \times N}

V=ϕT×θ.V∈RN×N,N=H×W.V = \phi^T \times \theta. \\ V \in \mathcal R^{N \times N}, N = H\times W.

3.
VV를 Non-local Neural Networks에서 언급한 방법처럼 normalization(ff function)을 거친다. 여기에서는 softmax, rescaling, none등의 선택지가 있는데 본 논문에서는 softmax(embedded gaussian)를 선택했다.

V⃗=f(V).\vec V = f(V).

4.
γ\gamma를 곱한다.

O=V⃗×γT,O∈RN×C^O = \vec V \times \gamma^T, \\ O \in \mathcal R^{N\times \hat C}

5.
최종 Output은 1×11\times 1 convolution WoW_o를 곱하여 C^\hat C에서 원래 채널 수 CC로 채널 수를 복원하고 Residual 구조처럼 입력 값 XX를 더한 값으로 한다.

Y=Wo(OT)+XY = W_o(O^T) + X

혹은 입력 XX와 최종 결과를 concatenate한다.

Y=cat(Wo(OT),X)Y = \mathrm{cat}(W_o(O^T), X)

3.2. Asymmetric Pyramid Non-local Block

위에서 서술한 Non-local network은 long range dependency를 포착하는 데에는 효과적이지만 시간적으로, 메모리적으로 매우 부담되는 연산이다.

@ Motivation and Analysis.
Semantic segmentation에선 세밀한 features를 뽑아내기 위해 큰 해상도의 output을 갖는 경우가 많다. 이 경우 O(C^N2)=O(C^H2W2)\mathcal O(\hat CN^2) = \mathcal O(\hat CH^2W^2)의 시간 복잡도는 굉장한 부담으로 작용한다.
본 논문의 연구진은 단순하게 NN의 숫자를 더 작은 숫자 SS로 NN의 일부를 샘플링하여 줄이는 것으로 해결하고자 했다((SS ≪\ll NN)).

@ Solution.
위에서의 분석을 토대로 NN에서 일부 SS를 sampling하는 모듈인 Pθ,Pγ\mathcal P_\theta, \mathcal P_\gamma를 θ,γ\theta, \gamma 각각에 대해 정의한다.

θP=Pθ(θ),γP=Pγ(γ),θP∈RC^×S,γP∈RC^×S\theta_P = \mathcal P_\theta(\theta), \gamma_P = \mathcal P_\gamma(\gamma), \\ \theta_P \in \mathcal R^{\hat C \times S}, \gamma_P \in \mathcal R^{\hat C \times S}

이후 절차는 기존 non-local block에서와 동일하다.

VP=ϕT×θP,V⃗P=f(VP)VP,V⃗P∈N×SV_P = \phi^T \times \theta_P, \\ \vec V_P = f(V_P) \\ V_P, \vec V_P \in N \times S
OP=V⃗P×γPT,YP=cat(Wo(OPT),X)OP∈RN×C^,YP∈RC×NO_P = \vec V_P \times {\gamma_P}^T, \\ Y_P = \mathrm{cat}(W_o({O_P}^T), X) \\ O_P \in \mathcal R^{N\times \hat C}, Y_P \in \mathcal R^{C\times N}

위와 같은 asymmetric matrix multiplication은 계산 복잡도 면에서 O(C^NS)\mathcal O(\hat CNS)로 기존 non-local block 보다 O(C^N2)\mathcal O(\hat CN^2)으로 눈에 띄게 낮은 모습을 볼 수 있다.

@ Asymmetric Pyramid Non-local Block.
그렇다면 전체 NN에서 일부 SS를 샘플링하는 방법은 어떻게 되는가?

논문의 저자들은 Global and multi-scale representations를 잡아내는 것에 효과적인 Spatial Pyramid Pooling을 Non-local block에도 적용할 수 있을 것이라는 생각을 했다.

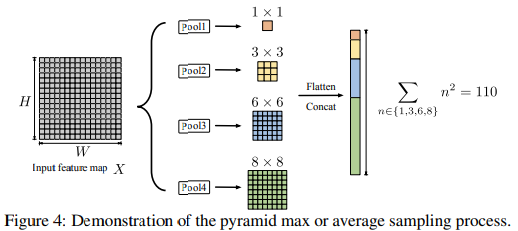
논문에서는 θ\theta와 γ\gamma에서 각각 네 개의 pooling 결과를 flatten하여 SS (=110=110)로 하였다.

S=110=∑n∈{1,3,6,8}n2S = 110 = \sum_{n\in \{1, 3, 6, 8\}} n^2

3.3. Asymmetric Fusion Non-local Block

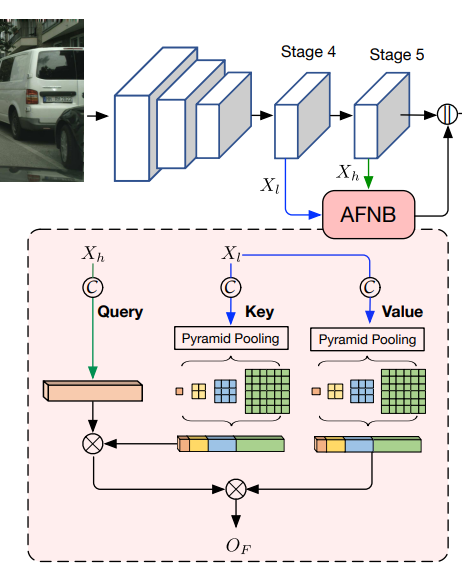
addition이나 concatenate와 같은 방식으로 다른 수준(level)의 두 요소를 fusion하는 것은 semantic segmentation에 좋은 영향을 줄 수 있다.

1.
기존 Non-local block이 하나의 feature map을 입력으로 하는 반면에 Fusion Non-local Block은 두 가지의 입력이 있다.

  • low-level feature map: Xl∈RCl×NlX_l \in \mathcal R^{C_l \times N_l}
    • NlN_l: low-level feature map의 크기
  • high-level feature map: Xh∈RCh×NhX_h \in \mathcal R^{C_h \times N_h}
    • NhN_h: high-level feature map의 크기

먼저 이 두 가지 입력을 각각의 1×11 \times 1 convolution 임베딩(Wl,WhW_l, W_h)을 거쳐 임베딩으로 만들어준다.

Eh=Wh(Xh),El=Wl(Xl),Eh∈RC^×Nh,El∈RC^×Nl\mathcal E_h = W_h(\mathcal X_h), \mathcal E_l = W_l(\mathcal X_l), \\ \mathcal E_h \in \mathcal R^{\hat C \times N_h}, \mathcal E_l \in \mathcal R^{\hat C \times N_l}

2.
이 두 행렬을 곱해 유사도 행렬 VF∈RNh×NlV_F \in \mathcal R^{N_h \times N_l}를 만들고, 동일하게 normalization 과정을 거친다.

VF=EhT×El,V⃗F=f(VF)V_F = \mathcal {E_h}^T \times \mathcal E_l, \\ \vec V_F = f(V_F)

3.
다음으로 low-level feature map과 곱해준다.

OF=V⃗F×ElT,OF∈RNh×C^O_F = \vec V_F \times \mathcal {E_l}^T, \\ O_F \in \mathcal R^{N_h \times \hat C}

4.
마지막으로 Residual 과정을 거치고 high-level feature map의 채널 수 ChC_h로 만들기 위해 1×11 \times 1 convolution을 거친다.

YF=cat(Wo(OFT),Xh).Y_F = \mathrm{cat}(W_o({O_F}^T), X_h).

PNB에서 적용했던 것처럼 Fusion Non-local Block에도 spatial pyramid pooling을 적용해 계산량 부담을 완화하였다. 이로인해 각각 Asymmetric PNB(APNB), Asymmetric FNB(AFNB)로 명명했다.

3.4. Network Architecture

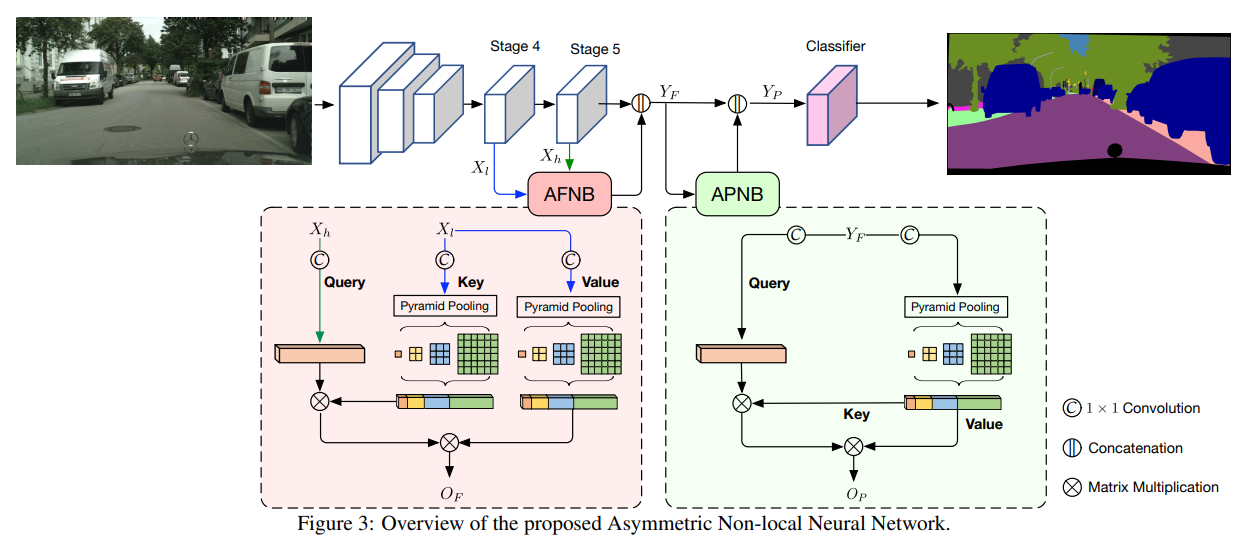
논문에서 ResNet101을 backbone network로 사용했으며 마지막 두 down-sampling 구간을 dilation convolution으로 대체했다. 이는 마지막 두 down-sampling 구간에서의 결과 feature map 크기를 동일하게 유지하기 위함이다. 결과적으로 그림 3에서 볼 수 있듯이 Stage 4, Stage 5, Classifier는 모두 같은 크기를 유지하고 있음을 알 수 있다.

4. Experiments

4.1. Datasets and Evaluations Metrics

@ Datasets

  • Cityscapes
  • ADE20K
  • PASCAL Context

@ Evaluation Metric

  • Mean IoU: Mean of class-wise intersection over union

4.2. Implementation Details

@ Training objectives
본 실험에서 사용한 손실함수는 아래와 같이 두 cross entropy loss로 이루어져 있다.

L=Lfinal+λLStage4,λ=0.4\mathcal L = \mathcal L_{\mathrm {final}} + \lambda \mathcal L_{\mathrm {Stage4}}, \\ \lambda = 0.4

이와 같이 손실함수를 구성한 배경에 대해선 논문에서 서술하고 있지 않지만 기존의 ResNet101의 일부 segmentation 성능을 가져가고 싶은 것 같다.

@ etc.

  • ResNet101 backbone pretrained on ImageNet
  • Stochastic Gradient Descent optimizer
  • learning rate
    • initial learning rate
      • Cityscapes: 0.01
      • PASCAL Context, ADE20K: 0.02
    • learning rate decay: 1−(itermaxiter)power1 - ({{\mathrm {iter}} \over {\mathrm {max_iter}}})^ \mathrm {power}, power=0.9\mathrm {power} = 0.9
  • Data
    • input size, batch size, epochs
      • Cityscapes: 769×769,8,60K769 \times 769, 8, 60\mathrm K
      • PASCAL Context: 480×480,16,28K480 \times 480, 16, 28\mathrm K
      • ADE20K: 520×520,16,150K520 \times 520, 16, 150\mathrm K
    • augmentation
      • random scaling in the range of [0.5,2.0][0.5, 2.0]
      • random horizontal filp
      • random brightness

4.4. Ablation Study

@ Efficacy of the APNB and AFNB

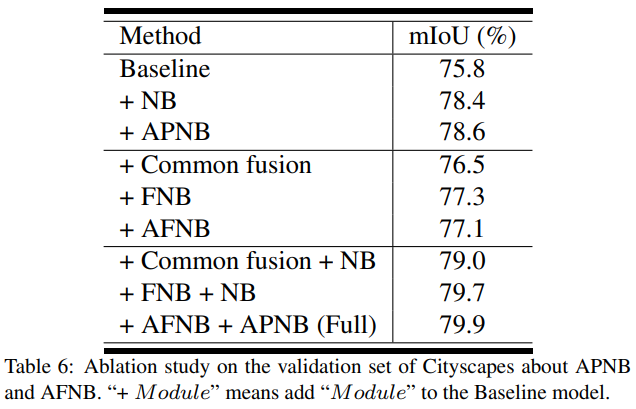
  • Baseline: FCN-like ResNet-101
  • + NB: Classifier 이전에 Non-local block 추가
  • + Common Fusion: Baseline에서 Stage4 -> Stage5 과정을
    Stage5 ++ ReLU(BatchNorm(Conv(Stage4)))로 변경

@ Selection of Sampling Methods
APNB 모듈에서 샘플링 방법의 선택은 그 성능에 많은 영향을 미친다.

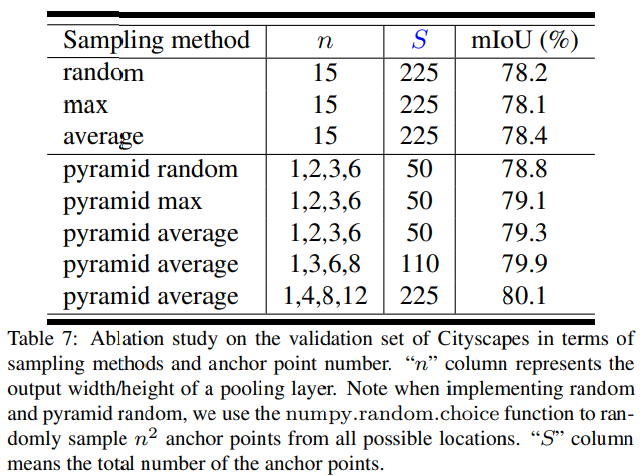
@ Influence of the Anchor Points Numbers
APNB 모듈에서 pyramid pooling layer의 크기 역시 그 성능에 큰 영향을 미친다. Table 7에서처럼 SS의 크기가 늘어날수록 성능이 향상되는 것 을 볼 수 있으며 논문에서 저자들은 efficacy와 efficiency의 적절한 지점인 (1,3,6,8)(1, 3, 6, 8)을 default setting으로 설정했다.

profile
riverdeer
딥 러닝을 공부하는
이전 포스트

[paper-review] Non-local Neural Networks

다음 포스트

[paper-review] GCNet: Non-local Networks Meet Squeeze-Excitation Networks and Beyond

0개의 댓글