[paper-review] GCNet: Non-local Networks Meet Squeeze-Excitation Networks and Beyond

Cao, Y., Xu, J., Lin, S., Wei, F., & Hu, H. (2019). Gcnet: Non-local networks meet squeeze-excitation networks and beyond. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops (pp. 0-0).

---

Non-local Series

아래에서 Non-local operation에 대한 내용을 먼저 다루었습니다.
1. Non-local Neural Networks
2. Asymmetric Non-local Neural Networks for Semantic Segmentation

---

1. Introduction

@ long-range dependency
Visual scene의 전체적인 이해를 위해 long-range dependency를 포착하는 것은 여러 연구들을 통해 중요하다는 점이 입증되었다.

하지만 Visual task에서 주류로 활용되고 있는 Convolution neural networks (CNN)은 구조 상으로 지역적인(local) 연산이다. 때문에 멀리 떨어진 요소들 간의 관계, long-range dependency를 포착하기 위해선 convolution 레이어들을 매우 크게, 깊게 쌓아야한다. 하지만 이는 컴퓨팅적으로 비효율적이고 최적화에도 어렵다.

@ Non-local
이러한 문제로 인해 Non-local Neural Networks에서는 self-attention 메커니즘을 통해 long-range dependency의 모델링을 제안했다. 하나의 input, 이미지 내에서 모든 픽셀 각각에 대해 그 픽셀과 다른 픽셀 간의 상관관계를 계산해 각각 픽셀 feature에 계산한 상관관계를 반영하는 방법으로 long-range dependency를 모델링할 수 있다고 했다.

하지만 각 query 픽셀 마다 attention map을 시각화해보면 그 attention map들이 유사한 것을 볼 수 있었고 이는 불필요한 계산 부담을 일으킨다고 주장한다.

때문에 논문에서는 모든 query point에 대해서 각각 따로 attention map을 계산할 것이 아니라 모든 query point에 동일한 한 가지 attention map을 사용할 것을 제안한다. 저자들은 이를 Simplified Non-local (SNL) Block으로 이름지었다.

@ Squeeze-and-Excitation
이렇게 동일한 한 가지 attention map을 사용해 Simplified Non-local Block의 구조는 Squeeze-and-excitation Networks에서 제안한 Squeeze-and-Excitation (SE) block과 유사하다고 판단했고, 이를 바탕으로 Simplified Non-local block과 Squeeze-and-Excitation block을 결합하여 Global Context (GC) Block을 최종적으로 제안하고 있다.

---

2. Related Work

@ Deep architecture

• ResNeXt & Xception
  • 신경망을 좁고 깊게 쌓을 것만이 아니라 한 블록에서 브랜치를 나누어 신경망을 구성하도록 했음 (inception block 처럼)
• Deformable Convolution Networks & Deformable ConvNets V2
  • Deformable Convolution을 제안함으로써 이미지의 'geometric'한 특성의 모델링 능력을 향상시킴
• Squeeze-Excitation Networks
  • feature의 채널 간 스코어를 계산해 채널 간 dependency를 모델링하도록 설계함

@ Long-range dependency modeling

1. Self-attention 메커니즘 사용
   • Relation Networks for Object Detection
     • Object detection에 self-attention을 활용, 물체 간의 관계를 모델링하는데 사용
   • Non-local Neural Networks
     • self-attention으로 pixel-level pairwise 관계를 모델링
   • CCNet: Criss-Cross Attention for Semantic Segmentation
     • 십자가 형태의 attention 연산을 하는 criss-cross block을 쌓음으로써 NLNet을 발전시켰고 이를 semantic segmentation에 적용했다.
   • 해당 방법은 각 query 포인트에 대한 query-indenpendent attention map을 학습하는 것이고 때문에 모든 픽셀에 대해 pixel-level pairwise를 계산해야 하기 때문에 지나친 컴퓨팅 비용이 필요한 방법이다.
2. query-independent global context 사용
   • Squeeze-Excitation Networks, Gather-Excite: GENet and PSANet: Point-wise Spatial Attention Network for Scene Parsing
     • feature map을 한 번 더 가공하여 global context 및 channel dependency를 모델링
   • CBAM: Convolution Block Attention Module
     • 역시 feature map을 가공하여 Spatial한 위치, channel-wise dependency를 모델링
   • 이 방법들은 feature map을 가공하여 global context를 획득하려는 방법들이다. 하지만 feature map을 가공한다고 해서 global context를 충분히 반영할 수 있다고는 할 수 없다.

---

3. Analysis on Non-local Networks

3.1. Revisiting the Non-local Block

기존 non-local block은 다른 위치에서의 정보를 결합함으로써 특정 쿼리 위치(query position)의 특징을 강화하는 것에 목표하고 있다.
같은 차원 수를 가진 입력, 출력 $\mathbf x, \mathbf z$에 대해서,

• $i$: index of query positions, $j$: enumerates all possible positions
• $\mathbf x = \{\mathbf x_i\}^{N_p}_{i=1}$
  • $N_p=H\times W$ for image, $N_p=H\times W\times T$ for video
• $\mathcal C(\mathbf x)$: normalization factor

이후 논문에서의 편의를 위해 ${f(\mathbf x_i, \mathbf x_j) \over \mathcal C(\mathbf x)} = \mathcal w_{ij}$로 표기한다.

기존 Non-local block을 제안했던 논문에선 네 가지 instantiations를 제안했다.

• (a) Gaussian, $\mathcal w_{ij} = {\exp ( \left\langle \mathbf x_i, \mathbf x_j \right\rangle) \over \sum_m \exp ( \left\langle \mathbf x_i, \mathbf x_m \right\rangle)}$
• (b) Embedded Gaussian, $\mathcal w_{ij} = {\exp ( \left\langle W_q\mathbf x_i, W_k\mathbf x_j \right\rangle) \over \sum_m \exp ( \left\langle W_q\mathbf x_i, W_k\mathbf x_m \right\rangle)}$
• (c) Dot product, $\mathcal w_{ij} = {\left\langle W_q\mathbf x_i, W_k\mathbf x_m \right\rangle \over N_p}$
• (d) Concat, $\mathcal w_{ij} = {\mathrm{ReLU}(W_q[\mathbf x_i, \mathbf x_j]) \over N_p}$

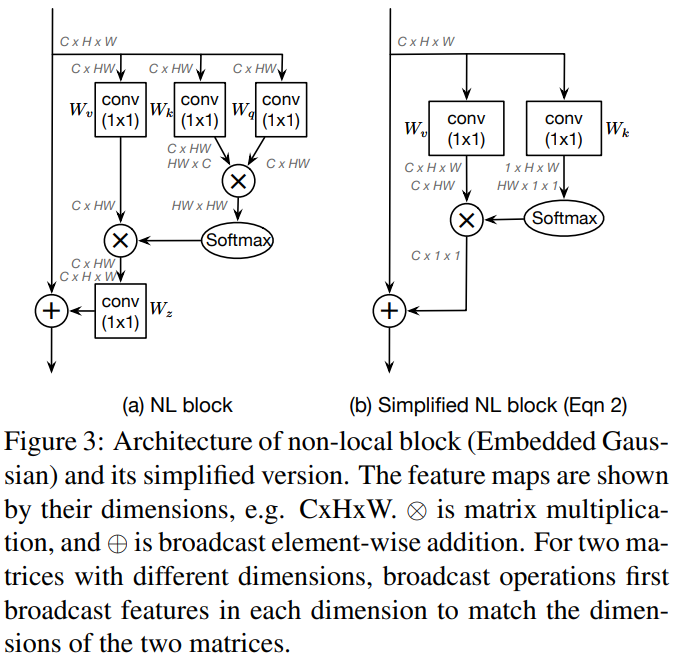
이 중 가장 널리 쓰이는 버전은 (b) Embedded Gaussian 이다. 이에 대한 도식은 Figure 3 (a)에서 볼 수 있다.

3.2. Analysis

@ Visualization
논문에서는 직관적인 non-local block의 이해를 위해 각기 다른 query position에서의 attention map을 시각화했다. 저자들은 COCO dataset에서 6장의 랜덤한 이미지를 선택했고 3개의 다른 query position (red point)에 대해서 attention map을 시각화했다. Figure 2에서 같은 사진에 대해 서로 다른 query point에 대한 attention map들이 비슷비슷함을 볼 수 있다.

@ Statistical Analysis
위에서의 시각화 결과와 더불어 attention map에 대해 통계적 분석을 통해 모든 attention map이 비슷하다는 것을 주장한다.
$\mathbf v_i$를 위치 $i$에 대한 feature vector라고 할 때,

으로 두 attention map간의 평균적 차이를 구할 수 있다. 여기에서 사용하는 $dist(\cdot, \cdot)$은 Cosine distance와 Jensen-Shannon divergence (JSD)를 사용한다.

• Cosine distance: $dist(\mathbf v_i, \mathbf v_j)=(1-\cos(\mathbf v_i, \mathbf v_j))/2$
• Jensen-Shannon divergence (JSD): $dist(\mathbf v_i, \mathbf v_j)={1\over 2}\sum_{k=1}^{N_p} \left( v_{ik} \log{2v_{ik} \over v_{ik} + v_{jk}} + v_{jk} \log{2v_{jk} \over v_{ik} + v_{jk}}\right)$

Why JSD can be distance function?. 저자들은 Gaussian, Embedded Gaussian function에 대해서 각각 attention map의 합이 $1$로 나타나기 때문에 이를 확률 분포로써 여길 수 있다고 생각했다. 때문에 확률 분포 간의 거리를 측정하는 데 쓰이는 Jensen-Shannon divergence를 distance function으로 사용할 수 있다고 주장하고 있다.

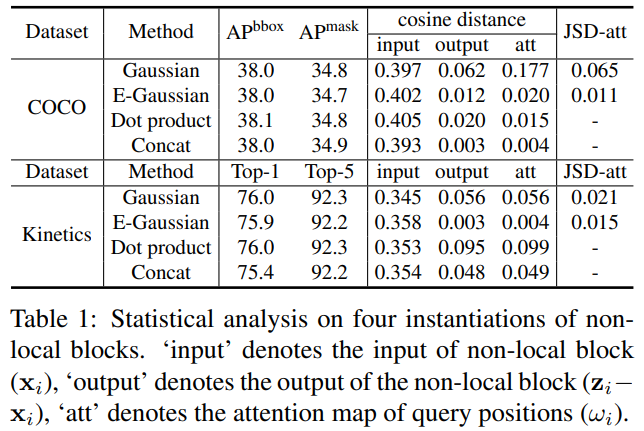
위 Table 1의 결과로 아래와 같은 시사점을 지적하고 있다.

1. $\mathrm{input}$ 이미지의 cosine distance가 충분하게 차이가 있는 것으로 보아 non-local block을 거치기 전에는 서로 다른 쿼리 위치에 대해 충분히 다름을 알 수 있다.
2. 반면, $\mathrm{output}$의 cosine distance는 충분히 작으므로 non-local block에 의해 모델링된 global context features가 서로 다른 쿼리 위치에 대해 거의 동일함을 알 수 있다.
3. 즉, non-local block은 각 쿼리 위치별로 특징적인 global context feature를 계산하려 하지만 학습이 된 후의 global context feature는 각 쿼리 위치에 영향을 받지 않고 있다.

@ 결론. 괜히 계산만 복잡하게 query-specific global context feature를 모두 계산할 필요없다.

---

4. Method

4.1. Simplifying the Non-local Block

본 논문에서는 Section 3에서의 실험 결과를 바탕으로 Non-local block을 단순화해야 한다고 주장한다. 여기에는 기존 Non-local block에서도 가장 성능이 좋았던 Embedded Gaussian pairwise function을 사용한 버전을 발전시켰다. 다만 이 때, Relation Networks for Object Detection에서 $W_z$의 효과가 미미하다고 주장했고 이를 받아들여 삭제했다.

위에서 제시했던 기존 Non-local block의 수식보다 훨씬 간결해진 것을 느낄 수 있다.

기존 non-local block과 가장 눈에 띄게 다른점은 residual 덧셈 부분인 $\mathbf x_i$를 제외하면 query 위치 $i$에 대해서 독립적으로 계산된다는 점이다. 즉 모든 쿼리 위치 $i$에 대해서 동일한 attention map 혹은 global context가 제공된다.
실험 결과에서도 기존 Non-local (NL) block에 비해서 이 simplified non-local (SNL) block의 성능이 ImageNet classification, Object detection on COCO, Action recognition의 세 가지 task에서 모두 좋았다.

4.2. Global Context Modeling Framework

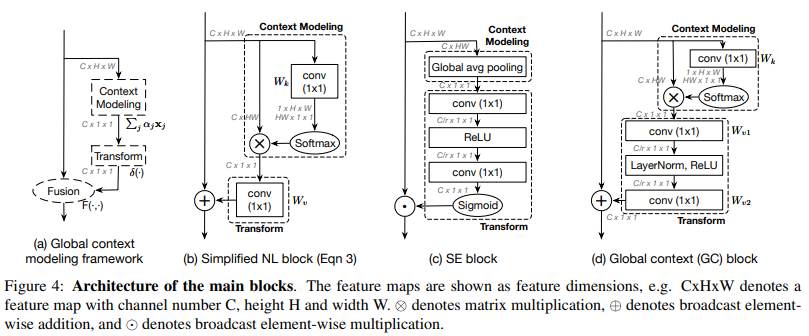
위에서 나타낸 Simplified non-local block을 간단하게 나타내면 아래 그림의 (a)와 같이 [a] Context modeling - [b] Transform - [c] Fusion의 구조로 나타낼 수 있다. 역시 마찬가지로 Squeeze-and-excitation Networks의 Squeeze Excitation (SE) block을 (a)와 같이 [a] Context modeling - [b] Transform - [c] Fusion의 구조로 생각할 수 있다.

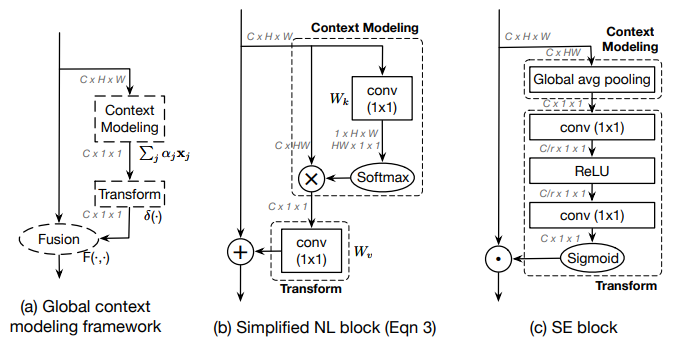
• $F$: [c] fusion
  • SNL block에선 matrix element-wise addition
  • SE block에선 matrix element-wise multiplication
• $\delta$: [b] Transform
  • SNL block에선 linear transformations matrix $W_v$를 이용한 임베딩 과정으로 구현
  • SE block에선 $\mathrm{conv}(1 \times 1) \rightarrow \mathrm{ReLU} \rightarrow \mathrm{conv}(1\times 1)$으로 이어지는 "Excitation" 과정으로 구현
• $\sum_{j=1}^{N_p}\alpha_j\mathbf x_j$: [a] Context modeling
  • SNL block에선 pairwise function $f$(embedded gaussian)를 통한 가중치 계산으로 구현
  • SE block에선 Global Average Pooling

4.3. Global Context Block

논문의 저자들은 위 Section 4.2에서의 구조 연구를 바탕으로 Global Context (GC) Block을 제안하고 있다. GC Block은 SNL block의 effective modeling on long-range dependency라는 장점과 SE block의 lightweight computation의 장점 두 가지를 모두 가지고 있는 블록이라고 주장한다.

@ lightweight computation
Simplified Non-local block의 [b] Transform 과정에서 computation 비용이 크다는 단점이 있다.
예를 들어 ResNet 아키텍처의 마지막 블록 $\mathrm{res}_5$는 채널 수 2048을 가지는데, 이 때 $1\times 1$ convolution을 사용하면 $C\times C=2048 \times 2048$로 어마어마한 파라미터 수를 갖게된다.

여기에서 SE block의 bottleneck transform 과정을 도입하면 $2\times C\times C/r$로 파라미터 수를 줄일 수 있게된다. $r$은 줄어드는 차원의 bottleneck ratio.

@ formulation