[paper-review] Non-local Neural Networks

Wang, X., Girshick, R., Gupta, A., & He, K. (2018). Non-local neural networks. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 7794-7803).

---

Abstract

Convolution과 recurrent 연산들은 모두 지역적으로 인접한 값들의 처리를 위해 설계되어 있다. 본 논문에서는 long-range dependencies 특징 추출에 반영하기 위한 non-local operation을 제안한다.

• non-local operation은 특정 한 위치에서의 모든 위치에 대한 특징 값들의 가중합으로 나타낼 수 있다.
  • 전역적인 특징(global features, long-range dependency)을 잡아낼 수 있다.
• non-local operation으로 설계한 non-local block은 기존 컴퓨터 비전 아키텍처에 쉽게 덧붙여 적용할 수 있다.

---

Introduction

long-range dependency를 포착하는 것은 컴퓨터 비전이나 음성, 언어 데이터와 같은 시퀀스 데이터에서 매우 중요한 작업이다. 이미지의 경우 사람이 이미지를 대하는 것처럼 전체적인 이미지를 볼 수 있어야하고 언어의 경우에도 글의 전체적 맥락을 파악하는 것은 중요하기 때문이다.

컴퓨터 비전 및 시퀀스 데이터에서 가장 많이 사용되는 convolution and recurrent 연산은 모두 공간적으로도 시간적으로도 local neighborhood에서의 연산을 처리한다. 때문에 convolution과 recurrent에서 long-range dependency를 반영하기 위해선 매우 깊게(very deep) convolution과 recurrent 연산을 반복해야 한다.

본 논문에서는 효율적이고 간단하며 기존에 사용되고 있는 딥러닝 아키텍처에 잘 녹아들 수 있는 요소들로 구성된 non-local operation을 제안한다.

non-local operation은 여러 장점이 있다.

• a) recurrent나 convolution과 다르게 non-local operation은 픽셀이나 시퀀스 요소 간의 거리에 무관하게 두 요소 간 상호작용을 계산한다
• b) 효율적이고 레이어의 수가 적을 때에도 최선의 결과를 달성할 수 있다.
• c) 입력과 출력값의 크기가 동일하여 입력값의 크기를 보존할 수 있으며 따라서 다른 convolution이나 recurrent에 쉽게 결합될 수 있다.

---

Related Work

@ Non-local image processing

• Buades et al.
  • image denoising을 위한 filtering 알고리즘
  • 한 이미지에서 모든 픽셀에 대한 weighted mean을 계산한다.

@ Graphical models
Long-range dependency는 Conditional Random Field (CRF)와 같은 graphocal models로도 모델링할 수 있다.

• L.-C. Chen et al.
  • semantic segmentation의 출력 값에 CRF를 적용하여 후처리에 사용했다.

@ Feedforward modeling for sequences
음성이나 언어 시퀀스를 모델링하기 위한 feedforward network를 사용하는 경향이 나타나고 있다. 이 때에는 very deep 1-D convolution과 large receptive field를 사용해 long-term dependency를 포착한다.

@ Self-attention

• Vaswani et al.
  • 본 연구는 self-attention과 많은 관련이 있다.
  • self-attention은 non-local mean 연산의 한 형태로 볼 수 있다.

---

Non-Local Neural Networks

Fomulation

• $\mathbf x$: 입력 값; 이미지, 시퀀스, 영상과 같은 입력 값의 features
• $i$: output index
• $j$: output index $i$와 관련 점수를 계산할 $\mathbf x$안에서의 모든 index들
• $\mathbf y$: 출력값, $\mathbf x$와 크기가 같다.
• $f$: pairwise function, $i$와 모든 $j$사이의 관계를 계산하는 함수이다.
• $g$: $j$ 위치에서의 입력값의 representation을 계산한다.
• $\mathcal C(\mathbf x)$: normalize factor

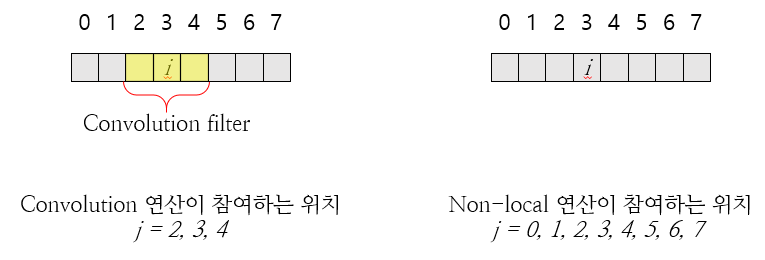
@ Convolution vs. Non-local
non-local 연산은 모든 위치($j$)가 연산에 참여한다.
반면 convolution은 local neighborhood에서의 위치만 연산에 참여한다.

kernel size가 3인 convolutional을 1D입력에 대해서 수행하면 $i-1 \le j \le i+1$에 해당하는 $j$만 연산에 참여한다.

@ Recurrent vs. Non-local
Recurrent은 심지어는 $j=i$ and $j=i-1$의 index의 요소들만 연산에 참여한다.

@ Fully-connected layer (fc layer) vs. Non-local

• 가중치의 사용 측면에서.
  • fc layer는 학습된 가중치를 단순 사용
  • non-local은 서로 다른 위치 간의 상관관계를 기반하여 계산
• 입력 및 출력 크기의 측면에서.
  • fc layer는 고정된 입력 및 출력의 크기가 정해져 있다.
  • non-local은 입력의 크기에 가변적이며 출력의 크기도 입력의 크기와 동일하다.

Instantiations

앞서 나타낸 non-local operation의 수식에서 pairwise function인 $f$의 여러가지 형태를 소개한다. 다만 실험을 통해 여러가지 형태에 결과가 크게 달라지지 않으며 non-local operation 자체가 의미가 있는 것임을 나타낼 수 있다.
$f$에 대해 소개하기 이전에 $g$는 단순 선형 임베딩의 형태로 사용했으며 $W_g$ 가중치 행렬을 학습하여 $g(\mathbf x_j)=W_g\mathbf x_j$의 형태로 계산된다.

@ Gaussian

$\mathbf x_i^T\mathbf x_j$; dot-product를 유사도로 사용한다. Euclidean distance 역시 두 벡터의 유사도를 측정하는데에 사용되는데 dot-product가 딥러닝 구현에 더 자연스럽다.

@ Embedded Gaussian
Gaussian function의 간단한 확장 버전이다. 위에서는 dot-product로 유사도를 계산하는 것을 embedding space에서 계산하는 방식이다.

저자들은 해당 embedded gaussian function이 "Attention is all you need"의 self-attention 및 attentional 접근 방법과 매우 유사하다고 인정하고 있다.
attentional behavior과 비슷함에도 불구하고 attention score가 본 논문에서의 연구의 핵심이 아님을 강조하고 있다. (non-local operation이 핵심이다)

@ Dot product

$N$은 input $\mathbf x$의 전체 수. $f$의 총합을 $\mathcal C(\mathbf x)$로 할 경우보다 gradient를 간단하게 할 수 있기 때문이다.
dot product와 embedded gaussian의 가장 큰 차이점은 softmax의 적용 유무이다.

@ Concatenation

Non-local Block

마지막으로 $\mathbf y_i = {1 \over \mathcal C(\mathbf x)} \sum_{\forall j} f(\mathbf x_i, \mathbf x_j)g(\mathbf x_j)$ 처럼 계산된 $\mathbf y_i$를 최종적으로 아래와 같이 계산하여 최종 결과물을 산출한다.

여기에서 $+ \mathbf x_i$는 residual connection을 의미한다. residual connection은 입력 값을 출력 값에 더해줌으로써 기존 입력의 특징을 보완해주는 역할을 한다.

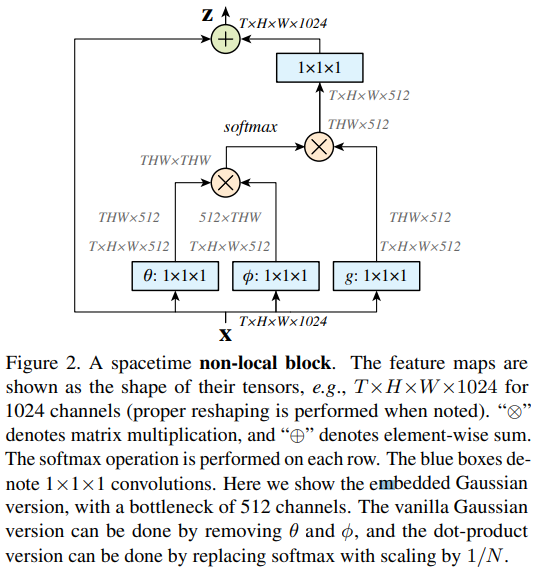
Implementation of Non-local Blocks.
$W_g, W_\theta, W_\phi$의 채널 수를 input $\mathbf x$의 절반으로 설정했다. 이를 통해 bottleneck design을 적용할 수 있으며 연산의 부담을 반으로 줄일 수 있다.