개인적인 논문해석을 포함하고 있으며, 의역 및 오역이 남발할 수 있습니다. 올바르지 못한 내용에 대한 피드백을 환영합니다 :)
1. Introduction
최근 deep neural network를 통한 metric learning이 활발히 연구되고 있다. 이 연구들은 의미적으로 비슷한 데이터들(semantically similar data)이 서로 가깝게 군집화될 수 있도록 어느 한 임베딩 공간(embedding space)에 projection하는 방법을 학습한다. 이러한 임베딩 공간의 퀄리티는 주로 신경망을 학습하는 데 사용되는 손실함수(loss function)에 의해 결정된다.
이와 같은 손실함수는 두 가지 종류로 나뉠 수 있다.
[@ Pair-based loss].
pair-based loss는 임베딩 공간에서의 데이터 간 pairwise 거리를 기반으로 설계된다. 이러한 loss들은 두 개 이상의 데이터 간의 관계를 이용해 데이터와 데이터를 비교하고 이들 간의 세밀한 관계(data-to-data relations)를 학습한다.
- 장점
- 데이터 간의 세밀한 관계를 비교하여 신경망을 학습.
- 풍부한 supervisory signals
- 단점
- 을 학습 데이터 수라고 할 때 학습의 계산복잡도가 및 으로 치솟는다.
- 따라서, 수렴속도가 느리다.
[@ Proxy-based loss]
proxy-based loss들은 proxy를 도입함으로써 위에 나타난 복잡도 문제를 해결했다. proxy는 학습 데이터의 일부 중에서 채택된다. proxy를 채택하는 것도 역시 모델의 파라미터로 학습될 수 있다. proxy를 제외한 나머지 데이터 포인트들에 대해서 하나씩 선택해 같은 클래스인 proxy와는 가깝게 될 수 있도록, 다른 클래스인 proxy와는 멀리 떨어질 수 있도록 학습한다.
- 장점
- 일반적으로 한 batch 내에서 데이터 포인트들을 샘플링하는 pair-based loss에 비해 proxy를 활용하기 때문에 샘플링할 필요가 없어 빠르게 계산할 수 있다.
- noise와 이상치에 강건할 수 있다.
- 단점
- 한 batch 내에서 data-to-proxy relations만 계산할 수 있다.
[@ Proxy-Anchor loss]
본 논문에서 제안하는 Proxy-Anchor loss는 위 두 손실함수들의 장점을 모두 갖추며, 단점을 모두 해결한 손실함수이다. Proxy-Anchor loss는 각 proxy를 하나의 anchor로써 활용해 한 batch안의 모든 데이터 포인트와 관계를 계산한다.
데이터 포인트들을 샘플링할 필요도 없으며 noise, 이상치에도 강건하다. 또한 데이터 포인트에 따라 gradient가 다르게 주어질 수 있기 때문에 data-to-data relations도 고려할 수 있는 손실함수이다.
2. Related work
2.1 Pair-based Losses
- Contrastive loss
- 두 데이터 포인트를 샘플링
- 두 데이터 포인트가 같은 클래스면 서로 가깝게 당기고 다른 클래스면 서로 멀리 떨어지도록 밀어낸다.
- Triplet loss
- anchor 데이터 포인트, anchor와 같은 클래스인 positive 데이터 포인트, anchor와 다른 클래스인 negative 데이터 포인트를 각각 샘플링
- anchor-positive 거리를 가깝게, anchor-negative 거리는 멀리 떨어지게 학습
- N-pair loss & Lifted Structure loss
- 하나의 anchor, 하나의 positive, 여러개의 negative 포인트를 샘플링
- 동일하게 anchor-positive 거리를 가깝게, anchor-negative 거리는 멀리 떨어지게 학습
- 이 때, negative 포인트들 간의 어려움(hardness)를 고려하여 다른 세기로 밀어낸다.
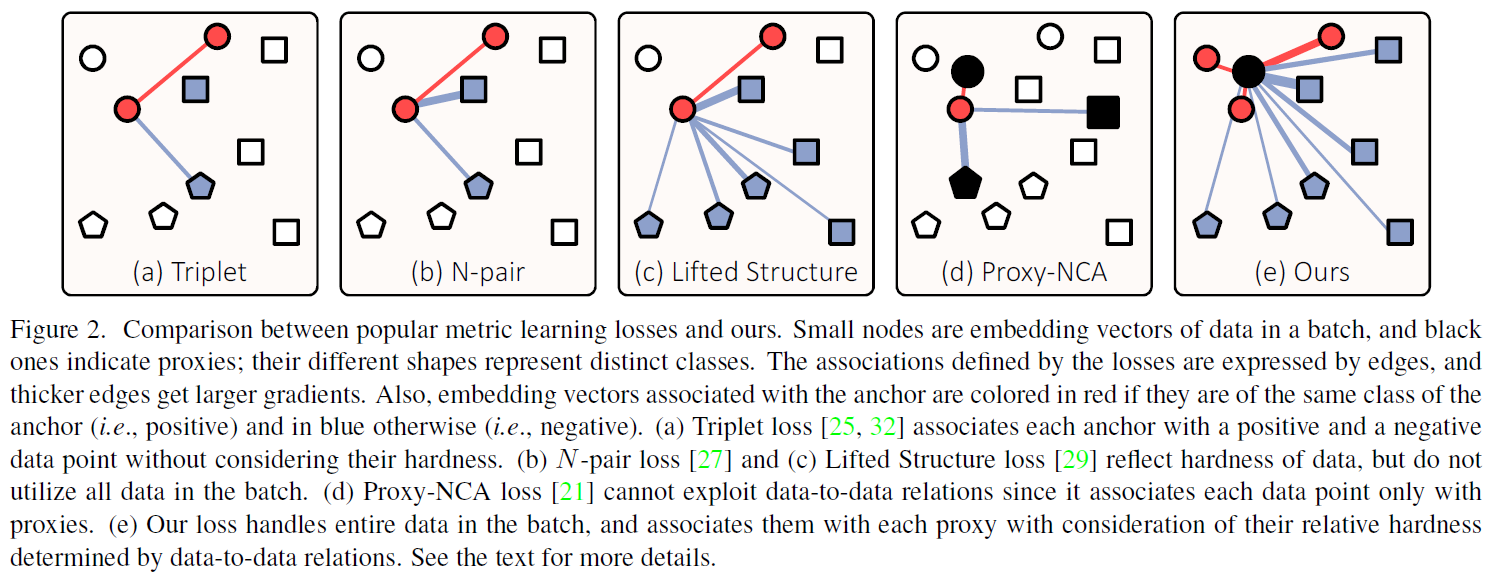
위 손실함수들은 그림 2에서 보는 것처럼 한 배치 내에서 모든 데이터 포인트를 활용하지 않는다. 따라서 유용한 데이터 샘플이 학습이 누락될 수 있다.
2.2 Proxy-based Losses
- Proxy-NCA
- proxy를 활용한 Neighborhood Component Anlysis(NCA).
- 각 클래스마다 하나의 proxy를 선정하고, 다른 한 데이터 포인트를 샘플링
Proxy-based loss는 근본적으로 각 데이터 포인트들을 proxy하고만 연관을 짓기 때문에 data-to-data relations를 학습하기 어렵다.
3. Our Method
3.1 Review of Proxy-NCA Loss
[@ Definition]. Proxy-NCA loss의 일반적인 환경 세팅은 각 클래스 마다 하나씩 proxy를 할당하여 총 proxy의 수는 클래스의 수와 같게 된다.
주어진 입력의 data point의 임베딩 벡터()를 anchor로 하면 입력과 같은 클래스를 가지는 proxy를 positive(), 입력과 다른 클래스를 가지는 proxy들을 negative()로 정의한다.
아래는 Proxy-NCA loss의 정의이다.
- 는 임베딩 벡터 a batch
- , cosine similarity
- , Log-Sum-Exp function
[@ Gradient]. 아래는 Proxy-NCA loss의 gradient이다. gradient를 보면 positive proxy의 경우에 일정한 힘으로 와 가 서로 당겨지는 반면에, negative proxy의 경우 와 가 가까울수록 서로 강력하게 밀려나는 것을 볼 수 있다.
두 벡터가 가까울수록, 즉 cosine similarity가 클수록(=1에 가까울수록), 값이 커진다.
따라서, gradient는 커지며, 서로 강력하게 밀려난다고 해석할 수 있다.
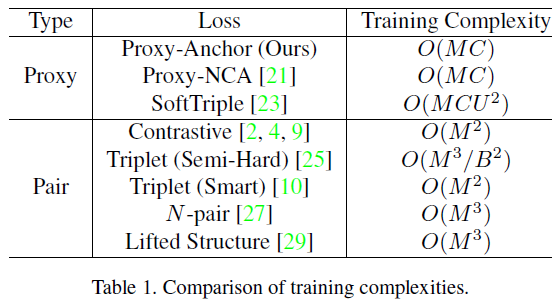
[@ Training complexity]. Proxy-NCA loss는 복잡도 로 기존 pair-based losses가 복잡도 , 를 갖는 것에 비해 빠른 수렴이 가능하다. (는 클래스의 수, 은 데이터 포인트의 수, 일반적으로 .)
3.2 Proxy-Anchor Loss
[@ Definition]. Proxy-Anchor loss의 주요 아이디어는 각각의 proxy를 anchor로 하여 한 batch 내의 모든 데이터와 연관성을 계산하는 것이다. 본 논문에서는 Proxy-NCA loss에서처럼 각 클래스 당 하나의 proxy를 할당했다. 아래는 Proxy-Anchor loss의 정의이다.
- , margin
- , scaling factor
- , 모든 proxy / , positive proxies
- , 한 batch 내의 모든 임베딩 벡터
- , positive 임베딩 벡터 집합
[@ How it works].
- 가 positive embedding vector일 때
- 의 값은 cosine similarity가 에 가까울수록 최대값을 갖는다.
- 따라서 hardest positive sample, 가장 proxy와 멀리 떨어진 positive sample은 같은 positive sample들 중에 최대값에 가장 근접한다. (cosine similarity가 에 가장 근접하기 때문!)
- 그렇다면 hardest positive sample이 positive sample 중에 가장 큰 함수값을 가진다.
- 자연스럽게 hardest positive sample이 손실함수에 가장 많은 영향을 준다.
- 가 negative embedding vector일 때
- 의 값은 cosine similarity가 에 가까울수록 최대값을 갖는다.
- 따라서 hardest negative sample, 가장 proxy와 가까운 negative sample은 같은 negative sample들 중에 최소값에 가장 근접한다.
- 그렇다면 hardest negative sample이 negative sample 중에 가장 큰 함수값을 가진다.
- 자연스럽게 hardest negative sample이 손실함수에 가장 많은 영향을 준다.
- 논문에서 제안하는 손실함수가 한 batch 내의 모든 샘플에 대해서 상대적으로 어려운 샘플들에 더 많은 gradient를 제공함으로써 더 나은 embedding space를 구성할 수 있다고 해석할 수 있다.
[@ Comparison to Proxy-NCA]. Proxy-Anchor loss의 가장 큰 장점은 positive sample들에 대해 상대적인 hardness에 따라 다른 gradient를 제공해줄 수 있다는 점이다. 반면 Proxy-NCA는 positive sample들에 대해 일정한 gradient를 제공한다. 이 점이 본 논문에서 제안하는 Proxy-Anchor loss가 data-to-data relations를 고려할 수 있음을 나타낸다.
또한 margin의 개념을 더할 수 있다는 점에서 장점이 있다. margin을 손실함수에 포함하게 되면 같은 클래스끼리는 더 조밀하게, 다른 클래스끼리는 더 멀리 벌어질 수 있게 embedding space를 학습할 수 있다.
그림 3에서 이 두 가지 장점을 확인할 수 있다.

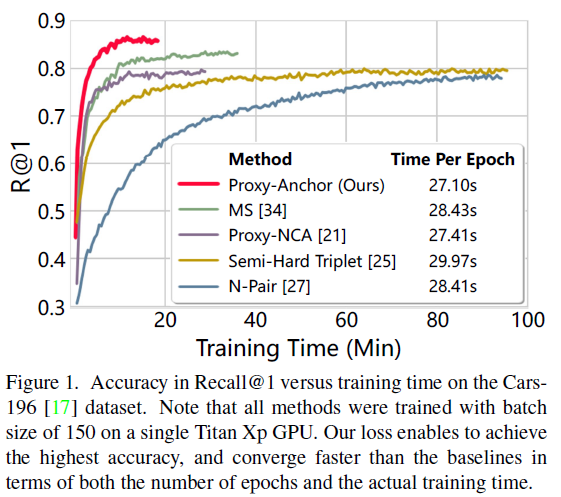
3.3 Training Complexity Analysis
4. Experiments
4.1 Datasets
- CUB-200-2011
- training: 5,864 images - 100 classes
- testing: 5,924 images - 100 classes
- Cars-196
- training: 8,054 images - 초기 98 classes
- testing: 8,131 images - training classes 제외한 전부
- Stanford Online Product (SOP)
- training: 59,551 images - 11,318 classes
- testing: 60,502 images - training classes 제외한 전부
- In-Shop
- training: 25,882 images - 3,997 classes
- testing: 28,760 images - training classes 제외한 전부
4.2 Implementation Details
[@ Embedding network]. 이전의 연구들과 동일하게 ImageNet classification에 사전학습된 Inception network with batch normalization을 모든 실험에 사용했다.
마지막에는 클래스 수에 맞는 fully connected layer를 붙이고 마지막 output에 -normalize를 적용했다.
[@ Proxy setting]. 이전 Proxy-NCA와 동일하게 클래스 수에 따라 하나씩 proxy를 사용했다. proxy는 단위 hyperspace에 균등하게 펼쳐질 수 있도록 normal distribution을 통해 초기화 진행했다.
[@ Image setting]. 학습 중에는 random cropping, horizontal flipping을 사용, 테스트 중에는 center-crop을 사용하여 잘라낸 이미지 크기는 를 기본으로 했지만 HORDE와의 비교를 위해 의 크기로도 실험을 진행했다.
[@ Hyperparameter setting]. 손실함수 수식에 사용된 ,
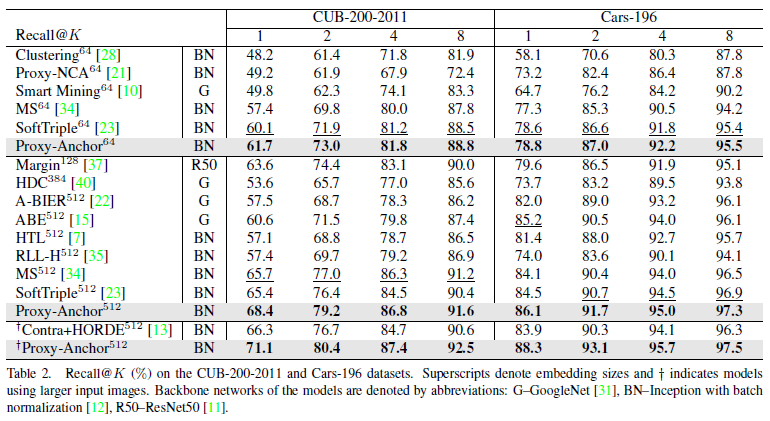
4.3 Comparison to Other Methods
.
한 샘플을 임베딩 공간에 사영했을 때, 모델이 정답 클래스로 추측한 상위 개의 클래스 중에서 정답 클래스가 속하는 경우를 로 하여 반복실험한다.
반복실험하여 해당 표본에 대한 Recall 값을 라 한다.

4.4 Qualitative results
아래는 각 데이터셋에 따라 query 이미지에 대해 검색했을 때 상위 4개의 결과를 나타낸 것이다.
일부 틀리는 경우도 있었지만 틀린 결과도 query 이미지와 외관상 흡사한 이미지이다.

4.5 Impact of Hyperparameters
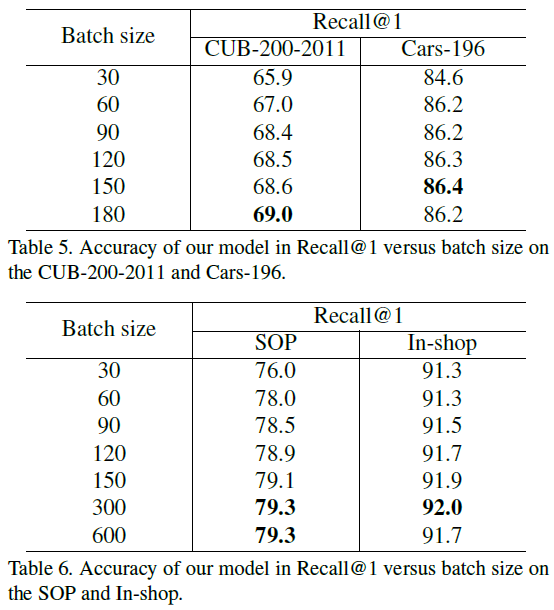
[@ Batch size]. 아래는 batch size에 따른 Recall@1의 값 변화이다.
많은 batch를 한 번에 처리할수록 data point들 간의 관계를 많이 파악할 수 있고 이에 따라 성능이 증가함을 확인할 수 있다.
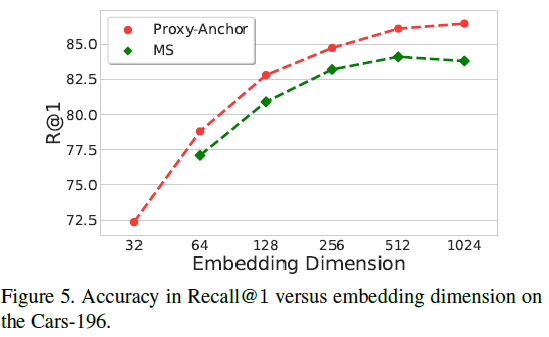
[@ Embedding dimension]. 임베딩 벡터의 차원은 speed and accuracy의 trade-off를 좌우하는 중요한 요소이다. 아래에서 보는 것과 같이 MS loss와 비교했을 때 임베딩 벡터의 차원에 상관없이 일관되게 Proxy-Anchor loss의 성능이 좋았다.
또한 MS loss에서는 1024차원의 높은 차원으로 가면 성능이 하락하는 것과 다르게 Proxy-Anchor loss는 높은 차원으로 갈수록 성능이 동일하게 향상되었다.
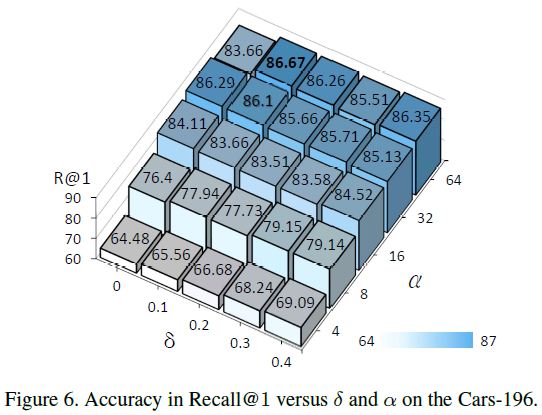
[@ and of our loss].
proxy가 normal distribution을 통해 초기화가 된다고 했는데 정확히 어떻게 proxy들을 잡는 것인가요? 이 부분은 논문을 그저 번역하신 것 같아서 질문 드립니다.