[paper-review] Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

개인적인 논문해석을 포함하고 있으며, 의역 및 오역이 남발할 수 있습니다. 올바르지 못한 내용에 대한 피드백을 환영합니다 :)

Liu, Z., Lin, Y., Cao, Y., Hu, H., Wei, Y., Zhang, Z., ... & Guo, B. (2021). Swin transformer: Hierarchical vision transformer using shifted windows. arXiv preprint arXiv:2103.14030.

---

1. Introduction

본 논문에서는 Transformer의 Computer Vision 분야로의 확장 가능성에 대한 연구를 진행했으며 Computer Vision에서의 general purpose backbone으로 사용될 수 있도록 하려했다.

[@ Scale]
언어 modality와 비전 modality 간의 차이 중 하나는 Scale의 포함 여부이다. 언어 태스크에서 활용되었던 Transformer가 언어를 처리함에 있어 가장 기본적인 단위인 단어 토큰과 다르게 시각적 요소는 크기가 다양하게 출현하게 된다. 이 점은 기존 Object detection과 같은 태스크에서 주된 연구 주제이기도 했다.
현존하는 Transformer 기반의 모델들은 모두 고정된 scale의 토큰들을 가지고 있으며 이는 vision task에 적합하지 않은 특성이다.

[@ Resolution & Computation complexity]
또 하나의 차이점은 텍스트 구절에 비해 이미지의 픽셀 해상도(데이터 밀집도)가 훨씬 높다는 점이다. 픽셀 수준에서 고밀도 예측(dense predictions)이 필요한 semantic segmentation과 같은 vision task에서는 Self-attention의 계산 복잡성이 이미지 크기에 따라 제곱으로 증가하기 때문에 고해상도 이미지에서는 Transformer의 사용이 어렵다.

[@ Swin Transformer]

• Scale
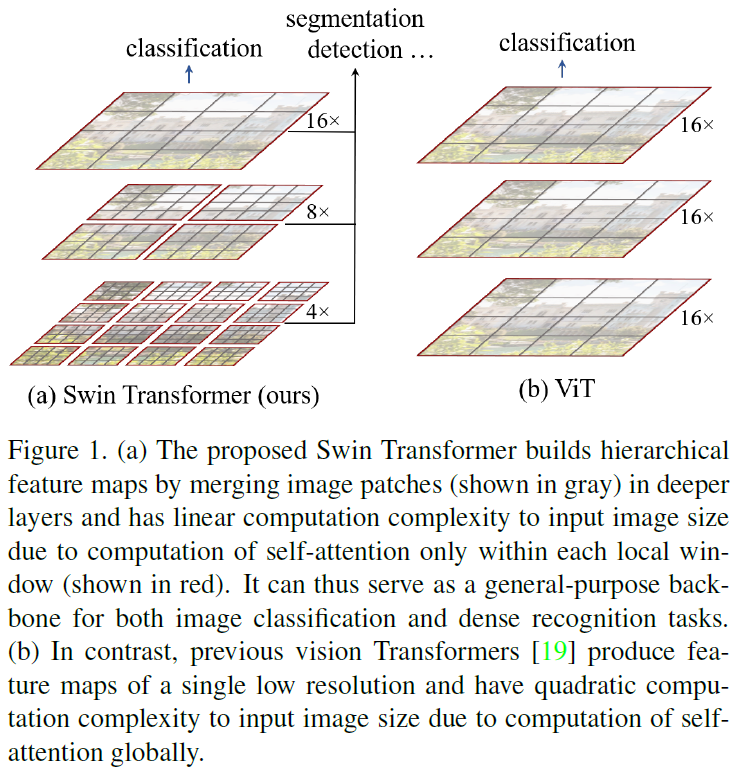
  • 아래 그림 1(a)에서처럼 Swin Transformer는 작은 크기의 패치(patch)에서 시작해 점차 더 모델이 깊어질수록 인점한 패치들을 병합하며 계층적인 특징표현(hierarchical representation)을 구성할 수 있게 된다.
  • Swin Transformer의 이러한 특성으로 인해 기존 Computer vision community에서 주로 사용되던 Object detection이나 Semantic segmentation과 같은 advanced task에도 backbone으로써 사용될 수 있다.
• Resolution & Computation complexity
  • Swin Transformer에서는 이미지를 분할하여 그 분할한 window에 대해서만 Self-attention을 계산하게 된다.
  • 따라서 window 크기를 한 번 지정하면 이미지가 늘어남에 따라 window 내부의 패치 수는 고정되며 따라서 계산복잡도는 이미지 크기에 대해 window 수에 따라서 선형적으로만 증가하게 된다.
  • 이 점은 기존 Vision Transformer가 이미지 크기에 대해 제곱으로 증가하는 것과 대비된다.

---

3. Method

3.1 Overall Architecture

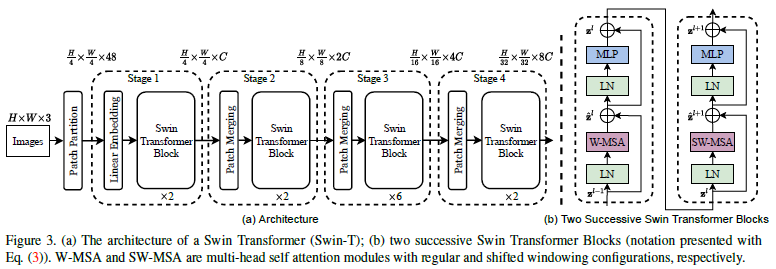
[@ Patch Partition, Patch Splitting Module]
(Vision Transformer와 같이) 입력되는 RGB 이미지를 서로서로 겹치지 않도록 patch로 분할하고 각 patch를 1차원으로 펼친다(flatten).
논문에서는 각 patch의 크기를 $4\times 4$로 사용했으며 따라서 펼친 1차원 patch는 $4\times 4 \times 3(\mathrm{RGB})=48$ 차원을 가진다.

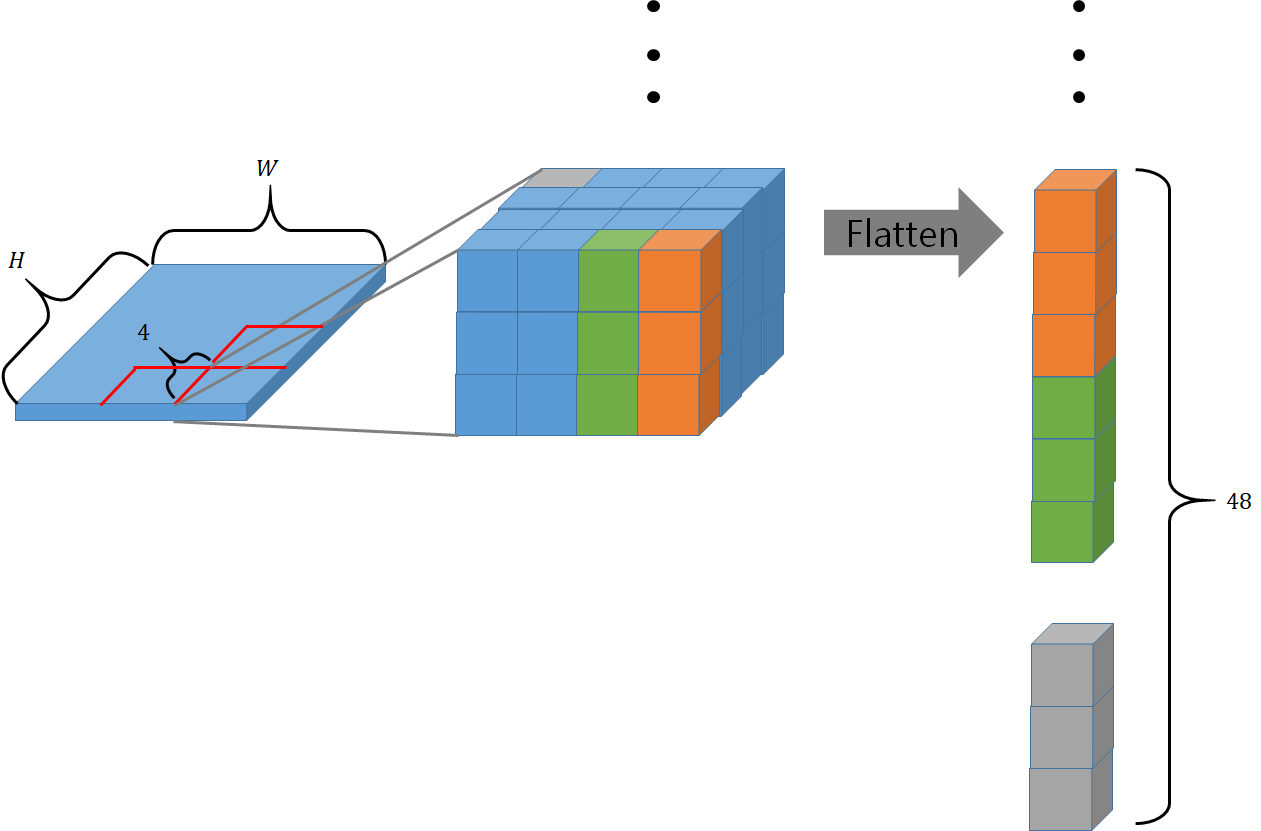
[@ Stage 1]

1. 먼저 Linear Embedding을 거쳐 $C$차원으로 사영(projection)된다.
   • ${H\over 4} \times {W\over 4} \times 48 \rightarrow {H\over 4} \times {W\over 4} \times C$
   • 이렇게 만들어진 $({H\over 4} \times {W\over 4})$개의 $C$차원 벡터들은 Transformer에서의 "token"으로써 사용된다.
2. 각 token들은 일정 갯수의 Transformer block을 통과한다.

[@ Stage 2]

여기에서는 hierarchical한 feature map을 생성하기 위해 patch의 크기를 조정하게 된다.

1. patch merging layer를 통과하여 서로서로 인접한 $(2\times 2)=4$개의 patch들끼리 결합하여 하나의 큰 patch를 새롭게 만든다.
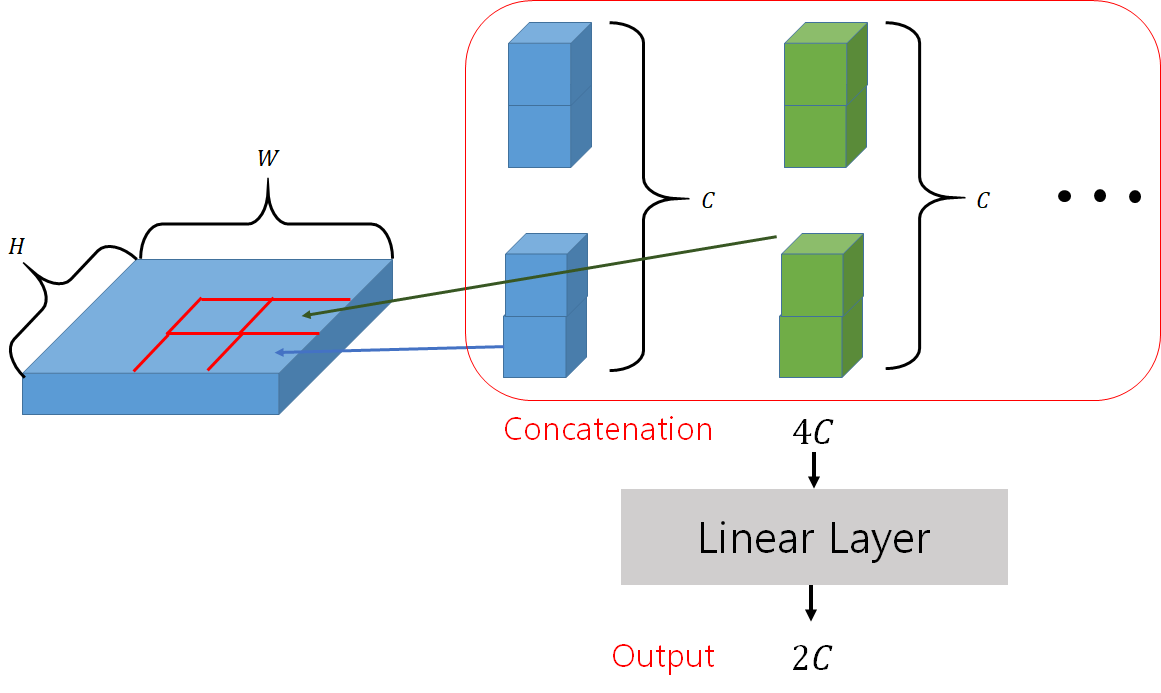
   • 아래는 patch merging layer의 계산 과정을 시각화한 것이다.
   • 인접한 $(2\times 2)=4$개의 patch들을 concatenate하는 과정에서 차원이 $4C$로 늘어나기 때문에 linear layer를 통과하여 $2C$로 조정한다.
2. Stage 1에서와 같이 일정 갯수의 Transformer block을 통과한다.
   • Output: ${H\over 8} \times {W\over 8} \times 2C$

[@ Stage 3 & 4]
Stage 2와 같은 방식으로 점차 patch size는 커지고 patch의 수는 많아지며 각 flattened patch(=token)의 차원은 두 배씩 늘어간다.

• Stage 3: ${H\over 16} \times {W\over 16} \times 4C$
• Stage 4: ${H\over 32} \times {W\over 32} \times 8C$
• 각 Stage에서의 Output은 기존 computer vision task에서 많이 사용되는 형태의 feature map으로 활용될 수 있게된다.

[@ Swin Transformer Block]
각 Stage들은 Swin Transformer Block들을 여러 차례 거치게 된다. Swin Transformer block들은 아래와 같이 구성된다. block 내부의 각 요소들에 대한 설명은 Section 3.2에서 설명하고 있다.

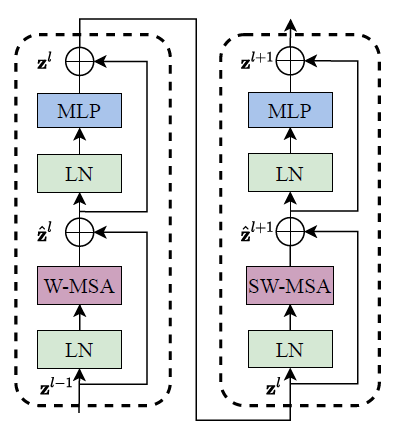
3.2 Shifted Window based Self-Attention

[@ 기존 Vision Transformers의 한계]
Image Classification에 활용된 기존 Transformer 아키텍처와 그 변형들은 토큰과 모든 토큰 사이의 관계를 계산하는 global self-attention을 적용했다.
하지만 이 방법은 계산 복잡도가 입력 이미지 해상도에 대해서 제곱으로 증가하게 되고 dense한 예측이나 높은 해상도의 이미지에 적용하기에는 어려움이 있다.

[@ Self-attention in non-overlapped windows]
논문에서는 위에서 제시한 한계 때문에 효율적인 모델링을 위해 window들 내부에서만 self-attention을 계산하는 것을 제안한다.
$M\times M$개의 패치들로 window가 구성되어 있다고 생각하면 아래와 같이 계산복잡도를 나타낼 수 있다.

기존 MSA 모듈에서 패치 내부의 해상도 $hw$에 제곱으로 증가하는 반면 W-MSA 모듈에서는 패치 내부에서만 계산이 발생하기 때문에 한 window 내부의 패치의 수 $M \times M$에 따라 증가한다.

[@ Shifted window partitioning in successive blocks]
위에서 언급한 W-MSA(window-based self-attention) 모듈은 window간의 연결성이 부족하고, 이는 모델링 성능을 저해시키는 요소이다.
논문에서는 연산의 효율을 유지하면서도 window들 간의 연결성을 반영할 수 있는 shifted window partitioning 방법을 제안한다.

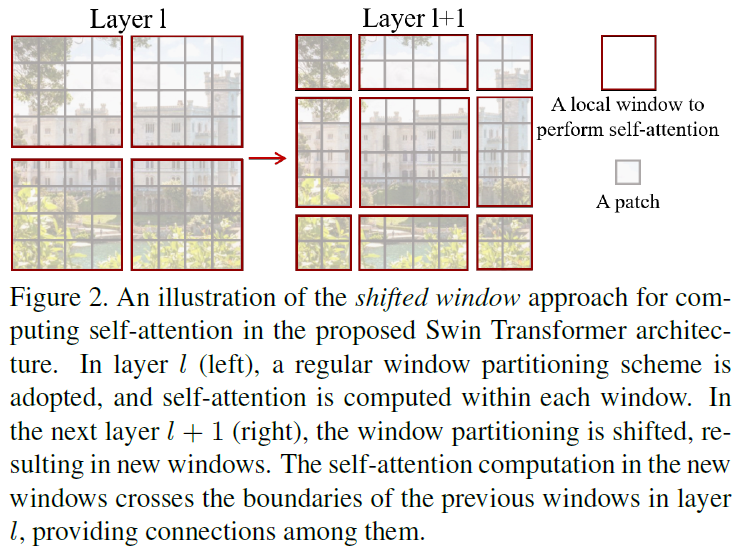
그림 2의 좌측은 W-MSA 모듈의 window 분할 방식, SW-MSA 모듈의 window 분할 방식이다.

• W-MSA
  • $8\times 8$ feature map을 $2\times 2 = 4$개의 window로 나누면 그림과 같이 $4\times 4(M=4)$ 크기의 window들로 구성되게 된다.
• SW-MSA
  • W-MSA 모듈에서 분할이 발생한 패치에서 $\left( \lfloor {M \over 2} \rfloor, \lfloor {M \over 2} \rfloor \right)$칸 떨어진 패치에서 window 분할이 발생
  • 그림 2의 예시에선, $\left( \lfloor {M \over 2} \rfloor, \lfloor {M \over 2} \rfloor \right) = (2, 2)$.

[@ Efficient batch computation for shifted configuration]
SW-MSA 모듈을 실제로 적용함에 있어 생각해야할 점이 존재한다.

• 먼저 SW-MSA 모듈에서처럼 window를 나누게 되면 window의 수가 늘어나게 된다. W-MSA에서 $\lceil {h \over M} \rceil \times \lceil {w \over M} \rceil (=2\times 2)$ 였던 window 수가 SW-MSA 모듈에서는 $(\lceil {h \over M} \rceil + 1) \times (\lceil {w \over M} \rceil + 1) (=3\times 3)$으로 늘어난다.
• 또한 일부 window들은 $M\times M$보다 작아지게 된다.

논문에서는 이를 위한 두 가지 방법을 제시한다.

• Naive solution
  • 작아진 window들에 padding을 두어 $M\times M$ 사이즈로 만드는 방법
  • window의 수는 여전히 늘어나게되고 그렇게 되면 W-MSA 모듈의 window 수, $\lceil {h \over M} \rceil \times \lceil {w \over M} \rceil (=2\times 2)$와 SW-MSA 모듈에서의 window 수, $(\lceil {h \over M} \rceil + 1) \times (\lceil {w \over M} \rceil + 1) (=3\times 3)$로 달라지게 된다.
  • 따라서 이 방법은 계산복잡도 상으로도, 효율 면으로도 적절하지 않다.
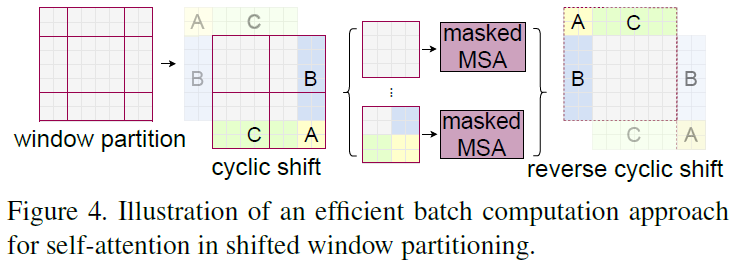
• Cyclic-shifting
  • 좌상단(top-left) 패치들부터 그림 4처럼 패치를 옮겨 $M\times M$ 크기로 만든다.
  • 이렇게 패치를 새롭게 구성하면 여러 window들이 인접하지 않는 패치들과 인접하게 되므로 이를 분리할 수 있는 계산을 적용해야 한다.
  • 논문에서는 여기에 마스킹 메커니즘(masking mechanism)을 통해 이를 분리한다.
    • 예를 들어 A window에 속하는 패치에 대한 self-attention을 계산할 때 B window에 속하는 패치들에는 마스킹을 적용하는 방식이다.
  • 이 방법을 통해 window들의 크기, 갯수를 W-MSA 모듈에서의 것과 동일하게 유지할 수 있으며 효율적인 방법이다.

[@ Relative position bias]
Self-attention을 계산하는 과정에서 Relative position bias $B \in \mathbb R^{M^2 \times M^2}$를 더함으로써 위치적 정보를 모델링할 수 있도록 했다. 이 bias는 window 내부에서의 위치를 모델링하는 것이다.

Vision Transformer에서 사용했던 position embedding(Absolute position embedding: 모든 패치의 위치에 따른 임베딩)을 사용했을 때 위에서 제시한 relative position bias를 사용했을 때보다 오히려 성능이 저하되는 것을 관찰했다.

3.3 Architecture Variants

• Swin-T: $C=96$, layer numbers $=\{2, 2, 6, 2\}$
• Swin-S: $C=96$, layer numbers $=\{2, 2, 18, 2\}$
• Swin-B: $C=128$, layer numbers $=\{2, 2, 18, 2\}$
  • base model, ViT-B와 DeiT-B의 모델 크기 및 복잡도가 비슷하도록 설계
• Swin-L: $C=192$, layer numbers $=\{2, 2, 18, 2\}$
• $C$는 Stage 1의 hidden layers의 채널 수

• window size, $M=7$
• query dimension of each head, $d=32$
• each MLP, $\alpha=4$

---

4. Experiments

4.1 Image Classification on ImageNet-1K

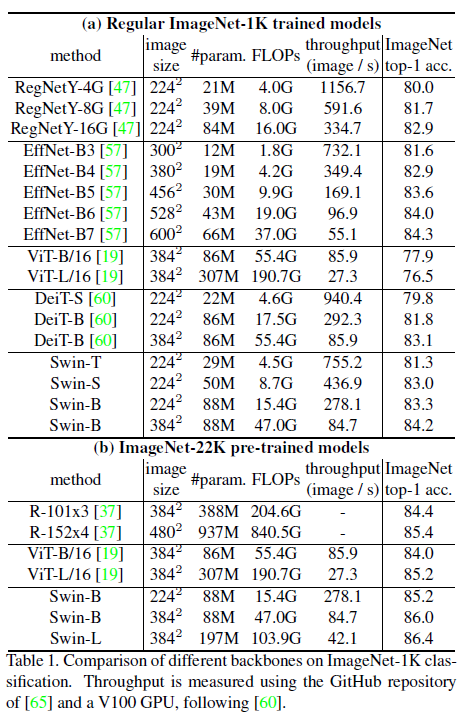
표 1(a)는 ImageNet-1K에 학습한 경우를 나타내며, 표 1(b)는 ImageNet-22K에 사전학습하고 ImageNet-1K에 미세조정한 경우를 나타낸다.
위와 같이 1. 거대한 데이터에 사전학습하고 미세조정을 수행할 경우는 물론이고 2. 사전학습을 거치지 않은 경우에도 최고의 결과를 보였다.

4.2 Object Detection on COCO

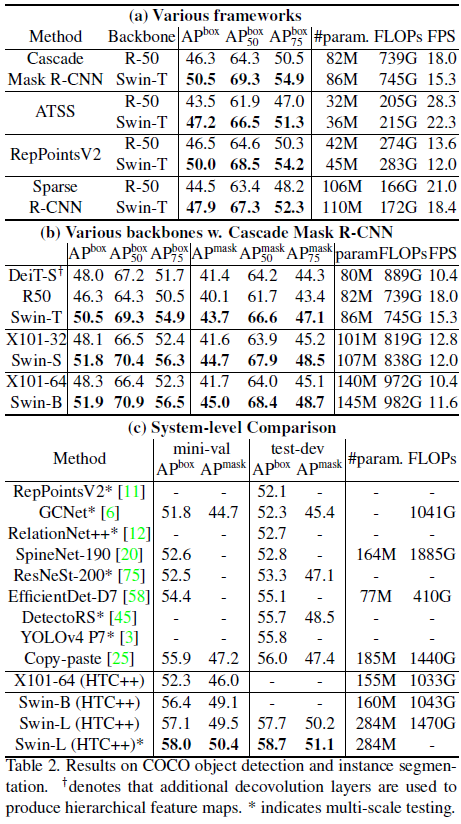
4.3 Semantic Segmentation on ADE20K

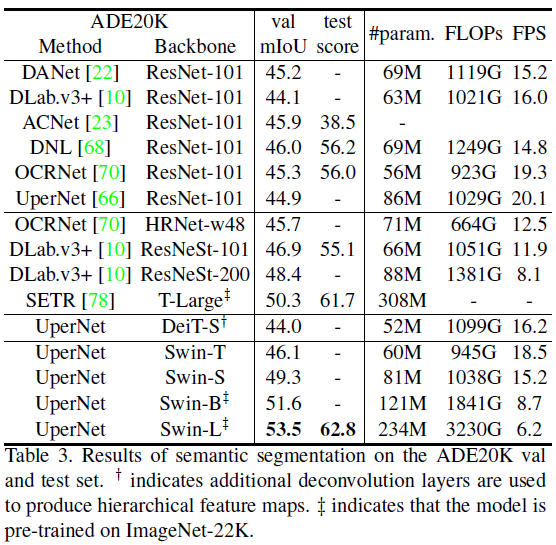
4.4 Ablation Study

아래 세 가지 task에 대해 Ablation study를 진행

• Image Classification ImageNet-1K
• Cascade Mask R-CNN을 방법으로 하여 COCO Object detection
• UperNet을 방법으로, ADE20K Semantic Segmentation

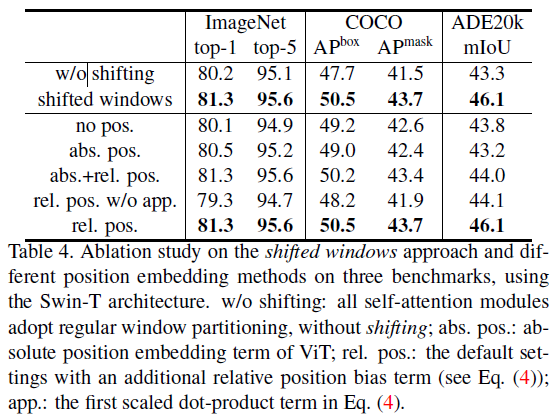
[@ Shifted windows] 세 가지 task 모두에게서 shifted windows 방법이 효과있음을 보이고 있다. 이 방법이 window들 간의 연관성을 모델링할 수 있음을 알 수 있다.

[@ Relative position bias] 기존 Vision Transformer에서 사용했던 [abs](absolute position embedding의 사용이 효과적임을 볼 수 있다.

[app](the first scaled dot-product term)는 아래 수식에서 $\sqrt d$를 의미하는 것으로 보인다.

$\mathrm{Attention}(Q, K, V) = \mathrm{SoftMax}(QK^T/\sqrt d + B)V$

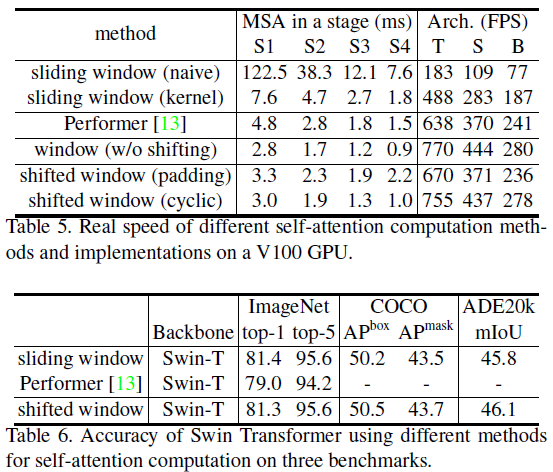
[@ Different Self-attention methods] 아래 표 5와 표 6은 cyclic shifting + shifted windows를 통한 window 내의 self-attention 계산의 효용성을 보인다. 기존 Vision Transformer 모델들의 sliding window에 비해 성능은 대등하지만 그 계산 복잡도는 현저한 차이를 보인다.
가장 빠른 Trnasformer 아키텍처 중 하나인 Performer와 비교해서도 본 논문에서 제안하는 방법이 더 나은 결과를 보였다.