[paper-review] EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks

Tan, M., & Le, Q. (2019, May). Efficientnet: Rethinking model scaling for convolutional neural networks. In International Conference on Machine Learning (pp. 6105-6114). PMLR.

개인적인 논문해석을 포함하고 있으며, 의역 및 오역이 남발할 수 있습니다. 올바르지 못한 내용에 대한 피드백을 환영합니다 :)

---

1. Introduction

[@ Scaling up ConvNets]

• ConvNets의 모델 크기를 늘리는 것은 정확도를 향상시키기 위한 가장 보편적인 방법
  • ResNet이 대표적이며, ResNet-18에서 ResNet-200으로 더 많은 레이어를 사용함으로써 모델의 크기를 늘릴 수 있다.
• 하지만 ConvNets의 Scaling에 대한 연구는 잘 이루어지지 않았다.
  • 이전에 모델의 depth, width, resolution을 확장하여 모델 성능을 높이려는 시도가 있었지만 이 세 가지 측면 중에서 한 가지 측면에만 모델을 확장하는 것이 일반적이었다.
  • 세 가지 측면 모두에 대한 확장도 있었긴 했지만 사람이 임의의 값으로 지정했었다.
  • depth: 모델 구성에서 레이어 수를 늘리는 것, ex) from ResNet-18 to ResNet-200
  • width: ConvNet 구성에서 convolution layer의 채널 수를 늘리는 것
  • resolution: 입력 이미지의 해상도를 키우는 것

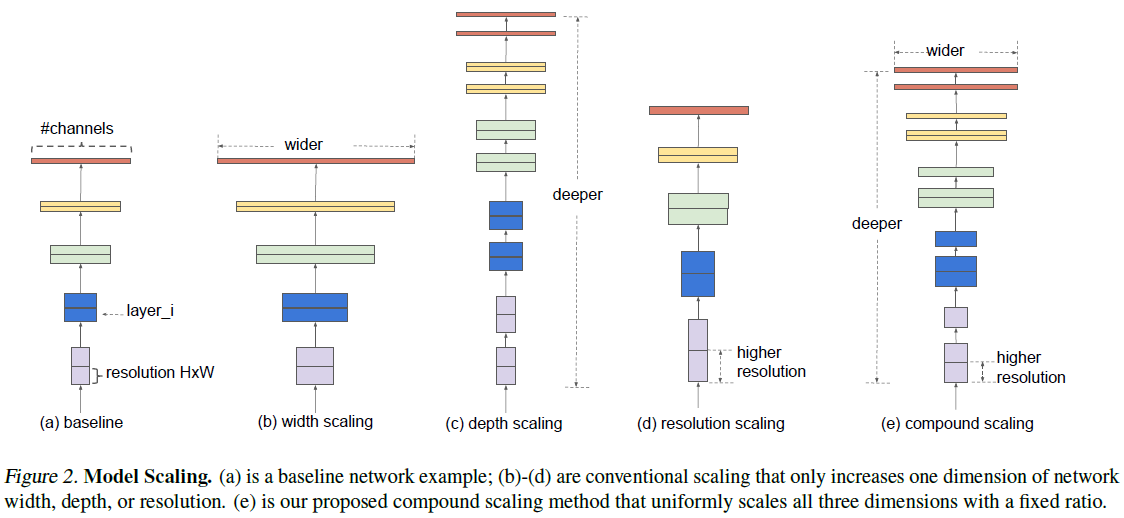
[@ Rethinking Model Scaling]

• 본 논문에서는 ConvNets의 크기를 확장하는 프로세스를 다시 생각해보고 연구했다.
  • 정확도(accuracy)와 효율성(efficiency)를 모두 달성할 수 있는 원칙적인 방법에 대한 연구
  • depth, width,resolution 모든 측면에서 균형을 맞추는 것이 중요
• 기존의 임의의 비율로 depth, width, resolution을 조정하던 것과 다르게 일정하게 고정된 scaling coefficient로 모델의 크기를 조정하게 된다.
  • $2^N$배 더 많은 컴퓨팅 자원을 사용할 수 있다면 depth, width, resolution을 각각 $\alpha^N, \beta^N, \gamma^N$배 하기만 하면 된다.
  • $\alpha, \beta, \gamma$는 간단한 grid search를 통해 찾을 수 있는 constant coefficient이다.
• 직관적으로도 이 scaling 방법은 합리적인 방법이다.
  • 입력 이미지 해상도(resolution)를 늘리면 더 많은 레이어를 쌓아 receptive field를 늘리고(depth), 더 많은 채널을 계산에 포함해 세분화된 패턴을 잘 포착해야 한다(width).

---

2. Related Work

[@ ConvNet Accuracy]

• 점차 ConvNets는 정확해지고는 있지만 그 크기도 커져가고 있다.
  • 2014년 ImageNet competition winner GoogleNet이 6.8M의 파라미터 수를 가지고 top-1 accuracy 74.8%
  • 2017년 ImageNet competition winner SENet은 145M의 파라미터 수를 가지고 top-1 accuracy 82.7%
  • 논문 발표 당시 GPipe는 557M의 파라미터 수로 84.3%의 top-1 accuracy
• 더 높은 정확도가 우리에게는 필요한데 현재 하드웨어의 메모리 한계에 도달했다.

[@ ConvNet Efficiency]

• Neural Architecture Search (NAS)가 효율적인 mobile-size의 ConvNets를 설계하는 데 널리 사용되고 있다.
  • depth, width, convolution kernel types and sizes 등등의 광범위하게 조정하여 최적의 ConvNets을 설계할 수 있다.
  • 다만, 훨씬 더 큰 사이즈를 가진 모델들에 대해서는 많은 계산 비용이 필요하기 때문에, 이 방법을 적용하기 어렵다.
• 본 논문에서, 거대한 ConvNets에 의 모델 효율성을 극대화하면서 정확도를 향상시킬 수 있는 방법에 대해 연구한다.

[@ Model Scaling]

• depth 확장
  • 대표적인 scaling 방법으로 레이어의 수를 조정하여 크기를 조정한다.
  • ResNet은 ResNet-18 부터 ResNet-200까지 모델의 크기를 조정할 수 있다. (He et al., 2016)
• width 확장
  • WideResNet(Zagoruyko & Komodakis, 2016) 이나 MobileNets(Howard et al., 2017)은 모델의 크기를 Conv Layer 채널 수로 조정한 대표적 예시
• depth와 width가 모두 중요하다라고 생각한 연구
  • (Raghu et al., 2017; Lin & Jegelka, 2018; Sharir & Shashua, 2018; Lu et al.,
    2018)
  • 여전히 ConvNet의 효율, 성능을 모두 향상 시킬 수 있는 방법에 대한 논의가 필요하다.

---

3. Compound Model Scaling

3.1. Problem Formulation

[@ Annotations]

• ConvNet Layer $i$를 함수 $Y_i=\mathcal F_i(X_i)$로 나타낼 수 있다. ($X_i=\left < H_i, W_i, C_i\right >$)
• ConvNet $\mathcal N$은 레이어들이 합성된 리스트의 형태로 표현할 수 있다:
  $\mathcal N = \mathcal F_k \bigodot...\bigodot\mathcal F_2\bigodot\mathcal F_1(X_1)$
  • 사실 ConvNet layer들이 모여 하나의 stage로 구성되고, 이 stage들의 모여 하나의 ConvNet을 이루며 이 stage 구조가 반복되는 경우가 많다.
    • 예를 들어, ResNet은 각 stage가 여러 layer로 구성된 5 stages가 존재
    • 모든 layer들은 같은 convolution type을 갖는다.
    • 모든 stage들은 같은 아키텍처를 갖는다.
• 따라서 아래와 같이 ConvNet을 정의할 수 있다.
  $\mathcal N = \bigodot_{i=1...s}\mathcal F_i^{L_i}(X_{\left < H_i, W_i, C_i\right >})$
  • $i$번째 stage에서 $\mathcal F_i$ layer가 $L_i$번 반복 -> $\mathcal F_i^{L_i}$

[@ 최적화문제 정의]
Model scaling은 baseline 아키텍처에서 ConvNet layer의 디자인을 변경하지 않은 채로 모델의 length($L_i$), width($C_i$), resolution($H_i, W_i$)을 수정하는 것이 일반적이다. 각 레이어 $i$에 대해 이 변수들($L_i, C_i, H_i, W_i$)을 최적으로 찾는 것만으로도 엄청난 경우의 수를 갖게 된다.
즉, 우리의 목적함수는 아래와 같이 정의할 수 있게 된다.

3.2. Scaling Dimensions

위 최적화에 있어 주요 문제점은 변수 $d, w, r$이 서로서로 영향이 있으며 각각 변수들을 조정함에 있어 서로 다른 컴퓨팅 자원의 한계 하에서 조정해야 한다는 점이다.

[@ Depth]

• ConvNets를 조정하는 데 가장 보편적인 방법
• 그 근거는 모델을 깊게 쌓을수록 더 풍부하고 복잡한 특징들을 포착하여 새로운 task에도 잘 일반화될 수 있을 것이라는 직관적인 추론이다.

• But. 신경망을 깊게 구성할수록 vanishing gradient 문제는 피할 수 없다. (ResNet-1000은 ResNet-101보다 훨씬 더 많은 레이어로 구성했음에도 비슷한 정확도를 보인다.)

[@ Width]

• ConvNets의 width를 조정하는 방법은 주로 작은 사이즈의 모델을 크게할 때 사용된다.
• 더 넓은 신경망을 구성할수록 fine-grained features를 잘 포착할 수 있으며 학습이 더 쉬워진다는 이전 연구도 있었다. (Zhagoruyko & Komodakis, 2016)

• But. 얇고 넓은 모델들은 higher level features를 포착하는 데 어려움을 가지는 경향이 있다.
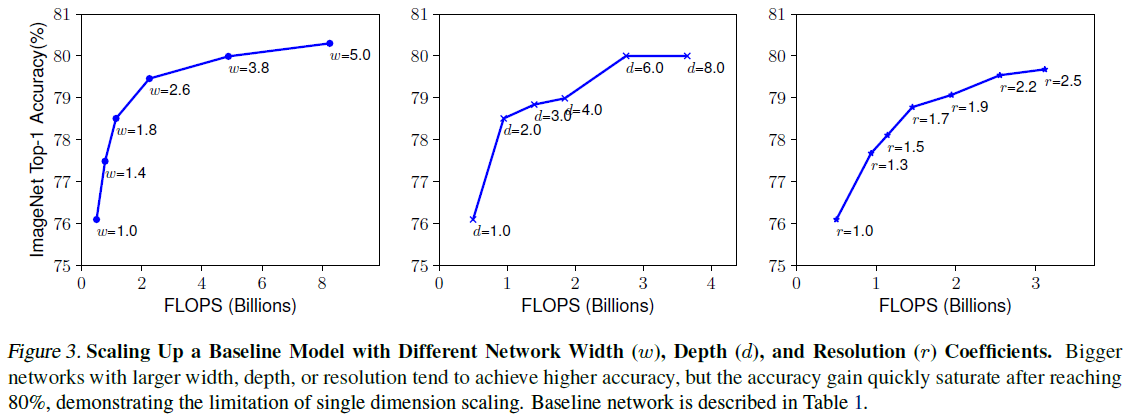
• 본 논문에서의 실험(Figure 3 (left))에서도 모델이 넓어질수록 금새 모델의 정확도가 포화됨을 볼 수 있다.

[@ Resolution]

• 입력 이미지의 해상도가 높은 해상도를 가질수록 ConvNets는 더 fine-grained patterns를 포착할 수 있다.
• 초기 ConvNets는 $224\times 224$의 해상도로 출발했으나 최근에는 $299\times 299, 331\times 331$ 크기의 이미지를 사용하는 경향이 있다.
• Object detection과 같은 task에서는 $600 \times 600$의 해상도를 높은 해상도를 사용한다.

• But. 본 논문에서의 실험 결과(figure 3 (right))를 보면 해상도가 점점 커질수록 정확도가 늘어나는 비율은 점차 줄어든다.

[Observation 1] - 신경망의 크기를 width, depth, resolution 중 한 가지 측면에서 조정하는 것은 정확도를 향상시킬 수 있지만 모델이 커질수록 그 효과는 줄어든다.

3.3. Compound Scaling

앞선 실험을 통해 depth, width, resolution 각각의 측면에서 크기를 조정하는 것이 독립적이지 않다는 점을 알 수 있었다. 직관적으로도 높은 해상도의 이미지는 더 깊은 모델을 사용하는 것이 올바르다고 느껴진다.
따라서 본 논문에서는 서로 다른 depth, width, resolution 측면의 스케일링 정도를 조정하고 각각이 균등하게 조정되야 함을 주장하고 있다.

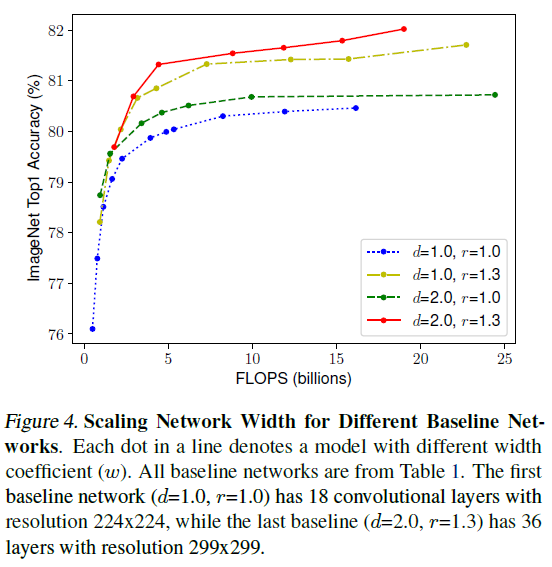
Figure 4는 이러한 직관적인 추론을 증명하는 결과이다.
$d$와 $r$을 조정하며 서로 다른 네 가지의 환경에서 $w$를 점차 늘려가며 실험한 결과, $d=1.0, r=1.0$일 때 즉, $w$만 차별적으로 조정할 때 정확도가 포화되는 속도가 가장 빨랐다.

[Observation 2] - 정확도와 효율성을 모두 잡아내기 위해선, width, depth, resolution을 균형있게 조정하는 것이 중요하다.

사실 일부 선행 연구에서 depth, width, resolution을 균형있게 조정하는 연구를 진행했었지만 이 수치를 모두 수동으로 조정했었다. (Zoph et al., 2018, Real et al., 2019)

[@ Compound Scaling Method]
본 논문에서는 사용자가 자신의 하드웨어 스펙에 맞게 크기 조정 정도를 compound coefficient $\boldsymbol\phi$로 조정할 수 있는 방법을 제안한다.

@ 제약조건 $\alpha\cdot\beta^2\cdot\gamma^2 \approx 2$ 에 대하여.

• ConvNets의 depth, width, resolution를 조정함에 따라 연산의 FLOPS는 각각 $d, w^2, r^2$으로 비례한다.
  • 즉, depth를 두 배 늘리면 FLOPS가 두 배 늘어나지만
  • width, resolution을 각각 두 배 늘리면 FLOPS는 각각 네 배씩 증가한다.
• ConvNet 중심의 모델들은 대부분의 계산 비용이 ConvNets에서 발생하기 때문에 총 모델의 FLOPS는 $\alpha\cdot\beta^2\cdot\gamma^2$에 근접하게 늘어난다.
• 본 논문에서는 $\alpha\cdot\beta^2\cdot\gamma^2$의 값을 $2$에 근접하게 제약조건을 걸었기 때문에 총 FLOPS는 $2^\boldsymbol\phi$만큼 증가한다고 볼 수 있다.

---

4. EfficientNet Architecture

Model Scaling은 baseline 모델의 각 레이어 연산을 수정하지 않기 때문에 좋은 baseline 모델을 갖추는 것이 중요하다. 현존하는 ConvNets 아키텍처들에도 본 논문에서 제안하는 scaling 방법을 적용할 것이지만 그 효과를 더 잘 보여주기 위해 EfficientNet이라는 새로운 baseline 모델을 제안한다.

Tan et al., 2019에서의 연구에서 처럼 Multi-objective neural architecture search (AutoML) 방법을 사용해 정확도와 FLOPS를 모두 최적화하는 모델 구조, EfficientNet-B0를 찾았다.

• Tan et al., 2019 에서의 연구와 같은 search space
• optimization goal: $ACC(m) \times [FLOPS(m)/T]^w$
  • $ACC(m), FLOPS(m)$: 모델 $m$에 대한 정확도와 FLOPS
  • $T$: target FLOPS
  • $w$: 정확도와 FLOPS의 trade-off를 조정하는 hyperparameter 논문에서는 $-0.07$ 사용

[@ Compound Scaling Method의 사용]
이 EfficientNet-B0를 baseline으로 compound scaling method를 사용

• Step 1. $\boldsymbol\phi=1$로 고정하고, 두 배의 컴퓨팅 자원이 사용 가능함을 가정하고 $\alpha, \beta, \gamma$를 작은 grid search를 통해 최적값 $\alpha=1.2, \beta=1.1, \gamma=1.15$를 얻을 수 있었다.
• Step 2. $\boldsymbol\phi$를 점차 늘려가며 차례로 EfficientNet-B1 ~ B7을 획득한다.
  • 모델의 몸집을 키운 다음에 최적의 $\alpha, \beta, \gamma$ 값을 찾는 것이 훨씬 더 나은 성능을 보장하겠지만 이 방법은 너무 계산비용이 크다.
  • 앞선 실험을 통해 $\alpha, \beta, \gamma$의 최적 조합이 있음을 밝혀내고 이를 작은 모델에서 최적 조합을 찾고 이를 점차 몸집을 늘려 성능이 뛰어난 모델을 만들었다는 점이 본 연구의 주요 contribution이라 볼 수 있을 것이다.

---

5. Experiments

5.1. Scaling Up MobileNets and ResNets

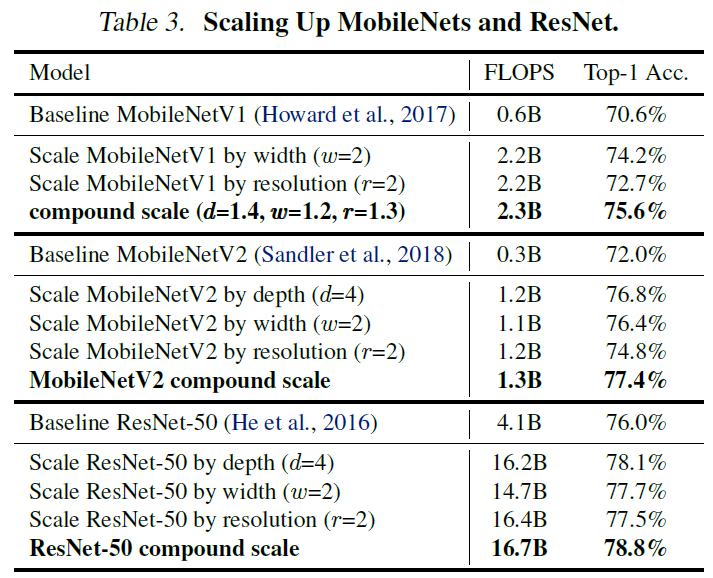
Table 3에서 MobileNets, ResNets 모두에서 논문에서 제안하는 Compound Scale Method가 FLOPS는 비슷하게 유지하면서 성능을 크게 향상시킴을 확인할 수 있다.

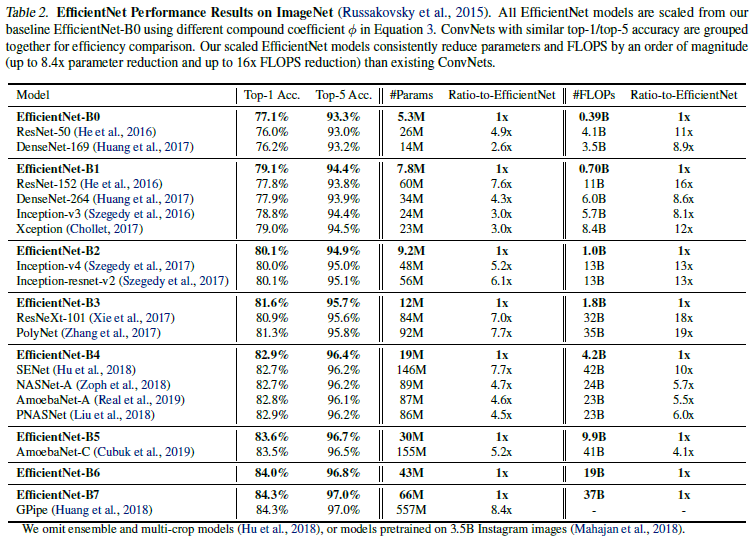
5.2. ImageNet Results for EfficientNet

Table 2는 각 EfficientNet이 비슷한 성능을 보이는 모델들이 계산 비용 면에서는 크게 앞서는 모습을 보여준다.

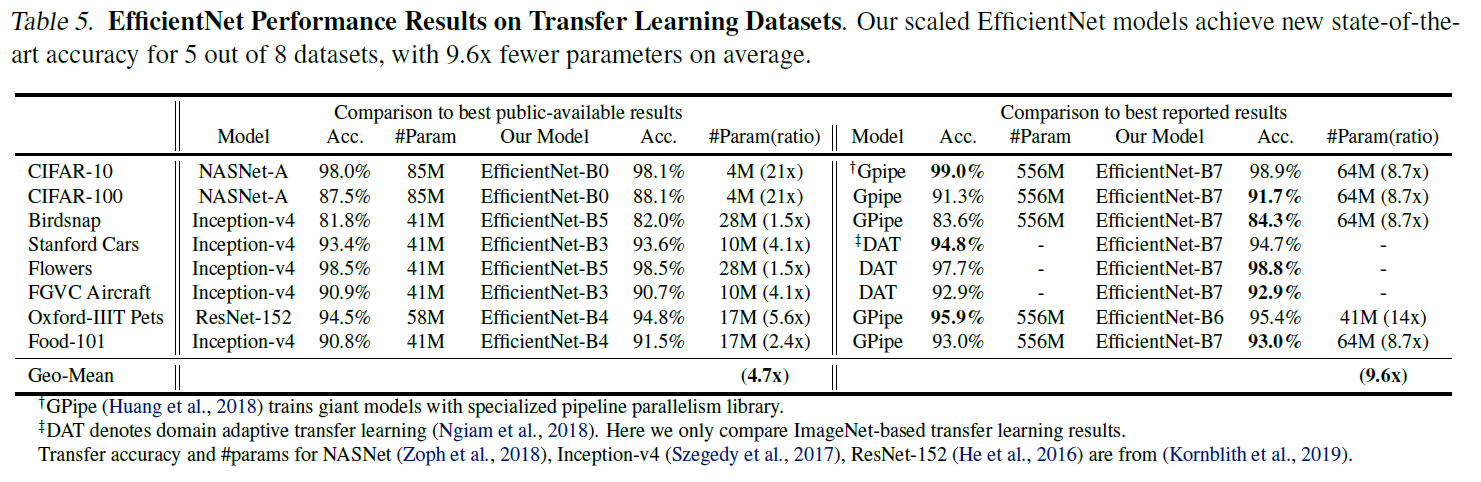
5.3. Transfer Learning Results for EfficientNet

전이학습에 사용되어도 파라미터 수를 현저하게 줄일 수 있다.

---

6. Discussion

[@ Compound Scaling Method 빼기 EfficientNet Architecture]
EfficientNet에서 논문에서 제안하는 Compound Scaling Method의 효과를 덜어내보았다. depth, width, resolution 한 가지 측면에서만 scaling을 진행하는 것보다 Compound Scaling Method가 확실히 더 나은 성능을 보임을 알 수 있다.

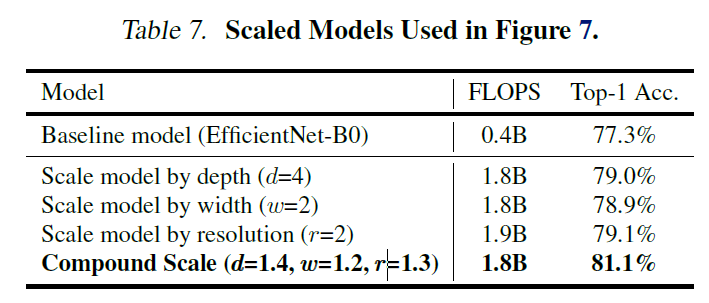
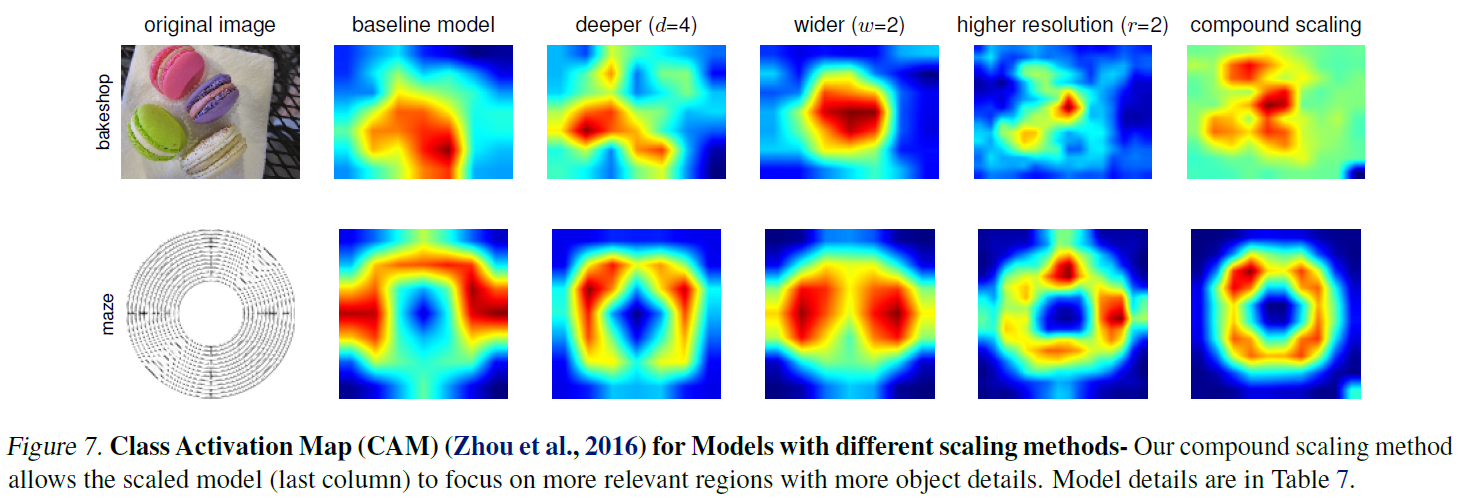
[@ Class Activation Map]
위 실험에서 사용된 모델들의 예측에 집중하는 영역을 살펴보면 Compound Scaling Method를 사용했을 때 물체의 디테일에 잘 집중하는 모습을 볼 수 있다.

---

7. Conclusion

• 중요하면서도 이전의 많은 연구들이 간과하고 있던 ConvNets을 몸집을 늘릴 때 depth, width, resolution을 균형있게 늘려야 한다는 점을 체계적으로 밝혀냈다.
• 이를 위한 Compound Scaling Method를 제안하였으며 간단하고 효과적으로 baseline ConvNets의 몸집을 키울 수 있었다. 이 과정에서 보다 원칙적인 방법으로 모델의 효율성까지 유지할 수 있었다.
• EfficientNet이라는 mobile-size의 baseline 모델을 제시했으며, 이 모델을 기반으로 Compound Scaling Method를 사용해 모델을 효과적으로 더 나은 성능을 위해 사이즈를 늘릴 수 있음을 보였다.
• 결과적으로 EfficientNet+Compound Scaling Method로 계산 비용을 최소화하며 최고 수준의 성능을 달성할 수 있었다.