[LightGBM] LightGBM: A Highly Efficient Gradient Boosting Decision Tree 리뷰

Sion Park·2022년 2월 20일

안녕하세요! 오늘은 LightGBM알고리즘을 소개한 논문 LightGBM: A Highly Efficient Gradient Boosting Decision Tree 를 리뷰해볼게요! 이 논문은 인공지능에서 아주 유명한 학회인 NIPS에서 발표된 논문으로 Kaggle에서도 아주 인기있는 알고리즘입니다. 마찬가지로 많은 분들이 이 알고리즘의 성능이 좋다는 것은 알고 계실텐데요. 저도 이용은 많이 해봐서 이 알고리즘이 비교적 빠르고, 메모리 효율도 굉장히 좋다는 것은 알고 있었습니다. 그럼 이 알고리즘이 왜 그러한 이점이 있는지 궁금해서 찾아 읽어봤는데 다소 흥미로운 부분이 많아서 리뷰하게 되었습니다!

이 리뷰게시글에서는 해당 논문에서 Theoretical한 부분과 Experiments섹션은 생략하고 알고리즘의 방법이나, 어떠한 부분이 이 알고리즘을 성공으로 이끌었는지 초점을 맞추어 소개하겠습니다.

1. Introduction

GBDT방법은 효율성, 정확도, 해성 가능성이 높아 기계학습알고리즘으로 널리 이용되고 있습니다. 하지만 빅데이터의 등장으로 정확도와 효율성을 trade-off해야하는 문제가 발생합니다. GBDT는 기본적으로 각 관측치와 변수마다 정보획득량을 평가하기때문에 계산복잡도가 표본의 수와 변수의 수에 비례하게 됩니다. 즉 효율성이 굉장히 떨어집니다.
해당논문에서는 이러한 문제를 해결하고자 두 가지 기술을 제안합니다
- GOSS(Gradient-based One-Side Sampling): GBDT는 기본적으로 Gradient를 이용하는데, 여기서 기울기가 큰 표본들은 더 많은 정보량을 가지고 있을 것입니다. 즉, 해당 표본에 대해 과소적합되어 있다는 말입니다. 따라서 큰 Gradient값을 가진 표본을 더 학습하는 것이 정보의 획득량이 더욱 많으며 반대로 Gradient가 작은 표본들은 큰 영향을 미치지 않을 것 입니다. 그러므로 Gradient값이 큰 표본들을 일정 비율 추출하고 그렇지 않은 표본들을 일정비율로 random하게 학습합니다.

- EFB(Exclusive Feature Bundling): 실제 데이터는 많은 변수를 갖지만 변수공간은 매우 희소하여 변수 개수를 효과적으로 줄일 수 있습니다. 예를 들면 One-hot encoding 된 변수들은 굳이 여러개의 변수로 나타낼 필요가 없이 하나의 변수로 묶을 수 있다는 것과 같은 원리입니다.(하지만 여기서 말하는 EFB방법은 One-hot encoding된 변수처럼 perfectly하게 배타적인 변수에만 적용하는 것이 아닙니다.) 해당 논문에서는 최적의 Bundle을 찾는 문제를 그래프 색칠 문제로 바꾸어 Greedy 알고리즘을 적용한 효율적인 방법을 제안했습니다. (뒷 부분에서 더 자세하게 설명하겠습니다.)
해당 논문에서는 GOSS와 EFB 방법을 적용한 GBDT를 LightGBM이라고 부릅니다. 논문에서 이 알고리즘은 기존 GBDT에 비해 20배 이상 빠른 훈련속도를 보여주면서 거의 동일한 성능을 보여준다고 합니다.

2. Preliminaries

GBDT

GBDT는 간단히 결정트리를 순차적으로 학습시키는 모형입니다.

순차적으로 잔차를 계산하고 이를 target으로 하는 새로운 결정트리를 만들어 가는 방식으로 학습이 되죠!

결국 결정트리를 만드는데 중요한 것은 최적 분할점을 찾는 것인데 이 부분이 가장 시간이 오래걸리는 부분입니다.

논문에서는 이러한 결정트리 알고리즘으로 Histogram-based Algorithm을 소개하고 있습니다. 해당 알고리즘이 메모리나 속도 측면에서 효율적이기 때문에 이 논문에서 이를 바탕으로 연구를 하였다고 합니다. Histogram-based Algorithm은 다음과 같습니다.

알고리즘은 간단하기 때문에 설명은 생략하겠습니다! 이 Histogram-based Algorithm은
- Histogram생성: $O(n\times p)$
- 분할점을 찾을 때 $O(\#bin \times p)$

만큼의 계산량이 필요하다고 합니다. ( $n$ : 데이터의 수, $p$ : 변수의 수) 여기서 $\# bin$ 은 데이터의 수인 $n$ 보다 아주 작기 때문에 결국 Histogram을 만들 때에 계산량이 아주 많다고 합니다.

즉, 데이터의 수와 변수의 수를 줄인다면 GBDT의 학습속도를 크게 향상시킬 수 있음을 언급합니다.

3. Gradient-based One-Side Sampling

GBDT는 표본에 따른 기본 가중치가 없으므로 AdaBoost와 같은 표본 가중치를 직접 적용하기 어렵다고 합니다.

하지만 GBDT의 Gradient의 크기를 이용하면 현재 모형으로부터 부족한 정보의 양을 알 수 있습니다.

여기서 단순히 기울기가 작은 데이터는 잘 학습된 데이터로 판단하여 버리게 되면 효율적으로 표본을 활용할 수 있을 것으로 기대 되지만, 이러한 방법은 데이터의 분포를 바꾸게 되므로 학습모형의 성능이 저하될 수 있다고 합니다.
GOSS방법은 기울기가 큰 표본을 모두 sampling하고 기울기가 작은 표본에 대해서는 random sampling을 진행합니다.

- 기울기의 크기에 따라 데이터를 정렬하여 상위 $a \times 100 \%$ 의 표본
- 기울기가 작은 표본데이터를 $b\times 100 \%$ 의 표본

이때 표본들의 효과를 보정하고자 기울기가 작은 표본에 $(1-a)/b$ 의 가중치를 주어 정보 획득량을 계산합니다.

4. Exclusive Feature Bundling

고차원 데이터는 일반적으로 매우 희소(Sparse)합니다. 보통 희소한 변수공간에서는 변수가 상호 배타적입니다.
('논문에서는 0이아닌 값을 동시에 갖지 않는다.' 라고 되어있는데 이는 scaling 된 경우를 말하는 것으로 보입니다)

즉, 이러한 성질을 통해 배타적인 변수를 단일 변수로 안전하게 묶을 수 있다고 합니다.

배타적 변수 묶음을 하게 되면 앞서 언급하였던 히스토그램 알고리즘의 계산복잡도는 $O(n\times p)$ 에서 $O(n\times \# bundle)$ 로 줄일 수 있게됩니다. 즉, GBDT의 훈련속도 자체를 크게 향상 시킬 수 있습니다.
변수 묶음 문제는 각각 변수를 노드로 갖는 그래프 문제로 생각해 볼 수 있습니다.

하지만 이러한 경우 모든 가능한 경우를 탐색하는 것은 NP-hard 입니다.

그렇기 때문에 이 논문에서는 배타적 변수묶음을 하기 위해 Greedy 알고리즘을 사용합니다.

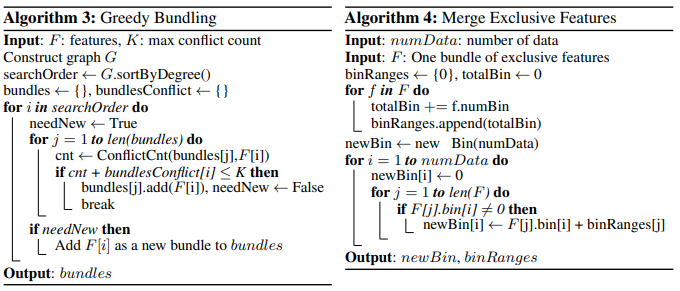
Greedy Bundling: 이 알고리즘은 변수에서 배타적이지 않은 부분(충돌)을 일정 허용하며 Bundle을 만드는 알고리즘으로 Algorithm 3에서 이전에 지정된 수 K 보다 작은 수의 충돌이 일어난 번들을 Greedy하게 만들어 나가는 알고리즘입니다.
Merge Exclusive Features: Greedy Bundling에서 얻은 묶음들을 각각 변수로 묶어주는 알고리즘으로 쉽게 말하면 각 변수의 히스토그램을 옆으로 쌓아가는 과정이라고 이해하면서 보시면 쉬울 것 같네요. 논문의 설명에 따르면 "원래의 변수 A는 [0, 10] 값을 취하고 변수 B는 [0, 20] 값을 취한다. 그렇다면 변수 B 값에 오프셋 10을 더하여 가공한 변수가 [10, 30]에서 값을 취하게 한다." 라고 합니다.
이 방법은 모형 학습전에 단 한번 실행되며 계산복잡도가 크지 않으므로 학습시간에 큰 영향이 없습니다.