Classification vs Regression

• 예측값이 카테고리와 같은 이산형 값일 경우, 분류 (Classification)
• 예측값이 연속형 숫자 값일 경우, 회귀 (Regression)

단순 선형 회귀분석 (Linear Regression)

sklearn.linear_model.LinearRegression
statsmodels.formula.api.ols

• 잔차(오류) - Residual
  • 실제값과 회귀모델에 의해 예측한 값의 차이
  • 음일수도 있고 양일수도 있음
• Residual 의 제곱 합이 최소로 하는 Method of Least Squares 기법을 이용
  • 잔차의 합이 최소가 되는 모델을 만든다!

package import

import numpy as np
import pandas as pd
import sklearn 
import statsmodels

from sklearn.model_selection import train_test_split

# Way1
from sklearn.linear_model import LinearRegression

# Way2
import statsmodels.formula.api as smf

from sklearn.metrics import r2_score

print(f"numpy version = {np.__version__}")
print(f"pandas version = {pd.__version__}")
print(f"sklearn version = {sklearn.__version__}")
print(f"statsmodels version = {statsmodels.__version__}")

데이터 불러오기

df = pd.read_csv("https://raw.githubusercontent.com/YoungjinBD/dataset/main/auto-mpg.csv")

df

다중공선성 분석 (Multicolinearity)

1. 상관행렬 (Correlation Matrix)

   df.corr()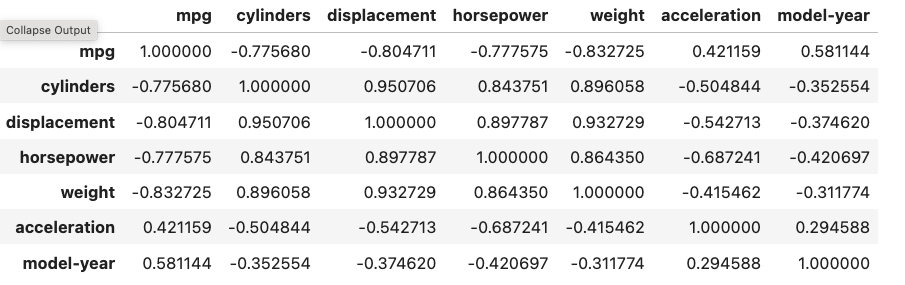

   

2. 산점도 행렬 (Scatter Plot)

   import seaborn as sns
   
   sns.pairplot(df)

3. VIF (Variance Inflation Factor) 계수

데이터 전처리

# 결측값 행 삭제
df = df.dropna()

train, test 데이터 준비

from sklearn.model_selection import train_test_split

# column = df.corr().iloc[0].abs().sort_values(ascending=False).index[1]
column = df.corr().iloc[0].abs().nlargest(2).index[1]

X = df[[column]]
y = df["mpg"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10)

print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

모델 적용 및 데이터 분석 수행

• sklearn.linear_model.LinearRegression 클래스 활용

  Lklearn.linear_model.inearRegression(
      *,
      fit_intercept=True,
      copy_X=True,
      n_jobs=None,
      positive=False,
  )

from sklearn.linear_model import LinearRegression

linearRegression = LinearRegression()

linearRegression.fit(X_train, y_train)

y_pred = linearRegression.predict(X_test)

assert y_pred.shape == y_test.shape

데이터 모델링 성능 평가

from sklearn.metrics import r2_score

print(f"독립변수 계수 = {linearRegression.coef_}")
print(f"y절편 = {linearRegression.intercept_}")

print(f"r2_score = {r2_score(y_test, y_pred)}")

y_train_pred = linearRegression.predict(X_train)
print(f"r2_score = {r2_score(y_train, y_train_pred)}")

statsmodels 을 통한 선형 회귀 분석

train, test 데이터 준비

# train, test 데이터 준비
columns = df.select_dtypes(np.number).corr().iloc[0].abs().iloc[1:].sort_values(ascending=False)
columns = columns[columns >= 0.7].index   # 상관계수 크기가 0.7 이상인 독립변수들만 추출

X = df[columns]
y = df["mpg"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=10)

print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape) 

모델 적용 및 데이터 분석 수행

• statsmodels.formula.api.ols 활용

  statsmodels.formula.api.ols(
  	formula, 
  	data, 
  	subset=None, 
  	drop_cols=None, 
  	*args, 
  	**kwargs
  ) -> Model

# Linear Regression (By statsmodels.formula.api.ols)
import statsmodels.formula.api as smf
# import statsmodels.api as sm

fomula = f"mpg ~ {' + '.join(columns)}"

ols = smf.ols(fomula, df).fit()

y_pred = ols.predict(X_test)

• 신뢰 구간 구하기

  • get_prediction(X_test).summary_frame()

    prediction_result = ols.**get_prediction**(X_test)
    
    prediction_result.**summary_frame**()

    

데이터 모델링 성능 평가

# 모델 유의성 검정 (t-검정, f-검정), 모델 적합성 검정 (R^2)
print(f"params = \n{ols.params}\n")              # 회귀계수 (regression coefficient)
# print(f"fittedvalues = {ols.fittedvalues}")    # 추정치
# print(f"resid = {ols.resid}")                  # 잔차 (Redisual)
print(f"tvalues = \n{ols.tvalues}\n")            # 각 독립변수 유의성 검정 (t-검정 임계치 critical value)
print(f"pvalues = \n{ols.pvalues}\n")            # t-검정 유의확률 
print(f"fvalue = {ols.fvalue}\n")                # f-검정 (모델 전체의 유의성 검정)
print(f"f_pvalue = {ols.f_pvalue}\n")            # f-검정 유의확률
print(f"rsquared = {ols.rsquared}\n")            # 결정계수 (R^2)
print(f"rsquared_adj = {ols.rsquared_adj}\n")    # 수정결정계수 (Adjusted R^2)

ols.summary()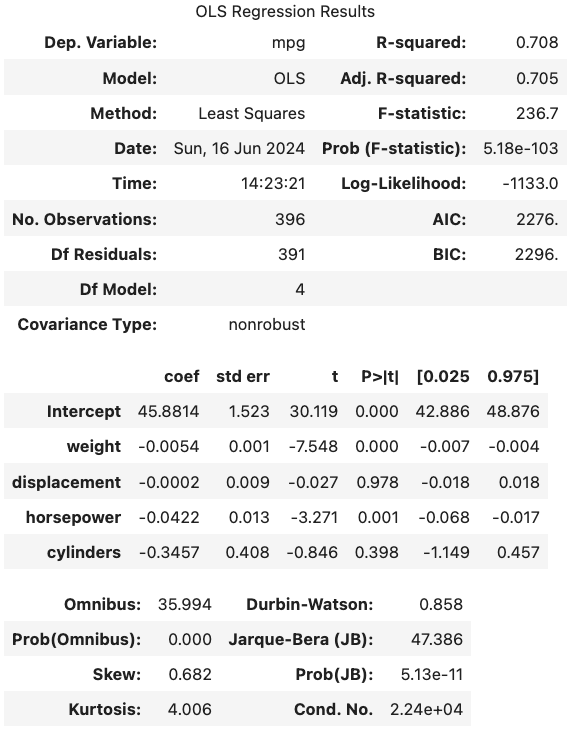

잔차 분석 (Residual Analysis)

import matplotlib.pyplot as plt

# Residual Plot (등분산성, 독립성)
plt.subplot(1, 2, 1)
plt.plot(df["mpg"], ols.resid, 'o')
plt.title("Residual Plot")
plt.xlabel("mpg")
plt.ylabel("Residual")
plt.tight_layout()

# QQ Plot (정규성)
import scipy.stats as stats
plt.subplot(1, 2, 2)
stats.probplot(ols.resid, plot=plt)
plt.title("QQ Plot")
plt.xlabel("Theoretical Quantiles")
plt.ylabel("Sample Quantiles")
plt.tight_layout()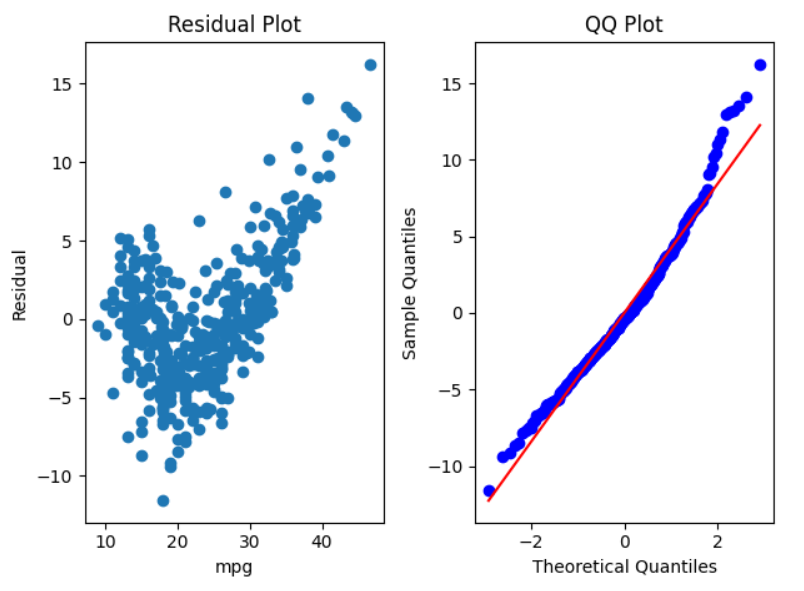

OLS, GLS, WLS 란?

1. OLS (Ordinary Least Squares)

• 개요: 가장 일반적인 회귀 분석 방법으로, 잔차(실제 값과 예측 값의 차이)의 제곱 합을 최소화하는 추정 방법입니다.
• 가정:
  • 오차 항이 정규분포를 따르고, 평균이 0이며, 분산이 일정하다 (등분산성).
  • 오차 항이 서로 독립적이다 (자기상관이 없다).
• 적용: 데이터의 오차 항이 등분산성을 가지며 서로 독립적인 경우에 적합합니다.
• 예시:

  import statsmodels.api as sm
  model = sm.OLS(y, X).fit()
  print(model.summary())

2. GLS (Generalized Least Squares)

• 개요: OLS의 가정을 만족하지 않을 때 사용됩니다. 특히, 오차 항이 등분산성을 가지지 않거나 자기상관이 있는 경우에 적용됩니다.
• 가정:
  • 오차 항이 서로 독립적이지 않거나, 분산이 일정하지 않을 수 있다.
• 적용: 오차 항의 분산이 일정하지 않거나 자기상관이 존재하는 경우에 적합합니다.
• 예시:여기서 sigma_matrix는 오차 항의 분산-공분산 행렬입니다.

  import statsmodels.api as sm
  model = sm.GLS(y, X, sigma=sigma_matrix).fit()
  print(model.summary())

3. WLS (Weighted Least Squares)

• 개요: 데이터 포인트마다 다른 가중치를 부여하는 회귀 방법입니다. 일반적으로 오차의 분산이 일정하지 않을 때 사용됩니다.
• 가정:
  • 오차 항이 독립적이지만, 등분산성을 가지지 않을 수 있다.
• 적용: 데이터의 분산이 일정하지 않아서 더 중요한 데이터 포인트에 더 많은 가중치를 부여하고 싶은 경우에 적합합니다.
• 예시:

  import statsmodels.api as sm
  weights = 1 / np.var(y)  # 가중치 정의 (예시)
  model = sm.WLS(y, X, weights=weights).fit()
  print(model.summary())

차이점 요약

• OLS는 오차 항의 분산이 일정하고 서로 독립적일 때 사용됩니다.
• GLS는 오차 항이 등분산성을 가지지 않거나 자기상관이 있을 때 사용됩니다.
• WLS는 데이터 포인트마다 가중치를 달리 부여할 수 있으며, 오차 항의 분산이 일정하지 않을 때 사용됩니다.

다중 선형 회귀분석 (Linear Regression)

sklearn.linear_model.LinearRegression
statsmodels.formula.api.ols

• 여러 개의 독립변수를 사용한 회귀분석 기법

package import

import numpy as np
import pandas as pd

import sklearn
import statsmodels
import scipy
import seaborn as sns
import matplotlib

from sklearn.model_selection import train_test_split

from sklearn.linear_model import LinearRegression

import statsmodels.formula.api as smf
import statsmodels.api as sm
import statsmodels.stats.api as sms

from sklearn.metrics import r2_score
import scipy.stats as stats
import matplotlib.pyplot as plt

print(f"numpy version = {np.__version__}")
print(f"pandas version = {pd.__version__}")
print(f"sklearn version = {sklearn.__version__}")
print(f"statsmodels version = {statsmodels.__version__}")
print(f"scipy version = {scipy.__version__}")
print(f"seaborn version = {sns.__version__}")
print(f"matplotlib version = {matplotlib.__version__}")

데이터 불러오기

df = pd.read_csv("https://raw.githubusercontent.com/YoungjinBD/dataset/main/housing.csv")

df.describe()

데이터 전처리

# 결측값이 있는 행 전체 제거
df = df.dropna()
assert df.isna().sum().sum() == 0

# ocean_proximity는 범주형 값이므로, 선형회귀분석에서는 제외
category_columns = df.select_dtypes("object").columns
# df.drop(category_columns, axis=1)
df = df.drop(columns=category_columns) 
assert len(df.select_dtypes("number").columns) == len(df.columns)

독립변수들 간의 상관관계 분석

상관계수 행렬 (Correlation Matrix)

df.corr().loc["median_house_value"].abs().sort_values(ascending=False)

산점도 행렬 (Scatter Plot Matrix)

import seaborn as sns

sns.pairplot(df)

train, test 데이터 준비

from sklearn.model_selection import train_test_split

dependentVariable = "median_house_value"
independentVariables = df.columns.drop(dependentVariable)

X = df[independentVariables] # df.drop(dependentVariable, axis=1), df.drop(columns=dependentVariable)
y = df[dependentVariable]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

모델 적용 및 데이터 분석 수행

statsmodels.formula.api 활용하는 방법

import statsmodels.formula.api as smf
import statsmodels.api as sm

dependentVariable = "median_house_value"
independentVariables = df.columns.drop(dependentVariable)

formula = f"{dependentVariable} ~ {' + '.join(independentVariables)}"

ols = smf.ols(formula=formula, data=df).fit()

y_pred = ols.predict(X_test)

assert y_pred.shape == y_test.shape

ols.summary()

sklearn.linear_model.LinearRegression 활용하는 방법

from sklearn.linear_model import LinearRegression 

lr = LinearRegression()

lr.fit(X_train, y_train)

print(f"params = {lr.coef_}")
print(f"intercept = {lr.intercept_}")

y_pred = lr.predict(X_test)

assert y_pred.shape == y_test.shape

데이터 모델링 성능 평가

from sklearn.metrics import r2_score

print(r2_score(y_test, y_pred))

y_train_pred = ols.predict(X_train)

print(r2_score(y_train, y_train_pred))

from sklearn.metrics import r2_score

print(r2_score(y_test, y_pred))

y_train_pred = lr.predict(X_train)

print(r2_score(y_train, y_train_pred))

잔차 분석 (Residual Analysis)

import matplotlib.pyplot as plt

plt.subplot(1, 2, 1)
plt.plot(df[dependentVariable], ols.resid, 'o')
plt.xlabel(dependentVariable)
plt.ylabel("Residual")
plt.title("Residual Plot")
plt.tight_layout()

import scipy.stats as stats

plt.subplot(1, 2, 2)
stats.probplot(ols.resid, plot=plt)
plt.xlabel("Thoretical Quantiles")
plt.ylabel("Sample Quantiles")
plt.title("QQ Plot")
plt.tight_layout()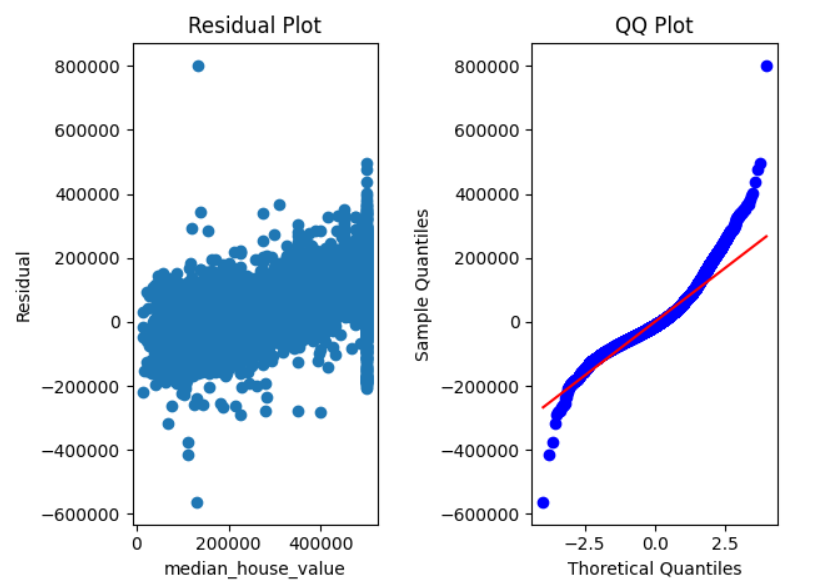

xgboost 라이브러리를 통한 선형 회귀 분석

from xgboost import XGBRegressor

xgb = XGBRegressor()

xgb.fit(X_train, y_train)

y_pred = xgb.predict(X_test)

from sklearn.metrics import r2_score
predict(y_test, y_pred, r2_score)

xgb.predict(X_val)

의사결정나무를 이용한 예측 문제 해결

sklearn.tree.DecisionTreeRegressor

• 의사결정을 위한 규칙을 나무 모양을 조합하여, 목표변수에 대한 예측을 수행하는 기법이다.
• 이전에 학습한 분류 기능과는 달리 각 항목에서의 범주를 예측하는 것이 아니다.
  • 값 자체를 예측하는 것
  • 의사결정나무를 학습하는 것은 최종적으로 회귀나무를 구축하는 과정
• 수치 데이터, 범주 데이터 모두 사용 가능

package import

import numpy as np
import pandas as np
import sklearn
import matplotlib

# from sklearn.tree import DecisionTreeClassifier 
from sklearn.tree import DecisionTreeRegressor

from sklearn.model_selection import train_test_split

from sklearn.metrics import mean_squared_error
# from sklearn.metrics import mean_absolute_error
# from sklearn.metrics import median_absolute_error

import matplotlib.pyplot as plt

print(f"numpy version = {np.__version__}")
print(f"pandas version = {pd.__version__}")
print(f"sklearn version = {sklearn.__version__}")
print(f"matplotlib version = {matplotlib.__version__}")

데이터 불러오기

df = pd.read_csv("https://raw.githubusercontent.com/YoungjinBD/dataset/main/housing.csv")

df

df.info()

df.describe()

데이터 전처리

# 결측값이 있는 행 제거
df = df.dropna()
assert df.isna().sum().sum() == 0

# ocean_proximity 범주형 값으로 분석에서 제외
df = df.drop(columns="ocean_proximity")

독립변수들 간 상관관계 분석

상관계수 행렬 (Correlation Matrix)

df.corr().loc["median_house_value"].abs().sort_values(ascending=False)

median_house_value    1.000000
median_income         0.688355
latitude              0.144638
total_rooms           0.133294
housing_median_age    0.106432
households            0.064894
total_bedrooms        0.049686
longitude             0.045398
population            0.025300
Name: median_house_value, dtype: float64

산점도 행렬 (Scatter Plot Matrix)

import seaborn as sns

sns.pairplot(df)

train, test 데이터 준비

from sklearn.model_selection import train_test_split

y_column = "median_house_value"
X_columns = df.drop(columns=y_column).columns

X = df[X_columns]
y = df[y_column]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

모델 적용 및 데이터 분석 수행

• sklearn.tree.DecisionTreeRegressor 클래스 활용

  DecisionTreeRegressor(
      *,
      criterion='squared_error',
      splitter='best',
      max_depth=None,
      min_samples_split=2,
      min_samples_leaf=1,
      min_weight_fraction_leaf=0.0,
      max_features=None,
      random_state=None,
      max_leaf_nodes=None,
      min_impurity_decrease=0.0,
      ccp_alpha=0.0,
      monotonic_cst=None,
  )

from sklearn.tree import DecisionTreeRegressor
# from sklearn.tree import DecisionTreeClassifier

dtr = DecisionTreeRegressor(max_depth=3, random_state=42)

dtr.fit(X_train, y_train)

y_pred = dtr.predict(X_test)

assert y_pred.shape == y_test.shape

데이터 모델링 성능 평가

from sklearn.metrics import mean_squared_error
# from sklearn.metrics import mean_absolute_error
# from sklearn.metrics import median_absolute_error

mse = mean_squared_error(y_test, y_pred)

print(mse)

y_train_pred = dtr.predict(X_train)

print(mean_squared_error(y_train, y_train_pred))

랜덤 포레스트를 이용한 예측 문제 해결

sklearn.ensemble.RandomForestRegressor

• 다수의 의사결정 트리들을 Bagging하여 분류 또는 회귀를 수행하는 앙상블(ensemble) 기법이다.
  • 각 트리는 전체 학습 데이터 중 서로 다른 데이터를 샘플링하여 일부 데이터를 제외한 후 최적의 특징을 찾아 트리를 분기한다.

package import

import numpy as np
import pandas as pd
import sklearn
import matplotlib
import scipy
import seaborn as sns

from sklearn.model_selection import train_test_split

# from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import RandomForestRegressor

from sklearn.metrics import mean_squared_error
# from sklearn.metrics import mean_absolute_error
# from sklearn.metrics import median_absolute_error

print(f"numpy version = {np.__version__}")
print(f"pandas version = {pd.__version__}")
print(f"sklearn version = {sklearn.__version__}")
print(f"matplotlib version = {matplotlib.__version__}")
print(f"scipy version = {scipy.__version__}")
print(f"seaborn version = {sns.__version__}")

데이터 불러오기

df = pd.read_csv("https://raw.githubusercontent.com/YoungjinBD/dataset/main/housing.csv")

df

df.info()

df.describe()

데이터 전처리

# 결측값이 있는 행 제거
df = df.dropna()
assert df.isna().sum().sum() == 0

# ocean_proximity 범주형 컬럼 제거
all_columns = set(df.columns)
number_columns = set(df.select_dtypes(np.number).columns)
category_columns = all_columns - number_columns
df = df.drop(columns=category_columns)

독립변수들 간의 상관관계 분석

상관계수 행렬 (Correlation Matrix)

df.corr().loc["median_house_value"].abs().sort_values(ascending=False)

산점도 행렬 (Scatter Plot Matrix)

import seaborn as sns

sns.pairplot(df)

train, test 데이터 준비

from sklearn.model_selection import train_test_split

y_column = "median_house_value"
X_columns = df.drop(columns=y_column).columns

X = df[X_columns]
y = df[y_column]

assert type(X) == pd.DataFrame
assert type(y) == pd.Series

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)

모델 적용 및 데이터 분석 수행

• sklearn.ensemble.RandomForestRegressor 클래스 활용

RandomForestRegressor(
    n_estimators=100,
    *,
    criterion='squared_error',
    max_depth=None,
    min_samples_split=2,
    min_samples_leaf=1,
    min_weight_fraction_leaf=0.0,
    max_features=1.0,
    max_leaf_nodes=None,
    min_impurity_decrease=0.0,
    bootstrap=True,
    oob_score=False,
    n_jobs=None,
    random_state=None,
    verbose=0,
    warm_start=False,
    ccp_alpha=0.0,
    max_samples=None,
    monotonic_cst=None,
)

from sklearn.ensemble import RandomForestRegressor

rfr = RandomForestRegressor(max_depth=3, random_state=42)

rfr.fit(X_train, y_train)

y_pred = rfr.predict(X_test)

assert y_pred.shape == y_test.shape

데이터 모델링 성능 평가

from sklearn.metrics import mean_squared_error

mse = mean_squared_error(y_test, y_pred)

print(mse)

print(mean_squared_error(y_train, rfr.predict(X_train)))