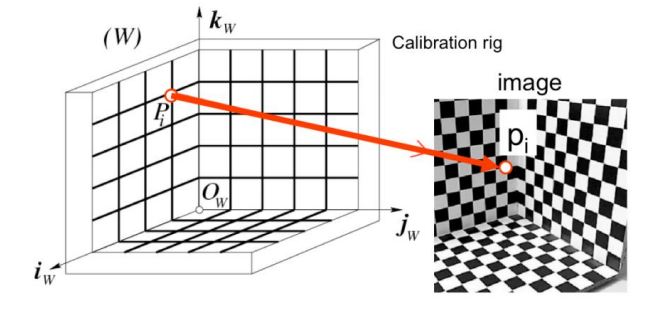
본 포스트는 Flexible Camera Calibration By Viewing a Plane From Unknown Orientations [Zhang et al. ICCV 1999]를 참고하였다.
Mapping to pixel coordinates
2차원 좌표 x와 3차원 좌표 Xcam의 관계는 다음과 같다.
xXcam=K[I∣0]Xcam=[R∣t]Xworld
이 때 Xcam은 원점 기준 3차원 좌표계이며 월드 좌표계의 3차원 좌표 Xworld는 회전 변환을 통해서 Xcam이 될 수 있을 것이다.
Camera Extrinsic matrix
위 수식 Xcam=[R∣t]Xworld에서 [R∣t]는 무엇일까?
[R∣t]를 정확히 표현하면 다음과 같다.
[R3×301×3T3×11]4×4
[R∣T]는 extrinsic matrix이고 카메라 좌표계와 월드 좌표계 사이의 변환을 의미하는 matrix이며 이는 월드 좌표에서 카메라 중심의 위치와 카메라의 방향을 정의한다.
R은 회전(Rotation)을, T는 평행이동(Translation)을 의미한다. 동시에, T는 Xworld의 원점(C)을 3차원 카메라 중심 좌표계에 투영한 위치를 의미한다.
C는 또한 다음과 같이 계산될 수 있다.
C=−R−1T=−RTT
R과 T는 월드 좌에서 3차원 카메라 좌표로의 변환을 의미하므로 카메라와 무관한 외부 파라미터이다. 이것이 extrinsic matrix로 불리는 이유이기도 하다.
extrinsic matrix는 먼저 intrinsic matrix를 구하고 이미 샘플링 된 3차원 월드 좌표와 2차원 이미지 좌표 간의 매칭 쌍을 이용해 구한다. Mapping to pixel coordinates에 있는 수식을 그대로 따라가는 셈이다.
Camera extrinsic matrix의 DoF(Degree of Freedom)는 얼마일까?
3차원 rotation을 의미하는 R은 다음과 같다.
R=⎣⎢⎡cos(β)cos(γ)cos(β)sin(γ)−sin(β)sin(α)sin(β)cos(γ)−cos(α)sin(γ)sin(α)sin(β)sin(γ)+cos(α)cos(γ)sin(α)cos(β)cos(α)sin(β)cos(γ)+sin(α)sin(γ)cos(α)sin(β)sin(γ)−sin(α)cos(γ)cos(α)cos(β)⎦⎥⎤
R은 α,β,γ를 통해 결정되므로 R에 의한 DoF는 3이며
T는 C가 투영된 3차원 좌표이므로 T에 의한 DoF 또한 3이다.
따라서 Camera extrinsic matrix의 DoF는 6이다.
World to Cam & Cam to World
그렇다면 임의의 3차원 좌표를 카메라 원점 기준 3차원 좌표로 옮기는 공식은 무엇일까?
Xcam=[Rw2c∣tw2c]Xworld
이 수식은 임의의 3차원 좌표 Xworld를 카메라 원점의 3차원 좌표 Xcam으로 mapping 하는 공식이다.
이러한 변환은 SLAM과 같은 mapping application이나 simultaneous localization 등에 적극 활용된다.
카메라 원점 3차원 좌표에서 임의의 3차원 좌표로 옮기는 공식은 무엇일까?
Xworld=[Rc2w∣tc2w]Xcam
공식 자체는 카메라를 알 때 world 좌표를 구하는 공식으로 보이지만 사실 tracking과 같이 know object의 world 좌표를 알 때 영상으로 좌표를 옮겨오는 task에서 주로 사용된다.
두 수식은 inverse 관계에 있으며 따라서 다음과 같은 수식 유도가 가능하다.
XcamXcam=[Rw2c∣tw2c][Rc2w∣tc2w]Xcam=Rw2c(Rc2wXcam+tc2w)+tw2c
이로부터 다음과 같은 수식을 얻을 수 있다.
Rw2cRc2w=IRw2ctc2w+tc2w=0
How to calculate Camera Calibration
Camera Calibration matrix K는 어떻게 구할까?
우리가 알 고 있는 정보는 각 이미지의 Xcam이다. 편의를 위해 Xcam의 z좌표가 0이라 하자. 즉, X=(X1,X2,0,1)이다.
반면 우리가 모르는 정보는 constant camera intrinsics K이며 camera pose인 R과 t도 알지 못한다.
이 때, 어떠한 카메라 상의 2차원 좌표 x는 다음과 같다.
∀λ∈Rλx=K[r1,r2,r3∣t]XcamXcam=λ′K[r1,r2∣t][X1,X2,1]T
λ는 scale invariant한 homography의 성질을 반영한 것이다.
마지막 수식은 3차원이였으나 z=0으로 인해 2차원이 된 Xcam과 이미지 2차원 좌표 x 간의 homography를 의미한다.
이 경우 앞선 2D Homography 포스트에서 다룬 공식을 적용할 수 있다.
Let H=K[r1,r2∣t]Xcam=λH[r1,r2∣t]⟺K−1H=λ[r1,r2∣t]
이 때, R의 r1과 r2가 orthonomal하므로 다음과 같은 관계가 만족한다.
(i) r1Tr2=0(ii) r1Tr1=r2Tr2=1
이를 이용하면 최종적으로 3×4 projection matrix H에 대해 다음과 같은 수식을 얻을 수 있다.
As K−1[h1,h2,h3]=λ[r1,r2∣t]r1=K−1h1r2=K−1h2Put r1,r2 into (i) and (ii)
(iii) h1TK−TK−1h2(iv) h1TK−TK−1h1=h2TK−TK−1h2
위 두 수식 (iii), (iv)을 바탕으로 최적화 기법인 Levenberg Marquardt Algorithm를 이용하여 Camera calibration matrix K를 구할 수 있다.
Degrees of Freedom of H
H의 DoF(Degrees of Freedom)은 얼마일까?
H는 3×4 projection matrix이다. 먼저 H의 식을 살펴보자.
H=K[R∣t]
이미 R의 DoF는 3, t의 DoF는 3임을 보았다. 즉, extrinsic matrix의 DoF는 6이다.
또한 앞선 포스트에서 calibration(intrinsic) matrix K의 DoF는 5임을 보았다.
따라서 H의 DoF는 11이다.
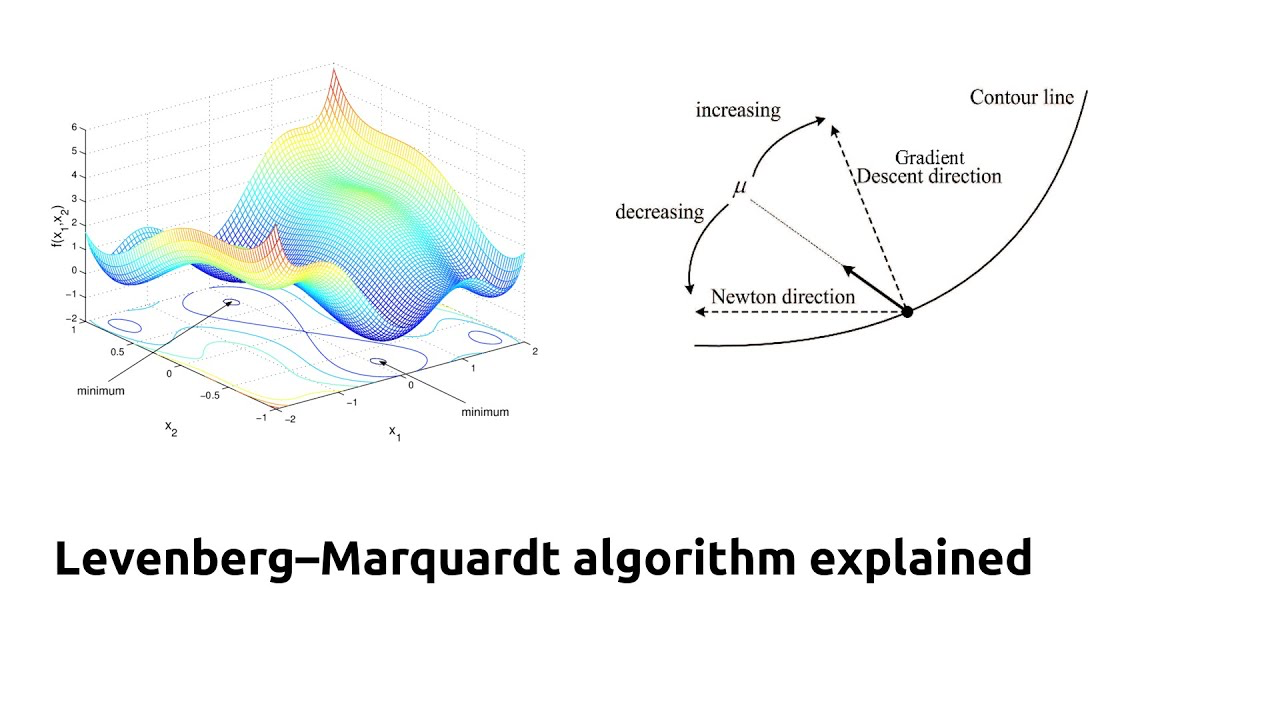
Levenberg Marquardt Algorithm
Levenberg Marquardt Algorithm에 대해서는 최적화 관련 포스트에서 다시한번 자세히 다룰 예정이다.

References
https://ieeexplore.ieee.org/document/791289
https://darkpgmr.tistory.com/142
https://eehoeskrap.tistory.com/511
https://www.semanticscholar.org/paper/Stereo-camera-system-calibration%3A-the-need-of-two-Beschi-Feng/cb01fe7e7fc8793e3d0b6ee43b8e41401af97c29
https://www.youtube.com/watch?v=dPZo74SbkeQ