Pinhole Camera & Camera Calibration

Henry·2023년 4월 15일

3D Vision Calibration DL ML focal length intrinsic pinhole radial distortion 캘리브레이션 핀홀

3D Vision

목록 보기

2/3

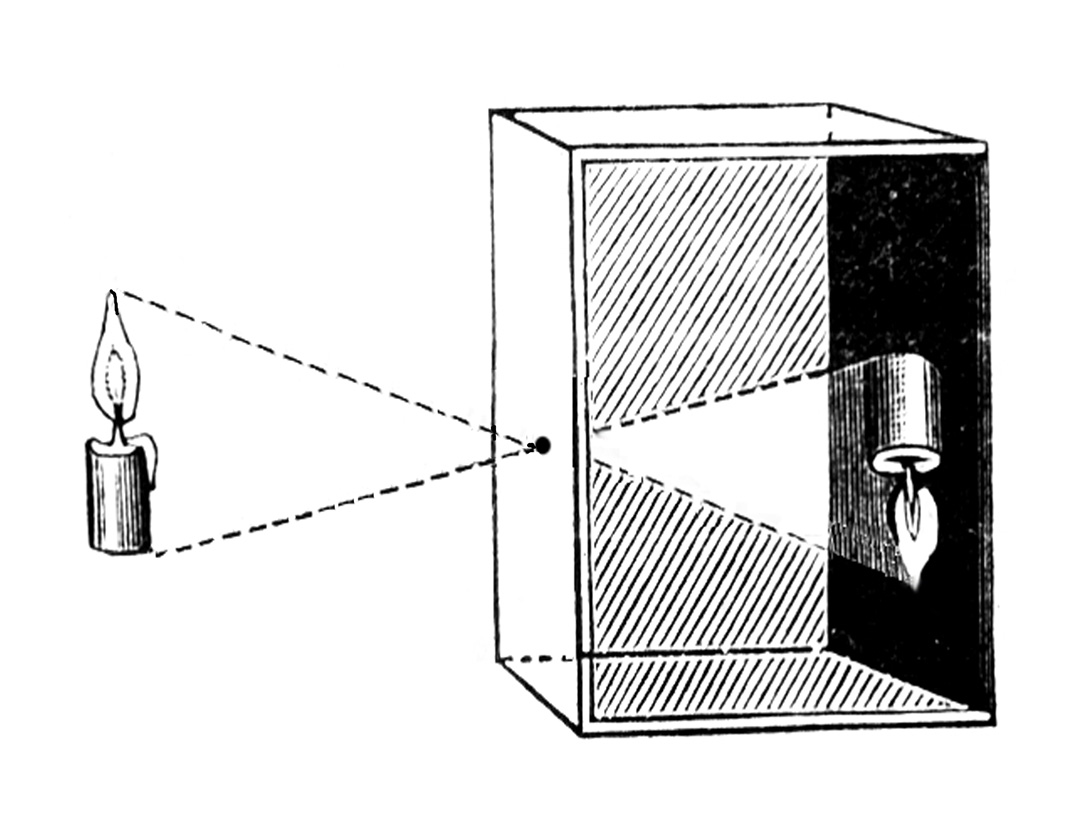
Pinehole camera model

핀홀 카메라는 무엇일까?

핀홀 카메라는 렌즈를 사용하지 않고 작은 구멍을 통해 빛을 받아 들여 촬영하는 사진기이다.

현대의 카메라야 당연히 렌즈가 있지만, 이 핀홀 카메라를 통해 수학적으로 가장 간단한 모델링할 수 있으므로 핀홀 상황을 가정해보자.

Mapping to pixel coordinates

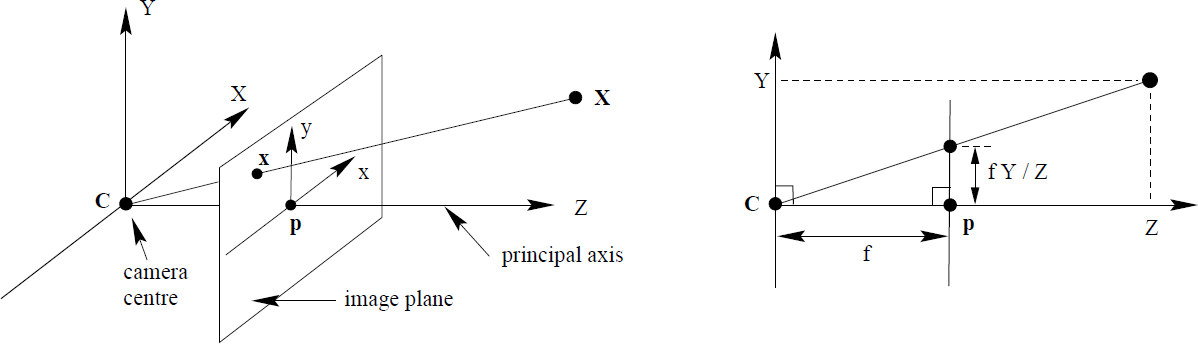
3차원 좌표를 어떻게 2차원 이미지 좌표로 바꿀 수 있을까?

2D homography에서와 같이, 3차원 좌표 $(X,\space Y, \space Z)$ 는 $(X, \space Y, \space Z, \space 1)$ 와 같이 표현할 수 있다.

카메라 중점을 원점이라고 가정한다면, 이미지 좌표(pixel coordinates)는 $z$ 축에 대해 단위거리마다 $Y \over Z$ 만큼 늘어날 것이므로 초점거리(focal length) $f$ 에 대해 3차원 좌표 $X = \begin{pmatrix} X & Y & Z \end{pmatrix}$ 를 다음과 같이 표현할 수 있다.

\begin{pmatrix} X \\ Y \\ Z \end{pmatrix} \mapsto \begin{pmatrix}fX/Z \\ fY/Z \end{pmatrix}

따라서 3차원 좌표 $(X, \space Y, \space Z, \space 1)$ 는 다음과 같다.

\begin{pmatrix} X \\ Y \\ Z \\ 1\end{pmatrix} \mapsto \begin{pmatrix}fX \\ fY \\ Z \end{pmatrix} = \begin{bmatrix}f & & & 0 \\ & f & & 0 \\ & & 1 & 0 \end{bmatrix} \begin{pmatrix}X \\ Y \\ Z \\ 1 \end{pmatrix}

물론 카메라 중점이 원점이 아닐 수 있다. 이 경우 옮겨진 $p_x$ 와 $p_y$ 만큼을 이동시켜주면 된다.

\begin{pmatrix} X \\ Y \\ Z \\ 1\end{pmatrix} \mapsto \begin{pmatrix}fX + Zp_x \\ fY + Zp_y \\ Z \end{pmatrix} = \begin{bmatrix}f & & p_x & 0 \\ & f & p_y & 0 \\ & & 1 & 0 \end{bmatrix} \begin{pmatrix}X \\ Y \\ Z \\ 1 \end{pmatrix}

Camera intrinsic matrix

위 수식에서 좌표 변환을 일으키는 matrix는 다음과 같다.

K = \begin{bmatrix}f & & p_x\\ & f & p_y\\ & & 1\end{bmatrix}

이 matrix를 Camera intrinsic matrix 또는 Camera calibration matrix라고 부른다. 약자로 $K$ 를 자주 쓰며 이러한 notation으로 앞서 살펴본 식을 정리해보자.

x = K[I|0]X_{cam}

이 때, $x$ 는 2차원 좌표 $(fX + Zp_x, \space fY + Zp_y, \space Z)$ 이며 $X_{cam}$ 은 3차원 좌표 $(X, \space Y, \space Z, \space 1)$ 이다. 또, 네번째 column의 모든 값이 $0$ 이므로 $[I|0]$ 와 같이 분리하여 표기한다.

이러한 $K$ 는 보통 calibration pattern으로 구한다.

Calibration is for 3D to 2D

착각하기 쉬운 내용이니 조심하자. Camera intrinsic matrix는 3차원에서 2차원으로 가는 수식이다. $Z$ 에 대해 알지 못하기 때문에 2차원에서 3차원으로의 mapping은 존재하지 않는다.

Pinhole과 Actual Camera의 차이

핀홀 카메라는 렌즈가 없음을 가정하였다. 하지만 현대의 카메라는 모두 렌즈가 있고, 렌즈의 왜곡 때문에 이론적 핀홀 모델과 차이를 보인다.

Radial distortion

핀홀 카메라의 가정과 다르게 실제 카메라는 렌즈로 인해 빛이 굴절한다. 일반적으로 이 때 사용되는 렌즈로 얇은 렌즈로 가정하며 이를 thin lense assumption이라고 한다. 또한, 위 가정에서의 카메라 모델을 paraxial refraction model이라 한다. 이 모델에서 빛이 렌즈의 어디를 통과하냐에 따라 굴절이 조금씩 다르게 되고, 광축까지의 거리가 상이하게 된다. 이로 인해 좌표에 변화를 주게되는 radial distortion이 발생한다.

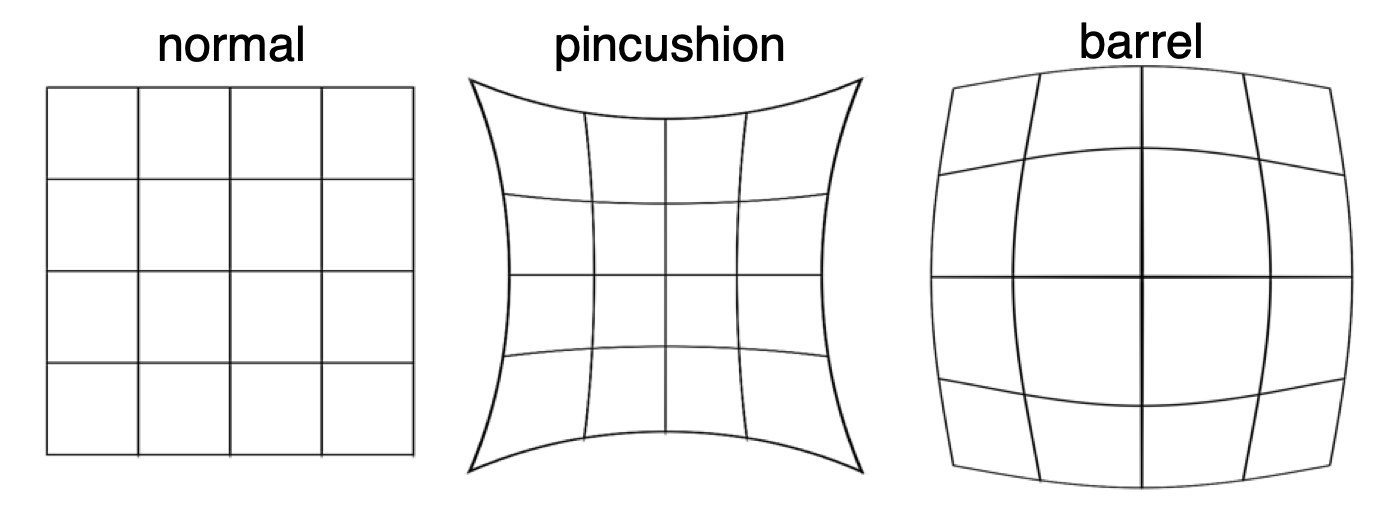
위 사진은 paraxial refraction model에서 발생하는 두 가지 radial distortion을 나타낸다. 배율이 증가하면 pincushion distortion이 나타나고, 배율이 감소하면 barrel distortion이 나타난다.

왜곡으로 인해 변화된 좌표 $(x_d, \space y_d)$ 는 원래의 좌표 $(\tilde{x}, \space \tilde{y})$ 에 대해 다음과 같다.

\begin{pmatrix} x_d \\ y_d \end{pmatrix} = L(\tilde{r}) \begin{pmatrix} \tilde{x} \\ \tilde{y} \end{pmatrix}

위 수식에서 변화를 의미하는 $L(\tilde{r})$ 은 보통 이차함수로 fitting한다.

3D vision을 수행하기 전에 이미지 전처리 과정에서 radial distortion을 보정해주어야하며, 앞서 살펴본 카메라 중점 또한 원점으로 옮겨주는 것이 좋다. $(p_x = p_y = 0)$

참고로 radial distortion은 DNN으로도 학습시켜 해결할 수도 있지만 이차함수를 두고 전처리하는 것 또한 충분히 괜찮은 성능을 보인다.

Skewness

현대의 카메라에는 센서가 있고 경우에 따라 센서 제조 과정에서 카메라 좌표계의 축이 90도를 이루지 못할 수 있다. 축이 이루는 각을 $\theta$ 라 할 때, $K$ 는 다음과 같이 표현된다.

K = \begin{bmatrix}\alpha & -\alpha cot\theta & p_x\\ & \beta \over sin\theta & p_y\\ & & 1\end{bmatrix}

물론 대부분의 카메라는 zero-skewed 상태이다.

Degrees of Freedom

Camera intrinsic matrix의 DoF(Degrees of Freedom)은 얼마일까?

skewness을 고려하면 Camera intrinsic matrix $K$ 는 focal length에 2개( $\alpha, \beta$ ), offset에 2개( $c_x, c_y$ ), skewness에 1개( $\theta$ )를 포함해 총 5개의 DoF를 갖는다.

Conclusion

핀홀 카메라 모델은 렌즈가 없는 카메라를 모델링한 것이다.
실제 카메라는 렌즈가 있어 빛이 굴절해 좌표를 왜곡한다.
따라서 radial distortion 보정과 카메라 중점을 원점으로 옮기는 전처리가 필요하다.
Camera intrinsic matrix의 DoF는 5이다.

Appendix

핀홀 카메라 모델에서의 초점거리(focal length) $f$ 는 카메라 중점(바늘구멍)부터 이미지까지의 거리이지만 실제 카메라에서의 초점거리는 렌즈부터 렌즈초점(focal point)까지의 거리이다.

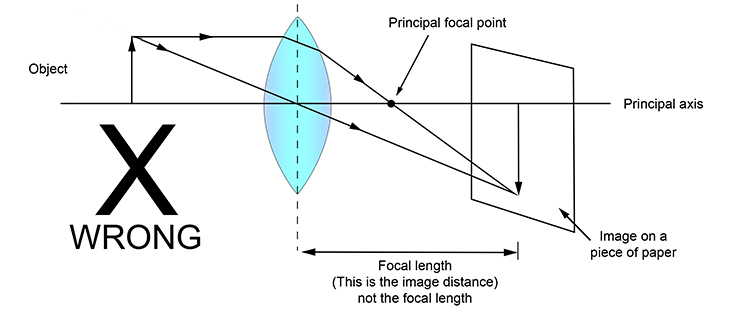
간혹 초점거리가 렌즈부터 이미지 센서까지라고 알려져있는데, 이는 잘못된 사실이다.

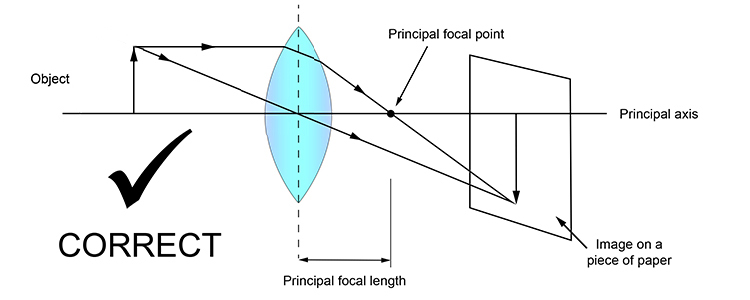
렌즈부터 이미지 센서까지의 거리는 이미지 거리(image distance)이고 렌즈부터 렌즈 초점까지의 거리가 초점 거리이다.