5.1 주성분 분석을 통한 비지도 차원 축소
특성 추출 : 데이터셋의 특성 개수를 줄이는 방법으로, 새로운 특성 곤간으로 데이터를 변환하거나 투영하여 원본 특성이 유지되지 않음
📍장점📍
1) 저장 공간 절약
2) 학습 알고리즘의 계산 효율성 향상
3) 차원의 저주 문제 감소 -> 예측 성능 향상
5.1.1 주성분 분석의 주요 단계
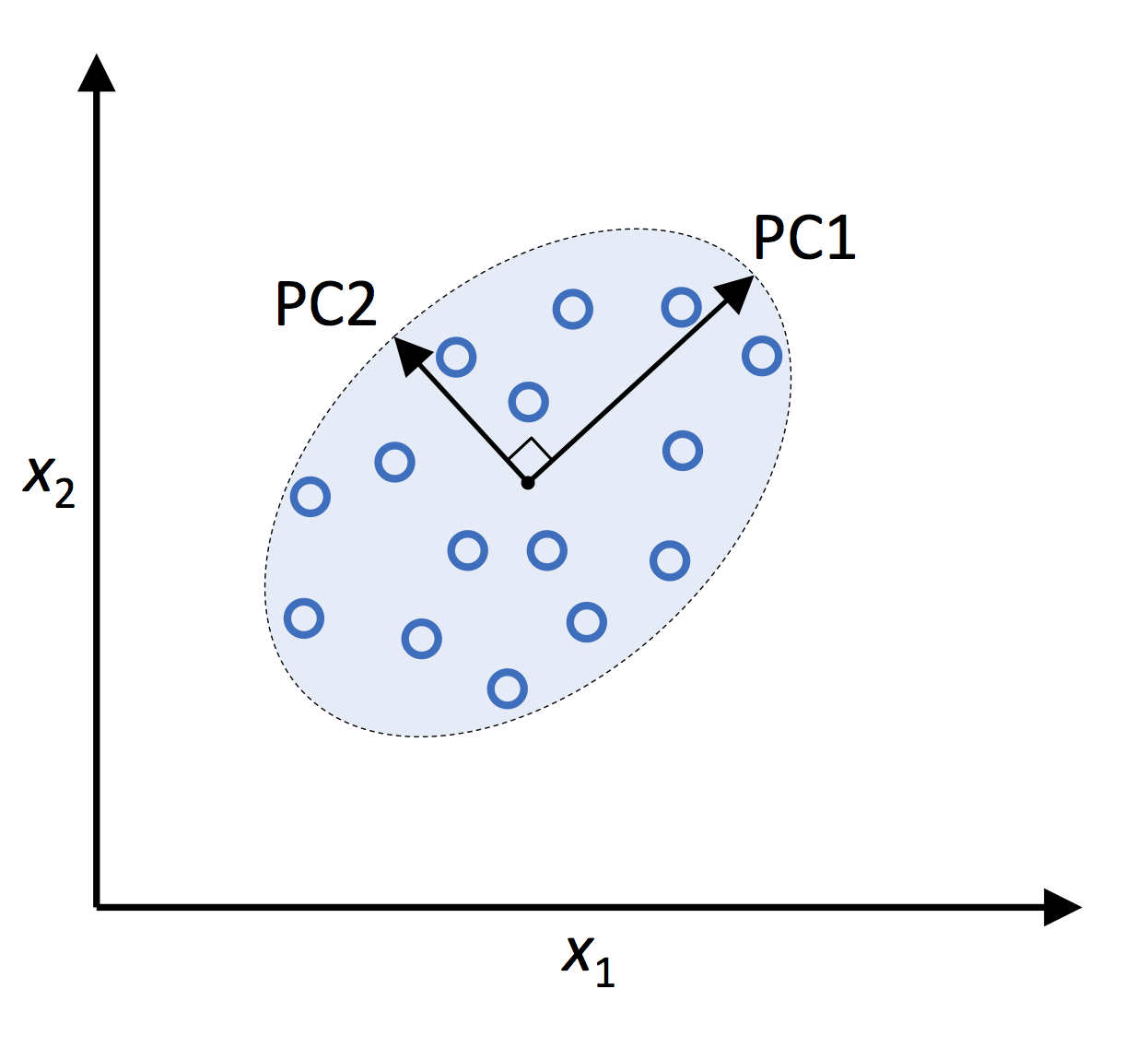
PCA : 비지도 선형 변환 기법, 고차원 데이터에서 분산이 가장 큰 방향을 찾고 좀 더 작거나 같은 수의 차원을 갖는 새로운 부분 공간으로 이를 투영
-> 사용 분야 : 탐색적 데이터 분석과 주식 거래 시장의 잡음 제거, 생물정보학 분야에서 게놈 데이터나 유전자 발현 분석
📍PCA 단계📍
1) d 차원 데이터셋을 표준화 전처리
2) 공분산 행렬을 만듦
3) 공분산 행렬을 고유 베거와 고유값으로 분해
4) 고윳값을 내림차순으로 정렬하고 그에 해당하는 고유 벡터의 순위를 매김
5) 고윳값이 가장 큰 k개의 고유 벡터를 선택. 여기서 k는 새로운 특성 부분 공간의 차원(k <= d)
6) 최상위 k개의 고유 벡터로 투영 행렬 w를 만듦
7) 투영 행렬 w를 사용해서 d 차원 입력 데이터셋 X를 새로운 k 차원의 특성 부분 공간으로 변환
5.1.2 주성분 추출 단계
📍네 단계 구성📍
1) 데이터를 표준화 전처리
2) 공분산 행렬을 구성
3) 공분산 행렬의 고윳값과 고유 벡터를 구함
4) 고윳값을 내림차순으로 정렬하여 고유 벡터의 순위를 매김
☑️Wine 데이터셋 로드☑️
import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/wine/wine.data',
header=None)☑️Wine 데이터셋 훈련 데이터셋과 테스트 데이터셋으로 나누기☑️
from sklearn.model_selection import train_test_split
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.3,
stratify=y,
random_state=0)☑️데이터 표준화 적용하여 단위 분산 갖게 하기☑️
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)☑️공분산 행렬의 고윳값 분해☑️
numpy.cov 함수 : 표준화 전처리된 훈련 데이터셋의 공분산 행렬을 계산
linalg.eig 함수 : 공분산 행렬에 대한 고윳값 분해를 수행
import numpy as np
cov_mat = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
print('\n고윳값 \n%s' % eigen_vals)
➡️ 13개의 고윳값이 들어있는 벡터(eigen_vals)와 각 고윳값에 대응하는 고유 벡터가 열에 저장된 13x13차원의 행렬(eigen_vals)을 얻음
5.1.3 총 분산과 설명된 분산
☑️설명된 분산 비율 그래프로 그려보기☑️
cumsum 함수 : 설명된 분산의 누적 합을 계산
step 함수 : 그래프로 그리기
tot = sum(eigen_vals)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
import matplotlib.pyplot as plt
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center',
label='Individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid',
label='Cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()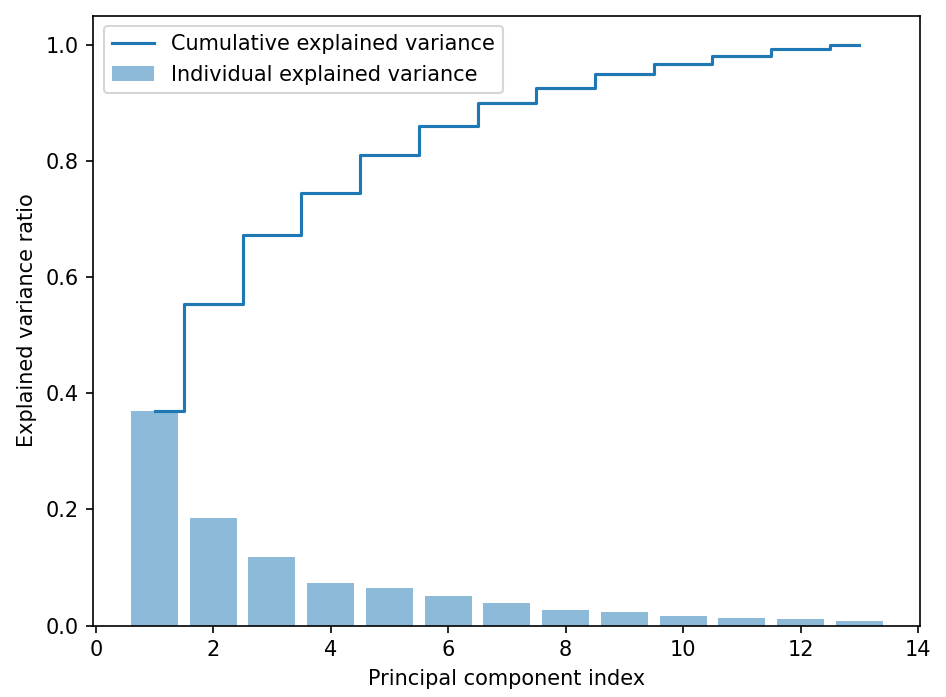
➡️첫 번째 주성분이 거의 분산의 40%를 커버하고 있음을 보여줌
➡️처음 두 개의 주성분이 데이터셋에 있는 분산의 대략 60%를 설명함
5.1.4 특성 변환
📍남은 단계📍
1) 고윳값이 가장 큰 k개의 고유 벡터를 선택. 여기서 k는 새로운 특성 부분 공간의 차원(k <= d)
2) 최상위 k개의 고유 벡터로 투영 행렬 w를 만듦
3) 투영 행렬 w를 사용해서 d 차원 입력 데이터셋 X를 새로운 k 차원의 특성 부분 공간으로 변환
☑️고윳값의 내림차순으로 고유 벡터와 고윳값의 쌍을 정렬☑️
# (고윳값, 고유벡터) 튜플의 리스트를 만듭니다
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
for i in range(len(eigen_vals))]
# 높은 값에서 낮은 값으로 (고윳값, 고유벡터) 튜플을 정렬합니다
eigen_pairs.sort(key=lambda k: k[0], reverse=True)☑️최상위 두 개의 고유 벡터로부터 13 x 2 차원의 투영 행렬 W를 만듦☑️
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
eigen_pairs[1][1][:, np.newaxis]))
print('투영 행렬 W:\n', w)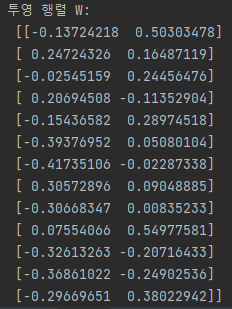
☑️샘플 x(13차원의 행 벡터)를 PCA 부분 공간(두 개의 주성분)을 투영하여 x' 얻기☑️
X_train_std[0].dot(w)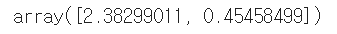
☑️훈련 데이터셋을 행렬 점곱으로 두 개의 주성분에 투영☑️
X_train_pca = X_train_std.dot(w)☑️변환된 Wine 훈련 데이터셋을 2차원 산점도로 시각화☑️
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train == l, 0],
X_train_pca[y_train == l, 1],
c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()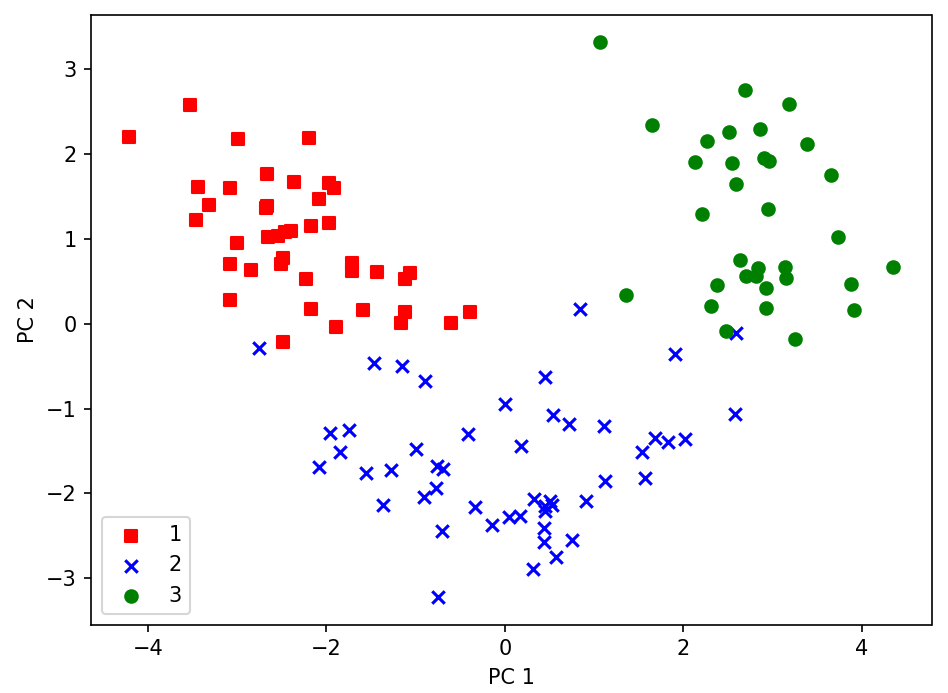
➡️데이터가 y축(두 번째 주성분)보다 x축(첫 번째 주성분)을 따라 더 넓게 퍼져 있음
➡️선형 분류기가 클래스들을 잘 분리할 수 있음을 직관적으로 알 수 있음
5.1.5 사이킷런의 주성분 분석
☑️결정 경계 만드는 함수 생성하여 파일로 저장☑️
import numpy as np
from matplotlib import pyplot as plt
from matplotlib.colors import ListedColormap
def plot_decision_regions(X, y, classifier, resolution=0.02):
# 마커와 컬러맵을 설정합니다
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# 결정 경계를 그립니다
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# 샘플의 산점도를 그립니다
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.8,
c=colors[idx],
marker=markers[idx],
label=cl,
edgecolor='black')☑️함수 이용하여 결정 경계 생성☑️
from sklearn.linear_model import LogisticRegression
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_std)
X_test_pca = pca.transform(X_test_std)
lr = LogisticRegression(random_state=1)
lr = lr.fit(X_train_pca, y_train)
plot_decision_regions(X_train_pca, y_train, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()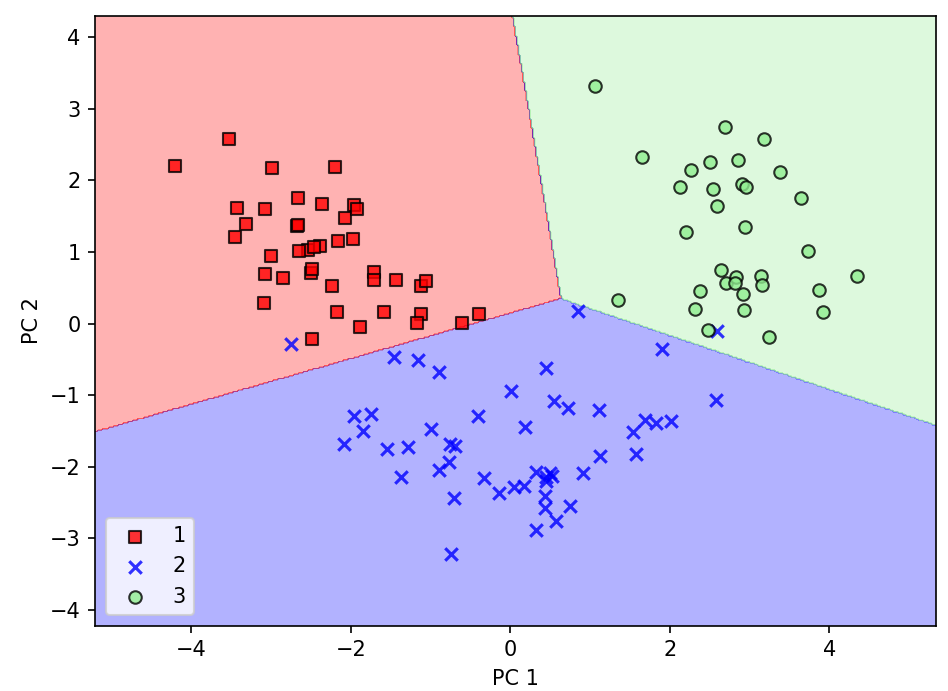
☑️테스트 데이터셋을 변환하고 로지스틱 회귀가 클래스를 잘 구분하는지 결정 경계 그리기☑️
plot_decision_regions(X_test_pca, y_test, classifier=lr)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()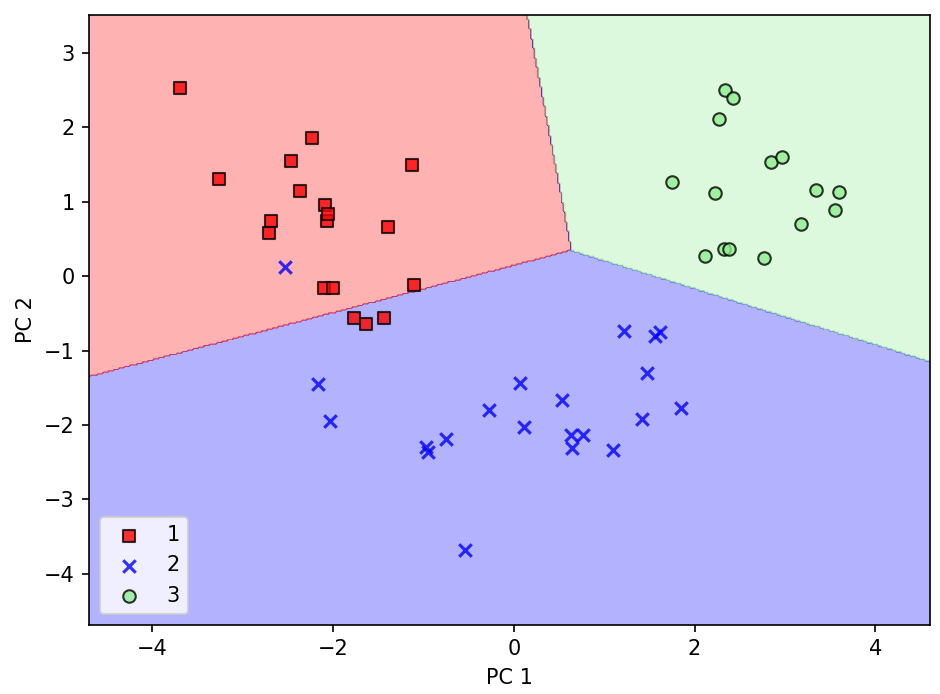
➡️로지스틱 회귀가 2차원 특성 부분 공간에서 매우 잘 작동함
5.2 선형 판별 분석을 통한 지도 방식의 데이터 압축
선형 판별 분석(LDA) : 규제가 없는 모델에서 차원의 저주로 인한 과대 적합 정도를 줄이고 계산 효율성을 높이기 위한 특성 추출의 기법으로 사용
📍LDA 목표📍
-> 클래스를 최적으로 구분할 수 있는 특성 부분 공간 찾는 것
5.2.1 주성분 분석 vs 선형 판별 분석
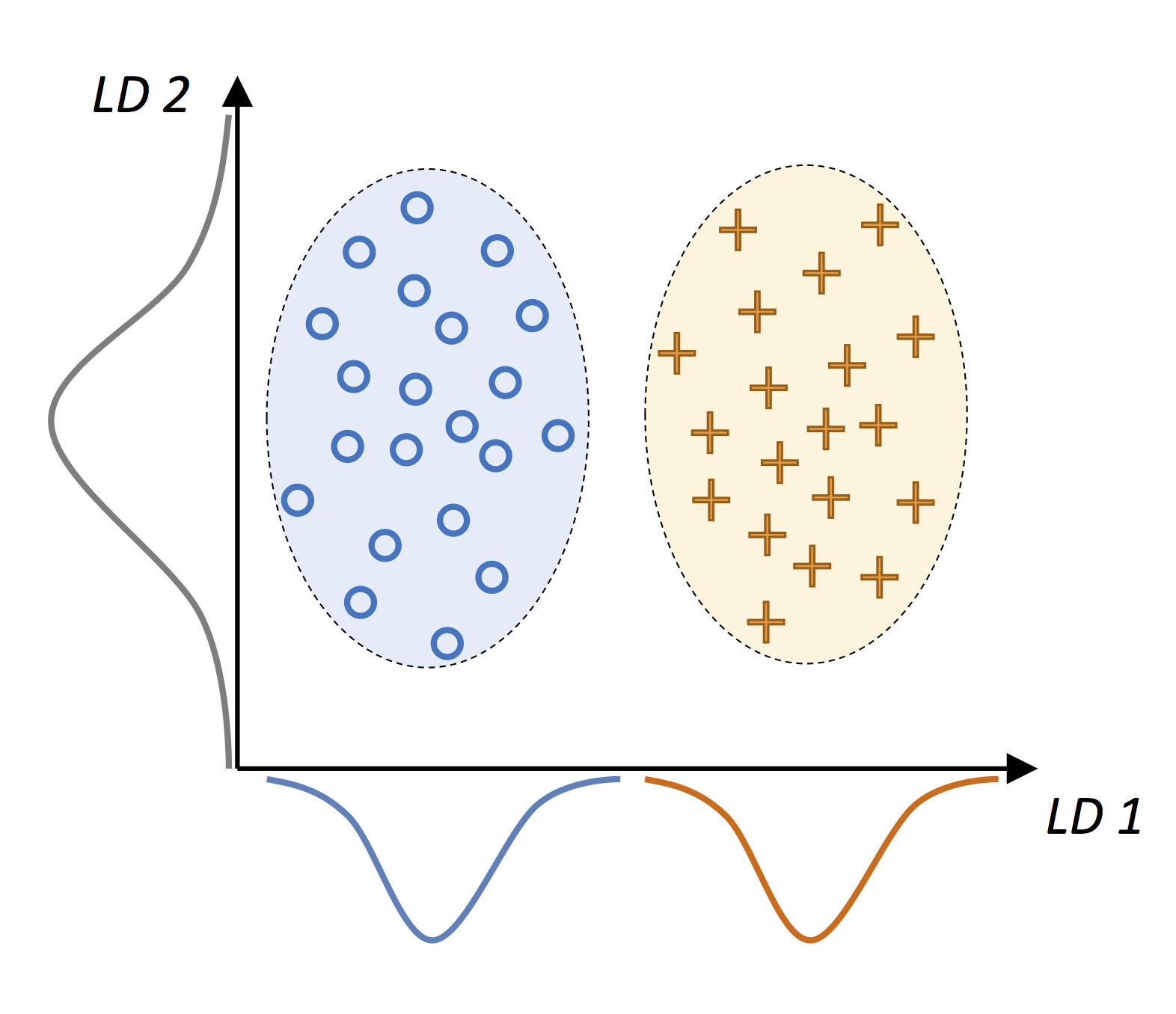
5.2.2 선형 판별 분석의 내부 동작 방식
📍LDA 수행에 필요한 주요 단계📍
1) d 차원의 데이터셋을 표준화 전처리(d는 특성 개수)
2) 각 클래스에 대해 d 차원의 평균 벡터를 계산
3) 클래스 간의 산포 행렬 SB와 클래스 내 산포 행렬 SW를 구성
4) SW-1SB행렬의 고유 벡터와 고윳값을 계산
5) 고윳값을 내림차순으로 정렬하여 고유 벡터의 순서를 매김
6) 고윳값이 가장 큰 k개의 고유 벡터를 선택하여 d x k 차원의 변환 행렬 W를 구성. 이 행렬의 열이 고유 벡터이다.
7) 변환 행렬 W를 사용하여 샘플을 새로운 특성 부분 공간으로 투영
5.2.3 산포 행렬 계산
☑️각 클래스에 대한 평균 벡터를 계산☑️
np.set_printoptions(precision=4)
mean_vecs = []
for label in range(1, 4):
mean_vecs.append(np.mean(X_train_std[y_train == label], axis=0))
print('MV %s: %s\n' % (label, mean_vecs[label - 1]))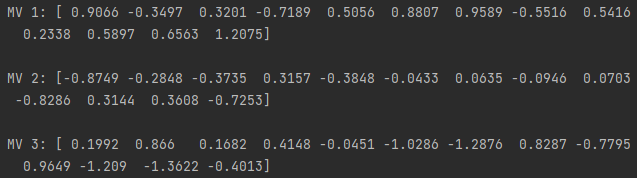
☑️클래스 내 산포 행렬 계산☑️
d = 13 # 특성의 수
S_W = np.zeros((d, d))
for label, mv in zip(range(1, 4), mean_vecs):
class_scatter = np.zeros((d, d)) # 각 클래스에 대한 산포 행렬
for row in X_train_std[y_train == label]:
row, mv = row.reshape(d, 1), mv.reshape(d, 1) # 열 벡터를 만듭니다
class_scatter += (row - mv).dot((row - mv).T)
S_W += class_scatter # 클래스 산포 행렬을 더합니다
print('클래스 내의 산포 행렬: %sx%s' % (S_W.shape[0], S_W.shape[1]))
☑️클래스 내 산포 행렬 스케일 조정☑️
d = 13 # 특성의 수
S_W = np.zeros((d, d))
for label, mv in zip(range(1, 4), mean_vecs):
class_scatter = np.cov(X_train_std[y_train == label].T)
S_W += class_scatter
print('스케일 조정된 클래스 내의 산포 행렬: %sx%s' %
(S_W.shape[0], S_W.shape[1]))
☑️클래스 간의 산포 행렬 계산☑️
mean_overall = np.mean(X_train_std, axis=0)
mean_overall = mean_overall.reshape(d, 1) # 열 벡터로 만들기
d = 13 # 특성 개수
S_B = np.zeros((d, d))
for i, mean_vec in enumerate(mean_vecs):
n = X_train_std[y_train == i + 1, :].shape[0]
mean_vec = mean_vec.reshape(d, 1) # 열 벡터로 만들기
S_B += n * (mean_vec - mean_overall).dot((mean_vec - mean_overall).T)
print('클래스 간의 산포 행렬: %sx%s' % (S_B.shape[0], S_B.shape[1]))
5.2.4 새로운 특성 부분 공간을 위해 선형 판별 벡터 선택
☑️행렬 SW-1SB의 고윳값 계산☑️
eigen_vals, eigen_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))☑️고윳값의 역순으로 고유 벡터를 정렬☑️
# (고윳값, 고유벡터) 튜플의 리스트를 만듭니다.
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
for i in range(len(eigen_vals))]
# (고윳값, 고유벡터) 튜플을 큰 값에서 작은 값 순서대로 정렬합니다.
eigen_pairs = sorted(eigen_pairs, key=lambda k: k[0], reverse=True)
# 고윳값의 역순으로 올바르게 정렬되었는지 확인합니다.
print('내림차순의 고윳값:\n')
for eigen_val in eigen_pairs:
print(eigen_val[0])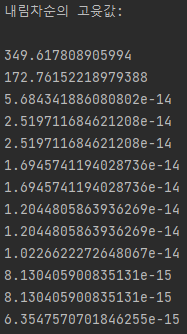
☑️고윳값의 내림차순으로 선형 판별 벡터 그리기☑️
tot = sum(eigen_vals.real)
discr = [(i / tot) for i in sorted(eigen_vals.real, reverse=True)]
cum_discr = np.cumsum(discr)
plt.bar(range(1, 14), discr, alpha=0.5, align='center',
label='Individual "discriminability"')
plt.step(range(1, 14), cum_discr, where='mid',
label='Cumulative "discriminability"')
plt.ylabel('"Discriminability" ratio')
plt.xlabel('Linear discriminants')
plt.ylim([-0.1, 1.1])
plt.legend(loc='best')
plt.tight_layout()
plt.show()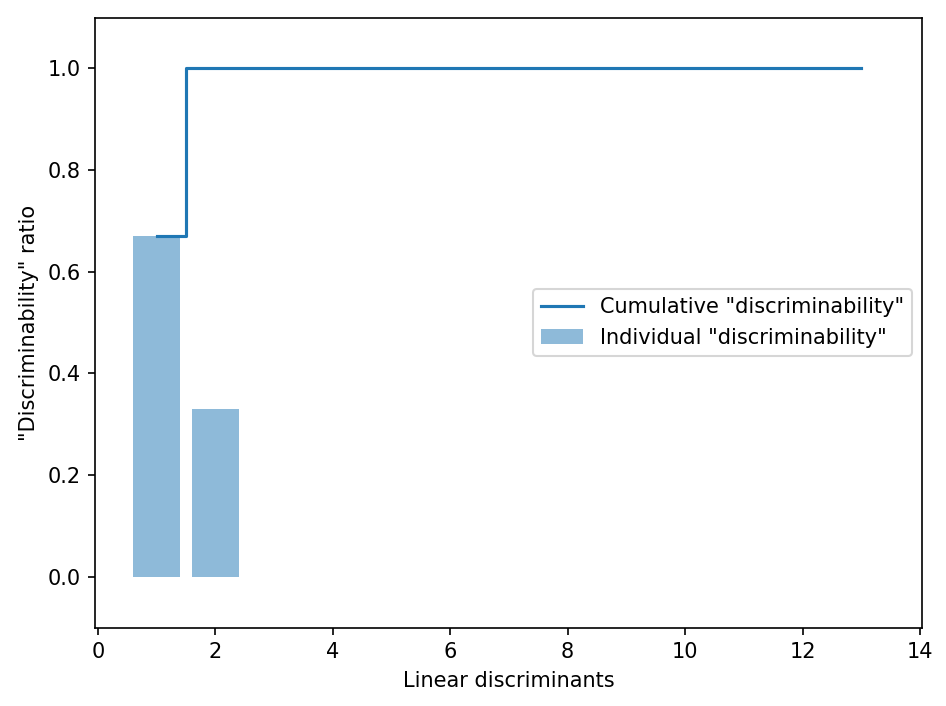
➡️처음 두 개의 선형 판별 벡터가 Wine 데이터셋에 있는 정보 중 거의 100%를 잡아냄
☑️두 개의 판별 고유 벡터를 열로 쌓아서 변환 행렬 W 만들기☑️
w = np.hstack((eigen_pairs[0][1][:, np.newaxis].real,
eigen_pairs[1][1][:, np.newaxis].real))
print('행렬 W:\n', w)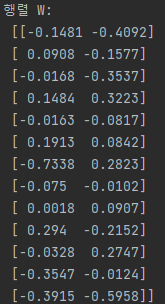
5.2.5 새로운 특성 공간으로 샘플 투영
☑️변환 행렬 W를 훈련 데이터셋에 곱해서 데이터 변환☑️
X_train_lda = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_lda[y_train == l, 0],
X_train_lda[y_train == l, 1] * (-1),
c=c, label=l, marker=m)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower right')
plt.tight_layout()
plt.show()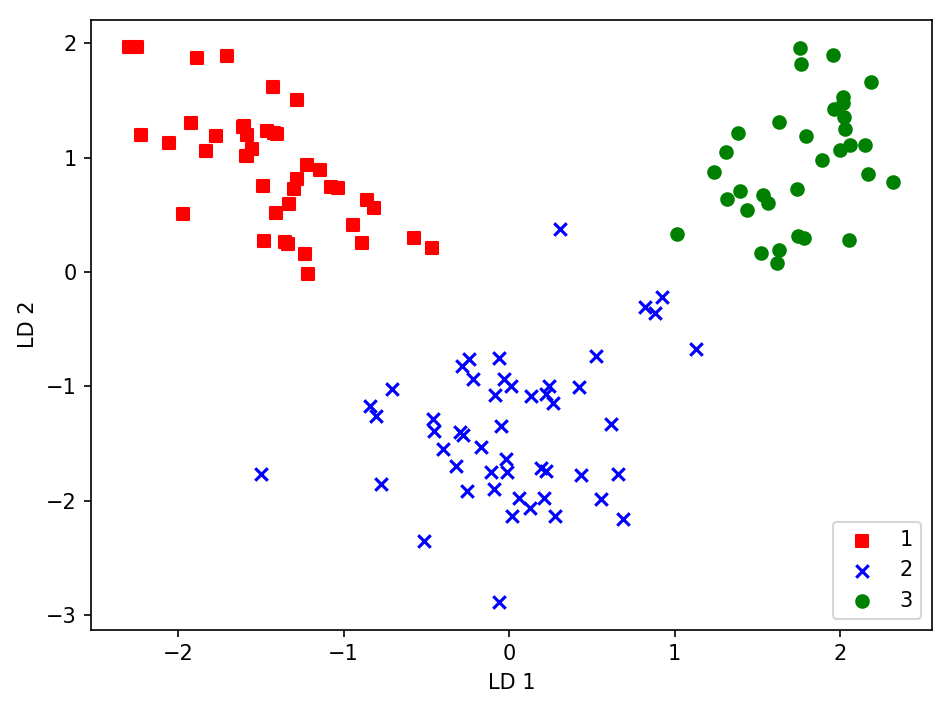
➡️세 개의 와인 클래스를 새로운 특성 부분 공간에서 선형적으로 완벽하게 구분
5.2.6 사이킷런의 LDA
☑️사이킷런에 구현된 LDA 클래스 불러오기☑️
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)
X_train_lda = lda.fit_transform(X_train_std, y_train)☑️LDA로 변환한 저차원 훈련 데이터셋에 로지스틱 회귀 분류기가 잘 동작하는지 확인☑️
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression(random_state=1)
lr = lr.fit(X_train_lda, y_train)
plot_decision_regions(X_train_lda, y_train, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()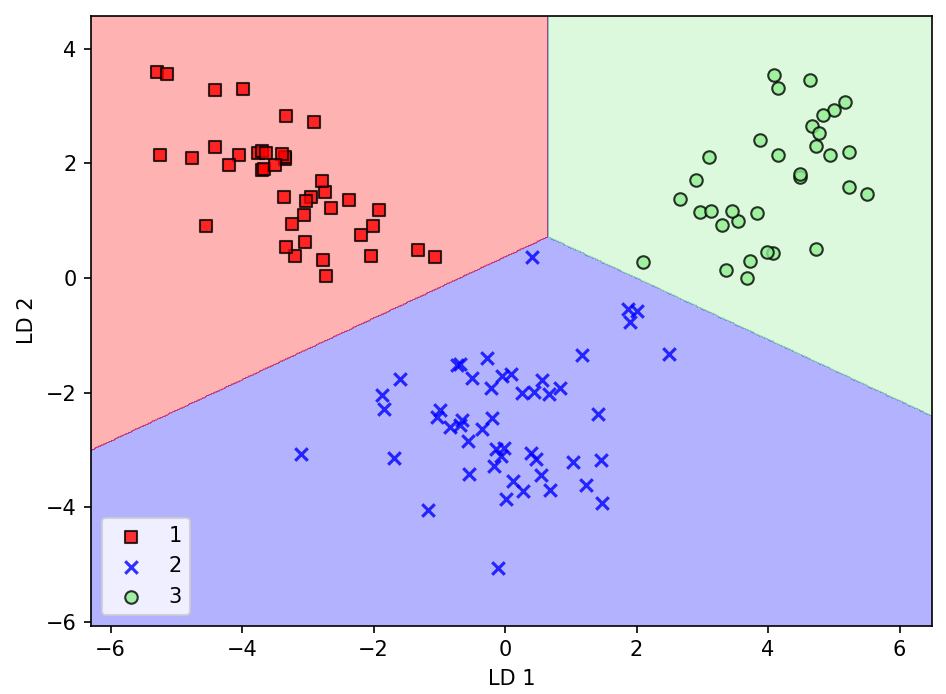
➡️클래스 2의 샘플 하나가 로지스틱 회귀 모델의 결정 경계에 가까이 놓여 있음
X_test_lda = lda.transform(X_test_std)
plot_decision_regions(X_test_lda, y_test, classifier=lr)
plt.xlabel('LD 1')
plt.ylabel('LD 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()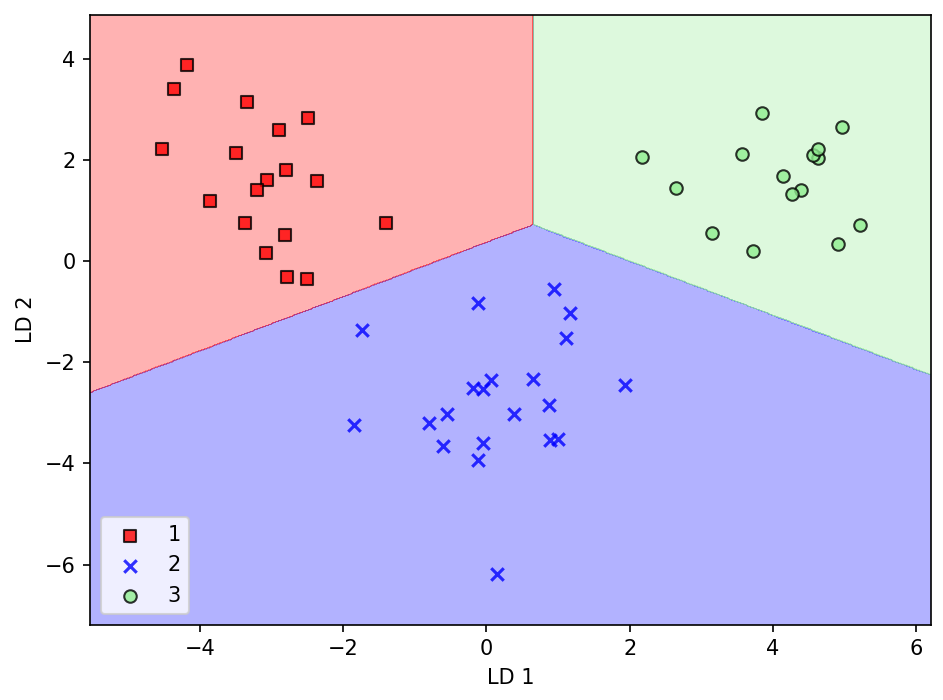
➡️모든 샘플을 완벽하게 분류
5.3 커널 PCA를 사용하여 비선형 매핑
커널 PCA -> 선형적으로 구분되지 않는 데이터를 선형 분류기에 적합한 새로운 저차원 부분 공간으로 변환
5.3.1 커널 함수와 커널 트릭
📍단계📍
1) 커널 PCA를 통한 비선형 매핑을 수행하여 데이터를 고차원 공간으로 변환
2) 고차원 공간에 표준 PCA를 사용하여 샘플이 선형 분류기로 구분될 수 있는 저차원 공간으로 데이터를 투영
커널 트릭 : 원본 특성 공간에서 두 고차원 특성 벡터의 유사도를 계산 가능 (계산 비용이 비싼 문제를 해결)
5.3.2 파이썬으로 커널 PCA 구현
from scipy.spatial.distance import pdist, squareform
from scipy.linalg import eigh
import numpy as np
from distutils.version import LooseVersion as Version
from scipy import __version__ as scipy_version
# scipy 2.0.0에서 삭제될 예정이므로 대신 numpy.exp를 사용합니다.
if scipy_version >= Version('1.4.1'):
from numpy import exp
else:
from scipy import exp
def rbf_kernel_pca(X, gamma, n_components):
"""
RBF 커널 PCA 구현
매개변수
------------
X: {넘파이 ndarray}, shape = [n_samples, n_features]
gamma: float
RBF 커널 튜닝 매개변수
n_components: int
반환할 주성분 개수
반환값
------------
X_pc: {넘파이 ndarray}, shape = [n_samples, k_features]
투영된 데이터셋
"""
# MxN 차원의 데이터셋에서 샘플 간의 유클리디안 거리의 제곱을 계산합니다.
sq_dists = pdist(X, 'sqeuclidean')
# 샘플 간의 거리를 정방 대칭 행렬로 변환합니다.
mat_sq_dists = squareform(sq_dists)
# 커널 행렬을 계산합니다.
K = exp(-gamma * mat_sq_dists)
# 커널 행렬을 중앙에 맞춥니다.
N = K.shape[0]
one_n = np.ones((N, N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# 중앙에 맞춰진 커널 행렬의 고윳값과 고유벡터를 구합니다.
# scipy.linalg.eigh 함수는 오름차순으로 반환합니다.
eigvals, eigvecs = eigh(K)
eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
# 최상위 k 개의 고유벡터를 선택합니다(결과값은 투영된 샘플입니다).
X_pc = np.column_stack([eigvecs[:, i]
for i in range(n_components)])
return X_pc예제 1 : 반달 모양 구분하기
☑️rbf_kernel_pca 함수를 비선형 데이터셋에 적용☑️
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, random_state=123)
plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X[y == 1, 0], X[y == 1, 1], color='blue', marker='o', alpha=0.5)
plt.tight_layout()
plt.show()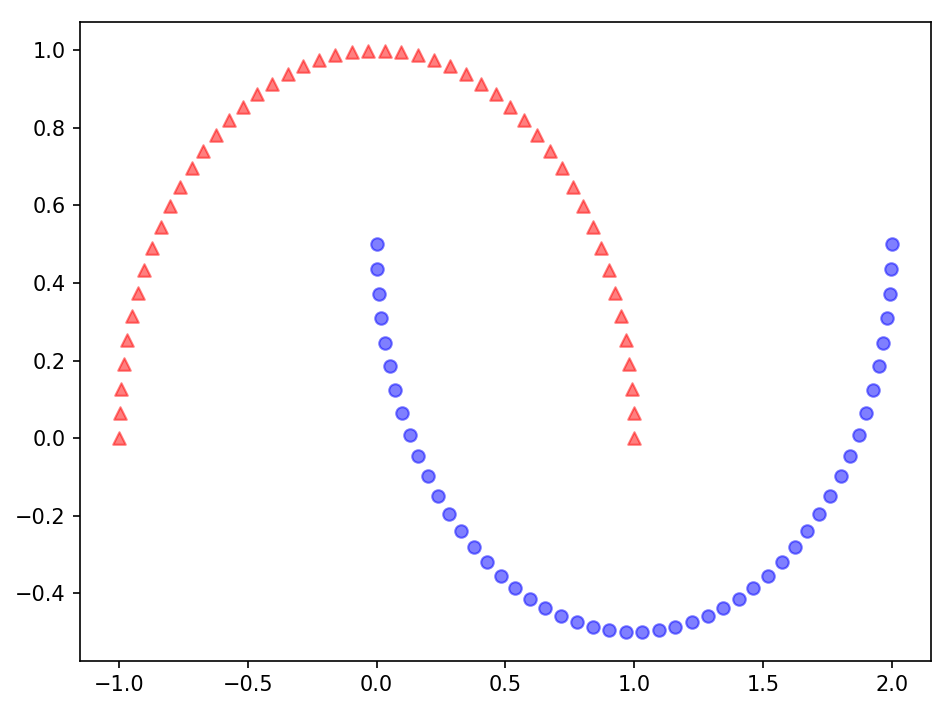
☑️기본 PCA의 주성분에 데이터셋을 투영하여 확인☑️
from sklearn.decomposition import PCA
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_spca[y == 0, 0], X_spca[y == 0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y == 1, 0], X_spca[y == 1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_spca[y == 0, 0], np.zeros((50, 1)) + 0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y == 1, 0], np.zeros((50, 1)) - 0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()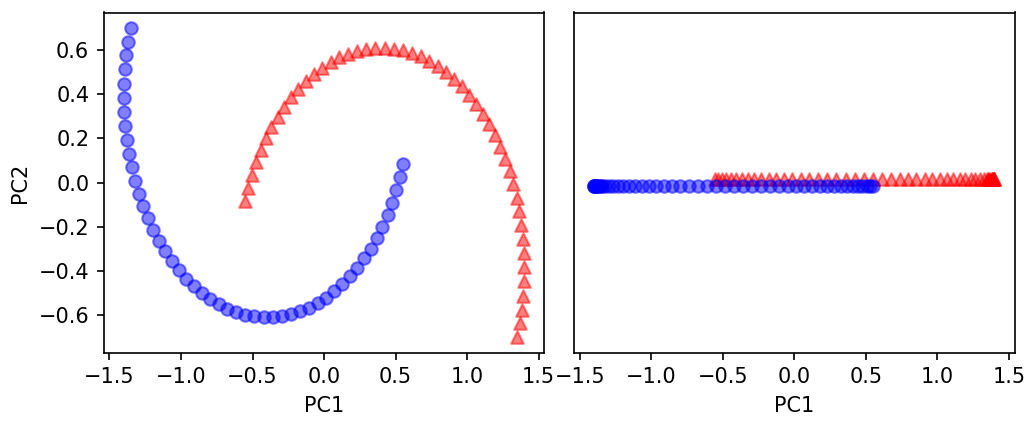
☑️커널 PCA 함수 rbf_kernel_pca를 적용☑️
X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_kpca[y==0, 0], X_kpca[y==0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y==1, 0], X_kpca[y==1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y==0, 0], np.zeros((50, 1))+0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y==1, 0], np.zeros((50, 1))-0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()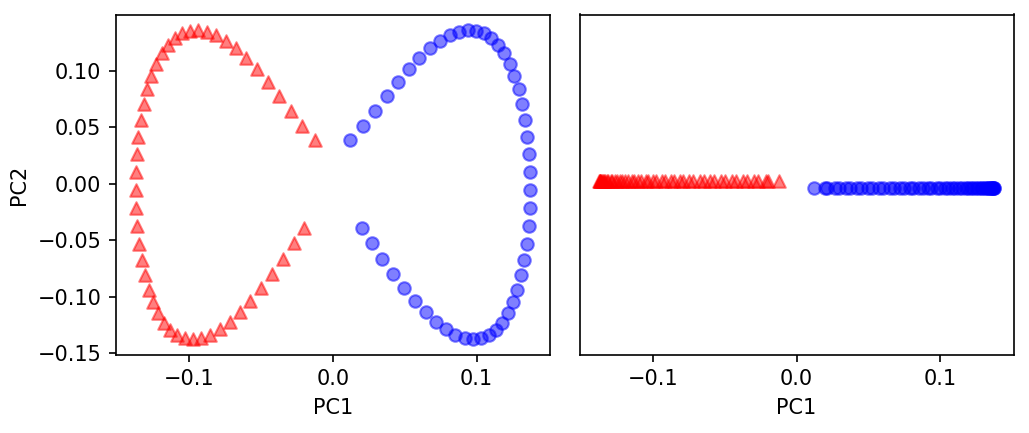
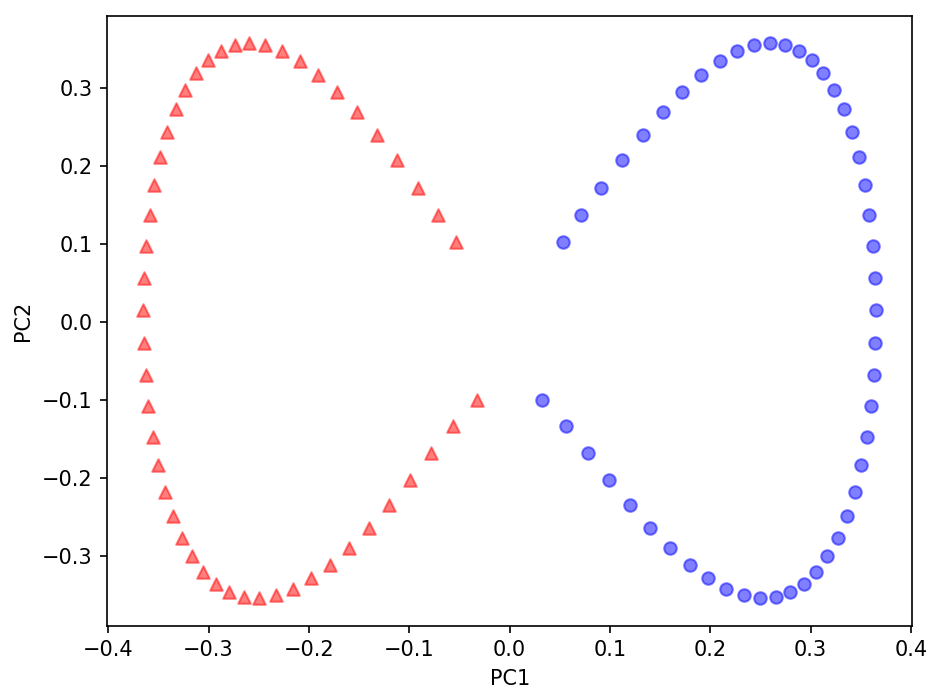
예제 2: 동심원 분리하기
☑️동심원 모양의 데이터셋☑️
from sklearn.datasets import make_circles
X, y = make_circles(n_samples=1000, random_state=123, noise=0.1, factor=0.2)
plt.scatter(X[y == 0, 0], X[y == 0, 1], color='red', marker='^', alpha=0.5)
plt.scatter(X[y == 1, 0], X[y == 1, 1], color='blue', marker='o', alpha=0.5)
plt.tight_layout()
plt.show()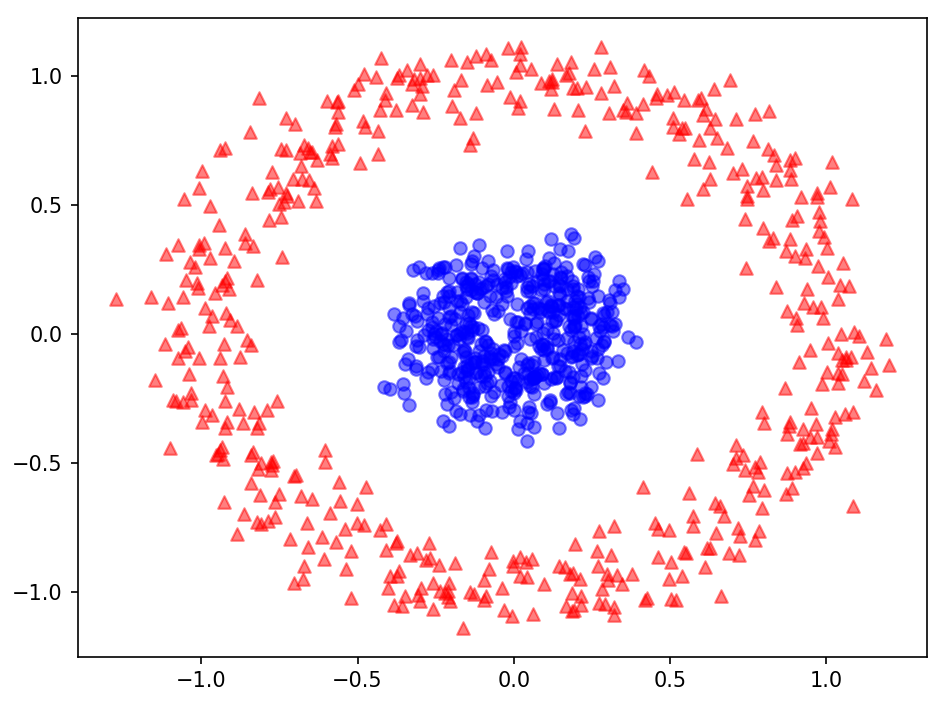
☑️기본 PCA를 적용☑️
scikit_pca = PCA(n_components=2)
X_spca = scikit_pca.fit_transform(X)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_spca[y == 0, 0], X_spca[y == 0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_spca[y == 1, 0], X_spca[y == 1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_spca[y == 0, 0], np.zeros((500, 1)) + 0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_spca[y == 1, 0], np.zeros((500, 1)) - 0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()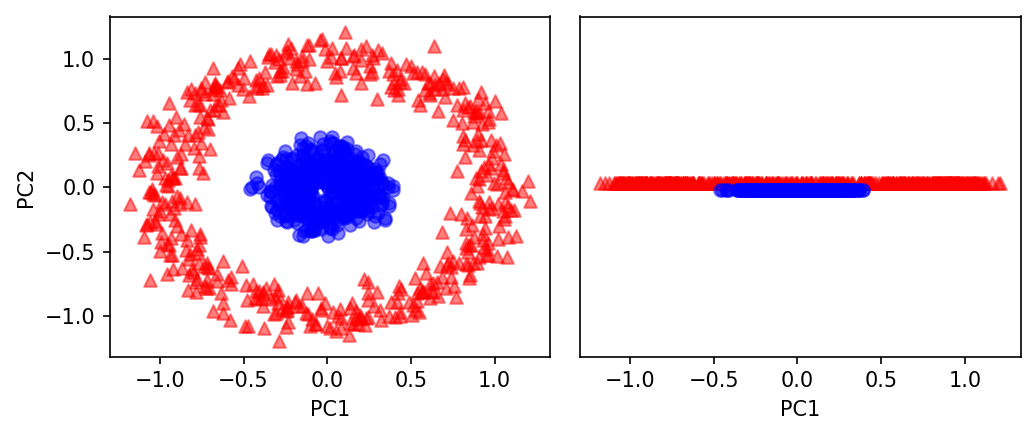
➡️선형 분류기에 적합한 결과 만들 수 ❌
☑️RBF 커널 PCA 구현 사용☑️
X_kpca = rbf_kernel_pca(X, gamma=15, n_components=2)
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(7, 3))
ax[0].scatter(X_kpca[y == 0, 0], X_kpca[y == 0, 1],
color='red', marker='^', alpha=0.5)
ax[0].scatter(X_kpca[y == 1, 0], X_kpca[y == 1, 1],
color='blue', marker='o', alpha=0.5)
ax[1].scatter(X_kpca[y == 0, 0], np.zeros((500, 1)) + 0.02,
color='red', marker='^', alpha=0.5)
ax[1].scatter(X_kpca[y == 1, 0], np.zeros((500, 1)) - 0.02,
color='blue', marker='o', alpha=0.5)
ax[0].set_xlabel('PC1')
ax[0].set_ylabel('PC2')
ax[1].set_ylim([-1, 1])
ax[1].set_yticks([])
ax[1].set_xlabel('PC1')
plt.tight_layout()
plt.show()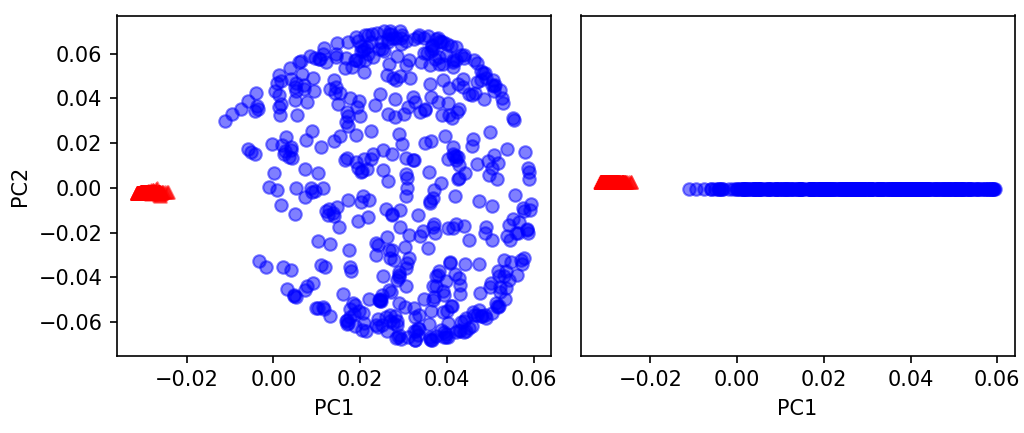
➡️RBF 커널 PCA가 두 클래스를 선형적으로 구분할 수 있는 새로운 부분 공간으로 데이터를 투영
5.3.3 새로운 데이터 포인트 투영
☑️rbf_kernel_pca 함수를 커널 행렬의 고윳값도 반환하도록 수정☑️
from scipy.spatial.distance import pdist, squareform
from numpy import exp
from scipy.linalg import eigh
import numpy as np
def rbf_kernel_pca(X, gamma, n_components):
"""
RBF 커널 PCA 구현
매개변수
------------
X: {넘파이 ndarray}, shape = [n_samples, n_features]
gamma: float
RBF 커널 튜닝 매개변수
n_components: int
반환할 주성분 개수
Returns
------------
alphas: {넘파이 ndarray}, shape = [n_samples, k_features]
투영된 데이터셋
lambdas: list
고윳값
"""
# MxN 차원의 데이터셋에서 샘플 간의 유클리디안 거리의 제곱을 계산합니다.
sq_dists = pdist(X, 'sqeuclidean')
# 샘플 간의 거리를 정방 대칭 행렬로 변환합니다.
mat_sq_dists = squareform(sq_dists)
# 커널 행렬을 계산합니다.
K = exp(-gamma * mat_sq_dists)
# 커널 행렬을 중앙에 맞춥니다.
N = K.shape[0]
one_n = np.ones((N, N)) / N
K = K - one_n.dot(K) - K.dot(one_n) + one_n.dot(K).dot(one_n)
# 중앙에 맞춰진 커널 행렬의 고윳값과 고유 벡터를 구합니다.
# scipy.linalg.eigh 함수는 오름차순으로 반환합니다.
eigvals, eigvecs = eigh(K)
eigvals, eigvecs = eigvals[::-1], eigvecs[:, ::-1]
# 최상위 k 개의 고유 벡터를 선택합니다(투영 결과).
alphas = np.column_stack([eigvecs[:, i]
for i in range(n_components)])
# 고유 벡터에 상응하는 고윳값을 선택합니다.
lambdas = [eigvals[i] for i in range(n_components)]
return alphas, lambdas☑️새로운 반달 데이터셋을 만들고 수정된 커널 PCA 구현을 사용하여 1차원 부분 공간에 투영☑️
X, y = make_moons(n_samples=100, random_state=123)
alphas, lambdas = rbf_kernel_pca(X, gamma=15, n_components=1)☑️원본 투영을 재현☑️
x_new = X[25]
x_proj = alphas[25] # 원본 투영
def project_x(x_new, X, gamma, alphas, lambdas):
pair_dist = np.array([np.sum((x_new - row)**2) for row in X])
k = np.exp(-gamma * pair_dist)
return k.dot(alphas / lambdas)
# 새로운 데이터포인트를 투영합니다.
x_reproj = project_x(x_new, X, gamma=15, alphas=alphas, lambdas=lambdas)☑️첫 번째 주성분에 투영한 것을 그래프로 그리기☑️
plt.scatter(alphas[y == 0, 0], np.zeros((50)),
color='red', marker='^', alpha=0.5)
plt.scatter(alphas[y == 1, 0], np.zeros((50)),
color='blue', marker='o', alpha=0.5)
plt.scatter(x_proj, 0, color='black',
label='Original projection of point X[25]', marker='^', s=100)
plt.scatter(x_reproj, 0, color='green',
label='Remapped point X[25]', marker='x', s=500)
plt.yticks([], [])
plt.legend(scatterpoints=1)
plt.tight_layout()
plt.show()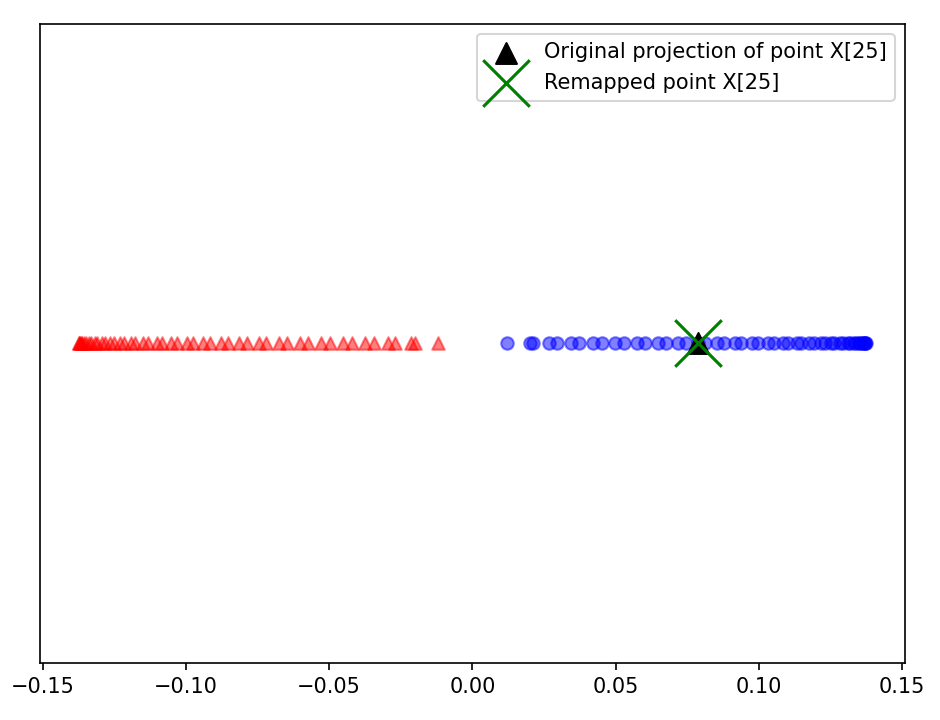
5.3.4 사이킷런의 커널 PCA
☑️사이킷런의 커널 PCA 사용하여 그려보기☑️
from sklearn.decomposition import KernelPCA
X, y = make_moons(n_samples=100, random_state=123)
scikit_kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_skernpca = scikit_kpca.fit_transform(X)
plt.scatter(X_skernpca[y == 0, 0], X_skernpca[y == 0, 1],
color='red', marker='^', alpha=0.5)
plt.scatter(X_skernpca[y == 1, 0], X_skernpca[y == 1, 1],
color='blue', marker='o', alpha=0.5)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.tight_layout()
plt.show()