합성곱 신경망
합성공 신경망(Convolutional Neural Network, CNN)이라는 키워드는 아마 굉장히 많이 들어봤을 것이다. 특히, 근래 연구를 시작한 사람이 아니라 2010년대 중반에 시작한 사람이라면 더더욱이 말이다.
일반적으로 이미지 인식과 같은 컴퓨터 비전 분야에서 주로 등장하는 이 키워드는과 같은 컴퓨터 비전 분야에서 주로 등장하는 이 키워드는 결국 임베딩 관점에서 보자면 공간적 픽셀 데이터(패턴)을 벡터 공간으로 임베딩하는 도구이다.
합성곱 신경망에서 당연 키워드는 합성곱(Convolution)일 것이다.
합성곱 연산은 이렇게 이루어져있는데, 쉽게 말하자면 겹쳐서 곱하고 더하는 연산이다. 이 합성곱 연산이 2차원 이미지에 가게 되면 마치 돋보기/필터의 역할을 하는데, 이미지 같은 2차원에서는 커널(작은 행렬)을 입력 이미지 위에서 슬라이딩하면서 곱하고 더해 새로운 값을 만드는 연산이 되기 때문이다. 이는 곧 이미지의 특정 영역에서 분포 또는 변화량을 계산해 출력 노드를 생성할 수 있기에 지역적 특징(Local Feature)을 파악할 수 있다.
또한, 이미지 데이터는 고정된 프레임 내에 객체들의 위치와 형태가 자유분방하므로 여러 영역의 지역 특징을 조합해 입력 데이터의 전반적인 전역 특징(Global Features)도 파악할 수 있다.
이러한 합성곱 신경망은 컴퓨터비전을 위해 고안되었지만, 자연어 처리에서도 우수한 성능을 보인다. 순환 신경망은 무조건 연산 순서의 제약이 존재하지만, 합성곱 신경망은 그런게 없기 때문이다.
이제 합성곱 신경망의 구조에 대해 알아보자.
합성곱 계층
합성곱 계층은 입력 데이터와 필터를 합성곱해 출력 데이터를 생성하는 계층이다. 합성곱 계층의 입력 데이터는 모든 위치에서 동일한 필터를 사용하므로 모델 매개변수를 공유하고, 모델이 학습해야 할 매개변수 수가 감소해 과대적합을 방지한다. 또한, 입력 데이터에서 특징을 추출할 때, 해당 특징이 이미지 내 다른 위치에 존재하더라도 필터를 사용해 특징을 추출하므로 특징이 어디에 있어도 동일하게 추출할 수 있다.
이러한 합성곱 계층을 여러 겹 쌓아 모델을 구성하며, 합성곱 계층이 많아질수록 모델의 복잡도가 증가하므로 더 다양한 특징을 추출해 학습할 수 있다.
필터
합성곱 계층은 입력 데이터에 필터(Filter)를 이용해 합성곱 연산을 수행하는 계층이다. 필터는 커널(Kernel) 또는 윈도우(Window)로 불리기도 하며, 일반적으로 3 X 3 / 5 X 5와 같은 작은 크기의 정방형으로 구성된다.
이 필터를 일정 간격으로 이동하면서 입력 데이터와 합성곱 연산을 수행해 특징 맵을 생성한다. 필터 영역마다 합성곱 연산이 수행되며, 필터의 가중치가 이 모델 학습 과정에서 갱신된다.
합성곱 신경망은 보통 여러 개의 필터를 사용해 다양한 특징을 추출하며, 이를 통해 입력 이미지의 다양한 특징을 인식하고 분류할 수 있다.
다음 영상은 필터를 이동시키며 특징 맵을 추출하는 과정을 보여준다
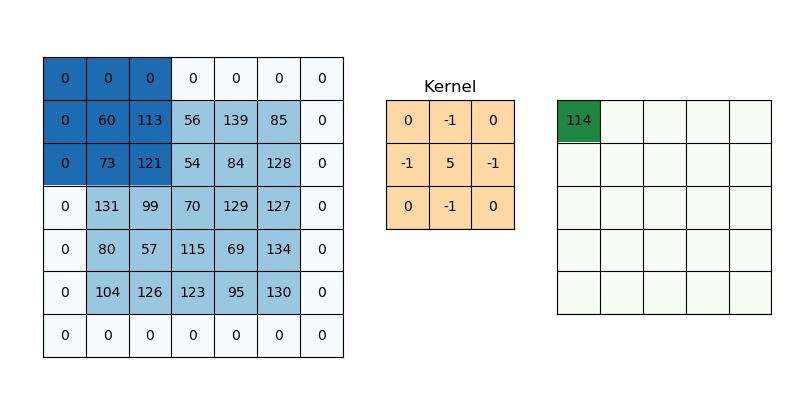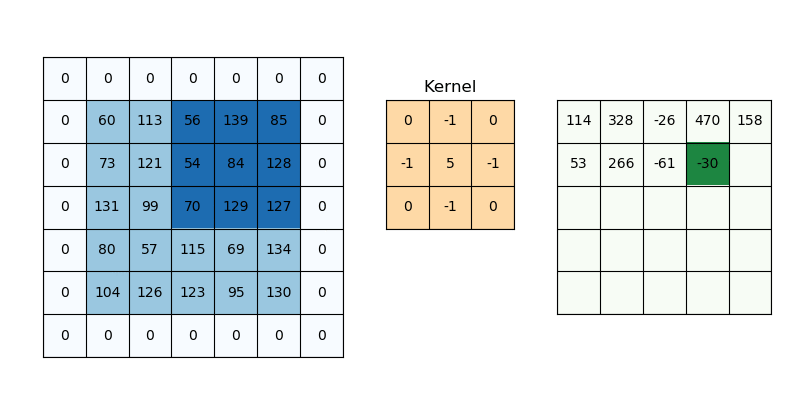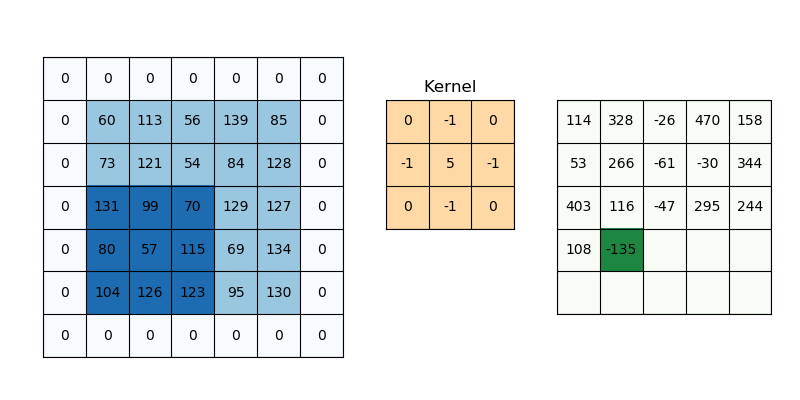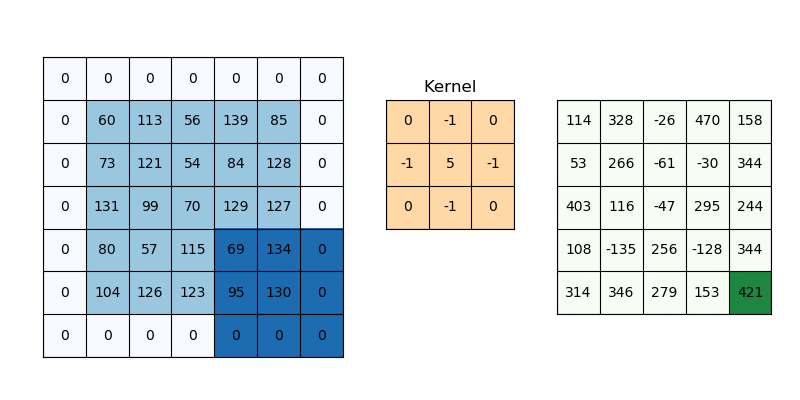
출처 : medium.com/@draj0718
합성곱 연산은 입력 이미지에서 필터와 대응하는 부분을 곱한 후, 모두 더한 값을 특징 맵의 한 원소로 사용한다. 필터는 일반적으로 이미지 왼쪽 상단부터 오른쪽 하단으로 이동하며 연산을 반복하며, 이를 통해 특징 맵 전체를 계산한다.
패딩
위 예시 영상과 같이 일반적으로 합성곱 연산을 수행하면 출력값인 특징 맵의 크기가 작아진다. 즉 입력값 크기 대비 출력값의 크기가 감소한다.
이는 합성곱 신경망을 더 깊게 쌓는 데 제약사항이 될 수 있거나 또는, 이미지의 가장자리에 있는 정보는 다른 위치에 있는 정보 대비 학습하기가 어려워진다.
이러한 현상을 방지하기 위해 입력 이미지나 입력으로 사용되는 특징 맵 가장자리에 특정 값을 덧붙이는 패딩(Padding)을 추가한다. 가장자리에 덧붙이는 패딩 값은 0으로 할당하는데, 이를 제로 패딩(Zero padding)이라고 한다. 예시는 아래 그림과 같다.
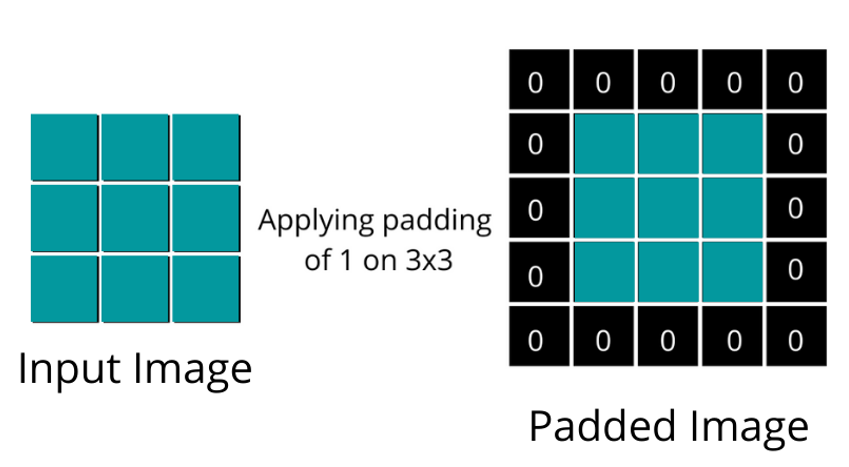
출처 : https://www.almabetter.com/bytes/articles/what-is-padding-in-convolutional-neural-network
패딩을 이렇게 추가하면 출력값의 크기가 작아지지 않고 입력값의 크기와 동일한 크기로 특징 맵이 계산된다. 합성곱 신경망에서는 패딩을 적절히 사용해 입력 데이터 크기를 조정하고 작은 크기의 필터로도 이미지 전체에 대한 정보를 반영할 수 있다.
간격
간격(Stride)이란 필터가 한 번에 움직이는 크기를 의미한다. 간격이 1이면 필터가 한 픽셀씩 움직이며, 2 이상이면 필터가 더 큰 간격으로 움직인다. 이때 합성곱 과정의 특성상, 간격의 크기가 커질수록 출력 데이터의 크기는 입력 데이터보다 더더욱이 작아진다. 즉 간격 조정은 공간적 정보를 유지하거나 감소시키는 역할을 한다. 작게 설정할 수록 공간적 정보를 보존하며 크게 설정하면 감소시킬 수 있다.
채널
입력 데이터와 필터 간의 연산은 채널(Channel)에서 수행된다. 채널은 입력 데이터와 필터가 3차원으로 구성되어 있을 때 같은 위치의 값끼리 연산되게 한다. 이를 통해 입력 데이터의 공간 정보를 유지하면서 추출되는 특징을 확장할 수 있다.
예를 들어, 입력 데이터가 RGB 이미지라면, 각각의 R, G, B 채널마다 동일한 필터가 존재하며, 각 필터는 해당 채널의 정보를 추출해 특징 맵을 생성한다. 특징 맵의 개수는 채널 개수만큼 존재한다. 채널 개수는 다시 일반적으로 합성곱 계층에서 설정되며, 이는 사용자의 목적에 따라 달라진다. 채널의 개수가 많아질수록 학습할 수 있느 ㄴ특징의 다양성이 증가한다.
팽창
팽창(Dilation)은 합성곱 연산을 수행할 때 입력 데이터에 더 넓은 범위의 영역을 고려할 수 있게 하는 기법으로, 필터와 입력 데이터 사이에 간격을 두는 기법이다. 일반적으로 합성곱 계층에서 팽창값은 1로 사용해 간격을 한 칸만 띄워 사용한다. 이 값이 커질수록 필터가 입력 데이터를 바라보는 범위가 넓어진다. 아래 그림은 팽창값에 따른 연산 결과의 차이를 보인다.
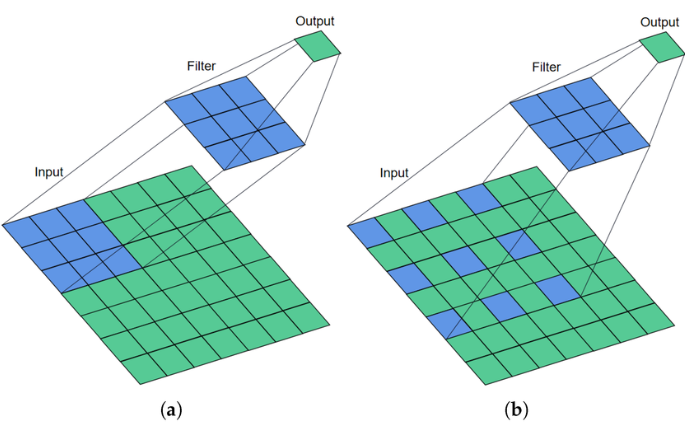
출처 : Bearing Fault Diagnosis via Improved One-Dimensional Multi-Scale Dilated CNN, (a) Dilation value = 1, (b) Dilation value = 2
팽창은 필터의 크기를 키우지 않고 입력 데이터에 더 넓은 영역을 고려할 수 있게 해 더 깊고 복잡한 모델을 구성할 수 있게 한다. 팽창을 적절히 적용하면 모델의 매개변수 수를 줄일 수 있어 메모리 사용량을 줄일 수 있다.
하지만, 팽창값을 ㅈ거절히 설정하지 못하면 입력 데이터의 범위가 커지므로 오히려 연산량이 늘어나거나 인접한 픽셀값을 고려하지못해 공간적 정보가 보존되지 못하는 경우도 있다.
활성화 맵
활성화 맵(Activation Map)은 합성곱 계층의 특징 맵에 활성화 함수를 적용해 얻어진 출력값을 의미한다. 합성곱 계층에서 입력 이미지와 필터의 합성곱 연산을 통해 특징 맵을 추출하면 이 값에 비선형성을 추가하기 위해 활성화 함수를 적용한다.
일반적으로 CNN에선 ReLU 함수가 많이 채택되며, 이렇게 얻은 활성화 맵은 다음 계층의 입력값으로 사용되며, 합성곱 연산과 활성화 함수를 여러 번 반복하여 신경망을 구성하면, 입력 이미지에서 추출된 추상적인 특징을 학습할 수 있게 된다.
풀링
풀링(Pooling)은 특징 맵의 크기를 줄이는 연산으로 합성곱 계층 다음에 적용된다. 풀링은 특징 맵의 크기를 줄여 연산량을 감소시키고 입력 데이터의 정보를 압축하는 효과를 가진다. 풀링은 합성곱 연산과 비슷하게 필터와 간격을 이용하며, 해당 필터 내에 최대값을 선택하거나, 혹은 평균값을 계산하여 사용하면서 특징 맵의 크기를 감소시킨다.
