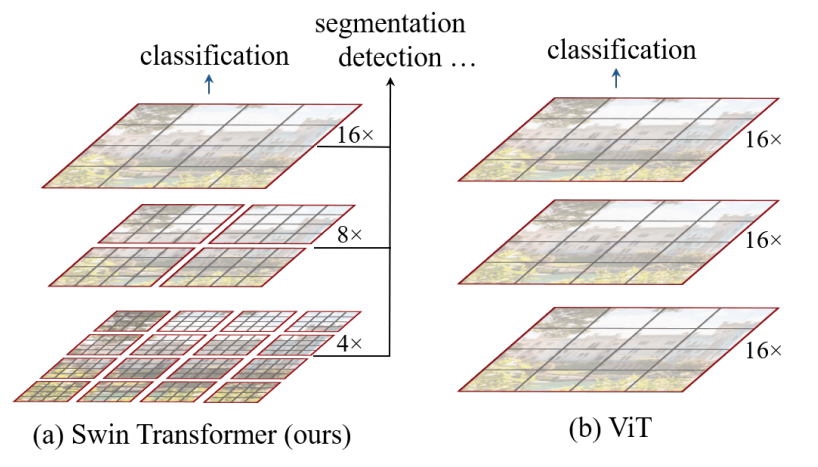
Swin Transformer : Hierarchical Vision Transformer using Shifted Windows

year : 2021
Code : https://github.com/microsoft/Swin-Transformer

Method

Overall Architecture

기존의 ViT와 동일하게 patch embedding으로 input을 만들어줍니다. 다른점이 있다면 패치 사이즈가 4x4라는 것입니다. ViT에서는 16x16의 패치가 디폴트값이었습니다. 패치사이즈가 작아지면 전체 패치의 갯수가 제곱으로 늘어나고 패치의 임베딩 차원이 동일하면 연산량도 그에 상응하게 늘어납니다. 따라서 4x4 사이즈는 상당히 작은 크기임을 알 수 있습니다.

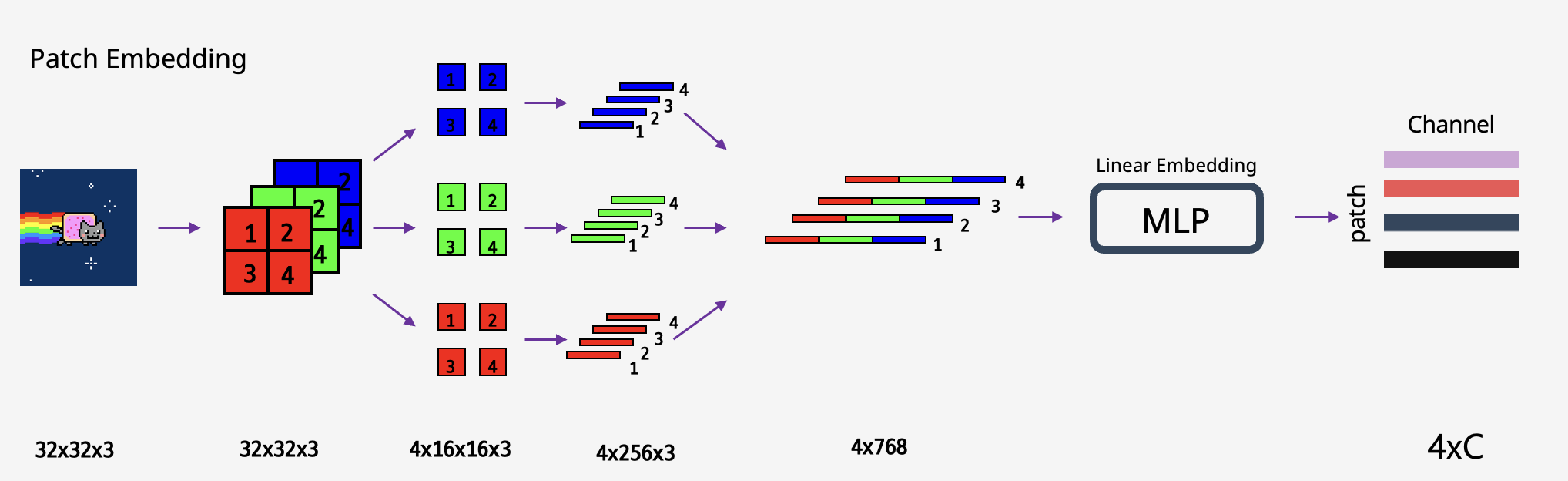
아래는 과거에 만들어 두었던 발표자료에서 가져온 패치 임베딩(패치사이즈 16) 예시입니다. 만약 4x4 패치가 된다면 16x16에 비해서 패치수가 16배 많으므로 리니어 임베딩을 지나면 64 x C(임의의 차원)이 됩니다.

Swin transformer는 여러개의 Stage로 구성되어 있으며 각 Stage에서는 패치의 갯수가 변하지 않습니다. 따라서 Stage 1에서는 전체 토큰의 갯수 $\frac{H}{4} \times \frac{W}{4}$가 유지됩니다. 논문의 제목처럼 계층적 표현을 위해서 Stage가 진행됨에 따라서 패치는 합쳐지고 이 과정에서 패치의 갯수는 줄어들게 됩니다.

Stage 2에서는 Stage 1에 있던 패치를 합치는 Patch merging layer를 통과합니다. Patch mergin layer는 인전한 2x2패치를 concat하고 linear layer를 통해서 채널을 절반으로 줄입니다. 이를 통해서 패치의 갯수를 1/4로 줄일 수 있습니다.

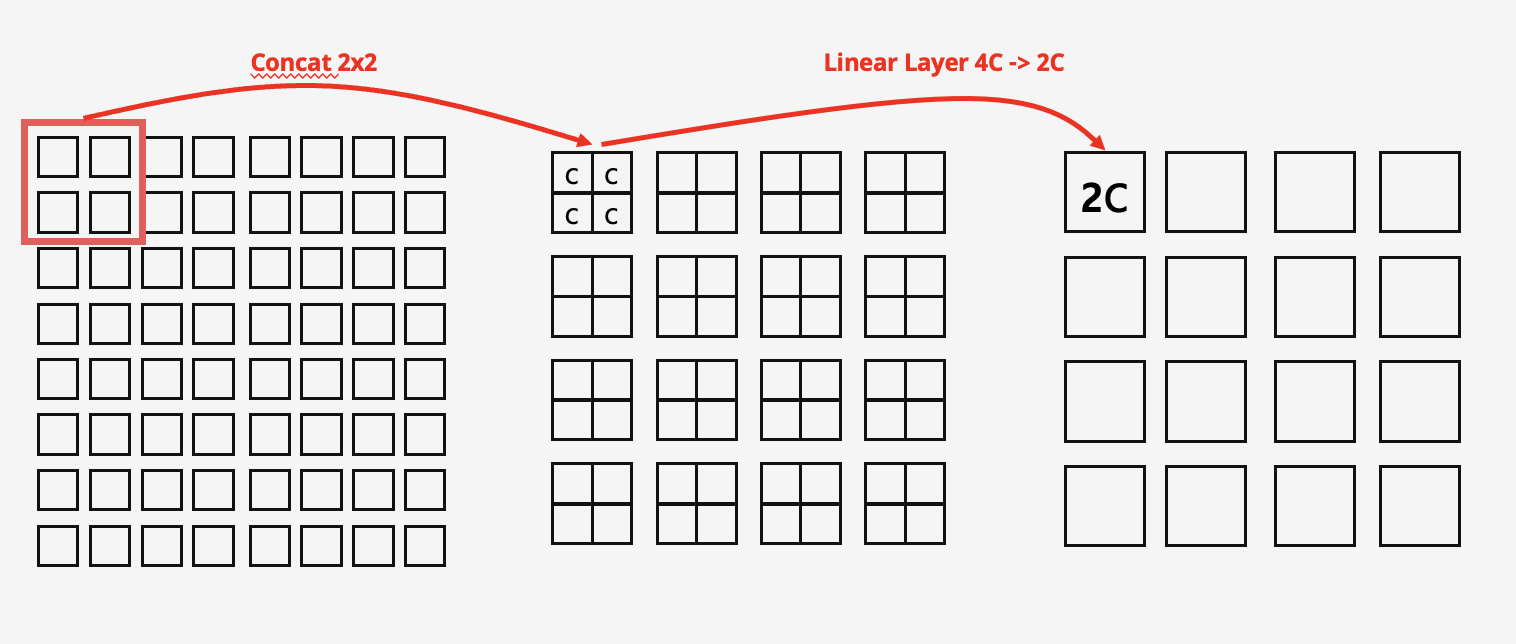
간단하게 그림을 표현해보았는데 실제 연산에서는 아래 그림과 같이 2차원 벡터의 연산이 아닌 1차원으로 flatten된 벡터로 연산됩니다.

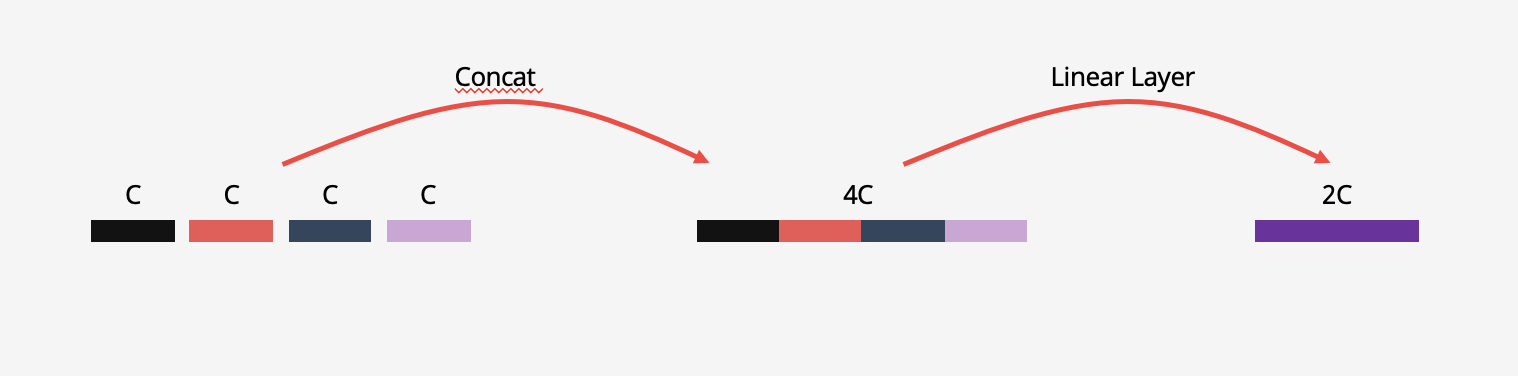
위와 같은 연산은 Stage를 지날때마다 동일하게 적용되어서 Stage 4까지 이어집니다. Stage 1에서는 4x4크기의 패치를 이용해서 Patch Embedding을 했기때문에 패치 갯수가 $\frac{H}{4} \times \frac{W}{4}$ 이지만, 위와 같이 4개의 패치를 하나로 묶었기 때문에 패치 갯수는 $\frac{H}{8} \times \frac{W}{8}$ 로 1/4이 됩니다. 이를 통해서 논문에서 제시하는 아래와 같은 계층적 구조가 완성됩니다.

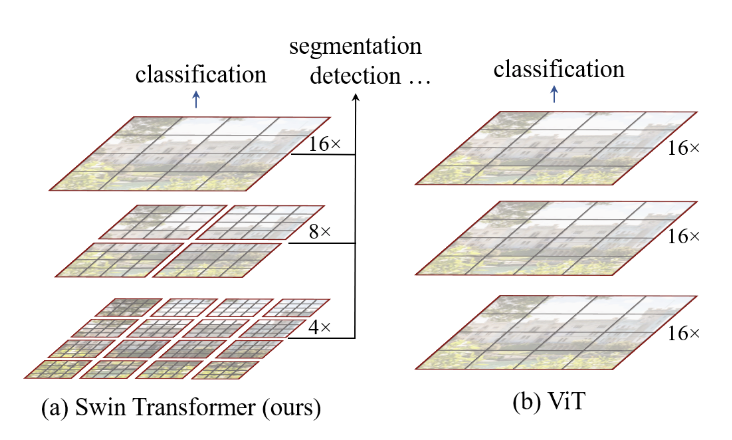
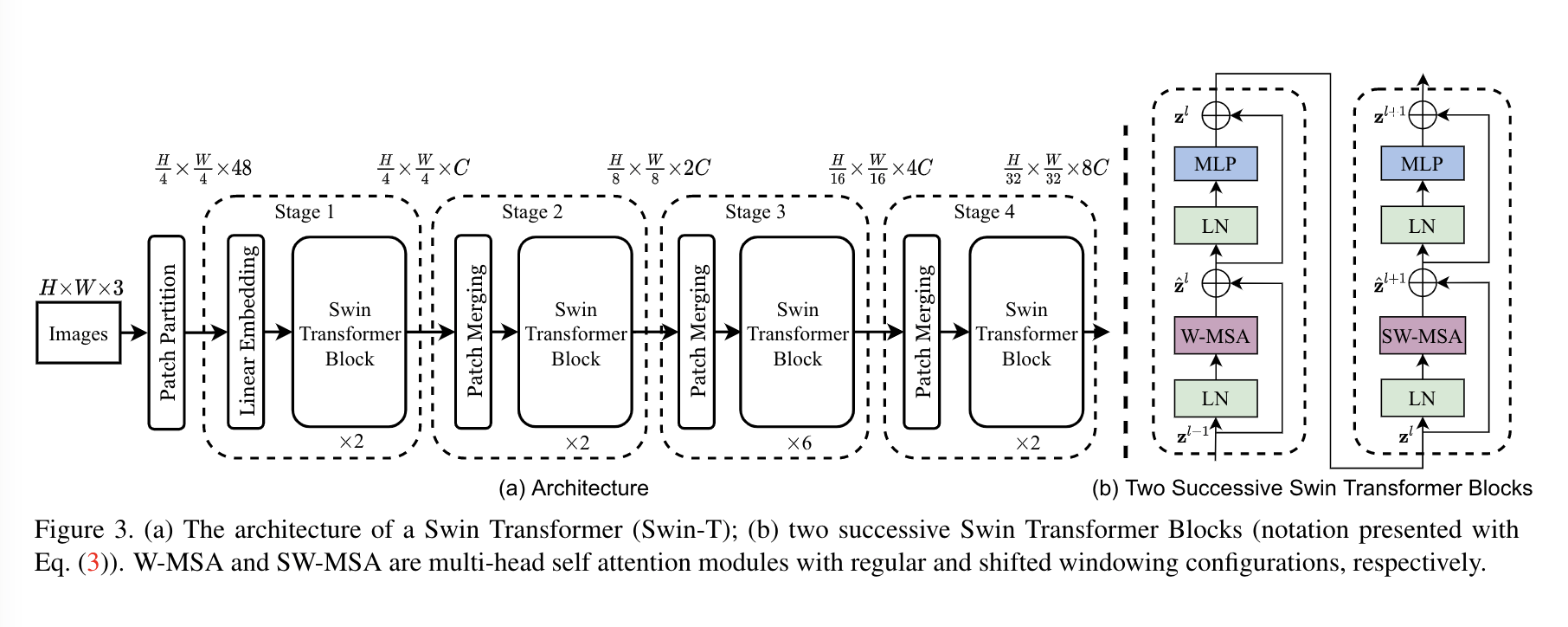
위 그림과 같이 총 4개의 Stage 를 지나면서 한번 지날때마다 패치의 크기가 4배씩 늘어나고 패치의 갯수는 1/4로 줄어들게 됩니다. 본 논문에서는 Swin Transformer Block을 제시하였는데 기존의 ViT에서 사용했던 MSA(Multi Head Self Attention)을 대체하는 W-MSA(Window based MSA), SW-MSA(Shifted Window MSA)로 이루어져있습니다. 이외의 구조는 기존 ViT와 동일하게 Pre-Norm구조에 2개의 Linear layer와 GELU를 사용하는 MLP block이 Attention 연산 다음에 적용되고 각 연산마다 residual connection이 존재합니다. 

Shifted Window based Self-Attention

본 논문의 가장 큰 기여점이라고 생각하는 Shifted Window 입니다. Swin transformer는 4x4라는 아주 작은 Patch를 사용합니다. ViT의 기본 모델이 사용한 16x16에 비교하면 $(\frac{16}{4} \times \frac{16}{4})^2$배 많은 연산이 필요합니다. 이를 해결하기 위해서 겹치지 않는(non overlapping) MxM(default 7)개의 패치를 하나의 Window로 설정하고 Window안에서만 Attention 연산을 수행합니다.

여담이지만 처음에 7이라는 숫자를 보고 왜 굳이 저 숫자로 설정했는지 의문이었습니다. 아마 pre-train과정에서 가장 많이 사용하는 이미지 해상도인 224(32x7 -> (2^5)x7)가 7의 배수이기 때문으로 생각합니다. Stage를 지나면서 패치의 갯수는 (8x7) x (8x7) -> (4x7) x (4x8) -> (2x7) x (2x7) -> (1x7) x (1x7) 순으로 줄어드는데 계속해서 7의 배수이기 때문에 Window size를 7x7로 설정하면 계속해서 나누어 떨어집니다.

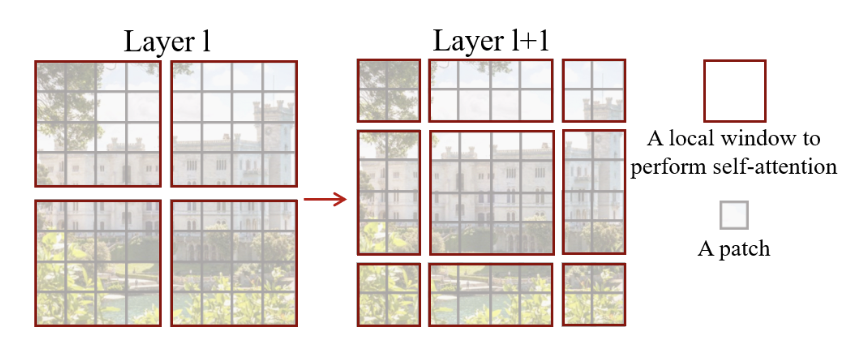
위 그림에서 왼쪽 예시가 4x4 Window 입니다.

기존의 Vanilla Transformer와 ViT가 채택한 Global Attention은 패치수에 Quadratic하게 연산량이 증가하지만 Window based Attention의 연산량은 패치의 수에 Linear하게 증가합니다. 이를 확인하기 위해서 임의로 Attention 연산을 3단계로 나누어서 행렬곱의 형태를 살펴보면 아래와 같습니다. 편의를 위해서 scale factor는 제외했으며, $N_{patch}$는 $\frac{H}{patch\_size} \times \frac{W}{patch\_size}$입니다.

-Input -> Q,K,V : $(N_{patch} \times C) * (C \times C) \rightarrow (N_{patch} \times C)$
-$Q * K^{T} * V$ : $(N_{patch} \times C) * (C \times N_{patch}) * (N_{patch} \times C) \rightarrow (N_{patch} \times C)$
-Attention -> Output : $(N_{patch} \times C) * (C \times C) \rightarrow (N_{patch} \times C)$

위 연산들의 연산량은 결국 행렬곱의 연산량을 구하면 알 수 있습니다. 간단한 예시로 Naive하게 행렬곱을 했다고 가정하면, (MxN)*(NxP)행렬곱의 연산량은 MNP 입니다. 이를 사용해서 위 연산들의 연산량을 구하면 아래와 같습니다.

-Input -> Q,K,V : $N_{patch}C^2$
-$Q * K^{T} * V$ : $2N_{patch}^{2}C$
-Attention -> Output : $N_{patch}C^2$

따라서 총 연산량은 $4N_{patch}C^2 +2 N_{patch}^{2}C$로 패치갯수의 제곱해서 연산량이 증가합니다.

하지만 본 논문에서는 Window 내에서만 Attention연산을 수행하기 때문에 총 연산량은 $4N_{patch}C^2 +2M^{2}hwC$로 $hw$에 대해서는 선형적으로 연상량이 증가합니다. 이를 통해서 작은 패치를 사용함에도 불구하고 적은 연산량을 유지할 수 있습니다.

Window based Attention은 분명 연산량을 선형적으로 줄임으로서 작은패치를 사용함에 있어서 부담을 덜 수 있지만 연산이 줄었다는건 그만큼 잃는 것도 있습니다. Global Attention과 같은 경우에 모든 패치들이 상호작용을 하지만 Window based Attention은 같은 Window 안에서만 상호작용이 이루어지기 때문에 멀리 떨어진 위치의 패치들과 상호작용이 불가능합니다.

Cyclic Shift

본 논문에서는 Window간의 연결을 추가하면서 동시에 적은 연산량을 유지하기 위해서 Shifted window partiotioning을 도입합니다. 위 그림에서 오른쪽이 Shifted 된 window의 예시입니다. $[\frac{M}{2}, \frac{M}{2}]$만큼 대각선으로 Window가 Shift된것을 볼 수 있습니다. 이런식으로 Window를 옮기게 되면 기존의 Window에서 연결성이 없었던 패치들간의 연결성이 생기지만 가장자리에는 원래 Window 크기보다 작은 Window들이 여러개 생기게 됩니다.

만약 패딩을 통해서 작은 window들을 크기를 원래 window 사이즈와 맞춰주면 전체 Window의 갯수가 늘어나기 때문에 계산 효율성이 떨어지게 됩니다.

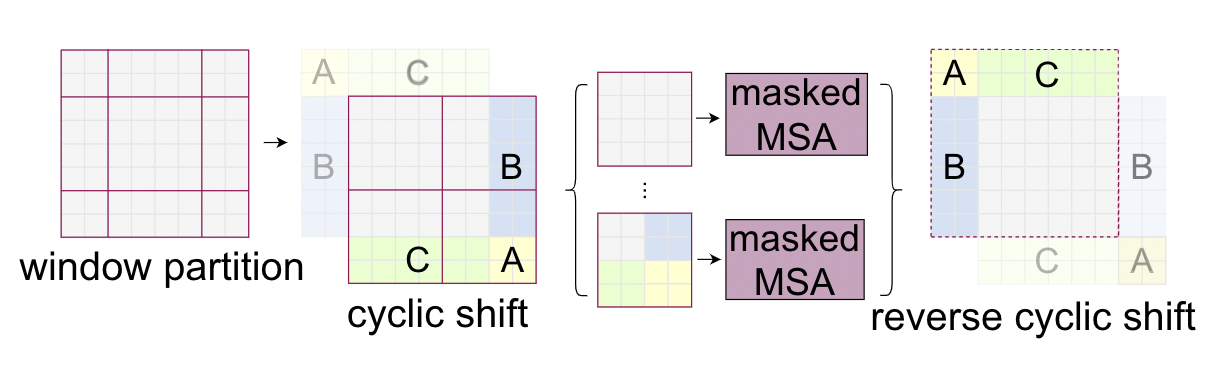
따라서 위 그림과같이 짜투리(?) Window들을 모아서 기존과 동일한 크기의 Window를 만들고 서로 다른 짜투리 Window에서 온 패치들끼리는 Attention 연산이 수행되지 않도록 mask를 적용합니다. 동일한 말이지만 Window가 shift되었다기 보다는 패치들이 옮겨졌다는 것이 더 적절할것 같습니다. Cyclic shift에 대해서는 이후 코드 리뷰에서 더 자세히 다루겠습니다.

Relative position bias

본 논문에서는 Attention 연산에 아래와 같이 relative position bias 를 추가했습니다.

M개의 패치를 가지는 window 내에서 상대적인 패치들간의 거리는 [-M+1, M-1]의 범위에 있습니다.

1번째 패치를 기준으로 M번째 패치의 거리는 M-1 이고 M번째 패치를 기준으로 1번째 패치는 -M+1입니다. 절대 거리는 같지만 방향이 다르므로 상대 거리를 사용합니다.

$B$는 $\hat{B} \in R^{(2M-1)\times(2M-1)}$에서 선택해서 사용합니다. 저자들은 이와 같은 상대적 위치를 사용하는 것이 성능향상에 큰 도움이 되었다고 밝혔습니다.