Intro

Stanford University의 CS231n 강의를 듣고 정리한 내용입니다.
궁금한 점이나 오류가 있다면 언제든지 댓글 남겨주시기 바랍니다.

1. Activation Functions

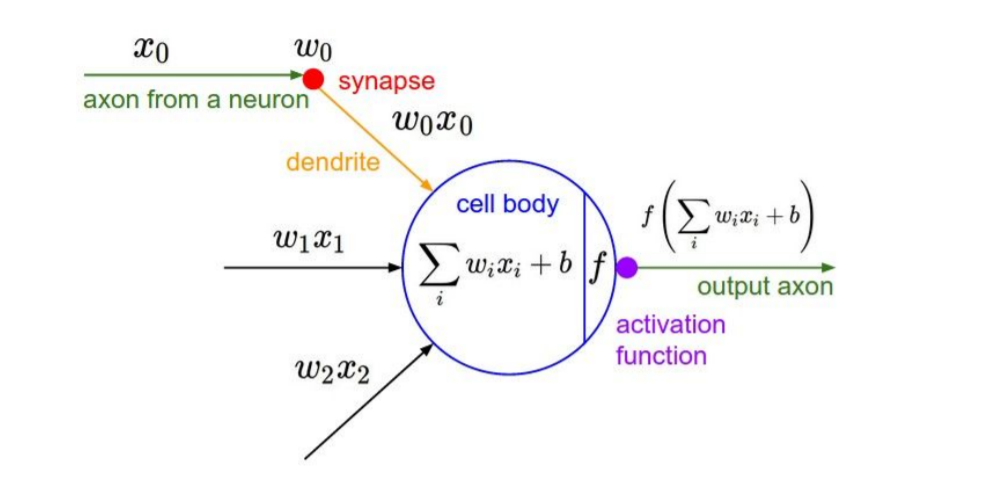
우선 neural networks를 학습하기에 앞서 activation function의 종류를 짚고 넘어가려 한다. 위의 그림에서 볼 수 있듯이 neural networks는 input data를 non-linearity한 activation function에 집어 넣은 결과값을 다음 layer로 넘기기 때문에 어떤 activation function을 사용하는 지에 따라 학습 결과가 달라질 수 있다.

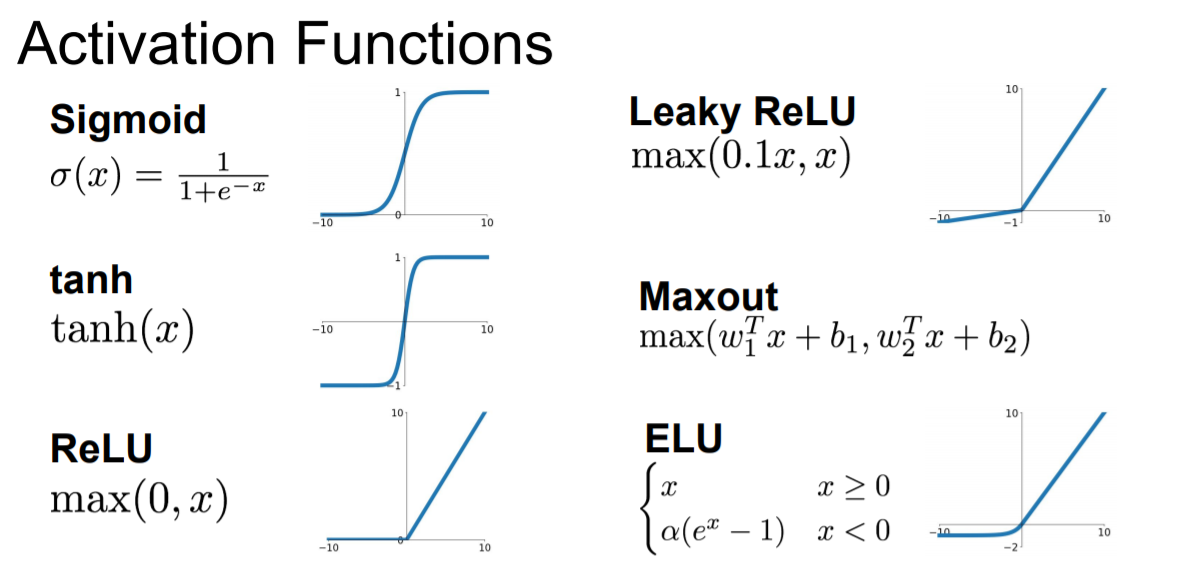
현재 자주 언급되는 activation function의 종류는 다음과 같으며 하나씩 살펴보려 한다.

1) Sigmoid Function

Sigmoid function은 전통적으로 많이 사용되던 함수인데 함숫값이 오로직 0과 1 사이에서만 결정이 된다는 특징이 있다.

다만 현재는 이 sigmoid를 잘 사용하지 않는데 그 이유는 다음과 같다.

1. Saturated neurons “kill” the gradients

우선 $x$가 $\infty$나 $-\infty$를 향해 갈 수록 sigmoid의 함숫값이 0 또는 1에 매우 가까워져 전체적으로 $x$축에 평행한 모습을 볼 수 있다. 이를 saturated 하다라고 표현하는데 이런 경우에는 backpropagation을 할 때 치명적인 문제가 발생한다.

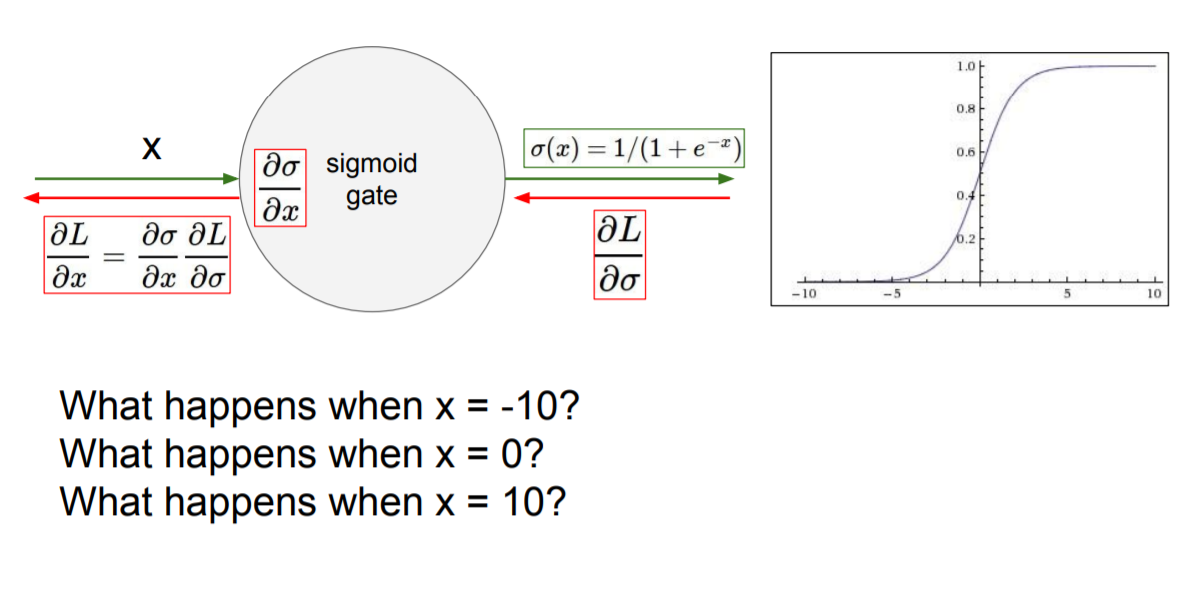
위의 그림을 보면 $x = -10$이나 $x = 10$일 때 gradient의 값은 모두 0임을 알 수 있다. 그렇게 되면 backpropagation 시 모두 0이 곱해지는 결과를 야기하게 된다. 즉 학습이 더 이상 진행되지 않는 것이다.

2. Sigmoid outputs are not zero-centered

Zero-centered란 그래프의 중심 0인 형태로 함숫값이 양수 혹은 음수에만 치우치지 않고 실수 전체에서 나타나는 형태를 의미한다. Sigmoid는 위의 그래프에서도 볼 수 있듯이 함숫값이 항상 0보다 크거나 같은 형태로 나타난다. 이러한 경우에는 어떤 문제점이 생길까? 아래의 그림을 보면서 생각해보자.

Neural networks에서 input은 이전 layer의 결과값이라고 생각하면 된다. 그런데 sigmoid 함수는 항상 양수이기에 sigmoid를 한번 거친 이후론 input 값은 항상 양수가 된다. 그렇게 되면 backpropagation을 할 때 문제가 생긴다. Backpropagation을 할 때 $\frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial f}\times \frac{\partial f}{\partial w_i}$ 식을 거친다. 이때 $\frac{\partial f}{\partial w_i}=x_i$이므로 $\frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial f}\times x_i$가 된다. 그런데 input 값인 $x_i$는 항상 양수이기에 $\frac{\partial L}{\partial w_i}$와 $\frac{\partial L}{\partial f}$의 부호는 같을 수 밖에 없다. 위의 2차원 평면에서 살펴보면 부호가 모두 같은 지점은 1,3 사분면 뿐이다. 따라서 지그재그의 형태로 학습이 될 수 밖에 없고 이는 학습을 오래 걸리게 한다.

3. exp() is a bit compute expensive

마지막으로 exp() 계산은 상대적으로 비싸다는 단점이 있다.

2) tanh

3) ReLU

가장 많이 사용되는 함수는 바로 ReLU 이다. ReLU는 $x$가 양수인 지점에 한해서 saturate 문제에서 벗어난다. 또한 단순히 max 함수를 이용하기 때문에 계산이 매우 빠르다는 장점이 있다.

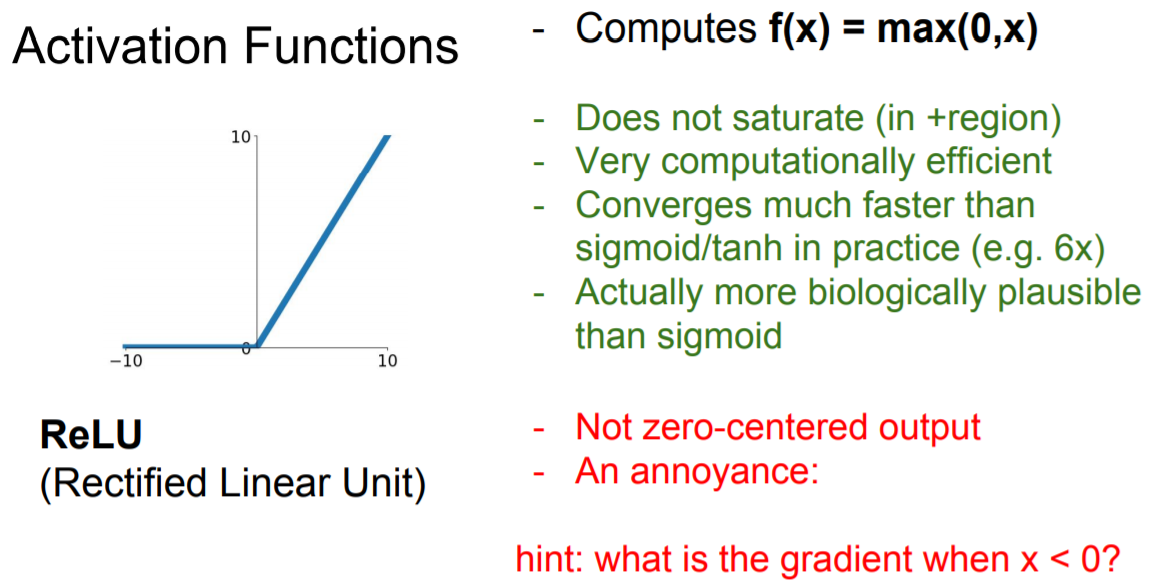
다만 여전히 함숫값은 모두 양수이기 때문에 output이 zero-centered 하지 못 하다는 단점이 있으며 $x$가 음수인 지역에서는 saturated 하기에 학습 시 gradient를 죽이게 되는 문제가 있다.

또한 learning rate을 너무 크게 잡으면 data cloud 밖에서 activate 되는 문제가 발생하는데 이를 dead ReLU라고 부르며 이러한 경우에는 다시 활성화되지 못 해서 update가 더 이상 진행되지 않는다는 치명적인 문제가 발생한다.

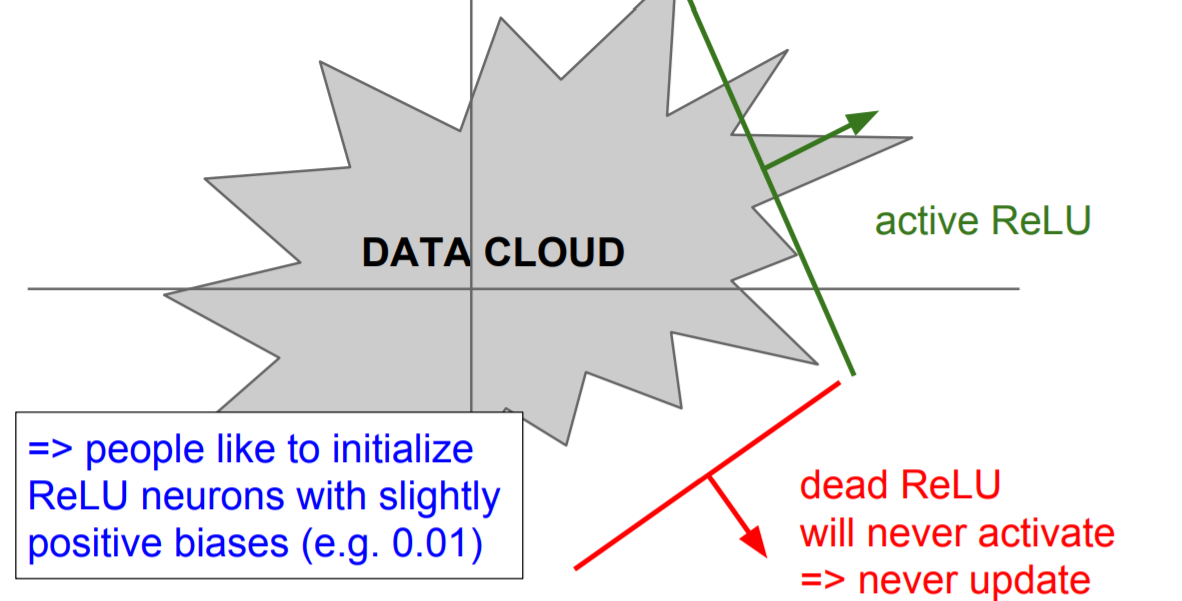
따라서 ReLU를 사용할 땐 learning rate를 작은 값으로 초기화 해야 한다.

4) Leaky ReLU & PReLU

ReLU가 $x$가 음수인 지역에서 saturate 되는 문제를 해결한 함수이다.

5) ELU

6) Maxout

Maxout은 ReLU와 Leaky ReLU를 합쳐서 계산한 것으로 각각의 단점을 상쇄시킨다는 장점이 있지만 연산량이 2배로 증가한다는 단점이 존재한다.

2. Data Preprocessing

1) Zero-centered & Normalized data

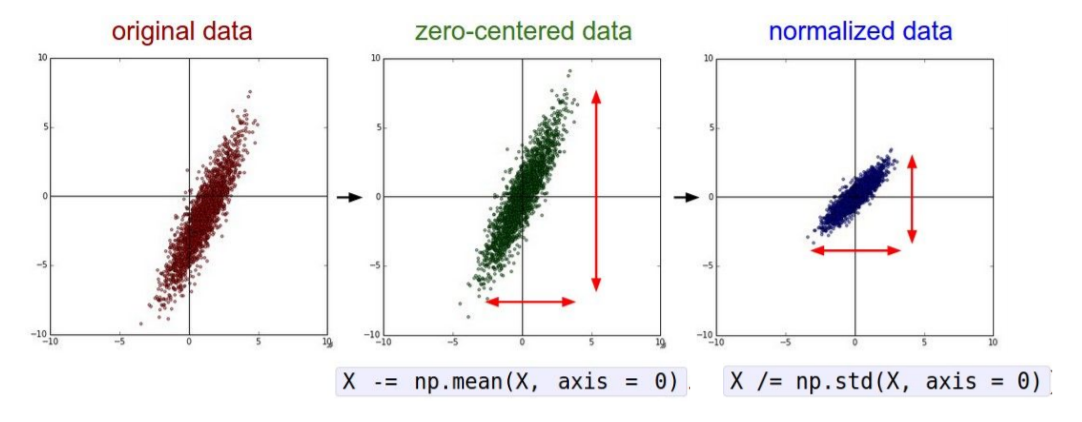
2) PCA & Whitening

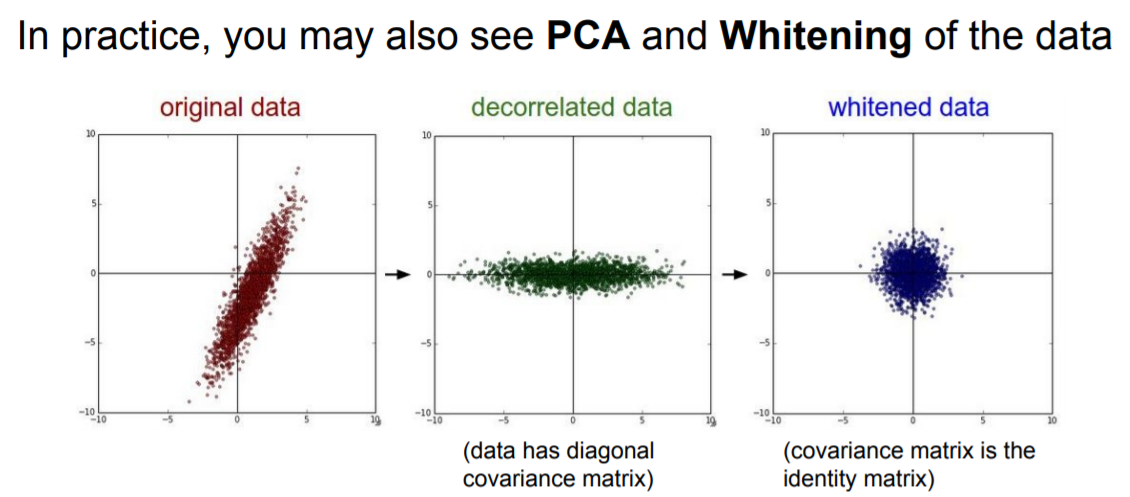
3) Image data의 전처리

Image data는 보통 zero-centered 처리까지만 진행한다.

3. Weight Initialization

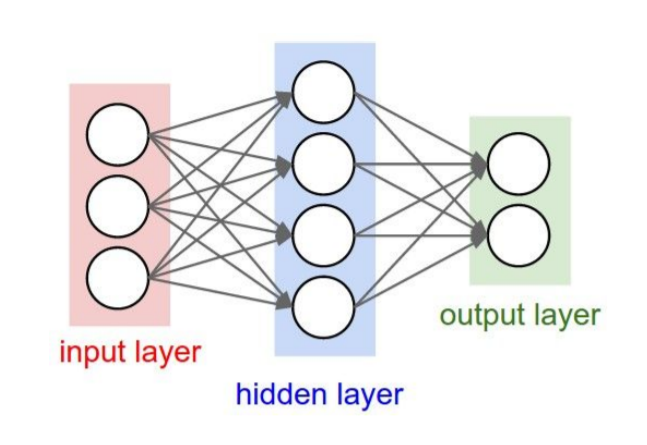
Weight 값을 0으로 초기화 하면 모두 동일한 gradient를 얻고 동일한 연산만 진행된다.

1) Small Random Numbers

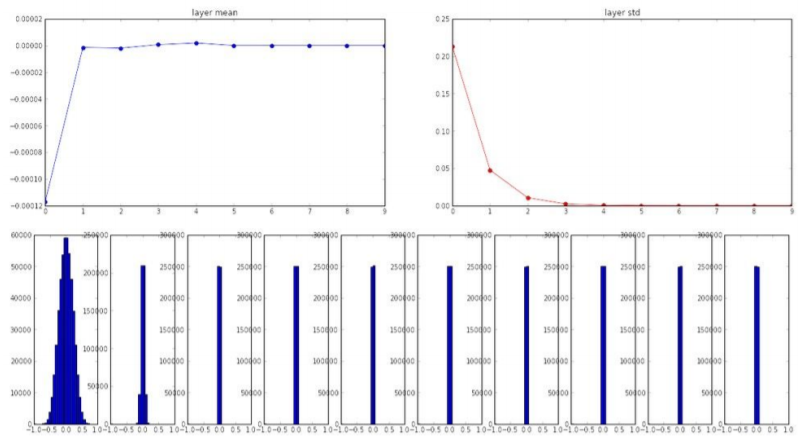
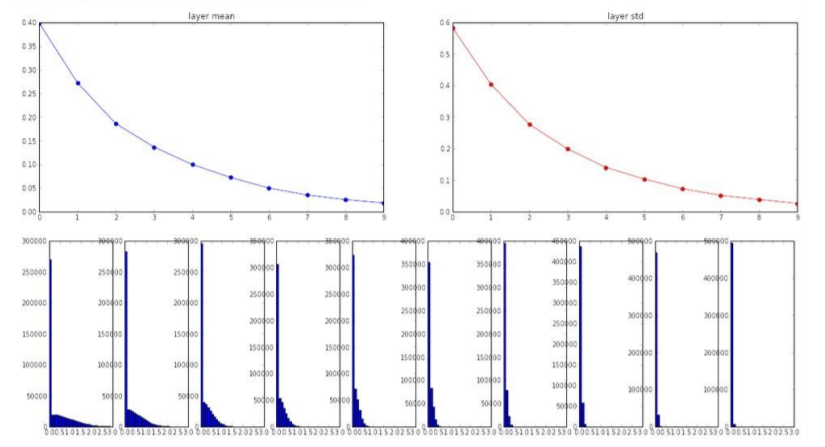
작은 값으로 초기화 하면 간단한 neural networks에선 괜찮지만 더 복잡해질 수록 위의 그래프에서 볼 수 있듯이 모든 값이 0에 가까워지는 문제가 발생한다.

2) Large Random Numbers

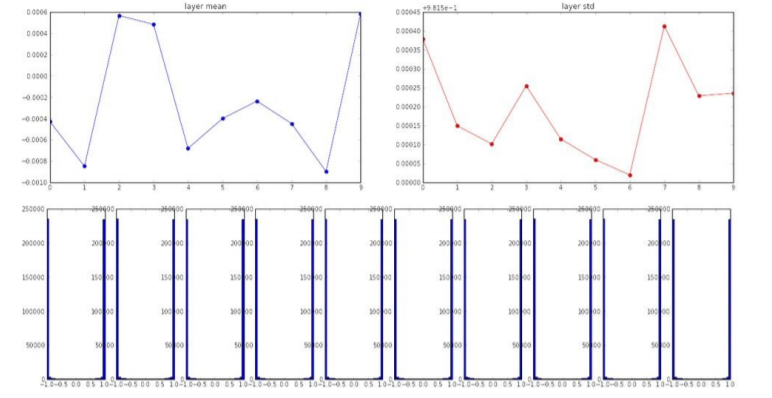
너무 큰 값도 saturate 문제가 발생하기에 좋지 않다.

3) Xavier Initialization

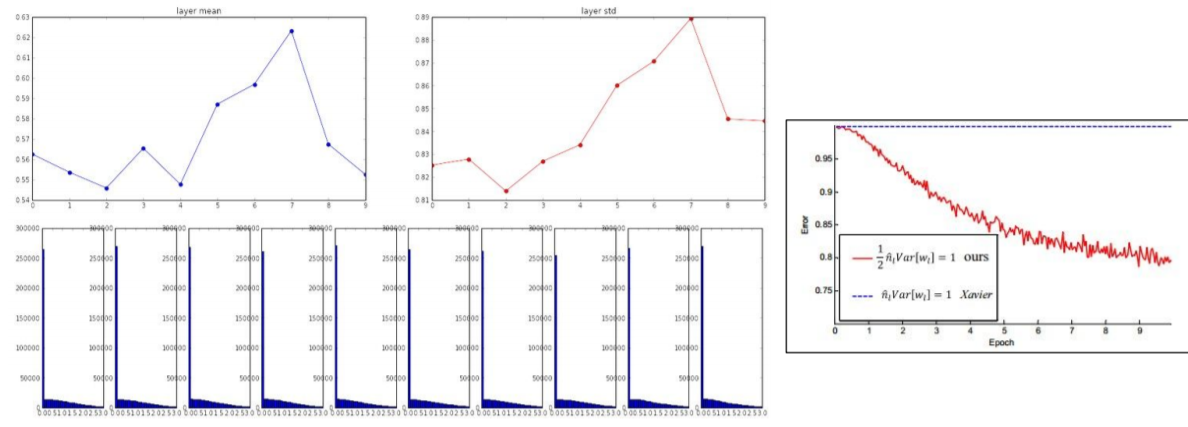
Input의 개수만큼 나눈 것이 xavier인데 이를 이용하면 위에서 발생하는 문제를 해결할 수 있다.

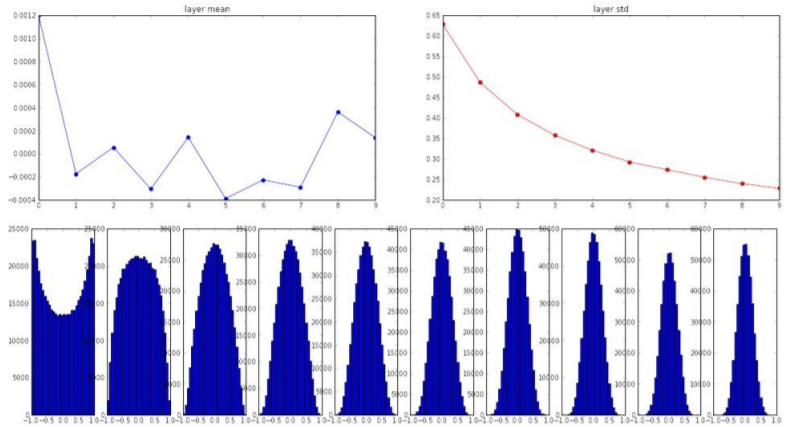
ReLU의 경우에는 input의 개수/2로 나눠준다.

참고자료

CS231n youtube 강의
CS231n 강의노트