GANs

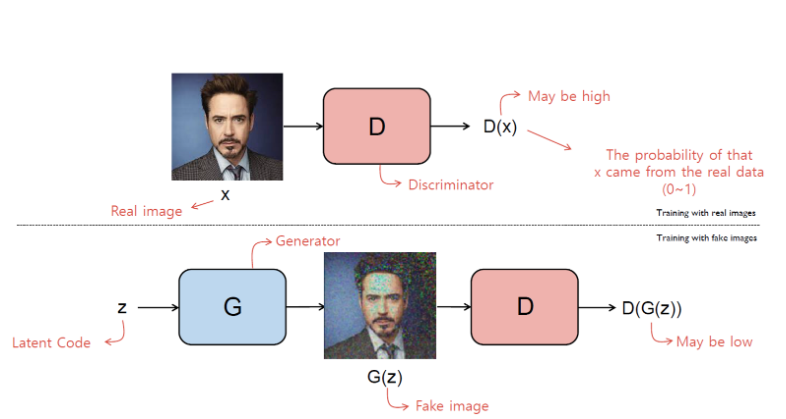
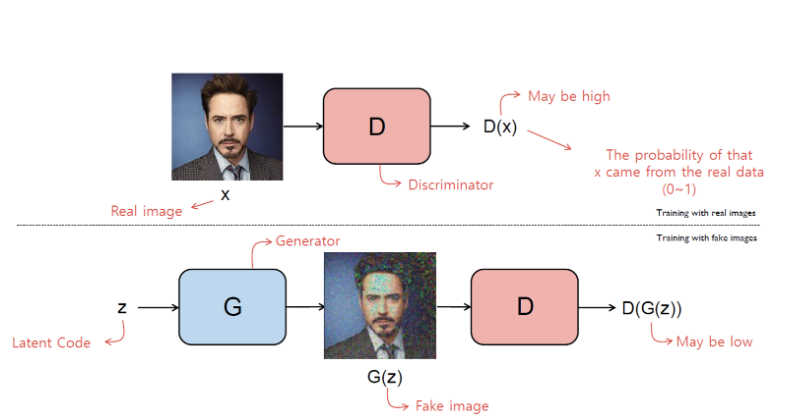
Generative Adversarial Networks (GANs)는 두 개의 네트워크인 생성자(Generator)와 판별자(Discriminator)가 서로 경쟁적으로 학습하는 구조로, Ian Goodfellow에 의해 처음 제안되었습니다. GAN의 목적은 생성자가 실제 데이터와 구별할 수 없을 정도로 진짜같은 데이터를 생성하는 것이며, 이를 통해 두 네트워크가 상호 학습하며 발전합니다.

1. GAN의 기본 개념

GAN은 생성자(Generator)와 판별자(Discriminator)라는 두 개의 신경망이 적대적 게임(adversarial game)을 수행하면서 학습하는 구조를 가집니다.

• 생성자(G): 임의의 노이즈 벡터를 받아들여 가짜 데이터를 생성하여 실제 데이터 분포를 모방하려고 합니다.
• 판별자(D): 입력된 데이터가 실제 데이터인지 생성자가 만든 가짜 데이터인지를 구분하려고 합니다.

이 두 네트워크는 서로의 성능을 향상시키기 위해 경쟁하며, 궁극적으로 생성자는 실제와 구별할 수 없는 데이터를 생성하는 것을 목표로 합니다.

2. GAN의 구성 요소 정의

GAN의 수식적 정의를 위해 필요한 구성 요소들을 먼저 정의하겠습니다.

2.1. 데이터 분포

• 실제 데이터 분포: $p_{data}(x)$
  • 실제 데이터 샘플 x가 따르는 분포입니다.
• 잠재 공간 노이즈 분포: $p_z(z)$
  • 생성자의 입력으로 사용되는 잠재 공간(latent space, z)에서의 노이즈 분포로, 일반적으로 다변량 표준 정규분포 $N(0,I)$를 사용합니다.

2.2. 생성자 (Generator)

• 생성자 함수: $G:z→x$
  • 노이즈 벡터 $z∼p_z(z)$를 받아들여 가짜 데이터 샘플 $x=G(z)$을 생성합니다.
• 생성 데이터 분포: $p_g(x)$
  • 생성자가 만들어낸 데이터 샘플들이 따르는 분포로, G에 의해 정의됩니다.

2.3. 판별자 (Discriminator)

• 판별자 함수: $D:x→[0,1]$
  • 입력 데이터 $x$가 주어졌을 때, 이 데이터가 실제 데이터일 확률을 출력합니다.
  • 즉, $D(x)$는 입력이 실제 데이터일 확률로 해석됩니다.

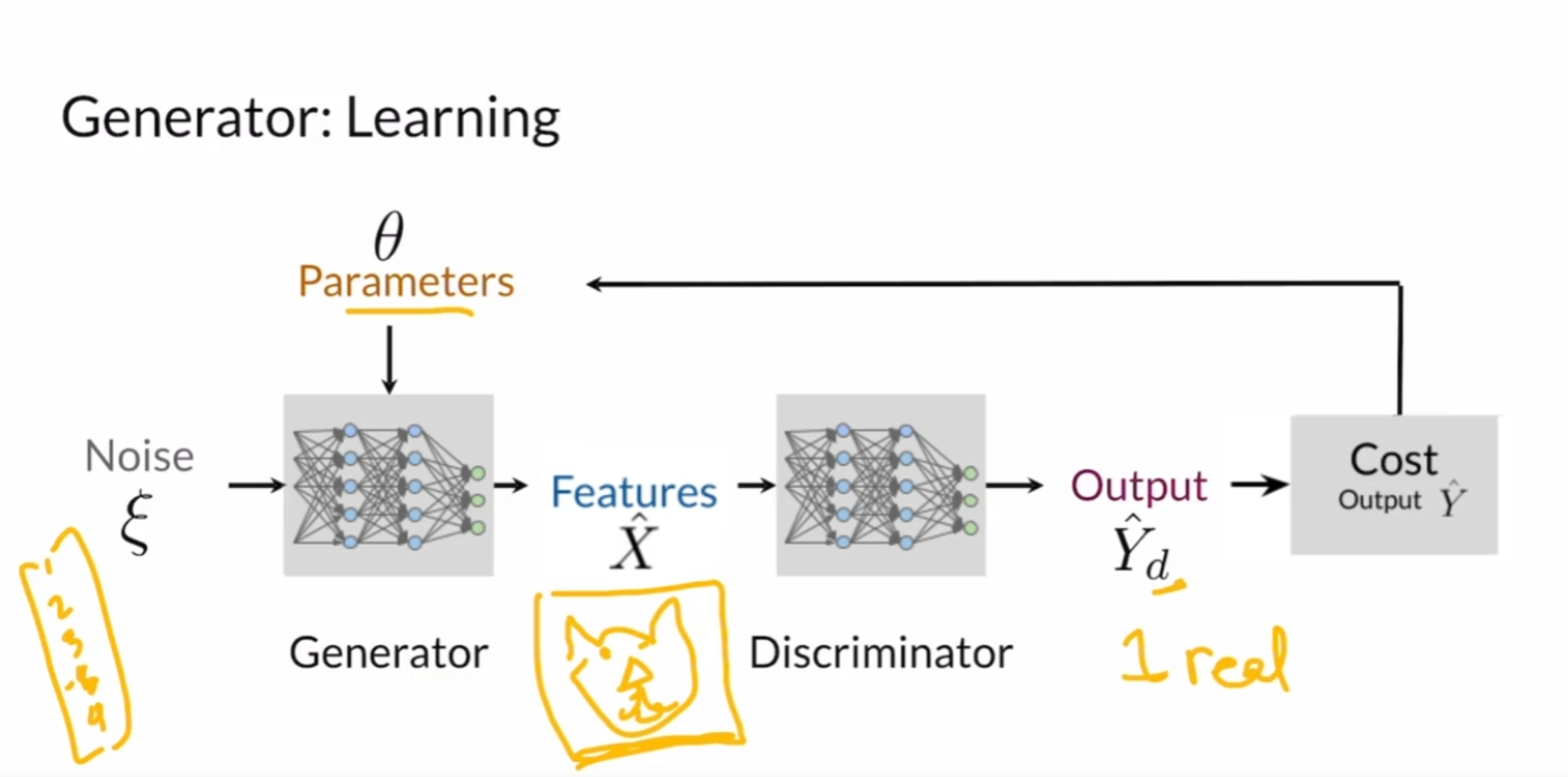
3. GAN의 목적 함수 (Objective(Loss) Function)

GAN의 학습은 미니맥스 게임(minimax game) 형태의 목적 함수를 최적화하는 것으로 표현됩니다. 생성자와 판별자는 다음과 같은 목적 함수를 가지고 있습니다.

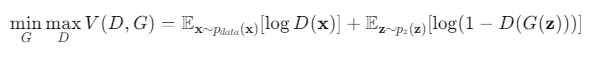
각 항의 의미

• $E_{x∼P_{data}(x)}[log⁡D(x)]$:
  • 실제 데이터에 대해 판별자가 올바르게 실제 데이터로 분류하도록 하는 것을 촉진합니다.
  • $x∼p_{data}(x)$ 실제 데이터에서 샘플링, 확률 밀도 함수
• $E_{z∼p_z(z)}[log⁡(1−D(G(z)))]$:
  • 생성된 가짜 데이터에 대해 판별자가 올바르게 가짜 데이터로 분류하도록 하는 것을 촉진합니다.
• 전체적으로:
  • 판별자(D)는 목적함수를 최대화하여 실제와 가짜 데이터를 정확하게 구분하려고 하고,
    • D(x)를 최대한 1에 가깝게 만들고, D(G(z))를 최대한 0에 가깝게 만듦
  • 생성자(G)는 목적함수를 최소화하여 판별자를 속이고자 합니다.
    • D(G(z))를 최대한 1에 가깝게 만듦

4. 최적의 판별자에 대한 분석

GAN의 목적 함수를 분석하기 위해 고정된 생성자 G에 대해 최적의 판별자 D를 찾는 과정을 살펴보겠습니다.

4.1. 목적 함수 재정의

우선, 목적 함수를 확률 밀도 함수를 이용하여 다시 표현합니다.

$V(D,G)=∫_xp_{data}(x)log⁡D(x)dx+∫_zp_z(z)log⁡(1−D(G(z)))dz$

이를 생성 데이터 분포 $p_g(x)$로 표현하면:

$V(D,G)=∫_x[p_{data}(x)log⁡D(x)+p_g(x)log⁡(1−D(x))]dx$

4.2. 최적의 D에 대한 유도

고정된 G에 대해, 목적 함수 V(D,G)를 D에 대해 최대화하려면 각 x에서의 D 값이 최대화되어야 합니다. 이를 위해 적분 내부의 표현을 각 x에 대해 최대화합니다.

즉, 다음 함수를 최대화하는 D를 찾습니다.

$f(D)=p_{data}(x)log⁡D(x)+p_g(x)log⁡(1−D(x))$

이를 D에 대해 미분하고 0으로 놓습니다.

${∂f\over ∂D}={p_{data}(x)\over D(x)}−{p_g(x)\over 1−D(x)}=0$

이를 정리하면:

$D^∗(x)={p_{data}(x)\over p_{data}(x)+p_g(x)}$

이는, 고정된 G에 대해 최적의 판별자 D*입니다.

4.3. 최적의 D*를 대입한 목적 함수

이제 최적의 D*를 목적 함수에 대입하여 생성자 G의 성능을 평가할 수 있습니다.

$V(G)=V(D^∗,G)=∫_x[p_{data}(x)log⁡D^∗(x)+p_g(x)log⁡(1−D^∗(x))]dx$

5. GAN의 최종 목적 함수와 JS Divergence

5.1. 목적 함수의 재정의

앞서 구한 최적의 D*를 목적 함수에 대입하여 정리합니다.

$V(G)=∫_x[p_{data}(x)log{p_{data}(x)\over{p_{data}(x)+p_g(x)}}+p_g(x)log{p_g(x)\over{p_{data}(x)+p_g(x)}}]$

이를 수학적으로 더 간결하게 표현하면:

$V(G)=−log⁡4+2⋅JSD(p_{data}∥p_g)$

여기서 JSD는 Jensen-Shannon Divergence로 두 분포 간의 유사성을 측정하는 지표입니다.(두 분포간의 거리 측정을 통해 유사성을 측정합니다.)

p.s. JSD는 양수이므로 loss는 -log4 보다 작아질 수 없습니다.

5.2. Jensen-Shannon Divergence의 정의

Jensen-Shannon Divergence는 다음과 같이 정의됩니다.

$JSD(p∥q)={1\over2}KL(p∥m)+{1\over2}KL(q∥m)$

여기서:

• KL은 Kullback-Leibler Divergence를 의미합니다.
• $m={1\over2}(p+q)$ 입니다.

5.3. 의미 해석

• 목적 함수 V(G)는 JSD에 비례하므로, 생성자 G를 학습시키는 것은 $p_g$와 $p_{data}$ 간의 Jensen-Shannon Divergence를 최소화하는 것과 동등합니다.
• JSD가 최소화될 때, 즉 $p_g = p_{data}$일 때, 생성자는 실제 데이터 분포를 정확히 모방하게 됩니다.

6. Non-Saturating GAN Loss

실제로 GAN을 학습시킬 때, 원래의 목적 함수로는 생성자의 학습이 느려지는 문제가 발생할 수 있습니다. 이를 해결하기 위해 Non-Saturating GAN Loss 함수를 사용합니다.

원래 목적 함수에서 생성자는 $log(1−D(G(z)))$를 최소화해야 합니다.

그러나 $D(G(z))$가 0에 가까울 때(학습 초반, 생성자(G)가 상당히 형편 없을 때), 이 로그 함수의 기울기가 0에 가까워져 학습이 느려집니다.

따라서 $*log(1−x)*$를 최소화 하는 대신 $*log(x)*$를 최대화하는 방식을 이용하게 됩니다.

이를 해결하기 위해 다음과 같은 손실 함수를 사용합니다.

$L(G)=−E_{z∼p_z(z)}[logD(G(z))]$

REFERENCE

https://velog.io/@sujin_yun_/GAN-완전-정복-1.-Generative-Adversarial-NetworkGAN **

https://process-mining.tistory.com/169

https://www.youtube.com/watch?v=vZdEGcLU_8U 25:14