Back Propagation(역전파)와 Loss function(손실함수) 선택 방법

유승한·2024년 10월 21일

딥러닝

목록 보기

2/15

1. 정의와 기본 원리

역전파(Backpropagation)는 인공 신경망에서 오차를 네트워크의 가중치로 다시 전파하여 가중치를 업데이트하는 과정입니다. 역전파는 딥러닝에서 가중치 학습의 핵심 알고리즘으로, 모델이 주어진 데이터에 대한 예측을 점진적으로 개선할 수 있도록 해줍니다.

해당 알고리즘은 Deep neural network기 등장한 이후 모델의 depth가 깊어지며 가중치의 수가 기하급수적으로 늘기 시작하며, 기존의 경사하강법을 여러 층에 존재하는 가중치들을 전부 업데이트하는 것이 너무도 많은 연산량과 메모리를 요구하게 되며 그 대안으로 등장하였습니다.

2. Forward Propagation(순전파)

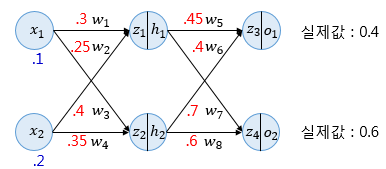
순전파는 신경망에서 입력 데이터를 각 층의 가중치와 활성화 함수를 통해 순차적으로 전달하여 출력값(예측값)을 얻습니다. 순방향 신경망은 입력층에 들어온 입력값을 순전파하여 예측값을 도출해냅니다.

위 예시는 딥 러닝을 이용한 자연어 처리 입문에서 가져온 예시입니다.

$z_1 = w_1x_1+w_2x_2=0.3*0.1+0.25*0.2=0.08$

$z_2 = w_3x_1+w_4x_2=0.4*0.1+0.35*0.2=0.11$

$h_1 = sigmoid(z_1) = 0.5199$

$h_2 = sigmoid(z_1) = 0.5274$

$z_3 = w_5h_1+w_6h_2=4449$

$z_4 = w_7h_1+w_8h_2=0.6804$

$o_1=sigmoid(z_3)=0.6094$

$o_2=sigmoid(z_4)=0.6638$

손실함수로 MSE(평균제곱오차)를 사용한다고 가정할 때,

$E_{o_1} = {1\over 2}(target_{o_1}-output_{o_1})^2 = 0.0219$

$E_{o_2} = {1\over 2}(target_{o_2}-output_{o_2})^2 = 0.0020$

$E_{total} = E_{o_1} + E_{o_2} = 0.0239$

3. Back Propagation(역전파)

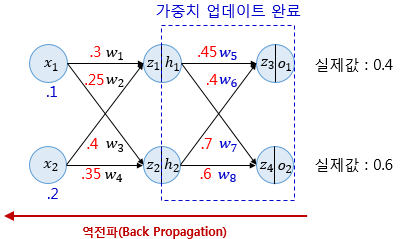
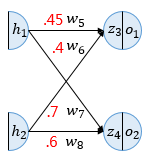
역전파는 순전파와 반대로 출력층에서 입력층 방향으로 계산하면서 가중치를 업데이트해갑니다. 처음 업데이트할 가중치는 $w5,w6,w7,w8$ 총 4개입니다. 경사 하강법을 수행하려면 가중치 w5를 업데이트 하기 위해서 $∂E_{total}\over ∂w_5$ 를 계산해야 합니다. 이때 chain rule(연쇄 법칙)에 따라 아래와 같이 풀어 쓸 수 있습니다.

$\frac{∂E_{total}}{∂w_{5}} = \frac{∂E_{total}}{∂o_{1}} \text{×} \frac{∂o_{1}}{∂z_{3}} \text{×} \frac{∂z_{3}}{∂w_{5}}$

$\frac{∂E_{total}}{∂o_{1}}=2 \text{×} \frac{1}{2}(target_{o1}-output_{o1})^{2-1} \text{×} (-1) + 0 = 0.2094$

시그모이드 함수의 미분은 $f(x)×(1−f(x))$ 입니다. 따라서

$\frac{∂o_{1}}{∂z_{3}}=o_{1}\text{×}(1-o_{1})=0.60944600(1-0.60944600)=0.2380$

$\frac{∂z_{3}}{∂w_{5}}=h_{1}=0.5199$ ( $z_3 = w_5h_1+w_6h_2$ 에서 $w_5$ 에 대한 미분)

학습률을 0.5라 가정했을 때 아래와 같이 가중치를 업데이트할 수 있습니다.

$w_{5}^{+}=w_{5}-α\frac{∂E_{total}}{∂w_{5}}=0.45- 0.5 \text{×} 0.02592286=0.43703857$

같은 원리로 $w_{6}^{+},\ w_{7}^{+},\ w_{8}^{+}$ 을 계산할 수 있습니다.

이와 같이 가중치를 업데이트해 나가는 과정을 역전파라고 하며, 이 과정을 끝가지 수행 시 기존의 전체 오차 $E_{total}$ 로부터 오차가 감소함을 알 수 있습니다. 즉 학습이란 순전파와 역전파를 반복하여 오차를 최소화하는 가중치를 찾는 과정입니다.

chain rule을 통해 모든 가중치에 관하여 미분을 한번에 진행하는 것보다 일련의 미분 과정을 통해 가중치 업데이트를 할수 있기에 연산에 있어서 이점을 얻을 수 있게 됩니다.

4. 역전파의 2가지 주요 가정

가정 1: 네트워크의 활성화 함수는 미분 가능하다.

설명: 연쇄 법칙이 적용되기 위해서는 각 계층의 활성화 함수(activation function)가 미분 가능해야 합니다. 즉, 입력값에 대한 출력값의 변화가 미분 가능해야만, 역전파 과정에서 각 가중치의 기울기를 계산할 수 있습니다.
수학적 원리: 네트워크의 손실 함수 LLL가 최종 출력층에 종속되어 있고, 출력층이 여러 활성화 함수로 이루어진 경우, 연쇄 법칙을 이용하여 손실 함수에 대한 각 가중치의 변화율을 계산할 수 있습니다.
연쇄 법칙 적용:
- 예를 들어, 신경망의 출력층이 $a=f(z)$ 이고, $z=w*x$ 라고 한다면, 연쇄 법칙에 따라 손실 함수 L에 대한 가중치 w의 기울기는 다음과 같이 계산됩니다: ${∂w\over ∂L}={∂a \over ∂L}⋅{∂z \over ∂a}⋅{∂w \over ∂z}$

이 과정에서 각 활성화 함수 f(z)는 미분 가능해야만 기울기를 계산할 수 있습니다. 따라서 역전파의 첫 번째 가정은 모든 활성화 함수가 미분 가능해야 한다는 것입니다.

가정 2: 손실 함수가 최소화 가능한 형태로 표현될 수 있다.

설명: 역전파 알고리즘이 기울기를 계산하여 손실 함수(오차)를 최소화하기 위한 경사 하강법을 적용하려면, 손실 함수는 최소화할 수 있는 형태여야 합니다. 즉, 손실 함수는 최소값이 존재해야 하며, 그 최소값을 향해 학습이 진행될 수 있어야 합니다.
수학적 원리: 역전파는 주어진 데이터에 대해 모델의 예측값과 실제 값 간의 차이를 나타내는 손실 함수 L의 기울기를 계산하여 가중치를 업데이트하는 방법입니다. 이때 가중치 업데이트의 목적은 손실 함수 L의 값을 최소화하는 것이므로, L이 최소값을 가질 수 있도록 설정되어야 합니다.
손실 함수의 예:
- MSE (Mean Squared Error): 연속적인 값을 예측할 때 주로 사용되며, 이 함수는 볼록(convex)하고 최소값을 가지므로, 경사 하강법을 통해 최소화할 수 있습니다.
- Cross Entropy: 이산적인 값을 예측하는 분류 문제에서 사용되며, 확률적인 예측 값을 실제 레이블과 비교하여 손실을 계산합니다.

5. MAE? CROSS ENTROPY?

위 예시에서는 손실함수로 MAE를 사용하고 있습니다. 하지만 손실함수로 Cross Entropy도 대중적으로 사용되는데 이때 어떤 손실함수를 사용하는게 좋을까요? 이는 수식을 자세히 살펴보면 알 수 있습니다.

“오토인코더의 모든 것” 강의에서 발췌한 그림입니다. 위 그림에서는 기울기 하강법과 역전파 알고리즘이 정리되어 있습니다. 위 수식을 바탕으로 아래 그림을 이해해봅시다.

역전파 관점

해당 그림에서는 간단한 네트워크를 예시로 들고 있습니다. 이 예시를 통해 딥러닝 학습에 사용되는 역전파 알고리즘에 있어서 어떤 손실함수가 유리한지 가늠해보도록 하겠습니다.

입력레이어에 해당하는 뉴런에 1이 들어갔을 때 출력 레이어에 해당하는 뉴런에서 0이 나와야합니다. 활성함수는 시그모이드입니다.

이때 MSE를 통해 손실을 계산할 시에 $c = (a-y)^2/2$ 가 나오게 됩니다.(2는 통상적으로 미분을 위해 넣은거니 무시하셔도 상관 없습니다.)

이후 c의 기울기(네트워크 출력값의 손실함수 미분값)를 구하게 된다면 $∇_a C = (a-y)$ 와 같이 나오게 됩니다. (∇는 gradient와 같습니다)

해당 기울기값에서 시그모이드 함수의 미분값을 곱해줍니다. $\delta = ∇_a C*\sigma'(z)$

역전파의 chain rule을 통해 계산한 에러 시그널 $\delta$ 에서 학습률을 곱한 뒤 가중치를 업데이트 한다면 최종적으로 $w = w - \eta\delta$ 와 같은 수식을 얻을 수 있습니다.

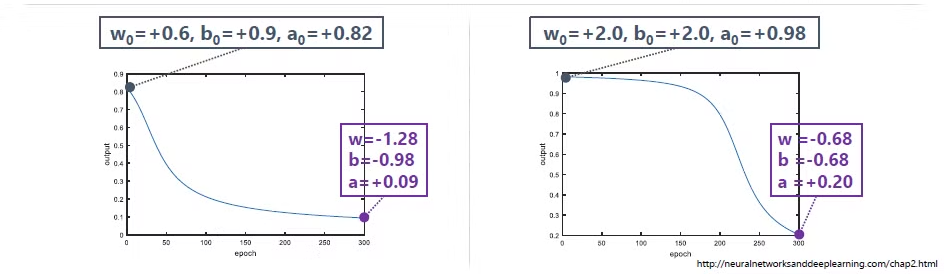
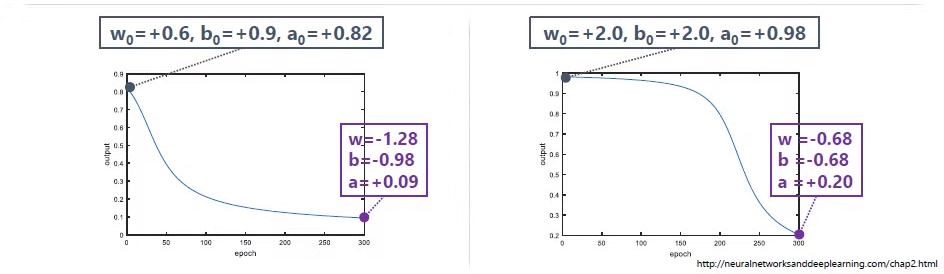
epoch(파라미터 업데이트 횟수라고 생각해주시면 됩니다)에 따른 학습 추이입니다. 두 그림에서는 초기 값을 달리 넣었을 때 왼쪽 그림에서 학습이 더 잘 됨을 a 의 값을 통해 알 수 있습니다.(0에 가까워야 학습이 잘된 것입니다.)

왜 오른쪽 그림의 초기값은 학습이 잘 이뤄지지 않았을까요? 그 이유는 역전파 수식에 $\sigma'(z)$ , 활성함수의 미분값이 들어가 있기 때문입니다. 앞선 예시에서 활성 함수로 시그모이드 함수를 사용했습니다.

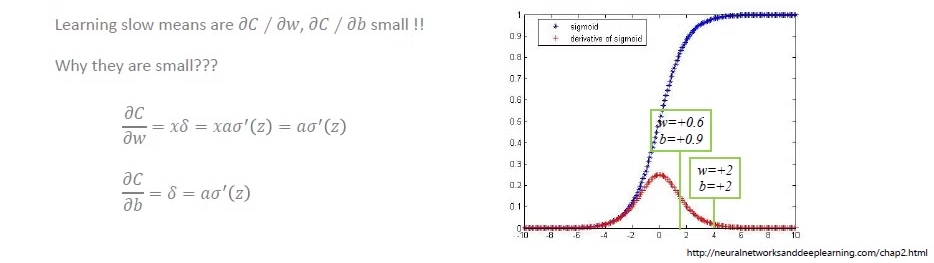
시그모이드 함수는 보시다시피 입력값이 0에서 멀어질 시 기울기가 상당히 낮음을 알 수 있습니다. 이로 인해 z 초기값에 따라 $\eta\delta$ 가 신경망의 레이어를 지나칠 수록 매우 작아지게 되고, 초반 학습이 많이 더디게 된다는 문제가 생깁니다. 이를 기울기 소실 문제라고 부릅니다.

이때 Cross Entropy를 손실함수로 이용할 시 MSE를 이용할 때보다 비교적 초기값에 의해 학습이 더뎌지는 현상이 훨씬 덜어집니다.

그 이유는 MSE와 달리 Cross Entropy는 출력 레이어에서의 error 값에 대한 활성화 함수의 미분 값이 곱해지지 않기 때문입니다. 위 수식에서 볼 수 있듯이 $\sigma'(z)$ 가 없어집니다.

4번에 걸친 역전파 수식에 있어서 기존의 출력레이어에 error 값에 대한 활성 함수의 미분 값이 곱해지지 않음을 통해서 기울기 소실 문제를 어느 정도 방지할 수 있습니다.

따라서 딥러닝 학습 측면에서 손실함수로는 cross entropy가 통상적으로 더 유리함을 알 수 있습니다.(활성 함수에 따라 달라질 수 있습니다.)

p.s. 해당 방법 외에도 대표적으로 사용하는 것이 활성화 함수를 Relu로 바꾸는 것입니다.

최대우도법 관점

$f_\theta(x)$ : 신경망의 출력값

$y$ : 정답(원하는 값)

$p(y| f_\theta(x))$ : 신경망(모델)의 출력값이 정해졌을 때 정답이 나올 확률

조건부 분포가 따르는 분포도 설정해줘야합니다. 이때 가우시안으로 설정해주고 진행해봅시다.

여기서 신경망(모델)은 가우시안의 파리미터(가우시안의 경우 평균과 표준편차)를 추정하기 위한 장치라고 볼 수 있습니다.

$p(y| f_\theta(x))$ (likely hood 값)이 최대값이 되는게 목표입니다. 앞서 설명드린 파라미터를 추정해가며 최대값을 구해보겠습니다. 파라미터는 예시로 평균이라고 하고, 평균을 추정해보겠습니다.

그림을 보면 $\theta_1$ 이 $\theta_2$ 보다 y에 가까우며, 그럴 시에 $p(y| f_\theta(x))$ 이 최대값애 가까워짐을 알 수 있습니다. 즉 평균값(파라미터)이 y일 때 $p(y| f_\theta(x))$ 최대값에 도달함을 알 수 있습니다.

손실함수는 $-log(p(y| f_\theta(x)))$ 이며 이를 이용해 최적의 파라미터인 $\theta^*$ 를 찾을 수 있게 됩니다. 최적의 파라미터인 $\theta_2$ 를 통해 도출하는 것은 새로운 확률분포인 $p(y| f_\theta^*(x))$ 입니다. 고전적인 머신러닝 기법에서는 고정 입력 고정 출력이 일반적이지만, 생성형 ai에서는 고정된 입력으로도 다른 출력이 도출됩니다. 따라서 auto encoder는 최대우도법을 이용해 도출된 확률분포에서 샘플링을 통해 새로운 이미지를 생성합니다.