Softmax Regression(소프트맥스 회귀)

1. 정의

Softmax Regression은 일반화된 로지스틱 회귀로, 단순 이진 분류를 위한 모델이 아닌, 여러 개의 다중 클래스를 분류하기 위한 다항 로지스틱 회귀(multinomial LR)입니다.

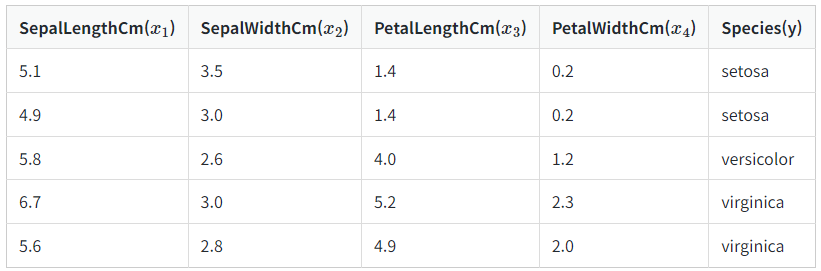
위의 붓꽃 품종 예측 데이터는 꽃받침과 꽃잎 길이와 넓이로부터 품종을 예측합니다. 로지스틱 회귀와 같이 시그모이드 함수를 적용한다면 setosa가 정답일 확률은 0.8, versicolor가 정답일 확률은 0.2, virginica가 정답일 확률은 0.4 등과 같은 출력을 얻게됩니다. 하지만 Softmax Regression은 품종 확률 합이 1인 예측값을 얻도록 합니다. 그리고 샘플 데이터가 입력으로 들어오면 모델이 setosa일 확률이 0.7, versicolor일 확률 0.05, virginica일 확률이 0.25로 예측값을 도출할 시에 setosa로 예측했다고 간주합니다.

2. Softmax Regression 이해

$s_k(x)=(θ^{(k)})^Tx$

샘플 $x$가 주어지면, 소프트맥스 회귀 모델이 각 클래스 k에 대한 점수 $s_k(x)$를 계산합니다.

$θ^{(k)}= n * 1$

각 클래스는 자신만의 파라미터 벡터 $θ^{(k)}$가 존재합니다.

$x= n * 1$

$θ= k * n$

이 벡터들은 파라미터 행렬인 $\theta$에 저장됩니다.

각 클래스의 점수를 소프트맥스 함수를 통과시켜 클래스 k에 대한 확률 클래스 k에 대한 확률 p를 추정합니다.

그렇기 때문에 소프트맥스 회귀 분류기의 예측은 아래와 같습니다.

더 쉽게 소프트맥스 함수를 이해하고자한다면, k차원의 벡터에서 i번째 원소를$z_i$, i번째 클래스가 정답일 확률을 $p_i$로 나타낸다고 하였을 때 소프트맥스 함수는 $p_i$ 다음과 같이 정의합니다.

$p_i = {e^{z_i}\over \sigma_{j=1}^3e^{z_j}} for i=1,2,…k$

위에서 풀어야하는 문제의 경우 k=3이므로 3차원 벡터 $z=[z1 z2 z3]$의 입력을 받으면 소프트맥스 함수는 아래와 같은 출력을 리턴합니다.

$softmax(z) = [{e^{z_1}\over \sigma_{j=1}^3e^{z_j}}{e^{z_2}\over \sigma_{j=1}^3e^{z_j}}{e^{z_3}\over \sigma_{j=1}^3e^{z_j}}] = [p_1,p_2,p_3] = 예측값 y hat$

p1,p2,p3 각각은 1번 클래스가 정답일 확률, 2번 클래스가 정답일 확률, 3번 클래스가 정답일 확률을 나타내며 각각 0과 1사이의 값으로 총 합은 1이 됩니다.

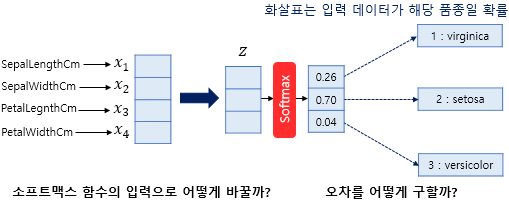
해당 그림에서 두가지를 집중해서 봐야합니다.

1. 입력 벡터는 4차원인데 분류 클래스는 3차원이기에 차원 축소가 이뤄져야한다는 점

   소프트맥스 함수의 입력 벡터 z의 차원수만큼 결과값이 나오도록 가중치 곱을 진행합니다. 이때 전부 다른 가중치를가지고 학습 과정에서 점차적으로 오차를 최소화하는 가중치로 값이 변경됩니다.
   

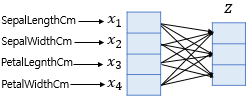
2. 오차 계산은 어떻게 이뤄지는지에 대한 의문

   소프트맥스 회귀에서는 실제값을 원-핫 벡터로 표현합니다.
   
   

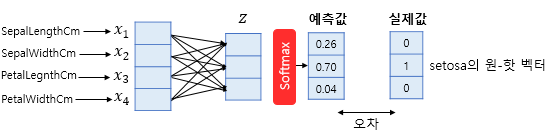
   도출된 예측값을 실제 값과 비교하여 오차를 도출한 뒤에 가중치를 업데이트합니다. 이 때 오차는 소프트맥스 회귀는 비용 함수로 크로스 엔트로피 함수를 사용합니다.